Simulation of Dampers Made of Viscoelastic Materials

Abstract

Taking damping into account in the problems of structural dynamics is an important and nontrivial problem. Its complexity is primarily determined by the required specification of correct characteristics of the materials used and the choice of a model suitable for analysis. We consider some models of viscoelastic materials as regards the possibility of applying these models in harmonic analysis of damping properties of various materials in the linear range of elastic strains. The proposed analysis is based on the use of parameters of viscoelastic materials, which are specified as coefficients of a differential equation of small forced vibrations. It is shown that the models considered here are characterized by different frequency dependences of parameters of materials being simulated. This makes it possible to combine a model with frequency dependences of its parameters close to the frequency characteristics of parameters of viscoelastic materials under investigation.

INTRODUCTION

Vibrations in dynamic (mechanical) constructions are often associated with rotating elements, the misbalance or change in the operating regimes of which cause undesirable vibrations both in the construction itself and in the ambient. Consequences of resonant effects manifested when the frequency of induced vibrations approaches the resonance frequency of a mechanical system can be extremely negative, which explains the importance of the analysis of frequency properties of constructions being designed even at the stage of modeling. This especially concerns the constructions in which frequencies of vibrations vary over a wide range. One striking example of such systems is a quadrocopter (multicopter), in which the sources of vibrations are motors with lift rotors, the rotational frequency of which can vary over wide limits, with the vibration-sensitive element (controller) being located on the same frame as the motors. Dampers of rigs in quadrocopters are often made of viscoelastic materials.¹ One often-used material is rubber, which is widely employed for damping vibrations in various mechanical constructions [2] (including those in aircraft construction) due to its properties. For example, rubber is the main damping element in the multilayer structure of the torsion bar connecting the blade of the main lift rotor with the shaft, which is an important element of new-generation light helicopters [3].

The required damping of undesirable vibrations necessitates correct modeling of dampers made of viscoelastic materials. Simulation of viscoelastic materials is based on the linear theory of viscoelasticity of materials with shape memory. The linear theory of viscoelasticity was developed on the basis of the concepts of properties of solids such as plasticity and creep [4–7]. Investigations of properties of viscoelastic materials (including those developed for damping of vibrations in various mechanical constructions) have been intensified. New monographs [8] and numerous publications devoted to individual theoretical and applied problems have appeared [3, 9–13]. In these publications, the approaches to estimation of damping properties of materials used for these purposes and various their models are described [4, 5, 8, 14]. However, the criteria for estimating the extent of correspondence of models to specific materials have not been worked out. Information on parameters of damping materials required for their simulation is also scarce. In this connection, the problem of correct measurement of parameters of viscoelastic materials becomes especially important [12, 13].

In this study, we demonstrate the difference in the frequency properties and the possibility of using the frequency dependence of parameters of damping materials for some available models of viscoelastic materials as a criterion for selecting parameters of an appropriate model.

1. FORCED VIBRATIONS OF A MECHANICAL SYSTEM. EQUATION AND VOIGT MODEL

The differential equation of small forced vibrations has the form

$$x{\kern 1pt} ''\, + rx{\kern 1pt} '\, + kx = F(t),$$

(1)

where F(t) is the generalized periodic external force connected with generalized coordinate x; x' and x'' are the first and the second derivatives of x with respect to time t, respectively; and m, r, and k are the generalized coefficients of inertia, friction, and elasticity, respectively.

Therefore, the external force is opposed by three forces: force of inertia

$${{F}_{m}}(t) = mx{\kern 1pt} '',$$

(2)

where m is the mass of the body to which the force is applied; generalized friction force

$${{F}_{r}}(t) = rx{\kern 1pt} ',$$

where r is the generalized friction coefficient; and quasi-elastic force

$${{F}_{k}}(t) = kx,$$

where k is the coefficient of the quasi-elastic force.

Equation (1) can also be written in the form

$$x{\kern 1pt} ''\, + 2\delta x{\kern 1pt} '\, + \Omega _{0}^{2}x = \frac{1}{m}F(t),$$

where δ and Ω₀ are the damping coefficient and the frequency of free vibrations of the system, respectively:

$$\delta = \frac{r}{{2m}},$$

$${{\Omega }_{0}} = \sqrt {\frac{k}{m}} .$$

In the simulation of a mechanical system, the representation of its dynamical modes in the form of a system with concentrated parameters is widely used [15, 16], which reflects in many cases the most significant factors determining the behavior of the system under preset actions with a high degree of accuracy. In constructing such models, the inertia properties of the mechanism are assumed to be concentrated at individual points in the form of reduced masses, and these points are connected by elastic, dissipative, and geometrical noninertial bonds [16].

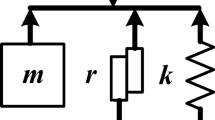
In such an approach, the mechanical system with forced vibrations described by Eq. (1) can be represented schematically in the form shown in Fig. 1. In this figure, the following notation is used: F(t) is the force acting on three elements (m is an inertial element of mass m, r is a dissipative element with friction coefficient r, and k is an elastic element with coefficient of elasticity k).

Fig. 1.

Schematic diagram of a system performing forced vibrations.

In such a representation, the viscoelastic material (damper) is represented using the Voigt model [5]. In the case considered here (harmonic analysis), the perturbing force varies in accordance with the harmonic law

$$F(t) = {{F}_{0}} + {{F}_{a}}\cos (\Omega t),$$

where F₀ and F_a are the constant component and the amplitude of the harmonic component of the external force, respectively, and Ω is the circular frequency of the harmonic component of the acting force.

Steady-state forced vibrations are also harmonic (having the same frequency, but shifted in phase relative to the external force):

$$x = {{X}_{0}} + {{X}_{a}}\cos (\Omega t + \varphi ),$$

where X₀ and X_a are the constant component and the amplitude of the harmonic component of displacement x under the action of force F(t), respectively; φ is the phase shift relative to the acting force; and X₀ = $\frac{{{{F}_{0}}}}{k}$.

Amplitude of vibrations X_a and phase shift φ depend on the vibrational frequency

$${{X}_{a}}(\Omega ) = \frac{{{{F}_{a}}}}{{m\sqrt {{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{(2\delta \Omega )}}^{2}}} }},$$

(3)

$$\tan \varphi (\Omega ) = - \frac{{2\delta \Omega }}{{\Omega _{0}^{2} - {{\Omega }^{2}}}}.$$

(4)

In the given case (harmonic action), we have

$$\begin{gathered} x{\kern 1pt} ' = - {{X}_{a}}(\Omega )\Omega \sin (\Omega t + \varphi (\Omega )) \\ = - {{X}_{a}}(\Omega )\Omega \cos (\Omega t - \beta (\Omega )), \\ \end{gathered} $$

where β(Ω) is the phase shift between force F(t) and the rate of variation of displacement x,

$$\beta (\Omega ) = \frac{\pi }{2} - \varphi (\Omega ),$$

$$\tan \beta (\Omega ) = - {{\tan }^{{ - 1}}}\varphi (\Omega ) = \frac{{\Omega _{0}^{2} - {{\Omega }^{2}}}}{{2\delta \Omega }},$$

$$x{\kern 1pt} '' = - {{X}_{a}}(\Omega ){{\Omega }^{2}}\cos (\Omega t + \varphi (\Omega )).$$

(5)

The dissipative loss in steady-state forced vibrations characterized by loss power P_d are described by dissipative function Φ [17]:

$${{P}_{d}} = 2\Phi ;\quad \Phi = \frac{{r{{{(x')}}^{2}}}}{2}.$$

Energy loss W_d(T) over the period of vibrations (where T = 2π/Ω) is given by

$${{W}_{d}}(T) = \int\limits_0^T {2\Phi dt = r\int\limits_0^T {{{{(x{\kern 1pt} ')}}^{2}}dt.} } $$

The integration gives

$${{W}_{d}}(T) = r\pi \Omega X_{a}^{2} = r\pi \Omega \frac{{F_{a}^{2}}}{{{{m}^{2}}[{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{(2\delta \Omega )}}^{2}}]}}.$$

The frequency dependence of the amplitude of vibration and the loss power has a resonance near Ω ≈ Ω₀ for δ < Ω₀/$\sqrt 2$ [4].

2. THE MAXWELL AND KELVIN–VOIGT MODELS

The Maxwell model is illustrated in Fig. 2. In this case, external force F(t) is opposed by two forces, i.e., inertial force F₁(t) = F_m(t) = mx'', where m is the mass of the body to which the force is applied, and damping force F₂(t) produced by series-connected elements of friction and elasticity.

Fig. 2.

Maxwell model in the system performing forced vibrations.

In this case, deformations² of elements of friction and elasticity (x_r and x_k, respectively) are determined by force F₂(t) = F₂cos(Ωt + ψ)), where ψ denotes the phase shift of force F₂(t) relative to force F(t):³

$${{F}_{2}}(t) = rx_{r}^{'},$$

(6)

$${{F}_{2}}(t) = k{{x}_{k}},$$

(7)

where $x_{r}^{'}$ is the derivative of displacement (deformation) of the friction element.

Total deformation x₂ of the damper equals total displacement x: x₂ = x_r + x_k = x. In this case (taking relations (6) and (7) into account), we have

$$\begin{gathered} {{x}_{r}} = \frac{{{{F}_{2}}}}{{\Omega r}}\sin (\Omega r + \psi ), \\ {{x}_{k}} = \frac{{{{F}_{2}}}}{k}\cos (\Omega t + \psi ), \\ {{x}_{2}} = {{F}_{2}}\left[ {\frac{1}{{\Omega r}}\sin (\Omega t + \psi ) + \frac{1}{k}\cos (\Omega t + \psi )} \right]. \\ \end{gathered} $$

(8)

Transforming relation (8), we obtain

$${{x}_{2}} = {{F}_{2}}\sqrt {{{{\left( {\frac{1}{{\Omega r}}} \right)}}^{2}} + {{{\left( {\frac{1}{k}} \right)}}^{2}}} \cos (\omega t + \psi - \xi ),$$

(9)

where ξ can be determined from the expression

$$\tan \xi = \frac{k}{{\Omega r}}.$$

(10)

To compare the characteristics of the Maxwell and Voigt models, it is convenient to transform the Maxwell model to the form of the Voigt model (see Fig. 1) with corresponding (equivalent) parameters. In such a transformation, F₂(t) is represented by the sum of two orthogonal components F_2r(t) and F_2k(t). The vector diagram in Fig. 3 shows the relation between all the interacting forces.

Fig. 3.

Vector diagram of interacting forces.

In Fig. 3, the amplitudes of vectors are denoted in the same way as the amplitudes of corresponding forces. The symbol φ denotes the phase shift of displacement x relative to acting force F(t). The symbol ψ denotes the phase shift of force F₂(t) relative to force F(t). Inertial force F₁(t) = F_m(t) is in antiphase relative to the displacement. Elastic force F_2k(t) (as a component of force F₂(t)) is synphase to the displacement. Friction force F_2r(t) (the other component of force F₂(t)) is orthogonal to the displacement (shifted in phase by 90° relative to the displacement):

$$\begin{gathered} {{F}_{2}} = \sqrt {F_{{2k}}^{2} + F_{{2r}}^{2}} , \\ {{F}_{{2k}}} = {{F}_{a}}\cos \varphi + {{F}_{m}}, \\ {{F}_{{2r}}} = {{F}_{a}}\sin \varphi . \\ \end{gathered} $$

(11)

Since the Maxwell model transformed to the Voigt model must still operate as before the transformation (i.e., ensure the same reaction to the same action), the parameters of elements of the transformed model (coefficients of friction and elasticity) must change in a certain way.

We denote the coefficients of friction and elasticity in the transformed Maxwell model by r_e and k_e, respectively. The expressions for F_2k, F_2r, and F₂ taking relations (2), (4), and (5) into account can, then, be written in the form

$${{F}_{{2k}}}(\Omega ) = \frac{{{{F}_{a}}\Omega _{0}^{2}}}{{\sqrt {{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}} }},$$

(12)

$$\begin{gathered} {{F}_{{2r}}}(\Omega ) = \frac{{{{F}_{a}}\Omega {{r}_{e}}}}{{m\sqrt {{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}} }}, \\ {{F}_{2}}(\Omega ) = {{F}_{a}}\sqrt {\frac{{\Omega _{0}^{4} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}{{{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}} . \\ \end{gathered} $$

(13)

Expression (9) for the total deformation in the Maxwell model taking relation (13) into account takes the form

$$\begin{gathered} {{x}_{2}}(\Omega ) = {{F}_{a}}\sqrt {{{{\left( {\frac{1}{{\Omega r}}} \right)}}^{2}} + {{{\left( {\frac{1}{k}} \right)}}^{2}}} \\ \times \,\,\sqrt {\frac{{\Omega _{0}^{4} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}{{{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}} \cos (\Omega t + \psi - \xi ). \\ \end{gathered} $$

(14)

In this case, deformation amplitude X₂ has the form

$$\begin{gathered} {{X}_{2}}(\Omega ) = {{F}_{a}}\sqrt {{{{\left( {\frac{1}{{\Omega r}}} \right)}}^{2}} + {{{\left( {\frac{1}{k}} \right)}}^{2}}} \\ \times \,\,\sqrt {\frac{{\Omega _{0}^{4} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}{{{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}} . \\ \end{gathered} $$

(15)

Since x₂ = x, we have X₂ = X_a, which yields, after transformation (15), taking (3) into account,

$$\Omega _{0}^{4} + {{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}^{2}} = \frac{1}{{{{m}^{2}}\left[ {{{{\left( {\frac{1}{{\Omega r}}} \right)}}^{2}} + {{{\left( {\frac{1}{k}} \right)}}^{2}}} \right]}}.$$

(16)

In the transformed Maxwell model, $\Omega _{0}^{2}$ = k_e/m, which reduces expression (16) to

$${{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}^{2}} = \frac{1}{{{{m}^{2}}\left[ {{{{\left( {\frac{1}{{\Omega r}}} \right)}}^{2}} + {{{\left( {\frac{1}{k}} \right)}}^{2}}} \right]}} - {{\left( {\frac{{{{k}_{e}}}}{m}} \right)}^{2}}.$$

(17)

Thus, we have obtained an equation connecting parameters r_e and k_e of the transformed Maxwell model with parameters r and k of the initial model.

The second equation is defined as F_2k = k_eX_a. Expression (12) defined component F_2k of force F₂ as a function of force F_a and parameters r_e and k_e of the transformed Maxwell model. However, this component can also be defined in terms of parameters r and k of the initial model; namely,

$${{F}_{{2k}}} = {{F}_{2}}\cos \xi ,$$

which yield, with taking relations (13) and (10) into account,

$${{F}_{{2k}}}(\Omega ) = \frac{{{{F}_{a}}}}{{\sqrt {1 + {{{\left( {\frac{k}{{\Omega r}}} \right)}}^{2}}} }}\sqrt {\frac{{\Omega _{0}^{4} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}{{{{{(\Omega _{0}^{2} - {{\Omega }^{2}})}}^{2}} + {{{\left( {\frac{{\Omega {{r}_{e}}}}{m}} \right)}}^{2}}}}} .$$

(18)

Equating expressions (12) and (18), after the transformation, we obtain

$${{k}_{e}} = \frac{{\Omega r}}{k}\Omega {{r}_{e}}.$$

(19)

Equations (17) and (19) form a system the solution of which for r_e and k_e gives

$${{r}_{e}} = \frac{r}{{1 + {{{\left( {\frac{{\Omega r}}{k}} \right)}}^{2}}}},$$

(20)

$${{k}_{e}} = \frac{k}{{1 + {{{\left( {\frac{k}{{\Omega r}}} \right)}}^{2}}}}.$$

(21)

It can be seen that the coefficients of the transformed model in this case become dependent on frequency.

If we consider the more complex Kelvin–Voigt model [8, 9] shown in Fig. 4 and transform it into the Voight model, the parameters of the transformed model will also depend on frequency in the manner characteristic of the given model:

$${{r}_{{ek}}} = r\frac{{{{{\left( {\frac{{{{k}_{1}}}}{{{{k}_{1}} + {{k}_{2}}}}} \right)}}^{2}}}}{{1 + {{{\left( {\frac{{\Omega r}}{{{{k}_{1}} + {{k}_{2}}}}} \right)}}^{2}}}},$$

$${{k}_{{ek}}} = \frac{{{{k}_{1}}{{k}_{2}}}}{{{{k}_{1}} + {{k}_{2}}}}\frac{{1 + \frac{{{{{(\Omega r)}}^{2}}}}{{({{k}_{1}} + {{k}_{2}}){{k}_{2}}}}}}{{1 + {{{\left( {\frac{{\Omega r}}{{{{k}_{1}} + {{k}_{2}}}}} \right)}}^{2}}}}.$$

(23)

Fig. 4.

Kelvin–Voigt model in a system performing forced vibrations.

In these expressions, indices k₁ and k₂ indicate an additional elastic element and the elastic element in the Voigt model, respectively (see Fig. 4).

The frequency dependences of the parameters of the transformed Kelvin–Voigt model were obtained using the method of electromechanical analogies [18–20], which considerably simplifies calculations in complex cases. The derivation of these dependences is given in the Appendix. These dependences are more complicated than in the case of the Maxwell model and are more adaptable as regards the possibility of their tuning to the frequency dependences of parameters of the viscoelastic material under investigation.

3. EXAMPLE OF CALCULATION OF FREQUENCY CHARACTERISTICS

By way of example, let us consider the Maxwell and Kelvin–Voigt models of rubber 57–7024–110, which are transformed to the Voigt model. The results of measurements of relaxation parameters of the rubber, which were taken for a sample strain of 50%, were given in [21]. These results were used for determining the elastic modulus of rubber at frequencies close to zero (E₀ = 1.73 MPa) and the elastic modulus for rubber in the range of high frequencies tending to infinity (E_∞ = 3.6 MPa). The parameters of the transformed Kelvin–Voigt model at frequencies tending to zero and infinity were chosen equal to the corresponding parameters of rubber at the same frequencies. In choosing the parameters of the Maxwell model, the equality of the elastic coefficients of the model and of the material was ensured only in the range of frequencies tending to infinity. For better visualization, Figs. 5 and 6 show examples of the frequency dependences of equivalent friction coefficients (r_e and r_ek) and coefficients of elasticity (k_e and k_ek) in the Maxwell and Kelvin–Voigt models transformed to the Voigt model.

Fig. 5.

Example of frequency dependences of the equivalent friction coefficients in the Maxwell model (solid curve) and in the Kelvin–Voigt model (dashed curve).

Fig. 6.

Example of frequency dependence of the equivalent coefficients of elasticity in the Maxwell model (solid curve) and in the Kelvin–Voigt model (dashed curve).

In Figs. 5 and 6, the following notation was used: r(M) and k(M) are the coefficients of viscous friction (r) and elasticity (k) in the Maxwell model, respectively; r(KF), k₁(KF), and k₂(KF) are the coefficients of viscous friction (r) and elasticity (k₁ and k₂) in the Kelvin—Voigt model, respectively; r_e and r_ek are the values of coefficients of viscous friction (r_e and r_ek) in the Maxwell and Kelvin–Voigt models transformed to the Voigt model, respectively; k_e and k_ek are the values of equivalent coefficients of elasticity (k_e and k_ek) of the Maxwell and Kelvin–Voigt models transformed to the Voigt model, respectively; and  f/f_n are the values of normalized frequencies.

The frequency normalization was performed so that the average value of the coefficient of elasticity in the Kelvin–Voigt model for such a material corresponded to a frequency of 1 Hz.

4. CONCLUSIONS. CHOICE OF THE MODEL OF A VISCOELASTIC MATERIAL

The models of viscoelastic materials reduced to the same form corresponding to the differential equation of forced vibrations are characterized by parameters differing in their frequency dependences. For example, the parameters in the Voigt model are frequency-independent, while the frequency dependences of the parameters of the Maxwell and Kelvin–Voigt models are defined by expressions (20)–(23).

The choice of an appropriate model for analysis of damping processes of the materials in question is a complicated problem, because the number of physical mechanisms of damping of vibrations in actual materials is very large [14] and these mechanisms are either unknown or immaterial in the context of the problem under investigation. Nevertheless, irrespective of damping mechanisms, the simulation of mechanisms of damping of vibrations in many practical problems is a necessary stage of designing mechanical systems. Our analysis of several models of a viscoelastic body shows that, to choose the model of a given damping material correctly, it is necessary not only to know (determine) its parameters in some specific conditions, but also to know the frequency dependence of these parameters in the range of frequencies typical of the system being designed. We can then use a model of the Voigt type as the model of the viscoelastic material, but with frequency-depending parameters. In this case, the frequency dependences of the model parameters and the corresponding parameters of the actual materials must be as close as possible in the preset frequency range. This model can be a transformation of a certain model (any of the known models or the model synthesized for the first time) with elements having frequency-independent parameters.

Summarizing the results, we can formulate the following conclusions.

1. Damping properties of viscoelastic materials in mechanical constructions are estimated by indices that can be determined in terms of the coefficient of the differential equation describing the behavior of the system under a harmonic action.

2. These coefficients are parameters of the mechanical Voigt model of a viscoelastic material.

3. In this study, it is shown that any mechanical model of a viscoelastic material, which is a combination of frequency-independent elements of viscous friction and elasticity, can be transformed to the Voigt model with frequency-dependent parameters.

4. We propose to use the frequency dependences of parameters of mechanical models (of viscoelastic materials) transformed to the Voigt model for estimating the extent of correspondence of the model to the viscoelastic material by comparing the frequency dependences of the parameters of the model and of the material.

5. To carry out such a comparison, the parameters of the viscoelastic material much be expressed in terms of the coefficients of the corresponding differential equation.

Appendices

APPENDIX

Application of the Method of Electromechanical Analogies in the Transformation of the Kelvin–Voigt Model to the Voigt Model

The Kelvin–Voigt model of a viscoelastic material and its electrical analog are illustrated in Figs. 7a and 7b, respectively.

Fig. 7.

(a) Kelvin–Voigt model and (b) its electrical analog.

In Fig. 7, the following notation is used: r_F and k_F are the dissipative and elastic elements (respectively) of the Voigt model, which is part of the Kelvin–Voigt model; k_K is an additional elastic element of the Kelvin–Voigt model; C_F and R_F are the electric capacitance and resistance, which are analogs of elements k_F and r_F, respectively, and C_K is the capacitance that is an analog of element k_K.

All elements of the Kelvin–Voigt model and their electric analogs shown in Fig. 7 are frequency-independent parameters. To analyze the frequency properties of the Kelvin–Voigt model, it is convenient to use its electrical analog or transform this model to the Voigt model with frequency-dependent parameters as shown in Fig. 8.

Fig. 8.

(a) Voigt model and (b) its electrical analog with frequency-dependent parameters.

In this figure, the following notation is used: C_e(f) and R_e(f) are frequency-dependent elements (electric capacitance and resistance, respectively) of the electric circuit equivalent to that shown in Fig. 7b, and k_e(f) and r_e(f) are frequency-dependent coefficients of elasticity and friction (respectively) of the elements of the Voigt model equivalent to those in the Kelvin–Voigt model shown in Fig. 7a.

Parameters k_e(f) and r_e(f) of the transformed model can easily be determined from the results of calculation of parameters C_e(f) and R_e(f). To determine parameters C_e(f) and R_e(f), we compare the expressions for the input resistance of two electrical analogs shown in Figs. 7b and 8b.

The expression for input resistance Z_k of the analog of the Kelvin–Voigt model has the form

$${{Z}_{k}} = \frac{1}{{{{Y}_{k}}}} = \frac{1}{{j\Omega {{C}_{k}} + \frac{1}{{{{R}_{F}} + {{{(j\Omega {{C}_{F}})}}^{{ - 1}}}}}}},$$

(A.1)

where Y_k is the input conductance of the electric circuit that is an analog of the Kelvin–Voigt model; Ω is the frequency; and C_k, R_F, and C_F are elements of the electric circuit that is an analog of the Kelvin–Voigt model.

Expression (A.1) can be transformed to

$$\begin{gathered} {{Z}_{k}} = {{R}_{F}}\frac{{{{{\left( {\frac{{{{C}_{F}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}}{{1 + {{{(\Omega {{R}_{F}})}}^{2}}{{{\left( {\frac{{{{C}_{F}}{{C}_{K}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}} \\ - \,j\frac{{\frac{1}{{\Omega ({{C}_{F}} + {{C}_{K}})}} + \Omega {{C}_{K}}R_{F}^{2}{{{\left( {\frac{{{{C}_{F}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}}{{1 + {{{(\Omega {{R}_{F}})}}^{2}}{{{\left( {\frac{{{{C}_{F}}{{C}_{K}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}}. \\ \end{gathered} $$

(A.2)

We compare this expression with the expression for input resistance Z_e of the transformed circuit shown in Fig. 8b:

$${{Z}_{e}} = {{R}_{e}}(f) + \frac{1}{{j\Omega {{C}_{e}}(f)}} = {{R}_{e}}(f) - j\frac{1}{{\Omega {{C}_{e}}(f)}}.$$

(A.3)

Here, R_e(f) and C_e(f) are frequency-dependent parameters of the transformed circuit.

Equating the real and imaginary parts of expressions (A.2) and (A.3), we obtain

$${{R}_{e}}(f) = {{R}_{F}}\frac{{{{{\left( {\frac{{{{C}_{F}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}}{{1 + {{{(\Omega {{R}_{F}})}}^{2}}{{{\left( {\frac{{{{C}_{F}}{{C}_{K}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}},$$

(A.4)

$$\frac{1}{{{{C}_{e}}(f)}} = \frac{{\frac{1}{{({{C}_{F}} + {{C}_{K}})}} + {{\Omega }^{2}}{{C}_{K}}R_{F}^{2}{{{\left( {\frac{{{{C}_{F}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}}{{1 + {{{(\Omega {{R}_{F}})}}^{2}}{{{\left( {\frac{{{{C}_{F}}{{C}_{K}}}}{{{{C}_{F}} + {{C}_{K}}}}} \right)}}^{2}}}}.$$

(A.5)

Taking into account the rules of transition from the mechanical model to the electrical analog, in accordance with which r_e(f) = R_e(f) and k_e(f) = $\frac{1}{{{{C}_{e}}(f)}}$ (see Fig. 6), and also r_F = R_F, k_F = $\frac{1}{{{{C}_{F}}}}$, and k_K = $\frac{1}{{{{C}_{K}}}}$ (see Fig. 7), we obtain, from expressions (A.4) and (A.5), after transformations, the sought relations for the parameters of the transformed model, which correspond to expressions (22) and (23):

$$\begin{gathered} {{r}_{e}}(f) = {{r}_{F}}\frac{{{{{\left( {\frac{{{{k}_{K}}}}{{{{k}_{F}} + {{k}_{K}}}}} \right)}}^{2}}}}{{1 + {{{\left( {\frac{{\Omega {{r}_{F}}}}{{{{k}_{F}} + {{k}_{K}}}}} \right)}}^{2}}}}, \\ {{k}_{e}}(f) = \frac{{{{k}_{F}}{{k}_{K}}}}{{{{k}_{F}} + {{k}_{K}}}}\frac{{1 + \frac{{{{{(\Omega {{r}_{F}})}}^{2}}}}{{({{k}_{F}} + {{k}_{K}}){{k}_{F}}}}}}{{1 + {{{\left( {\frac{{\Omega {{r}_{F}}}}{{{{k}_{F}} + {{k}_{K}}}}} \right)}}^{2}}}}. \\ \end{gathered} $$

In this case, the Voigt model with parameters r_e(f) and k_e(f) of the transformed model fully corresponds to the Kelvin–Voigt model with parameters r_F, k_F, and k_K.