1 Introduction

The necessity to reduce oscillations that occur in dynamic mechanical systems under the influence of external and internal forces is explained by the negative impact of oscillations of various system elements on its operational behaviour. This impact is appeared in the instability of the overall system behaviour, decrease in service life of its individual elements, which malfunction can lead to the destruction of the entire system. A typical pattern of structures that are sensitive to oscillations is, for example, an aircraft with air propellers. Rotation of these propellers is accompanied by undesirable oscillations of structural units of an aircraft.

Dampers made of viscoelastic materials are widely used to damp oscillations that occur in various mechanical structures under the action of periodic forces [1,2,3]. The analysis of the behaviour of viscoelastic dampers under harmonic inputs becomes particularly acute when forces, occurred in the mechanical system, induce oscillations in a wide frequency range.

The frequency analysis of viscoelastic materials is usually based on the theory of linear viscoelasticity [4,5,6,7,8]. According to this theory, properties of viscoelastic materials that describe the relationship between strains and stresses under harmonic inputs are characterized by a complex elastic modulus at small strains in a linear region [6, 9].

This approach allows, when designing viscoelastic dampers, to avoid considering the specific structure of viscoelastic materials and physical mechanisms of viscoelasticity, which are very diverse for different materials [9]. A huge number of studies and publications are devoted to the nature of viscoelasticity and methods of describing the properties of viscoelastic materials (from polymers to carbon-containing materials and metals). Let us note the works [8, 10,11,12,13,14,15]. In these papers, the nature of the viscoelasticity of various materials is analyzed, the corresponding models and theories describing the materials’ properties are proposed, and a significant bibliography on these issues is given. Modern theories of dynamic analysis of viscoelasticity consider structures at the nano-level, take into account the local gradient behavior of deformation, extend it to the non-local level, introducing the concept of an integral complex modulus of elasticity [13,14,15].

Thus, the complex modulus of elasticity considered in the paper is a characteristic of a viscoelastic material that fully reflects the relationship between stresses and strains in a viscoelastic shock absorber, regardless of the physical mechanisms of viscoelasticity and the models used.

Let us consider a mechanical system with a damper made of viscoelastic materials in the forced-oscillation regime. The system’s behaviour is described by a differential equation with parameters dependent on properties of viscoelastic materials as well as damped masses [16,17,18]. As it shown in [19], coefficients of the differential equation for induced oscillations in a system with a viscoelastic damper can be determined through parameters of any mechanical damper model, i.e., through the coefficients of viscous friction and elasticity coefficients of the model elements. Various mechanical models of viscoelastic materials are described in [4,5,6, 20]. A study of the relationship between parameters of the differential equation and characteristics of a viscoelastic damper (in particular, components of its complex elastic modulus) is developed in the proposed paper.

Complex elastic modulus of the model can be expressed using the model parameters. The modulus helps to evaluate the adequacy of the assumed damper model to the real viscoelastic material. Also, it helps to investigate the influence of the damper made with the studied viscoelastic material on the behaviour of the system on exposure of a coercive force of the particular frequency.

Quality of the model can be evaluated by comparing components of the complex elastic modulus in a required frequency range with such components of the complex elastic modulus of the used material. It is important to measure the parameters of viscoelastic materials accurately, which is rather difficult and labour-consuming, especially when components of the complex elastic modulus are measured in a wide frequency range. Measurement techniques for parameters of viscoelastic materials are presented, for example, in papers [6, 21,22,23,24,25].

The influence of the damper on the system behaviour described by the differential equation is expressed as a relationship between equation parameters and components of the complex elastic modulus of the model adequate to the viscoelastic material. In this case, components of the complex elastic modulus of the model should be expressed in terms of its parameters. The parameters of the model, in turn, determine the values of the coefficients of the differential equation. The mentioned relationships are discussed in this article.

In [18], difficulties are noted in determining the loss coefficient (matrix) of a differential equation. It should also be noted that losses in the material determined through the coefficient of viscous friction used in the differential equation, are proportional to the rate of deformation changes [16,17,18]. While the losses determined by the loss modulus of the complex modulus of elasticity are proportional to the magnitude of the relative deformations [9].

However, the relationship between these two approaches has not been determined so far, and, even now, some researchers doubt the fact that these methods for describing the properties of viscoelastic materials are equivalent. They suppose that components of the complex elastic modulus of the viscoelastic material (and those of its adequate model) and parameters of the differential equation, which describe the behaviour of these materials in mechanical structures, cannot be connected one-to-one [9].

This paper shows that this alleged contradiction can be resolved when the complex elastic modulus of the model adequate to the viscoelastic material is represented through the parameters of the model. On the other hand, these parameters are expressed using parameters of the differential equation for the system with a damper, performing induced harmonic oscillations. This relationship is easily established by direct comparison of stresses in a viscoelastic material at specified harmonic strains with a force that induces harmonic oscillations of a certain level in the system with a damper.

The established relations between parameters of damping material and parameters of the differential equation allow us to simulate oscillations of different elements of the mechanical system with a damper. Also, the relations make it possible to determine parameters of a viscoelastic material suitable for the protection of system elements vulnerable to vibrations in a required frequency range.

Thus, the main novelty of the article is that we express the coefficients of the differential equation in terms of the components of the complex elastic modulus of the viscoelastic material. Therefore, we can determine the system frequency response by the parameters of the damper model. Also, vice versa, we specify the material parameter requirements for the damper to be used in a specific mechanical system with a certain frequency response.

2 Induced oscillations in a single-mass system with a damper

The mechanical system at given impacts will be represented in the form of the model with lumped parameters [18, 26, 27]. This model reflects the most critical properties of the system with the specified degree of accuracy [26, 27]. In such a system, the viscoelastic damper is also represented as a mechanical model with lumped parameters [18]. Mechanical models are not tied to the structure of a specific viscoelastic material and are used in this paper to determine the characteristics of a damping material suitable for use in the system being developed [28]. In contrast to mechanical models, analytical models of viscoelastic materials are widely used in the synthesis of materials with the required characteristics [1, 29].

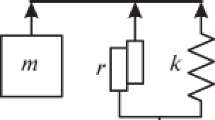
Let us first consider the system with a damper positioned between a lumped mass, which is affected by a disturbance force, and a bed of infinite mass. We will call these systems as single-mass systems. The effect of a damper on the level of damped mass oscillations in the required frequency range of the coercive force is the subject to study in these systems.

2.1 The differential equation for induced oscillations and a generalized model of the damper [17]

The differential equation for induced oscillations of the mechanical system with lumped parameters is given by [16, 17]:

$$mx^{\prime\prime} + rx^{\prime} + kx = F(t),$$
(1)

where F(t) is the generalized periodic external force related to the generalized coordinate x;

x′, x″ are the first and second derivatives of x with respect to t, respectively;

m, r и k are generalized factors of inertia, friction, and elasticity, respectively.

Values of the damping ratio of free oscillations δ, the frequency of free oscillations \(\Omega_{0}\) and the resonant frequency \(\Omega_{r}\) are also typical for the system described by Eq. (1) [9, 17]:

$$\delta = r/2m,\,\,\,\Omega_{0} = \sqrt {k/m} ,\,\,\,\,\Omega_{r} = \sqrt {\Omega_{0}^{2} - 2\delta^{2} } .$$

According to Eq. (1), the external force is counteracted by three forces:

  • the inertial force:

    $$F_{m} (t) = mx^{\prime\prime},$$
    (2)

    where m is the mass of the body to which the force is applied,

  • the friction force:

    $$F_{r} (t) = rx^{\prime},$$
    (3)

    where r is the coefficient of viscous friction of the dissipative element of the system,

  • the elastic force;

    $$F_{k} (t) = kx,$$
    (4)

    where k is the coefficient of elasticity (stiffness) of the elastic element.

The system described by this equation can be schematically represented in the form shown in Fig. 1.

Fig. 1
figure 1

Schematic representation of a mechanical system with a damper. F(t)—acting force; m—inertial element; r—dissipative element; k—elastic element

Full size image

Dissipative and elastic elements connected in parallel combine a damper. Its scheme corresponds to the Voigt model of a viscoelastic material. Parameters of this model (coefficient of internal friction and elastic coefficient) are frequency-independent and equal to the corresponding parameters of the differential equation. Any model that relevantly reflects properties of the used viscoelastic material can be transformed into the Voigt model [19]. Moreover, parameters of this transformed model (equivalent coefficient of internal friction and elastic coefficient, which generally depend on the frequency) will also be equal to the parameters of the differential equation. We will call this transformed model with frequency-dependent parameters, which is matched the differential equation of induced oscillations, as the equivalent Voigt model. This model will be taken as a generalized model of the damper.

2.2 The complex elastic modulus of the damper model and the parameters of the differential equation

In the case of steady-state harmonic oscillations, the complex relationship between the stress in the material and the strain can be written as [6]:

$$\sigma_{a} e^{j\Omega t} = G(\Omega )\varepsilon_{a} e^{j(\Omega t - \varphi )} = G_{a} (\Omega )e^{j\varphi } \varepsilon_{a} e^{j(\Omega t - \varphi )} ,$$
(5)

where \(\sigma_{a} e^{j\Omega t}\) is a harmonic stress function with the frequency Ω and amplitude \(\sigma_{a}\);

\(\varepsilon_{a} e^{j(\Omega t - \varphi )} = \varepsilon (t)\) is a harmonic function of relative strains of the material, with an amplitude εa relative to the stress by an angle φ;

\(G(\Omega )\) is a complex elastic modulus of the material, equal to:

$$G(\Omega ) = G^{|} (\Omega ) + jG^{||} (\Omega ) = G_{a} (\Omega )e^{j\varphi } ;$$

\(G^{|} (\Omega )\) is a storage modulus (real part of the complex elastic modulus);

\(G^{||} (\Omega )\) is a loss modulus (imaginary part of the complex elastic modulus);

\(G_{a} (\Omega )\) is an absolute value of the complex elastic modulus;

\(\varphi = \tan^{ - 1} (G^{||} /G^{|} )\)—the phase shift relative to the stress (loss angle).

The delay of deformations relative to the stress at steady—state harmonic oscillations in a system with a damper is due to the presence of losses in the dissipative element of the damper. From a mathematical point of view, this fact determines the appearance of an imaginary component in the elastic modulus [9].

In this paper, we will be limited to the study of axial linear elastic strains of viscoelastic materials. In this case, the relationship between the complex modulus of elasticity and parameters of the differential equation can be demonstrated simply and clearly, taking into account the basic properties of viscoelastic materials. Obviously, it is necessary to consider the possibility of the appearance of orthogonal components of deformations under axial force impact when the certain constructions of dampers are studied [14, 30].

Passing from stresses \(\sigma\) and relative values of strains \(\varepsilon\) to forces \(F_{a}\) acting on the damper made of viscoelastic material (with a base area S and height l), and to displacements \(x_{a}\) under the influence of these forces, using (5), we will get:

$$\frac{{F_{a} (t)}}{S} = \frac{{F_{a} }}{S}e^{j\Omega t} = G(\Omega )\frac{{x_{a} }}{l}e^{j(\Omega t - \varphi )}$$
(6)

or

\(F_{a} (t) = \frac{S}{l}G(\Omega )X_{a} e^{j(\Omega t - \varphi )} = G_{a} (\Omega )\frac{S}{l}e^{j\varphi } X_{a} e^{j(\Omega t - \varphi )}\) where \(F_{a} (t) = F_{a} e^{j\Omega t}\) is harmonic function of the force acting on the damper;

\(X_{a} e^{j(\Omega t - \varphi )} = x_{a} (t)\)—harmonic shift function.

Taking the force acting on the damper as \(F_{a} (t) = F_{a} \cos (\Omega t),\) and the displacement as \(x_{a} (t) = X_{a} \cos (\Omega t - \varphi ),\) taking the equation \(F_{a} (t) = F_{k} (t) + F_{r} (t)\) into account, and in accordance with (3) and (4), we get:

$$\begin{gathered} F_{a} (t) = kx + rx^\prime \hfill \\ = kX_{a} \cos (\Omega t - \varphi ) - r\Omega X_{a} \sin (\Omega t - \varphi ). \hfill \\ \end{gathered}$$
(7)

On the other hand, in accordance with (6):

$$\begin{gathered} F_{a} (t) = \frac{S}{l}G(\Omega )X_{a} \cos (\Omega t - \varphi ) = \hfill \\ = \frac{S}{l}X_{a} (G^{|} (\Omega )\cos (\Omega t - \varphi ) - G^{{||}} (\Omega )\sin (\Omega t - \varphi ) \hfill \\ \end{gathered}$$
(8)

Comparing expressions (7) and (8) we get:

$$G^{|} (\Omega ) = k\frac{l}{S};$$
(9)
$$G^{||} (\Omega ) = r\Omega \frac{l}{S}.$$
(10)

Components of the complex elastic modulus of viscoelastic materials (and models that relevantly reflect their properties) are frequency-dependent [7]. Hence, both parameters k and r of a differential equation for induced harmonic oscillations in a viscoelastic material should also have a certain frequency dependence, as it follows from Eqs. (9) and (10).

Thus, it is possible to establish a relation between components of the complex elastic modulus of the model of viscoelastic material and oscillation parameters in the system when frequency-dependent parameters of the differential equation for induced harmonic oscillations in a viscoelastic material are used.

2.3 Frequency dependences for components of the complex elastic modulus of damper models

It was noted in [19], the model in the form of a certain combination of dissipative and elastic components with constant parameters ri and kj can be transformed to the Voigt model with equivalent frequency-dependent parameters \(r_{e} (\Omega )\) and \(k_{e} (\Omega )\) .

This model will show accurately damping properties of the damper made of a viscoelastic material. Frequency properties of the material are defined by a complex elastic modulus in accordance with relations (9) and (10) with parameters k and r equal to ke and re , respectively.

Expressions for the equivalent parameters of some models [19], as well as ones for the components of the complex elastic modulus of corresponding models of dampers, are summarized in Table 1.

Table 1 Models and their parameters
Full size table

The standard solid model combined from a series coupling of an elastic element kK and the Voigt model (“KV” model), shown in Table 1, is, in fact, the two-section generalized Voigt model. In the model, one section (an elastic element) can be considered as a degenerated Voigt section. Similarly, the standard solid model combined from a parallel coupling of an elastic element kK and the Maxwell model can also be considered as the two-section generalized Maxwell model (“KM” model), where one section is a degenerated Maxwell section.

Frequency profiles of the storage modulus and the loss modulus of the Voigt, Maxwell, and "KM" standard solid models are shown in Fig. 2. Frequency profiles of the complex elastic modulus of the "KV" model are identical to similar profiles of the complex elastic modulus of the "KM" model if certain parameters of this model are chosen.

Fig. 2
figure 2

Frequency profile of components of the complex elastic modulus of the Voigt, Maxwell, and “KM” models

Full size image

Ratios of damper sizes for all models are set to \(\frac{l}{S} = \frac{1}{3}\left[ {m^{ - 1} } \right]\). For the Voigt model, the parameter kF is set to the value of the storage modulus of the "KM" model at the point \(\Omega = 0\) (\(k_{F} = G_{KM}^{|} (0)\) ), and the parameter rF is set to the value of the frequency derivative of the loss modulus of the "KM" model at the point \(\Omega = 0\) (thus, \(r_{F} = G_{KM}^{|} (\infty ) - G_{KM}^{|} (0)\)). These parameters of the Voigt model result in the lowest difference between compared dependencies in the low-frequency range. For the Maxwell model, the value of the kM parameter is set to the total value of kK and \(k_{M}^{K}\) parameters of the "KM" model, where storage modules of these models become equal at the frequency \(\Omega = \infty\) : \(G_{M}^{|} (\infty ) = G_{KM}^{|} (\infty )\) . Values of the "KM" model parameters and the normalising frequency Ω0 are determined from relations validated for this example: \(\frac{{k_{K} }}{{k_{M}^{K} }} = 0.2;\) \((\Omega_{0} )^{2} = \frac{{k_{K} }}{m}\) with m = 1. The value of the parameter rM of the Maxwell model is set to the value of the parameter \(r_{M}^{K}\) of the KM model. Thus, the higher values of the loss modules in both models occur at the same frequency.

As it shown in Fig. 2, the both plots of the Voigt model and of the standard solid model are closely approximated within the low frequency band.

For the Maxwell model, the storage modulus of the Maxwell model tends toward zero at any values of rM and kM parameters at low frequencies (at \(\Omega \to 0\) ) unlike other models [6]. This circumstance makes it impossible to use this model over the low frequency range, at least for solid viscoelastic materials. However, it is possible to use the Maxwell model within the higher frequency bands.

2.4 Frequency response of the system with a viscoelastic damper

At first, it is necessary to determine the requirements for a viscoelastic material suitable for use in the damper in the designed system.

The frequency profile of an oscillation amplitude Xa of the inertial element in the simplest system shown in Fig. 1 (at frequency-independent parameters r and k) has a resonant behaviour at values of the damping ratio \(\delta < \frac{{\Omega_{0} }}{\sqrt 2 }\) [9, 16]:

$$\begin{gathered} X_{a} = \frac{{F_{a} }}{{m\sqrt {(\Omega _{0}^{2} - \Omega ^{2} )^{2} + (2\delta \Omega )^{2} } }} \hfill \\ = \frac{{F_{a} }}{{m\Omega _{0}^{2} \sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega _{0} }}} \right)^{2} } \right)^{2} + 4\left( {\frac{\delta }{{\Omega _{0} }}} \right)^{2} \left( {\frac{\Omega }{{\Omega _{0} }}} \right)^{2} } }}, \hfill \\ \end{gathered}$$
(11)

where the values δ and Ωo are determined by parameters of the model of the viscoelastic damper and the damped mass.

The frequency dependence of an oscillation amplitude of the system’s inertial element against its oscillation amplitude at low frequencies (at \(\Omega \to 0\) ) is the amplitude-frequency response of the system [14, 17]:

$$a = \frac{{X_{a} }}{{X_{a0} }} = \frac{1}{{\sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega_{0} }}} \right)^{2} } \right)^{2} + c_{0} \left( {\frac{\Omega }{{\Omega_{0} }}} \right)^{2} } }},$$
(12)

where: a is a relative oscillation level of the inertial element of the system, Xa0—amplitude of the inertial element oscillation at low frequencies (at \(\Omega \to 0\) ), \(c_{0} = 4\left( {\frac{\delta }{{\Omega_{0} }}} \right)^{2}\) .

We will find characteristic points of the studied amplitude-frequency response (taking into account 12). The value square of the relative damping factor \(\left( {\frac{\delta }{{\Omega_{0} }}} \right)^{2}\) at the maximum acceptable value of the relative oscillation level ax at a resonant frequency \(\Omega_{r}\) can be represented as:

$$\left( {\frac{\delta }{{\Omega_{0} }}} \right)^{2} = \frac{1}{2}\left( {1 - \sqrt {1 - \frac{1}{{a_{x}^{2} }}} } \right).$$
(13)

Therein, the resonant frequency can be determined from the following expression:

$$\left( {\frac{{\Omega_{r} }}{{\Omega_{0} }}} \right)^{2} = \sqrt {1 - \frac{1}{{a_{x}^{2} }}} .$$
(14)

We also present expressions for the determination of frequencies that exceed the resonant frequency, where the value of relative oscillation level decreases to 1 and 0.707 (respectively \(\Omega_{1}\) and \(\Omega_{0.7}\) ):

$$\left( {\frac{{\Omega_{1} }}{{\Omega_{0} }}} \right)^{2} = 2\sqrt {1 - \frac{1}{{a_{x}^{2} }}} = 2\left( {\frac{{\Omega_{r} }}{{\Omega_{0} }}} \right)^{2} .$$
(15)

and

$$\left( {\frac{{\Omega_{0.7} }}{{\Omega_{0} }}} \right)^{2} = \sqrt {1 - \frac{1}{{a_{x}^{2} }}} + 2\sqrt {2 - \frac{1}{{a_{x}^{2} }}} .$$
(16)

Amplitude-frequency response of the system at \(\delta \ge \frac{{\Omega_{0} }}{\sqrt 2 }\) behaves as a monotonically decreasing function (with frequency-independent parameters k and r), and the value of \(\frac{{\Omega_{0.7} }}{{\Omega_{0} }}\) is determined by the expression:

$$\left( {\frac{{\Omega_{0.7} }}{{\Omega_{0} }}} \right)^{2} = \sqrt {\left( {2\left( {\frac{\delta }{{\Omega_{0} }}} \right)^{2} - 1} \right)^{2} + 1} - \left( {2\left( {\frac{\delta }{{\Omega_{0} }}} \right)^{2} - 1} \right).$$
(17)

The value of \(\frac{{\Omega_{0.7} }}{{\Omega_{0} }}\) is maximal and equal to 1 at \(\left( {\frac{\delta }{{\Omega_{0} }}} \right)^{2} = \frac{1}{2}\) . In this case, \(\Omega_{0.7} = \Omega_{0}\) and the studied frequency response is as flat as possible in the low-frequency range with the largest drop at frequencies higher than \(\Omega_{0}\) . This dependence corresponds to the frequency response of a two-section low-pass filter with the cut-off frequency (boundary frequency) \(\Omega_{b}\) at the level of 0.707 equal to the frequency \(\Omega_{0.7}\) of the damper.

2.5 The frequency response of the system and the parameters of the damper model

For the given cutoff frequency value and acceptable value of oscillations in a damper (low-pass filter) bandpass, determined by its operation conditions in the system, and for the given value of the damped mass, values of parameters r and k for the required frequency profile are determined from given equations as follows.

Values of differential equation parameters for oscillations in the studied system with a damper can be expressed at \(a_{x} \ge 1\) using (13), (14), and (16) through required values of frequency response parameters as:

$$k = m\Omega_{0}^{2} = \frac{{m\Omega_{0.7}^{2} }}{{1 + \sqrt {1 - \frac{1}{{a_{x}^{2} }}} }};$$
(18)
$$\begin{gathered} r = 2m\delta = m\Omega _{0} \sqrt {2\left( {1 - \sqrt {1 - \frac{1}{{a_{x}^{2} }}} } \right)} \hfill \\ = m\Omega _{{0.7}} \sqrt {2\frac{{1 - \sqrt {1 - \frac{1}{{a_{x}^{2} }}} }}{{1 + \sqrt {1 - \frac{1}{{a_{x}^{2} }}} }}} . \hfill \\ \end{gathered}$$
(19)

At \(\delta \ge \frac{{\Omega_{0} }}{\sqrt 2 }\) we can submit δ in the form \(\delta = \delta_{n} k_{\delta }\) . Here, the parameter \(k_{\delta }\) (\(k_{\delta } \ge 1\) ) defines a magnification value of the damping ratio against its minimal value \(\delta_{n}\), equal to \(\delta_{n} = \frac{{\Omega_{0} }}{\sqrt 2 },\) where the frequency response starts to behave as a monotonically decreasing function. The cutoff frequency \(\Omega_{0.7}\) at \(\delta > \delta_{n}\) becomes less than \(\Omega_{0}\). Thus, in accordance with (17) \(k_{\delta }\) can be expressed as a function of \(\frac{{\Omega_{0.7} }}{{\Omega_{0} }} = k_{\Omega }\): \(k_{\delta }^{2} = 1 + \frac{{1 - k_{\Omega }^{2} }}{{2k_{\Omega } }}.\) In this case (\(k_{\delta } \ge 1\)), values of k and r parameters will be equal to:

$$k = m\Omega_{0}^{2} = \frac{{m\Omega_{0.7}^{2} }}{{k_{\Omega }^{2} }};$$
(20)
$$r = 2m\delta = 2m\delta_{n} k_{\delta } = m\frac{{\Omega_{0.7} }}{{k_{\Omega } }}\sqrt {2 + \frac{{1 - k_{{_{\Omega } }}^{2} }}{{k_{\Omega } }}} .$$
(21)

Thus, parameters of the differential equation should comply with relations (18) and (19) at \(\delta \le \frac{{\Omega_{0} }}{\sqrt 2 }\) (\(a_{x} \ge 1\) ), or with relations (20) and (21) at \(\delta \ge \frac{{\Omega_{0} }}{\sqrt 2 }\) (\(a_{x} = 1\) ) to meet the requirements for the amplitude-frequency response of a system with a damper.

If the viscoelastic material is defined by the Voigt model (which is acceptable over the low-frequency band in many cases), parameters of the model will be equal to parameters of the differential equation: \(k_{F} = k,\) \(r_{F} = r.\) Components of the complex elasticity modulus of the viscoelastic damper model (and material) will be equal to (Table 1):

\(G_{F}^{|} = \frac{l}{S}k_{F} ,\) \(G_{F}^{||} (\Omega ) = \frac{l}{S}k_{F} \frac{\Omega }{{\Omega_{F} }},\) where l and S—are determined to subject to conditions of the damper operation in the system.

We can evaluate the performance of the damper in a wider frequency range by using the standard solid "KM" model.

Amplitude-frequency response of the system in this case (\(a_{KM}\) ) can be obtained from (12) by replacing k with ke in the expression \(\Omega_{0}^{2} = \frac{k}{m}\) , and by replacing r with re in the expression \(\delta = \frac{r}{2m}\) (for the “KM” model according Table 1).

On rearrangement (12), we have:

$$\begin{gathered} a_{{KM}} = \frac{1}{{\sqrt {\left( {1 - R\frac{{1 + c_{k}^{2} c_{{00}} R}}{{1 + c_{k} (c_{k} + 1)c_{{00}} R}}} \right)^{2} + \,c_{{00}} \frac{R}{{D^{2} }}} }},\, \hfill \\ \;where\;\,\Omega _{{00}}^{2} = \frac{{k_{K} }}{m};\,\,R = \left( {\frac{\Omega }{{\Omega _{{00}} }}} \right)^{2} ;\,\, \hfill \\ D = 1 + c_{k} (c_{k} + 1)c_{{00}} R,\,\,\delta _{{00}} = \frac{{r_{M}^{K} }}{{2m}};\,\, \hfill \\ c_{{00}} = 4\left( {\frac{{\delta _{{00}} }}{{\Omega _{{00}} }}} \right)^{2} = \left( {\frac{{r_{M}^{K} }}{m}} \right)^{2} \frac{m}{{k_{K} }};\,\,c_{K} = \frac{{k_{K} }}{{k_{M}^{K} }}. \hfill \\ \end{gathered}$$
(22)

The " KM " model is transformed into the Voigt model at \(k_{M}^{K} = \infty\) . In this case, frequency response characteristics of both models (a and \(a_{KM}\)) will be equal at \(\Omega_{00} = \Omega_{0}\), \(\delta_{00} = \delta\) and \(c_{00} = c_{0}\) . In this case, parameters \(k_{K}\) and \(r_{M}^{K}\) of the "KM" model are determined by coefficients of the differential equation: \(k_{K} = k\) and \(r_{M}^{K} = r\) . It is convenient to express the value of the \(c_{0}\) parameter as \(c_{0} = \frac{1}{{a^{2} (\Omega_{0} )}}\) , where \(a(\Omega_{0} )\) is the relative oscillation amplitude of the mass m at the frequency \(\Omega_{0}\), when the Voigt model with parameters \(k_{F} = k_{K} = k\) and \(r_{F} = r_{M}^{K} = r\) is used.

In case of real materials \(k_{M}^{K} \ne \infty\) , and at finite values of \(k_{M}^{K}\), the frequency response of the "KM" model will basically be equal to the same characteristic of the Voigt model only over the low-frequency band. The acceptable value of the \(k_{M}^{K}\) parameter (which is acceptable in the sense of the influence on the amplitude-frequency response of the system) can be determined via variation of the \(c_{K}\) parameter. The variation is performed when modelling the frequency profile \(a_{KM}\) and choosing the studied amplitude-frequency response behaviour in the range of medium and high frequencies, which meets the requirements for the damper. Values of \(k_{K}\) and \(r_{M}^{K}\) parameters can also be specified during the simulation.

Some results of the simulation are shown in Fig. 3.

Fig. 3
figure 3

Amplitude-frequency response of the one-mass system with dampers, represented by the Voigt and “KM” models

Full size image

Three curves represented by thick lines in Fig. 3, show the frequency response of the system when the damper is approximated by the Voigt model at different values of the relative damping coefficient. The middle thick line corresponds to the critical value of the damping ratio \(\left( {\frac{\delta }{{\Omega_{0} }} = \frac{1}{\sqrt 2 }} \right)\) when the amplitude-frequency response characteristic is as flat as possible with the largest drop within the range of attenuation. In this case, the normalized frequency \(\Omega_{0}\) is chosen to fulfil the equation \(\frac{{\Omega_{0.7} }}{{\Omega_{0} }} = 1\) . Thick line in the left corresponds to the case of a higher damping ratio \(\left( {\frac{\delta }{{\Omega_{0} }} = 1} \right)\) when the slope of the frequency response decay and the boundary frequence \(\left( {\frac{{\Omega_{0.7} }}{{\Omega_{0} }} = 0.644} \right)\) are decreasing. The right thick line corresponds to the case when a certain increase in the level of oscillations in a filter (damper) bandpass is allowed (in this case it increases to the level of \(a_{r} = 1.05\) at \(\frac{\delta }{{\Omega_{0} }} = 0.588\) ). This leads to an increase of the slope drop of the frequency response characteristic and a moderate increase of the boundary frequence (\(\frac{{\Omega_{0.7} }}{{\Omega_{0} }} = 1.164\) ).

The Voigt model parameters for the selected cases at m = 1[kg] and \(\Omega_{0} = 1\)[HZ] are:

  • for the case \(\frac{\delta }{{\Omega_{0} }} = 1\) : \(k_{F} = m\Omega_{0}^{2} = 1\left[ {\tfrac{N}{m.}} \right]\) ; \(r_{F} = 2m\delta = 2\left[ {\tfrac{Ns}{{m.}}} \right]\) ;

  • for the case \(\frac{\delta }{{\Omega_{0} }} = \frac{1}{\sqrt 2 }\) : \(k_{F} = m\Omega_{0}^{2} = 1\left[ {\tfrac{N}{m.}} \right]\) ; \(r_{F} = 2m\delta = 1.414\left[ {\tfrac{Ns}{{m.}}} \right]\) ;

  • for the case \(\frac{\delta }{{\Omega_{0} }} = 0.588\) : \(k_{F} = m\Omega_{0}^{2} = 1\left[ {\tfrac{N}{m.}} \right]\) ; \(r_{F} = 2m\delta = 1.176\left[ {\tfrac{Ns}{{m.}}} \right]\) .

Thin lines in Fig. 3 show frequency response characteristics of the system when the damper is represented by the standard solid model “KM”. Characteristics of this model are calculated to match with the Voigt model (\(k_{K} = k_{F}\) и \(r_{M}^{K} = r_{F}\) ) in a low frequency range. The behavior of the amplitude-frequency response in the higher frequency range is determined by the value of the \(c_{K} = \frac{{k_{K} }}{{k_{M}^{K} }}\) parameter. Simulation shows, that a decrease of the parameter \(k_{M}^{K}\) from infinity to a certain final value results in a shift of an initial amplitude-frequency response of the system with a Voigt model to a higher frequency region. The shift occures without sacrificing its general behaviour (as well as a gradual amplification of oscillations within the resonant area). A significant amplification of oscillations in the resonant region occurs with a further decrease of the parameter \(k_{M}^{K}\) . Resonant area appears even on monotonically decreasing profiles (for cases \(\frac{\delta }{{\Omega_{0} }} \ge \frac{1}{\sqrt 2 }\) ). This behaviour of the frequency response characteristic is shown in Fig. 3 as the thin solid line on the right. It corresponds to the case \(\frac{\delta }{{\Omega_{0} }} = \frac{1}{\sqrt 2 }\) at \(c_{K} = 0.16\) . The value of \(c_{K}\) is selected to reach the maxumum value \(a = a_{X}\) (at the resonant frequency) of 1. The value \(c_{K} = 0.2\) for the case \(\frac{\delta }{{\Omega_{0} }} = 0.707\) (thin dashed line) is selected from the condition that the frequency response \(a_{KM}\) remains as flat as possible over the largest part of the range. The value \(c_{K} = 0.17\) for the case \(\frac{\delta }{{\Omega_{0} }} = 0.588\) (thin solid line on the left) is selected from the condition for an acceptable increase of the level \(a_{KM}\) to the value of \(a_{X} = 1.1\).

The "KM" model parameters for the selected cases at m = 1[kg] and \(\Omega_{0} = 1\)[HZ] are:

  • for the case \(\frac{\delta }{{\Omega_{0} }} = 1\) and \(c_{K} = 0.16\), \(k_{K} = 1\left[ {\tfrac{N}{m.}} \right]\) ; \(r_{M}^{K} = 2\left[ {\tfrac{Ns}{{m.}}} \right]\) ; \(k_{M}^{K} = \frac{{k_{K} }}{{c_{K} }} = 6.25\left[ {\tfrac{N}{m.}} \right]\) ;

  • for the case \(\frac{\delta }{{\Omega_{0} }} = \frac{1}{\sqrt 2 }\) and \(c_{K} = 0.2\), \(k_{K} = 1\left[ {\tfrac{N}{m.}} \right]\) ; \(r_{M}^{K} = 1.414\left[ {\tfrac{Ns}{{m.}}} \right]\) ; \(k_{M}^{K} = 5\left[ {\tfrac{N}{m.}} \right]\) ;

  • for the case \(\frac{\delta }{{\Omega_{0} }} = 0.588\) and \(c_{K} = 0.17\), \(k_{K} = 1\left[ {\tfrac{N}{m.}} \right]\) ; \(r_{M}^{K} = 1.176\left[ {\tfrac{Ns}{{m.}}} \right]\) ; \(k_{M}^{K} = 5.88\left[ {\tfrac{N}{m.}} \right]\)

Thus, the parameters of the "KM" model are defined for the characteristics with the desired shape as follows. Parameters \(k_{K}\) and \(r_{M}^{K}\) are calculated from Eqs. (18)–(21) as parameters \(k_{F}\) and \(r_{F}\) of the original Voigt model, equal to coefficients k and r of the differential equation.

Parameter \(k_{M}^{K}\) is calculated from the equation \(c_{K} = \frac{{k_{K} }}{{k_{M}^{K} }}\) (the value of \(c_{K}\) is determined during the simulation of its effect on the frequency response characteristic).

Components of the complex elastic modulus of the viscoelastic damper model (and material) that provide the required amplitude-frequency response of the system are determined through the parameters of the model, as shown in Table 1.

Frequency profiles for components of the complex elastic modulus of the damper model wich ensure the maximal flat amplitude-frequency response of the damping system using the Voigt and “KM” models are shown in Fig. 4. Parameters of these models are taken from the example shown in Fig. 3, and the relation \(\frac{l}{S} = \frac{1}{3}\) [m.−1]. Frequency profiles of the system with these dampers are also shown in this picture for illustrative purposes.

Fig. 4
figure 4

Frequency profiles of components of the complex elastic modulus of the Voigt and “KM” models of the damper and the relative oscillation level of the damped mass

Full size image

Thus, the frequency response of a damper will correspond to the plot aF, when the behaviour of a viscoelastic material selected for the damper is closely approximated by the Voigt model with the storage modulus \(G_{F}^{|}\) and the loss modulus \(G_{F}^{||}\) in a required frequency range (as shown in Fig. 4). If frequency dependences of components of the complex elastic modulus of the studied material are closely approximated in a required frequency range by corresponding dependences of the standard solid model "KM", shown in the figure, the frequency response characteristic of the damper will correspond to the plot \(a_{KM}\).

The proposed approach to the analysis of the behaviour of viscoelastic dampers, which is based on the use of a generalized model of the damper in the form of the equivalent Voigt model with frequency-dependent parameters, allows us to determinate frequency response characteristics of designed dampers, as well as characteristics of viscoelastic materials approximated with more complex models.

2.6 Frequency characteristics of a system with a damper approximated by a multisectional generalized Maxwell model

As an example, we will estimate the frequency properties of a system with a damper, represented by a three-section generalized Maxwell model (with one degenerate section), which is shown in Fig. 5. We call this model (with two complete and one degenerate Maxwell sections) as "KMM" one.

Fig. 5
figure 5

Three-section generalized Maxwell model

Full size image

We can express the parameters \(k_{e}\) and \(r_{e}\) of the "KMM" model transformed to the equivalent Voigt model (generalized damper model) in terms of the parameters of the original model:

$$k_{e} = k_{K} + k_{1} \frac{{\left( {\frac{\Omega }{{\Omega_{1} }}} \right)^{2} }}{{1 + \left( {\frac{\Omega }{{\Omega_{1} }}} \right)^{2} }} + k_{2} \frac{{\left( {\frac{\Omega }{{\Omega_{2} }}} \right)^{2} }}{{1 + \left( {\frac{\Omega }{{\Omega_{2} }}} \right)^{2} }}$$
(23)
$$r_{e} = \frac{{r_{1} }}{{1 + \left( {\frac{\Omega }{{\Omega_{1} }}} \right)^{2} }} + \frac{{r_{2} }}{{1 + \left( {\frac{\Omega }{{\Omega_{2} }}} \right)^{2} }},$$
(24)

where \(\Omega_{1} = \frac{{k_{1} }}{{r_{1} }}\); \(\Omega_{2} = \frac{{k_{2} }}{{r_{2} }}\); \(k_{K}\), \(k_{1}\), \(k_{2}\), \(r_{1}\), \(r_{2}\)–elasticity coefficients and coefficients of internal friction of elastic and dissipative elements of the studied system.

Therefore, expressions for components of the complex elastic modulus of the damper model (and of the corresponding viscoelastic material) are ([12]):

$$G^{|} = \frac{l}{S}\left( {k_{K} + k_{1} \frac{{\left( {\frac{\Omega }{{\Omega_{1} }}} \right)^{2} }}{{1 + \left( {\frac{\Omega }{{\Omega_{1} }}} \right)^{2} }} + k_{2} \frac{{\left( {\frac{\Omega }{{\Omega_{2} }}} \right)^{2} }}{{1 + \left( {\frac{\Omega }{{\Omega_{2} }}} \right)^{2} }}} \right)$$
(25)
$$G^{||} = \frac{l}{S}\left( {k_{1} \frac{{\frac{\Omega }{{\Omega_{1} }}}}{{1 + \left( {\frac{\Omega }{{\Omega_{1} }}} \right)^{2} }} + k_{2} \frac{{\frac{\Omega }{{\Omega_{2} }}}}{{1 + \left( {\frac{\Omega }{{\Omega_{2} }}} \right)^{2} }}} \right)$$
(26)

Full sizes of a damper (l and S) are selected with respect to the actual loading of a damper in the studied system and strength properties of the proposed material.

Frequency profiles for components of the complex elastic modulus are shown in Fig. 6. In this case, the model is formed by adding one section to the "KM" model which characteristics are used in the example shown in Fig. 4 (\(\frac{l}{S} = \frac{1}{3}\) [m−1]). For comparison, Fig. 6 shows the characteristics \(a_{KMM}\) and \(a_{KM}\) of both models “KMM” and “KM”.

Fig. 6
figure 6

Frequency response characteristics of the "KMM" and "KM" models

Full size image

Parameters of the "KMM" model section additional to the "KM" model are specially selected in this case to obtain the deviation of the frequency characteristic from the average value (equal to 1) not more than 0.1 within the damper bandpass. In any other (optional) case, we can at least determine a frequency response characteristic of a damper made of a particular material, which frequency properties are simulated by more intricated models, on the basis of this suggested approach.

We now give the general expression for the frequency response characteristic of the system with a damper, when a viscoelastic material is expressed by a multisectional generalized Maxwell model with one degenerate section:

$$a_{c} = \frac{1}{{\sqrt {\left( {1 - \frac{R}{D}} \right)^{2} + \,4\left( {\frac{{\delta_{0} }}{{\Omega_{0} }}} \right)^{2} R\frac{{\sum\nolimits_{i} {\frac{{\frac{{r_{i} }}{{\sum\nolimits_{i} {r_{i} } }}}}{1 + R}} }}{D}} }},$$
(27)

where \(\Omega_{0}^{2} = \frac{{k_{K} }}{m}\) ; \(R = \left( {\frac{\Omega }{{\Omega_{0} }}} \right)^{2}\), \(D = 1 + \sum\nolimits_{i} {\frac{{\frac{{k_{i} }}{{k_{K} }}R}}{1 + R}}\), \(\delta_{0} = \frac{{\sum\nolimits_{i} {r_{i} } }}{2m}\) ; \(\Omega_{i} = \frac{{k_{i} }}{{r_{i} }}\) ; m—the damped mass; i—index corresponding to the number of the complete Maxwell section; \(k_{K}\), \(k_{i}\), \(r_{i}\)—parameters of the model.

Expression (27) can also be submitted in a form:

$$a_{c} = \frac{1}{{\sqrt {\left( {1 - \frac{R}{D}} \right)^{2} + \,4\left( {\frac{{\delta_{0} }}{{\Omega_{0} }}} \right)^{2} R\frac{{\sum\nolimits_{i} {\frac{{\frac{{r_{i} }}{{\sum\nolimits_{i} {r_{i} } }}}}{{1 + c_{i}^{2} d_{i} R}}} }}{D}} }},$$

The last expression uses the following notations: \(c_{i} = \frac{{k_{K} }}{{k_{i} }}\) ; \(D = 1 + \sum\nolimits_{i} {\frac{{c_{i} d_{i} R}}{{1 + c_{i}^{2} d_{i} R}}}\), \(d_{i} = 4\left( {\frac{{\delta_{i} }}{{\Omega_{0} }}} \right)^{2}\) , where \(\delta_{i} = \frac{{r_{i} }}{2m}\) .

3 Induced oscillations in a dual-mass system with a damper

3.1 Basic relations for a dual-mass system with a damper

In a dual-mass system, the damper is positioned between two oscillating masses (m и M), as shown in Fig. 7.

Fig. 7
figure 7

A damper in a dual-mass system. F(t)—driving (coercive) force; Fm and FM—inertial forces of masses m and M; Fr, Fk—an internal friction force and an elasticity force respectivly

Full size image

In this case:

$$F^{M} = F^{r} + F^{K} ,$$
(28)
$$F(t) = F^{m} + F^{r} + F^{K} = F^{m} + F^{M} .$$
(29)

Assuming

$$F(t) = F_{a} \cos (\Omega t),$$
(30)
$$x_{m} = X_{m} \cos (\Omega t - \varphi ),$$
(31)
$$x_{M} = X_{M} \cos (\Omega t - \psi ),$$
(32)

where the current values of m and M masses’ displacements are indicated by symbols \(x_{m}\) and \(x_{M}\), respectively; Xm and XM are amplitudes of these displacements; \(\varphi\) and \(\psi\) are phase shifts of the displacements relative to the driving force. Thus, we obtain:

$$F^{m} = m(x_{{^{m} }} )^{\prime\prime} = - m\Omega^{2} X_{m} \cos (\Omega t - \varphi ),$$
(33)
$$F^{M} = M(x_{{^{M} }} )^{\prime\prime} = - M\Omega^{2} X_{M} \cos (\Omega t - \psi ).$$
(34)

Since the deformation of the damper model (in the accepted approximation of linear, axial deformations of the viscoelastic body) can be represented by a difference between displacement of its ends, i.e. \(x_{m} - x_{M}\) , the equations for the damper resistance forces in accordance with (31) and (32) are:

$$\begin{gathered} F^{r} = r(x_{m} - x_{M} )^{\prime}, \hfill \\ = - r\Omega (X_{m} \sin (\Omega t - \varphi ) - X_{M} \sin (\Omega t - \psi )), \hfill \\ \end{gathered}$$
(35)
$$\begin{gathered} F^{k} = k(x_{m} - x_{M} ) \hfill \\ = - k(X_{m} \cos (\Omega t - \varphi ) - X_{M} \cos (\Omega t - \psi )). \hfill \\ \end{gathered}$$
(36)

From (29), with consideration to (30), (33), and (34), we find:

$$\begin{gathered} F_{a} \cos (\Omega t) \hfill \\ = - \Omega ^{2} (mX_{m} \cos (\Omega t - \varphi ) + MX_{M} \cos (\Omega t - \psi )). \hfill \\ \end{gathered}$$
(37)

From (35) we get:

$$X_{m} = \frac{{F_{a} \sin \psi }}{{m\Omega^{2} \sin (\varphi - \psi )}},$$
(38)
$$X_{M} = \frac{{F_{a} \sin \varphi }}{{M\Omega^{2} \sin (\psi - \varphi )}}.$$
(39)

Converting (28) with consideration to (34), (35), (36), we get:

$$\begin{gathered} X_{M} (k\cos (\Omega t - \psi ) - r\Omega \sin (\Omega t - \psi )) \hfill \\ - X_{m} (k\cos (\Omega t - \varphi ) - r\Omega \sin (\Omega t - \varphi )) \hfill \\ = M\Omega ^{2} X_{M} \cos (\Omega t - \psi ). \hfill \\ \end{gathered}$$
(40)

From (40) it follows:

$$\begin{gathered} X_{m} \sqrt {k^{2} + (r\Omega )^{2} } \sin (\gamma - (\Omega t - \varphi )) \hfill \\ = X_{M} \sqrt {(k - M\Omega ^{2} )^{2} + (r\Omega )^{2} } \sin (\beta - (\Omega t - \psi )), \hfill \\ \end{gathered}$$
(41)

where \(\gamma\) and β are defined by the relations:

$$\tan \gamma = \frac{k}{r\Omega },$$
(42)
$$\tan \beta = \frac{{k - M\Omega^{2} }}{r\Omega }.$$
(43)

From (41) it follows:

$$\varphi - \psi = \beta - \gamma$$
(44)

and

$$X_{m} \sqrt {k^{2} + (r\Omega )^{2} } = X_{M} \sqrt {(k - M\Omega^{2} )^{2} + (r\Omega )^{2} } .$$
(45)

Converting (38) and (39) in consideration of (44), we find:

$$\sin \psi = \frac{{ - \frac{{mX_{m} }}{{MX_{M} }}\sin (\beta - \gamma )}}{{\sqrt {1 + 2\frac{{mX_{m} }}{{MX_{M} }}\cos (\beta - \gamma ) + \left( {\frac{{mX_{m} }}{{MX_{M} }}} \right)^{2} } }},$$
(46)
$$\sin \varphi = \frac{{\frac{{MX_{M} }}{{mX_{m} }}\sin (\beta - \gamma )}}{{\sqrt {1 + 2\frac{{MX_{M} }}{{mX_{m} }}\cos (\beta - \gamma ) + \left( {\frac{{MX_{M} }}{{mX_{m} }}} \right)^{2} } }}.$$
(47)

Then (38) and (39), taking into account (44), (46) and (47), give:

$$X_{m} = \frac{{F_{a} }}{{m\Omega^{2} }}\frac{{ - \frac{{mX_{m} }}{{MX_{M} }}}}{{\sqrt {1 + 2\frac{{mX_{m} }}{{MX_{M} }}\cos (\beta - \gamma ) + \left( {\frac{{mX_{m} }}{{MX_{M} }}} \right)^{2} } }}$$
(48)

and

$$X_{M} = \frac{{F_{a} }}{{m\Omega^{2} }}\frac{{ - \frac{{MX_{M} }}{{mX_{m} }}}}{{\sqrt {1 + 2\frac{{MX_{M} }}{{mX_{m} }}\cos (\beta - \gamma ) + \left( {\frac{{MX_{M} }}{{mX_{m} }}} \right)^{2} } }}.$$
(49)

Transforming (48, 49) with consideration to (42), (43), (44), we have:

$$\begin{gathered} \left| {X_{m} } \right| = \frac{{F_{a} \sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega_{M} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}{{(m + M)\Omega^{2} \sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }} \hfill \\ = \frac{{F_{a} \sqrt {\left( {1 - \left( {1 + \frac{M}{m}} \right)\left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}{{(m + M)\Omega^{2} \sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}, \hfill \\ \end{gathered}$$
(50)
$$\left| {X_{M} } \right| = \frac{{F_{a} \sqrt {1 + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}{{(m + M)\Omega^{2} \sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }},$$
(51)

where: \((\Omega_{0}^{e} )^{2} = \frac{k}{{m_{e} }}\) , \(m_{e} = \frac{M}{{1 + \frac{M}{m}}}\) , \(c_{0}^{e} = 4\left( {\frac{{\delta^{e} }}{{\Omega_{0}^{e} }}} \right)^{2} = \frac{r}{{m_{e} }}\frac{r}{k}\), \(\delta^{e} = \frac{r}{{2m_{e} }}\) , \((\Omega_{M} )^{2} = \frac{k}{M}\) .

The fundamental difference between oscillations in a dual-mass system and oscillations in a system with one damped mass is an increase of oscillation amplitude in the low-frequency range (at \(\Omega \to 0\) ): \(\left| {X_{m} } \right|_{\Omega \approx 0} \simeq \left| {X_{M} } \right| \simeq \frac{{F_{a} }}{{\Omega^{2} (M + m)}}\) . (For a single-mass system \(\left| {X_{a} } \right|_{\Omega \approx 0} \simeq \frac{{F_{a} }}{{\Omega^{2} m}}\) ).

3.2 Frequency response of the dual-mass system with a damper, represented by the Voigt model

We will study oscillations of mass m, which are affected by a driving force when the damper is positioned between two masses (as it shown in Fig. 7), relative to oscillations in the system without damper.

When the Voigt model (with constant parameters \(k_{F}\) and \(r_{F}\) equal to parameters of the differential equation k and r) is used as the damper model, the frequence responce (\(a_{m}^{m}\) ) can be represented as follows, taking (50) into account:

$$a_{m}^{m} = \frac{{\sqrt {\left( {1 - (1 + \frac{M}{m})\left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}{{\sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}.$$
(52)

Analysis of the Eq. (52) shows that the local minimum and maximum in a frequency response take place at frequencies \(\Omega_{n}\) and \(\Omega_{x}\) respectivly at \(c_{0}^{e} < \frac{2q}{{q + 1}}\), where \(q = 1 + \frac{M}{m}\) . The values of these frequencies are determined by the expressions: \(\Omega_{n}^{2} = \frac{{q + 1 - \sqrt {(q - 1)^{2} + 2c_{0}^{e} (q + 1)} }}{{2q - c_{0}^{e} (q + 1)}}\) and \(\Omega_{x}^{2} = \frac{{q + 1 + \sqrt {(q - 1)^{2} + 2c_{0}^{e} (q + 1)} }}{{2q - c_{0}^{e} (q + 1)}}\) , so \(\Omega_{n} < \Omega_{x}\) .

Maximum in the high frequency region disappears at \(c_{0}^{e} \ge \frac{2q}{{q + 1}}\) , and the frequency response tends monotonically to the value \(1 + \frac{M}{m}\) : \(a_{m}^{m} \mathop{\longrightarrow}\limits_{{\Omega \to \infty }}^{}1 + \frac{M}{m}\) . As we can see, this value is determined by the ratio of oscillating masses, and it can far exceed the oscillation level over the low-frequency band. The minimum value of \(a_{m}^{m}\) takes place at the frequency \(\Omega_{n} = \frac{{q + 1 - \sqrt {(q - 1)^{2} + 2c_{0}^{e} (q + 1)} }}{{2q - c_{0}^{e} (q + 1)}}\) at \(c_{0}^{e} \ge \frac{2q}{{q + 1}}.\)

The relative frequency profile of oscillations amplitude of the mass M under the impact of a driving force on the mass m (\(a_{M}^{m}\) ) in view of (51) can be represented as:

$$a_{M}^{m} = \frac{{\sqrt {1 + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}{{\sqrt {\left( {1 - \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } \right)^{2} + c_{0}^{e} \left( {\frac{\Omega }{{\Omega_{0}^{e} }}} \right)^{2} } }}.$$
(53)

This function has a maximum on the frequency, determined from: \(\frac{{\Omega_{x} }}{{\Omega_{0}^{e} }} = \sqrt {\frac{{\sqrt {1 + 2c_{0}^{e} } - 1}}{{c_{0}^{e} }}}\) . This maximum is equal to

$$a_{x} = \frac{{\sqrt[4]{{1 + 2c_{0}^{e} }}}}{{\sqrt {\left( {\frac{{1 + c_{0}^{e} - \sqrt {1 + 2c_{0}^{e} } }}{{c_{0}^{e} }}} \right)^{2} + \sqrt {1 + 2c_{0}^{e} } - 1} }}.$$

Oscillation level of the mass M decreases monotonically with increasing of frequency: \(a_{M}^{m} \mathop{\longrightarrow}\limits_{{\Omega \to \infty }}^{}0\) , when the frequency is higher than \(\Omega_{x}\) In this region, \(a_{M}^{m}\) becomes equal to 1 at \(\left( {\frac{{\Omega_{1} }}{{\Omega_{0}^{e} }}} \right)^{2} = 2\) and reaches the value of 0.707 at the \(\frac{{\Omega_{0.7} }}{{\Omega_{0}^{e} }} = \sqrt {\frac{{2 + c_{0}^{e} + \sqrt {\left( {2 + c_{0}^{e} } \right)^{2} + 4} }}{2}}\) frequency.

Examples of such frequency profiles of a dual-mass system under the impact of a coercive (driving) force on the mass m are shown in Fig. 8. These plots were calculated at various values of the \(c_{0}^{e}\) parameter, which characterizies the value of oscillations in a system with a damper, represented by the Voigt model at \(\frac{M}{m} = 5\) .

Fig. 8
figure 8

Frequency profiles of oscillations in the dual-mass system with a damper, represented by the Voigt model, on exposure to the coercive force on the mass m

Full size image

Dashed thick lines in the figure represent frequency profiles of the mass m oscillations at three different values of the relative damping coefficient \(c_{0}^{e}\). Solid thick lines represent the frequency profiles of the mass M oscillations at the same values of the relative damping coefficient. For the comparison, the dashed thin line represents the initial extremely flat frequency profile of the mass m oscillations (\(a_{m}\)) in the single-mass system at \(\frac{\delta }{{\Omega_{0} }} = \frac{1}{\sqrt 2 }\). As it shown in the figure, use of the damper in a dual-mass system over a low frequency band allows to decrease the level of the mass m oscillations, affected by a coercive force, withoit a significant increase of the mass M oscillations. However, suppression of oscillations of the mass M with a significant increase in the mass m oscillations is observed in the high frequency range.

Thus, parameters of the differential equation of induced oscillations in the studied system can be determined as a result of the simulation of a viscoelastic material by the Voigt model, on the basis of the maximum acceptable value of the relative oscillation level and the cut-off frequency value (\(\Omega_{0.7}\) or \(\Omega_{1}\) ). As described above, values of these coefficients are used as the initial data to determine the required values of the parameters of the viscoelastic material which is acceptable for the designed damper.

3.3 Frequency response characteristics of the dual-mass system with a damper, represented by the “KM” model

We now give expressions for the relative oscillations of masses m and M used in a simulation of a viscoelastic material with the standard solid model "KM". These expressions can be obtained from (50) and (51) by the subtitution of k and r parameters in the expressions for \(\Omega_{0}^{e}\) and \(\delta_{0}^{e}\) (45) with parameters \(k_{e}\) and \(r_{e}\) of the "KM" model (Table 1). The substitution can be done in the same way as it was done for a single-mass system:

$$a_{m}^{m} = \frac{{\sqrt {\left( {\left( {1 - (1 + \frac{M}{m}} \right)R\frac{{1 + c_{k}^{2} c_{00}^{e} R}}{D}} \right)^{2} + \frac{{c_{00}^{e} R}}{{D^{2} }}} }}{{\sqrt {\left( {1 - R\frac{{1 + c_{k}^{2} c_{00}^{e} R}}{D}} \right)^{2} + \,\frac{{c_{00}^{e} R}}{{D^{2} }}} }}$$
(54)
$$a_{M}^{m} = \frac{{\sqrt {1 + \frac{{c_{00}^{e} R}}{{D^{2} }}} }}{{\sqrt {\left( {1 - R\frac{{1 + c_{k}^{2} c_{00}^{e} R}}{D}} \right)^{2} + \,\frac{{c_{00}^{e} R}}{{D^{2} }}} }}$$
(55)

In expressions (54), (55) \(R = \left( {\frac{\Omega }{{\Omega_{00}^{e} }}} \right)^{2}\), \(D = 1 + c_{k} (c_{k} + 1)c_{00}^{e} R\), \(\delta_{00}^{e} = \frac{{r_{M} }}{{2m_{e} }}\) , \(\left( {\Omega_{00}^{e} } \right)^{2} = \frac{{k_{K} }}{{m_{e} }}\) , \(c_{00}^{e} = 4\left( {\frac{{\delta_{00}^{e} }}{{\Omega_{00}^{e} }}} \right)^{2}\) .

Frequency profiles of the relative oscillation level of masses m and M in the dual-mass system with a damper, represented by the "KM" model (comparing with the Voigt model) on exposure \(\frac{M}{m} = 5\) to the coercive force on the mass m, are represented in Fig. 9.

Fig. 9
figure 9

Frequency profiles of oscillations in the dual-mass system with a damper, represented by the "KM" model, on exposure to the coercive force on the mass m

Full size image

Dashed thick lines in the figure represent frequency profiles of oscillation amplitudes of masses m and M of the Voigt model at \(c_{00}^{e} = \frac{2q}{{q + 1}}\) , and thin lines represent similar dependences of the "KM" model calculated for the same k and r parameters of the differential equation and the value of the \(c_{k} = 0.1\) parameter. The dashed thin line represents the initial extremely flat frequency profile of the relative level of mass m oscillations amplitude in the one-mass system.

Figure 10 shows similar frequency profiles of the relative level of masses’ oscillations in the dual-mass system with a damper for the case of exposure to the coercive force on the mass M (at \(\frac{M}{m} = 5\)).

Fig. 10
figure 10

Frequency plots of the dual-mass system with a damper, represented by the "KM" model, on exposure to the coercive force on the mass M

Full size image

As it can be shown in the simulation, the stronger the difference between frequency parameters of the viscoelastic material and frequency parameters of the Voigt model, the higher level of mass oscillations is observed within the medium frequency band.

The proposed approach to estimate oscillations in a dual-mass system with a damper is also applicable for more complex models of viscoelastic materials, similar to the data shown in Sects. 2.3–2.6 for a single-mass system.

4 Conclusion

Summing up, we note the following points.

The behaviour of viscoelastic damping materials under harmonic inputs is described by the differential equation for induced oscillations in a system with a damper. A system damper behaviour is determined by two parameters of the differential equation—the elasticity (stiffness) coefficient k and the coefficient of viscous friction r. Basic regularities of the damper behaviour are described by the theory of linear viscoelasticity and characterized by the complex modulus of elasticity. Frequence dependences of components of the complex elastic modulus determine the frequence dependences of the coefficients k and r of the differential equetion.

In this way, a viscoelastic material is represented by some initial model with frequency-independent parameters \(k_{i}\) and \(r_{j}\) of elastic and dissipative elements respectivly. Components of the complex elastic modulus of the initial model, represented in terms of \(k_{i}\) and \(r_{j}\) , might be adequate to the corresponding components of the viscoelastic material. The initial model is transformed to the equivalent Voigt model containing two elements with \(k_{e}\) and \(r_{e}\) parameters wich are equal to k and r coefficients of the differential equation. Thus, coefficients of the differential equation for oscillations in the system with a viscoelastic damper can be expessed in terms of frequency-independent parameters of an arbitrary model of a viscoelastic material. In this case, levels of oscillations of inertial elements of a system with a damper in the required frequency range (i.e. frequency response characteristics of the system) can also be determined in terms of frequency-independent parameters of the initial damper model.

The proposed approach to the analysis of the behaviour of viscoelastic dampers allows us to determine the requirements for viscoelastic materials suitable for use in the designed dampers. The approach is based on the use of a generalized damper model in form of the equivalent Voigt model with frequency-dependent parameters. Therefore, it allows to determine parameters of the initial damper model corresponding to the requirements for the frequence response of the designed system.

Naturally, difficulties to select an acceptable model of viscoelastic materials increase when the operating frequency range expands, and simple models cannot adequately reflect properties of real materials. Nevertheless, simple models can be used to determine the required values of parameters of the studied model, which defines its behavior in the low-frequency range.

Intensive studies in the field of dynamic analysis of beam-type structures at the nano-level with local gradient behaviour of deformation and its propagation to the non-local level lead to the analysis of device models, the parameters of which depend on the device dimensions. The study of the features of the application of the proposed approach to the analysis of such structures and models is supposed to be implemented while continuing the work on the design of viscoelastic dampers.