Solar wind interaction with dusty plasma produces electrostatic instabilities and solitons

Abstract

It is shown that the solar wind interaction with dusty plasma in planetary magnetospheres gives rise to electrostatic instabilities and solitary structures. Non-Maxwellian electrons increase the growth rate of shear flow instability and reduce the amplitude of solitary pulses formed by the modified dust ion acoustic wave (mDIAW) in nonlinear regime. Dust number density plays the similar role. The kappa ($\kappa$) and Cairns distribution functions are used to take into account the role of non-Maxwellian electrons in the presence of stationary dust and flowing ions along the external magnetic field with inhomogeneous velocity. This theoretical model is general and it can be applied to various dusty plasma environments such as interstellar medium, cometary tails and planetary magnetospheres. Here it has been applied to the Saturn’s $F$-ring plasma.

1 Introduction

Solar wind prevails everywhere in the interplanetary space and its interaction with the magnetized planets form complex structures of magnetospheres. Boundaries of magnetospheres act as obstacles on the way of solar wind and it does not penetrate into the atmospheres of magnetized planets directly. At the boundaries it is incident on the planetary plasmas at different angles and in some regions it is almost parallel to the field lines. Since solar wind consists of two parts slow and fast (Lang 2001) and flows are not homogeneous everywhere, therefore we think that field-aligned shear flow is able to produce electrostatic instability pointed out long ago (D’Angelo 1965) at those boundary regions of the magnetospheres where wind flow is almost parallel to the field lines. In the presence of heavier stationary dust fluid, the electrons and ions of solar wind can sustain dust ion acoustic wave (DIAW) (Shukla and Silin 1992; Shukla and Mamun 2002) which has larger frequency compared to the usual ion acoustic wave (IAW). Research on ion acoustic wave was initiated long ago using Maxwellian velocity distribution for electrons (Davidson 1972; Rudakov and Sagdeev 1960). It has also been shown that IAW becomes an electromagnetic wave in an unmagnetized inhomogeneous plasma (Saleem 1996) and it couples with drift wave and Alfven wave in the magnetized plasma (Pottelette et al. 1990; Weiland 2000). Most of space (Amatucci 1999; Main et al. 2010; Gavrishchaka et al. 1998) and astrophysical (Havnes 1988; Lazarian and Yan 2002; Shan et al. 2008) plasmas have uniform and non-uniform flows. Laboratory plasmas also have flows and associated instabilities appear because of free energy available in the system (Sen et al. 2000; McGarthy and Maurer 1998).

It is difficult to attain and maintain the laboratory plasmas in Maxwellian state in general. On the other hand, flows of plasma species are very common in space plasmas and in the presence of such flows the charge particles may not follow Maxwellian distribution (Yoon 2005, 2018; Kourakis et al. 2012). The nonthermal distributions are now considered to be the stationary states arising naturally in space plasmas which have flows and nonuniformities. Nonthermal distributions have important effects on linear and nonlinear wave dynamics. For example, Cairns et al. (1995) showed that if electrons follow a nonthermal distribution (which is now called Cairns distribution) then the nonlinear ion acoustic waves produce both density humps and density dips contrary to usual KdV solitons with only density humps when electrons are assumed to follow Boltzmann distribution. Kappa (or nonthermal) distribution function for electrons in magnetosphere was observed long ago (Vasyliunas 1968) which has broader electron velocity distribution than Maxwellian. Several authors have presented detailed analysis on understanding the plasmas containing species with kinetic energies higher than the average thermal energy, and their consequent impacts on linear and nonlinear propagation of the waves in different plasma scenarios (Kourakis et al. 2012; Baluku et al. 2010; Lazar et al. 2018; Hellberg et al. 2009). Effects of electron beam propagation in a plasma having cold ions and kappa distributed electrons has also been investigated on ion acoustic solitary waves (Saini et al. 2010). Recently in a review article, the effects of kappa distribution of electrons on nonlinear ion acoustic waves in $O$-$H$ plasma of upper ionosphere have been pointed out (Saleem and Shan 2020).

In addition to kappa and Cairns distribution functions, $q$ non-extensive distribution was also proposed (Tsallis 1988) which has been discussed by many researchers in literature (Livadiotis and McComas 2009, 2011; Williams et al. 2013; Verheest et al. 2013). Electrostatic instabilities and nonlinear structures in the presence of field aligned shear flow have been investigated using Cairns-Tsallis distribution for electrons (Shan and Saleem 2017). Vertical sizes of 1-D and 2-D electrostatic solitons in $O$-$H$ plasma of upper ionosphere using nonextensive and trapped electrons have been estimated (Shan and Saleem 2018).

We expect that after attaining steady state with the incoming solar wind, the plasma of planetary dusty magnetospheres has non-Maxwellian electrons and if ion temperature $T_{i}$ is smaller than electron temperature $T_{e}$, then electrons may follow kappa ($\kappa$) or Cairns velocity distributions while the ions remain Maxwellian. Density concentration of dust particles and non-Maxwellian electrons have significant influence on both the electrostatic linear instability and formation of solitary structures. In case of Maxwellian electron velocity distribution the linear dispersion relation of DIAW in unmagnetized plasma for $T_{i}< T_{e}$ is given as follows (Shukla and Silin 1992; Shukla and Mamun 2002),

$$ \omega ^{2}=\frac{n_{i0}}{n_{e0}}\biggl(\frac{c_{s}^{2}k^{2}}{1+\lambda _{De}^{2}k^{2}}\biggr) $$

(1)

In this case Poisson equation is used to have dispersion in the waves. Here $c_{s}=(K_{B}T_{e}/m_{i})^{\frac{1}{2}}$ is phase speed of IAW, $\lambda _{De}=(K_{B}T_{e}/4\pi n_{e0}e^{2})^{\frac{1}{2}}$ is electron Debye length, $n_{i0}$ $(n_{e0})$ is the ion (electron) equilibrium density and quasi-neutrality demands $n_{i0}=n_{e0}+Z_{d}n_{d0}$ while $n_{d0}$ is the dust equilibrium density and $Z_{d}$ is the number of negative charges on the dust particle.

In magnetized plasma, quasi neutrality gives the linear dispersion relation of DIAW in the following form (Saleem 2018),

$$ \omega^{2} = \frac{n_{i0}}{n_{e0}} \biggl(\frac{c_{s}^{2}k_{z}^{2}}{1+\rho_{s}^{2} k_{\perp}^{2}} \biggr) $$

(2)

In this case dispersion occurs due to $\rho _{s}^{2}k_{\perp }^{2}\neq 0$ where $\rho _{s}=c_{s}/\Omega _{i}$ is the ions larmor radius at electron temperature and $\Omega _{i}=eB_{0}/cm_{i}$ is the ion gyro frequency.

In unmagnetized plasma, the dispersion term $\lambda _{De}^{2}k^{2}$ in Eq. (1) appears due to the use of Poisson equation when we do not assume quasi-neutrality. In magnetized plasma even if we assume quasi-neutrality, the dispersion in ion acoustic waves occurs through the term $\rho _{s}^{2}k_{\perp }^{2}$as given in Eq. (2). Since $\lambda _{De}^{2} << \rho _{s}^{2}$ because $v_{A}^{2} << c^{2}$ (where $v_{A}$ is Alfven wave speed and $c$ is speed of light), therefore quasi-neutrality is used in magnetized plasma.

Several authors have studied different aspects of dusty plasmas (Waksman et al. 2012; Poedts et al. 2000; Birk and Wiechen 2002; Pandey et al. 2012). Linear and nonlinear waves in plasmas having stationary and mobile dust have also been investigated (Onishchenko et al. 2002; Vranjes and Poedts 2010; Garai et al. 2014, 2015; Saleem and Haque 2004). More than a decade ago (Saleem 2006), solar wind interaction with dusty magnetospheres of planets and comets was considered, but the main effect of shear flow instability was neglected.

In the present investigation we shall use the non-Maxwellian Cairns and Kappa distributions for the electrons and analyze their effects on the linear shear flow driven instability and solitary electrostatic pulses formed by these waves in nonlinear regime. In the next section theoretical model is described. In Section 3, linear dispersion relation is written. Solution of nonlinear equations is presented in Section 4. In Section 5, the analytical results are applied to the dusty plasma of Saturn’s $F$-ring. The last Section contains summary of the work.

2 Theoretical model

We assume that ions have shear flow parallel to external magnetic field i.e. along $z$-axis such that $B_{0}=B_{0}\hat{z}$, $v_{i0}=v_{0}(x)\hat{z}$, $v_{0}(x)$ is the ions shear flow speed, and heavier dust particles are stationary. Cairn’s distribution for electrons is given as (Cairns et al. 1995),

$$\begin{aligned} f_{e}(v) =&\frac{n_{e0}}{(3\alpha +1)\sqrt{2\pi v_{e}^{2}}}\bigl[1+\alpha \bigl(v^{4}/v_{e}^{4}-2 \Phi \bigr)^{2}\bigr] \\ &\times\exp \bigl[-v^{2}/2v_{e}^{2}+ \Phi \bigr] \end{aligned}$$

(3)

where $\Phi =e\varphi /K_{B}T_{e}$ is the normalized potential, $n_{e0}$ is the equilibrium density, $v$ is the fluid speed, $v_{e}=\sqrt{K_{B}T_{e}/m_{e}}$ is the characteristic thermal velocity, $m_{e}$ is the electron temperature and $\alpha$ is a non-zero nonthermal parameter which is a measure of the degree of deviation from Maxwellian behavior of the Cairns distribution. Allowing $\alpha$ to vary from zero to infinity and integrating $f_{e}(v)$ over velocity space under appropriate boundary conditions, we obtain electron number density expression as,

$$ n_{e}=n_{e0}\bigl\{ 1+\beta _{1}\Phi +\beta _{2}\Phi ^{2}\bigr\} $$

(4)

In the limit $\Phi \ll 1$, we have $\beta _{1}=1-\beta _{0}$, $\beta _{2}=1/2$ and $\beta _{0}=4\alpha /(3\alpha +1)$ (Cairns et al. 1996). The value of $\beta _{0}$ is restricted between $0\leq$ $\beta _{0}<4/3$. It is to be noted that for larger values of $\beta _{0}$ the distribution function develops wings for higher velocities and becomes multi-peaked. Equation (4) reduces to Maxwell Boltzmann distribution for $\alpha =0$. The three-dimensional, isotropic Kappa distribution function (Summers and Thorne 1991, 1992; Shan and Haque 2012; Rehman et al. 2017) can be written as

$$ f_{\kappa e}(v)=\frac{n_{0}}{(\pi \kappa \theta _{e}^{2})^{\frac{3}{2}}}\frac{\Gamma (\kappa +1)}{\Gamma (\kappa -1/2)} \biggl(1+\frac{v_{e}^{2}}{\kappa \theta _{e}^{2}}\biggr)^{-(\kappa +1)}, $$

(5)

where $n_{0}$ is the species equilibrium number density, $\theta _{e}=\sqrt{((\kappa -3/2)/\kappa )2K_{B}T_{e}/m_{e}}$ is the effective thermal speed which is modified by the spectral index Kappa ($\kappa$), $T_{e}$ is the kinetic temperature, and $\Gamma (x)$ is the gamma function. Clearly, for a physically realistic thermal speed, the above mentioned distribution function is convergent for $\kappa >3/2$.

In order to obtain electron’s density expression, the distribution function (5) can be integrated over the velocity space (Hellberg et al. 2009) which yields,

$$ n_{e}=n_{e0}\biggl[1-\frac{e\varphi }{(\kappa -3/2)K_{B}T_{e0}} \biggr]^{-\kappa +1/2}. $$

(6)

For $e\varphi /(\kappa -3/2)K_{B}T_{e}<1$, we apply Taylor series expansion to obtain

$$ n_{e}=n_{e0}\bigl(1+K_{1}\Phi +K_{2}\Phi ^{2}\bigr), $$

(7)

and in this case coefficients of $\Phi$ and $\Phi ^{2}$ terms become,

$$ K_{1}=\frac{(\kappa -1/2)}{(\kappa -3/2)},\quad \text{and}\quad K_{2}= \frac{(\kappa ^{2}-1/4)}{2(\kappa -3/2)^{2}} $$

Now we consider ions equation of motion,

$$ (\partial _{t}+\mathbf{v}_{i}\cdot \nabla ) \mathbf{v}_{i}=\frac{e}{m_{i}}\biggl(\mathbf{E}+ \frac{1}{c}\biggr)\mathbf{v}\times \mathbf{B}-\mathbf{\nabla }p_{i} $$

(8)

where $m_{i}$, and $p_{i}=(n_{i}K_{B}T_{i})$ are the ionic mass and ionic pressure, respectively. The electric field $E$ and electrostatic potential $\varphi$ are linked $E=-\nabla \varphi$, whereas $e(c)$ is the magnitude of the electronic charge (the speed of light in vacuum) such that $\nabla =(0 , \partial _{y}, \partial _{z})$. In order to obtain the expression for component of ions velocity perpendicular to $B_{0}$, we take cross product of this equation with unit vector $\hat{z}$ which yields,

$$\begin{aligned} \mathbf{v}_{i\perp } \simeq& \frac{c}{B_{0}}\mathbf{E}_{\perp } \times \hat{z}-\frac{1}{\Omega _{i}}(\partial _{t}+ \mathbf{v}_{i}\cdot \nabla )\mathbf{v}_{i\perp } \times \hat{z} \\ &{}-\frac{{v}_{Ti}^{2}}{\Omega _{i}}\nabla \ln n_{i}\times \hat{z} = \mathbf{v}_{E}+\mathbf{v}_{P}+\mathbf{v}_{D} \end{aligned}$$

(9)

where $v_{Ti}=(K_{B}T_{i}/m_{i})^{\frac{1}{2}}$ is thermal speed of ions, $\Omega _{i}=eB_{0}/cm_{i}$ is the ions gyro-frequency. For low frequency waves using drift approximation $\mid \partial _{t}\mid <<\Omega _{i}$, we obtain

$$ \mathbf{v}_{i\perp }\simeq \mathbf{v}_{E}+ \mathbf{v}_{P}+\mathbf{v}_{D} $$

Here $D_{\mathbf{e}}=cT_{e}/eB_{0}$, the quantity $v_{E}=\frac{c}{B_{0}}E_{\perp }\times \hat{z}$ is the electric drift, whereas

$$ \mathbf{v}_{pi}=-\frac{D_{e}}{\Omega _{i}} \bigl[ \partial _{t}+\mathbf{v}_{0}(x)\cdot \mathbf{\nabla }+v_{iz}\partial _{z}+\mathbf{v}_{E}\cdot \mathbf{\nabla } \bigr] (1+T_{i}/T_{e})\mathbf{\nabla }_{\perp }\Phi $$

and

$$ \mathbf{v}_{Di}=-K_{B}T_{i}\nabla _{\perp }\ln n_{i}\times \hat{z}/m_{i} \Omega _{i} $$

are polarization and diamagnetic drift velocities, respectively. It should be noted that we are considering uniform density (i.e., $\mathbf{\nabla }n_{0}\mathbf{=0}$), therefore $\mathbf{v}_{Di}$ contains perturbed part of density. This term appears because we are not ignoring ions pressure effects because phase velocity of the wave is larger than ions thermal velocity due to $1<<n_{i0}/n_{e0}$ in dusty plasma. If Boltzmann density distribution for electrons is used, then we can obtain dispersion relation Eq. (2) in this limit (Saleem 2018) if ions temperature is ignored. It may be mentioned here that our theoretical model is also valid if we assume $T_{i}<<T_{e}$ and in this case $\mathbf{v}_{Di}$ term will disappear in Eq. (9).

Parallel components of ions equation of motion are written, respectively, as,

$$\begin{aligned} &(\partial _{t}+v_{0}\partial _{z}+ \mathbf{v}_{E}\cdot \nabla +v_{iz}\partial _{z})v_{iz}+\mathbf{v}_{E}\cdot \nabla v_{0} \\ &\quad =\frac{e}{m_{i}}E_{z}-v_{Ti}^{2} \partial _{z}\ln n_{i} \end{aligned}$$

(10)

Perturbation has been assumed to be electrostatic $E=-\nabla \varphi$, obliquely propagating relative to $B_{0}$ with $\mid \partial _{z}\mid <<\mid \nabla _{\perp }\mid$ and having phase speed in between electron (ion) thermal speeds such that $v_{Ti}<<\omega /k_{z}<<v_{Te}$ where $\omega$ is the frequency of the modified dust ion acoustic wave, $v_{Te}=(K_{B}T_{e}/m_{e})^{\frac{1}{2}}$ is the electrons thermal speed, and $\omega /k_{z}$ is the phase speed of the modified dust ion acoustic wave (mDIAW).

The ions continuity equation for $\mathbf{\nabla }\cdot \mathbf{v}_{E}=0$ can be expressed as,

$$\begin{aligned} &(\partial _{t}+v_{0}\partial _{z})n_{i}+n_{i0}( \partial _{z}v_{iz}+\nabla _{\perp }\cdot \mathbf{v}_{P})+\nabla n_{i}\cdot \mathbf{v}_{E} \\ &\quad + \partial _{z}(n_{i}v_{iz})=0 \end{aligned}$$

(11)

3 Linear dispersion relation

We assume that the wave propagates in the $yz$-plane with frequency $\omega$ making an angle with $\mathbf{B}_{0}$ such that $k_{z}<<k_{y}$ where $k_{z}(k_{y})$ is the parallel (perpendicular) component of the wave vector $\mathbf{k}$. In magnetized plasma, we can use quasi-neutrality $n_{i} \simeq (n_{e}+Z_{d} n_{d})$ which can be expressed as $(n_{i0} + n_{i}) \simeq (n_{e0}+n_{e}) + Z_{d} (n_{d0} +n_{d})$ whereas in this expression the quantities without the subscript naught (0) are the perturbed parts of densities of the species. Since we are investigating ion acoustic waves which have phase speed much greater than phase speed of dust acoustic waves in the plasma containing heavy dust fluid, therefore dust density fluctuations $(n_{d})$ are ignored. Then under equilibrium condition mentioned above, the quasi-neutrality expression in the presence of stationary dust becomes $n_{i} \sim n_{e}$ for fluctuating densities. We estimate $n_{i}$ using Eq. (11) along with Eqs. (9) and (10) whereas electron perturbed density $n_{e}$ is obtained from Eq. (4). In linear limit, perturbations are assumed to be proportional to $e^{i(k_{y}y+k_{z}z-\omega t)}$, and dispersion relation under quasi-neutrality turns out to be,

$$ \Omega _{0}^{2}=\biggl(\frac{n_{i0}}{n_{e0}}\biggr) \frac{c_{s}^{2}k_{z}^{2}}{(1+\frac{n_{i0}}{n_{e0}}\rho _{s}^{2}k_{y}^{2})} \biggl( 1+\frac{\beta _{1}n_{e0}\sigma _{i}}{n_{i0}}-\frac{k_{y}}{k_{z}}S_{i} \biggr) $$

(12)

where $\Omega _{0}=(\omega -k_{z}v_{0})$ is the Doppler shifted frequency of the wave, $S_{i}=v_{0}^{\prime }/\Omega _{i}$ is a shear flow parameter, $v_{0}^{\prime }=dv_{0}/dx$ and $\sigma _{i}=T_{i}/T_{e}$. The linear dispersion relation of DIAW is modified if $S_{i}<0$ or $\mid \frac{k_{y}}{k_{z}}S_{i}\mid <1$. Equation (12) is the same as Eq. (17) of Ref. (Saleem 1996). If the following condition

$$ \biggl(1+\frac{\beta _{1}n_{e0}\sigma _{i}}{n_{i0}}\biggr)< \frac{k_{y}}{k_{z}}S_{i} $$

(13)

holds, then instead of DIAW a purely growing instability appears. This non-resonant mode is similar to D’Angelo mode (D’Angelo 1965) but it has larger growth rate because $1< n_{i0}/n_{e0}$ holds in dusty plasmas, in general (Saleem and Ali 2017). When the wave attains larger amplitude, then a balance between dispersion and nonlinear wave breaking in $yz$-plane produces electrostatic solitons.

Linear dispersion relation of DIAW is modified because of the term containing $\beta _{1}$ in Eq. (12) for the case of Cairns distribution of electrons. On the other hand, whenever we consider Kappa distribution function of electrons, then the factor $\beta _{1}$ should be replaced by $K_{1}$ in the linear dispersion relation Eq. (12). Let us assume the linear flow profile $v_{0}=a_{0}x+b_{0}$ where $a_{0}$ and $b_{0}$ are constants, then $v_{0}^{\prime }=a_{0}$ and when the inequality Eq. (13) holds the RHS of Eq. (12) becomes negative. One obtains $\Omega _{0}=\pm i\gamma$ for $0<\gamma$, where $\gamma$ is a real quantity having frequency unit. In this case one of the roots give purely growing instability (D’Angelo 1965) and DIAW does not appear. On the other hand when $S_{i}<0$ or the inequality (13) is reversed, one obtains modified dust ion acoustic wave (mDIAW) in the presence of shear flow of ions. When the wave attains larger amplitude, then a balance between dispersion and nonlinear wave breaking in $yz$-plane produces electrostatic solitons.

4 Nonlinear analysis

To investigate the effects of non-thermal electrons on the development of electrostatic solitary pulses, we define a co-moving frame $\eta =y+\delta z-ut$ where $\delta <<1$ and $u$ is the speed of the solitons, because we are considering oblique propagation of the perturbation in yz-plane as has been mentioned in linear analysis. If we consider the $x$-dependence of perturbed quantities then convective derivative in nonlinear dynamics will appear as $(\mathbf{v}_{E}\cdot \nabla )\mathbf{v}_{E}\neq 0$ and vorticity in the plasma will be finite. In this case vortex structure may appear (Saleem 2018),

Parallel component of ion momentum equation (11) in $\eta$-frame is expressed in the following form as,

$$\begin{aligned} \frac{dv_{iz}}{d\eta }& =\frac{\delta c_{s}^{2}}{a}\frac{d\Phi }{d\eta }-\frac{c_{s}^{2}}{\Omega _{i}}\frac{dv_{0}}{dx}\frac{d\Phi }{d\eta }+ \frac{\delta }{2a}\frac{dv_{iz}^{2}}{d\eta } \\ & +\frac{\delta v_{Ti}^{2}}{a}\biggl\{ \frac{d(n_{i}/n_{i0})}{d\eta }-\frac{1}{2}\frac{d(n_{i}/n_{i0})^{2}}{d\eta }\biggr\} \end{aligned}$$

(14)

where $a=u-\delta v_{0}$. Ion continuity equation in $\eta$-frame is,

$$ \frac{dn_{i}}{d\eta }-n_{i0}\rho _{s}^{2} \frac{d^{3}\Phi }{d\eta ^{3}}-\frac{n_{i0}\delta }{a}\frac{dv_{iz}}{d\eta }= \frac{\delta }{a}\frac{d(n_{i}v_{iz})}{d\eta } $$

(15)

We can express $n_{i}$ in terms of $\Phi$ using quasi-neutrality $n_{i}\simeq n_{e}$. First we deal with the case of nonthermal electrons assuming that they follow Cairns distribution. In this case (14) can be written as,

$$ \frac{dv_{iz}}{d\eta }=\frac{c_{s}^{2}}{a}(\delta l_{1}-S_{i}) \frac{d\Phi }{d\eta }+\frac{\delta v_{ti}^{2}}{a}l_{2}\frac{d\Phi ^{2}}{d\eta }+ \frac{\delta }{2a}\frac{dv_{iz}^{2}}{d\eta } $$

where $l_{1}=(1+\beta _{1}T_{i}n_{e0}/T_{e}n_{i0})$ and $l_{2}=[\beta _{2}n_{e0}/n_{i0}-\beta _{1}^{2}(n_{e0}/n_{i0})^{2}/2]$. Integration of this equation using the boundary conditions $\Phi$, $v_{iz}\rightarrow 0$ as $\eta \rightarrow \pm \infty$ yields the integration constant to be zero. Thus we have,

$$ v_{iz}=\frac{c_{s}^{2}}{a}(\delta l_{1}-S_{i}) \Phi +\frac{\delta v_{ti}^{2}}{a}l_{2}\Phi ^{2}+ \frac{\delta v_{iz}^{2}}{2a} $$

(16)

In the next step, we take advantage of the small amplitude approximation and substitute the dominant first term on RHS of (16) in the term containing $v_{iz}^{2}$ and re-write it in the following form,

$$ v_{iz}\simeq R_{1}\Phi +R_{2}\Phi ^{2} $$

(17)

where $R_{1}=(\delta l_{1}-S_{i})c_{s}^{2}/a$, $R_{2}=\delta l_{2}v_{Ti}^{2}/a+\delta R_{1}^{2}/2a$. Since $\Phi$ is now a function of only $\eta$, therefore using Eqs. (15) and (17) along with quasi-neutrality, we write an ordinary differential equation in terms of $\Phi$ as,

$$ -\frac{d\Phi }{d\eta }+\frac{1}{2}A\Phi \frac{d\Phi }{d\eta }+B\rho _{s}^{2}\frac{d^{3}\Phi }{d\eta ^{3}}=0 $$

(18)

where $A=2P_{2}/P_{1}$, $B=n_{i0}/n_{e0}P_{1}\$such that

$$ P_{1}=(\beta _{1}-\delta n_{i0}R_{1}/an_{e0})\text{, }P_{2}= \biggl\{ \frac{n_{i0}\delta R_{2}}{n_{e0}a}+\frac{\beta _{1}\delta R_{1}}{a}-\beta _{2}\biggr\} $$

Note that the $\beta _{2}$-term in the expression of $P_{2}$ is smaller and hence can be neglected. Let $\xi =\eta /\rho _{s}$, then (18) becomes,

$$ -\frac{d\Phi }{d\xi }+A\Phi \frac{d \Phi }{d\xi }+B\frac{d ^{3}\Phi }{d\xi ^{3}}=0 $$

(19)

where $\xi =\eta /\rho _{s}$.

The equation differential equation (19) in $\xi$-frame admits soliton solution as,

$$ \Phi =\Phi _{0}\ \text{sech}^{2} ( \xi /W ) $$

(20)

where $\Phi _{0}=3/A$ is the maximum amplitude and $W=\sqrt{4B}$ is the width of the electrostatic solitons. Similar procedure is adopted to deal with kappa distribution of electrons to investigate the nonlinear solitary structures of DIAW as has been used for the case of Cairns distribution function. For the case of Kappa distribution, we substitute the Eq. (7) in quasi-neutrality which yields the same nonlinear differential equation (18) with modified nonlinear and dispersive coefficients $A$ and $B$, which become,

$$ A=2Q_{2}/Q_{1}\text{, }B=(n_{i0}/n_{e0})Q_{1} $$

(21)

In this case, the quantities $l_{1}$ and $l_{2}\$will be modified as $l_{1}^{\prime }=(1+K_{1}T_{i}n_{e0}/T_{e}n_{i0})$ and $l_{2}^{\prime }=[K_{2}n_{e0}/n_{i0}-K_{1}^{2}(n_{e0}/n_{i0})^{2}/ 2]$ for Kappa distributed electrons case, while the factors $P_{1}$ and $P_{2}\$have been changed to $Q_{1}$ and $Q_{2}$ as $Q_{1}=(K_{1}-\delta n_{i0}R_{1}/an_{e0})$, and $Q_{2}=\{n_{i0}\delta R_{2}/n_{e0}a+K_{1}\delta R_{1}/a-K_{2}\}$. However in this case, the expressions $R_{1}$ and $R_{2}$ will change into $R_{1}^{\prime }$ (with $l_{1}^{\prime }$) and $R_{2}^{\prime }$ (with $l_{2}^{\prime }$). The $\kappa$- distribution case reduces to Maxwell distribution case for $\kappa \rightarrow \infty$, and in this case we find the factor $K_{1}$ $\rightarrow 1$ while $K_{2}\rightarrow 1/2$ and hence electrons will be behaving as Maxwellian in this limit. The factors $l_{1}^{\prime }$ and $l_{2}^{\prime }$ will be modified as,

$$ l_{1}^{\prime \prime }=(1+T_{i}n_{e0}/T_{e}n_{i0})\text{ and }l_{2}^{\prime \prime }= \bigl[n_{e0}/2n_{i0}-(n_{e0}/n_{i0})^{2}/2 \bigr] $$

Also the factors appearing as $Q_{1}$ and $Q_{2}$ will be modified as follows,

$$ Q_{1}=(1-\delta n_{i0}R_{1}/an_{e0})\text{, }Q_{2}= \biggl\{ \frac{n_{i0}\delta R_{2}}{n_{e0}a}+\frac{\delta R_{1}}{a}-1/2\biggr\} $$

with $R_{1}^{\prime \prime }=(\delta l_{1}^{\prime \prime }-S_{i})c_{s}^{2}/a$, $R_{2}^{\prime \prime }=\delta l_{2}^{\prime \prime }v_{Ti}^{2}/a+\delta (R_{1}^{\prime \prime })^{2}/2a$. With these $Q_{1}$ and $Q_{2}$, the coefficients $A$ and $B$ are modified for the case of Maxwellian electrons.

The impact of larger values of $\kappa$ (approaching Maxwellian case) is shown in Fig. 2e. It shows that larger value of Mach number i.e. $M=0.46$ is needed to form solitary structures. All these Figs. 2a-2e are indicative of the fact that linear wave and solitary structures are modified significantly under the impact of superthermal electrons and shear flow.

5 Results and discussion

Now we apply our theoretical results to the dusty plasma of Saturn’s $F$-ring considering the region where electrons and ions have inhomogeneous flows parallel to field lines. The plasma parameters of this region are chosen (Shukla and Mamun 2002) as $B_{0}=0.1\ \text{G}$, $T_{e}=100\ \text{eV}$, $T_{i}=10\ \text{eV}$, $z_{d}=10^{3}$, $n_{d0}=10\ \text{cm}^{-3}$ and $n_{e0}=10^{3}\ \text{cm}^{-3}$. Corresponding to these parameters we find, $\Omega _{i}=957.9$ rad/S, $v_{ti}=3.09\times 10^{6}$ cm/S, $c_{s}=9.7\times 10^{6}$ cm/S, $\rho _{s}=1.02\times 10^{4}$, $\rho _{i}=3.23\times 10^{3}$, $v_{0n}=v_{0}/c_{s}$, ($n$ for normalized), $v_{0}=5\times 10^{6}$ cm/S, $\omega _{s}=c_{s}k_{z}$, $\Omega _{Ds}=\frac{n_{i0}}{n_{e0}}\omega _{s}=1.07\times 10^{4}$, $\omega _{0}=k_{z}v_{0}=0.1$. Thus the conditions $\omega _{s}<<\omega _{Ds}<<k_{z}v_{te}$ and $\omega _{Ds}<<\Omega _{i}$ hold for this low-frequency wave. Since $n_{i0}/n_{e0}=11$, therefore, the growth rate of this instability is large. If shear in flow is along negative $x$-direction then the frequency of the DIAW increases and it becomes modified dust ion acoustic wave (mDIAW) (Saleem 2006).

When mDIAW is excited by a physical mechanism, then the nonlinear interactions may give rise to solitary pulses. Presence of non-thermal and superthermal electrons has effect on both linear shear flow instability and the size of the structures.

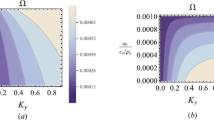
Using Cairns distribution, we have found that the growth rate $Im(\Omega _{0})$ of the instability increases for the larger values of $\alpha$, but this increase is small as shown in Fig. 1a. Figure 1b illustrates the increase in growth rate corresponding to an increase in dust concentration. Amplitude of the soliton decreases when $\alpha$ increases (Fig. 1c) or if the dust concentration rises (Fig. 1d).

Fig. 1a

The Doppler shifted growth rate from Eq. (12) is plotted against the wave number $k_{y}$ for $\alpha$ variation, with fixed parameters $\delta _{d}=Z_{d}n_{d0}/n_{e0}=11$, $k_{z}=10^{-4}$ $k_{y}$, $\sigma _{i}=0.1$, $\delta =0.12$, $S_{i}=0.008$

Fig. 1b

The Doppler shifted growth rate from Eq. (12) is plotted against the wave number $k_{y}$ for dust variation $\delta _{d}=Z_{d}n_{d0}/n_{e0}$ with fixed parameters $k_{z}=10^{-4}$ $k_{y}$, $\delta =0.12$, $\alpha =0.12$, $S_{i}=0.008$

Fig. 1c

The soliton profile for different values of $\alpha$ with fixed parameters $\delta=0.12$, $S_{i}=0.008$, $M=0.55$, $\delta_{d}=11$, and $v_{0n}=0.52$

Fig. 1d

The soliton profile for different values of $\delta _{d}$ with fixed parameters $\delta =0.12$, $S_{i}=0.008$, $M=0.53$, $\alpha =0.1$, and $v_{0n}=0.52$

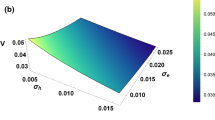
Assuming that the electrons follow kappa distribution, we plot Doppler shifted frequency $Im(\Omega _{0})$ vs $k_{y}$ in Fig. 2a choosing $v_{0}^{\prime }=8\times 10^{-3}$ $\Omega _{i}$ and fixed $k_{z}=10^{-3}$ $k_{y}$. The effect of nonthermal electrons on the linear instability is small, but the rise in dust concentration causes notable increase in the growth rate which is obvious in Fig. 2b. We ignore $K_{2}$ (being smaller term) in $R_{2}$ and plot solitary nonlinear pulses. Figure 2c shows that the increase in number density of the dust also decreases the amplitude of the soliton. The larger number of hot electrons (i.e. increase in $\kappa$-values) significantly modify the size of the nonlinear structure as shown in Fig. 2d.

Fig. 2a

The Doppler shifted growth rate from Eq. (12) is plotted against the wave number $k_{y}$ for $\kappa$ variation, with fixed parameters $\delta _{d}=11$, $k_{z}=10^{-4}$ $k_{y}$, $\delta =0.1$, $S_{i}=0.008$

Fig. 2b

The Doppler shifted growth rate from Eq. (12) is plotted against the wave number $k_{y}$ for dust variation $\delta _{d}=Z_{d}n_{d0}/n_{e0}$ with fixed parameters $k_{z}=10^{-4}$ $k_{y}$, $\kappa=5$, $S_{i}=0.008$

Fig. 2c

The soliton profile for different values of $\delta _{d}$ with fixed parameters $\delta =0.12$, $S_{i}=0.008$, $M=0.41$, $\kappa =5$, and $v_{0n}=0.52$

Fig. 2d

The soliton profile for different values of $\kappa$ with fixed parameters $\delta =0.12$, $S_{i}=0.008$, $M=0.43$, $\delta _{d}=11$, and $v_{0n}=0.52$

Fig. 2e

The soliton profile for different values of $\kappa$ with fixed parameters $\delta =0.12$, $S_{i}=0.008$, $M=0.46$, $\delta _{d}=11$, and $v_{0n}=0.52$

6 Summary

The effects of non-Maxwellian electrons on purely growing shear flow driven instability and the solitary pulses of modified dust ion acoustic wave (mDIAW) have been investigated. Cairns and Kappa distribution functions for electrons have been used. It is found that the non-thermal electrons contribute to the increase in the growth rate of shear flow instability. But this effect is small. However, the increase in concentration of dust particles has significant effect on this growth rate.

Increase in non-thermality of electrons (i.e. increase in $\alpha$ for the case of Cairns distributed electrons) reduces the amplitude of the electrostatic solitary pulses. However, increase in superthermality of electrons (i.e. decrease in values of $\kappa$ for the case of Kappa distributed electrons) increases the amplitude of the electrostatic solitary pulses The increase in number density of dust also increases the growth rate of linear instability and reduces the size of the structure. Thus number density of non-thermal electrons and stationary dust play similar role in increasing the growth rate of shear flow instability and destroying the solitary pulses. As an illustration, the results of analytical calculations have been applied to the plasma of Saturn’s F-ring. However, the theoretical results are general and are applicable to dusty plasmas in the inter-stellar clouds, magnetospheres of planets and cometary tails.