1 INTRODUCTION

Yttrium iron garnet films with a thickness from a few to tens of microns and length from a few to tens of centimeters have the properties of a ferromagnetic medium in the range from 1 to 20 GHz. This frequency range has been intensively studied due to the possibility of exciting exchange–dipole spin waves propagating along a film. One of the main results of such a study has been the discovery of spin-wave envelope solitons in ferromagnetic films [1–3]. While in the theory of linear waves one speaks of the effects of exchange and dipole–dipole interactions when the corresponding energies are comparable in an order of magnitude, the formation conditions and the structure of even weakly nonlinear solitons are largely determined by the competition between two types of spatial dispersion, the exchange and magnetostatic ones, rather than by their energies [4]. In addition, taking into account magnetostatics makes the problem not only non-one-dimensional but also nonlocal and requires correct consideration of the boundary conditions on the surface of a sample.

To analyze small-amplitude excitations in magnetic films, one usually applies the local nonlinear Schrödinger equation (NLSE):

$$i{{\partial }_{\tau }}\psi - \frac{{\partial _{k}^{2}\omega (k)}}{2}\partial _{X}^{2}\psi + g{\text{|}}\psi {{{\text{|}}}^{2}}\psi = 0.$$
(1)

The complex field ψ(X, τ) describes the space–time modulation of a traveling activation wave

$$\psi (X,\tau ){{e}^{{ikx + i\omega (k)t}}} \equiv \psi {{e}^{{i\theta }}},$$

where k and ω(k) are the wave number and the frequency of the main harmonic, x and t are the spatial coordinate and time, and X and τ are the corresponding slow variables. The deviations of normalized magnetization mi(x, t) (i = 1, 2, 3) from the equilibrium position (0, 0, 1) are expressed in terms of ψ(X, τ):

$${{m}_{1}} + i{{m}_{2}} = \psi {{e}^{{i\theta }}},\quad {{m}_{3}} \approx - {\text{|}}\psi {{{\text{|}}}^{2}}/2.$$
(2)

A simplified derivation of the NLSE assumes the differentiability of the dispersion law of linear spin waves ω(k) with respect to the wave number k. The interaction constant g of waves is traditionally calculated in the limit as k → 0 from the expansion of the ferromagnetic resonance frequency in terms of the oscillation amplitude [5]. However, in the region of small wave numbers (|kd| ≪ 1, d is the film thickness), the frequency ω(k) of exchange–dipole spin waves is a nondifferentiable function of k [6]. In [4, 7] the authors showed that, for wave numbers k and frequencies ω(k) satisfying the conditions

$$L \gg \lambda \gg {{k}^{{ - 1}}} > d \gg a,\quad \lambda \ll c{\text{/}}\omega ,\quad \partial _{k}^{2}\omega (k) \ne 0,$$
(3)

the nonlinear and nonlocal dynamic equations of a ferromagnetic plate in the absence of spin pinning at its surface and with correct consideration of the exchange and magnetostatic interactions can be reduced to the simplified local model (1). Here L is the size of the sample, λ is the characteristic size of magnetic inhomogeneities, a is the lattice constant, and c is the speed of light. The neighborhoods of zero dispersion points, where \(\partial _{k}^{2}\)ω(k) ≈ 0 (due to the competition between exchange and magnetostatic dispersions), as well as long-wavelength excitations with |kd| < 1, require separate consideration [4]. During a step-by-step derivation of the NLSE, the interaction constant of waves takes into account the inhomogeneities in the distribution of magnetization along the normal to the plate and nontrivially depends on the wave vector of the main harmonic and the plate thickness. As a result, one can describe the interaction features of spin waves with close values of nonzero wave vectors that are inhomogeneous across the thickness of the plate and propagate along the plate. These results allow one to pass from model (1) to observable quantities in a more detailed manner.

In sufficiently thin films with free surface spins only the lower branch of the spectrum of exchange–dipole waves with an almost uniform distribution of magnetization along the normal to the plane is excited by an alternating magnetic field [8]. In this branch, there exist large ranges of wave numbers (3) in which g > 0 and \(\partial _{k}^{2}\)ω(k) < 0. Hence, the Lighthill criterion [9]

$$g\partial _{k}^{2}\omega < 0,$$
(4)

holds, which allows the formation of bright exponential solitons from localized pulses of external action. In this case, model (1) is reduced by scaling transformations to the standard form of the focusing NLSE:

$$i{{\partial }_{t}}\psi + \partial _{x}^{2}\psi + 2{\text{|}}\psi {{{\text{|}}}^{2}}\psi = 0.$$
(5)

In the case of an infinite plate (–∞ < x < ∞), Eq. (5) is equivalent to the commutativity of two differential operators depending on a complex spectral parameter [10, 11]. Such a representation (U–V-pair) allows one to find a mapping of the solutions of model (5) to the scattering data of the auxiliary spectral problem. In the simplest case, when ψ(x, t) tends to zero as x → ±∞, the evolution of the scattering data is determined by linear equations and is explicitly calculated by the magnetization distribution ψ(x, t = 0) defined at the initial time. The inverse spectral transformation makes it possible to find a complete solution of the initial boundary value problem for NLSE (5) by the scattering data. Strictly speaking, these results are applicable only for unbounded samples. Therefore, the main applications of NLSE (5) and its generalization were found in nonlinear optics and fluid dynamics: in designing optical fiber communication lines and in the simulation of wave processes in water basins (see [12–15] and references cited there).

In the case of finite variation ranges of x, one cannot obtain a simple mapping of the initial and boundary conditions formulated for the initial fields to the scattering data. Nevertheless, the traditional inverse scattering problem method on the whole axis –∞ < x < ∞ allows one to solve initial boundary value problems for wave processes on the half-line 0 ≤ x < ∞ [16–19]. In the case of NLSE (5) for the field ψ(x, t) = χ(x, t) on the half-line 0 ≤ x < ∞, practically important boundary conditions

$$[{{\partial }_{x}}\chi - \beta \chi ]{{{\text{|}}}_{{x = + 0}}} = 0;$$
(6)
$$\chi \to 0,\quad {\text{and}}\quad {{\partial }_{x}}\chi \to 0\quad {\text{as}}\quad x \to + \infty .$$
(7)

turn out to be integrable.

The positive or negative surface anisotropy constant β determines the character of spin pinning at the edge of the film. From the physical viewpoint, the parameter β takes into account the single-ion anisotropy and/or the external magnetic field on the face x = 0 of the sample. The effective magnetic field and the anisotropy axis are directed along the normal to the developed surface of the film.

In the limiting case of β → 0, the first relation in (6) turns into the Neumann condition ∂xχ|x = +0 = 0 (free spins at the edge of the plate); in the formal limit as |β| → ∞, this relation reduces to the Dirichlet condition χ|x = +0 = 0 (complete spin pinning at the point x = 0).

In [16–19], the authors proposed a modification of the inverse scattering problem method for solving NLSE on the half-line for given initial perturbation χ(x, t = 0) and boundary conditions (6), (7). The integration scheme is analogous to the method of images used in solving linear boundary value problems of electrostatics with certain spatial symmetry. However, the above-cited works do not contain an analysis of multisolitons. For instance, in [19] the author discusses from the very beginning only dispersive waves without solitons. In the present work, we analyze the initial boundary value problem in a semi-infinite ferromagnetic film in the presence of spin waves and solitons. We show that solitons near the boundary of the film have qualitatively new properties that are absent in the infinite medium. We study the changes in the dynamic properties and the structure of solitons for different degrees of spin pinning at the boundary x = 0 of the sample and obtain new conservation laws for nonlinear collective excitations in a semi-infinite film.

The article is organized as follows. In Section 2, we give formulas from [16, 17] that are necessary for the theoretical description of the nonlinear dynamics of a semi-infinite ferromagnetic film. Section 3 gives a solution of the initial boundary value problem for the NLSE on the half-line. The advantage of the method consists not only in the direct relation to the conventional integration scheme of the NLSE on the interval –∞ < x < ∞ [11], but also in that, in contrast to other approaches [18, 19], it allows generalization and opens up the possibility of a detailed analysis of quasi-one-dimensional solitons and dispersive waves in semi-infinite samples with integrable boundary conditions [20] within the basic Landau–Lifshitz models for the Heisenberg ferromagnet and for ferromagnets with anisotropy quadratic in magnetization [4].

In Section 4 we obtain explicit formulas for soliton excitations in a semi-infinite plate. We show that there exist two classes of solitons. Multisolitons of the first class are localized near the edge x = 0 of the film and represent near-boundary oscillations of magnetization with specific frequency and amplitude properties. The second class consists of moving particle-like objects that are elastically reflected from the edge of the film. At large distances from the edge of the film, these objects are transformed into precessing magnetic solitons, typical for an infinite medium, that elastically collide with each other.

In Section 5, we find a series of local integrals of motion for a semi-infinite ferromagnetic film each of which represents the additive sum of contributions of solitons and quasiparticles of the continuous spectrum of spin waves. We establish additional conservation laws that ensure the localization of solitons near the boundary of a sample or their reflection from the boundary.

2 STATEMENT OF THE PROBLEM

Recall that, in solving the initial boundary value problem for the NLSE on the whole axis   –∞ < x < ∞, it is assumed that the field ψ(x, t) is differentiable the necessary number of times with respect to the variables x and t. Then Eq. (5) is equivalent to the commutativity of two operators [11],

$$[{{\partial }_{x}} - U(\lambda ),{{\partial }_{t}} - V(\lambda )] = 0,$$
(8)

where

$$U(\lambda ) = - \frac{{i\lambda }}{2}{{\sigma }_{3}} + i(\psi {\text{*}}{{\sigma }_{ + }} + \psi {{\sigma }_{ - }}),$$
$$\begin{gathered} V(\lambda ) = i{{\sigma }_{3}}\left( {\frac{{{{\lambda }^{2}}}}{2} - \,{\text{|}}\psi {{{\text{|}}}^{2}}} \right) \\ - \,[({{\partial }_{x}}\psi - i\lambda \psi ){{\sigma }_{ - }} - ({{\partial }_{x}}\psi {\text{*}} + i\lambda \psi {\text{*}}){{\sigma }_{ + }}], \\ \end{gathered} $$

σi (i = 1, 2, 3) are the Pauli matrices, σ± = (σ1 ± iσ2)/2, and λ is a complex spectral parameter. Representation (8) can be rewritten in the integrated form, using the translation matrix T0(x, y, λ) along the x axis from point y to point x. Henceforth, when it does not cause confusion, we do not indicate dependence on time t. The matrix T0(x, y, λ) satisfies the equations [11]

$$\begin{gathered} {{\partial }_{x}}{{T}_{0}}(x,y,\lambda ) = U(x,\lambda ){{T}_{0}}(x,y,\lambda ), \\ {{\partial }_{y}}{{T}_{0}}(x,y,\lambda ) = - {{T}_{0}}(x,y,\lambda )U(y,\lambda ); \\ {{\partial }_{t}}{{T}_{0}}(x,y,\lambda ) = V(x,\lambda ){{T}_{0}}(x,y,\lambda ) - {{T}_{0}}(x,y,\lambda )V(y,\lambda ) \\ \end{gathered} $$
(9)

with the conditions T0(x, x, λ) = I and detT0(x, y, λ) = 1 and has the superposition property

$${{T}_{0}}(x,z,\lambda ){{T}_{0}}(z,y,\lambda ) = {{T}_{0}}(x,y,\lambda ).$$

In particular, the relation T0(x, y, λ) = \(T_{0}^{{ - 1}}\)(y, x, λ) holds. The matrix functions U(λ) and V(λ) have a special form:

$$U{\text{*}}(\lambda {\text{*}}) = {{\sigma }_{2}}U(\lambda ){{\sigma }_{2}},\quad V{\text{*}}(\lambda {\text{*}}) = {{\sigma }_{2}}V(\lambda ){{\sigma }_{2}}.$$
(10)

Therefore, Eqs. (9) imply the involution property

$$T_{0}^{*}(x,y,\lambda {\text{*}}) = {{\sigma }_{2}}{{T}_{0}}(x,y,\lambda ){{\sigma }_{2}}.$$
(11)

Let us proceed to the consideration of the NLSE (5) for the field ψ(x, t) = χ(x, t) on the half-line 0 ≤ x < ∞ for boundary conditions (6), (7). To include this problem in the scheme of the inverse problem method, we extend the field χ(x, t) to the whole axis in an even way. To this end, we define ψ(x, t) as a continuous piecewise differentiable function

$$\psi (x,t) = \left\{ \begin{gathered} \chi (x,t),\quad x \geqslant 0, \hfill \\ \chi ( - x,t),\quad x < 0. \hfill \\ \end{gathered} \right.$$
(12)

The function ψ(x, t) is continuous at the point x = 0:

$$\psi (x = + 0,t) = \psi (x = - 0,t) = \chi (x = 0,t),$$

but its first derivative experiences a jump [16, 17]:

$${{\partial }_{x}}\psi {{{\text{|}}}_{{x = + 0}}} - {{\partial }_{x}}\psi {{{\text{|}}}_{{x = - 0}}} = 2{{\partial }_{x}}\chi (x = + 0,t).$$

These relations allow us to consider the previous boundary condition (6) as additional constraint on the field ψ(x, t) at the point x = 0:

$$\Delta \psi {{{\text{|}}}_{{x = 0}}} = 0,\quad [\Delta {{\partial }_{x}}\psi - 2\beta \psi ]{\kern 1pt} {\kern 1pt} {{{\text{|}}}_{{x = 0}}} = 0$$
(13)

that are analogous to similar constraints in the procedure of integration of the linearized NLSE on the half-line 0 ≤ x < ∞ by the image method. Here Δ f  |x = 0 = f(x = +0) – f(x = –0).

We can verify by direct calculation that the constraint (13) is equivalent to the relation [20]

$${{V}_{ + }}(\lambda )K(\lambda ) - K(\lambda ){{V}_{ - }}(\lambda ) = 0,$$
(14)

where V±(λ) ≡ V(λ)|x = ±0, K(λ) = λI + iβσ3, and I is the identity matrix. To take into account the relation (14), we modify T0(x, y, λ) and introduce a new translation matrix T(x, y, λ) [16],

$$\begin{gathered} T(x,y,\lambda ) \\ = \left\{ \begin{gathered} {{T}_{0}}(x,y,\lambda ),\quad xy > 0, \hfill \\ {{T}_{0}}(x, + 0,\lambda )K(\lambda ){{T}_{0}}( - 0,y,\lambda ),\quad x > 0 > y, \hfill \\ {{T}_{0}}(x, - 0,\lambda ){{K}^{{ - 1}}}(\lambda ){{T}_{0}}( + 0,y,\lambda ),\quad x < 0 < y, \hfill \\ \end{gathered} \right. \\ \end{gathered} $$
(15)

which includes the factors K(λ) and K–1(λ). From representation (15) we conclude that the new translation matrix is not unimodular:

$$\det T(x,y,\lambda ) = {{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{({\text{sgn}}x - {\text{sgn}}y)/2}}}.$$
(16)

It satisfies the relations

$$\begin{gathered} T(x,x,\lambda ) = I\quad {\text{for}}\quad x \ne 0, \\ T(x,y,\lambda ) = {{T}^{{ - 1}}}(y,x,\lambda )\quad {\text{for}}\quad x \ne y \\ \end{gathered} $$
(17)

and

$$T( + 0, - 0,\lambda ) = {{T}^{{ - 1}}}( - 0, + 0,\lambda ) = K(\lambda ).$$
(18)

When x ≠ 0 and y ≠ 0, taking into account (14) and (15), we obtain the following differential equations for T(x, y, λ):

$$\begin{gathered} {{\partial }_{x}}T(x,y,\lambda ) = U(x,\lambda )T(x,y,\lambda ), \\ {{\partial }_{y}}T(x,y,\lambda ) = - T(x,y,\lambda )U(y,\lambda ); \\ {{\partial }_{t}}T(x,y,\lambda ) = V(x,\lambda )T(x,y,\lambda ) - T(x,y,\lambda )V(y,\lambda ), \\ \end{gathered} $$
(19)

which are the same as Eqs. (9) for an infinite plate. This allows us to include the boundary value problem (6), (7) for the NLSE (5) on the half-line 0 ≤ x < ∞ in the scheme of the inverse scattering problem on the whole axis –∞ < x < ∞. At the same time, the specificity of extending the field ψ(x, t) (12) leads to the modification of the calculations. Let us dwell on this in more detail.

3 INTEGRATION OF THE NLSE ON THE HALF-LINE BY THE IMAGE METHOD

3.1 Direct Scattering Problem

Following the scheme of the inverse scattering problem on the whole axis –∞ < x < ∞ [11], we introduce the matrix functions

$${{T}_{ \pm }}(x,t,\lambda ) = \mathop {\lim }\limits_{y \to \pm \infty } \left[ {T(x,y,\lambda )\exp \left( { - \frac{{i\lambda y}}{2}{{\sigma }_{3}}} \right)} \right]$$
(20)

which are the Jost basis solutions of the auxiliary linear system [11, 16]

$${{\partial }_{x}}{{T}_{ \pm }} = U{{T}_{ \pm }}.$$
(21)

The asymptotic behavior of these solutions

$${{T}_{ \pm }}(x,t,\lambda ) \to \exp \left( { - \frac{{i\lambda x{{\sigma }_{3}}}}{2}} \right)\quad {\text{as}}\quad x \to \pm \infty $$

is consistent with condition (7).

We can easily verify that, for x ≥ 0, the matrix p(x, t) in the expansion of the Jost solution T+(x, t, λ) in inverse powers of λ (as λ → ∞),

$${{T}_{ + }}(x,\lambda ) = \left( {I + \frac{{p(x,t)}}{\lambda } + ...} \right)\exp \left( { - \frac{{i\lambda x{{\sigma }_{3}}}}{2}} \right),$$

satisfies the relation

$$[{{\sigma }_{3}},p] = 2(\chi {\text{*}}{{\sigma }_{ + }} + \chi {{\sigma }_{ - }}).$$

Hence we immediately obtain an explicit solution of NLSE (5) for x ≥ 0 in terms of the matrix element [T+(x, t, λ)]21:

$$\chi (x,t) = - \mathop {\lim }\limits_{\lambda \to \infty } \left[ {{{{[{{T}_{ + }}(x,t,\lambda )]}}_{{21}}}\exp \left( {\frac{{i\lambda x}}{2}} \right)\lambda } \right].$$
(22)

The evenness ψ(x, t) = ψ(–x, t) (12) leads to an additional symmetry of the matrices U and V:

$$\begin{gathered} U(x,\lambda ) = - {{\sigma }_{3}}U( - x, - \lambda ){{\sigma }_{3}}, \\ V(x,\lambda ) = {{\sigma }_{3}}V( - x, - \lambda ){{\sigma }_{3}}, \\ \end{gathered} $$

with regard to which system (19) implies the proportionality of the matrix functions T(x, y, λ) and σ3T(‒x, –y, –λ)σ3. The proportionality factor is fixed by equality (18):

$$\begin{gathered} T(x,y,\lambda ) = {\text{sgn}}(xy){{\sigma }_{3}}T( - x, - y, - \lambda ) \\ \times \,{{\sigma }_{3}}{{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{({\text{sgn}}x - {\text{sgn}}y)/2}}},\quad \lambda \in R. \\ \end{gathered} $$
(23)

Here we used the relation

$${{K}^{{ - 1}}}(\lambda ) = - \frac{{K( - \lambda )}}{{{{\lambda }^{2}} + {{\beta }^{2}}}}.$$

Since K*(λ*) = σ2K(λ)σ2, formulas (11) and (15) preserve the previous reduction for the new translation matrix:

$$T{\text{*}}(x,y,\lambda {\text{*}}) = {{\sigma }_{2}}T(x,y,\lambda ){{\sigma }_{2}}.$$
(24)

From (16), (23), and (24) we obtain the key properties of the Jost functions for λ ∈ R:

$$\begin{gathered} \det {{T}_{ \pm }}(x,\lambda ) = {{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{({\text{sgn}}x \mp 1)/2}}}, \\ {{T}_{ \pm }}(x,\lambda ) = \pm {\text{sgn}}x{{\sigma }_{3}}{{T}_{ \mp }}( - x, - \lambda ){{\sigma }_{3}}{{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{({\text{sgn}}x \mp 1)/2}}}, \\ T{\text{*}}(x,\lambda ) = {{\sigma }_{2}}T(x,\lambda ){{\sigma }_{2}}. \\ \end{gathered} $$
(25)

On the real λ axis, the fundamental solutions are determined simultaneously; therefore, they are related by the transition matrix T(λ):

$${{T}_{ - }}(x,\lambda ) = {{T}_{ + }}(x,\lambda )T(\lambda ),$$
(26)

whose algebraic structure is determined by the reductions (25):

$$\begin{gathered} T(\lambda ) = \left( {\begin{array}{*{20}{c}} {a(\lambda )}&{ - \bar {b}(\lambda )} \\ {b(\lambda )}&{\bar {a}(\lambda )} \end{array}} \right), \\ a(\lambda )\bar {a}(\lambda ) + b(\lambda )\bar {b}(\lambda ) = {{\lambda }^{2}} + {{\beta }^{2}}, \\ \bar {a}(\lambda ) = a{\text{*}}(\lambda ),\quad \bar {b}(\lambda ) = b{\text{*}}(\lambda ), \\ a{\text{*}}( - \lambda ) = - a(\lambda ),\quad b( - \lambda ) = - b(\lambda ),\quad \lambda \in R. \\ \end{gathered} $$
(27)

Introduce the notation \(T_{ \pm }^{{(i)}}\) for the ith column of the matrix T± = (\(T_{ \pm }^{{(1)}}\), \(T_{ \pm }^{{(2)}}\)). The columns \(T_{ - }^{{(1)}}\)(x, λ) and \(T_{ + }^{{(2)}}\)(x, λ) of the Jost solutions are analytically continued from the real axis to the domain Imλ > 0, and the columns \(T_{ - }^{{(2)}}\)(x, λ) and \(T_{ + }^{{(1)}}\)(x, λ) are analytical functions in the lower half-plane Imλ < 0 except, possibly, simple poles of the matrix T+(x, λ) for x < 0 at the points λ = ±iβ, which are inherited from the matrix K–1(λ).

From (26) we obtain a representation for a(λ) in the form

$$\begin{gathered} a(\lambda ) = \frac{{\det [T_{ - }^{{(1)}}(x,\lambda ),T_{ + }^{{(2)}}(x,\lambda )]}}{{\det {{T}_{ + }}(x,\lambda )}} \\ = {{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{(1 - {\text{sgn}}x)/2}}}\det [T_{ - }^{{(1)}}(x,\lambda ),T_{ + }^{{(2)}}(x,\lambda )]. \\ \end{gathered} $$
(28)

This implies that the function a(λ) admits an analytical continuation to the upper half-plane Imλ > 0, where it generally has zeros that are assumed to be simple. Moreover, this function may have a zero at the point λ = i|β| (see (15), (20), and (28)). We can show that an element \(\bar {a}\)(λ) of the transition matrix is continued from the real axis to the domain Imλ < 0, where it is expressed in terms of a(λ*): \(\bar {a}\)(λ) = a*(λ*).

The reduction a*(–λ) = –a(λ) (27) is transferred from the real axis to the domain Imλ > 0, where it takes the form

$$a{\text{*}}( - \lambda {\text{*}}) = - a(\lambda ).$$
(29)

According to (29), the zeros of the function a(λ) either appear in pairs,

$$\begin{gathered} {{\lambda }_{j}} = \{ {{\lambda }_{k}}, - \lambda _{k}^{*}\} ,\quad \operatorname{Im} {{\lambda }_{k}} > 0, \\ k = 1,2,...,N,\quad j = 1,2,...,2N; \\ \end{gathered} $$
(30)

or are purely imaginary,

$${{\lambda }_{j}} = \{ i{{\nu }_{s}}\} ,\quad {{\nu }_{s}} > 0,\quad s = 1,2,...,M.$$
(31)

If a(λi) = 0, then we conclude from (28) that the columns \(T_{ - }^{{(1)}}\)(x, λj) and \(T_{ + }^{{(2)}}\)(x, λj) are proportional:

$$T_{ - }^{{(1)}}(x,{{\lambda }_{j}}) = \gamma ({{\lambda }_{j}})T_{ + }^{{(2)}}(x,{{\lambda }_{j}}).$$
(32)

The continuation of the composition of the last two equalities in (25) to the complex λ plane gives a relation

$$\begin{gathered} {{T}_{ \pm }}(x,\lambda ) = \pm {\text{sgn}}x{{\sigma }_{1}}T_{ \mp }^{*}( - x, - \lambda {\text{*}}){{\sigma }_{1}} \\ \, \times {{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{({\text{sgn}}x \mp 1)/2}}}, \\ \end{gathered} $$
(33)

where the values of λ are chosen in the analyticity domains of the corresponding columns. In particular, from (33) we obtain

$$\begin{gathered} T_{ - }^{{(1)}}(x,\lambda ) = - {\text{sgn}}x{{\sigma }_{1}}T_{ + }^{{(2)*}}( - x, - \lambda {\text{*}}){{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{({\text{sgn}}x + 1)/2}}}, \\ T_{ + }^{{(2)}}(x,\lambda ) = {\text{sgn}}x{{\sigma }_{1}}T_{ - }^{{(1)*}}( - x, - \lambda {\text{*}}){{[{{\lambda }^{2}} + {{\beta }^{2}}]}^{{({\text{sgn}}x - 1)/2}}}, \\ \end{gathered} $$
(34)

where Imλ > 0.

Using (32) and (34), we derive a relation between the normalization constants:

$$\gamma ({{\lambda }_{k}})\gamma {\text{*}}( - \lambda _{k}^{*}) = - (\lambda _{k}^{2} + {{\beta }^{2}}),\quad k = 1,2,...,N;$$
(35)
$${\text{|}}\gamma (i{{\nu }_{s}}){{{\text{|}}}^{2}} = \nu _{s}^{2} - {{\beta }^{2}} > 0,\quad s = 1,2,...,M.$$
(36)

The constraint (36) is valid only for νs > |β|.

In the limit of large λ, the Jost functions have the following asymptotics [16]:

$$\begin{gathered} {{T}_{ + }}(x,\lambda ) = \exp \left( { - \frac{{i\lambda x}}{2}{{\sigma }_{3}}} \right)[I + o(1)],\quad x > 0; \\ {{T}_{ + }}(x,\lambda ) = {{\lambda }^{{ - 1}}}\exp \left( { - \frac{{i\lambda x}}{2}{{\sigma }_{3}}} \right)[I + o(1)],\quad x < 0; \\ {{T}_{ - }}(x,\lambda ) = \lambda \exp \left( { - \frac{{i\lambda x}}{2}{{\sigma }_{3}}} \right)[I + o(1)],\quad x > 0; \\ {{T}_{ - }}(x,\lambda ) = \exp \left( { - \frac{{i\lambda x}}{2}{{\sigma }_{3}}} \right)[I + o(1)],\quad x < 0. \\ \end{gathered} $$
(37)

The element a(λ) of the transition matrix is recovered by its zeros, poles, the asymptotic behavior for large λ, and the reflection coefficient b(λ) [11, 16]:

$$\begin{gathered} a(\lambda ) = (\lambda + i\alpha )\prod\limits_{s = 1}^M {\left( {\frac{{\lambda - i{{\nu }_{s}}}}{{\lambda + i{{\nu }_{s}}}}} \right)} \prod\limits_{k = 1}^N {\frac{{(\lambda - {{\lambda }_{k}})(\lambda + \lambda _{k}^{*})}}{{(\lambda + {{\lambda }_{k}})(\lambda - \lambda _{k}^{*})}}} \\ \times \exp \left( {\frac{1}{{2\pi i}}\int\limits_{ - \infty }^{ + \infty } {{\text{d}}\mu \frac{{\ln [1 - \,{\text{|}}b(\mu ){{{\text{|}}}^{2}}{{{({{\mu }^{2}} + {{\beta }^{2}})}}^{{ - 1}}}]}}{{\mu - \lambda }}} } \right), \\ \operatorname{Im} \lambda > 0,\quad {{\alpha }^{2}} = {{\beta }^{2}}. \\ \end{gathered} $$
(38)

The numbers N and M in (38) define, respectively, the number of complex (30) and purely imaginary (31) zeros of the coefficient a(λ).

To specify the relation between the parameter α and the anisotropy constant β in (38), we construct an appropriate representation for the elements of the transition matrix. Such a representation follows from (26) with regard to (15) in the limit as x → +0:

$$T(\lambda ) = T_{ + }^{{ - 1}}( + 0,\lambda )K(\lambda ){{T}_{ - }}( - 0,\lambda ).$$
(39)

Using (33), we express T–(–0, λ) in terms of T+(+0, λ) for x → +0,

$${{T}_{ - }}( - 0,\lambda ) = {{\sigma }_{1}}T_{ + }^{*}( + 0, - \lambda {\text{*}}){{\sigma }_{1}},$$

and rewrite (39) as

$$T(\lambda ) = T_{ + }^{{ - 1}}( + 0,\lambda )(\lambda + i\beta {{\sigma }_{3}}){{\sigma }_{1}}T_{ + }^{*}( + 0, - \lambda {\text{*}}){{\sigma }_{1}}.$$
(40)

Taking into account that detT+(+0, λ) = 1, from (40) we obtain formulas for the elements of the transition matrix that are useful for further analysis:

$$\begin{gathered} a(\lambda ) = (\lambda + i\beta ){{[{{T}_{ + }}( + 0,\lambda )]}_{{22}}}[{{T}_{ + }}( + 0, - \lambda {\text{*}})]_{{22}}^{*} \\ - \,(\lambda - i\beta ){{[{{T}_{ + }}( + 0,\lambda )]}_{{12}}}[{{T}_{ + }}( + 0, - \lambda {\text{*}})]_{{12}}^{*}, \\ \operatorname{Im} \lambda > 0; \\ \end{gathered} $$
(41)
$$\begin{gathered} b(\lambda ) = - (\lambda + i\beta ){{[{{T}_{ + }}( + 0,\lambda )]}_{{21}}}[{{T}_{ + }}( + 0, - \lambda {\text{*}})]_{{22}}^{*} \\ + \,(\lambda - i\beta ){{[{{T}_{ + }}( + 0,\lambda )]}_{{11}}}[{{T}_{ + }}( + 0, - \lambda {\text{*}})]_{{12}}^{*}, \\ \lambda \in R. \\ \end{gathered} $$
(42)

Recall that a(λ) is an analytical function in the upper half-plane of the parameter λ. In (41) it is expressed in terms of the elements of the column \(T_{ + }^{{(2)}}\)(λ), which are analytical in the same domain. On the contrary, the function b(λ) does not have any definite properties of analyticity and is defined only for λ ∈ R. Therefore, on the right-hand side of (42), we should take the limits of the components of \(T_{ + }^{{(2)}}\)(λ) and \(T_{ + }^{{(1)}}\)(λ) from their domains Imλ > 0 and Imλ < 0 to the contour –∞ < λ < ∞.

In the limit as λ → +i0, representation (41) gives the following value with regard to the last formula in (25):

$$a(\lambda = 0) = i\beta \det {{T}_{ + }}( + 0,\lambda ) = i\beta .$$

On the other hand, in view of the evenness of the function |b(μ)|2, we obtain

$$a(\lambda = 0) = i\alpha {{( - 1)}^{M}}$$

from the dispersion relation (38). Thus, the relation between the parameters α and β is given by the equality

$$\beta = \alpha {{( - 1)}^{M}},$$
(43)

which depends on the number of imaginary zeros of the coefficient a(λ).

Using the auxiliary linear equation (21), we have constructed a mapping of the solutions of the original initial boundary value problem for the NLSE on the half-line to the complete set of scattering data. This set contains the spectral densities b(λ), where

$$ - \infty < \lambda < + \infty ,$$

the discrete zeros λj of the coefficient a(λ) (Imλj > 0), and the normalization constants γ(λj) (j = 1, 2, …, 2N + M). In the new variables, the problem of integration of the NLSE reduces to the solution of linear problems. The last equation in (19) implies a typical dependence of the scattering data on time:

$$\begin{gathered} a(t,\lambda ) = a(0,\lambda ),\quad b(t,\lambda ) = b(0,\lambda ){{e}^{{ - i{{\lambda }^{2}}t}}}, \\ \gamma ({{\lambda }_{j}},t) = \gamma (0,{{\lambda }_{j}}){{e}^{{ - i\lambda _{j}^{2}t}}}. \\ \end{gathered} $$
(44)

The values of the integration constants b(0, λ), λj, and γ(0, λj) are obtained from Eq. (21) by a given initial distribution of magnetization χ(x, t = 0).

3.2 Inverse Scattering Problem

The spectral function b(λ, t) parameterizes spin-wave trains that spread in time due to the dominance of dispersion phenomena over the effects of compression of wave packets due to the interaction of harmonics. The zeros λj of the coefficient a(λ) parameterize structurally stable particle-like objects—solitons. In the absence of dispersive waves, long-lived magnetic solitons correspond to the coefficient a(λ) with zeros under the condition b(λ) = \(\bar {b}(\lambda )\) ≡ 0.

To theoretically describe the evolution of the initial magnetization distribution in a semi-infinite plate with boundary conditions (6), (7), we should pass from the scattering data to the observable quantity χ(x, t). A specificity of the works [16, 17] consists in that the inverse mappings on the intervals

$$0 < x < \infty \quad {\text{and}}\quad - \infty < x < 0$$

turn out to be different and can be considered independently. Although the finally constructed solutions of the NLSE, the real one for x > 0 and the fictitious one for x < 0, are related by symmetry (12), the corresponding Jost functions do not have such a property.

To construct the sought solutions ψ(x, t) = χ(x, t) of the Cauchy problem for the NLSE (5) with the boundary conditions (6), (7) on the interval 0 < x < ∞, we proceed from the first column of the matrix relation (26) of the Jost functions on the real λ axis. We write the corresponding equality in a form convenient for further calculations:

$$\begin{gathered} \frac{{T_{ - }^{{(1)}}(x,\lambda )}}{{a(\lambda )}}\exp \left( {\frac{{i\lambda x}}{2}} \right) - \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right) \\ = T_{ + }^{{(1)}}(x,\lambda )\exp \left( {\frac{{i\lambda x}}{2}} \right) - \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right) \\ + \,T_{ + }^{{(2)}}(x,\lambda )r(\lambda )\exp \left( {\frac{{i\lambda x}}{2}} \right),\quad \lambda \in R, \\ \end{gathered} $$
(45)

where r(λ) = b(λ)/a(λ). For now, we omit the dependence on time t.

Recall that the vector function \(T_{ - }^{{(1)}}\)(x, λ)a‒1(λ) × exp(iλx/2) is analytical in the domain Imλ > 0 everywhere except the poles, which coincide with the zeros of the coefficient a(λ) (38). In the general case, the positions of these zeros are determined by formulas (30) and (31). For α < 0, the element a(λ) has an additional special zero λ = i|α| in the domain Imλ > 0. The function \(T_{ + }^{{(1)}}\)(x, λ)exp(iλx/2) is analytical in the lower half-plane of λ. The asymptotic behavior of these functions for x > 0 and λ → ∞ is given by the formulas (see (37) and (38))

$$\begin{gathered} \frac{{T_{ - }^{{(1)}}(x,\lambda )}}{{a(\lambda )}}\exp \left( {\frac{{i\lambda x}}{2}} \right) - \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right) = O\left( {\frac{1}{\lambda }} \right), \\ T_{ + }^{{(1)}}(x,\lambda )\exp \left( {\frac{{i\lambda x}}{2}} \right) - \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right) = O\left( {\frac{1}{\lambda }} \right). \\ \end{gathered} $$
(46)

The construction of linear integral equations of the inverse scattering problem for the NLSE on the half-line (for 0 < x < ∞) differs from that on the whole axis [10] only by the presence of additional reductions and the appearance of a special zero λ = i|α| with α < 0 of the function a(λ). Let us discuss what this leads to.

Consider a piecewise analytical function of the parameter λ:

$$F(x,\lambda ) = \left\{ \begin{gathered} \frac{{T_{ - }^{{(1)}}(x,\lambda )}}{{a(\lambda )}}\exp \left( {\frac{{i\lambda x}}{2}} \right),\quad \operatorname{Im} \lambda > 0, \hfill \\ T_{ + }^{{(1)}}(x,\lambda )\exp \left( {\frac{{i\lambda x}}{2}} \right),\quad \operatorname{Im} \lambda < 0. \hfill \\ \end{gathered} \right.$$
(47)

In view of estimates (46), the values of this function at any point of the λ plane are expressed by the Cauchy theorem [10] in terms of the integral of the jump of the function F(x, λ) along the real axis when crossing this axis, as well as in terms of the residues of the function \(T_{ - }^{{(1)}}\)(x, λ)a–1(λ)exp(iλx/2) at the zeros of the denominator a(λ). For α > 0, only the residues at the points λ = λj (30) and (31) remain, at which, according to (32), we have

$$\begin{gathered} {\text{Res}}{\kern 1pt} {{s}_{{\lambda = {{\lambda }_{j}}}}}\left[ {T_{ - }^{{(1)}}(x,\lambda ){{a}^{{ - 1}}}(\lambda )\exp \left( {\frac{{i\lambda x}}{2}} \right)} \right] \\ = \gamma ({{\lambda }_{j}})T_{ + }^{{(2)}}(x,{{\lambda }_{j}}){{[a'({{\lambda }_{j}})]}^{{ - 1}}}\exp \left( {\frac{{i{{\lambda }_{j}}x}}{2}} \right). \\ \end{gathered} $$

In contrast to [10], now the derivatives a'(λj) and the normalization constants γ(λj) are related by the reductions (29), (35), and (36). For α < 0, the element a(λ) has a special zero λ = i|α| in its analyticity domain; therefore, the function F(x, λ) may have a pole at this point. Actually, there is no such a pole because, according to the reduction (36), γ(i|α|) = 0, and hence \(T_{ - }^{{(1)}}\)(x, i|α|) = 0 for α < 0 and x > 0.

The integral representation for the piecewise analytical function F(x, λ) has the form

$$\begin{gathered} F(x,\lambda ) = \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right) + \sum\limits_n^{} {\frac{{{{c}_{n}}y(x,{{\lambda }_{n}})}}{{\lambda - {{\lambda }_{n}}}}} \\ + \frac{1}{{2\pi i}}\int\limits_{ - \infty }^{ + \infty } {{\text{d}}\mu \frac{{T_{ + }^{{(2)}}(x,\mu )}}{{\mu - \lambda }}r(\mu )\exp \left( {\frac{{i\mu x}}{2}} \right),} \\ \end{gathered} $$
(48)

where

$$y(x,{{\lambda }_{n}}) = T_{ + }^{{(2)}}(x,{{\lambda }_{n}})\exp (i{{\lambda }_{n}}x{\text{/}}2),$$
$${{c}_{n}} = \gamma ({{\lambda }_{n}}){\text{/}}a'({{\lambda }_{n}}),\quad \gamma ({{\lambda }_{n}})\gamma {\text{*}}( - \lambda _{n}^{*}) = - ({{\alpha }^{2}} + \lambda _{n}^{2}).$$

The quantities cn and r(μ) in this and subsequent formulas depend on time:

$${{c}_{n}}(t) = {{c}_{n}}(t = 0){{e}^{{ - i\lambda _{n}^{2}t}}},\quad r(\mu ,t) = r(\mu ,t = 0){{e}^{{ - i{{\mu }^{2}}t}}}.$$

The last property in (25) is transferred from the real λ axis to the complex plane and takes the following form for the columns \(T_{ + }^{{(1)}}\)(x, λ) and \(T_{ + }^{{(2)}}\)(x, λ):

$$T_{ + }^{{(1)}}(x,\lambda ) = i{{\sigma }_{2}}[T_{ + }^{{(2)}}(x,\lambda {\text{*}})]{\text{*}},\quad \operatorname{Im} \lambda \leqslant 0.$$
(49)

Together with (49), representation (48) yields a closed system of linear integral equations for calculating the functions \(T_{ + }^{{(2)}}\)(x, λ) for –∞ < λ < ∞ and discrete values of y(x, λn) (Imλn > 0):

$$\begin{gathered} i{{\sigma }_{2}}[T_{ + }^{{(2)}}(x,\lambda )]{\text{*}}\exp \left( {\frac{{i\lambda x}}{2}} \right) = \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right) + \sum\limits_n^{} {\frac{{{{c}_{n}}y(x,{{\lambda }_{n}})}}{{\lambda - {{\lambda }_{n}}}}} \\ + \frac{1}{{2\pi i}}\int\limits_{ - \infty }^{ + \infty } {{\text{d}}\mu \frac{{T_{ + }^{{(2)}}(x,\mu )}}{{\mu - \lambda + i0}}r(\mu )\exp \left( {\frac{{i\mu x}}{2}} \right),\quad \lambda \in R;} \\ i{{\sigma }_{2}}y{\text{*}}(x,{{\lambda }_{n}}) = \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right){{e}^{{ - ix\lambda _{n}^{*}}}} + \sum\limits_m^{} {\frac{{{{c}_{m}}y(x,{{\lambda }_{m}}){{e}^{{ - ix\lambda _{n}^{*}}}}}}{{\lambda _{n}^{*} - {{\lambda }_{m}}}}} \\ + \frac{1}{{2\pi i}}\int\limits_{ - \infty }^{ + \infty } {{\text{d}}\mu \frac{{T_{ + }^{{(2)}}(x,\mu )}}{{\mu - \lambda _{n}^{*}}}r(\mu )\exp \left( {\frac{{i\mu x}}{2} - ix\lambda _{n}^{*}} \right).} \\ \end{gathered} $$
(50)

After the solution of Eqs. (50) is found, formula (48) gives the values of the function F(x, λ) at all points of the upper and lower λ half-planes.

For soliton states, the reflection coefficient r(μ) ≡ 0; hence, the function F(x, λ) has no jump on the real axis λ. Therefore, only algebraic equations remain for calculating the functions y*(x, λn) and y(x, λn). After straightforward transformations, we can eliminate y*(x, λn) and obtain a closed system of linear equations for calculating y(x, λn):

$$\begin{gathered} y(x,{{\lambda }_{n}}) = \left( \begin{gathered} 0 \\ 1 \\ \end{gathered} \right){{e}^{{ix{{\lambda }_{n}}}}} + \left( \begin{gathered} 1 \\ 0 \\ \end{gathered} \right)\sum\limits_m^{} {\frac{{c_{m}^{*}{{e}^{{ix({{\lambda }_{n}} - \lambda _{m}^{*})}}}}}{{\lambda _{m}^{*} - {{\lambda }_{n}}}}} \\ + \,\sum\limits_{p,m}^{} {\frac{{c_{m}^{*}{{c}_{p}}{{e}^{{ix({{\lambda }_{n}} - \lambda _{m}^{*})}}}y(x,{{\lambda }_{p}})}}{{(\lambda _{m}^{*} - {{\lambda }_{n}})(\lambda _{m}^{*} - {{\lambda }_{p}})}}.} \\ \end{gathered} $$
(51)

The formulas for multisolitons are simplified if we introduce

$$\begin{gathered} \tilde {\gamma }(\lambda ,t) = \frac{{\gamma (\lambda ,t)}}{{\lambda + i\alpha }}, \\ \tilde {a}(\lambda )\, = \,\frac{{a(\lambda )}}{{\lambda + i\alpha }}\, = \,\prod\limits_{s = 1}^M {\left( {\frac{{\lambda - i{{\nu }_{s}}}}{{\lambda + i{{\nu }_{s}}}}} \right)} \prod\limits_{k = 1}^N {\frac{{(\lambda - {{\lambda }_{k}})(\lambda + \lambda _{k}^{*})}}{{(\lambda + {{\lambda }_{k}})(\lambda - \lambda _{k}^{*})}}} \\ \end{gathered} $$
(52)

instead of the functions γ(λ, t) and a(λ). Then

$$\begin{gathered} {{c}_{n}}(t) = \tilde {\gamma }(\lambda ,t){\text{/}}\tilde {a}'({{\lambda }_{n}}), \\ \tilde {\gamma }({{\lambda }_{n}},t)\tilde {\gamma }{\text{*}}( - \lambda _{n}^{*},t) = f( - {{\lambda }_{n}}), \\ \tilde {\gamma }({{\lambda }_{n}},t) = \tilde {\gamma }({{\lambda }_{n}},t = 0){{e}^{{ - i\lambda _{n}^{2}t}}}, \\ \end{gathered} $$
(53)

where f(λ) = (λ + iα)/(λ – iα).

It follows from system (51) that the projections of the vectors y(x, t, λn) are independent. According to (47), (48), and (22), the soliton solutions of the NLSE are expressed in terms of the second projections of these vectors:

$$\chi (x,t) = - \sum\limits_n^{} {{{c}_{n}}(t){{y}_{2}}(x,t,{{\lambda }_{n}}),\quad 0 \leqslant x < \infty ,} $$
(54)

and by construction satisfy the boundary condition (6) with relation (43):

$$[{{\partial }_{x}}\chi - \beta \chi ]{{{\text{|}}}_{{x = 0}}} = 0,\quad \beta = {{( - 1)}^{M}}\alpha ,$$
(55)

where M is the number of zeros of the coefficient \(\tilde {a}\)(λ) of the form λ = iνs (νs > |α|).

4 ANALYSIS OF SOLITONS IN A SEMI-INFINITE FERROMAGNETIC FILM

4.1 Precessing Solitons Localized near the Edge of the Film

First we discuss collective excitations, which are parameterized by imaginary zeros of the function \(\tilde {a}\)(λ) (52). It turns out that all of them correspond to stationary solitons whose cores have oscillatory degrees of freedom and are localized near the edge x = 0 of the film.

Let M = 1, \(\tilde {a}\)(λ) = (λ – iν)/(λ + iν), and ν > |α|. From (53) we find |\(\tilde {\gamma }\)(iν)| = \(\sqrt {(\nu - \alpha ){\text{/}}(\nu + \alpha )} \) and write an expression for c1(t) ≡ c(t) in the form

$$c(t) = 2\nu {{\left( {\frac{{\nu - \alpha }}{{\nu + \alpha }}} \right)}^{{1/2}}}{{e}^{{i\varphi (t)}}},\quad \varphi (t) = {{\nu }^{2}}t + {{\delta }_{0}},$$
(56)

where δ0 is an arbitrary real constant. Then system (51) yields the components of the vector y(iν):

$${{y}_{1}}(i\nu ) = \frac{{ic{\text{*}}(t){{e}^{{ - \nu x}}}}}{{2\nu \Delta (x)}},\quad {{y}_{2}}(i\nu ) = \frac{1}{{\Delta (x)}},$$
(57)

where Δ(x) = eνx + |c(t)/(2ν)|2e–νx, and formulas (54) and (55) give a soliton solution of the NLSE:

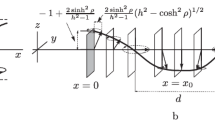
$$\begin{gathered} \chi (x,t) = - \frac{{c(t)}}{{\Delta (x)}} = - \frac{{\nu \sqrt {{{\nu }^{2}} - {{\alpha }^{2}}} }}{{\nu \,{\text{cosh}}(\nu x) + \alpha \,{\text{sinh}}(\nu x)}}{{e}^{{i{{\nu }^{2}}t + i{{\delta }_{0}}}}}, \\ {{\nu }^{2}} > {{\alpha }^{2}},\quad 0 < x < \infty , \\ \end{gathered} $$
(58)

with the boundary condition ∂xlnχ|x = 0 = –α (55). The soliton (58) adjoins the edge x = 0 of the film. According to formulas (2), magnetization components in the core of the soliton (58) perform precession with frequency ω = ν2 around the normal to the plane of the film.

For α = 0, expression (58) simplifies:

$$\chi (x,t) = - \frac{\nu }{{\cosh (\nu x)}}{{e}^{{i{{\nu }^{2}}t + i{{\delta }_{0}}}}},$$
(59)

and describes a soliton in the absence of spin pinning at the boundary x = 0 of the sample. In this case, the width of the soliton is l \(\sim \) ν–1, the precession frequency is ω = ν2, and the maximum amplitude A = ν satisfies algebraic constraints that admit experimental verification:

$${{l}^{{ - 1}}}\,\sim \,\sqrt \omega \,\sim \,A.$$

For a semi-infinite film in the absence of spin pinning at its boundary, when ∂xχ|x = 0 = 0, the energy of the model (5) is expressed as

$$H = \int\limits_0^\infty {({\text{|}}{{\partial }_{x}}\chi (x,t){{{\text{|}}}^{2}} - \,{\text{|}}\chi (x,t{\text{)}}{{{\text{|}}}^{4}}){\text{d}}x.} $$

The terms in brackets take into account the contribution of exchange–dipole interactions, interaction with a constant external magnetic field, and the bulk uniaxial magnetic anisotropy energy [5, 7]. The soliton (59) is localized near the boundary x = 0 of the film because it is attracted to its imaginary image χ(‒x, t) in the nonphysical region –∞ < x < 0.

The partial pinning of spins at the boundary of the film and the boundary condition [∂xχ – βχ]|x = 0 = 0 are associated with the appearance of the surface magnetic anisotropy energy in the Hamiltonian of the system:

$$H = \int\limits_0^\infty {({\text{|}}{{\partial }_{x}}\chi (x,t){{{\text{|}}}^{2}} - \,{\text{|}}\chi (x,t){{{\text{|}}}^{4}}){\text{d}}x + \beta {\text{|}}\chi (x = 0,t){{{\text{|}}}^{2}}.} $$

When the surface anisotropy constant β is positive, it is energetically favorable for the soliton to move back from the boundary of the sample. When β < 0, on the contrary, the total energy of the system decreases when the soliton moves closer to the film edge x = 0. The compression rate of the soliton core increases with increasing |β|. In the general case, the parameter α of multisolitons is related to the surface magnetic anisotropy constant β by formula (43). For the soliton (58), M = 1, and hence β = –α. The structure of such a soliton near the film edge x = 0 changes quantitatively and qualitatively under the variation of the magnitude and sign of the parameter α (see Fig. 1).

Fig. 1.
figure 1

A soliton localized near the edge of the sample for (a) α = 0, (b) α < 0 and 2νx0 = ln[(ν + |α|)/(ν – |α|)], and (c) α > 0.

Full size image

It is interesting that, for partial spin pinning at the edge of the film (for |α| < ∞), the precession frequency of the soliton (58) is always higher than a certain threshold value

$$\omega = {{\nu }^{2}} > {{\alpha }^{2}} = {{\beta }^{2}}.$$

For a two-soliton excitation with two imaginary zeros λ = iν1, 2 (52), the functions c1, 2(t) (53) are given by

$${{c}_{{1,2}}}(t) = \pm 2{{\nu }_{{1,2}}}\left[ {\frac{{{{\nu }_{1}} + {{\nu }_{2}}}}{{{{\nu }_{1}} - {{\nu }_{2}}}}} \right]{{\left( {\frac{{{{\nu }_{{1,2}}} - \alpha }}{{{{\nu }_{{1,2}}} + \alpha }}} \right)}^{{1/2}}}{{e}^{{i{{\varphi }_{{1,2}}}(t)}}},$$
$${{\nu }_{{1,2}}} > {\text{|}}\alpha {\text{|}};\quad {{\varphi }_{{1,2}}}(t) = \nu _{{1,2}}^{2}t + {{\delta }_{{1,2}}},$$

where δ1, 2 are arbitrary real constants. Calculations similar to previous ones give a solution of the NLSE:

$$\begin{gathered} \chi (x,t) = - \frac{1}{{{{D}_{0}}}}[{{c}_{1}}({{e}^{{{{\nu }_{2}}x}}} + {{e}^{{ - {{\nu }_{2}}x}}}f( - i{{\nu }_{2}})) \\ \, + {{c}_{2}}({{e}^{{{{\nu }_{1}}x}}} + {{e}^{{ - {{\nu }_{1}}x}}}f( - i{{\nu }_{1}}))], \\ \end{gathered} $$
(60)
$$\begin{gathered} {{D}_{0}} = {{e}^{{({{\nu }_{1}} + {{\nu }_{2}})x}}} + {{e}^{{ - ({{\nu }_{1}} + {{\nu }_{2}})x}}}f( - i{{\nu }_{1}})f( - i{{\nu }_{2}}) \\ + {{\left( {\frac{{{{\nu }_{1}} + {{\nu }_{2}}}}{{{{\nu }_{1}} - {{\nu }_{2}}}}} \right)}^{2}}[{{e}^{{ - ({{\nu }_{1}} - {{\nu }_{2}})x}}}f( - i{{\nu }_{1}}) + {{e}^{{({{\nu }_{1}} - {{\nu }_{2}})x}}}f( - i{{\nu }_{2}})] \\ \, + (c_{1}^{*}{{c}_{2}} + {{c}_{1}}c_{2}^{*}){{({{\nu }_{1}} + {{\nu }_{2}})}^{{ - 2}}}, \\ \end{gathered} $$

where f(–iν) = (ν – α)/(ν + α).

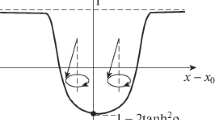
In this case, M = 2; therefore, the field (60) satisfies the boundary condition ∂xlnχ|x = 0 = α (55). It describes a nonlinear superposition of two solitons (58). Such solitons are localized near the edge x = 0 of the sample in layers of thickness of about \(\nu _{1}^{{ - 1}}\) and \(\nu _{2}^{{ - 1}}\). Magnetization in the cores of the solitons precesses with frequencies \(\nu _{1}^{2}\) and \(\nu _{2}^{2}\) around the normal to the developed surface of the film.

Due to the interaction of solitons, the amplitude of each of them oscillates with frequency |\(\nu _{1}^{2}\) – \(\nu _{2}^{2}\)|. While, for a single-soliton state (58), the magnetization component m3 at the film edge was constant, for a two-soliton excitation it performs oscillations with frequency |\(\nu _{1}^{2}\) – \(\nu _{2}^{2}\)| between two limiting values (see (Fig. 2):

$$\begin{gathered} |{\kern 1pt} \chi (x = 0,t){\kern 1pt} {{|}^{2}} = {{(\nu _{1}^{2} - \nu _{2}^{2})}^{2}}[\nu _{1}^{2} + \nu _{2}^{2} - 2{{\alpha }^{2}} \\ - 2\sqrt {(\nu _{1}^{2} - {{\alpha }^{2}})(\nu _{2}^{2} - {{\alpha }^{2}})} \cos ({{\varphi }_{1}}(t) - {{\varphi }_{2}}(t)){{]}^{{ - 1}}}, \\ {\text{|}}\chi {\text{|}}_{{\min }}^{2} = {{(\nu _{1}^{2} - \nu _{2}^{2})}^{2}}{{[{{(\nu _{1}^{2} - {{\alpha }^{2}})}^{{1/2}}} + {{(\nu _{2}^{2} - {{\alpha }^{2}})}^{{1/2}}}]}^{{ - 2}}}, \\ {\text{|}}\chi {\text{|}}_{{\max }}^{2} = {{(\nu _{1}^{2} - \nu _{2}^{2})}^{2}}{{[{{(\nu _{1}^{2} - {{\alpha }^{2}})}^{{1/2}}} - {{(\nu _{2}^{2} - {{\alpha }^{2}})}^{{1/2}}}]}^{{ - 2}}}. \\ \end{gathered} $$
(61)
Fig. 2.
figure 2

Two-soliton excitation (60) for α = ε|α|, ε = 1 (solid lines) and ε = –1 (dashed lines) in the extreme positions corresponding to the values of |χ|(x = 0) = |χ|min and |χ|(x = 0) = |χ|max.

Full size image

In the absence of spin pinning (for α = 0), from (61) we obtain

$${\text{|}}{{\nu }_{2}} - {{\nu }_{1}}{\text{|}} \leqslant {\text{|}}\chi (x = 0,t){\text{|}} \leqslant {\text{|}}{{\nu }_{1}} + {{\nu }_{2}}{\text{|}}.$$

In the general case, multisolitons parameterized by different sets of imaginary zeros (31) of the coefficient \(\tilde {a}\)(λ) describe a series of long-lived near-boundary oscillations of magnetization with discrete frequencies of amplitude and phase modulations of the field χ(x, t).

4.2 Reflection of Moving Solitons from the Edge of the Film

Each pair of complex conjugate zeros of the function \(\tilde {a}\)(λ) (30) parameterizes one moving particle-like object. At large distances from the edge of the film, this object takes the form of a soliton typical of the infinite medium. Paired interactions of solitons are elastic: after a collision, only the initial phase of internal oscillations and the coordinate of the center of each soliton are changed. At the same time, near the film edge, the core of the moving soliton is strongly deformed due to the interaction with this edge. The interaction with the edge can be formally interpreted as the interaction of a real soliton with a fictitious image soliton. Therefore, the collision of each soliton with the edge of the film is also elastic. Let us explain this assertion by an example of a simple soliton that is parameterized by two zeros λ = λ0, –\(\lambda _{0}^{*}\) (Imλ0 > 0) of the coefficient \(\tilde {a}\)(λ) (52):

$$\tilde {a}(\lambda ) = \frac{{(\lambda - {{\lambda }_{0}})(\lambda + \lambda _{0}^{*})}}{{(\lambda + {{\lambda }_{0}})(\lambda - \lambda _{0}^{*})}}.$$

From (53) we find the functions c1, 2(t):

$${{c}_{1}}(t) = \frac{{2{{\lambda }_{0}}({{\lambda }_{0}} - \lambda _{0}^{*})}}{{({{\lambda }_{0}} + \lambda _{0}^{*})}}{{\gamma }_{0}}{{e}^{{ - i\lambda _{0}^{2}t}}},$$
$${{c}_{2}}(t) = \frac{{2\lambda _{0}^{*}({{\lambda }_{0}} - \lambda _{0}^{*})}}{{({{\lambda }_{0}} + \lambda _{0}^{*})\gamma _{0}^{*}}}f{\text{*}}( - {{\lambda }_{0}})\,{{e}^{{ - i\lambda _{0}^{{*2}}t}}},$$

where γ0 is an arbitrary complex constant and f(λ) = (λ + iα)/(λ – iα). Formulas (51) and (54) define a soliton solution of model (5),

$$\begin{gathered} \chi (x,t) = - \frac{2}{D}\left( {\frac{{{{\lambda }_{0}} - \lambda _{0}^{*}}}{{{{\lambda }_{0}} + \lambda _{0}^{*}}}} \right) \\ \times \left[ {{{\lambda }_{0}}{{\gamma }_{0}}{{e}^{{ - i\lambda _{0}^{2}t}}}{{{({{e}^{{i\lambda _{0}^{*}x}}} + f{\text{*}}( - {{\lambda }_{0}})\,{{e}^{{ - i\lambda _{0}^{*}x}}})}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \left. { + \frac{{\lambda _{0}^{*}f{\text{*}}( - {{\lambda }_{0}})}}{{\gamma _{0}^{*}}}{{e}^{{ - i\lambda _{0}^{{*2}}t}}}({{e}^{{ - i{{\lambda }_{0}}x}}} + f( - {{\lambda }_{0}})\,{{e}^{{i{{\lambda }_{0}}x}}})} \right], \\ \end{gathered} $$
$$\begin{gathered} D = {{e}^{{ - ix({{\lambda }_{0}} - \lambda _{0}^{*})}}} + \,{\text{|}}f( - {{\lambda }_{0}}){{{\text{|}}}^{2}}{{e}^{{ix({{\lambda }_{0}} - \lambda _{0}^{*})}}} \\ + {{\left( {\frac{{2{\text{|}}{{\lambda }_{0}}{\text{|}}}}{{{{\lambda }_{0}} + \lambda _{0}^{*}}}} \right)}^{2}} \\ \end{gathered} $$
(62)
$$\begin{gathered} \times \left( {{\text{|}}{{\gamma }_{0}}{{{\text{|}}}^{2}}{{e}^{{ - i(\lambda _{0}^{2} - \lambda _{0}^{{*2}})t}}} + {{{\left| {\frac{{f( - {{\lambda }_{0}})}}{{{{\gamma }_{0}}}}} \right|}}^{2}}{{e}^{{i(\lambda _{0}^{2} - \lambda _{0}^{{*2}})t}}}} \right) \\ + {{\left( {\frac{{{{\lambda }_{0}} - \lambda _{0}^{*}}}{{{{\lambda }_{0}} + \lambda _{0}^{*}}}} \right)}^{2}} \\ \times \left( {f( - {{\lambda }_{0}}){{e}^{{i({{\lambda }_{0}} + \lambda _{0}^{*})x}}} + f{\text{*}}( - {{\lambda }_{0}}){{e}^{{ - i({{\lambda }_{0}} + \lambda _{0}^{*})x}}}} \right), \\ \end{gathered} $$

which satisfies the boundary condition (55) with M = 2:

$${{\partial }_{x}}{\text{ln}}\chi {{{\text{|}}}_{{x = 0}}} = \alpha = \beta .$$
(63)

The validity of (63) can be easily verified by a straightforward calculation with regard to the equalities

$${{\partial }_{x}}D{{{\text{|}}}_{{x = 0}}} = 0,\quad 1 - f( - {{\lambda }_{0}}) = \frac{{2i\alpha }}{{{{\lambda }_{0}} + i\alpha }},$$
$$1 + f( - {{\lambda }_{0}}) = \frac{{2{{\lambda }_{0}}}}{{{{\lambda }_{0}} + i\alpha }}.$$

Formula (62) describes the propagation of a particle-like excitation from the bulk of the plate, where 0 < x < ∞, to the boundary x = 0, its reflection from the boundary, and the subsequent propagation into the bulk of the sample again. Let us show that, at large distances from the edge of the plate, the excitation (62) is transformed into a moving precession soliton, the same, as in an infinite sample. To this end, we notice that the character of the solution (62) for x ≫ 1 is determined by the competition between the terms in the numerator with exponential factors exp[±u(x + νt)/2] and exp[±u(x – νt)/2] and the leading terms in the denominator with coefficients e±ux and e±uνt, where ν + iu = 2λ0. Since Imλ0 > 0, the parameter u is always positive. Assume for definiteness that the parameter ν is also positive. The values of u and ν define, respectively, the size l0 \(\sim \) u–1 of the soliton and its velocity. Indeed, for x ≫ 1 in the limit as t → ±∞, the structure of a soliton in the co-moving reference frame is described by the following expression for x \( \mp \) νt = const:

$$\begin{gathered} \chi (x,t \to \pm \infty ) \\ \approx \operatorname{Im} {{\lambda }_{0}}\exp \left[ {i\left( {\frac{{({{u}^{2}} - {{\nu }^{2}})t}}{4} \pm \frac{{\nu x}}{2} - \frac{\pi }{2} + {{\varphi }_{ \pm }}} \right)} \right] \\ \times {{\cosh }^{{ - 1}}}\left[ {\frac{u}{2}(x \mp \nu t - {{x}_{ \pm }})} \right], \\ {{\varphi }_{ + }} = \arg ({{\gamma }_{0}}{{\lambda }_{0}}),\quad {{\varphi }_{ - }} = - \arg \left( {\frac{{{{\lambda }_{0}}f( - {{\lambda }_{0}})}}{{{{\gamma }_{0}}}}} \right), \\ {{x}_{ + }} = \frac{2}{u}\,\,\ln \left| {\frac{{2{{\lambda }_{0}}{{\gamma }_{0}}}}{{{{\lambda }_{0}} + \lambda _{0}^{*}}}} \right|,\quad {{x}_{ - }} = \frac{2}{u}\,\,\ln \left| {\frac{{2{{\lambda }_{0}}f( - {{\lambda }_{0}})}}{{({{\lambda }_{0}} + \lambda _{0}^{*}){{\gamma }_{0}}}}} \right|. \\ \end{gathered} $$
(64)

Formulas (64) define a simple soliton in an infinite sample [10, 11] that moves along the x axis with the velocity ±ν. It follows from (64) that, at large distances from the edge x = 0 of the film, the only result of the interaction of the soliton with the boundary is a change in the phase of the internal precession and a shift of the soliton center. The magnetization of soliton in its co-moving reference frame performs a precession performs a precession with frequency Ω = (u2 + ν2)/4 around the normal to the film plane. The change in the initial phase of the soliton precession after its reflection from the boundary has the form

$${{\varphi }_{ + }} - {{\varphi }_{ - }} = \arg \left[ {{{\lambda }_{0}}\left( {\frac{{{{\lambda }_{0}} - i\alpha }}{{{{\lambda }_{0}} + i\alpha }}} \right)} \right].$$

The phase shift depends on the pinning parameter of surface spins α (α2 = β2), as well as on the complex number λ0 = (ν + iu)/2, instead of which we can use appropriate observable parameters, for example, the width u–1 and the velocity ν of the soliton, or the velocity ν of the soliton and its precession frequency Ω. Hence, the measurement of the phase shift of the soliton after its reflection from the sample boundary gives information about the parameter α. This fact can be used for diagnosing the state of spins at the film edge. In [21], the authors theoretically predicted and experimentally confirmed the reflection of a longitudinal deformation soliton from the end face of a nonlinear elastic rod. Similar processes are also typical for solitons in ferromagnetic films.

Complete spin pinning at the edge of a film corresponds to the Dirichlet condition

$$\chi (x = 0,t) = 0,$$
(65)

which is obtained from the general condition (55) in the limit |β| = |α| → ∞. In this case, the function \(\tilde {a}\)(λ) (52) does not have purely imaginary zeros, since their existence contradicts the constraint (36). This implies that, for complete spin pinning, there are no long-lived localized oscillations near the face x = 0 of the plate. At the same time, the plate allows the formation of moving multisolitons. In the limit α → ∞, the function f(–λ0) → –1; therefore, from (62) we immediately obtain an analytical expression for the simplest of such solitons:

$$\begin{gathered} \chi (x,t) = - \frac{{2i}}{D}\left( {\frac{u}{\nu }} \right)\exp \left( { - \frac{{i({{u}^{2}} - {{\nu }^{2}})t}}{2}} \right) \\ \times \left( {{{\lambda }_{0}}{{\gamma }_{0}}\left[ {\exp \left( {\frac{{i\nu x}}{2} + \frac{u}{2}(x + \nu t)} \right)} \right.} \right. \\ \left. {\, + \theta \exp \left( { - \frac{{i\nu x}}{2} - \frac{u}{2}(x - \nu t)} \right)} \right] \\ + \frac{{\lambda _{0}^{*}}}{{\gamma _{0}^{*}}}\left[ {\exp \left( {\frac{{i\nu x}}{2} - \frac{u}{2}(x + \nu t)} \right)} \right. \\ \left. {\left. { + \,\theta \exp \left( { - \frac{{i\nu x}}{2} + \frac{u}{2}(x - \nu t)} \right)} \right]} \right), \\ \end{gathered} $$
(66)
$$\begin{gathered} D = 2\left[ {\cosh (ux) + {{{\left( {\frac{{2{\text{|}}{{\lambda }_{0}}{\text{|}}}}{\nu }} \right)}}^{2}}\cosh (u\nu t + \ln {\text{|}}{{\gamma }_{0}}{{{\text{|}}}^{2}})} \right. \\ \left. {\, - \theta {{{\left( {\frac{u}{\nu }} \right)}}^{2}}\cos (\nu x)} \right], \\ \end{gathered} $$

where ν + iu = 2λ0 and θ ≡ –1. We can easily check that (66) satisfies the boundary condition (65).

The opposite case of free spins (α = 0) is described by the same expression (66) with θ ≡ 1. In this case, f(‒λ0) = 1. In both cases of α = 0 and α → ∞, after reflection from the boundary, the soliton has the same shift of the center of gravity Δx = x+ – x– = 4u–1lnγ0 (Fig. 3).

Fig. 3.
figure 3

Soliton (66) at times t = ±t0, t0 ≫ 1 (solid lines), t = 0 for α = ∞ (dashed line), and t = 0 for α = 0 (dash-and-dot line).

Full size image

5 INTEGRALS OF MOTION FOR NONLINEAR EXCITATIONS IN A SEMI-INFINITE FILM

The considered procedure can be interpreted as a nonlinear analog of the solution of a boundary value problem for a linear differential equation by the Fourier method. Indeed, in a small-amplitude limit in the absence of solitons, when the relations

$$\alpha = \beta ,\quad a(\lambda ) = \lambda + i\beta ,\quad {{[T_{ + }^{{(2)}}(x,\lambda )]}_{2}} \approx \exp \left( {\frac{{i\lambda x}}{2}} \right),$$

hold, the wave field χ(x, t) found by formulas (48) and (22) has the form

$$\begin{gathered} \chi (x,t) \approx \frac{1}{{2\pi i}}\int\limits_{ - \infty }^{ + \infty } {{\text{d}}\mu \,r(\mu ,t)\,{{e}^{{ix\mu }}}} \\ = \frac{1}{{2\pi i}}\int\limits_0^{ + \infty } {{\text{d}}\mu \,b(\mu ,t = 0)\,{{e}^{{ - i{{\mu }^{2}}t}}}} \left[ {\frac{{{{e}^{{ix\mu }}}}}{{\mu + i\beta }} + \frac{{{{e}^{{ - ix\mu }}}}}{{\mu - i\beta }}} \right], \\ x \geqslant 0, \\ \end{gathered} $$
(67)

and, consequently, is related to the reflection coefficient r(μ) of the scattering problem by standard Fourier transform. When passing to the right-hand side of (67), we took into account that b(λ) (27) is an odd function. We can easily check by direct calculation that formula (67) gives a solution of the linearized equation (5) on the interval 0 < x < ∞ with boundary conditions (6), (7).

It is well known that distant Fourier components of functions that have no singularities on the real axes are exponentially small [22]. In this problem, since the field χ(x) is extended to the whole real axis, its derivatives have jumps at the point x = 0. When the wave field ψ(x) or its derivatives have jumps on the real axis, the exponential decay of its Fourier components r(μ) as μ → ∞ turns into a power-law decay [22]. This property of Fourier transforms is inherited by the spectral densities b(μ) of the inverse scattering problem. In this section, we obtain a power-law expansion for the coefficient b(μ) as μ → ∞. To construct purely soliton excitations in a semi-infinite plate, the difference of the functions b(μ) from those in the infinite plate is not significant since, for solitons, b(μ) ≡ 0 by definition. At the same time, we show that the condition b(μ) ≡ 0 leads to additional conservation laws for the wave field at the boundary of the sample that ensure the localization of soliton oscillations near the edge of the film and the elastic reflection of moving solitons from the sample boundary.

We obtain a series of local integrals of motion for solitons and dispersive waves in a plate from the expansion of the time-independent functional a(λ) in powers of λ–1.We apply formula (41) for a(λ) into which we introduce the representation of the Jost function T+(+0, λ) in the form

$${{T}_{ + }}( + 0,\lambda ) = (I + W( + 0,\lambda )){{e}^{{Z( + 0,\lambda )}}}.$$
(68)

The expansion of the antidiagonal matrix W(x, λ) for x ≥ 0 in inverse powers of λ was obtained in [11]:

$$W(x,\lambda ) = \sum\limits_{n = 1}^\infty {\frac{1}{{{{\lambda }^{n}}}}[\omega _{n}^{*}(x){{\sigma }_{ + }} - {{\omega }_{n}}(x){{\sigma }_{ - }}],\quad x \geqslant 0.} $$
(69)

Here ω1 = χ(x), and the following coefficients are defined recursively:

$$\begin{gathered} {{\omega }_{{n + 1}}}(x) = - i{{\partial }_{x}}{{\omega }_{n}}(x) - \chi {\text{*}}(x)\sum\limits_{k = 1}^{n - 1} {{{\omega }_{k}}(x){{\omega }_{{n - k}}}(x),} \\ n = 1,2,.... \\ \end{gathered} $$

For n = 1, the second term on the right-hand side of the equality is absent. The diagonal matrix Z(+0, λ) is expressed in terms of ωn(x):

$$\begin{gathered} Z( + 0,\lambda ) = \frac{i}{2}\sum\limits_{n = 1}^\infty {\frac{1}{{{{\lambda }^{n}}}}\int\limits_0^\infty {[\chi {\text{*}}(z){{\omega }_{n}}(z)(I + {{\sigma }_{3}})} } \\ - \,\chi (z)\omega _{n}^{*}(z)(I - {{\sigma }_{3}})]{\text{d}}z. \\ \end{gathered} $$
(70)

After straightforward calculations, we find the first most important integrals of motion [16]:

$$\ln \frac{{a(\lambda )}}{{\sqrt {{{\lambda }^{2}} + {{\beta }^{2}}} }} = - \frac{{2iN}}{\lambda } - \frac{{2i}}{{{{\lambda }^{3}}}}H + ...,$$
(71)

where

$$N = \int\limits_0^\infty {{\text{|}}{{\partial }_{x}}\chi (x,t){{{\text{|}}}^{2}}{\text{d}}x - \frac{\beta }{2}} $$

is the number of spin deviations [23, 24] and

$$\begin{gathered} H = \int\limits_0^\infty {({\text{|}}{{\partial }_{x}}\chi (x,t){{{\text{|}}}^{2}}\, - \,{\text{|}}\chi (x,t){{{\text{|}}}^{4}}){\text{d}}x} \\ + \,\beta {\text{|}}\chi (x = 0,t){{{\text{|}}}^{2}} + \frac{{{{\beta }^{3}}}}{6} \\ \end{gathered} $$

is the Hamiltonian (energy) of magnetic oscillations in the film.

On the other hand, the series in powers of λ–1 for the function a(λ) follows immediately from (38). Recall that β = (–1)Mα. A comparison of two expansions for a(λ)/\(\sqrt {{{\lambda }^{2}} + {{\beta }^{2}}} \) yields explicit formulas for N and H in the presence of solitons and dispersive waves in a semi-infinite plate:

$$\begin{gathered} N = \int\limits_0^\infty {n(\mu ){\text{d}}\mu } + 2\sum\limits_{k = 1}^N {\operatorname{Im} {{\lambda }_{k}}} + \sum\limits_{s = 1}^M {{{\nu }_{s}} - \frac{\alpha }{2};} \\ H = \int\limits_0^\infty {{{\mu }^{2}}n(\mu ){\text{d}}\mu } + \frac{2}{3}\sum\limits_{k = 1}^N {\operatorname{Im} \lambda _{k}^{3}} - \frac{1}{3}\sum\limits_{s = 1}^M {\nu _{s}^{3} + \frac{{{{\alpha }^{3}}}}{6}.} \\ \end{gathered} $$
(72)

The quantity

$$n(\mu ) = - \frac{1}{{2\pi }}\ln \left( {1 - \frac{{{\text{|}}b(\mu ){\text{|}}}}{{{{\mu }^{2}} + {{\alpha }^{2}}}}} \right) > 0$$

has the meaning of the density of spin-wave modes with wave number μ. The discrete terms in (72) correspond to the additive contributions of different solitons to the integrals of motion.

Let us show that, for a semi-infinite plate with boundary conditions (6), (7), in contrast to the case of an infinite sample, the spectral density of spin waves b(λ) in the limit λ → ∞ exhibits a power-law, rather than an exponential, decay. To this end, we apply formula (42). The calculations are simplified if, using relations (49), we express the right-hand side of equality (42) in terms of the same functions that were used in formula (41) for the coefficient a(λ):

$$\begin{gathered} b(\lambda ) = (\lambda + i\beta )[{{T}_{ + }}( + 0,\lambda {\text{*}})]_{{12}}^{*}[{{T}_{ + }}( + 0, - \lambda {\text{*}})]_{{22}}^{*} \\ + \,(\lambda - i\beta )[{{T}_{ + }}( + 0,\lambda {\text{*}})]_{{22}}^{*}[{{T}_{ + }}( + 0, - \lambda {\text{*}})]_{{12}}^{*}, \\ \lambda \in R. \\ \end{gathered} $$
(73)

Using (68)–(70) and (73), we find an asymptotic expansion for the function b(λ) for λ ≫ 1:

$$\begin{gathered} b(\lambda ) = 2\sum\limits_{k = 1}^\infty {\frac{1}{{{{\lambda }^{{2k - 1}}}}}({{\omega }_{{2k}}} + i\beta {{\omega }_{{2k - 1}}}){{{\text{|}}}_{{x = 0}}}} \\ \times \exp \left( {2i\sum\limits_{n = 1}^\infty {\int\limits_0^\infty {\chi {\text{*}}(z){{\omega }_{{2n}}}(z){{\lambda }^{{ - 2n}}}{\text{d}}z} } } \right). \\ \end{gathered} $$
(74)

The first term of the series has the form

$$\begin{gathered} b(\lambda ) = \left[ {\frac{{2i}}{{{{\lambda }^{3}}}}(\partial _{x}^{3}\chi - \beta \partial _{x}^{2}\chi + 4\beta {\text{|}}\chi {{{\text{|}}}^{2}}\chi ){{{\text{|}}}_{{x = 0}}} + O\left( {\frac{1}{{{{\lambda }^{5}}}}} \right)} \right] \\ \times \exp \left( {\frac{2}{{{{\lambda }^{2}}}}\int\limits_0^\infty {\chi {\text{*}}(z){{\partial }_{z}}\chi (z)\,{\text{d}}z + O\left( {\frac{1}{{{{\lambda }^{4}}}}} \right)} } \right). \\ \end{gathered} $$

Of course, for pure soliton states, all pre-exponential factors in (74) vanish. For the simplest soliton (58), we can easily verify by direct calculation that the following identity is valid:

$$(\partial _{x}^{2}\chi - \beta \partial _{x}^{2}\chi + 4\beta {\text{|}}\chi {{{\text{|}}}^{2}}\chi ){{{\text{|}}}_{{x = 0}}} = 0.$$

Thus, for multisolitons in a semi-infinite plate (0 ≤ x < ∞), there exists a series of nontrivial relations between the field χ(x, t) and its spatial derivatives at the boundary x = 0 of the sample.

6 CONCLUSIONS

In this work we have shown that, in a semi-infinite plate at any localized initial distribution of magnetization, there exists, in addition to the series of local integrals of motion each of which is a sum of additive contributions of solitons and dispersive waves, a series of new conservation laws for the wave field at the edge of the film. The latter provide the possibility of localization of soliton-like oscillations of magnetization near the boundary of the sample and the elastic reflection of moving solitons from this boundary.

The formulas obtained for multisolitons can be used as test ones for the analytical description of soliton states near the boundaries of finite-size samples. They are useful for verifying numerical calculations and can serve as a basis for new experiments on the diagnostics of spin pinning at the surface of a sample by measuring the phase shift of solitons after their reflection from the boundary.

In conclusion, we discuss the conditions under which solitons are generated in a semi-infinite film. Let λ, T, and A be the characteristic spatial and temporal scales of spin wave modulation and the amplitude of spin waves, respectively. Since the effects of dispersion and nonlinearity during the formation of solitons are balanced, from the dimensional NLSE (1) we obtain the estimates

$${{\lambda }^{2}}\,\sim \,\,\frac{{{\text{|}}\partial _{k}^{2}\omega (k){\text{|}}}}{{g{{A}^{2}}}},\quad T\,\sim \,\,\frac{1}{{g{{A}^{2}}}}.$$

Here ω(k) is the frequency of the main harmonic depending on the wave number k, and g is the interaction constant of waves. Recall that the Lighthill criterion (4) holds in the excitation region of solitons. Suppose that solitons are formed (at the boundary or in the bulk of the film) by pulses of duration τext. Then λ \(\sim \) cgτext, where cg = ∂kω(k) is the group velocity of spin waves, and we obtain the following estimate for the threshold pump amplitude starting from which soliton generation becomes possible:

$$g{{A}^{2}}\,\sim \,{\text{|}}\partial _{k}^{2}\omega (k){\text{|}}\,/\,{{({{c}_{g}}{{\tau }_{{{\text{ext}}}}})}^{2}}.$$

In this case, the formation of envelope solitons is conditioned by the inequality λ ≫ k–1. According to [4, 7], for τext = 10–20 ns, the wave numbers k > 103–104 cm–1 in the existence region of soliton states. The consideration of smaller wave numbers is not allowed. The point is that the dispersion law ω(k) is not differentiable at the point k = 0, and the nonlinear dynamics of the magnetic film is described in the neighborhood of this point by a different equation with a nonlocal dispersion term [25]. The nonlocal part of the magnetostatic dispersion smoothes out the inhomogeneities in the distribution of magnetization in the film. As a result, exponential solitons typical for the local NLSE are absent in the long-wavelength limit. Instead, new weakly localized algebraic-soliton-type exchange–dipole states are formed.

The generation of solitons localized near the edge of a film by external pulses occurs in a threshold manner with respect to the pump amplitude. The change in the number of such solitons should give rise to discrete frequencies of resonant oscillations of magnetization near the edge of the sample and should manifest itself in characteristic frequency and amplitude modulations of the magnetization component perpendicular to the plane of the film.