Solitons in a semi-infinite ferromagnet with anisotropy of the easy axis type

Abstract

We propose a special variant of the inverse scattering transform method to construct and analyze soliton excitations in a semi-infinite sample of an easy-axis ferromagnet in the case of a partial pinning of spins at its surface. We consider the limit cases of free edge spins and spins that are fully pinned at the sample boundary. We find frequency and modulation characteristics of solitons localized near the sample surface. In the case of different degrees of edge spin pinning, we study changes in the cores of moving solitons as a result of their elastic reflection from the sample boundary. We obtain integrals of motion that control the dynamics of magnetic solitons in a semi-infinite sample.

1. Introduction

To date, the nonlinear dynamics of quasi-one-dimensional solitons and waves in extended magnetic media [1]–[3] has been studied most comprehensively. The fact is that the basic equations of the theory of magnetism often admit representations in the form of commutativity conditions for two differential operators. In unbounded samples, these representations are used to map the magnetization distributions into the scattering data of auxiliary spectral problems. The evolution of the scattering data is determined by linear equations and can be calculated explicitly using the initial magnetization distributions. The inverse map gives the complete solution of each specific initial boundary-value problem.

Unfortunately, this technique (the inverse scattering transform method) runs into significant difficulties when extended to finite-size systems. For bounded samples, there is no simple map of the initial–boundary conditions into the scattering data [4]–[6]. The exceptions are semi-infinite samples with a preferred class of boundary conditions [7]–[10]. In principle, an approach similar to the method of “images” in electrostatics can be used for them [11]–[13]. The initial boundary-value problem on the semiaxis (the spatial coordinate $0 \leq x<\infty$) with a certain symmetry can be continued to the entire axis $-\infty<x<\infty$. After that, the problem is solved in accordance with the traditional integration scheme for a nonlinear model on the line.

For basic equations of magnetism, physically meaningful integrable boundary conditions were described in [14]. However, the nonlinear magnetization dynamics in semi-infinite samples was barely studied until now. In [15], [16], the features of magnetic solitons in semi-infinite samples were analyzed in the framework of the nonlinear Schrödinger equation and the Landau–Lifshitz equation for an isotropic Heisenberg ferromagnet. The interaction of solitons with the sample boundary leads to special dynamical properties that are absent in an infinite medium and are useful for technological applications.

In this paper, we take the effect of the crystallographic magnetic anisotropy into account and study the nonlinear dynamics of an easy-axis ferromagnet in a semi-infinite sample with the energy

$$H =\frac{1}{2}\int_{0}^{\infty} dx\,[\alpha(\partial_{x} \mathbf{M})^2-K (M_3^2-M_0^2)]+h M_3 (x, t)|_{x=0}. $$

(1.1)

Here, $\mathbf{M}(x, t)$ is the material magnetization ($\mathbf{M}^2 (x, t)=M_0^2=\mathrm{const}$); $\alpha>0$ and $K>0$ are the exchange interaction and magnetic anisotropy constants; $h \mathbf{e}$ is the external magnetic field along the boundary $x=0$ of the sample or the effective unidirectional-anisotropy field of surface spins [17]–[19], $\mathbf{e}=(0, 0, 1)$; and $0 \leq x <\infty$ and $0 \leq t < \infty$ are the spatial coordinate and the time.

After passing to the dimensionless variables

$$x'=x \sqrt{\frac{K}{\alpha}},\qquad t'=\gamma M_0 Kt, \qquad h' =\frac{h}{M_0 \sqrt{K \alpha}}, \qquad \mathbf{n}=-\frac{\mathbf{M}}{M_0},$$

where $\gamma$ is the magnetomechanical ratio and $M_0$ is the nominal magnetization, the Landau–Lifshitz equation for the calculation of the normalized magnetization $\mathbf{n}(x,t)$ becomes

$$\partial_{t'} \mathbf{n}=[\mathbf{n} \times (\partial_{x'}^2 \mathbf{n}+\mathbf{e} (\mathbf{n} \cdot \mathbf{e}))], \qquad \mathbf{n}^2=1, $$

(1.2)

where $0 < x' <\infty$, $0 < t' < \infty$, with the integrable boundary conditions

$$\mathbf{n} \to \mathbf{e}, \quad\partial_{x'} \mathbf{n} \to 0 \qquad \text{for} \quad x' \to +\infty,$$

(1.3)

$$[\mathbf{n} \times (\partial_{x'}\mathbf{n}+h' \mathbf{e})]|_{x'=0}=0$$

(1.4)

and the given initial magnetization field perturbation

$$\mathbf{n}(x',t')|_{t'=0}=\mathbf{n}_0 (x'). $$

(1.5)

We omit the primes over the dimensionless variables in what follows. The choice of asymptotic boundary condition (1.3) corresponds to the energy minimum of the homogeneous ground state.

Mixed boundary condition (1.4) takes the partial pinning of spins at the sample boundary $x=0$ into account. In the limit cases $h=0$ and $|h| \to \infty$, we obtain the corresponding problem for free edge spins

$$[\mathbf{n} \times \partial_{x} \mathbf{n}] |_{x=0}=0 $$

(1.6)

and the problem with the full spin pinning at the sample boundary

$$n_3 |_{x=0}=\pm 1. $$

(1.7)

We choose the sign in the right-hand side of (1.7) in the course of further analysis.

We note that in [20], the simplest nonlinear excitation localized near the end of a semibounded spin chain was first obtained. The considered model in the continuum approximation reduces to the Landau–Lifshitz equation of an easy-axis ferromagnet. Its approximate solution was found under a dynamical condition reflecting the absence of neighbors in the region $x<0$ at the edge spin of the chain. In this paper, we present a complete study of the nonlinear dynamics of solitons and dispersive spin waves in a semibounded easy-axis ferromagnet with boundary conditions that describe the partial pinning of spins at the sample boundary.

This paper is organized as follows. In Sec. 2, we substantiate the application of the method of “images.” In Sec. 3, we present basic formulas that are necessary to describe the nonlinear dynamics of a semi-infinite sample. In Sec. 4, we obtain and analyze two classes of new solitons. As in [15], [16], the first one contains solitons localized near the sample boundary. The second class includes moving solitons, which are characterized by elastic collisions with each other and the sample boundary. Edge solitons have specific frequency and modulation properties. Moving solitons change the core structures during the collision with the sample boundary. It is shown in Sec. 5 that any perturbation of a semi-infinite sample can be described in terms of the ideal gas of magnetic solitons and quasiparticles of the spin wave spectrum. We obtain a series of new conservation laws guaranteeing that solitons satisfy the correct conditions at the sample boundaries.

2. Method of “images”

We recall that when integrating the Landau–Lifshitz model

$$\partial_{t} \mathbf{S}=[\mathbf{S} \times (\partial_{x}^2 \mathbf{S}+\mathbf{e} (\mathbf{S} \cdot \mathbf{e}))], \qquad \mathbf{S}^2=1, $$

(2.1)

in the interval $-\infty<x<\infty$, the field $\mathbf{S}(x,t)$ is assumed to be differentiable with respect to $x$ and $t$ a required number of times. Equation (2.1) is then equivalent to the commutativity condition for two differential operators [3], [21]:

$$\begin{aligned} \, &[\partial_x - L, \partial_t - A]=0, \\ &L=-i\sum_{\alpha=1}^{3} w_\alpha (\lambda)S_\alpha \sigma_\alpha, \qquad A =-i\sum_{\alpha=1}^{3}(w_\alpha(\lambda) [\mathbf{S} \times \partial_x \mathbf{S}]_\alpha+2 a_\alpha (\lambda) S_\alpha) \sigma_\alpha, \nonumber \end{aligned}$$

(2.2)

where $w_\alpha(\lambda)$ are rational functions of the spectral parameter:

$$w_1=w_2 = \frac{1}{4}(\lambda+\lambda^{-1}),\qquad w_3 = \frac{1}{4}(\lambda-\lambda^{-1}),$$

$\sigma_\alpha$ are the Pauli matrices, and $a_1 (\lambda) =-w_2 (\lambda) w_3 (\lambda)$, with cyclic permutations of subscripts $1,2,3$ for other coefficients $a_\alpha(\lambda)$.

We rewrite representation (2.2) in the integrated form. For this, we introduce the matrix $T_0 (x, y, \lambda)$ of translation along the axis $Ox$ from a point $y$ to a point $x$ [21]. Here and hereafter, whenever this does not cause a misunderstanding, we do not indicate the dependence of functions on the time $t$. The matrix function $T_0$ satisfies the equations

$$ \begin{aligned} \, &\partial_x T_0(x, y, \lambda) = L(x, \lambda) T_0(x, y, \lambda),\qquad \partial_y T_0(x, y, \lambda) = - T_0(x, y, \lambda) L(y, \lambda), \\ &\partial_t T_0(x, y, \lambda) =A(x, \lambda) T_0(x, y, \lambda) - T_0(x, y, \lambda) A(y, \lambda) \end{aligned}$$

(2.3)

with the normalization condition $T_0(x, x, \lambda)=I$, where $I$ is the unit matrix. Hence, in view of the tracelessness of the matrix $L$, we obtain $\det T_0(x, y, \lambda) = 1$. The superposition property

$$T_0(x, y, \lambda) T_0(y, z, \lambda)=T_0(x, z, \lambda)$$

holds. Because the matrices $L(\lambda)$ and $A(\lambda)$ have the special forms

$$\begin{alignedat}{2} L(-\lambda^{-1}) &= \sigma_3 L(\lambda) \sigma_3, &\qquad L^*(\lambda^*) &= \sigma_2 L(\lambda) \sigma_2,\\ A(-\lambda^{-1}) &= \sigma_3 A(\lambda) \sigma_3, &\qquad A^*(\lambda^*) &= \sigma_2 A(\lambda) \sigma_2, \end{alignedat}$$

Eqs. (2.3) imply the involution properties

$$T_0(x, y, -\lambda^{-1}) = \sigma_3 T_0(x, y, \lambda) \sigma_3, \qquad T_0^*(x, y, \lambda^*) = \sigma_2 T_0(x, y, \lambda) \sigma_2.$$

To make initial boundary-value problem (1.2)–(1.5) on the semiaxis $0 \leq x< \infty$ tractable by the traditional scheme of the inverse scattering transform method, we continue the field $\mathbf{n}(x, t)$ to the negative axis as an even function:

$$\mathbf{S}(x, t)=\begin{cases} \mathbf{n}(x, t), & 0 \leq x <+\infty, \\ \mathbf{n}(-x, t), & -\infty<x < 0.\end{cases} $$

(2.4)

The continuation $\mathbf{S}(x, t)$ is continuous at $x=0$,

$$\mathbf{S}(-0, t)=\mathbf{S}(+0, t)=\mathbf{n}(x=+0, t), $$

(2.5)

but its first derivative with respect to $x$ has a jump:

$$\partial_x \mathbf{S}|_{x=+0}-\partial_x \mathbf{S}|_{x=-0}=2 \partial_x \mathbf{n}|_{x=+0}.$$

Taking these formulas into account, we treat initial boundary condition (1.4) for the field $\mathbf{n}(x, t)$ as additional constraints imposed on the choice of the functions $\mathbf{S}(x, t)$:

$$\Delta \mathbf{S}|_{x=0}=0, \qquad [\mathbf{S} \times (\Delta \partial_x \mathbf{S} + 2 h \mathbf{e})]|_{x=0}=0, $$

(2.6)

where $\Delta f|_{x=0}=f(x=+0)-f(x=-0)$.

It was shown in [14] that constraint (2.6) is equivalent to the matrix relation

$$A_{+}(\lambda) K(\lambda) - K(\lambda) A_{-}(\lambda)=0, $$

(2.7)

where $A_\pm (\lambda) \equiv A(x, \lambda)|_{x = \pm 0}$, $K(\lambda)=2 w_3 (\lambda) I+ ih \sigma_3$. Following [11], [12], to take Eq. (2.7) into account, we modify $T_0 (x, y, \lambda)$ and introduce the new translation matrix

$$T(x, y, \lambda)=\begin{cases} T_0 (x, y, \lambda),& x y>0, \\ T_0 (x, +0,\lambda) K(\lambda) T_0 (-0, y, \lambda),& x>0>y, \\ T_0 (x, -0,\lambda) K^{-1}(\lambda) T_0 (+0, y, \lambda),& x<0<y, \end{cases} $$

(2.8)

which is not unimodular:

$$\det T(x, y, \lambda)=[4 w_3^2 (\lambda)+h^2]^{(\operatorname{sgn} x - \operatorname{sgn} y)/2}.$$

Its normalization and superposition properties change,

$$ \begin{aligned} \, &T(x, x, \lambda)=I \quad \text{for}\quad x\ne 0,\qquad T(x, y, \lambda)=T^{-1}(y, x, \lambda), \\ &T(+0, -0, \lambda)=T^{-1}(-0, +0, \lambda)=K(\lambda), \end{aligned}$$

(2.9)

but the involutions

$$T(x, y, -\lambda^{-1}) = \sigma_3 T(x, y, \lambda) \sigma_3, \qquad T^*(x, y, \lambda^*) = \sigma_2 T(x, y, \lambda) \sigma_2 $$

(2.10)

are preserved. In accordance with (2.3) and (2.8), the translation matrix $T(x, y, \lambda)$ satisfies the differential equations

$$ \begin{aligned} \, &\partial_x T(x, y, \lambda) = L(x, \lambda) T(x, y, \lambda),\qquad \partial_y T(x, y, \lambda) = -T(x, y, \lambda) L(y, \lambda),\\ &\partial_t T(x, y, \lambda) =A(x, \lambda) T(x, y, \lambda) - T(x, y, \lambda) A(y, \lambda), \end{aligned}$$

(2.11)

which coincide with Eqs. (2.3) for $T_0(x, y, \lambda)$ on the interval $-\infty<x< \infty$. This allows including initial boundary-value problem (1.2)–(1.5) for the Landau–Lifshitz equation on the semiaxis into the traditional scheme of the inverse scattering transform method on the interval $-\infty<x<\infty$. The distinctions are related to the necessity to take the additional symmetry of the field $\mathbf{S}(x, t)$ into account:

$$\mathbf{S}(-x, t)=\mathbf{S}(x, t). $$

(2.12)

We next consider this in more detail.

3. Jost functions and spectral data

Symmetry (2.12) generates new properties of the operators:

$$A(-x, -\lambda) = A(x, \lambda), \qquad L(-x, -\lambda) = -L(x, \lambda), \qquad (4 w_3^2 (\lambda)+h^2) K^{-1}(\lambda)=-K(-\lambda);$$

if they are taken into account, relations (2.11) imply the proportionality of the translation matrices $T(x, y, \lambda)$ and $T(-x, -y, -\lambda)$. The proportionality coefficient is fixed by the last equality in (2.9):

$$T(x, y, \lambda) = \operatorname{sgn}(x y) T(-x, -y, -\lambda)\,[4 w_3^2 (\lambda)+h^2]^{(\operatorname{sgn} x -\operatorname{sgn} y)/2}. $$

(3.1)

Following the standard scheme of the inverse scattering transform method for an infinite medium, we introduce the Jost functions

$$\begin{aligned} \, & T_\pm (x, \lambda, t)=\lim_{y \to \pm \infty} [T(x, y, \lambda) e^{-i w_3(\lambda) y\sigma_3}], \nonumber\\ & \det T_\pm (x, \lambda) = [4 w_3^2 (\lambda)+h^2]^{(\operatorname{sgn} x \mp 1)/2}. \end{aligned}$$

(3.2)

They serve as fundamental solutions of the auxiliary linear system

$$\partial_x T_\pm = L(\lambda) T_\pm $$

(3.3)

under the asymptotic boundary conditions

$$T_{\pm}(x, t, \lambda) \to \varphi_0 (x, \lambda) \equiv e^{-i w_3(\lambda) x\sigma_3}, \qquad x \to \pm \infty, $$

(3.4)

which are consistent with the behavior of the initial field $\mathbf{n}(x, t)$ (1.3) as $x \to \pm \infty$.

The Jost solutions are defined simultaneously on the real $\lambda$ axis and are therefore related to each other by a transition matrix $Q(\lambda)$:

$$T_{-} (x, \lambda)=T_{+} (x, \lambda) Q(\lambda), \qquad \lambda \in \mathbb{R}. $$

(3.5)

In what follows, we use the notation $\Psi^{(1)}$ and $\Psi^{(2)}$ for the first and second columns of the matrix $\Psi$. The column vectors $T_{-}^{(1)}(x, \lambda)$ and $T_{+}^{(2)}(x, \lambda)$ of the matrices $T_\pm (x, \lambda)$ are analytically continued from the real $\lambda$ axis to the domain $\operatorname{Im} \lambda>0$, and the columns $T_{-}^{(2)}(x, \lambda)$ and $T_{+}^{(1)}(x, \lambda)$ are analytic functions in the lower half-plane $\operatorname{Im} \lambda< 0$, except, possibly, the simple poles of the function $T_{+}(x, \lambda)$ at points that are roots of the equations $2 w_3(\lambda) \pm ih=0$. These poles are inherited from the matrix $K^{-1}(\lambda)$ (see (2.8) and (3.2)).

The properties of the symmetry of translation matrix (2.10), (3.1) and of asymptotic conditions (3.4) are taken over by Jost solutions (3.2) and can be continued from the real $\lambda$ axis to the complex plane:

$$\begin{aligned} \, &T_\pm^*(x, \lambda^*)=\sigma_2 T_\pm (x, \lambda) \sigma_2, \qquad T_\pm (x, -\lambda^{-1})=\sigma_3 T_\pm (x, \lambda) \sigma_3, \nonumber\\ &T_\pm (x, \lambda) = \pm \operatorname{sgn} x\sigma_2 T_\mp^*(-x, -\lambda^*) \sigma_2 [4 w_3^2 (\lambda)+h^2]^{(\operatorname{sgn} x \mp 1)/2}. \end{aligned}$$

(3.6)

These relations refine the algebraic structure of the transition matrix:

$$ \begin{aligned} \, &Q(\lambda)= \begin{pmatrix} a(\lambda) & - \bar{b}(\lambda) \\ b(\lambda) & \bar{a}(\lambda) \end{pmatrix}, \qquad a(\lambda)\bar{a}(\lambda)+b(\lambda)\bar{b}(\lambda)=4 w_3^2 (\lambda)+h^2,\\ &a(\lambda)=a(-\lambda^{-1})=-a^*(-\lambda^*),\quad \operatorname{Im} \lambda \geq 0, \qquad \bar{a}(\lambda)=a^*(\lambda^*),\quad \operatorname{Im} \lambda \leq 0, \\ &\bar{b}(\lambda)=b^*(\lambda), \qquad b(-\lambda)=b(\lambda)=-b(-\lambda^{-1}),\qquad \lambda \in \mathbb{R}. \end{aligned}$$

(3.7)

In writing formulas (3.7) for $a(\lambda)$ and $\bar{a}(\lambda)$, we took into account that the relation between Jost solutions (3.5) leads to the representations

$$a(\lambda)= \frac{\det[T_{-}^{(1)}(x, \lambda),T_{+}^{(2)}(x, \lambda)]}{\det T_{+}(x, \lambda)}, \qquad \bar{a}(\lambda)= \frac{\det[T_{+}^{(1)}(x, \lambda),T_{-}^{(2)}(x, \lambda)]}{\det T_{+}(x, \lambda)}, $$

(3.8)

where $\det T_{+}(x, \lambda)=[4 w_3^2 (\lambda)+h^2]^{(\operatorname{sgn} x - 1)/2}$. It hence follows that the functions $a(\lambda)$ and $\bar{a}(\lambda)$ can be analytically continued from the real $\lambda$ axis to the respective domains $\operatorname{Im} \lambda>0$ and $\operatorname{Im} \lambda<0$ (except, possibly, the points where $2 w_3 (\lambda) \pm i h =0$).

In the domain of its analyticity, the function $a(\lambda)$ can have zeros $\lambda\!=\!\lambda_j$ ($\operatorname{Im} \lambda_j\!> 0$), which we assume to be simple. In addition, it can vanish at the points $\lambda=\lambda_0$ ($\operatorname{Im} \lambda_0>0$), which are roots of the equations $2 w_3 (\lambda) \pm i h =0$. In what follows, we show that the zeros $\lambda_j$ parameterize solitons, and the zeros $\lambda_0$ do not define soliton states. The positions of the zeros of the coefficient $a(\lambda)$ (if they exist) must satisfy constraints (3.7):

$$a(\lambda_j)=a(-\lambda^{-1}_j)=-a^*(-\lambda^*_j)=0.$$

Therefore, imaginary zeros combine to form the pairs

$$\lambda=ib_s, \, ib_s^{-1},\qquad b_s>0,\qquad s=1,2,\ldots, M, $$

(3.9)

and the complex zeros combine to form “quartets”:

$$\lambda =\lambda_k,\;-\lambda_k^{-1},\;-\lambda_k^*,\;(\lambda_k^*)^{-1},\qquad \operatorname{Im} \lambda_k>0,\qquad k=1,2,\ldots, N. $$

(3.10)

It follows from representation (3.8) that the condition $a(\lambda_j)=0$ implies the proportionality of the columns $T_{-}^{(1)}(x, \lambda_j)$ and $T_{+}^{(2)}(x, \lambda_j)$:

$$T_{-}^{(1)}(x, \lambda_j)=\gamma(\lambda_j)T_{+}^{(2)}(x, \lambda_j). $$

(3.11)

Reductions (3.6) lead to constraints imposed on the choice of the normalization constants $\gamma(\lambda_j)$:

$$\gamma(ib_s^{-1})=-\gamma(ib_s), \qquad |\gamma(ib_s)|^2 =4 w_3^2 (ib_s)+h^2 >0, \qquad s=1,2,\ldots, M;$$

(3.12)

$$\gamma(-\lambda_k^{-1})=-\gamma(\lambda_k), \qquad \gamma(\lambda_k) \gamma(-\lambda_k^*)=4 w_3^2(\lambda_k)+h^2, \qquad k=1,2,\ldots, N.$$

(3.13)

Relations (3.12) are valid only for

$$|h|>\max_{s} \biggl[\frac{b_s+b_s^{-1}}{2}\biggr]. $$

(3.14)

The transition matrix $Q(\lambda)$ is independent of the coordinate $x$. Hence, using formulas (2.8), (2.9), (3.5), and (3.6), we obtain the representation

$$\begin{aligned} \, Q(\lambda)&=T_{+}^{-1}(x, \lambda)|_{x=+0}\, K(\lambda) T_{-}(x, \lambda)|_{x=-0}={} \nonumber\\ &=\sigma_2 T_{+}^{\mathrm{T}}(x, \lambda)|_{x=+0}\, \sigma_2 K(\lambda) \sigma_2 T_{+}^*(x, -\lambda^*)|_{x=+0}\, \sigma_2 ={} \nonumber\\ &=T^\dagger_{+}(x, \lambda^*)|_{x=+0}\, K(\lambda) \sigma_2 T_{+}^*(x, -\lambda^*)|_{x=+0}\, \sigma_2, \end{aligned}$$

(3.15)

which is useful for the further analysis. Here, the superscript ${}^\mathrm{T}$ denotes transposition and the symbol ${}^\dagger$, Hermitian conjugation.

We calculate the matrix element $a(\lambda)$ using the formula that is next to the last one in chain (3.15):

$$\begin{aligned} \, a(\lambda)={}& (2 w_3(\lambda)+ ih)[T_{+}(x, \lambda)|_{x=+0}]_{22} [T_{+}^*(x, -\lambda^*)|_{x=+0}]_{22} +{} \nonumber\\ &+(2 w_3(\lambda)- ih)[T_{+}(x, \lambda)|_{x=+0}]_{12} [T_{+}^*(x, -\lambda^*)|_{x=+0}]_{12}. \end{aligned}$$

(3.16)

To calculate $b(\lambda)$, we use the last expression in the right-hand side of (3.15). The element $b(\lambda)$ is then expressed in terms of the same functions as $a(\lambda)$:

$$\begin{aligned} \, b(\lambda)={}&(2 w_3(\lambda)+ ih)[T_{+}^*(x, \lambda^*)|_{x=+0}]_{12} [T_{+}^*(x, -\lambda^*)|_{x=+0}]_{22} -{} \nonumber\\ &-(2 w_3(\lambda)- ih)[T_{+}^*(x, \lambda^*)|_{x=+0}]_{22} [T_{+}^*(x, -\lambda^*)|_{x=+0}]_{12}. \end{aligned}$$

(3.17)

The function $b(\lambda)$ is defined for $\lambda \in \mathbb{R}$. Therefore, the right-hand side of (3.17) contains the limits of the components of $T_{+}^{(2)}(\lambda)$ on the real $\lambda$ axis taken in the domain of their definition $\operatorname{Im} \lambda> 0$.

To construct solutions of Landau–Lifshitz equation (1.2) and the conservation laws, we need information about the asymptotic behavior of the function $a(\lambda)$ as $\lambda \to \infty$. In accordance with (3.16), finding a series in powers of $\lambda^{-1}$ for $a(\lambda)$ reduces to expanding the Jost function $T_{+}(x, \lambda)$ for $x>0$, $|\lambda|\gg 1$.

We seek the required solution of system (3.3), (3.4) in the form [3], [21]

$$T_{+}(x, \lambda) =(I+\Phi(x, \lambda)) e^{-iw_3 (\lambda) x \sigma_3+Z(x, \lambda)}, $$

(3.18)

where we represent the antidiagonal ($\Phi$) and diagonal ($Z$) matrix functions as series

$$\Phi(x, \lambda) =\sum_{n=1}^{\infty} \frac{\Phi_n (x)}{\lambda^n},\qquad Z(x, \lambda) =\sum_{n=1}^{\infty} \frac{Z_n (x)}{\lambda^n}$$

with the asymptotic behavior

$$\Phi(x, \lambda) \to 0,\quad Z(x, \lambda) \to 0 \quad \text{for} \quad x \to+\infty.$$

We substitute (3.18) in Eq. (3.3) and separate the diagonal and antidiagonal parts. After simple calculations, we obtain

$$ \begin{aligned} \, &Z(x, \lambda) = i\int_x^{\infty} [w_3 (\lambda) (n_3 (x')-1) \sigma_3 +w_1 (\lambda) [n_1 (x') \sigma_1 + n_2 (x') \sigma_2] \Phi(x',\lambda)]\, d x', \\ &\partial_x \Phi + 2 i w_3 n_3 \sigma_3 \Phi - iw_1 \Phi (n_1 \sigma_1 + n_2 \sigma_2) \Phi +iw_1 (n_1 \sigma_1 + n_2 \sigma_2)=0. \end{aligned}$$

(3.19)

Equating the coefficients at like powers of $\lambda$, we sequentially calculate the coefficients $\Phi_n (x)$ and $Z_n (x)$. We present the first ones:

$$\Phi_0 = \frac{(n_1 \sigma_1 + n_2 \sigma_2) \sigma_3}{1+n_3},\qquad 2 Z_0=\ln \frac{1+n_3}{2}+i\sigma_3 \int_{x}^{\infty}\, d x' p(x'),$$

where $p(x)=(n_1 \partial_x n_2 - n_2 \partial_x n_1)/(1+n_3)$,

$$ \begin{aligned} \, &\Phi_1= -2 i \partial_x \biggl(\frac{n_1 \sigma_1 + n_2 \sigma_2}{1+n_3} \biggr),\\ &Z_1= -i\biggl(\frac{\sigma_3 \partial_x n_3}{1+n_3} -ip\biggr)+\frac{i\sigma_3}{2}\int_{x}^{\infty} d x'\, [(\partial_{x'}\mathbf{n})^2+1-n_3^2]. \end{aligned}$$

(3.20)

For $x>0$, $|\lambda|\gg 1$, the leading term of the asymptotic expansion of $T_{+}(x, \lambda)$ has the form

$$T_{+}(x, \lambda) =(I+\Phi_0(x)+O(\lambda^{-1}))\exp \biggl[-\frac{i\lambda x}{4} \sigma_3+Z_0(x)+O(\lambda^{-1}) \biggr]. $$

(3.21)

The asymptotic expansion of the Jost function $T_{-}(x, \lambda)$ in powers of $\lambda^{-1}$ for $x>0$ follows from $T_{+}(x, \lambda)$ by the formal replacement

$$\mathbf{n}(x) \to \mathbf{S}(x),\qquad \int_{x}^{+\infty} \to \int_{x}^{-\infty}.$$

We note that for $x>0$, the identity

$$\int_{x}^{-\infty}d x' \biggl(\frac{S_1 \partial_{x'} S_2 - S_2 \partial_{x'} S_1}{1+S_3}\biggr)=\int_{x}^{+\infty} d x'\, p(x')$$

holds. If these remarks are taken into account, the comparison of formulas (2.8) and (3.2) for $T_{+}(x, \lambda)$ and $T_{-}(x, \lambda)$ leads to the conclusion that the leading term of the expansion of $T_{-}(x, \lambda)$ for $x>0$, $|\lambda|\gg 1$ differs from (3.21) only in the factor $\lambda/2$ inherited from the matrix $K(\lambda)$:

$$T_{-}(x, \lambda) = \frac{\lambda}{2}\,(I+\Phi_0(x)+O(\lambda^{-1}))\exp \biggl[-\frac{i\lambda x}{4} \sigma_3+Z_0(x)+O(\lambda^{-1}) \biggr]. $$

(3.22)

The series for the Jost functions $T_{\pm}(x, \lambda)$ in powers of $|\lambda|\ll 1$ near the second singular point $\lambda=0$ are reconstructed from the asymptotic expansions for $|\lambda|\gg 1$ using second reduction (3.6).

Taking these remarks into account, we use representation (3.16) to obtain the estimates

$$a(\lambda)=\frac{\lambda}{2}+O(1) \quad \text{for} \quad |\lambda|\gg 1;\quad a(\lambda)=-\frac{1}{2 \lambda}+O(1) \quad \text{for} \quad |\lambda|\ll 1. $$

(3.23)

The explicit form of the analytic function $a(\lambda)$ can be reconstructed from its zeros, poles, asymptotic behavior near singular points, and the reflection coefficient $b(\lambda)$ [3], [21]:

$$\begin{aligned} \, a(\lambda)={}&[2 w_3(\lambda)+i\alpha]\prod_{s=1}^M \biggl(\frac{\lambda- ib_s}{\lambda+ ib_s}\biggr)\biggl(\frac{\lambda- ib_s^{-1}}{\lambda+ ib_s^{-1}}\biggr)\prod_{k=1}^N \biggl(\frac{\lambda- \lambda_k}{\lambda+ \lambda_k}\biggr) \times{} \nonumber\\ &\times \biggl(\frac{\lambda+ \lambda_k^*}{\lambda- \lambda_k^*}\biggr) \biggl(\frac{\lambda+ \lambda_k^{-1}}{\lambda- \lambda_k^{-1}}\biggr)\biggl(\frac{\lambda- (\lambda_k^*)^{-1}}{\lambda+ (\lambda_k^*)^{-1}}\biggr)\times{} \nonumber\\ &\times\exp \biggl(\frac{1}{2 \pi i} \int_{-\infty}^{+\infty} d\mu \,\frac{\ln[1-|b(\mu)|^2 (4 w_3^2 (\mu)+h^2)^{-1}]}{\mu-\lambda} \biggr). \end{aligned}$$

(3.24)

Here, $\operatorname{Im} \lambda \geq 0$, $\alpha^2=h^2$. To have a specific relation between the parameters $\alpha$ and $h$, we set $\lambda=1$ in representation (3.16). Using reductions (3.6), we bring the result to the form

$$a(\lambda=1)=i h \det T_{+}(+0, \lambda=1)=i h.$$

On the other hand, from (3.24) with $\lambda=1$, we find

$$a(\lambda=1)=i\alpha (-1)^M.$$

In the calculations, we took the symmetry properties of the functions $b(\lambda)$ and $w_3 (\lambda)$ into account. The comparison of the formulas yields a relation between the parameters $h$ and $\alpha$,

$$h=\alpha (-1)^M, $$

(3.25)

which depends only on the number $M$ of pairs of imaginary zeros of the coefficient $a(\lambda)$.

Thus, using auxiliary equation (3.3), we mapped the solutions of the initial boundary-value problem for the Landau–Lifshitz model on the semiaxis into the complete set of scattering data. This set contains the spectral densities $b(\lambda)$, $-\infty<\lambda<+\infty$, discrete zeros $\lambda_j$ of the coefficient $a(\lambda)$, and the normalization constants $\gamma(\lambda_j)$, $j=1,2,\ldots, 2 M+4 N$. In the new variables, the integration of the Landau–Lifshitz model reduces to solving linear differential equations. From the second equation in (2.11), we obtain the usual time dependence of scattering data [3]:

$$a(t, \lambda)=a(0, \lambda),\quad b(t, \lambda)=b(0, \lambda) e^{-4 i w_1^2(\lambda) t},\quad \gamma(t, \lambda_j)=\gamma(0, \lambda_j)e^{-4 iw_1^2(\lambda_j) t}. $$

(3.26)

We determine the values of the integration constants $a(0, \lambda)$, $b(0, \lambda)$, $\gamma(0, \lambda_j)$ from (3.3) using the given initial distribution of magnetization $\mathbf{n}_0(x)$ in Eq. (1.5).

From the physical standpoint, the spectral densities $b(\lambda, t)$ parameterize dispersive spin waves, and the discrete parameters $\lambda_j$ parameterize particle-like magnetic solitons. In the next section, we calculate purely soliton states in a semi-infinite sample in the absence of dispersive waves (for $b(\lambda)=\bar{b}(\lambda) \equiv 0$).

4. Construction of soliton solutions using the Riemann problem

To pass from the scattering data to the description of magnetization in the sample, methods of the theory of functions of complex variables are to be used. The inverse spectral transform on the semiaxis ${0<x<+\infty}$ differs from the spectral transform on the interval $-\infty<x<0$. However, it is possible to write the underlying Riemann problems uniformly using piecewise constant functions of the coordinate $x$. We introduce matrix functions $P_{+}(x, \lambda)$ and $P_{-}(x, \lambda)$ that are analytic in the respective upper ($\operatorname{Im} \lambda>0$) and lower ($\operatorname{Im} \lambda<0$) half-planes of the complex $\lambda$-plane:

$$ \begin{aligned} \, &P_{+}(x, \lambda)=(T_{-}^{(1)}(x, \lambda), T_{+}^{(2)}(x, \lambda))\varphi_0^{-1}(x, \lambda)\operatorname{diag}[S_2^*(x, \lambda^*), S_1^*(x, \lambda^*)],\\ &P_{-}(x, \lambda)=(T_{+}^{(1)}(x, \lambda), T_{-}^{(2)}(x, \lambda))\varphi_0^{-1}(x, \lambda)\operatorname{diag}[S_1(x, \lambda), S_2(x, \lambda)]. \end{aligned}$$

(4.1)

Their explicit forms are different for $x>0$ and $x<0$ and are defined concretely by factors that are piecewise constant with respect to $x$,

$$\begin{aligned} \, &S_1(x, \lambda)=H(x)+(2 w_3 (\lambda) -i\alpha) H(-x),\\ &S_1^{-1}(x, \lambda)=H(x)+(2 w_3 (\lambda) -i\alpha)^{-1} H(-x),\\ &S_2(x, \lambda)=H(-x)+(2 w_3 (\lambda) -i\alpha)^{-1} H(x),\\ &S_2^{-1}(x, \lambda)=H(-x)+(2 w_3 (\lambda) -i\alpha) H(x), \end{aligned}$$

where $H(x)=(1+\operatorname{sgn}x)/2$ is the Heaviside step function. The calculation of $P_\pm(x, \lambda)$ reduces to solving the matrix Riemann problem that is formulated as follows.

In the domains $\operatorname{Im} \lambda \geq 0$ and $\operatorname{Im} \lambda \leq 0$, construct the respective analytic functions $P_{+}(x, \lambda)$ and $P_{-}(x, \lambda)$ that satisfy the matching condition on the real $\lambda$ axis

$$P_{-}(x, \lambda)=\frac{P_{+}(x, \lambda)\,\varphi_0 (x, \lambda)}{a_m (x, \lambda)} \begin{pmatrix} 1 & - \bar{b}_m(x, \lambda) \\ -b_m(x, \lambda) & 1 \end{pmatrix} \varphi_0^{-1} (x, \lambda),\qquad \lambda \in \mathbb{R}, $$

(4.2)

and the constraints

$$\begin{aligned} \, &P_{\pm}(x, -\lambda^{-1})=\sigma_3 P_\pm(x, \lambda) \sigma_3, \end{aligned}$$

$$P_\pm(x, \lambda)=\mp i\operatorname{sgn}x \sigma_2 P_\pm^*(-x, -\lambda^*) \sigma_1 \operatorname{diag}[\theta(\mp x, \lambda), \theta(\pm x, -\lambda)],$$

(4.3)

$$P_{+}(x, \lambda)=\sigma_2 P^*_{-}(x, \lambda^*) \sigma_2.$$

(4.4)

To simplify the expressions, we use the notation

$$\begin{aligned} \, &\begin{alignedat}{2} &a_m (x, \lambda)= \det P_{+}(x, \lambda)= a(\lambda) S_1^{-1}(x, \lambda) S_2^*(x, \lambda^*),&\quad &\operatorname{Im} \lambda \geq 0,\\ &\bar{a}_m (x, \lambda)= \det P_{-}(x, \lambda)= a_m^*(x, \lambda^*),&\quad &\operatorname{Im} \lambda \leq 0; \end{alignedat}\\ &b_m (x, \lambda)= b(\lambda) [S_1^*(x, \lambda^*)]^{-1} S_2^*(x, \lambda^*),\qquad \bar{b}_m (x, \lambda)=b_m^* (x, \lambda),\qquad \lambda \in \mathbb{R};\\ &\theta(x, \lambda)=H(x)+f(\lambda) H(-x),\qquad f(\lambda)=\frac{i\alpha-2 w_3 (\lambda)}{i\alpha+2 w_3 (\lambda)}. \end{aligned}$$

Matching condition (4.2) is another form of the relation between Jost solutions (3.5) for $\lambda \in \mathbb{R}$. Reductions (4.3) and (4.4) follow from reductions (3.6) for the Jost functions. It is useful for the further analysis to rewrite relation (4.4) in another form

$$P_{+}^{-1}(x, \lambda)=\frac{\sigma_2 P^{\mathrm{T}}_{+}(x, \lambda) \sigma_2}{\det P_{+}(x, \lambda)}=\frac{P_{-}^\dagger (x, \lambda^*)}{a_m (x, \lambda)},\qquad \operatorname{Im} \lambda \geq 0. $$

(4.5)

We note that solutions of Riemann problem (4.2) are defined up to multiplication by a nondegenerate matrix that is independent of $\lambda$. We use asymptotic formulas for $P_{\pm}(x, \lambda)$ as $\lambda \to \infty$ to eliminate this arbitrariness. An important feature of the used approach is that solutions of Riemann problem (4.2)–(4.4) on the intervals $-\infty<x<0$ and $0<x<\infty$ are calculated independently. To obtain the magnetization field in the sample, it suffices to carry out calculations only on the semiaxis $0 \leq x<\infty$. For $x>0$, as $\lambda \to \infty$, the asymptotics of the function $P_{-}(x, \lambda)$ is given by formulas (3.21) and (3.22):

$$\begin{aligned} \, &P_{-}(\lambda) \to g_0 =\begin{pmatrix} 1 & -\dfrac{n_{-}}{1+n_3} \\ \dfrac{n_{+}}{1+n_3}&\hphantom{-}1 \end{pmatrix} \begin{pmatrix} r & 0 \\ 0 & r^* \end{pmatrix},\nonumber\\ &r=\sqrt{\frac{1+n_3}{2}}\,\exp\biggl(\frac{i}{2} \int_x^{\infty} dx'\, p(x')\biggr), \end{aligned}$$

(4.6)

where $n_{\pm}=n_1 \pm i n_2$ and $g_0^\dagger g_0 =I$.

We then restrict ourself to constructing purely soliton excitations ($b=\bar{b}=0$). Matching condition (4.2) is then simplified: for $x>0$ and with expression (4.5) taken into account, it becomes

$$P_{-}(\lambda) P_{-}^\dagger(\lambda^*)=I,\qquad \lambda \in \mathbb{R}. $$

(4.7)

The soliton matrix $P_{-}(\lambda)$ is a meromorphic function in the complex $\lambda$ plane. Its poles coincide with zeros $\lambda=\lambda_j$ (Eqs. (3.9) and (3.10)) of the expression

$$\det P_{-}^\dagger (\lambda^*)=\frac{a(\lambda)}{2 w_3 (\lambda)+i\alpha}.$$

Therefore, $P_{-}(\lambda)$ admits the representation

$$P_{-}(\lambda) =g_0 \Psi(\lambda),\qquad \Psi(\lambda)=I+\sum_{k=1}^{2 M+4 N} \frac{A_k}{\lambda-\lambda_k}. $$

(4.8)

The requirement of the absence of poles in the left-hand side of (4.7) leads to the $2 M+4 N$ independent matrix equations

$$P_{-}(\lambda_j^*) A_j^\dagger =0,\qquad j=1,2,\ldots, 2M+4 N,$$

which imply that the matrix $A_j$ is degenerate and can be written in the form [21], [22]

$$(A_j)_{\alpha \beta}=(X_j)_\alpha (\xi_j^*)_\beta,\qquad \alpha, \beta =1, 2,$$

where $\xi_j \in \mathrm{Ker} P_{-}(\lambda_j^*)$, i.e.,

$$P_{-}(\lambda_j^*) \xi_j = 0. $$

(4.9)

Using formulas (3.11) and (4.1), we find the algebraic structure of the second degenerate matrix $P_{-}(\lambda_j^*)$ for $x>0$:

$$\begin{aligned} \, P_{-}(\lambda_j^*)&=(T_{+}^{(1)}(\lambda_j^*), T_{-}^{(2)}(\lambda_j))\,\varphi_0^{-1}(\lambda_j^*)\operatorname{diag}[1,(2 w_3 (\lambda_j^*)-i\alpha)^{-1}]={} \\ &=i\sigma_2 (T_{+}^{*(2)}(\lambda_j^*), -\gamma^*(\lambda_j) T_{+}^{*(2)}(\lambda_j^*))\varphi_0^{-1}(\lambda_j^*)\operatorname{diag}[1,(2 w_3 (\lambda_j^*)-i\alpha)^{-1}]. \end{aligned}$$

Hence, we immediately find the vectors $\xi_j$:

$$\xi_j = \begin{pmatrix} \nu^*_j (x,t) \\ 1 \end{pmatrix},\qquad \nu_j (x,t)=\kappa(\lambda_j) e^{2 i w_3 (\lambda_j) x -4 i w_1^2 (\lambda_j) t}. $$

(4.10)

The constant complex parameters

$$\kappa(\lambda_j) = \frac{\gamma(\lambda_j, t)|_{t=0}}{2 w_3 (\lambda_j)+i\alpha}$$

satisfy the constraints

$$\kappa(-\lambda_j^{-1})=-\kappa(\lambda_j),\qquad \kappa(\lambda_j)\kappa^*(-\lambda_j^*)=f(\lambda_j), $$

(4.11)

where $f(\lambda)=[i\alpha-2 w_3 (\lambda_j)]/[i\alpha+2 w_3 (\lambda_j)]$. The values of $\lambda_j$ are the same as in (3.9) and (3.10).

As a result of the substitution of $\xi_j$ defined in (4.10) in Eq. (4.9), we obtain a linear system for the vectors $X_k$,

$$\xi_j+\sum_{k=1}^{4 N+2 M} M_{j k} X_k =0, \qquad M_{j k}=\frac{(\xi_k^* \cdot \xi_j)}{\lambda_j^*-\lambda_k}.$$

Its solution determines the soliton matrix function $P_{-}(x, t, \lambda)$ for $x>0$:

$$ \begin{aligned} \, &P_{-}(\lambda)=g_0 \Psi(\lambda),\\ &\Psi_{\alpha \beta}(\lambda)=\delta_{\alpha \beta}-\sum_{k,j=1}^{4 N+2 M}\frac{(M^{-1})_{k j} (\xi_j)_{\alpha}(\xi_k^*)_{\beta}}{\lambda-\lambda_k},\qquad \alpha,\beta=1,2, \end{aligned}$$

(4.12)

where

$$(M^{-1})_{k j} =\frac{\partial \ln \det M}{\partial M_{j k}}.$$

We substitute the expression for $P_{-}(\lambda)$ (4.12) in the first formula in (4.3) and set $\lambda=0$ in the obtained equality. This leads to a matrix equation for the components of the easy-axis ferromagnet magnetization:

$$g_0^\dagger \sigma_3 g_0 = \begin{pmatrix} n_3 & -n_{-} e^{i\gamma_0} \\ -n_{+} e^{i\gamma_0}&-n_3 \end{pmatrix} =\Psi(\lambda)|_{\lambda=0}\, \sigma_3,\qquad \gamma_0 = \int_{x}^{+\infty} dx'\, p(x'). $$

(4.13)

The further calculation is simplified by the parameterization

$$\mathbf{n}=(\sin \theta \cos \Phi, \sin \theta \sin \Phi, \cos \theta),$$

where

$$n_3 = \cos \theta, \qquad n_{+}=\sin \theta e^{i\Phi},\qquad \gamma_0 = \int_{x}^{\infty} (1-\cos \theta) \partial_{x'}\Phi\, dx'. $$

(4.14)

Using formulas (4.13) and (4.14), we reconstruct the fields $\theta(x, t)$ and $\Phi(x, t)$ of magnetic solitons in a semi-infinite sample:

$$\cos \theta=\Psi_{11}(\lambda)|_{\lambda=0},\qquad \partial_x \Phi = \frac{1}{2i} \biggl[\frac{1}{\Psi_{11}(x, \lambda)} \frac{\partial}{\partial x}\ln \frac{\Psi_{21}(x, \lambda)}{\Psi_{21}^*(x,\lambda)} \biggr] \Bigg|_{\lambda=0}. $$

(4.15)

We show in what follows that for soliton solutions, the integral that defines the $\Phi$ field can be calculated in explicit form.

5. Interaction of solitons with the sample boundary

5.1. Edge solitons

Magnetic solitons on the semiaxis are divided into two classes as functions of the choice of zeros of the coefficient $a(\lambda)$. Imaginary zeros (3.9) parameterize fixed solitons, whose cores are localized near the sample surface. A pair of zeros of $a(\lambda)$

$$\lambda_1 =ie^\rho,\qquad \lambda_2 =ie^{-\rho},\qquad -\infty<\rho<\infty$$

corresponds to the simplest soliton. Its structure is specified by the functions $\nu_j (x, t)$ in (4.10),

$$\nu_1 (x, t)=-\nu_2 (x, t)=\sqrt{\frac{\alpha-\cosh \rho}{\alpha+\cosh \rho}}\, e^{-x\cosh \rho+it\sinh^2 \rho},$$

where $|\alpha|\!>\!\cosh \rho$. Consequently, such solitons form in a threshold manner in the case where the surface field amplitude is $|h|>\cosh \rho$. In formulas (4.13) and (4.15), $\frac{\Psi_{21}^*}{\Psi_{21}}\big|_{\lambda=0}=e^{2 it \sinh^2 \rho}$; hence, after simple calculations, we find

$$n_3=1 -\frac{2}{1+\sinh^2 y \tanh^2 \rho},\qquad n_{+}=n_1 + in_2 = \frac{2\sinh y\tanh \rho}{1+\sinh^2 y \tanh^2 \rho} e^{i(t \sinh^2 \rho+\varphi_0)}, $$

(5.1)

where $\varphi_0$ is an arbitrary real integration constant,

$$y = x\cosh \rho-\frac{1}{2} \ln \frac{\alpha-\cosh \rho}{\alpha+\cosh \rho}.$$

In this case, $M=1$, and therefore solution (5.1) satisfies boundary condition (1.4) with $h=-\alpha$ (3.25).

In the soliton core, magnetization vector (5.1) performs uniform precession with the frequency ${\omega=\sinh^2 \rho}$ around the axis $Oz$. The position of the soliton center and its core structure depend on the value and the sign of the surface field $h$. In relatively weak positive fields $\cosh \rho<h \leq \sqrt{\cosh (2 \rho)}$, the soliton core has the width

$$d= x_2 - x_1 = \frac{2}{\cosh \rho}\ln \biggl(\coth \rho+\sqrt{1+\coth^2 \rho}\,\biggr)$$

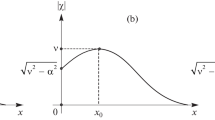
(see Fig. 1), where $x_{1,2}$ are the points where the $n_3$ component vanishes.

Fig. 1.

(a) The $n_3$ component of soliton (5.1) and (b) the spatial distribution of spins in the soliton for field values $\cosh \rho<h \leq \sqrt{\cosh (2 \rho)}$.

We recall that in the exchange approximation, near-boundary solitons have no constraints imposed on their size [16]. The presence of a uniaxial-anisotropy field gives rise to a finite domain of the spatial localization of solitons. In dimensional variables, the characteristic localization scale is determined in units of the magnetic length $l_0=\sqrt{K/\alpha}$. In dimensionless variables, $l_0=1$.

At the center $x_0=[2 \cosh \rho]^{-1} \ln[(h+\cosh \rho)/(h-\cosh \rho)]$ of soliton (5.1), the magnetization reaches the value $n_3=-1$. At the sample boundary $x=0$, for $\cosh \rho < h <\sqrt{\cosh(2\rho)}$, the value $n_3 (x)|_{x=0} = -1+2 \sinh^2 \rho/(h^2-1) \equiv n_3^{(0)}$ varies in the range $0 \leq n_3^{(0)} < 1$. In the soliton localization domain, the vector $\mathbf{n}$ rotates about the axis $Oz$ in an in-phase way; on the left and on the right of the center (for $x<x_0$ and $x>x_0$), the rotation phases differ by $\pi$.

In strong positive fields $h>\sqrt{\cosh (2 \rho)}$, the left soliton edge closely approaches the sample boundary. The soliton has a width of the order of $x_0+d/2$, and $n_3$ varies in the range $-1 \leq n_3^{(0)}<0$ at the sample boundary (Fig. 2a).

Fig. 2.

The $n_3$ component of soliton (5.1) for the field values (a) $h > \sqrt{\cosh (2 \rho)}$, (b) $-\sqrt{\cosh (2 \rho)}<h <-\cosh \rho$, and (c) in the case of the full pinning of surface spins.

Edge solitons of another structure form in the case of the opposite direction of the surface field, $h \leq - \cosh \rho$. In the range $-\sqrt{\cosh (2 \rho)}\ll h< -\cosh \rho$, such solitons are small-amplitude ones (Fig. 2b). In this case, the center of soliton (5.1) coincides with the sample boundary $x=0$. The remagnetization in the soliton core enhances as $|h|$ increases. At the sample boundary, the magnetization approaches the saturation $n_3 \approx -1$.

In the limit $h \to -\infty$, solution (5.1) becomes

$$n_3=1 -\frac{2}{1+[\sinh(x\cosh \rho)\tanh \rho]^2},\qquad n_{+}=\frac{2\sinh(x\cosh \rho)\tanh \rho e^{it\sinh^2 \rho+i\varphi_0}}{1+[\sinh(x\cosh \rho)\tanh \rho]^2}$$

and describes a precessing soliton in the case of the full pinning of edge spins (Fig. 2c):

$$n_3|_{x=0}=-1,\qquad n_3 \to 1 \qquad \text{for} \qquad x \to +\infty.$$

The center of such a soliton coincides with the sample boundary. The magnetization precession is concentrated on the near-boundary layer with a width of the order of $\cosh^{-1} \rho$.

In [20], an approximate solution describing a nonlinear excitation localized near the chain end was described for a semibounded spin chain with a weak exchange anisotropy. In this paper, we discuss the dynamics of the easy-axis ferromagnet with different boundary conditions, one-soliton state (5.1) is close in its structure to the localized excitation obtained in [20]. The soliton can localize near the sample boundary only in the case of a sufficiently nonuniform magnetization field near the sample surface. Therefore, for the formation of solitons (5.1), there is a threshold with respect to the absolute value of the surface anisotropy $h$. At the same time, the core structures of near-boundary solitons and hence their energies are different as functions of the sign of $h$. In Sec. 6, we calculate the total energy of a semibounded sample in the presence of solitons and magnons in it (see (6.5)). The case where an even number of precessing solitons for $h>0$ and an odd number of them for $h<0$ are localized near the sample boundary is energetically advantageous.

The interaction of precessing edge solitons is manifested in additional oscillations of their cores at combination frequencies. We discuss the two-soliton solution of problem (1.2)–(1.5) with four imaginary zeros (3.9) of the coefficient $a(\lambda)$. The final formulas are simplified if the parameterization

$$\lambda_{1,2}=ie^{\pm \rho_1},\qquad \lambda_{3,4}=ie^{\pm \rho_2},\qquad -\infty<\rho_{1,2}<\infty$$

is used. In this case, the vectors $\xi_j$ in (4.10) are

$$\begin{aligned} \, &\xi_{1,2}=\begin{pmatrix} \pm \nu^*_1 \\ 1 \end{pmatrix},\qquad \xi_{3,4} = \begin{pmatrix} \pm \nu^*_2 \\ 1 \end{pmatrix},\\ &\nu_{1,2}=e^{-y_{1,2}+is_{1,2}},\qquad y_{1,2}=x\cosh \rho_{1,2}-\frac{1}{2}\ln \frac{\alpha-\cosh \rho_{1,2}}{\alpha+\cosh \rho_{1,2}},\qquad s_{1,2}=t\sinh^2 \rho_{1,2} + s^{(0)}_{1,2}, \end{aligned}$$

where $s^{(0)}_{1,2}$ are real constants of integration. The independent elements of the matrix $\Psi(\lambda=0)$ in Eq. (4.12) can be represented as

$$\Psi_{11}(\lambda)|_{\lambda=0}=\frac{|u|^2-|q|^2}{|u|^2+|q|^2},\qquad \Psi_{21}(\lambda)|_{\lambda=0}=\frac{2 uq}{|u|^2+|q|^2}, $$

(5.2)

where the functions $u(x, t)$ and $q(x, t)$ are

$$ \begin{aligned} \, &q=\gamma [\tanh \rho_2 \sinh y_2 e^{is_1}-\tanh \rho_1 \sinh y_1 e^{is_2}],\qquad \gamma = \frac{\cosh \rho_{1}-\cosh \rho_{2}}{\cosh \rho_{1}+\cosh \rho_{2}},\\ &u= \frac{1}{2}\tanh \rho_1 \tanh \rho_2[\gamma^2\cosh(y_1+y_2)-\cosh(y_1-y_2)]+\frac{\sinh^2 \rho_1 e^{-i (s_2-s_1)}+\sinh^2 \rho_2 e^{i (s_2-s_1)}}{(\cosh \rho_{1}+\cosh \rho_{2})^2}. \end{aligned}$$

(5.3)

If relations (5.2) and (5.3) are used, the right-hand side of the second equation in (4.15) can be written as a derivative,

$$\frac{1}{2i\Psi_{11}}\,\partial_x \ln \frac{\Psi_{21}}{\Psi_{21}^*} \Bigg|_{\lambda=0}=\frac{1}{2i}\,\partial_x \ln \frac{u^* q}{q^* u}. $$

(5.4)

Therefore, the angles $\theta$ and $\Phi$, and hence the magnetization components of the two-soliton excitation can be explicitly calculated as

$$n_3=1-\frac{2 |q|^2}{|u|^2+|q|^2},\qquad n_{+}=\frac{2 u^* q}{|u|^2+|q|^2}. $$

(5.5)

We recall that in this case, $M=2$, and therefore solution (5.3), (5.5) satisfies mixed boundary condition (1.4) with $h=\alpha$ (3.25). It describes a nonlinear superposition of two edge solitons (5.1). We note that two-soliton excitation (5.3), (5.5) forms only under the condition that the surface field is larger than a certain threshold value: $|h|>\max_{s=1,2} \cosh \rho_{s}$.

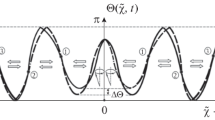
To be more specific, we assume that $\rho_1 > \rho_2$. Then it is easy to verify that the first soliton (the one with $\rho=\rho_1$) is always located closer to the sample boundary than the second one. In the cores of solitons of type (5.1), the magnetization $\mathbf{n}$ precesses with frequencies $\omega_{1,2}=\sinh^2 \rho_{1,2}$ around the anisotropy axis $Oz$. The soliton interaction is manifested in that at the sample boundary $x=0$, the magnetization component $n_3$ does not remain constant, as in the case of single solitons, but oscillates with the frequency $\omega_1-\omega_2$ equal to the difference between the precession frequencies of individual solitons,

$$n_3 (x, t)|_{x=0,t=0}=n_3^{\min} \leq n_3 (x, t)|_{x=0} \leq n_3^{\max}=n_3 (x, t)|_{x=0, t=T/2},$$

where $T=2 \pi/(\omega_1-\omega_2)$ is the oscillation period.

Two-soliton complex (5.3), (5.5) periodically approaches the sample boundary and is then repulsed from it. It then moves as a single whole. The longitudinal shift of the multisoliton as a whole is accompanied by transverse magnetization modulations along the axis $Oz$ with the frequency $\omega_1-\omega_2$ and hence by nutation oscillations of the magnetization precession axis about the $Oz$ direction.

The component $n_3$ for two-soliton solution (5.3), (5.5) is schematically shown in Fig. 3 for $h>0$ and $h<0$ at the time instants $t=0$ (solid lines) and $t=T/2$ (dashed lines). For positive values of the field $h$, the component $n_3$ has only one extremum point, a minimum at point $B$. For negative values of $h$, the $n_3$ component has two extremum points at any instant of time: a maximum at point $A$ and a minimum that periodically shifts between limit positions $B$ and $B'$. Point $A$ barely shifts with time: $A=A'$. At point $A'$, $n_3=1$; and at point $B'$, $n_3=-1$.

Fig. 3.

The $n_3$ component of two-soliton excitation (5.3), (5.5) for (a) $h> 0$ and (b) $h<0$ at the time instants $t=0$ (solid lines) and $t=T/2$ (dashed lines).

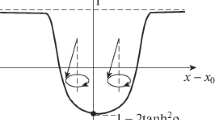
The peak-to-peak magnitude $\Delta x$ of longitudinal oscillations of two-soliton excitation (5.3), (5.5) essentially depends on the ratio of the quantities $\rho_1$ and $\rho_2$ that parameterize the solitons. For $\rho_2\ll \rho_1$, the longitudinal oscillations are not pronounced, and the magnetization dynamics in the two-soliton complex is predominantly determined by nutation oscillations about the precession axis. In such a case, the magnetization behavior in soliton (5.3), (5.5) is illustrated by Fig. 4, which, for $h<0$, shows the trajectories traced by the end of the vector $\mathbf{n}$ with time at different sample points $x$. Figure 4a shows the trajectory located on the right of point $A$ and slightly away from it (Fig. 3b). In Fig. 4(b–d), as $x$ increases, the projection of $n_3$ decreases gradually. Figure 4e corresponds to point $x$ located between limit positions $B$ and $B'$. In Fig. 4(f–i), the projection of $n_3$ increases, tending to the limit value $n_3=1$ as the distance from the sample boundary increases.

Fig. 4.

Trajectories traced by the end of the vector $\mathbf{n}(x=\mathrm{const}, t)$ on the surface of the sphere $\mathbf{n}^2=1$ for soliton (5.3), (5.5) for different values of $x$ in the case $h<0$ and $\rho_2 \ll \rho_1$.

In the limit $|h|=|\alpha|\to \infty$, we have

$$\ln \biggl(\frac{\alpha-\cosh \rho_s}{\alpha+\cosh \rho_s}\biggr) \to 0, \qquad s=1,2.$$

Therefore, for $x=0$, the relations $y_{1,2}=0$ and $q(x, t)|_{x=0}=0$ are valid, and hence two-soliton solution (5.3), (5.5) describes near-boundary magnetization oscillations in the case of the full pinning of surface spins in accordance with the edge condition $n_3|_{x=0}=1$, which differs from boundary condition (1.3) by the sign of the right-hand side for the one-soliton state. Thus, depending on the character of the full pinning of edge spins, the sample boundary captures either an even or an odd number $M$ of precessing solitons:

$$n_3|_{x=0}=(-1)^M. $$

(5.6)

The same dependence was established in [16] for edge solitons in the Heisenberg ferromagnet model.

For $\rho_2 \sim \rho_1$, excitation (5.3), (5.5) periodically shifts to the sample boundary at a significant distance, of the order of its width. In the limit $\rho_1=\rho_2 + \varepsilon$, $\rho_2 \equiv \rho$ ($\varepsilon\ll 1$), the peak-to-peak magnetization of longitudinal oscillations increases without bound. As $\varepsilon \to 0$, we obtain a degenerate exponential–polynomial solution. It is described by (5.5) where $u$ and $q$ are

$$\begin{aligned} \, &u=\frac{\tanh^2 \rho}{2}[\sinh^2 y -\bar{x}^2 \cosh^2 \rho - 4t^2 \cosh^4 \rho]+\frac{\coth^2 \rho}{2}+2 i t \cosh^2 \rho, \nonumber\\ &q=-[2 \sinh^{-1} (2 \rho) \sinh y+ \bar{x} \sinh \rho \cosh y-it\sinh(2 \rho)\sinh y] e^{it \sinh^2 \rho + i s_0}, \\ &y=x \cosh \rho -\frac{1}{2} \ln \biggl(\frac{h-\cosh \rho}{h+\cosh \rho}\biggr),\qquad \bar{x}=x+\frac{h}{h^2-\cosh^2 \rho}, \nonumber \end{aligned}$$

(5.7)

where $s_0$ is a real constant of integration. Excitation (5.5), (5.7) is the soliton in Eq. (5.1) moving towards the sample boundary for $t\ll -1$ and away from it for $t\gg 1$:

$$ \begin{aligned} \, &n_3 (x, |t|\gg 1)=1 -\frac{2}{1+\sinh^2 [y-\ln(4 |t| \cosh^2 \rho)] \tanh^2 \rho},\\ &n_{+}(x, |t|\gg 1)=n_1 + in_2 = \frac{2 \sinh [y-\ln(4 |t| \cosh^2 \rho)] \tanh \rho}{1+\sinh^2 [y-\ln(4 |t| \cosh^2 \rho)]\tanh^2 \rho} e^{it \sinh^2 \rho + i s_0}i\operatorname{sgn} t. \end{aligned}$$

(5.8)

The velocity of soliton (5.8) is $V \backsim (\cosh \rho |t|)^{-1}$ as $|t| \to \infty$. Approaching the sample boundary $x=0$ at $t=0$, soliton (5.8) is reflected from it, acquiring an additional phase shift by $\pi$. This follows from the presence of the factor $\operatorname{sgn} t$ in formula (5.8).

The soliton width (the distance between the points where $n_3=0$) barely changes in this case. In the case of different field values at the collision instant, the magnetization component $n_3$ in excitation (5.5), (5.7) is qualitatively the same as in Fig. 3(a, b) at $t=0$ (solid lines). However, it is interesting that at the instant of collision with the boundary (at $t=0$), all spins in excitation (5.5), (5.7) simultaneously land on the plane obtained by rotating the $Oxz$ plane counterclockwise through the angle $s_0$ about the $Oz$ axis. In Fig. 5a, for clarity, we assume that $s_0=0$. Then at $t = 0$ all spins land on the plane $Oxz$. In this case, for positive field values $h>0$, all of them are tilted in the direction towards the sample boundary: $n_1 (x, t)|_{t=0} \leq 0$ (Fig. 5a); for negative field values $h<0$, only spins located to the left of the point where $n_3=1$ (Fig. 5b) are tilted towards the sample boundary.

Fig. 5.

Excitation (5.5), (5.7) at the instant $t=0$ of collision with the sample boundary for (a) $h>0$ and (b) $h<0$.

5.2. Reflection of solitons from the sample boundary

Complex zeros (3.10) of the function $a(\lambda)$ parameterize another class of solitons. It is formed by moving precessing objects that typically experience elastic pair collisions with each other and elastic reflections from the sample boundary. In the process of approaching the boundary, each such soliton significantly changes its internal structure. It is therefore impossible to describe the soliton motion in finite-size samples in the framework of the traditional nonlinear perturbation theory, which suggests small changes in the structures and dynamical properties of solitons in unbounded mediums.

The simplest soliton moving in a semi-infinite sample is parameterized by four zeros (3.10) of $a(\lambda)$. We write them in the form

$$\lambda_1=\lambda_0,\qquad \lambda_2=-\lambda_0^{-1},\qquad \lambda_3=-\lambda_0^*,\qquad \lambda_4=\lambda_0^{*-1},\qquad \lambda_0 = e^{\rho+i\delta},$$

$-\infty<\rho<\infty$, $0<\delta<\pi$. Then the functions $\nu_j (x, t)$ are defined by formulas (4.10):

$$\begin{alignedat}{2} &\nu_1=\kappa(\lambda_0)\exp[ix\sinh(\rho+i\delta)-it\cosh^2(\rho+i\delta)],&\qquad &\nu_2=-\nu_1,\\ &\nu_3 =\frac{f^*(\lambda_0)}{\kappa^*(\lambda_0)}\exp[-ix\sinh(\rho-i\delta)-it\cosh^2(\rho-i\delta)],&\qquad &\nu_4=-\nu_3, \end{alignedat} $$

(5.9)

where $f(\lambda_0)=[i\alpha-\sinh(\rho+i\delta)]/[i\alpha+\sinh(\rho+i\delta)]$and $\kappa(\lambda_0)$ is an arbitrary complex constant.

Straightforward but more tiresome algebraic calculations lead to the above representation (5.2) for independent elements of the soliton matrix $\Psi(\lambda)|_{\lambda=0}$ and to Eqs. (4.15) and (5.4) for the angles $\theta$ and $\Phi$. Therefore, the magnetization distribution for a soliton moving in a semi-infinite ferromagnet can be written in the same form (5.5) as previously. Only the functions $u(x, t)$ and $q(x, t)$ are different:

$$\begin{aligned} \, q={}&\frac{\tanh \rho\cot \delta}{2 |\sinh(\rho+i\delta)|^2} \biggl[i\sinh \rho\cosh \rho \biggl((|\nu_3|+|\nu_3|^{-1})\frac{\nu_1}{|\nu_1|}-(|\nu_1|+|\nu_1|^{-1})\frac{\nu_3}{|\nu_3|} \biggr)+{}\nonumber\\ & + \sin \delta\cos \delta \biggl((|\nu_1|-|\nu_1|^{-1})\frac{\nu_3}{|\nu_3|}+(|\nu_3|-|\nu_3|^{-1})\frac{\nu_1}{|\nu_1|} \biggr) \biggr],\nonumber\\ u ={}&\frac{1}{4}\biggl[ (|\nu_1 \nu_3|+|\nu_1 \nu_3|^{-1})\tanh^2 \rho\cot^2 \delta |\coth(\rho+i\delta)|^2+\biggl(\biggl|\frac{\nu_1}{\nu_3}\biggr|+\biggl|\frac{\nu_3}{\nu_1}\biggr| \biggr)(\cot^2 \delta-\tanh^2 \rho)+{}\nonumber\\ & +\frac{(\nu_1^* \nu_3+\nu_1 \nu_3^*)}{|\nu_1 \nu_3|}|\coth(\rho+i\delta)|^2\biggr]+\frac{i}{2}\biggl(\biggl|\frac{\nu_1}{\nu_3}\biggr|-\biggl|\frac{\nu_3}{\nu_1}\biggr| \biggr)\tanh\rho\cot\delta. \end{aligned}$$

(5.10)

In this case, $M=0$, and therefore solution (5.5), (5.10) satisfies edge condition (1.4) with $h=\alpha$ (3.25).

To analyze the properties of soliton reflection from the boundary, we separate the real and imaginary parts in the exponential factors of the fields $\nu_j (x, t)$ (5.9):

$$ \begin{aligned} \, &\nu_1 = \kappa(\lambda_0)e^{- y_1 + is_1},\qquad \nu_3 = \frac{f^*(\lambda_0)}{\kappa^*(\lambda_0)}e^{- y_2 - is_2}, \\ &y_{1,2}=l_0^{-1} (x \mp V t),\qquad s_{1,2}=k x \mp \omega t, \qquad l_0^{-1}=\cosh \rho \sin \delta>0, \\ &V = 2 \sinh \rho \cos \delta = 2 k, \qquad \omega = \cosh^2 \rho\cos^2 \delta-\sinh^2 \rho\sin^2 \delta. \end{aligned}$$

(5.11)

We show that at large distances from the boundary, soliton (5.5), (5.10) moves as a single whole with the velocity $V$ or $-V$. The parameter $l_0$ determines the characteristic thickness of domain walls bounding the soliton core. The precession wave of the vector $\mathbf{n}$ with the frequency $\omega$ and wave number $k$ propagates through the core. The wave is generated near one soliton edge and disappears near another one. To substantiate these statements, we note that for $x\gg 1$, at large times, the asymptotic behavior of fields $n_3$ and $n_{+}$ (5.5) is determined by the competition between exponentially increasing terms in the numerators and denominators of formulas (5.5). To be more specific, we assume that the parameter $V$ is positive. Then for $x\gg 1$ and as $t \to \pm \infty$, in the reference frame related to the soliton, where $x \mp V t=\mathrm{const}$, its structure is described by the expressions

$$\begin{aligned} \, &n_3= 1- \frac{2}{\cot^2 \delta+\tanh^2 \rho}\biggl[\cosh^2 y_\pm + \frac{\sin^2 \delta}{\sinh^2 \rho+\cos^2 \delta} \biggr]^{-1},\nonumber\\ &n_{+}=\frac{2 \kappa e^{i\varphi_{\pm}}}{|\kappa| (\cot^2 \delta+\tanh^2 \rho)}(\cot \delta\cosh y_{\pm}\pm i\tanh \rho \sinh y_\pm)\biggl[\cosh^2 y_\pm + \frac{\sin^2 \delta}{\sinh^2 \rho+\cos^2 \delta} \biggr]^{-1}, \end{aligned}$$

(5.12)

where we introduce the notation

$$\begin{aligned} \, &y_\pm=l_0^{-1} (x \mp V t - x_{+}^{(0)}),&\qquad &x_{+}^{(0)}=l_0 \ln \frac{|\kappa \sinh(\rho+i\delta)|}{\sinh \rho\cos \delta},\\ &x_{-}^{(0)}=x_{+}^{(0)}+l_0 \ln \biggl|\frac{f(\lambda_0)}{\kappa(\lambda_0)} \biggr|,&\qquad &f(\lambda_0)=\frac{i\alpha-\sinh(\rho+i\delta)}{i\alpha+\sinh(\rho+i\delta)},\\ &\varphi_\pm=\pm(k x \mp \omega t)+\varphi_\pm^{(0)},&\qquad &\varphi_{+}^{(0)}=\frac{\pi}{2}+\frac{1}{2i} \ln \biggl[\frac{\sinh(\rho+i\delta)\cosh^2(\rho-i\delta)}{\sinh(\rho-i\delta)\cosh^2(\rho+i\delta)}\biggr], \end{aligned}$$

$\varphi_{-}^{(0)}=-\varphi_{+}^{(0)}-\operatorname{arg} f(\lambda_0)$, and $\kappa(\lambda_0)$ is an arbitrary complex integration constant. Formulas (5.12) describe precessing breathers propagating with the velocities $V$ and $-V$ in an infinite easy-axis ferromagnet. The complete analysis of their properties is contained in [1], [3]. Thus, at large distances from the sample boundary, particle-like excitation (5.5), (5.10) transforms into a typical magnetic soliton in an unbounded medium. The result of the soliton reflection from the sample edge amounts to a change in the internal precession phase and a shift of the soliton center. The phase shift $\varphi_{+}-\varphi_{-}=2 \varphi_{+}+\operatorname{arg} f(\lambda_0)$ depends on the spin pinning parameter $\alpha$ on the sample boundary and on the complex parameter $\sinh(\rho+i\delta)$, instead of which observable quantities can be used such as, e.g., the soliton velocity $V$ and size $l_0$:

$$\sinh(\rho+i\delta)=\frac{V}{2}+il_0^{-1}.$$

It hence follows that the measurement of the phase shift acquired by the soliton after its reflection from the sample boundary gives information about the parameter $\alpha$, and therefore about the spin pinning on the sample surface.

We note that in the limit case $\rho \to 0$, $\delta \ne \pi/2$ (or $\delta \to \pi/2$, $\rho \ne 0$), $x_\pm =\mathrm{const}\gg 1$, expressions (5.12) describe immovable breathers far from the sample boundary. Meanwhile, the breather localization near the sample edge is impossible because $q$ is zero in the complete solution (5.5), (5.10) at $\rho=0$ or $\delta=\pi/2$, and therefore the soliton state does not exists.

Edge multisolitons form under the condition that the surface field $|h|$ exceeds certain threshold values, while there is no such constraint for the formation of moving solitons.

In the limit $h \to 0$, we have the factor $f(\lambda_0)=-1$ in formulas (5.5), (5.9), and (5.10); they can then be simplified and determine a solution of Landau–Lifshitz equations (1.2) with free spins at the sample boundary:

$$[\mathbf{n} \times \partial_x \mathbf{n}]|_{x=0}=0.$$

In the opposite limit $|h| \to \infty$, we have the factor $f(\lambda_0)=1$. Therefore, at $x=0$, the equalities

$$\nu_{3}|_{x=0}=\nu_{1}^{*-1}|_{x=0},\qquad q|_{x=0}=0$$

hold. It hence follows that in this limit, solution (5.5), (5.9), (5.10) describes the reflection of a precessing soliton from the sample boundary with spins fully pinned at it:

$$n_3|_{x=0}=1.$$

Effects of the multisoliton reflection from the sample edge can be verified experimentally.

6. Integrals of motion

As in an infinite medium, the element $a(\lambda)$ of the transition matrix is independent of time and therefore serves as a generating functional for integrals of motion for an infinite ferromagnet. We obtain their explicit expressions from formula (3.16) for $a(\lambda)$ by substituting asymptotic series for elements of Jost function (3.18) there:

$$T_{+}(x, t, \lambda)=\biggl(I+\sum_{n=0}^{\infty} \frac{\Phi_n (x, t)}{\lambda^n} \biggr)\exp\biggl(-iw_3 (\lambda)x\sigma_3+ \sum_{k=0}^{\infty}\frac{Z_k (x, t)}{\lambda^k} \biggr). $$

(6.1)

The expansion coefficients in (6.1) are defined recursively by Eqs. (3.19) and have the algebraic structure

$$\Phi_n (x, t)=\begin{pmatrix} 0 & -w_n^*(x, t) \\ w_n (x, t) & 0 \end{pmatrix},\qquad Z_n (x, t)= \begin{pmatrix} z_{n}(x, t) & 0 \\ 0 & z_{n}^*(x, t) \end{pmatrix}.$$

The first functions $w_n (x, t)$ and $z_n (x, t)$ are given by (3.20),

$$\begin{aligned} \, &w_0=\frac{n_{+}}{1+n_3},\qquad w_1 = -2 i\,\partial_x w_0,\qquad z_0 =\frac{1}{2}\ln \frac{1+n_3}{2}+\frac{i}{2}\int_{x}^{\infty} p(x')\, dx', \nonumber\\ &p=\frac{n_1 \partial_x n_2 -n_2 \partial_x n_1 }{1+n_3}, \qquad z_1 =-\frac{i\partial_x n_3}{1+n_3}-p+\frac{i}{2} \int_{x}^{\infty}[(\partial_{x'} \mathbf{n})^2+1-n_3^2]\, dx'. \end{aligned}$$

(6.2)

Using Eqs. (3.16), (6.1), and (6.2), we calculate the first term of the asymptotic expansion:

$$\ln \biggl(\frac{a(\lambda)}{[4 w_3^2 (\lambda)+\alpha^2]^{1/2}}\biggr)=-\frac{2i}{\lambda}H+O\biggl(\frac{1}{\lambda^2} \biggr). $$

(6.3)

The expression

$$H=\frac{1}{2}\int_{0}^{\infty}[(\partial_{x'} \mathbf{n})^2+1-n_3^2]\, dx' - h n_3|_{x=0} $$

(6.4)

coincides with dimensionless energy (1.1) of a semi-infinite easy-axis ferromagnet. On the other hand, the expansion in terms of the inverse powers of $\lambda$ in the left-hand side of (6.3) can be immediately found using dispersion relation (3.24). The comparison of two expansions allows expressing the integrals of motion of the system in terms of spectral data. For the system energy, we obtain

$$H=-\alpha+\sum_{s=1}^{M}(b_s+b_s^{-1})+2 \sum_{k=1}^{N} \operatorname{Im} \lambda_k(1+|\lambda_k|^{-2})+\int_{-\infty}^{\infty}[1+4 w_3^2 (\mu)] \rho(\mu)\,d \mu, $$

(6.5)

where $\alpha =(-1)^M h$. The quantity

$$\rho(\mu)=-\frac{1}{16\pi w_1^2 (\mu)}\ln \biggl(1-\frac{|b(\mu)|^2}{4 w_3^2 (\mu)+h^2} \biggr)>0$$

has the meaning of the density of spin-wave modes with the wave number $\kappa=2 w_3 (\mu)$ and the dispersion law $\Omega=1+\kappa^2$.

In terms of the spectral data, the total system energy (6.4) is the sum of independent discrete contributions of solitons and quasiparticles of the continuous spectrum of spin waves. Therefore, the set of nonlinear excitations of a semi-infinite ferromagnet can be treated as an ideal gas of solitons and magnons.

The applied procedure for the integration of Landau–Lifshitz model (1.2)–(1.5) is a nonlinear analogue of the Fourier method. As in [15], [16], it can be shown that in the small-amplitude limit, the spin-wave field $n_{+}(x, t)$ ($|n_{+}|\ll 1$) of the linearized Landau–Lifshitz equation is related to the spectral density $b(\lambda, t)$ of the inverse scattering problem by the usual Fourier transformation. It is well known that distant Fourier components of functions with no singularities on the real axis are exponentially small. In this paper, because of the continuation to the entire real axis of the field $n_{+}(x, t)$ defined on the semiaxis ${0<x<\infty}$, the derivatives of the continuation $S_{+}(x, t)$ acquire a jump at $x=0$. In such cases, the distant Fourier components of the functions $S_{+}(x, t)$ have a power-law dependence as $\lambda \to \infty$ rather than the exponential one [23]. The spectral function $b(\lambda, t)$ of the inverse scattering transform inherits this feature of the Fourier transformation. We recall that for purely soliton states, $b(\lambda, t) \equiv 0$. This means that all coefficients of the expansion of $b(\lambda, t)$ in inverse powers of $\lambda$ must vanish. Thus, in a semi-infinite sample, the element $b(\lambda, t)$ of the transition matrix is a generating functional of additional integrals of motion for mutisolitons (4.12), (4.14), and (4.15) that we have obtained.

Using (3.17), (6.1), and (6.2), we find the asymptotic series for $b(\lambda, t)$:

$$b(\lambda, t) = \biggl[-2 ih w_0-w_1+\sum_{s=1}^{\infty} \frac{1}{\lambda^{2 s}} (w_{2 s -1}- 2 ih w_{2 s}-w_{2 s+1}) \biggr] \exp \biggl(2 \sum_{k=0}^{\infty} \frac{z_{2 k}}{\lambda^{2 k}} \biggr)\Bigg|_{x=0}. $$

(6.6)

In the case of purely soliton states, all preexponential factors vanish in this formula:

$$(2 ih w_0+w_1)|_{x=0}=0, \qquad (w_{2 s -1}- 2 ihw_{2 s}-w_{2 s+1})|_{x=0}=0, \qquad s=1,2,\ldots\;. $$

(6.7)

These constraints provide ensure the correct edge conditions for solitons and the localization of solitons near the sample boundary or their reflection from it.

The first additional integral of motion takes the form

$$\partial_x \ln \biggl(\frac{n_{+}(x, t)}{1+n_3 (x, t)}\biggr)\Bigg|_{x=0}=h. $$

(6.8)

For elementary soliton (5.1), it is easy to verify that identity (6.8) holds.

7. Conclusions

In this paper, using the inverse scattering transform method, we obtained and analyzed new soliton solutions of the Landau–Lifshitz equation for a semi-infinite ferromagnet with an anisotropy of the easy axis type. Under the influence of “image” forces, such solitons fundamentally change their structure and dynamical properties near the sample surface. Therefore, they cannot be studied using previously known methods for an unbounded medium.

We found the conditions for soliton localization near the sample boundary. We discovered the possibility of controlling the number of edge solitons by changing the degree of surface spin pinning. We showed that the edge solitons have a discrete set of eigenfrequencies, and the magnetization on the sample boundary undergoes regular modulations. We predicted and analytically described elastic reflections of moving precession solitons from the sample boundary. The obtained results indicate that the uniaxial anisotropy field leads to the narrowing and boundedness of the spatial localization regions for all types of solitons. Measurements of the phase shift acquired by solitons after their reflections from the boundary can be used to diagnose the degree of surface spin pinning.

We constructed the spectral expansions of a series of integrals of motion, which allow interpreting arbitrary localized perturbations in a semi-infinite ferromagnetic sample in terms of an ideal gas of solitons and magnons. We obtained additional conservation laws, which ensure the soliton localization near the sample surface or their reflection from it.

The results in this paper can be useful in verifying numerical calculations and in simulating the nonlinear dynamics of solitons in real finite-size samples. They stimulate the design of new experiments on the study of solitons in bounded samples.