On the Evolution of Orbits in a Photo-Gravitational Circular Three-Body Problem: The Inner Problem

Abstract

We consider the spatial restricted circular three-body problem in the nonresonant case. The massless body (satellite) is assumed to have a large sail area and, therefore, the light pressure is taken into account. We study the evolution of the satellite orbit based on Gauss’s scheme: the averaged equations of motion are investigated in Keplerian phase space, when a Keplerian ellipse with its focus in the main body (Sun) is taken as an unperturbed orbit located inside a sphere whose radius is equal to the orbital radius of the outer planet (inner problem). An investigation of the averaged model in the classical case, where the light pressure is neglected, is known to run into considerable difficulties both in calculating the averaged force function and in analyzing the evolving orbits. We have shown for the first time that the twice-averaged force function admits of an explicit analytical representation via hypergeometric (generalized hypergeometric) functions expandable into convergent power series based on the application of Parseval’s formula. We have also shown that the averaged equations of motion including the additional influence of light pressure are Liouville-integrated (we have three independent first integrals in involution). We have investigated, at fixed values of the Lidov–Kozai integral, the stationary regimes of oscillations in the case of low values of the satellite’s unperturbed semimajor axis (Hill’s case), their bifurcation as a function of the light pressure coefficient $\delta$. In the plane of Keplerian elements $e$ and $\omega$ we have constructed the phase portraits of the oscillations at various values of the light pressure coefficient. The portrait rearrangement due to both equilibrium position bifurcations and separatrix splitting is described. The separatrix splitting is shown to reverse the direction of evolution of the argument of pericenter $\omega$ in the case of rotational motions.

INTRODUCTION

The light pressure is of considerable importance in calculating the parameters of the motion of celestial objects with a large frontal area-to-mass ratio. Musen (1960) and Parkinson et al. (1960) were the first to be faced with the necessity to take into account this effect in their calculations related to the Vanguard I satellite, when it was required to also take into account the light pressure on the satellite to explain the orbital degradation. The light pressure played a major role in investigating the motion of the Echo 1, Echo 2, and PAGEOS balloon satellites, to which a number of papers are devoted. Among them we should mention the paper by Kozai (1961), where the shadow equation was solved, the paper by Ferraz-Mello (1964), where it was proposed to take into account the satellite’s entry into the shadow by introducing the shadow function, and the papers by Vashkov’yak (1974, 1976), where it was proposed to calculate the shadow function in the form of a series in Legendre polynomials and to express it via orbital elements, as a result of which the secular and long-period perturbations of the orbital elements under the influence of light pressure were obtained. The influence of light pressure and the Earth’s shadow on the evolution of Keplerian orbital elements in the first approximation of the small-parameter method was investigated in the monograph by Aksenov (1977).

Investigating the motion of objects with a large sail area is particularly important in connection with space debris moving in high orbits. For example, in addition to the perturbations from zonal harmonics, Krivov et al. (1995) considered the perturbations from light pressure forces. The same problem, but supplemented by the perturbations from electromagnetic forces, was considered by Hamilton and Krivov (1996).

In August 2018 the Parker Solar Probe was launched (Szabo 2018), with the study of the solar corona being among its objectives. The Probe corresponds in its parameters to objects with a large frontal area-to-mass ratio.

In particular, the averaging method, whose applications to the classical three-body problem were analyzed in detail by Moiseev (1945), is used to investigate the orbits of the above-mentioned objects on significant time scales. Using the ideas of the averaging method, Bryant (1961) described a clear change in the semimajor axis over the orbital period of a satellite by taking into account the light pressure and the shadow effect. He also showed that the semimajor axis of the satellite orbit retains its unperturbed value in the absence of a shadow. Lidov (1961, 1962) described the orbital evolution of a planetary satellite in terms of the elliptical three-body problem for Hill’s case (the case of a small ratio of the unperturbed semimajor axis of the satellite orbit to the radius of the planetary orbit); the fall of the satellite to the central body, when the orbital plane of the satellite is perpendicular to the orbital plane of the perturbing body, was described. Kozai (1962) derived an approximate expression for the twice-averaged disturbing force function in an asteroidal circular three-body problem and calculated the critical orbital inclinations. Sidorenko (2018) investigated the eccentric Lidov–Kozai effect, which can be interpreted as a resonant effect. Aksenov (1967) derived an analytical expression for the twice-averaged disturbing force function in the circular three-body problem in the form of a Fourier series whose coefficients are expressed via special functions written as quadratures. This author gave a justification for Gauss’s averaging method, which replaces the procedure of averaging over the mean anomaly of the planet’s motion by a uniform smearing of the planet’s mass over its orbit. Aksenov (1979a, 1979b) investigated the plane restricted elliptical three-body problem by the twice-averaging method and studied the evolution of the trajectories of a satellite and, in particular, described the trajectories of its fall to the central body. The topology of motions in the averaged circular three-body problem (inner problem) was studied numerically in the remarkable paper by Vashkov’yak (1981).

Note also that the averaging method is efficiently used in problems of the rotational motions of satellites in evolving orbits as well: averaging is used in Tikhonov et al. (2017) and Aleksandrov and Tikhonov (2020) to investigate the stability of the programmed rotational motion of a satellite around its center of mass in an evolving orbit. The method of Lyapunov functions in combination with the method of averaging the equations of rotational motion for a satellite was efficiently used to justify the asymptotic stability of the motion being stabilized (Aleksandrov and Tikhonov 2020). Amelkin (2019) determined the mean displacement of Mercury’s perihelion in a plane planetary problem by the averaging method.

Previously, we investigated the three-body problem with light pressure in the plane elliptical three-body problem (Dobroslavskiy and Krasilnikov 2018). Unfortunately, when writing the light pressure force function, we made a mistake ¹ and, as a consequence, the superfluous equilibria $e=\textrm{const}$ and $\omega=\pi/2$ appeared; the remaining results changed little. In the next paper (Dobroslavskiy and Krasilnikov 2020) devoted already to the four-body (Earth–Moon–Sun–Earth satellite) problem including the light pressure, we constructed the phase portraits of the oscillations in Keplerian orbital elements and studied the rearrangement of the phase portraits at various values of the light pressure coefficient. In these papers the effect of entry into the Earth’s shadow was neglected, because at a semimajor axis of the elliptical satellite orbit comparable to or exceeding that for the Moon the mean time of the satellite’s stay in the shadow is ${\sim}0.62\%$ in one revolution (Dobroslavskiy 2020).

The goal of this paper is to investigate the evolution of the spatial orbits of a close stellar satellite (solar probe) by taking into account the perturbations from an outer planet (Jupiter) and solar light pressure.

Fig. 1

Unperturbed trajectories of celestial bodies. Angular variables.

STATEMENT OF THE PROBLEM

Consider a circular spatial restricted three-body problem with light pressure forces $\mathbf{F}_{\lambda}$. Suppose that a massless body (satellite) $P$, having a large surface area-to-mass ratio, is in the gravitational field of two massive bodies moving relative to each other in a circular orbit of radius $r_{J}$; the central body $S$ (Sun) has a mass $m_{S}$ and acts on the satellite with a force $\mathbf{F}_{S}$, the second body $J$ (Jupiter) of mass $m_{J}$ exerts a perturbing effect with a force $\mathbf{F}_{J}$. We assume that the unperturbed trajectory of the satellite is a Keplerian ellipse with its focus at $S$ whose plane $\Pi$ forms an angle $i$ with the plane of motion $\Pi_{0}$ of the attractive bodies (Fig. 1).

Note that in the classical case, where the light pressure on the satellite is negligible, the problem was studied in detail in the paper by Vashkov’yak (1981). The goal of our paper is to describe the new effects in the averaged motion of the satellite produced by the light pressure.

Let us introduce a heliocentric coordinate system with the center at $S$. We will direct the $Sx$ axis to the point of vernal equinox, $SN$ is the line of nodes of the satellite orbit, the remaining axes forming a right-handed coordinate system are not specified in Fig. 1. Let $\mathbf{r}$ be the radius vector of body $P$ and $\mathbf{r}_{J}$ be the radius vector of body $J$.

Let $\Omega$ be the longitude of the ascending node of the unperturbed satellite orbit in plane $\Pi_{0}$, $e$ and $\omega$ be the eccentricity and argument of pericenter of this orbit, $\lambda_{J}$ is the longitude of body $J$, and $\lambda$ is the longitude of body $P$ in plane $\Pi_{0}$.

Consider the ‘‘inner’’ version of the three-body problem, where body $P$ moves inside a sphere of radius $r_{J}$:

$$a(1+e)<r_{J}.$$

Here, $a$ is the semimajor axis of the unperturbed satellite orbit.

Let us write the expression for the perturbed force function of the problem:

$$R=R_{J}+R_{S}.$$

(1)

Here, $R_{J}$ is the force function of the gravitational effect from body $J$, which is

$$R_{J}=fm_{J}\left(\frac{1}{\varDelta}-\frac{\left(\mathbf{r}_{J},\mathbf{r}\right)}{r_{J}^{3}}\right),$$

(2)

$$\varDelta=r_{J}\sqrt{1-2\left(\frac{r}{r_{J}}\right)\cos\gamma+\left(\frac{r}{r_{J}}\right)^{2}},$$

where $f$ is the gravitational constant, $\gamma$ is the angle between $\mathbf{r}_{J}$ and $\mathbf{r}$,

$$\cos\gamma=\cos{\left(\lambda_{J}-\Omega\right)}\cos{\left(\omega+\nu\right)}$$

(3)

$${}+\sin{\left(\lambda_{J}-\Omega\right)}\sin{\left(\omega+\nu\right)}\cos{i},$$

$\nu$ is the true anomaly in the motion of the satellite along the unperturbed orbit.

The function (2) can be expanded into a series in Legendre polynomials to terms independent of the coordinates of body $P$:

$$R_{J}=\frac{fm_{J}}{r_{J}}\sum_{n=2}^{\infty}\left(\frac{r}{r_{J}}\right)^{n}P_{n}(\cos\gamma).$$

The force function of the light pressure on a spherical satellite in a circular orbit can be represented as

$$R_{S}=-\frac{\delta r_{0}^{2}}{r}.$$

Here, $\delta>0$ is the light pressure coefficient (Aksenov 1977)

$$\delta=\frac{\varkappa\pi\rho^{2}E_{0}}{mc},$$

(4)

$\rho$ is the satellite’s surface radius, $m$ is its mass, $\varkappa$ is the reflection coefficient of the satellite’s surface, which is 1 for total absorption and 1.44 for diffuse scattering. $E_{0}$ is the solar constant defined as the light flux at distance $r_{0}$ (1 AU) from the Sun (approximately 1367 $\text{W}\text{m}^{-2}$), and $c$ is the speed of light in a vacuum.

Then, given the expressions for $R_{J}$ and $R_{S}$, the force function of the problem takes the form

$$R=-\frac{\delta r_{0}^{2}}{r}+\frac{fm_{J}}{r_{J}}\sum_{n=2}^{\infty}\left(\frac{r}{r_{J}}\right)^{n}P_{n}(\cos\gamma).$$

(5)

AVERAGING THE FORCE FUNCTION

The longitude $\lambda$ of body $P$ in the ecliptic plane is known to be described by the formulas (Aksenov 1967)

$$\cos{\lambda}=\frac{\cos{\left(\nu+\omega\right)}}{\sqrt{1-\sin^{2}{i}\sin^{2}{\left(\nu+\omega\right)}}},$$

$$\sin{\lambda}=\frac{\sin{\left(\nu+\omega\right)}\cos{i}}{\sqrt{1-\sin^{2}{i}\sin^{2}{\left(\nu+\omega\right)}}}.$$

Then, (3) can be rewritten as

$$\cos{\gamma}=\cos\left(\lambda_{J}-\Omega-\lambda\right)$$

(6)

$${}\times\sqrt{1-\sin^{2}{i}\sin^{2}{\left(\nu+\omega\right)}}.$$

To transform Eq. (5) to a form convenient for averaging, we will use the addition theorem for Legendre polynomials. Given (6), we will have

$$P_{n}(\cos\gamma)=P_{n}(0)P_{n}\left[\sin{i}\sin(\nu+\omega)\right]$$

(7)

$${}+2\sum_{k=1}^{n}\frac{(n-k)!}{(n+k)!}P_{n}^{(k)}(0)P_{n}^{(k)}\left[\sin{i}\sin(\nu+\omega)\right]$$

$${}\times\cos{k\left(\lambda_{J}-\Omega-\lambda\right)}.$$

Here, $P_{n}^{(k)}$ are associated Legendre functions, which can be represented at zero as

$$P_{n}^{(k)}(0)=\begin{cases}(-1)^{(n-k)/2}\dfrac{(n+k)!}{2^{n}\left(\frac{n-k}{2}\right)!\left(\frac{n+k}{2}\right)!},\\ n-k=2m,\quad m\in\mathbb{Z}\\ 0,\quad n-k=2m+1,\quad m\in\mathbb{Z}.\end{cases}$$

Next, we assume that the frequency $\dot{\lambda}_{J}$ does not resonate with the frequency $n$ of the unperturbed satellite motion. Averaging (5) over the longitude $\lambda_{J}$ of body $J$, we will obtain, given (3), (7), and the equality $P_{2n+1}(0)=0$, the once-averaged force function $R^{*}$ of the problem:

$$R^{*}=\frac{1}{2\pi}$$

(8)

$${}\times\int\limits_{0}^{2\pi}\left[-\frac{\delta r_{0}^{2}}{r}+\frac{fm_{J}}{r_{J}}\sum_{n=2}^{\infty}\left(\frac{r}{r_{J}}\right)^{n}P_{n}(\cos\gamma)\right]d\lambda_{J}$$

$${}=-\frac{\delta r_{0}^{2}}{r}+\frac{fm_{J}}{r_{J}}\sum_{n=1}^{\infty}\left(\frac{r}{r_{J}}\right)^{2n}$$

$${}\times P_{2n}\left(0\right)P_{2n}\left[\sin{i}\sin\left(\nu+\omega\right)\right].$$

Expression (8) coincides, to within the light pressure term, with the force function of a Gaussian ring (Duboshin 1961), which was first established in Aksenov (1967).

Let us now average the derived expression (8) over the true anomaly $\nu$ of body $P$. This requires writing the expression for $r$ via the true anomaly $\nu$ using the formulas for unperturbed motion and substituting it into (8). Our calculations show that the function $R^{*}$ contains a product of two functions periodic in $\nu$ under the summation sign: $\left(1+e\cos\nu\right)^{-2n}$ and $P_{2n}(\sin{i}\cos{\theta})$, where $\theta=\nu+\omega-\pi/2$. The main technical problem of any studies is to calculate the mean of this product. Modern software packages, such as Wolfram Mathematica and Maple, do not cope with this problem. For this purpose, we will use Parseval’s formula (Gradshteyn and Ryzhik 1963) describing the principal (secular) term of the product of two Fourier series:

$$\frac{1}{2\pi}\int\limits_{0}^{2\pi}(1+e\cos{\nu})^{-2n}$$

(9)

$${}\times P_{2n}\left(\sin{i}\cos{\theta}\right)d\nu$$

$${}=\frac{a_{0}\alpha_{0}}{4}+\frac{1}{2}\sum_{m=1}^{\infty}\left(a_{m}\alpha_{m}+b_{m}\beta_{m}\right).$$

Here, $\{a_{0},a_{m},b_{m}\}$ are the coefficients of the Fourier function $\left(1+e\cos\nu\right)^{-2n}$ and $\{\alpha_{0},\alpha_{m},\beta_{m}\}$ are the coefficients of the Fourier function $P_{2n}(\sin{i}\cos{\theta})$. The expressions for these coefficients are

$$a_{0}=\frac{1}{\pi}\int\limits_{0}^{2\pi}(1+e\cos\nu)^{-2n}d\nu$$

(10)

$${}=\frac{2}{(1-e)^{2n}}F_{2,1}\left(\frac{1}{2},2n;1;\frac{2e}{e-1}\right),$$

$$a_{m}=\frac{2}{(1-e)^{2n}}$$

$${}\times F_{3,2}^{\textrm{reg}}\left(\frac{1}{2},1,2n;1-m,1+m;\frac{2e}{e-1}\right),$$

$$b_{m}=0,$$

$$\alpha_{0}=\frac{1}{\pi}\int\limits_{0}^{2\pi}P_{2n}(\sin{i}\cos{\theta})d\nu$$

(11)

$${}=2P_{2n}(0)P_{2n}(\cos{i}),$$

$$\alpha_{m}=\begin{cases}2\cos\left(\dfrac{m\pi}{2}-m\omega\right)\dfrac{(2n-m)!}{(2n+m)!}\\ {}\times P_{2n}^{(m)}(0)P_{2n}^{(m)}(\cos{i}),\quad m\leq 2n\\ 0,\quad m>2n,\end{cases}$$

$$\beta_{m}=0.$$

As a result, the twice-averaged perturbed force function takes the form

$$R^{**}=\frac{1}{2\pi}\int\limits_{0}^{2\pi}R^{*}d\nu=-\frac{\delta r_{0}^{2}}{a(1-e^{2})}$$

(12)

$${}+\frac{fm_{J}}{r_{J}}\sum_{n=1}^{\infty}\left[\frac{a(1-e^{2})}{r_{J}}\right]^{2n}$$

$${}\times P_{2n}\left(0\right)I_{2n}(i,e,\omega).$$

Here,

$$I_{2n}(i,e,\omega)=\frac{1}{2\pi}\int\limits_{0}^{2\pi}(1+e\cos{\nu})^{-2n}$$

(13)

$${}\times P_{2n}\left(\sin{i}\cos{\theta}\right)d\nu=\frac{1}{(1-e)^{2n}}$$

$${}\times\Biggl{[}P_{2n}(0)P_{2n}(\cos{i})F_{2,1}\left(\frac{1}{2},2n;1;\frac{2e}{e-1}\right)$$

$${}+2\sum_{m=1}^{2n}F_{3,2}^{\textrm{reg}}\left(\frac{1}{2},1,2n;1-m,1+m;\frac{2e}{e-1}\right)$$

$${}\times\cos\left(\frac{m\pi}{2}-m\omega\right)\frac{(2n-m)!}{(2n+m)!}P_{2n}^{(m)}(0)P_{2n}^{(m)}(\cos{i})\Biggr{]},$$

$F_{2,1}$ is a hypergeometric function and $F_{3,2}^{\textrm{reg}}$ is a generalized regularized hypergeometric function,

$$F_{3,2}^{\textrm{reg}}\left(\alpha_{1},\alpha_{2},\alpha_{3};\beta_{1},\beta_{2};z\right)$$

$${}=\sum_{k=0}^{\infty}\frac{\left(\alpha_{1}\right)_{k}\left(\alpha_{2}\right)_{k}\left(\alpha_{3}\right)_{k}}{\Gamma\left(\beta_{1}+k\right)\Gamma\left(\beta_{2}+k\right)}\frac{z^{k}}{k!},$$

where $\Gamma(a)$ is the gamma function and $\left(x\right)_{k}$ is the Pochhammer symbol:

$$(x)_{k}=\frac{\Gamma(x+k)}{\Gamma(x)}.$$

Formula (13) was validated numerically—the results of our calculations of the left and right parts of the formula coincide in all significant figures for the following Cartesian product of the parameters: $e$ from 0 to 1 with a 0.1 step, $\omega$ from 0 to $2\pi$ with a $\pi/6$ step, $i$ from $-\pi/2$ to $\pi/2$ with a $\pi/6$ step, and $n$ from 1 to 15 with a 1 step.

Expressions (12) and (13) for the averaged force function can be expanded into a Fourier series in $\omega$. Our calculations show that this series is

$$R^{**}=-\frac{\delta r_{0}^{2}}{a(1-e^{2})}$$

(14)

$${}+\frac{fm_{J}}{r_{J}}\sum_{n=1}^{\infty}\Biggl{[}B_{2n}(e)P_{2n}(0)P_{2n}(\cos{i})$$

$${}\times F_{2,1}\left(\frac{1}{2},2n;1;\frac{2e}{e-1}\right)$$

$${}+(-1)^{n}\left(\sum_{k=n}^{\infty}B_{2k}(e)A_{2n}^{(2k)}(e,\cos i)\right)\cos{2n\omega}\Biggr{]}.$$

Here,

$$B_{2k}(e)=\frac{a^{2k}(1+e)^{2k}}{r_{J}^{2k}}P_{2k}(0),$$

$$A_{2n}^{(2k)}(e,\cos i)$$

$${}=\begin{cases}2F_{3,2}^{\textrm{reg}}\left(\dfrac{1}{2},1,2k;1-2n,1+2n;\dfrac{2e}{e-1}\right)\\ \times\dfrac{(2k-2n)!}{(2k+2n)!}P_{2k}^{(2n)}(0)P_{2k}^{(2n)}(\cos{i}),\\ 1\leq n\leq k\\ 0,\quad n>k.\end{cases}$$

When deriving Eq. (14), we used the well-known equality $P_{2k}^{(2n+1)}(0)=0$ nulling the terms containing $\sin 2n\omega$.

Here, it should be noted that an analytical representation of the twice-averaged force function for the problem in the form of a Fourier series in $\omega$ was first derived by Aksenov (1967). This author expressed the coefficients of this series via some unknown special functions in the form of quadratures. Unfortunately, the quadratures were not expanded into convergent series; the author restricted himself to the description of the recurrence relations for the quadratures. Therefore, it is very difficult to use the results from Aksenov’s paper in analytical studies.

AVERAGED EQUATIONS OF MOTION

The averaged equations in osculating variables (Lagrange equations) are (Duboshin 1968)

$$\frac{da}{dt}=0,$$

(15)

$$\frac{de}{dt}=-\frac{\sqrt{1-e^{2}}}{na^{2}e}\frac{\partial R^{**}}{\partial\omega},$$

$$\frac{di}{dt}=\frac{\cot{i}}{na^{2}\sqrt{1-e^{2}}}\frac{\partial R^{**}}{\partial\omega},$$

$$\frac{d\Omega}{dt}=\frac{\csc{i}}{na^{2}\sqrt{1-e^{2}}}\frac{\partial R^{**}}{\partial i},$$

$$\frac{d\omega}{dt}=\frac{\sqrt{1-e^{2}}}{na^{2}e}\frac{\partial R^{**}}{\partial e}-\frac{\cot{i}}{na^{2}\sqrt{1-e^{2}}}\frac{\partial R^{**}}{\partial i}.$$

The first integrals of the system are described by the equalities

$$a=c_{0},\quad(1-e^{2})\cos^{2}i=c_{1},\quad R^{**}=c_{2}.$$

The second of these integrals is commonly called the Lidov–Kozai integral. Note that the integral was first derived by von Zeipel (1910) and, subsequently, by Moiseev (1945). Using it, we eliminate the angle $i$,

$$i=\arccos\left(\pm\sqrt{\frac{c_{1}}{1-e^{2}}}\right)$$

from the averaged force function $R^{**}$ and derive a reduced system of equations with one degree of freedom:

$$\frac{de}{dt}=-\frac{\sqrt{1-e^{2}}}{na^{2}e}\frac{\partial\hat{R}}{\partial\omega},\quad\frac{d\omega}{dt}=\frac{\sqrt{1-e^{2}}}{na^{2}e}\frac{\partial\hat{R}}{\partial e}.$$

(16)

The force function $\hat{R}=\hat{R}\left(e,\omega\right)$ is the result of eliminating the angle $i$. Obviously, the energy integrals in Eqs. (16) is $\hat{R}\left(e,\omega\right)=\textrm{const}$.

A constraint on the range of variation of the osculating orbital eccentricity follows from the Lidov–Kozai integral: $0\leq e\leq\sqrt{1-c_{1}}$.

Fig. 2

Diagram of equilibria at $c_{1}=0.3$.

QUALITATIVE ANALYSIS

To perform a qualitative analysis, first of all note that the manifolds $e=0$ and $\sqrt{1-c_{1}}$ are integral in the reduced system of equations (16). Indeed, the derivative of $\hat{R}$ with respect to $\omega$ is

$$\frac{\partial\hat{R}}{\partial\omega}=-\frac{fm_{J}}{r_{J}}\sum_{n=1}^{\infty}(-1)^{n}$$

$${}\times 2n\left(\sum_{k=n}^{\infty}B_{2k}(e)A_{2n}^{(2k)}(e,\cos i)\right)\sin 2n\omega.$$

It becomes zero at $e=\sqrt{1-c_{1}}$, because, in this case, $\cos i=\pm 1$ and $A_{2n}^{(2k)}(e,\pm 1)=0$. The integrality of the manifold $e=0$ follows from the expansion of this derivative into a series in $e$:

$$\frac{\partial\hat{R}}{\partial\omega}=-\frac{fm_{J}}{r_{J}}\sum_{n=1}^{\infty}(-1)^{n}$$

$${}\times 4n\Bigg{\{}\sum_{k=n}^{\infty}\left(\frac{a}{r_{J}}\right)^{2k}\frac{(2k-2n)!}{(2k+2n)!}$$

$${}\times P_{2k}(0)P_{2k}^{(2n)}(0)P_{2k}^{(2n)}(\cos i)$$

$${}\times\bigg{[}\frac{1}{\Gamma(1-2n)\Gamma(1+2n)}+\bigg{(}\frac{2k}{\Gamma(1-2n)\Gamma(1+2n)}$$

$${}-\frac{2k}{\Gamma(2-2n)\Gamma(2+2n)}\bigg{)}e+O(e^{2})\bigg{]}\Bigg{\}}\sin{2n\omega}.$$

Indeed, the coefficients at $e^{0}$ and $e^{1}$ become zero, because the integers $m=0,-1,-2,\ldots$ are first-order poles of the gamma function $\Gamma(z)$. As a consequence, the derivative is equal to zero at $e=0$.

Hence we get

$$\frac{\partial\hat{R}}{\partial\omega}\sim e^{2}\sin 2\omega.$$

Note that this relation was previously derived by Ziglin (1976) using a special transformation of the averaged force function without an explicit description in a finite form and represented as a quadrature in mean longitude of point $P$.

Let us expand the reduced function $\hat{R}\left(e,\omega\right)$ into a series in $\left(a/r_{J}\right)$ and retain the terms to the second order inclusive:

$$\hat{R}^{(2)}=-\frac{\delta r_{0}^{2}}{a\left(1-e^{2}\right)}-\frac{fm_{J}a^{2}}{8r_{J}^{3}}$$

(17)

$${}\times\frac{1}{\sqrt{1-e^{2}}}\bigg{\{}\left[6\left(1-e^{2}\right)^{3/2}+9e^{2}-6\right]$$

$${}\times\left(\frac{c_{1}-1}{e^{2}}+1\right)\cos 2\omega-3c_{1}-e^{2}+1\bigg{\}}.$$

The equations of stationary points written to terms of the fifth order of smallness in $e$ are then brought to the form

$$\frac{\partial\hat{R}^{(2)}}{\partial e}=\bigg{\{}-\frac{2\delta}{a}$$

(18)

$${}+\frac{a^{2}fm_{J}}{8r_{J}^{3}}\bigg{[}-\frac{9}{2}(c_{1}-1)\cos 2\omega+3c_{1}+1\bigg{]}\bigg{\}}e$$

$${}+\bigg{\{}-\frac{4\delta}{a}-\frac{a^{2}fm_{J}}{16r_{J}^{3}}[6(2c_{1}+1)\cos 2\omega$$

$${}-9c_{1}-1]\bigg{\}}e^{3}+\dots=0,$$

$$\frac{\partial\hat{R}^{(2)}}{\partial\omega}=\frac{3a^{2}fm_{J}}{16r_{J}^{3}}[3(c_{1}-1)e^{2}$$

$${}+(2c_{1}+1)e^{4}+\dots]\sin 2\omega=0.$$

Fig. 3

Phase portrait at $\delta=0$.

The set of stationary solutions is $e=e(\delta,\omega,c_{1})$ and $\omega=\{0,\pi/2\}$. The following results take place for the parameters $a$ and $e$ from the ranges $0\leqslant a/r_{J}\leqslant 0.5$ and $0\leqslant e<1$. The $e(\delta,\omega,c_{1})$ equilibrium curves were constructed at different values of $\omega$ and fixed $c_{1}$ (Fig. 2) for the Sun–Jupiter–satellite system, when $a/r_{J}=0.384$, $m_{J}=0.00095$, $r_{J}=5.204$ AU, $c_{1}=0.3$, $0\leq e\leq 1$, and $0\leq\delta\leq 6\times 10^{-9}$. Some reference points $A_{j}$ with coordinates $(\delta_{j},e_{j})$ are specified in this figure: $A_{1}=(0,0.3998)$, $A_{2}=(0.054\times 10^{-9},0.83666)$, $A_{3}=(1.15\times 10^{-9},0.6432)$, $A_{4}$ $=$ (1.274 $\times$ $10^{-9}$, 0.83666), $A_{5}$ $=$ (1.365 $\times$ $10^{-9}$, 0.7683), and $A_{6}=(5.102\times 10^{-9},0)$.

Retaining more $e$ terms in (18) changes little the picture: we numerically compared the results obtained with the results of our calculations of Eqs. (18) containing the terms up to the seventh order of smallness in $e$ inclusive and showed that the equilibrium curves in Fig. 2slightly shifted in the direction of increasing eccentricity $e$.

For stationary values of $e$ and $\omega$ the longitude of the ascending node $\Omega$ is found by the quadrature from the corresponding equation of system (16). It can be seen that

$$\Omega=\Omega_{0}-\frac{2\sqrt{c_{1}}}{na^{2}}\textrm{sgn}(\cos i)\frac{\partial\hat{R}}{\partial c_{1}}t.$$

Fig. 4

Phase portrait at $\delta=0.5\times 10^{-9}$.

Thus, the elliptical orbits with their focus in the main attractive body having a constant inclination $i$ with respect to the plane of motion of the main bodies precessing slowly and uniformly around the normal to this plane correspond to the stationary solutions of Eqs. (16). At the same time, the orbital semimajor axis coincides with the line of nodes $SN$ ($\omega=0$) in the entire time of motions or is perpendicular to it ($\omega=\pi/2$).

A saddle–node bifurcation corresponds to point $A_{5}$, the unstable equilibria are highlighted by the dashed line. The real equilibria disappear at points $A_{2}$, $A_{4}$, and $A_{6}$, because the equilibrium curves go to the imaginary regions $e>\sqrt{1-c_{1}}$ or $e<0$ (the entire equilibrium curve at $\omega=\pi/2$ containing the pieces belonging to the the imaginary region $e>\sqrt{1-c_{1}}$ of possible motions is shown in Fig. 2). Two identical precessing elliptical orbits with their focus in the Sun, but with different arguments of pericenter correspond to point $A_{3}$. The equilibrium of the classical three-body problem, when $\delta=0$, corresponds to point $A_{1}$.

It follows from Fig. 2that in the small interval $(\delta_{1},\delta_{2})=(0,0.054\times 10^{-9})$ we have one stable equilibrium position ($\omega=\pi/2$). In the interval $\delta\in(\delta_{2},\delta_{4})=(0.054\times 10^{-9},1.274\times 10^{-9})$ a second stable equilibrium position appears for $\omega=0$. In the interval $\delta\in(\delta_{4},\delta_{5})=(1.274\times 10^{-9},1.365\times 10^{-9})$ another unstable equilibrium appears on the $\omega=\pi/2$ curve. At the bifurcation point $A_{5}$ the two equilibria on the $\omega=\pi/2$ curve merge into one and then vanish. So, only one stable equilibrium belonging to the $\omega=0$ curve remains in the interval $\delta\in(\delta_{5},\delta_{6})=(1.365\times 10^{-9},5.102\times 10^{-9})$, while at $\delta\in(\delta_{6},+\infty)$ the equilibrium positions disappear completely.

Fig. 5

Phase portrait at $\delta=1.0352\times 10^{-9}$.

Fig. 6

Phase portrait at $\delta=1.1497\times 10^{-9}$.

Fig. 7

Phase portrait at $\delta=1.3\times 10^{-9}$.

Fig. 8

Phase portrait at $\delta=2.88\times 10^{-9}$.

Fig. 9

Phase portrait at $\delta=5.5\times 10^{-9}$.

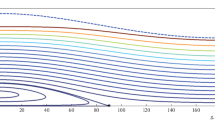
For all of the listed $\delta$ intervals we constructed the phase portraits of the oscillations shown in Figs. 3–9 by numerically integrating Eqs. (16). The results of our numerical integration were confirmed by the construction of level lines for the integral $\hat{R}^{(2)}$. Since the Fourier series for $\hat{R}$ contains only the even harmonics $\cos{2n\omega}$, the integral $\hat{R}=h$ curves are symmetric relative to $\omega=\pi/2$. The phase portrait in Fig. 3 was constructed for the parameters $c_{1}=0.3$, $a=2$ AU, and $\delta=0$ and qualitatively coincides with the phase portrait in Vashkov’yak (1981). This picture is qualitatively retained for any $\delta$ from the interval $(\delta_{1},\delta_{2})$. Here, we can see a center-type stationary point with coordinates $e=0.2472$ and $\omega=\pi/2$. In region $A$ we observe librational motions of the line of apsides, while in region $B$ the line of apsides executes a rotational motion in the direction of increasing argument of pericenter. Two integral manifolds, $e=0$ and $\sqrt{1-c_{1}}$, bounding the region of possible motions are shown on the phase portrait. These integral manifolds are also specified on other phase portraits.

Two center-type stationary points for $\omega=0$ and $\pi/2$ are present on the phase portrait in Fig. 4 constructed for the parameters $c_{1}=0.3$, $a=2$ AU, and $\delta=0.5\times 10^{-9}\in(\delta_{2},\delta_{4})$. In the neighborhood of the stationary points we have librational motions; in region $B$ we have rotational motions in the direction of increasing argument of pericenter. As $\delta$ increases, we observe a vertical upward elongation of region $A$ until the upper point of this region touches the upper manifold $e=\sqrt{1-c_{1}}$. The point of tangency, which is an equilibrium on this manifold, bifurcates as the parameter $\delta$ increases further and two separatrices (heteroclinic trajectories) correcting the lower equilibria with the upper ones appear (Fig. 5). The parameter $\delta=1.0352\times 10^{-9}$ (see Fig. 5) is bifurcational, because it leads to separatrix splitting. Each of the two separatrices splits into a pair of curves in such a way that the two newly appeared curves from region $A$ approach asymptotically (as $t\rightarrow\pm\infty$) the upper equilibria, forming a single curve bounding the new libration region $B$ (Fig. 6). The pair of the extreme curves that appeared leftward and rightward of region $A$ in Fig. 5 retain the asymptotic approach to the lower equilibria as $t\rightarrow\pm\infty$, asymptotically approaching the manifold $e=\sqrt{1-c_{1}}$ (Fig. 6).

The described splitting of the separatrices gives rise to an initially narrow and subsequently expanding region of rotational motions when the argument of pericenter $\omega$ decreases monotonically. Along these trajectories the satellite orbit slowly rotates in its osculating plane in a direction opposite to the case of $\delta=0$.

An additional unstable stationary point $D$ located near the integral manifold $e=\sqrt{1-c_{1}}$ appears on the phase portrait in Fig. 7 corresponding to $\delta=1.3\times 10^{-9}\in(\delta_{4},\delta_{5})$. A further increase in $\delta$ leads to the merging of the stable and unstable points at $\delta=1.365\times 10^{-9}$ and their subsequent disappearance, with the stationary point being retained on the second equilibrium branch $\omega=0$ (Fig. 8, $\delta\in(\delta_{5},\delta_{6})$).

For $\delta>\delta_{6}$ the phase portrait of the oscillations is shown in Fig. 9. It contains no stationary points; we have a secular drift of the line of apsides in the direction of decreasing argument of pericenter.

We showed that the terms of the fourth and sixth orders of smallness in $a/r_{J}$ in the reduced force function $\hat{R}$ have virtually no effect on the phase portrait of the oscillations, slightly shifting the equilibrium points along a vertical straight line and changing little the bifurcation values of $\delta$.

CONCLUSIONS

We considered the osculating elliptical motions of an asteroid (solar probe) with an infinitesimal mass around a star (Sun) under the action of two perturbations: the gravitational attraction from an outer planet (Jupiter) and the solar light pressure. We used Gauss’s scheme for twice averaging the perturbed force function of the problem over the planet’s longitude and the true anomaly of the satellite’s unperturbed motion. For the first time we have derived an explicit analytical expression for the averaged force function in the form of a Fourier series whose coefficients are expressed via known special functions. The analytical expression for the averaged force function allows one to obtain any approximation of the function in small parameter $a/r_{J}$ quickly and efficiently and to easily prove the integrality of some manifolds, in particular, the integrality of the manifold $e=\sqrt{1-c_{1}}$ in the reduced system, which is also a new result in the classical three-body problem.

An analysis of evolutionary motions showed that the influence of solar light pressure is very significant even at low values of the light pressure coefficient, when $\delta\sim 10^{-9}$: in the ranges $0\leqslant a/r_{J}\leqslant 0.5$ and $0\leqslant e<1$ an additional branch of the family of stationary motions $e(\delta)=\textrm{const},\omega=0$ appears, a saddle–node bifurcation of equilibria is observed on the branch for the traditional case of $\omega=\pi/2$, the real equilibria disappear when the family of stationary points goes beyond the region of possible motions.

The phase portrait of the oscillations is complicated significantly in comparison with the phase portrait of osculating motions in the classical circular three-body problem. For instance, saddle points appear near the manifold $e=\sqrt{1-c_{1}}$ in the region $(\delta_{4},\delta_{5})$, separatrix splitting is observed for $\delta$ from the interval $(\delta_{2},\delta_{4})$, reversing the direction of evolution of the argument of pericenter $\omega$ in the case of rotational motions.

The specified values of the parameter $\delta$ are typical, in order of magnitude, for the Parker Solar Probe. Thus, the results obtained can be used to estimate the parameters of motion when the light pressure on a given probe is taken into account.