Some Peculiarities of the Evolution of Orbits in the Satellite Restricted Elliptic Doubly Averaged Three-Body Problem

Abstract—

The inner (or satellite) version of the restricted elliptic three-body problem is considered. The terms up to the fourth order inclusive in small parameter are retained in the expansion of the perturbing function for the problem. The ratio of the orbital semimajor axes of perturbed and perturbing bodies is such a parameter, while their mean longitudes are the fastest variables. The Gauss scheme of independent double averaging over fast variables is used to analyze the orbital evolution of a body of negligible mass. Explicit analytical expressions for the doubly averaged perturbing function and its derivatives with respect to the elements on the right-hand sides of the evolution equations are presented. The integrable cases of the doubly averaged problem are studied in detail: planar and orthogonal apsidal orbits. The evolution system is numerically integrated in the general (nonintegrable) case for some special values of the problem parameters and initial conditions, in particular, for a set of orbital elements in which the so-called “flips”, i.e., transitions of the orbit from prograde to retrograde and vice versa, manifest themselves. In the Sun–Jupiter–asteroid model using some special asteroid orbits as an example, we show the influence of the retained fourth-order terms and the ellipticity of Jupiter’s orbit on their evolution.

INTRODUCTION AND FORMULATION OF THE PROBLEM

The averaged problems of celestial mechanics are both the subject of independent analytical and numerical research and one of the methodological foundations for studying the dynamics of real astronomical objects on long time scales. Various averaged schemes of the three-body problem, both general and restricted ones, are of special interest. The so-called Gauss scheme of independently averaging the force function of the problem over the two fastest variables, i.e., the mean longitudes of perturbing and perturbed bodies when their mean motions are incommensurable, is particularly prominent. N.D. Moiseev obtained a complete system of independent first integrals of the averaged (evolution) equations in elements in the restricted problem for a circular orbit of the perturbing body relative to the central one (Moiseev, 1945). Qualitative and analytical studies of the evolution equations were carried out by M.L. Lidov for the satellite version of the problem, when only the second-order terms are retained in the expansion of the perturbing function in powers of the small parameter α (the ratio of the semimajor axes of perturbed and perturbing bodies) (Lidov, 1961). Almost concurrently, Kozai investigated the asteroid version of the problem by including the terms ~α⁸ inclusive (Kozai, 1962). Apart from applications to the dynamics of satellites of planets and asteroids, these authors revealed the fall of a body of infinitesimal mass to a central body if its orbit is highly inclined to the orbital plane of the perturbing body. The monograph by I.I. Shevchenko (2017) is devoted to describing this effect called the Lidov–Kozai effect, along with its astrophysical applications. The paper by Ito (2016), where the doubly averaged perturbing function of the restricted circular three-body problem was expanded up α¹⁴ inclusive for the inner version (α < 1) and up to α^–15 inclusive for the outer version (α > 1), served as an elaboration of the study by Kozai (1962). Undoubtedly, a misprint in the last row of Eq. (33) from the Ito’s paper should be noted.

A natural generalization of the evolution three-body problem is its elaboration to the more realistic case where the orbit of a perturbing body is noncircular. The corresponding doubly averaged restricted elliptic problem has only a few integrable cases (Vashkov’yak, 1984) and is generally nonintegrable. Nevertheless, the Lidov–Kozai effect also manifests itself in this problem and, as a consequence, a new qualitative feature arises—highly eccentric orbits that change their type from prograde to retrograde and vice versa during their evolution. This phenomenon, which is related to the passage of the orbital inclination through 90° and was discovered by Katz et al. (2011) and Naoz et al. (2011), was called a “flip”. Quite a few papers are devoted to this phenomenon in the doubly averaged elliptic three-body problem (both general and restricted ones) with applications to the dynamics of exoplanets, triple star systems, and small bodies of the Solar system. Their extensive bibliography is contained in the already mentioned book by Shevchenko (2017). Among the recent works we will point out the papers by Naoz (2016) and Sidorenko (2018) devoted to the “eccentric Kozai–Lidov effect”.

In this paper we obtain a special form of the expansion of the doubly averaged perturbing function for the restricted elliptic three-body problem up to α⁴ inclusive (in particular, the terms ~α⁴ contain the square of the orbital eccentricity of a perturbing body). We consider the integrable cases of the problem in more detail and numerically integrate the evolution system with initial data corresponding to both a flip orbit and a stable equilibrium solution of the corresponding planar elliptic problem. In addition, we perform numerical calculations showing that including the terms ~α⁴ is necessary when analyzing the evolution of special asteroid orbits, in particular, a series of orbits of numbered asteroids with libration of the argument of perihelion: nos. 143 219, 159 518, 417 444, and 1866.

Consider the motion of a particle Р of negligible mass under the attraction of a central point S of mass m and a perturbing point J of mass m₁ ⪡ m moving relative to S in an elliptical orbit with a semimajor axis а₁ and eccentricity е₁. Let us introduce a rectangular coordinate system Oxyz with the origin at point S whose reference plane xOy coincides with the orbital plane of point J. Let the Ox axis be directed to the pericenter of the orbit of point J, the Oy axis be in the direction of its motion from the pericenter in the reference plane, and the Oz axis complements the coordinate system to a right-handed one. The perturbed orbit of point Р is characterized by osculating Keplerian elements: the semimajor axis а, the eccentricity е, the inclination i, the argument of pericenter ω, and the longitude of the ascending node Ω. The inner version of the problem suggests that the apocenter distance of point Р during the evolution of its orbit does not exceed the pericenter distance of the perturbing point J, i.e.,

$$a(1 + e) < {{a}_{1}}(1 - {{e}_{1}}).$$

As a rule, the secular part W of the complete perturbing function is used to investigate the orbital evolution of point Р:

$$W\left( {a,e,i,\omega ,\Omega ,{{a}_{1}},{{e}_{1}}} \right) = \frac{{f{{m}_{1}}}}{{4{{\pi }^{2}}}}\int\limits_0^{{{2\pi }}} {\int\limits_0^{{{2\pi }}} {\frac{{{\text{d}}{{\lambda }_{1}}{\text{d}}\lambda }}{{\Delta \left( {\lambda ,{{\lambda }_{1}}} \right)}}} } .$$

Here, in addition to the already introduced notation for the orbital elements, f is the gravitational constant, Δ is the distance between the perturbed and perturbing points Р and J, λ and λ₁ are the mean longitudes of these points, respectively. The procedure of such (independent) double averaging over fast variables is called the Gauss scheme, in which the absence of low-order commensurabilities between the mean motions of points J and Р is assumed. As a consequence, the first integrals of the equations of perturbed motion in elements appear in the doubly averaged problem,

(1)

while one more first integral (1 – e²)cos²i = const exists in the case of е₁ = 0 (Moiseev, 1945). In the function Wа₁ and е₁, along with а, play the role of parameters in the evolution problem.

A SPECIAL EXPRESSION FOR THE AVERAGED PERTURBING FUNCTION OF THE SATELLITE VERSION OF THE PROBLEM AND EVOLUTION EQUATIONS

Another equivalent expression for the function W via well-known formulas is also commonly used in analytical studies:

$$\begin{gathered} W\left( {a,e,i,\omega ,\Omega ,{{a}_{1}},{{e}_{1}}} \right) = \frac{1}{{2\pi }}\int\limits_0^{{{2\pi }}} {\left( {1 - e{{\cos}}E} \right)V\left( E \right)dE} , \\ V\left( E \right) = \frac{{f{{m}_{1}}}}{{2\pi a_{1}^{2}\sqrt {1 - e_{1}^{2}} }}\int\limits_0^{{{2\pi }}} {\frac{{r_{1}^{2}}}{{\Delta \left( {E,{{\nu }_{1}}} \right)}}d{{\nu }_{1}}} . \\ \end{gathered} $$

(2)

Here, Е is the eccentric anomaly of the perturbed point, ν₁ is the true anomaly of the perturbing point, r₁ = a₁ (1 – e₁²)/(1 + e₁ cos ν₁), and V is the force function of the elliptical Gaussian ring simulating the averaged influence of point J. In what follows, the so-called inner or satellite version of the problem will be considered by assuming r ⪡ r₁, while the terms up to the fourth order inclusive will be retained in the expansion of the function 1/Δ in Legendre polynomials P_n (or in powers of the ratio r/r₁), so that

$$\begin{gathered} \frac{1}{\Delta } = \frac{1}{{{{r}_{1}}}}{{\sum\limits_{n = 0}^{N = 4} {\left( {\frac{r}{{{{r}_{1}}}}} \right)} }^{n}}{{P}_{n}}\left( {{{\cos}}H} \right), \\ {{\cos}}H = \frac{1}{r}\left( {x{{\cos}}{{\nu }_{1}} + y{{\sin}}{{\nu }_{1}}} \right), \\ V\left( E \right) = \frac{{f{{m}_{1}}}}{{2\pi a_{1}^{2}\sqrt {1 - e_{1}^{2}} }} \\ \times \,\,\int\limits_0^{{{2\pi }}} {{{r}_{1}}\left[ \begin{gathered} 1 + \frac{r}{{{{r}_{1}}}}{{\cos}}H + \frac{{{{r}^{2}}}}{{2r_{1}^{2}}}\left( {3{{\cos}}{^{2}}H - 1} \right) \hfill \\ + \frac{{{{r}^{3}}}}{{2r_{1}^{3}}}\left( {{5\cos}}{{^{3}}H - 3{{\cos}}H} \right) \hfill \\ + \frac{{{{r}^{4}}}}{{8r_{1}^{4}}}\left( {{{35\cos}}{^{4}}H - 30{{\cos}}{^{2}}H + 3} \right) \hfill \\ \end{gathered} \right]d{{\nu }_{1}}} . \\ \end{gathered} $$

(3)

Performing the standard integration procedure in (3), we obtain an explicit expression for the function V:

$$\begin{gathered} V\left( E \right) = \frac{{3f{{m}_{1}}}}{{2a_{1}^{3}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\left\{ {\frac{1}{2}\left( {{{x}^{2}} + {{y}^{2}}} \right) - \frac{1}{3}{{r}^{2}}_{{}}^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}} \right. \\ + \frac{{{{e}_{1}}x}}{{4{{a}_{1}}\left( {1 - e_{1}^{2}} \right)}}\left[ {5\left( {{{x}^{2}} + {{y}^{2}}} \right) - 4{{r}^{2}}} \right] + \frac{1}{{64a_{1}^{2}{\kern 1pt} {{{\left( {1\, - \,e_{1}^{2}} \right)}}^{2}}}}{\kern 1pt} \\ \times \,\left. {\,\left[ \begin{gathered} 35\left( {2 + 5e_{1}^{2}} \right){{x}^{4}} + 70{\kern 1pt} \left( {2 + 3e_{1}^{2}} \right){{x}^{2}}{{y}^{2}} + \hfill \\ + \,\,35{\kern 1pt} \left( {2 + 5e_{1}^{2}} \right){\kern 1pt} {{y}^{4}} - 20{\kern 1pt} \left( {4 + 9e_{1}^{2}} \right){\kern 1pt} {{r}^{2}}{{x}^{2}} - \hfill \\ - \,\,20\left( {4 + 9e_{1}^{2}} \right){{r}^{2}}{{y}^{2}} + 8\left( {2 + 3e_{1}^{2}} \right){{r}^{4}} \hfill \\ \end{gathered} \right]} \right\}{\kern 1pt} , \\ \end{gathered} $$

(4)

where x, y, r are expressed via the eccentric anomaly Е using the well-known formulas for unperturbed elliptical Keplerian motion. Performing a similar integration procedure, we obtain the function W.

In the adopted approximation with respect to α the expression for the function W is given in Yokoyama et al. (2003). However, all of the subsequent results referring to the stability of Jupiter’s outer satellites were obtained for the resonant part of the function W containing only the terms ∼cos(Ω ± ω) and ∼cos2(Ω ± ω). In contrast to the expression given in this paper, in the following more compact formulas we directly separate out the dependence of W on the longitude of the ascending node Ω (it is this dependence that is an obstacle to the integrability of the doubly averaged restricted elliptic three-body problem):

$$\begin{gathered} W\left( {e,i,\omega ,\Omega ,\alpha ,{{e}_{1}}} \right) = \frac{{3f{{m}_{1}}{{\alpha }^{2}}}}{{8{{a}_{1}}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}w, \\ w = {{w}_{0}} - A{{w}_{1}} + B{{w}_{2}},\,\,\,\,{{w}_{0}} = {{e}^{2}} - {\text{si}}{{{\text{n}}}^{2}}i \\ + \,\,{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}i\left( {1 - 5{\text{si}}{{{\text{n}}}^{2}}\omega } \right),\,\,\,\,{{w}_{1}} = {{A}_{1}}{\text{cos}}\Omega + {{B}_{1}}{\text{sin}}\Omega , \\ {{w}_{2}} = \left( {1 + \frac{3}{2}e_{1}^{2}} \right){{A}_{0}} + e_{1}^{2}\left( {{{A}_{2}}{\text{cos2}}\Omega + {{B}_{2}}{\text{sin2}}\Omega } \right), \\ \alpha = \frac{a}{{{{a}_{1}}}},\,\,\,\,A = \frac{{5\alpha {{e}_{1}}}}{{8\left( {1 - e_{1}^{2}} \right)}},\,\,\,\,B = \frac{{15{{\alpha }^{2}}}}{{64{{{\left( {1 - e_{1}^{2}} \right)}}^{2}}}}, \\ \alpha \left( {1 + e} \right) < 1 - {{e}_{1}}. \\ \end{gathered} $$

(5)

Here, the coefficients А_{0, 1, 2} and В_{1, 2} dependent on the elements e, i, ω and independent of Ω are defined by the formulas

$$\begin{gathered} {{A}_{1}} = {{C}_{1}}e{\text{cos}}\omega ,\,\,\,\,{{B}_{1}}\,{\text{ = }}\left[ {10\left( {1 - {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i - {{C}_{1}}} \right] \\ \times \,\,e{\text{cos}}i{\text{sin}}\omega ,\,\,\,\,{{C}_{1}} = 4 + 3{{e}^{2}} - 5{\text{si}}{{{\text{n}}}^{2}}i \\ \times \,\,\left( {1 - {{e}^{2}} + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right),\,\,\,\,{{A}_{0}} = {{e}^{2}}\left( {8 + 3{{e}^{2}}} \right) \\ - \,\,2{\text{si}}{{{\text{n}}}^{2}}i\left[ {\left( {1 - {{e}^{2}}} \right)\left( {4 + 3{{e}^{2}}} \right) + 21{{e}^{2}}} \right. \\ \left. { \times \,\,\left( {2 + {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}\omega } \right] + {{C}_{2}},\,\,\,\,{{A}_{2}} = 7{{e}^{2}}\left( {2 + {{e}^{2}}} \right) \\ \times \,\,{\text{cos}}2\omega + 2{\text{si}}{{{\text{n}}}^{2}}i\left[ {\left( {1 - {{e}^{2}}} \right)\left( {3 - 10{{e}^{2}}} \right) + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right. \\ \left. { \times \,\,\left( {8 - 17{{e}^{2}} + 21{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right)} \right] - {{C}_{2}}, \\ {{B}_{2}} = 7{{e}^{2}}{\text{cos}}i{\text{sin2}}\omega \times \\ \times \,\,\left[ {7{\text{si}}{{{\text{n}}}^{2}}i\left( {1 - {{e}^{2}} + 3{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right) - \left( {2 + {{e}^{2}}} \right)} \right], \\ {{C}_{2}} = 7{\text{si}}{{{\text{n}}}^{4}}i\left\{ {{{{\left( {1 - {{e}^{2}}} \right)}}^{2}} + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega \times } \right. \\ \left. { \times \,\,\left[ {2\left( {1 - {{e}^{2}}} \right) + 3{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right]} \right\}. \\ \end{gathered} $$

(6)

The function w₁ contains factor e and is multiplied by the value proportional to е₁, while the function w₂ contains the terms of the zeroth and second order in е₁.

Below, it is convenient to introduce a new independent variable, a “dimensionless time” τ, according to the formula

$$\tau = \frac{{3f{{m}_{1}}}}{{8a_{1}^{3}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}n}}\left( {t - {{t}_{0}}} \right),$$

(7)

where $n = \frac{{\sqrt {fm} }}{{{{a}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}$ is the mean motion of point Р.

To describe the evolution of orbits, we will use the Lagrange equations in elements with the function w that is their first (and generally unique) integral:

$$\begin{gathered} \frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\frac{{di}}{{d\tau }} = \frac{1}{{{\text{sin}}i\sqrt {1 - {{e}^{2}}} }} \\ \times \,\,\left( {{\text{cos}}i\frac{{\partial w}}{{\partial \omega }} - \frac{{\partial w}}{{\partial \Omega }}} \right),\,\,\,\,\frac{{d\omega }}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}} \\ - \,\,\frac{{{\text{cos}}i}}{{{\text{sin}}i\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}},\,\,\,\,\frac{{d\Omega }}{{d\tau }} = \frac{1}{{{\text{sin}}i\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}}. \\ \end{gathered} $$

(8)

For arbitrary orbits of point Р and е₁ > 0 a rigorous solution of Eqs. (8) can be apparently found only by a numerical method for specified initial conditions, while the process of calculations can be controlled by the constancy of the function w along this solution. For completeness of the set of formulas, we provide expressions for the derivatives of w₀, w₁, and w₂ in elements. They are needed to calculate the right parts of the evolution equations.

The derivatives of the function w₀ are

$$\begin{gathered} \frac{{\partial {{w}_{0}}}}{{\partial e}} = 2e\left[ {1 + {\text{si}}{{{\text{n}}}^{2}}i\left( {1 - 5{\text{si}}{{{\text{n}}}^{2}}\omega } \right)} \right], \\ \frac{{\partial {{w}_{0}}}}{{\partial i}} = {\text{sin}}2i\left[ {{{e}^{2}}\left( {1 - 5{\text{si}}{{{\text{n}}}^{2}}\omega } \right) - 1} \right], \\ \frac{{\partial {{w}_{0}}}}{{\partial \omega }} = - 5{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}i{\text{sin2}}\omega ,\,\,\,\,\frac{{\partial {{w}_{0}}}}{{\partial \Omega }} = 0. \\ \end{gathered} $$

The derivatives of the function w₁ are

$$\begin{gathered} \frac{{\partial {{w}_{1}}}}{{\partial e}} = \frac{{\partial {{A}_{1}}}}{{\partial e}}{\text{cos}}\Omega + \frac{{\partial {{B}_{1}}}}{{\partial e}}{\text{sin}}\Omega , \\ \frac{{\partial {{A}_{1}}}}{{\partial e}} = {\text{cos}}\omega \left\{ {4 + 9{{e}^{2}} - 5{\text{si}}{{{\text{n}}}^{2}}i} \right. \\ \left. { \times \,\,\left[ {1 - 3{{e}^{2}}\left( {1 - 7{\text{si}}{{{\text{n}}}^{2}}\omega } \right)} \right]} \right\},\,\,\,\,\frac{{\partial {{B}_{1}}}}{{\partial e}} = {\text{cos}}i{\text{sin}}\omega \\ \times \,\,\left\{ { - \left( {4 + 9{{e}^{2}}} \right) + 15{\text{si}}{{{\text{n}}}^{2}}i\left[ {1 - {{e}^{2}}\left( {3 - 7{\text{si}}{{{\text{n}}}^{2}}\omega } \right)} \right]} \right\}, \\ \end{gathered} $$

$$\begin{gathered} \frac{{\partial {{w}_{1}}}}{{\partial i}} = \frac{{\partial {{A}_{1}}}}{{\partial i}}{\text{cos}}\Omega + \frac{{\partial {{B}_{1}}}}{{\partial i}}{\text{sin}}\Omega , \\ \frac{{\partial {{A}_{1}}}}{{\partial i}} = - 5e{\text{cos}}\omega {\text{sin}}2i\left( {1 - {{e}^{2}} + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right), \\ \frac{{\partial {{B}_{1}}}}{{\partial i}} = e{\text{sin}}i{\text{sin}}\omega \left\{ {4 + 3{{e}^{2}} + 5\left( {2 - 3{\text{si}}{{{\text{n}}}^{2}}i} \right)} \right. \\ \left. { \times \,\,\left[ {3\left( {1 - {{e}^{2}}} \right) + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right]} \right\}, \\ \end{gathered} $$

$$\begin{gathered} \frac{{\partial {{w}_{1}}}}{{\partial \omega }} = \frac{{\partial {{A}_{1}}}}{{\partial \omega }}{\text{cos}}\Omega + \frac{{\partial {{B}_{1}}}}{{\partial \omega }}{\text{sin}}\Omega ,\,\,\,\,\frac{{\partial {{A}_{1}}}}{{\partial \omega }} = - e{\text{sin}}\omega \\ \times \,\,\left\{ {4 + 3{{e}^{2}} - 5{\text{si}}{{{\text{n}}}^{2}}i\left[ {1 - 3{{e}^{2}}\left( {5 - 7{\text{si}}{{{\text{n}}}^{2}}\omega } \right)} \right]} \right\}, \\ \frac{{\partial {{B}_{1}}}}{{\partial \omega }} = e{\text{cos}}i{\text{cos}}\omega \\ \times \,\,\left[ {15{\text{si}}{{{\text{n}}}^{2}}i\left( {1 - {{e}^{2}} + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right) - \left( {4 + 3{{e}^{2}}} \right)} \right], \\ \end{gathered} $$

$$\frac{{\partial {{w}_{1}}}}{{\partial \Omega }} = {{B}_{1}}{\text{cos}}\Omega - {{A}_{1}}{\text{sin}}\Omega .$$

The derivatives of the function w₂ are

$$\begin{gathered} \frac{{\partial {{w}_{2}}}}{{\partial e}} = \left( {1 + \frac{3}{2}e_{1}^{2}} \right)\frac{{\partial {{A}_{0}}}}{{\partial e}}{\text{ + }}e_{1}^{2}\left( {\frac{{\partial {{A}_{2}}}}{{\partial e}}{\text{cos2}}\Omega + \frac{{\partial {{B}_{2}}}}{{\partial e}}{\text{sin2}}\Omega } \right), \\ \frac{{\partial {{A}_{0}}}}{{\partial e}} = 4e\left[ {4 + 3{{e}^{2}} + \left( {1 + 6{{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i - 42\left( {1 + {{e}^{2}}} \right)} \right. \\ \left. { \times \,\,{\text{si}}{{{\text{n}}}^{2}}i{\text{si}}{{{\text{n}}}^{2}}\omega } \right] + \frac{{\partial {{C}_{2}}}}{{\partial e}}, \\ \frac{{\partial {{A}_{2}}}}{{\partial e}} = 4e\left[ {7\left( {1 + {{e}^{2}}} \right){\text{cos2}}\omega - } \right.\left( {13 - 20{{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i \\ + \,\,14\left( {4 - 17{{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i{\text{si}}{{{\text{n}}}^{2}}\omega + \left. {294{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}i{\text{si}}{{{\text{n}}}^{4}}\omega } \right] - \frac{{\partial {{C}_{2}}}}{{\partial e}}, \\ \frac{{\partial {{B}_{2}}}}{{\partial e}} = 14e{\text{cos}}i{\text{sin2}}\omega \\ \times \,\,\left[ {7\left( {1 - 2{{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i + 42{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}i{\text{si}}{{{\text{n}}}^{2}}\omega - 2\left( {1 + {{e}^{2}}} \right)} \right], \\ \frac{{\partial {{C}_{2}}}}{{\partial e}} = 28e{\text{si}}{{{\text{n}}}^{4}}i\left[ {{{e}^{2}}\, - \,1\, + \,7\left( {1 - 2{{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}\omega + 21{{e}^{2}}{\text{si}}{{{\text{n}}}^{4}}\omega } \right], \\ \end{gathered} $$

$$\begin{gathered} \frac{{\partial {{w}_{2}}}}{{\partial i}} = \left( {1 + \frac{3}{2}e_{1}^{2}} \right)\frac{{\partial {{A}_{0}}}}{{\partial i}}{\text{ + }}e_{1}^{2}\left( {\frac{{\partial {{A}_{2}}}}{{\partial i}}{\text{cos2}}\Omega + \frac{{\partial {{B}_{2}}}}{{\partial i}}{\text{sin2}}\Omega } \right), \\ \frac{{\partial {{A}_{0}}}}{{\partial i}} = - 2{\text{sin2}}i\left[ {\left( {1 - {{e}^{2}}} \right)\left( {4 + 3{{e}^{2}}} \right)} \right. \\ + \,\,\left. {21{{e}^{2}}\left( {2 + {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}\omega } \right] + \frac{{\partial {{C}_{2}}}}{{\partial i}},\,\,\,\,\frac{{\partial {{A}_{2}}}}{{\partial i}} = 2{\text{sin2}}i \\ \times \,\,\left[ {\left( {1 - {{e}^{2}}} \right)\left( {3 - 10{{e}^{2}}} \right) + 7{{e}^{2}}\left( {8 - 17{{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}\omega } \right. \\ + \,\,\left. {147{{e}^{4}}{\text{si}}{{{\text{n}}}^{4}}\omega } \right] - \frac{{\partial {{C}_{2}}}}{{\partial i}},\,\,\,\,\frac{{\partial {{B}_{2}}}}{{\partial i}} = 7{{e}^{2}}{\text{sin}}i{\text{sin2}}\omega \\ \times \,\,\left[ {16 - 13{{e}^{2}} - 21\left( {1 - {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i + 21{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right. \\ \times \,\,\left. {\left( {2 - 3{\text{si}}{{{\text{n}}}^{2}}i} \right)} \right],\,\,\,\,\frac{{\partial {{C}_{2}}}}{{\partial i}} = 28{\text{si}}{{{\text{n}}}^{3}}i{\text{cos}}i \\ \times \,\,\left[ {{{{\left( {1 - {{e}^{2}}} \right)}}^{2}} + 14{{e}^{2}}\left( {1 - {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}\omega + 21{{e}^{4}}{\text{si}}{{{\text{n}}}^{4}}\omega } \right], \\ \end{gathered} $$

$$\begin{gathered} \frac{{\partial {{w}_{2}}}}{{\partial \omega }} = \left( {1 + \frac{3}{2}e_{1}^{2}} \right)\frac{{\partial {{A}_{0}}}}{{\partial \omega }}{\text{ + }}e_{1}^{2}\left( {\frac{{\partial {{A}_{2}}}}{{\partial \omega }}{\text{cos2}}\Omega + \frac{{\partial {{B}_{2}}}}{{\partial \omega }}{\text{sin2}}\Omega } \right), \\ \frac{{\partial {{A}_{0}}}}{{\partial \omega }} = - 42{{e}^{2}}\left( {2 + {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i{\text{sin2}}\omega + \frac{{\partial {{C}_{2}}}}{{\partial \omega }}, \\ \frac{{\partial {{A}_{2}}}}{{\partial \omega }} = 14{{e}^{2}}{\text{sin2}}\omega \left[ {\left( {8 - 17{{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i} \right. \\ \left. { + \,\,42{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}i{\text{si}}{{{\text{n}}}^{2}}\omega - \left( {2 + {{e}^{2}}} \right)} \right] - \frac{{\partial {{C}_{2}}}}{{\partial \omega }}, \\ \frac{{\partial {{B}_{2}}}}{{\partial \omega }} = 14{{e}^{2}}{\text{cos}}i\left\{ {\left[ {7\left( {1 - {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i - \left( {2 + {{e}^{2}}} \right)} \right]} \right. \\ \left. { \times \,\,{\text{cos}}2\omega + 21{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}i{\text{si}}{{{\text{n}}}^{2}}\omega \left( {3 - 4{\text{si}}{{{\text{n}}}^{2}}\omega } \right)} \right\}, \\ \frac{{\partial {{C}_{2}}}}{{\partial \omega }} = 98{{e}^{2}}{\text{si}}{{{\text{n}}}^{4}}i{\text{sin2}}\omega \left( {1 - {{e}^{2}} + 3{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right), \\ \frac{{\partial {{w}_{2}}}}{{\partial \Omega }} = 2e_{1}^{2}\left( {{{B}_{2}}{\text{cos2}}\Omega - {{A}_{2}}{\text{sin2}}\Omega } \right). \\ \end{gathered} $$

INTEGRABLE CASES OF THE ELLIPTIC PROBLEM

Planar Orbits

If sin i = 0, then the orbit of point Р is always located in the reference coordinate plane $\left( {\frac{{di}}{{d\tau }} = 0} \right),$ while the evolution equations are simplified. With the introduction of the longitude of periastron of point Р

$$g = \Omega + \omega \delta ,$$

(9)

where δ = sign(cos i), the evolution system takes the form

$$\frac{1}{\delta }\frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial g}},\,\,\,\,\frac{1}{\delta }\frac{{dg}}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}}.$$

(10)

In this case, it is obvious that the prograde (δ = 1) and retrograde (δ = –1) orbits evolve identically with time inversion, while the existence of the first integral

$$w(e,g) = h = {\text{const}}$$

(11)

makes the planar evolution problem integrable as a system with one degree of freedom.

The integrability of this (planar) version of the doubly averaged restricted elliptic problem was first established by E.P. Aksenov for B = 0, where the terms ~α⁴ and higher are disregarded in the expansion of the function W. A qualitative study of the problem was carried out in Aksenov (1979a), while the quadratures were analytically inverted and the time dependences of the orbital elements were obtained in Aksenov (1979b). E.P. Aksenov’s studies were elaborated by Veresh (1980a; 1980b; 1980c) in terms of both a qualitative analysis of the problem and the construction of its approximate analytical solution for α < 1. Subsequently, Vashkov’yak (1982) investigated the planar case of the problem for arbitrary α using a numerical-analytical method, which envisaged a numerical calculation of the function W and an analytical determination of the function V in Eqs. (2). In what follows, the results of these papers will be used and, where possible, the notation introduced in them will be retained.

Our goal is to derive refined quantitative evolution characteristics compared to the case of B = 0 and a more detailed qualitative study of the problem for B > 0 than that performed in Veresh (1980a).

From Eqs. (5) at sin i = 0 we obtain

$$\begin{gathered} w\left( {e,g,\alpha ,{{e}_{1}}} \right) = {{e}^{2}} - Ae\left( {4 + 3{{e}^{2}}} \right){\text{cos}}g + B{{e}^{2}} \\ \times \,\,\left[ {\left( {1 + \frac{3}{2}e_{1}^{2}} \right)\left( {8 + 3{{e}^{2}}} \right) + 7e_{1}^{2}\left( {2 + {{e}^{2}}} \right){\text{cos}}2g} \right] = h, \\ \end{gathered} $$

(12)

and Eqs. (10) take the form

$$\begin{gathered} \frac{1}{\delta }\frac{{de}}{{d\tau }} = - \sqrt {1 - {{e}^{2}}} \\ \times \,\,\left[ {A\left( {4 + 3{{e}^{2}}} \right) - 28Be_{1}^{2}e\left( {2 + {{e}^{2}}} \right){\text{cos}}g} \right]{\text{sin}}g, \\ \frac{1}{\delta }\frac{{dg}}{{d\tau }} = \sqrt {1 - {{e}^{2}}} \left\{ {2 - \frac{A}{e}\left( {4 + 9{{e}^{2}}} \right){\text{cos}}g + 2B} \right. \\ \left. { \times \,\,\left[ {\left( {2 + 3e_{1}^{2}} \right)\left( {4 + 3{{e}^{2}}} \right) + 14e_{1}^{2}\left( {1 + {{e}^{2}}} \right){\text{cos}}2g} \right]} \right\}. \\ \end{gathered} $$

(13)

At fixed parameters α and е₁ the integral (12) defines an h-family of integral curves in the (g, e) plane. For А = 0.1 and В = 0 Aksenov (1979a) constructed such a family, studied in detail its qualitative structure, found the stationary values of the variables e*, g* = 0, and revealed three possible types of phase trajectories: I—libration of both variables е and g; II— libration of е and circulation of g; III—degeneracy of trajectories, when the phase point reaches a boundary value of е = 1 in a finite time as g changes monotonically, which at a = const corresponds to the collision of point Р with the central point S. For α = 0.5 and е₁ = 0.3 Veresh (1980a) constructed similar families for both В = 0 (E.P. Aksenov’s solution) and В > 0. In this case, it was established that including the terms of higher orders in α does not change the qualitative structure of the families of integral curves, does not give rise to any new types of phase trajectories, but affects only their quantitative characteristics.

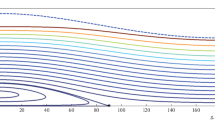
For completeness, we provide here the h-families of integral curves (12) for α = 0.24, e₁ = 0.5, A = 0.1, B = 0.024 (Fig. 1), and B = 0 (Fig. 2).

Fig. 1.

The family of integral curves (12) in the (g, е) plane for α = 0.24, e₁ = 0.5, A = 0.1, and B = 0.024 (F. Veresh’s solution).

In view of the existing symmetry of phase trajectories, only the regions 0° < g < 180° are shown. The open circles in the figures mark the stationary points (g = 0, e = e*) and the points (g = 0, e = e_s) and (g = 90°, e = 0) on the integral curves that bound the libration zones of the argument of pericenter. The filled circles mark the points (g = 0, e = 1) and (g = 90°, e = е_с) on the separatrices separating the circulation regions from the regions corresponding to degenerate trajectories. The phase point moves along these curves in such a way that е → 1 as t → ±∞. As was also noted in Veresh (1980a), a comparison of Figs. 1 and 2 makes it possible to estimate the influence of the factor В on the quantitative characteristics of the family of phase trajectories for the problem. Below, such characteristics will be presented for a fairly wide domain of parameters α and е₁.

The stationary solutions of system (13) are found by setting the right-hand sides of both equations equal to zero. From the first equation in (13) we have

$$\begin{gathered} g{\text{ }} = {\text{ }}0,\,\,\,\,{\text{or}}\,\,\,\,g = \pi ,~\,\,\,\,{\text{or}} \\ g = {\text{arccos}}\left[ {\frac{{A\left( {4 + 3{{e}^{2}}} \right)}}{{28Be_{1}^{2}e\left( {2 + {{e}^{2}}} \right)}}} \right]. \\ \end{gathered} $$

(14)

It can be shown that for the last two equalities the right-hand side of the second equation in (13) is positive for any α, е₁ and е ≠ 1. Therefore, for е < 1 the only stationary value of the variable g is

$$g = {{g}^{*}} = 0.$$

(15)

The stationary value of the eccentricity 0 < е* < 1 is found as the corresponding real root of the cubic equation

$${{c}_{3}}{{e}^{{*3}}} + {{c}_{2}}{{e}^{{*2}}} + {{c}_{1}}e{\text{*}} + {{c}_{0}} = 0,$$

(16)

where

$$\begin{gathered} {{c}_{3}} = 2B\left( {6 + 23e_{1}^{2}} \right),\,\,\,\,{{c}_{2}} = - 9A, \\ {{c}_{1}} = 2\left[ {1 + 2B\left( {4 + 13e_{1}^{2}} \right)} \right],\,\,\,\,{{c}_{0}} = - 4A. \\ \end{gathered} $$

(17)

At В = 0 Eq. (16) is quadratic and the stationary value of the eccentricity is defined by one of its roots by the formula (Aksenov, 1979a)

$$e^* = \frac{1}{{9A}}\left( {1 - \sqrt {1 - 36{{A}^{2}}} } \right).$$

(18)

Since А and В depend on the problem parameters α and е₁, for clarity, it is natural to present the results of the solution of Eq. (16) in the form of a family of isolines е*(α, е₁) = const (Fig. 3). The numerical values of е* are plotted vertically near the right ends of the thick lines. The corresponding dashed lines (В = 0) virtually coincide with the thick lines at small α. At α differing noticeably from zero the solid and dashed lines diverge, which gives an estimate of the influence of the terms ~α⁴ in the expansion of the averaged perturbing function on е*. In particular, for the parameters α = 0.24 and e₁ = 0.5 adopted when constructing the families in Figs. 1 and 2, е* ≈ 0.155 and 0.230, respectively.

Fig. 2.

Same as Fig. 1, but for В = 0 (E.P. Aksenov’s solution).

Fig. 3.

The family of isolines of the stationary values for the eccentricity е*(α, е₁) = const (the solution for В > 0—the thick lines; the solution for В = 0—the dashed lines).

In the domain of parameters α and е₁ under consideration the values of е* are relatively small and do not exceed about 0.2.

Remark. Going beyond the planar integrable case, we will note the recent paper by Neishtadt et al. (2018), where the spatial stability of stationary solutions was investigated in the linear approximation in i. It is also pointed out that the KAM theory guarantees the Lyapunov stability of stationary solutions for all values of the parameters in the α, e₁ plane, except, possibly, for the parameters belonging to some finite set of analytical curves.

The families е_s(α, е₁) = const (Fig. 4) and е_с(α, е₁) = const (Fig. 5), which characterize the sizes of the libration and circulation zones, are constructed similarly to the family of isolines for е*.

Fig. 4.

Same as Fig. 3, but for е_s(α, е₁) = const.

Fig. 5.

Same as Fig. 3, but for е_c(α, е₁) = const.

The following equations serve to determine е_s and е_с, respectively:

$$\frac{1}{4}{{c}_{3}}e_{s}^{3} + \frac{1}{3}{{c}_{2}}e_{s}^{2} + \frac{1}{2}{{c}_{1}}{{e}_{s}} + {{c}_{0}} = 0,$$

(19)

$$\frac{1}{4}{{c}_{3}}e_{c}^{4} - \frac{1}{3}{{c}_{2}}e_{c}^{3} + \frac{1}{2}{{c}_{1}}e_{c}^{2} - {{c}_{0}}{{e}_{c}} - {{h}_{c}} = 0.$$

(20)

In Eq. (20)h_c is defined by the formula

$${{h}_{{\text{c}}}} = {\text{1}}-{\text{7}}A + {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} \mathord{\left/ {\vphantom {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} {\text{2}}}} \right. \kern-0em} {\text{2}}}.$$

(21)

For the parameters α = 0.24 and e₁ = 0.5 adopted when constructing the families in Figs. 1 and 2, е_s ≈ 0.32 and 0.48, respectively, while е_с ≈ 0.595 and 0.370, respectively.

In addition to the above special values of the eccentricity, finding its extreme values for each of the characteristic ranges of the constant h of the integral (12) is of interest. As our analysis shows, h can vary within the range

$$\begin{gathered} \min h = h{\kern 1pt} ^* = h(e^*,0) \leqslant {{h}_{s}} = h({{e}_{s}},0) = h\left( {0, - } \right) \leqslant {{h}_{c}} = \\ = h({{e}_{c}},\pi ) \leqslant h{\kern 1pt} ^*{\kern 1pt} ^* = h(1,\pi ) = \max h. \\ \end{gathered} $$

(22)

Here, e* is the stationary value of the eccentricity, е_s is its value at g = 0, and е_с is its minimum value at g = π/2 corresponding to the circulation of g, whereby е(g = 0) = 1.

From the known е* for В > 0 it is easy to find

$$h^* = e{\text{*}}\left( {\frac{1}{4}{{c}_{3}}{{e}^{{*3}}} + \frac{1}{3}{{c}_{2}}{{e}^{{*2}}} + \frac{1}{2}{{c}_{1}}e{\text{*}} + {{c}_{0}}} \right),$$

(23)

which corresponds to the stationary solution. The remaining special values in the system of inequalities (22) are defined as

$${{h}_{{\text{s}}}} = 0,\,\,h{\text{**}} = {\text{1}} + {\text{7}}A + {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} \mathord{\left/ {\vphantom {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} {\text{2}}}} \right. \kern-0em} {\text{2}}}$$

(24)

and by Eq. (21) for h_c.

The types of phase trajectories revealed by E.P. Aksenov at В = 0 (Aksenov, 1979b) are also retained for B > 0, but their extreme characteristics undergo changes. Figures 6 and 7 present the h dependences of the extreme values of the eccentricity constructed at α = 0.24, e₁ = 0.5, and А = 0.1 for В = 0.024 and В = 0, respectively. The Roman numerals mark three regions with different types of change in elements.

Fig. 6.

Extreme values of the eccentricity versus h for α = 0.24, e₁ = 0.5, А = 0.1, and В = 0.024.

Fig. 7.

Same as Fig. 6, but for В = 0 (E.P. Aksenov’s solution).

For region I (h* ≤ h < 0, the libration of е and g) the extreme values of the eccentricity 0 < е_ex < 1 are defined by the two positive roots of the quartic polynomial

$$\frac{1}{4}{{c}_{3}}e_{{{\text{ex}}}}^{4} + \frac{1}{3}{{c}_{2}}e_{{{\text{ex}}}}^{3} + \frac{1}{2}{{c}_{1}}e_{{{\text{ex}}}}^{2} + {{c}_{0}}{{e}_{{{\text{ex}}}}} - h = 0.$$

(25)

For region II (0 < h < h_c, the libration of е and the circulation of g) the minimum value of the eccentricity 0 < е_min < 1 is defined by the positive root of the polynomial

$$\frac{1}{4}{{c}_{3}}e_{{{\text{ex}}}}^{4} - \frac{1}{3}{{c}_{2}}e_{{{\text{ex}}}}^{3} + \frac{1}{2}{{c}_{1}}e_{{{\text{ex}}}}^{2} - {{c}_{0}}{{e}_{{{\text{ex}}}}} - h = 0,$$

(26)

while its maximum value 0 < е_max < 1 is defined by the root of the polynomial (25), but with a different range of change in h.

Finally, for region III (degenerate trajectories, h_c < h ≤ h**) the minimum value of the eccentricity 0 < е_min <1 is defined by the positive root of the polynomial (26).

The procedure for calculating the roots of polynomials is among the standard ones in many computing systems, in particular, in Matlab, while the choice of the necessary roots is straightforward. Furthermore, the above algebraic equations allow, if necessary, dependences similar to those in Figs. 1 and 6 to be constructed for any admissible values of the problem parameters α and е₁.

It can be seen from a comparison of Figs. 6 and 7 presented on the same scale that our inclusion of the terms ∼α⁴ leads to a reduction in the extreme values of the eccentricity and allows their more accurate values differing significantly from those in the case of В = 0 to be obtained.

Orthogonal Apsidal Orbits

If cos i = 0 and sin Ω = 0, then the orbit of point Р is always orthogonal to the orbital plane of the perturbing point J$\left( {{{{\text{d}}i} \mathord{\left/ {\vphantom {{{\text{d}}i} {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = 0,\,\,{{{\text{d}}\Omega } \mathord{\left/ {\vphantom {{{\text{d}}\Omega } {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = 0} \right).$ A general qualitative study of this case, including the possible intersections of the orbits of points Р and J, was carried out using a numerical-analytical method by Vashkov’yak (1984) for arbitrary α. Here, the satellite version of the problem is investigated with the derivation of more detailed quantitative evolution characteristics.

In the approximation under consideration the evolution equations (8) are also simplified and take the form

$$\frac{{{\text{d}}e}}{{{\text{d}}\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\frac{{{\text{d}}\omega }}{{{\text{d}}\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}}.$$

(27)

Here,

$$\begin{gathered} w\left( {e,\omega ,\alpha ,{{e}_{1}}} \right) = {{e}^{2}}\left( {5{\text{co}}{{{\text{s}}}^{2}}\omega - 3} \right) + A{{\delta }_{1}}e{\text{cos}}\omega \\ \times \,\,\left[ {1 + {{e}^{2}}\left( {27 - 35{\text{co}}{{{\text{s}}}^{2}}\omega } \right)} \right] + B \\ \times \,\,\left\{ \begin{gathered} \left( {10 + 3e_{1}^{2}} \right){{e}^{2}} + \frac{1}{2}\left( {46 + 95e_{1}^{2}} \right){{e}^{4}} - 7{{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega \hfill \\ \times \,\,\left[ {2 + e_{1}^{2} + \left( {22 + 53e_{1}^{2}} \right){{e}^{2}} - \frac{{21}}{2}\left( {2 + 5e_{1}^{2}} \right){{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega } \right] \hfill \\ \end{gathered} \right\} \\ = h = {\text{const}}, \\ \end{gathered} $$

(28)

δ₁ = sign(cosΩ), so that

$$\begin{gathered} \frac{{{\text{d}}e}}{{{\text{d}}\tau }} = \sqrt {1 - {{e}^{2}}} {\text{sin}}\omega \left\{ \begin{gathered} 10e{\text{cos}}\omega + A{{\delta }_{1}}\left[ {1 + 3\left( {9 - 35{\text{co}}{{{\text{s}}}^{2}}\omega } \right){{e}^{2}}} \right] \hfill \\ + 14Be{\text{cos}}\omega \left[ {21\left( {2 + 5e_{1}^{2}} \right){{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega - \left( {22 + 53e_{1}^{2}} \right){{e}^{2}} - 2 - e_{1}^{2}} \right] \hfill \\ \end{gathered} \right\}, \\ \frac{{{\text{d}}\omega }}{{{\text{d}}\tau }} = \sqrt {1 - {{e}^{2}}} \left\{ \begin{gathered} 2\left( {5{\text{co}}{{{\text{s}}}^{2}}\omega - 3} \right) \hfill \\ + 2B\left[ \begin{gathered} 10 + 3e_{1}^{2} + \left( {46 + 95e_{1}^{2}} \right){{e}^{2}} \hfill \\ - \,7\left( {2 + e_{1}^{2} + 2\left( {22 + 53e_{1}^{2}} \right){{e}^{2}} - 21\left( {2 + 5e_{1}^{2}} \right){{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega } \right){\text{co}}{{{\text{s}}}^{2}}\omega \hfill \\ \end{gathered} \right] + \hfill \\ + A{{\delta }_{1}}\frac{{{\text{cos}}\omega }}{e}\left[ {1 + 3\left( {27 - 35{\text{co}}{{{\text{s}}}^{2}}\omega } \right){{e}^{2}}} \right] \hfill \\ \end{gathered} \right\}. \\ \end{gathered} $$

(29)

At fixed parameters α and е₁ the integral (28) defines an h-family of integral curves in the (ω, e) plane. One of these families for α = 0.3 and е₁ = 0.4 is presented in Figs. 8 and 9 (for two ranges of eccentricities). For greater detail, Figs. 8 and 9 show the ranges 0 < e < 0.1 and 0.1 < e < 1, respectively. As in the well-known case of orthogonal orbits in the doubly averaged Hill problem, where е₁ = 0 and α → 0 (В = 0) (Lidov, 1961; 1962), all phase trajectories intersect with the boundary straight line е = 1 in a finite time (except for the separatrices) and point Р collides with the central point S. A slight qualitative change is the appearance of a saddle stationary point at the boundary ω = 180°.

Fig. 8.

The family of integral curves (28) in the (ω, е) plane.

Fig. 9.

Same as Fig. 8, but for 0.1 < e < 1.  

In view of the existing symmetry of phase trajectories, Figs. 8 and 9 also show only the regions 0° < ω < 180°. The open circles in the figures mark the boundary points of the singular integral curves (ω = 90°, e = 0). The filled circles mark the points (ω = 180°, e = е*) on the separatrices. The phase point moves along these curves in such a way that е → 1 as t → ±∞.

The stationary solutions of system (29), or the singular points in the (ω, е) phase plane, are found by setting the right-hand sides of both equations equal to zero. In general, the existence of singular points within the rectangular region under consideration is not ruled out at arbitrary values of the constants А and В. Their coordinates can satisfy the system of two equations derived by setting the expressions in braces (29) equal to zero. However, here we consider only the solutions sin ω = 0 following from the first equation in (29), i.e.,

$${{\omega }^{*}} = 0,\,\,\,\,or\,\,\,\,{{\omega }^{*}} = \pi ,\,\,\,\,{{\delta }_{2}} = {\text{sign(cos}}{{\omega }^{*}}).$$

(30)

The stationary value of the eccentricity 0 < е* < 1 is found as the corresponding real root of the cubic equation

$${{p}_{3}}{{e}^{{*3}}} + {{p}_{2}}{{e}^{{*2}}} + {{p}_{1}}e{\text{*}} + {{p}_{0}} = 0,$$

(31)

where

$$\begin{gathered} {{p}_{3}} = 16B\left( {4 + 11e_{1}^{2}} \right),\,\,\,\,{{p}_{2}} = - 24A{{\delta }_{1}}{{\delta }_{2}}, \\ {{p}_{1}} = 4\left[ {1 - 2B\left( {1 + e_{1}^{2}} \right)} \right],\,\,\,\,{{p}_{0}} = A{{\delta }_{1}}{{\delta }_{2}}. \\ \end{gathered} $$

(32)

At В = 0 Eq. (31) is quadratic and its solution is given in Vashkov’yak (1984):

$$e^* = \frac{1}{{12A}}\left( {\sqrt {1 + 6{{A}^{2}}} - 1} \right).$$

(33)

The solution satisfying the condition 0 < e* < 1 exists only at δ₁δ₂ < 0, i.e.,

$$\begin{gathered} {\text{either at (}}\Omega = 0\,\,{\text{and}}\,\,{{\omega }^{*}} = \pi ) \\ \,\,{\text{or}}\,\,{\text{at}}\,\,(\Omega = \pi \,\,{\text{and}}\,\,{{\omega }^{*}} = 0). \\ \end{gathered} $$

(34)

This corresponds to the opposite directions of motion of point Р, with the stationary value in both cases being g* = Ω + ω* = π.

For the general case of В > 0 the isolines е*(α, е₁) = const are shown in Fig. 10. The numerical values of е* are plotted vertically near the right ends of the thick lines. The corresponding dashed lines virtually coincide with the thick ones at small α. At α differing noticeably from zero the solid and dashed lines diverge. This gives an estimate of the influence of the terms ~α⁴ in the expansion of the averaged perturbing function, which were included in this paper, on е*.

Fig. 10.

The family of isolines of the stationary values for the eccentricity е*(α, е₁) = const (the solution for В > 0—the thick lines; the solution for В = 0—the dashed lines).

In the domain of parameters α and е₁ under consideration the values of е* are relatively small and do not exceed about 0.2.

NUMERICAL SOLUTION OF THE EVOLUTION SYSTEM

Model Examples

In this section we present the results of our numerical solution of Eqs. (8) in the model of a system that includes the Sun—a central attracting point and one main perturbing point—Jupiter (а₁ = 5.2 AU, е₁= 0.048). Our calculations were performed with various initial data for a series of evolving orbits of hypothetical and real asteroids.

As one of the test model examples for demonstrating a “flip” (a well-known phenomenon that takes place in the restricted elliptic doubly averaged three-body problem and that consists in the transition of an asteroid orbit during its evolution from prograde to retrograde and vice versa), we consider an orbit with a semimajor axis а =2.2 AU and initial elements е₀ = 0.15, i₀= 75°, ω₀ = 0. This orbit, which is highly inclined to the reference plane, to a certain extent is close to the one in Naoz et al. (2013), in which, however, no initial longitude of the ascending node is specified. It is well known that flips can exist only in some domain of initial orbital elements. Lithwick and Naoz (2011) constructed the boundaries of these domains in the (е₀, cosi₀) plane for fixed values of the small parameter ε = 8A/5 numerically. In particular, Sidorenko (2018) proposed a satisfactory asymptotic approximation for the analytical fit of these boundaries in the case of ε ≤ 0.1.

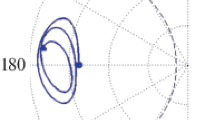
In the example given here Ω₀ = 120° was chosen in a special way, while Fig. 11 shows the time dependences of the inclination and the quantity log(1–e) (convenient for a graphical representation instead of е) in a time interval of 3 Myr.

Fig. 11.

Time variations of the inclination and eccentricity of an orbit with initial elements а = 2.2 AU, е₀ = 0.15, i₀= 75°, ω₀ = 0, and Ω₀ = 120°.

As the orbital inclination approaches 90° (the dashed straight line in the upper panel of Fig. 11), the eccentricity becomes very close to one. In reality, given the Sun’s nonzero radius, this, of course, would lead to the fall of an asteroid to its “surface” already at t ≈ 0.4 Myr (the first intersection of the dashed straight line with the graph in the lower panel of Fig. 11). Interestingly, a fairly subtle flip effect is detected even when using one of the simplest numerical integration methods (in this paper the fourth-order Runge–Kutta method).

Tracing the transformation of the stable stationary solution in the planar integrable case of the problem with initial conditions е₀= е*(α, е₁), i₀= 0, and g₀= g* = 0 as i₀ increases serves as another model example. For this purpose, we numerically integrated system (8) for the adopted constant parameters а₁, е₁, а = 2.2 AU. (α = 0.423), е₀ =0.019 and initial angular elements ω₀ = Ω₀ = 0. The results of these calculations are illustrated by Table 1, where the extreme values of the elements in a time interval of 1 Myr are presented. At initial inclinations no greater than about 32°.7 the argument of pericenter and the longitude of the ascending node circulate, while the elements e, i, and g librate, although the oscillation amplitude of g can approach 180°, with the minimum values of the eccentricity and the maximum values of the inclination being fairly close to the initial ones. For i₀ ≥ 33° both variables g and ω change monotonically with time, but the oscillation amplitudes of the eccentricity and inclination increase significantly. Such trends are also typical for the circular doubly averaged problem (Lidov, 1961; 1962; Kozai, 1962). They are retained at inclinations that are not too close to 90°. In the elliptic problem for this example, flips where the inclination passes through 90° (its maximum values are about 147°) and the eccentricity reaches a value very close to one begin to manifest themselves starting from i₀ = 76°. Interestingly, as our calculations show, there are no flips for the slightly smaller i₀ = 75°, at least in an interval of 5 Myr.

Table 1.   Extreme values of the elements of evolving orbits in a time interval of 1 Myr for а = 2.2 AU, е₀ = е* = 0.019, ω₀ = Ω₀ = 0, and various initial inclinations i₀

Thus, for the chosen values of the parameters а₁ and е₁ the data in Table 1 allow us to trace the qualitative changes of the “asteroid” orbit as its initial inclination changes. This orbit ultimately turns into a highly evolving one in eccentricity and inclination with its passage through 90° starting from the stationary position in the plane of motion of the perturbing body at a low eccentricity.

On the Evolution of Some Special Asteroid Orbits

In the problem of the evolution of asteroid orbits the influence of Jupiter’s orbital eccentricity is usually a secondary factor, as is the influence of the terms of the perturbing function with an order higher than α². Nevertheless, there exist orbits of real asteroids that absolutely require taking into account these factors for a proper description of their evolution. These include the asteroids with orbital elements satisfying some special conditions. These are primarily the orbits for which the constants of the first integrals of the doubly averaged Hill problem (Lidov, 1961; 1962)

(35)

satisfy the Lidov–Kozai resonance conditions с₁ < 3/5 and c₂ < 0. Skripnichenko and Kuznetsov (2018) provided a sample of 52 such numbered asteroids with ω-libration orbits. Interestingly, for three of them (143219, 159518, and 417444) the corresponding constants с₂ are less than 10^–3 in absolute value. This means that in the (ω–е) plane the phase point is very close to the separatrix separating the libration and circulation regions of the argument of perihelion. For such asteroids the simplified evolution model that disregards the terms ~α⁴ in the averaged perturbing function generally leads to incorrect quantitative and even qualitative results.

Table 2 gives the evolution characteristics of these orbits (along with the orbit of asteroid 1866) calculated by numerically integrating system (8) in a time interval of 1 Myr for two main cases: В = 0 (model ∼α³) and В > 0 (model ∼α⁴). The symbols characterizing the type of evolution of the argument of pericenter are given together with the extreme values of the eccentricity: С for circulation and L for libration. For asteroid 143219 including the terms ∼α⁴ refines only the range of eccentricities compared to the model ∼α³. However, for the remaining asteroids neglecting the terms ∼α⁴ additionally also leads to qualitative changes in the pattern of evolution of ω.

Table 2.   Qualitative and quantitative evolution characteristics of special asteroid orbits in two different models: В = 0 (model ∼α³) and В > 0 (model ∼α⁴)

As an illustration, Figs. 12 and 13 show the variations in the orbital eccentricity and the argument of perihelion for the last asteroid 417444 in the models ∼α³ and ∼α⁴, respectively.

Fig. 12.

Variations of the orbital eccentricity and the argument of perihelion for asteroid 417444 in the simplified model ∼α³.

Fig. 13.

Same as Fig. 12, but for the model ∼α⁴.

In the plane of these elements in Fig. 12 the initial point marked in the figure by the filled circle initially passes from the regime of ω libration relative to 90° to the regime of its circulation (along the arrow) and then returns to the regime of libration, but already relative to 270°. In the more accurate model (Fig. 13) ω liberates relative to 90° in the entire time interval under consideration.

In conclusion, note some possibilities for the development of this study. Apart from tracing the spatial transformation of planar equilibrium satellite orbits, a numerical search for so-called periodically evolving orbits with equal (commensurable) periods of variations in all elements could be of interest. An examination of the outer version of the restricted elliptic doubly averaged three-body problem will also serve as a supplement to this study.