An Improved Non-Rigid Point Set Registration Algorithm by Preserving Local Topology

Abstract

The previous works on point registration based on graph model formulate registration as a graph matching problem. The key step is to keep local neighborhood structure of a point stable because the local neighborhood structure may not change freely even under non-rigid deformation. However, the traditional methods do not give a correspondence between local point sets. In this paper, we propose to define a sub-graph which is compose of point and its adjacent points. A correspondence is obtained by arranging the edges of two sub-graphs according to length and angle, respectively. Finally, a local support probability is computed based on the correspondence. The performance of our method is validated with different synthetic data and real data, showing that the proposed method can improve the robustness and accuracy to the traditional techniques.

1 INTRODUCTION

Image registration or shape matching is a fundamental problem in computer vision, image analysis and pattern recognition. It is the key component in many applications such as visual enhancement, context-based image retrieval and medical image processing. According to the objects processed, registration algorithm is divided into gray registration and point registration. However, the former is time consuming. Thus, the real-time application prefers the latter. Point registration would have more extensive application prospect. The goal of point registration is to find meaningful correspondence between two different point sets and determine the transformation that maps one set to the other. These point sets are often extracted from other types of data such as images representing feature points.

Generally speaking, there are also two categories of methods on point registration, one is based on classification and the other is based on graph matching. The classification-based registration methods mainly adopt finite mixture model, especially Gaussian mixture model (GMM), which formulas the alignment of two point sets as a probability density estimation. Points from one set are normally distributed around points belonging to the other set. The point-to-point assignment problem can be recast into that of estimating the parameters of a mixture distribution.

The iterative closest point (ICP), introduced by Besl and Mckay [2] and Zhang [15], is one of the methods commonly used, which iteratively assigns correspondence based on the Euclidean distance and finds the least squares based transformation related to these point sets. A nonlinear version of ICP [6] and a TriICP algorithm [3] are the variants of ICP.

Chui and Rangarajan [4] formulate registration problem as likelihood estimation problem by using mixture model. The approach is the embedding of the expectation maximization (EM) algorithm with in a deterministic annealing scheme in order to directly control the fuzziness of the correspondences. Coherence point drift (CPD) Myronenko and Song [11] defines a velocity function for the template point set, namely the centroid of the Gaussian mixture model, and iteratively calculates the unknown parameters in the GMM by EM. An expectation conditional maximization (ECM) algorithm for point registration (ECMPR) is proposed by Horaud et al. [7], which adopts the anisotropic covariance model and ECM to resolve the rigid and articulated point registration. Sanroma et al. [14] propose a rigid point set registration method that uses neighboring relation and extends a non-rigid registration version. Sang et al. [13] and Ma et al. [10] introduce the local feature measured by shape context [1] to assign the membership probabilities of the mixture model. Nevertheless, the local feature is computed by comparing the histogram of shape context. As we know, a histogram shows statistical property of the numerical data. But the number of neighborhood points is always small. It is not accurate to describe the local topology of point just according to the distribution of only several points. Meanwhile, these methods include an extra uniform component, see Hennig and Coretto [8], in the mixture model in order to enhance robustness. But this strategy cannot fit outliers in both point sets at the same time.

In the second category, point registration is formulated as a graph matching problem. Each point is a node in the graph, and two nodes are connected by an edge if their Euclidean distance is less than a threshold. The optimal match between two graphs is the one that maximizes the number of matched edges. As computing the similarity matrix between two point sets, an extra column and an extra row are adopted to fit the outliers in two point sets. Chui et al. [5] propose the robust point matching (TPS-RPM) which adopting soft assignment and deterministic annealing techniques. Zheng et al. [16] introduce robust point matching for non-rigid shapes by preserving local neighborhood structure (PLNS) which takes advantage of the notion of a neighborhood structure for the general point matching problem. Lee et al. [9] propose topology preserving relaxation labeling algorithm (TPRL) using relaxation labeling and discrete values to measure the correlation between point pairs. Under the framework of registration based-on graph matching, the key question is how to precisely measure the local structure of point and quantize the differences of local structure. However, the methods mentioned above do not give an explicit correspondences when computing the local matching probability. In this paper, a new local structure named sub-graph is introduced and a corresponding method is proposed to compute correspondence between two sub-graphs. Above all, an improved registration algorithm based on topology invariance is proposed.

The paper is organized as follows. The non-rigid point set registration method is proposed in Section 2. In Section 3, the proposed method is applied to artificial point sets and medical image data. The experimental results are presented. Conclusions are drawn in Section 4.

2 METHOD

2.1 Point Registration Based on Graph Matching

In [16], the authors formulate point registration as a graph matching problem. According to that, each point is treated as a node in the graph, and two node are connected by an edge. The registration problem is the one that maximizes the number of matched edges of two graphs. Here point set T is composed with M points, T = t₁, t₂, …, t_M. And point set D is composed with N points, D = d₁, d₂, …, d_N. A mapping function f: T $\Leftrightarrow$ D is used to define the correspondence between point sets. When two point sets have different number of points, a dummy or nil point is introduced. The point sets T and D are augmented to $T{\kern 1pt} '$ = t₁, t₂, …, t_M, nil and $D{\kern 1pt} '$ = d₁, d₂, …, d_N, nil. Thus, the function $\hat {f}$: $T{\kern 1pt} ' \Leftrightarrow D{\kern 1pt} '$ may match multiple points to a dummy point. Under non-rigid deformation, the distance between a pair of points cannot be preserved. However, the local structure of a point may not change freely due to physical constraints. Therefore, the optimal matching $\hat {f}$ is:

$$\hat {f} = {{\operatorname{argmax} }_{f}}S\left( {T,D,f} \right),$$

(1)

where

$$\begin{gathered} S\left( {T,D,f} \right) = \mathop \sum \limits_{m = 1}^M \,\mathop \sum \limits_{i \in {{N}_{m}}} \,\delta (f(m),f(i)) \\ + \;\mathop \sum \limits_{n = 1}^N \,\mathop \sum \limits_{j \in {{N}_{n}}} \,\delta ({{f}^{{ - 1}}}(n),{{f}^{{ - 1}}}(j)). \\ \end{gathered} $$

(2)

N_m is the neighborhood of point t_m. If connected nodes m and i in one graph are matched to connected nodes f(m) and f(i) in the other graph, δ( f(m), f(i)) = 1. δ(i, j) is defined as 1 – dis(i, j). The value of dis(i, j) is 1 if point i and point j are a pair of neighbors; otherwise, dis(i, j) = 0. The optimal solution of (2) maximizes the number of matched edges of two graphs. The matching function in (1) with a set of supplemental variables is organized as a matrix P with dimension (M + 1) × (N + 1). The probability matrix P denotes the global similarity. If point t_m is matched to point d_n, then ${{P}_{{mn}}}$ = 1; otherwise, ${{P}_{{mn}}}$ = 0. And P satisfies

$$\mathop \sum \limits_{n = 1}^{N + 1} \,{{P}_{{mn}}} = 1\quad {\text{for}}\quad m = 1,2, \ldots ,M,$$

(3)

$$\mathop \sum \limits_{m = 1}^{M + 1} \,{{P}_{{mn}}} = 1\quad {\text{for}}\quad n = 1,2, \ldots ,N.$$

(4)

The objective function (2) can be written as

$$S\left( {T,D,P} \right) = 2\,\mathop \sum \limits_{m = 1}^M \,\mathop \sum \limits_{i \in {{N}_{m}}} \,\mathop \sum \limits_{n = 1}^N \,\mathop \sum \limits_{j \in {{N}_{n}}} \,{{P}_{{mn}}}{{P}_{{ij}}}.$$

(5)

The probability matrix P is initialized by shape context [1], which is a coarse histogram of the relative coordinates of the neighbor points as follows

$${{h}_{i}}\left( k \right)=\,\,{\kern 1pt} \left\{ q\ne {{x}_{i}}:\left( q-{{t}_{i}} \right)\in bin\left( k \right) \right\}.$$

(6)

The shape context of a point is a measure of the distribution of other points relative to it. Consider two points ${{t}_{i}}$ in one shape and ${{d}_{i}}$ in the other shape. Their shape contexts are ${{h}_{i}}\left( k \right)$ and ${{h}_{j}}\left( k \right)$, for $k = 1,2, \ldots ,K$, respectively. And the cost is denoted by ${{C}_{{ij}}}$. Based on the ${{{{\chi }}}^{2}}$ test statistic

$$~{{C}_{{ij}}} = \frac{1}{2}\mathop \sum \limits_{k = 1}^K \frac{{{{{\left[ {{{h}_{i}}\left( k \right) - {{h}_{j}}\left( k \right)} \right]}}^{2}}}}{{{{h}_{i}}\left( k \right) + {{h}_{j}}\left( k \right)}},$$

(7)

where K is the number of bins.

And relaxation labeling [12, 17] is adopt to resolve the optimal question. Based on relaxation labeling, the contextual constraints are expressed in the compatibility function ${{R}_{{mn}}}\left( {i,j} \right)$, which measures the strength of compatibility between ${{t}_{m}}$ matching ${{d}_{n}}$ and ${{t}_{i}}$ matching ${{d}_{j}}$. The support function ${{S}_{{mn}}}$ measures the overall support the match between points ${{t}_{m}}$ and ${{d}_{n}}$ gets from its neighbors

$${{S}_{{mn}}} = \mathop \sum \limits_{i \in {{N}_{m}}} \,\mathop \sum \limits_{j \in {{N}_{n}}} \,{{R}_{{ij}}}{{P}_{{ij}}}.$$

(8)

In [16], the compatibility function is ${{R}_{{mn}}}\left( {i,j} \right) = 1$ if a pair of neighbors ${{t}_{m}}$ and ${{t}_{i}}$ are matched to a pair of neighbors ${{d}_{n}}$ and ${{d}_{i}}$; otherwise, ${{R}_{{mn}}}\left( {i,j} \right) = 0$. The original updating rule is [12]

$${{P}_{{mn}}} = \frac{{{{P}_{{mn}}}{{S}_{{mn}}}}}{{\sum\limits_{j = 1}^N {{{P}_{{mj}}}{{S}_{{mj}}}} }}.$$

(9)

According to the objective function of (5), ${{S}_{{mn}}}$ is defined as

$${{S}_{{mn}}} = 4\,\mathop \sum \limits_{i \in {{N}_{m}}} \,\mathop \sum \limits_{j \in {{N}_{n}}} \,{{P}_{{ij}}}.$$

(10)

2.2 Point Registration by Preserving Local Structure

Formula (10) in above section is a local support function, which is used to update local context to achieve a globally consistent result. Meanwhile, it is also a local similarity probability used to correct global matching probability. Nevertheless, the method in [16] just takes the sum of global probability of adjacent points as local support without determining the correspondences between neighborhoods. TPRL algorithm in [9] takes advantage of a local structure of point to correct global matching probability. The authors firstly define a point and its neighborhoods. For a given point ${{t}_{i}} \in T$, one can select adjacent point $n_{x}^{{{{t}_{i}}}}$, $x = 1, \ldots ,X$, which reside in the circle centered at ${{t}_{i}}$. Similarly, for a point ${{d}_{j}} \in D$, adjacent points are $n_{y}^{{{{d}_{j}}}}$, $y = 1, \ldots ,Y$. The local structure is defined as an edge which compose of a point and its nearest adjacent point. The log distance and polar angle bins are used to capture the coarse location information [9]. The mass center of a point set is used as a reference point for the computation of the angle between point pairs.

The local similarity is computed by comparing the angle and radius of the two local neighborhood structures (namely, the two edges), which is used to replace the global probability when computing local support. Then three constraints are defined as:

$$\alpha ({{t}_{i}},n_{x}^{{{{t}_{i}}}};{{d}_{j}},n_{y}^{{{{d}_{j}}}}) = 1 - \frac{{\left| {{{l}_{i}}({{t}_{i}},n_{x}^{{{{t}_{i}}}}) - {{l}_{j}}({{d}_{j}},n_{y}^{{{{d}_{j}}}})} \right|}}{{{{{\max }}_{{m,n}}}({{l}_{m}}({{t}_{m}},n_{x}^{{{{t}_{m}}}}),{{l}_{n}}({{d}_{n}},n_{y}^{{{{d}_{n}}}}))}},$$

(11)

$$\beta ({{t}_{i}},n_{x}^{{{{t}_{i}}}};{{d}_{j}},n_{y}^{{{{d}_{j}}}})\, = \,1 - \frac{{\left| {{{\theta }_{i}}({{t}_{i}},n_{x}^{{{{t}_{i}}}}) - {{\theta }_{j}}({{d}_{j}},n_{y}^{{{{d}_{j}}}})} \right|}}{{{{{\max }}_{{m,n}}}({{\theta }_{m}}({{t}_{m}},n_{x}^{{{{t}_{m}}}}),{{\theta }_{n}}({{d}_{n}},n_{y}^{{{{d}_{n}}}}))}},$$

(12)

$$\gamma ({{t}_{i}},n_{x}^{{{{t}_{i}}}}) = 1 - \frac{{l({{t}_{i}},n_{x}^{{{{t}_{i}}}})}}{{{{{\max }}_{m}}{{l}_{m}}({{t}_{m}},n_{x}^{{{{t}_{m}}}})}},$$

(13)

where ${{l}_{i}}({{t}_{i}},n_{x}^{{{{t}_{i}}}})$ and ${{\theta }_{i}}({{t}_{i}},n_{x}^{{{{t}_{i}}}})$ denote the length and angle of edge composed of point ${{t}_{i}}$ and its nearest adjacent point $n_{x}^{{{{t}_{i}}}}$, respectively, and ${{\max }_{m}}{{l}_{m}}(\, \cdot \,)$ is used to obtain the longest edge and the biggest angle of point adjacent point pairs. Thus, α(·) computes the length difference, β(·) computes the angle difference, and γ(·) measures the salient. Thus, a compatibility coefficient is defined as

$$\begin{gathered} {{r}_{{{{t}_{i}}{{d}_{j}}}}}(n_{x}^{{{{t}_{i}}}},n_{y}^{{{{d}_{j}}}}) = \alpha ({{t}_{i}},n_{x}^{{{{t}_{i}}}};{{d}_{j}},n_{y}^{{{{d}_{j}}}}) \\ \times \;\beta ({{t}_{i}},n_{x}^{{{{t}_{i}}}};{{d}_{j}},n_{y}^{{{{d}_{j}}}}) \times \gamma ({{t}_{i}},n_{x}^{{{{t}_{i}}}}). \\ \end{gathered} $$

(14)

The value of formula (14) reaches the maximum value one when the local structure of two points are totally the same. Nevertheless, the local structure is just composed of two points and it assumes that the nearest adjacent points are in correspondence to each other, which is not robust.

2.3 Point Registration by Preserving Local Topology

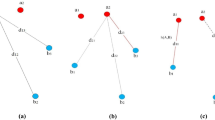
In this paper, we propose an improved point registration by preserving the local topology of point. In order to accurately computer the similarity of local topology, a concept of sub-graph is introduced as illustrated in Fig. 1. The sub-graph describes the local structure of point. A correspondence between edges of sub-graph is computed by matching two sub-graphs. The local support is the sum of cost of corresponding edges.

Fig. 1.

Example of sub-graph. The corresponding color indicates the correspondence between two sub-graphs.

The sub-graph is defined firstly. For point ${{t}_{i}} \in T$, the circle neighborhood of ${{t}_{i}}$ is defined as $n_{x}^{{{{t}_{i}}}}$, x = 1, 2, …, I. I is the number of neighborhood points and is set with fixed values (generally, 3–5). The point ${{t}_{i}}$ and one point in $n_{x}^{{{{t}_{i}}}}$ are connected to be an edge $e_{{{{t}_{i}}}}^{{n_{x}^{{{{t}_{i}}}}}}$. The sub-graph of point ${{t}_{i}}$ is composed of the I edges defined above and is a general case contrasting to the local structure defined in [9]. When the value of I is set to one, our method is degraded to TRPL [9]. In order to computing the similarity of two sub-graphs, the correspondence between edges must be confirmed. We notice that the relative positions between a point and its adjacent points in sub-graph are always stable. The reason is that the relative positions would not change freely because of physical constrain. The changes of local topology are isotropic in other words. Secondly, two partial ordering relations are defined to describe the topology mentioned above. And, a correspondence could be determined between two sub-graphs. Let $l({{t}_{i}},n_{x}^{{{{t}_{i}}}})$ be the distance between origin point ${{t}_{i}}$ and its adjacent point $n_{x}^{{{{t}_{i}}}}$ and $\theta ({{t}_{i}},n_{x}^{{{{t}_{i}}}})$ be the angle between point ${{t}_{i}}$ and its adjacent point $n_{x}^{{{{t}_{i}}}}$. Thus, two ordered set $S_{d}^{{{{t}_{i}}}}$ = $\{ n_{u}^{{{{t}_{i}}}}$, $u = 1,2, \ldots ,I\}$ satisfying $l({{t}_{i}},n_{u}^{{{{t}_{i}}}})$ < $l({{t}_{i}},n_{{u + 1}}^{{{{t}_{i}}}})$ and $S_{\theta }^{{{{t}_{i}}}}$ = $\{ n_{{v}}^{{{{t}_{i}}}}$, ${v} = 1,2, \ldots ,I\}$ satisfying $\theta ({{t}_{i}},n_{{v}}^{{{{t}_{i}}}})$ < $\theta ({{t}_{i}},n_{{{v} + 1}}^{{{{t}_{i}}}})$ are defined, respectively. As mentioned above, the relative position of point and its neighborhood points would not change freely because of physical constrain. Even if non-rigid deformation, the change of local point set is always smoothed within the local position of point. Namely, the order of edges remain stable in the most situation. From Fig. 1 we can clearly notice that. Thus, the local topology invariance can be represented by the two ordinal relations. If point ${{t}_{i}}$ is the corresponding point of ${{d}_{j}}$, their two ordinal relations of sub-graph edges would be almost identical. Thus, two correspondences $z_{{x'}}^{{y'}}$ and $z_{{x''}}^{{y''}}$ would be obtained based on $(S_{d}^{{{{t}_{i}}}},S_{d}^{{{{d}_{j}}}})$ and $(S_{\theta }^{{{{t}_{i}}}},S_{\theta }^{{{{d}_{j}}}})$. If edge $e_{{{{t}_{i}}}}^{{n_{x}^{{{{t}_{i}}}}}}$ has the same corresponding edge $e_{{{{d}_{j}}}}^{{n_{y}^{{{{d}_{j}}}}}}$ according to $z_{{x'}}^{{y'}}$ and $z_{{x''}}^{{y''}}$, the two edges are correspondent and would be marked with matched. Otherwise, unmatched. Supposing there are k sub-graph edges unmatched, where k ≥ 2. Thus, I – k sub-graph edges are matched and the correspondence is denoted by $z_{x}^{y}$. For the sub-graph edges matched, a matching probability is computed by

$$P_{{mn}}^{'} = \left\{ \begin{gathered} 0\quad {\text{if}}\quad k = I \hfill \\ \frac{{\sum\limits_{\left( {x,y} \right) \in z_{x}^{y}} {C(({{t}_{m}},n_{x}^{{{{t}_{m}}}}),({{d}_{n}},n_{y}^{{{{d}_{n}}}}))} }}{{(I - k)}}\quad {\text{else}}, \hfill \\ \end{gathered} \right.$$

(15)

and for the unmatched sub-graph edges, a matching probability is computed as

$$P_{{mn}}^{{''}} = \left\{ \begin{gathered} 0\quad {\text{if}}\quad k = 0 \hfill \\ \frac{{\sum\limits_{x = 1}^k {\sum\limits_{y = 1}^k {C(({{t}_{m}},n_{x}^{{{{t}_{m}}}}),({{d}_{n}},n_{y}^{{{{d}_{n}}}}))} } }}{{{{k}^{2}}}}\quad {\text{else}}, \hfill \\ \end{gathered} \right.$$

(16)

where a cost between any two edges is defined as follows

$$\begin{gathered} C(({{t}_{i}},n_{x}^{{{{t}_{i}}}}),({{d}_{j}},n_{y}^{{{{d}_{j}}}}))\, = \,\left( {1 - \frac{{\left| {{{l}_{i}}({{t}_{i}},n_{x}^{{{{t}_{i}}}})\, - \,{{l}_{j}}({{d}_{j}},n_{y}^{{{{d}_{j}}}})} \right|}}{{{{{\max }}_{{m,n}}}({{l}_{m}}({{t}_{m}},n_{x}^{{{{t}_{m}}}}),{{l}_{n}}({{d}_{n}},n_{y}^{{{{d}_{n}}}}))}}} \right) \\ \times \;\left( {1 - \frac{{\left| {{{\theta }_{i}}({{t}_{i}},n_{x}^{{{{t}_{i}}}}) - {{\theta }_{j}}({{d}_{j}},n_{y}^{{{{d}_{j}}}})} \right|}}{{{\text{ma}}{{{\text{x}}}_{{m,n}}}({{\theta }_{m}}({{t}_{m}},n_{x}^{{{{t}_{m}}}}),{{\theta }_{n}}({{d}_{n}},n_{y}^{{{{d}_{n}}}}))}}} \right), \\ \end{gathered} $$

(17)

where ${{\max }_{{m,n}}}({{l}_{m}}({{t}_{m}},n_{x}^{{{{t}_{m}}}}),{{l}_{n}}({{d}_{n}},n_{y}^{{{{d}_{n}}}}))$ and ${{\max }_{{m,n}}}({{\theta }_{m}}({{t}_{m}}$, $n_{x}^{{{{t}_{m}}}}),{{\theta }_{n}}({{d}_{n}},n_{y}^{{{{d}_{n}}}}))$ represent longer edge and larger angle, respectively. An improved local support function is introduced as

$${{S}_{{mn}}} = P_{{mn}}^{'} + P_{{mn}}^{{''}}.$$

(18)

Obviously, the number of edge pairs matched is I and the cost between edges is equal to one when the topology of two sub-graphs is totally the same. In this situation, the value of support function reach the maximum. As mentioned above, all the edges of two sub-graphs are marked as matched in Fig. 1b. Hence, ${{S}_{{mn}}} = P_{{mn}}^{'}$ where I = 3, k = 0. When the two ordinal relations of edges is completely different, the value of k is equal to I. There are no a priori correspondences. Then, formula (16) would degenerate into formula (8) which may be regarded as a special case of our algorithm.

At last, the thin plate spline (TPS) deformation model is adopted as physical constraints to bring two point sets closer in each iteration.

Thus, the algorithm proposed in this paper can be listed as follows

Algorithm 1. Framework of point registration by preserving topology algorithm.
	1:	Input: Two point sets: T and D.
	2:	Calculate the shape context for two point sets to initialize the matching probability matrix P and convert it to a generalized doubly stochastic matrix.
	3:	while No convergence or iteration < Nummax(300) do
	4:		Use formula (15)–(17) to computer the local matching probability of two sub-graphs.
	5:		Use the local support probability ${{S}_{{mn}}}$ formula (18) to update the global matching probability matrix P formula (9), and convert matrix P to a generalized doubly stochastic matrix.
	6:		Compute the transform parameters of TPS according to the matching probability of P and transform template point set T.
	7:	end while
	8:	Output: The correspondence between two point sets according to the final matching probability matrix P.

3 EXPERIMENT RESULT

In this section, the experiment results are shown. Our method is implemented in C++ and tested on an i5 CPU with 8 GB RAM. Three state-of-the-art algorithms: TPS-RPM [5], PLNS [16], and TPRL [9] are adopted to compare with our method. The log-polar bins [9] are used to compute the length and angle. The number of edges of sub-graph is set to three. We have performed registration experiments with synthetic and real data. Experiments with synthetic data consists in matching point sets of a fish and a Chinese character templates under non-rigid deformations, noise outliers, occlusion, and rotation. Experiments with real data consists in registering point sets extracted from ultrasound elastography image with histopathology images and two sequences of heart and chest slice images.

3.1 Synthetic Data

In this section we have performed matching experiments on synthetic data set [4]. The test data consist of two shape model. One is a fish shape that has 96 points, the other is a Chinese character with more complex pattern consisting of 108 points, as shown in Fig. 2a.

Fig. 2.

The examples of (a) original data sets and point shapes degenerated under (b) deformation, (c) outlier, (d) noise, (e) occlusion, and (f) rotation. Left col: data set of fish shape. Right col: data set of Chinese character shape.

Firstly, three sets of data are designed to measure the robustness of an algorithm under deformation, noise in point position, and outliers. The degeneration levels are set from one to five according to ascending extent. In each test, one point set is subjected to one of the above distortions to create a target point set. A total of 100 test point sets are randomly generated at each level. The examples degenerated are illustrated in Figs. 2b–2d. Our algorithm is run to find the correspondence between two sets of points and use the estimated correspondence to warp the target point set. The accuracy of the match is quantified as the average Euclidean distance between a point in the warped point set and the corresponding point in the original point set. The same evaluation metric is used as in [5] for evaluating the performance of different algorithms. The algorithm performances are compared by the mean and standard deviation of the registration error of 100 trials in each level. The statistical results for each setting are shown in Fig. 3.

Fig. 3.

Comparison of our result with TPS-RPM, PRNS, and TPRL under (a) deformation, (b) outlier, and (c) noise. The error bars indicate the standard deviation of the error over 100 random trials.

In the deformation test results (Fig. 3a) four algorithms achieve similar registration results in both two test point sets at low deformation ratio. However, as the degree of deformation increasing, our method shows more robustness. For the corresponding point pairs, their local topology are similar even if they are degenerated with non-rigid deformation. Our method accurately quantifies the topology differences between point pairs so that the corresponding point pairs obtain more local support than these unmatched point pairs. Our method shows more robustness in the case of severe deformation.

A similar situation happens when testing on data set with outliers. As a different number of outliers were added in point set according to different degenerated levels, the error ratio of the fourth algorithm increases. From the results of Fig. 3b, we note that the others algorithms easily fall into local optimum and get false correspondences, especially in high outlier level. Our method shows more robustness regardless of the outlier level. However, the neighborhood of a point changes significantly when a large number of outliers are present, which violates our assumption on topology preserving. The performance of our method begin to decrease, but it is still better than the previous ones in general.

For the noise test set, the presence of a much amount of noise make the location of point ambiguous. So the experiment is more challenging than the others. The results in Fig. 3c show that all algorithms are affected by the noise. When a mass of noise is added to point sets, the local topology may be destroyed. The mechanism of topology preserving will work as long as the noise does not disorder whole shape to unrecognizable. Thus, all the performances are declining greatly. The test result of our method shows that more accurate correspondences can be found compared to the others algorithms.

Secondly, the experiments are conducted under occlusion and rotation.

Occlusion is often present in most of real applications and is a challenge for many algorithms.

So, we test the four algorithms under occlusion. A moderate amount of non-rigid deformation is applied to two point sets. A point is randomly selected and removed together with some of its adjacent points. Six occlusion levels are used: from 0 to 50%, and 100 samples are generated for each level. Figure 2e shows two synthesized samples. Quantitative evaluation results are shown in Fig. 4a.

Fig. 4.

Comparison of our result with TPS-RPM, PRNS, and TPRL under (a) occlusion and (b) rotation. The error bars indicate the standard deviation of the error over 100 random trials.

In some applications, rotation invariance is also a critical property of a matching algorithm. We test our algorithm under rotations using synthesized data of the same fish and Chinese character shapes. A moderate amount of non-rigid deformation is applied. We then rotate the deformed shape. Six rotations are used: 0°, 30°, 60°, 90°, 120°, and 180°. One hundred samples are generated for each rotation. Figure 2f shows two synthesized rotation samples. Quantitative evaluation results are shown in Fig. 4b. We can see that our method consistently outperforms the others.

At last, we show comparative computation times for the three algorithms in Table 1. A standard PC with a 3.0 GHz processor and 8.0 GB of memory is used. A total of 500 fish point sets under different non-rigid deformation are used as test data. The average computation time is shown. Although it would take a little more time to compute the matching probability of sub-graphs in our method, the speed of convergence of our method is faster, because the local support function corrects the global matching probability. Although the time of one iteration may be longer, the total registration time is shorter. Thus, the cost of our method is better than PRNS and close to TPRL.

Table 1. The average computation time to register 500 pairs of fish point sets with different non-rigid deformations (s)

3.2 Real Data

We have performed real experiments with medical image data. The quantitative evaluation is conducted on two image sets which include heart slice sequence and chest slice sequence. Heart slice sequence is consisting of 30 image slices. Chest slice sequence is consisting of 24 image slices. As shown in Figs. 5a and 5b, we illustrate six and three slices of them, respectively. The order of images reflects a gradual change process of human organs. The deformations of heart and chest principal features, such as its contour, are non-rigid. At the same time, the point sets would in general have outliers when feature points are automatically extracted. Finding the correspondence points between slice pairs is always a key step for image registration or image 3D interpolation, etc. For each image, landmark points are extracted by Canny’s algorithm and the ground truths of correspondence are manually marked for performance evaluation. The adjacent image pairs are used to match. So we run 29 experiments for heart sequence and 23 experiments for chest sequence. After applying PRNS, TPRL, and our method, we get a projection between two correspondence points, as shown in Figs. 5c and 5d. Since we know the ground truth of correspondence, we take advantage of the number of feature point mismatched as error measure. Figure 6 shows the compared results.

Fig. 5.

Feature points registration between heart slices and chest slices. (a) Heart slice sequence. (b) Chest slice sequence. (c) An example matches from heart slice sequence. (d) An example matches from chest slice sequence.

Fig. 6.

Comparison of our result with PRNS and TPRL with heart slice sequence and chest slice sequence. The error bars indicate the standard deviation of the number of points mismatched.

4 CONCLUSIONS

This paper introduces an improved point set registration based on graph matching by preserving local topology. Unlike the previous methods, we firstly define the neighborhoods of point as a sub-graph. Secondly, two ordinal relations based topology stable are proposed to determine the correspondences between two sub-graphs, which is more reasonable and precise for measuring the local topology transformation. Finally, a matching probability is computed based on the correspondence as the local support. Extensive experiments were presented to show the robustness and accuracy. Compared with the other three well-known algorithms, our approach shows better performance. Nevertheless, the local topology may be destroyed when a large amount of outlier or noise exists. The performance of algorithm would decrease. How to improve the robustness would be addressed in our future research.