Abstract
This paper presents the bending and buckling analyses of simply supported nanowires using various classical and nonclassical higher-order shear deformation theories (HSDTs). A one-dimensional structure is modeled with including the surface effects based on the Gurtin–Murdoch surface elasticity theory (nonclassical beam theory) and the small-scale effect based on the Eringen nonlocal theory (nonlocal beam theory); the transverse displacement is divided into two bending and shear components. A system of governing equations is derived with the help of the minimum total potential energy principle and resolved via Navier’s solutions. Several numerical results are presented and compared with those given in the literature. The results showed that the influence of the surface effects on the bending and buckling load of nanowires is more pronounced than that of the nonlocal parameter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1. INTRODUCTION
Nanowires (NWs) belong to the family of thin materials that have a dimension 1D, such as nanobeams and nanotubes (NT). A wide range of uses of nanowire-based devices exists in the fields of engineering, physics applications, and others sectors. Nanowires are commonly used in devices based on advanced technologies, such as transistors, sensors, resonators in nano- (NEMS) and microelectro-mechanical (MEMS) systems and actuators [1–4]. They have wide applications in environmental monitoring, medical diagnostics, food processing, mining, bioengineering, and defense [5, 6].
For the first time, Gurtin and Murdoch [7, 8] proposed a generic theoretical framework based on the concept of continuum mechanics that represents the surface energy/interface. As is well known, the surface/volume ratio is high in nanoscale structures. Hence, the surface effect is one of the most important influences on the nanostructures compared to those on the macroscale. This way was clearly indicated and explained by Ansari and Sahmani [9] who adopted various theories of beams for the analysis of the buckling of nanobeams with surface effect. Others, for example Song et al. [10], used a continuum model for the mechanical behavior of nanowires including surface and surface-induced initial stresses. Dingreville et al. [11] demonstrated that the structure size influences the general elastic behavior and this dependence is important when at least one of the structural dimensions reduces to nanometers.
Nonlocal elasticity has been used widely to study the wave propagation in composites, elastic waves, dislocation mechanics and dynamic/static responses of FG-structures, carbon nanotubes, microtubules, and nanorods. For example the authors of works [12–14], as well as Reddy and Pang [15], modified analytical models (EBT and TBT) using the nonlocal elasticity theory of Eringen to analyze the static and dynamic behaviors of CNTs with various boundary conditions. Phadikar and Pradhan [16] analyzed the static bending and buckling of nanobeams and nanoplates in which nonlocal elasticity was included. Civalek and Demir [17] investigated the static flexural behavior of microtubules (MTs) using nonlocal elasticity, classical beam theory, and the differential quadrature method (DQM). Based on FEM and using a nonlocal continuum model, Demir and Civalek [18] analyzed the longitudinal and torsional frequency and the wave response of microtubules. Attia [19] developed a new analytical model to examine the responses of a PFG-nanobeam based on classical EBT, modified couple stress, nonlocal and surface elasticity. Based on the EBT model and Eringen’s nonlocal elasticity, Dihaj et al. [20] investigated the vibrational response of a chiral DW-CNT resting on the Winkler elastic foundation. The vibrational analysis of armchair SW-CNTs in thermal environment and embedded in an elastic medium was performed by Hamidi et al. [21] using the nonlocal Timoshenko beam theory. Ebrahimi et al. [22] studied the stability and free vibrational responses of simply supported, simply-clamped and clamped-clamped FG nanobeams using the HSDT model, nonlocal elasticity, and Chebyshev–Ritz method. Based on nonlocal elasticity, Bensattalah et al. [23] examined analytically the effects of the small-scale coefficient, vibrational mode and geometry parameters on frequency of chiral SW-CNTs using the TBT formulation and nonlocal elasticity. Civalek et al. [24] examined the free vibrational response of silica carbide and carbon nanotubes with various boundary conditions using the EBT formulation, Hamilton’s principle, and finite element-method. Based on nonlocal continuum elasticity and FSDT formulation (Timoshenko’s model), Bensattalah et al. [25] examined the mechanical stability of zigzag TW-CNTs. Shanab et al. [26] studied the static (bending, buckling) and dynamic (free vibration) behaviors of FG-nanobeams on the Winkler–Pasternak elastic foundation using Timoshenko’s beam theory with including the effects of surface energy and microstructure.
In this investigation, several nonclassical HSDTs (shear deformation theories) are developed to examine the buckling and bending responses of nonlocal nanowires (NWs) with taking into account the surface stress and small-scale effects. The accuracy of the current model is checked by comparing the obtained results with those found in the literature. The influence of the parameters of small-scale and surface stress effects on the critical buckling load and maximum center deflection are examined and discussed in detail through several numerical examples.
2. PROBLEM FORMULATION
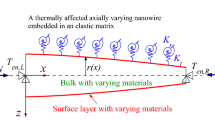
Consider a straight uniform beam with the length L; the area and perimeter of the cross section are A (A = b × h, where h and b are the thickness and width) and s, respectively. A coordinate system x, y, z is taken along the length, width and height of the beam, respectively (where 0 ≤ x ≤ L, –b/2 ≤ y ≤ b/2, –h/2 ≤ z ≤ h/2), as shown in Fig. 1. The NW is subjected to transverse load q (point load or uniform load) and axial forces p at both ends.
2.1. Surface Effects
The stress–strain relation with surface effect proposed by [7, 8] can be expressed in the general simple form as
where μs, λs are the Lamé constants of the surface, and τs is the surface stress (residual).
Based on nonlocal elasticity proposed by [27–30], the stress–strain relations are given as
where σx is the normal stress, τxz is the transverse shear stress, E and G are Young’s modulus and shear modulus, x is the origin coordinate at the left end of the one-dimensional structure, the depth is along the z axis, and the nonlocal parameter μ is zero. We obtain the constitutive relations of the local theories, where μ = (e0a)2, e0 is a material constant which is to be determined experimentally or by calibrating with atomistic modeling, and a is the internal characteristic length (e.g., lattice parameter, molecular diameter, and grain size).
2.2. Displacement Field
Based on assumptions of higher-order shear deformation theories [31–37] that the components of axial displacement u and the transverse displacement of any point of the beam w along the x, y, z axes are only dependent on the x and z coordinates, in a general form, the following displacement field can be written:
where the transverse displacement is partitioned with two components: the bending part wb and the shear part ws; the nonzero strains of the proposed beam theory are
where εx is the longitudinal strain, and γxz is the transverse shear strain. f (z) and g(z) are the shape functions and are chosen to satisfy the stress-free boundary conditions on the top and bottom surfaces of the beam. Thus the shear correction factor k is not needed.
The shape functions f (z) used in this work are model 1 (TBT) of [38]:
model 2 (SBT) of [39]:
model 3 (HBT) of [40]:
The following sections present the stress-displacement relations based on the developed surface elasticity beam model. The effects of surface stresses on the beam are assumed to be governed by the Gurtin–Murdoch theory of surface elasticity [7, 8] and can be simplified in the present study as
In this work, we consider a superposition between the quantities corresponding to the surface and the bulk, and this summation is considered to facilitate only the mathematical formulation:
The superscript s is used to denote the quantities corresponding to the surface, and the superscript b is employed to represent the quantities corresponding to the bulk, τs is the residual surface stress under unconstrained conditions, and μs, λs are the Lamé surface elasticity moduli determined by atomistic simulations or experimental measurements [41, 42].
For the classical beam theories, the stress component σzz = 0 because σzz << τxz.
For the nonclassical beam theories, the surface is not in balance with the above assumption. It is supposed that the stress component σzz changes linearly within the beam thickness and satisfies the balance conditions on the top and bottom surfaces [43], with
(71)
According to this assumption, σzz can be determined as
(72)
Using Eq. (4) along with Eq. (5), the components of surface stress for the present beam theories can be obtained in the following form:
The nonzero components of stress for the bulk σbxx, τbxz of the beam can be determined as
where ν is Poisson’s ratio.
3. NONLOCAL BEAM THEORY INCLUDING SURFACE EFFECTS
3.1. Stress–Strain Relationships
The following section presents the stress–displacement relations and the related Euler–Lagrange equations corresponding to each type of beam theory based on the developed nonlocal beam theory including the surface effects (N-HSDTs). The components of surface stress for N-HSDTs are given as
The nonzero components of stress for the bulk for N-HSDTs are given as
where
In this work, we consider
We have also
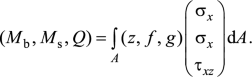 (13)
(13)
By substituting Eq. (4) into Eqs. (10), (11) and the subsequent results into Eq. (13), the stress resultants are obtained as
3.2. Governing Equations
The minimum total potential energy principle [44–48] is employed here to obtain the governing equations:
where δUint is the virtual variation of the strain energy and δWext is the variation of work done by external forces. The strain energy variation is given as
The variation of the potential energy of the applied loads can be expressed as
Substituting the expressions for δU, δW from Eqs. (16), (17) into Eq. (15), integrating by parts, and collecting the coefficients of δwb, δws, the following governing equations of the beam are obtained:
By replacing the stress resultants of Eq. (14) into Eq. (18), the nonlocal governing equations of N-HSDTs including surface effects can be expressed in terms of displacements δwb, δws as
(19-1)
where
where the constant parameter H is obtained by the residual surface tension τs and the shape of cross section. In this study for a rectangular beam, we have H = 2bτs.
In case if the nonlocal parameter μ is equal to zero and the surface effect is completely neglected, the equilibrium equation (19) becomes the classical beam theory; we denoted it by symbol CL.
In case if the surface effect is completely neglected, the equilibrium equation (19) becomes the nonlocal beam theory; we denoted it by symbol NL.
In case if the nonlocal parameter μ is set to zero, the equilibrium equation (19) becomes the nonclassical beam theory; we denoted it by symbol SE.
4. CLOSED-FORM SOLUTION FOR SIMPLY SUPPORTED NANOWIRES
In this study, analytical solutions are given for simply supported isotropic nanobeams in bending and buckling. The boundary conditions of simply supported beams are
The following two coefficients of displacements (wb, ws) are chosen to satisfy the above boundary conditions of simply supported beams as [49–52]:
where Wsn are arbitrary parameters to be determined, with α = nπ/L.
The transverse load q is also expanded in the Fourier sine series as
(221)
The Fourier coefficients Qn associated with uniform and point loads are given for sinusoidal load [53]
(222)
for uniform load
Substituting Eqs. (21) and (22) for the expansion of displacement components wb, ws and transverse load q into governing equations (18), the analytical solutions can be obtained from the following matrix system:
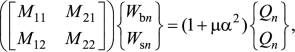 (23)
(23)
where M11 = S11 – Pα2(1 + μα2), M12 = S12 – Pα2(1 + μα2), M21 = S21 – Pα2(1 + μα2), M22 = S22 – Pα2(1 + μα2) and
The buckling load is obtained from Eq. (22) by setting q to zero:
The static deflection is obtained from Eq. (22) by setting p to zero:
5. RESULTS AND DISCUSSION
5.1. Nonlocality Validation for the Surface Effect is Completely Neglected
This first part is devoted to the buckling analysis of a simply supported nanobeam with including only the nonlocality effect.
The geometrical and material properties of a nonlocal beam used in this section, according to [54], are L = 10 nm, E = 3 × 106 N/m2, v = 0.3, h = b = 1 nm. τs = μs = λs = 0 and μ ≠ 0 correspond to the nonlocal beam theory, but μ = 0 corresponds to the local beam theory.
The presented results are for a wide range of small-scale coefficients and the length-to-depth ratio L/h = 10. From Table 1, we can see that the obtained results are in good agreement with those given by Aydogdu [14] and Reddy [54]. It can be also observed that an increase in the nonlocality parameter tends to decrease the critical buckling load. This emphasizes the significance of the size effect on the critical buckling load of the beams.
5.2. Surface Stress Including Nonlocal Elasticity Model for Nanowires
Analytical solutions for the bending and buckling response of simply supported nanobeams with taking into account the coupling effect of nonlocality and surface properties are presented in Tables 2–6.
* Taken from [9].
* Taken from [9].
* Taken from [9].
* Taken from [55].
* Taken from [55].
The material properties used in this investigation are [8] E = 17.73 × 1010 N/m2, ν = 0.27, λs = –8 N/m, μs = 2.5 N/m, τs = 1.7 N/m, and b = h = 1 nm.
Tables 2–4 present the values of the critical buckling load Pcr of simply supported nanobeams corresponding to the first, second and third buckling modes, respectively. The given results are compared with those obtained by Ansari and Sahmani [9] using the first shear deformation theory (FSDT) and refined beam theory (RBT) for the case of μ = 0. The tabulated results indicate that the current model is in good agreement with the results of Ansari and Sahmani [9] for various values of the aspect ratio L/h. It can also be observed that the values of the critical buckling load increase in the case of τs ≠ 0, 2μs + λs ≠ 0 (the surface stress effect is taken into account). It is clear from Tables 1–3 that the critical buckling load is in inverse relation with the values of the small-scale effect μ. The largest values of Pcr are obtained for the ratios L/h = 10 because the structure is slender. Comparisons of Tables 1–3 show that the largest values of the critical buckling load Pcr are obtained for the third mode where the effect of the small scale is more pronounced. We conclude from the tables that the critical buckling load is influenced a lot by the surface effect in the case of higher values of L/h.
Figure 2 plots the variation of the critical buckling loads versus the nonlocal parameter μ = 0.0, 0.5, 1.0, 1.5, 2.0 nm2 and slenderness ratio L/h for the simply supported beam with E s = –3 N/m, τs = 1.7 N/m, and b = h = 1 nm. From the obtained curves we can see that the critical buckling load is in inverse relation with the ratio L/h because the structure becomes slender. We can also observe that an increase in the nonlocal parameter μ leads to a decrease in the values of the buckling parameter Pcr.
Figure 3 presents a comparison of the critical buckling loads of simply supported nanowires E s = –3 N/m, τs = 1.7 N/m, and b = h = 1 nm predicted by the classical theory (CL), nonclassical nanobeam theory (SE), nonlocal theory (NL), and nonlocal theory with surface effect (NL-SE). The curves indicate that the critical buckling loads computed using the nonclassical theory (SE) are larger than those predicted by the nonlocal theory with surface effect (NT-SE) for the small values of ratio L/h, but the values of Pcr computed via SE and NL-SE are almost the same for higher values of L/h. The nonlocal theory (NL) gives small values of Pcr compared to the classical theory (CL).
Figure 4 illustrates the effect of E s, nonlocality parameter μ and slenderness ratio on the critical buckling load of the beam with τs = 0. The plotted curves clearly show that an increase in the nonlocality parameter μ and ratio L/h reduces the values of the critical buckling load. The highest values of the critical buckling load are obtained for 2μs + λs = 5.
Figure 5 shows the variation of the critical buckling load versus the value of the residual surface stress τs and small-scale effect parameter μ with E s = 0. We can see from the graphs that an increase in the magnitude of τs leads to an increase in the values of the critical buckling parameter for various values of the parameter μ. We can conclude again that the critical buckling load is in inverse relation with the slenderness ratio L/h and small-scale parameter μ.
Tables 5 and 6 present the maximum center deflections of nanowires under uniform and sinusoidal transverse mechanical load, respectively. The obtained results are compared with those given by Ould Youcef et al. [55] using FBT and HBT classical and nonclassical theories. The tabulated results for the maximum center deflections of nanowires confirm a good agreement between the current results and those of Ould Youcef et al. [55]. It is remarkable that the classical theory gives the highest values of the maximum center deflections because of neglecting the surface effect. The transverse displacement is in direct correlation with the nonlocality parameter μ. The maximum deflection increases with increasing span-to-thickness ratio L/h because the nanowire becomes slender and flexible.
The variation of the maximum transverse deflection of nanowires with E s = –3 N/m, τs = 1.7 N/m versus the span-to-depth ratio L/h and nonlocality parameter μ is illustrated in Fig. 6. It is seen that an increase in the ratio L/h leads to an increase in the values of the maximum deflection because the nanowire becomes flexible. The results obtained with allowance for the small-scale effect are higher than those obtained with the local theory.
Figure 7 presents a comparison of the transverse deflection of nanowires predicted by various analytical models (CL, SE, NL-SE and NL) for different values of the span-to-depth ratio L/h. The comparison demonstrates that the effect of nonlocality on the maximum deflection is more significant than the surface effect. We can confirm again that the higher values of deflection are obtained for slender nanowires.
The influence of the slenderness ratio L/h, nonlocal parameter μ, and the magnitudes of Es on the maximum center deflection of simply supported nanowires with τs = 0 is presented in Fig. 8. One can see from the plotted curves that the maximum transverse displacement increases with increasing parameter μ and length-to-thickness ratio. The low values of deflections are obtained for the positive values of E s.
The variation of the maximum center deflection versus the slenderness ratio L/h, residual surface stress τs, and small-scale effect parameter μ with E s = 0 is illustrated in Fig. 9. It can be seen that the center deflection increases with an increase in the nonlocality parameter μ and span-to-depth ratio L/h because the structure becomes flexible. An increase in the residual surface stress τs reduces the values of the center deflection for various values of L/h and parameter μ.
6. CONCLUSIONS
This work presents analytical solutions of the mechanical buckling and flexural behavior of simply supported nanowires under axial and transverse mechanical load. The structure is modeled on the basis of the cubic, sinusoidal and hyperbolic higher-order shear deformation theories. The surface stress and small-scale effects are considered based on the Gurtin–Murdoch surface elasticity theory and Eringen’s nonlocal theory. The governing equations are determined via virtual work principle. The obtained differential equations are solved analytically with the help of the Navier procedure. The accuracy of the developed model is checked by comparing the obtained results with those existing in the literature. Several examples are considered to show the influence of different parameters on the static responses of nanowires. The formulation can be extended to examine others types of structures and materials, as in [56–60].
REFERENCES
Lee, Z., Ophus, C., Fischer, L.M., Nelson-Fitzpatrick, N., Westra, K.L., Evoy, S., Radmilovic, V., Dahmen, U., and Mitlin, D., Metallic NEMS Components Fabricated from Nanocomposite Al–Mo films, Nanotechnology, 2006, vol. 17, no. 12, pp. 3063–3070. https://doi.org/10.1088/0957-4484/17/12/042
Witvrouw, A. and Mehta, A., The Use of Functionally Graded Poly-SiGe Layers for MEMS Applications, Mater. Sci. Forum, 2005, vol. 492–493, pp. 255–260. https://doi.org/10.4028/www.scientific.net/msf.492-493.255
Craighead, H.G., Nanoelectromechanical Systems, Science, 2000, vol. 290, no. 5496, pp. 1532–1535. https://doi.org/10.1126/science.290.5496.1532
Ekinci, K.L. and Roukes, M.L., Nanoelectromechanical Systems, Rev. Sci. Instrum., 2005, vol. 76, no. 6, p. 061101. https://doi.org/10.1063/1.1927327
Ahn, M.-W., Park, K.-S., Heo, J.-H., Park, J.-G., Kim, D.W., Choi, K.J., Lee, J.H., and Hong, S.-H., Gas Sensing Properties of Defect-Controlled ZnO-Nanowire Gas Sensor, Appl. Phys. Lett., 2008, vol. 93, no. 26, p. 263103. https://doi.org/10.1063/1.3046726
Venkatesan, B.M., Dorvel, B., Yemenicioglu, S., Watkins, N., Petrov, I., and Bashir, R., Highly Sensitive, Mechanically Stable Nanopore Sensors for DNA Analysis, Adv. Mater., 2009, vol. 21, no. 27, pp. 2771–2776. https://doi.org/10.1002/adma.200803786
Gurtin, M.E. and Murdoch, A.I., A Continuum Theory of Elastic Material Surfaces, Arch. Ration. Mech. Anal., 1975, vol. 57, no. 4, pp. 291–323. https://doi.org/10.1007/bf00261375
Gurtin, M.E. and Murdoch, A.I., Surface Stress in Solids, Int. J. Solids Struct., 1978, vol. 14, no. 6, pp. 431–440. https://doi.org/10.1016/0020-7683(78)90008-2
Ansari, R. and Sahmani, S., Bending Behavior and Buckling of Nanobeams Including Surface Stress Effects Corresponding to Different Beam Theories, Int. J. Eng. Sci., 2011, vol. 49, pp. 1244–1255. https://doi.org/10.1016/j.ijengsci.2011.01.007
Song, F., Huang, G.L., Park, H.S., and Liu, X.N., A Continuum Model for the Mechanical Behavior of Nanowires Including Surface and Surface Induced Initial Stresses, Int. J. Solids Struct., 2011, vol. 48, pp. 2154–2163. https://doi.org/10.1016/j.ijsolstr.2011.03.021
Dingreville, R., Qu, J., and Cherkaoui, M., Surface Free Energy and Its Effect on the Elastic Behavior of Nanosized Particles, Wires and Films, J. Mech. Phys. Solids, 2005, vol. 53, pp. 1827–1854. https://doi.org/10.1016/j.jmps.2005.02.012
Peddieson, J., Buchanan, G.R., and McNitt, R.P., Application of Nonlocal Continuum Models to Nanotechnology, Int. J. Eng. Sci., 2003, vol. 41, no. 3–5, pp. 305–312. https://doi.org/10.1016/s0020-7225(02)00210-0
Sudak, L.J., Column Buckling of Multiwalled Carbon Nanotubes Using Nonlocal Continuum Mechanics, J. Appl. Phys., 2003, vol. 94, no. 11, pp. 7281–7287. https://doi.org/10.1063/1.1625437
Aydogdu, M., A General Nonlocal Beam Theory: Its Application to Nanobeam Bending, Buckling and Vibration, Physica. E, 2009, vol. 41, pp. 1651–1655. https://doi.org/10.1016/j.physe.2009.05.014
Reddy, J.N. and Pang, S.D., Nonlocal Continuum Theories of Beams for the Analysis of Carbon Nanotubes, J. Appl. Phys., 2008, vol. 103, no. 2, p. 023511. https://doi.org/10.1063/1.2833431
Phadikar, J.K. and Pradhan, S.C., Variational Formulation and Finite Element Analysis for Nonlocal Elastic Nanobeams and Nanoplates, Comput. Mater. Sci., 2010, vol. 49, no. 3, pp. 492–499. https://doi.org/10.1016/j.commatsci.2010.05.040
Civalek, O. and Demir, C., Bending Analysis of Microtubules Using Nonlocal Euler–Bernoulli Beam Theory, Appl. Math. Model, 2011, vol. 35, no. 5, pp. 2053–2067. https://doi.org/10.1016/j.apm.2010.11.004
Demir, C. and Civalek, O., Torsional and Longitudinal Frequency and Wave Response of Microtubules Based on the Nonlocal Continuum and Nonlocal Discrete Models, Appl. Math. Model, 2013, vol. 37, no. 22, pp. 9355–9367. https://doi.org/10.1016/j.apm.2013.04.050
Attia, M.A., On the Mechanics of Functionally Graded Nanobeams with the Account of Surface Elasticity, Int. J. Eng. Sci., 2017, vol. 115, pp. 73–101. https://doi.org/10.1016/j.ijengsci.2017.03.011
Dihaj, A., Zidour, M., Meradjah, M., Rakrak, K., Heireche, H., and Chemi, A., Free Vibration Analysis of Chiral Double-Walled Carbon Nanotube Embedded in an Elastic Medium Using Non-Local Elasticity Theory and Euler–Bernoulli Beam Model, Struct. Eng. Mech., 2018, vol. 65, no. 3, pp. 335–342. https://doi.org/10.12989/sem.2018.65.3.335
Hamidi, A., Zidour, M., Bouakkaz, K., and Bensattalah, T., Thermal and Small-Scale Effects on Vibration of Embedded Armchair Single-Walled Carbon Nanotubes, J. Nano Res., 2018, vol. 51, pp. 24–38. https://doi.org/10.4028/www.scientific.net/JNanoR.51.24
Ebrahimi, F., Barati, M.R., and Civalek, Ö., Application of Chebyshev–Ritz Method for Static Stability and Vibration Analysis of Nonlocal Microstructure-Dependent Nanostructures, Eng. Comput, 2019. https://doi.org/10.1007/s00366-019-00742-z
Bensattalah, T., Zidour, M., and Daouadji, T.H., A New Nonlocal Beam Model for Free Vibration Analysis of Chiral Single-Walled Carbon Nanotubes, Compos. Mater. Eng., 2019, vol. 1, no. 1, pp. 21–31. https://doi.org/10.12989/cme.2019.1.1.021
Civalek, O., Uzun, B., Yayli, M.O., and Akgöz, B., Size-Dependent Transverse and Longitudinal Vibrations of Embedded Carbon and Silica Carbide Nanotubes by Nonlocal Finite Element Method, Eur. Phys. J. Plus., 2020, vol. 135, p. 381. https://doi.org/10.1140/epjp/s13360-020-00385-w
Bensattalah, T., Hamidi, A., Bouakkaz, K., Zidour, M., and Daouadji, T.H., Critical Buckling Load of Triple-Walled Carbon Nanotube Based on Nonlocal Elasticity Theory, J. Nano Res., 2020, vol. 62, pp. 108–119. https://doi.org/10.4028/www.scientific.net/JNanoR.62.108
Shanab, R.A., Attia, M.A., Mohamed, S.A., and Mohamed, N.A., Effect of Microstructure and Surface Energy on the Static and Dynamic Characteristics of FG Timoshenko Nanobeam Embedded in an Elastic Medium, J. Nano Res., 2020, vol. 61, pp. 97–117. https://doi.org/10.4028/www.scientific.net/jnanor.61.97
Eringen, A.C., Nonlocal Polar Elastic Continua, Int. J. Eng. Sci., 1972, vol. 10, pp. 1–16. https://doi.org/10.1016/0020-7225(72)90070-5
Eringen, A.C., On Differential Equations of Nonlocal Elasticity and Solutions of Screw Dislocation and Surface Waves, J. Appl. Phys., 1983, vol. 54, pp. 4703–4710. https://doi.org/10.1063/1.332803
Eringen, A.C. and Edelen, D.G.B., On Nonlocal Elasticity, Int. J. Eng. Sci., 1972, vol. 10, pp. 233–248. https://doi.org/10.1016/0020-7225(72)90039-0
Eringen, A.C., Nonlocal Continuum Field Theories, New York: Springer-Verlag, 2002.
Kar, V.R. and Panda, S.K., Large Deformation Bending Analysis of Functionally Graded Spherical Shell Using FEM, Struct. Eng. Mech., 2015, vol. 53, no. 4, pp. 661–679. https://doi.org/10.12989/sem.2015.53.4.661
Chandra, B.M., Ramji, K., Kar, V.R., Panda, S.K., Lalepalli, K.A., and Pandey, H.K., Numerical Study of Temperature Dependent Eigenfrequency Responses of Tilted Functionally Graded Shallow Shell Structures, Struct. Eng. Mech., 2018, vol. 68, no. 5, pp. 527–536. https://doi.org/10.12989/sem.2018.68.5.527
Madenci, E., A Refined Functional and Mixed Formulation to Static Analyses of FGM Beams, Struct. Eng. Mech., 2019, vol. 69, no. 4, pp. 427–437. https://doi.org/10.12989/sem.2019.69.4.427
Ahmed, R.A., Fenjan, R.M., and Faleh, N.M., Analyzing Post-Buckling Behavior of Continuously Graded FG Nanobeams with Geometrical Imperfections, Geomech. Eng., 2019, vol. 17, no. 2, pp. 175–180. https://doi.org/10.12989/gae.2019.17.2.175
Vinyas, M., On Frequency Response of Porous Functionally Graded Magneto-Electro-Elastic Circular and Annular Plates with Different Electro-Magnetic Conditions Using HSDT, Compos. Struct., 2020, vol. 240, p. 112044. https://doi.org/10.1016/j.compstruct.2020.112044
Hadji, L., Influence of the Distribution Shape of Porosity on the Bending of FGM Beam Using a New Higher Order Shear Deformation Model, Smart Struct. Syst., 2020, vol. 26, no. 2, pp. 253–262. https://doi.org/10.12989/sss.2020.26.2.253
Sahoo, B., Mehar, K., Sahoo, B., Sharma, N., and Panda, S.K., Thermal Frequency Analysis of FG Sandwich Structure under Variable Temperature Loading, Struct. Eng. Mech., 2021, vol. 77, no. 1, pp. 57–74. https://doi.org/10.12989/sem.2021.77.1.057
Reddy, J.N., A Simple Higher-Order Theory for Laminated Composite Plates, J. Appl. Mech., 1984, vol. 51, no. 4, pp. 745–752. https://doi.org/10.1115/1.3167719
Touratier, M., An Efficient Standard Plate Theory, Int. J. Eng. Sci., 1991, vol. 29, no. 8, pp. 901–916. https://doi.org/10.1016/0020-7225(91)90165-y
Soldatos, K., A Transverse Shear Deformation Theory for Homogeneous Monoclinic Plates, Acta Mech., 1992, vol. 94, no. 3, pp. 195–220. https://doi.org/10.1007/bf01176650
Miller, R.E. and Shenoy, V.B., Size-Dependent Elastic Properties of Nanosized Structural Elements, Nanotechnology, 2000, vol. 11, no. 3, pp. 139–147. https://doi.org/10.1088/0957-4484/11/3/301
Jing, G.Y., Duan, H.L., Sun, X.M., Zhang, Z.S., Xu, J., Li, Y.D., Wang, J.X., and Yu, D.P., Surface Effects on Elastic Properties of Silver Nanowires: Contact Atomic-Force Microscopy, Phys. Rev. B, 2006, vol. 73, no. 23. https://doi.org/10.1103/physrevb.73.235409
Lu, P., He, L.H., Lee, H.P., and Lu, C., Thin Plate Theory Including Surface Effects, Int. J. Solid. Struct., 2006, vol. 43, no. 16, pp. 4631–4647. https://doi.org/10.1016/j.ijsolstr.2005.07.036
Reddy, J.N., Energy Principles and Variational Methods in Applied Mechanics, John Wiley & Sons Inc., 2002.
Daouadji, T.H. and Hadji, L., Analytical Solution of Nonlinear Cylindrical Bending for Functionally Graded Plates, Geomech. Eng., 2015, vol. 9, no. 5, pp. 631–644. https://doi.org/10.12989/gae.2015.9.5.631
Kiani, Y., NURBS-Based Thermal Buckling Analysis of Graphene Platelet Reinforced Composite Laminated Skew Plates, J. Thermal. Stress, 2019, pp. 1–19. https://doi.org/10.1080/01495739.2019.1673687
Rachedi, M.A., Benyoucef, S., Bouhadra, A., Bachir Bouiadjra, R., Sekkal, M., and Benachour, A., Impact of the Homogenization Models on the Thermoelastic Response of FG Plates on Variable Elastic Foundation, Geomech. Eng., 2020, vol. 22, no. 1, pp. 65–80. https://doi.org/10.12989/gae.2020.22.1.065
Merzoug, M., Bourada, M., Sekkal, M., Ali Chaibdra, A., Belmokhtar, C., Benyoucef, S., and Benachour, A., 2D and Quasi 3D Computational Models for Thermoelastic Bending of FG Beams on Variable Elastic Foundation: Effect of the Micromechanical Models, Geomech. Eng., 2020, vol. 22, no. 4, pp. 361–374. https://doi.org/10.12989/gae.2020.22.4.361
Hadji, L., Zouatnia, N., and Bernard, F., An Analytical Solution for Bending and Free Vibration Responses of Functionally Graded Beams with Porosities: Effect of the Micromechanical Models, Struct. Eng. Mech., 2019, vol. 69, no. 2, pp. 231–241. https://doi.org/10.12989/sem.2019.69.2.231
Safa, A., Hadji, L., Bourada, M., and Zouatnia, N., Thermal Vibration Analysis of FGM Beams Using an Efficient Shear Deformation Beam Theory, Earthquakes Struct., 2019, vol. 17, no. 3, pp. 329–336. https://doi.org/10.12989/eas.2019.17.3.329
Zouatnia, N. and Hadji, L., Effect of the Micromechanical Models on the Bending of FGM Beam Using a New Hyperbolic Shear Deformation Theory, Earthquakes Struct., 2019, vol. 16, no. 2, pp. 177–183. https://doi.org/10.12989/eas.2019.16.2.177
Jena, S.K., Chakraverty, S., Malikan, M., and Mohammad-Sedighi, H., Hygro-Magnetic Vibration of the Single-Walled Carbon Nanotube with Nonlinear Temperature Distribution Based on a Modified Beam Theory and Nonlocal Strain Gradient Model, Int. J. Appl. Mech., 2020. https://doi.org/10.1142/s1758825120500544
Sedighi, H.M. and Bozorgmehri, A., Dynamic Instability Analysis of Doubly Clamped Cylindrical Nanowires in the Presence of Casimir Attraction and Surface Effects Using Modified Couple Stress Theory, Acta Mech., 2016, vol. 227, no. 6, pp. 1575–1591. https://doi.org/10.1007/s00707-016-1562-0
Reddy, J.N., Nonlocal Theories for Bending, Buckling and Vibration of Beams, Int. J. Eng. Sci., 2007, vol. 45, pp. 288–307. https://doi.org/10.1016/j.ijengsci.2007.04.004
Ould Youcef, D., Kaci, A., Houari, M.S.A., Tounsi, A., Benzair, A., and Heireche, H., On the Bending and Stability of Nanowire Using Various HSDTs, Adv. Nano Res., 2015, vol. 3, no. 4, pp. 177–191. https://doi.org/10.12989/anr.2015.3.4.177
Avcar, M., Free Vibration of Imperfect Sigmoid and Power Law Functionally Graded Beams, Steel Compos. Struct., 2019, vol. 30, no. 6, pp. 603–615. https://doi.org/10.12989/scs.2019.30.6.603
Sedighi, H.M. and Bozorgmehri, A., Nonlinear Vibration and Adhesion Instability of Casimir-Induced Nonlocal Nanowires with the Consideration of Surface Energy, J. Brazil. Soc. Mech. Sci. Eng., 2016, vol. 39, no. 2, pp. 427–442. https://doi.org/10.1007/s40430-016-0530-x
Shariati, A., Jung, D. won, Mohammad-Sedighi, H., Żur, K.K., Habibi, M., and Safa, M., On the Vibrations and Stability of Moving Viscoelastic Axially Functionally Graded Nanobeams, Materials, 2020, vol. 13, no. 7, p. 1707. https://doi.org/10.3390/ma13071707
AlSaid-Alwan, H.H.S. and Avcar, M., Analytical Solution of Free Vibration of FG Beam Utilizing Different Types of Beam Theories: A Comparative Study, Comput. Concret., 2020, vol. 26, no. 3, pp. 285–292. https://doi.org/10.12989/cac.2020.26.3.285
Hadji, L. and Avcar, M., Free Vibration Analysis of FG Porous Sandwich Plates under Various Boundary Conditions, J. Appl. Comput. Mech., 2021, vol. 7, no. 2, pp. 505–519. https://doi.org/10.22055/JACM.2020.35328.2628
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizicheskaya Mezomekhanika, 2021, Vol. 24, No. 3, pp. 36–39.
Rights and permissions
About this article
Cite this article
Lounis, A., Youcef, D.O., Bousahla, A.A. et al. Surface Effects and Small-Scale Impacts on the Bending and Buckling of Nanowires Using Various Nonlocal HSDTs. Phys Mesomech 25, 42–56 (2022). https://doi.org/10.1134/S1029959922010064
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1029959922010064




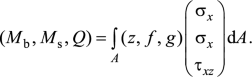 (13)
(13)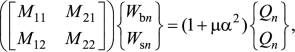 (23)
(23)






