1 Introduction

Because of excellent physical properties of nanowire-based nano-structures, e.g. small size with large ratio of surface-area to volume, the applications of these structures are growing rapidly. Nanowires are of great interest for detecting nano-objects with high sensitivity and also have noticeable applications in several industries such as optics [1], nanoelectromechanical systems (NEMS) [2], biological or gas sensing devices [3], flexible electronics and renewable energy technologies [4], ultrasensitive biological and chemical sensors [5], pH measurements [6], resonators and actuators [7, 8] and multifunctional NEMS.

When the electronic and mechanical systems are fabricated at nano-scale size, some new phenomena that originated from the nano-size quantum effects have become more important and the motion of nanowire-based structure is affected by the small-scale quantum electrodynamic interactions such as vacuum fluctuations. The effect of vacuum fluctuation forces is usually modeled through the Casimir attraction which is the dominant phenomenon in sub-micron separations [9]. By integrating a force-sensing micromechanical beam and an electrostatic actuator on a single chip, Zou et al. [10] demonstrated the Casimir effect between two micromachined silicon components on the same substrate. Lombardo et al. [11] numerically evaluate the Casimir interaction energy for configurations involving two perfectly conducting eccentric cylinders and a cylinder in front of a plane. Emig et al. [12] found the exact Casimir force between a plate and a cylinder by assuming an intermediate geometry between parallel plates and the plate-sphere. Tercas et al. [13] considered the mechanical coupling between a two-dimensional Bose–Einstein condensate and a graphene sheet via the vacuum fluctuations of the electromagnetic field which are at the origin of the so-called Casimir–Polder potential. By deriving a self-consistent set of governing equations of the condensate and the flexural modes of the graphene, they could show the formation of a new type of purely acoustic quasi-particle excitation, a quasi-polariton resulting from the coherent superposition of quanta of flexural and Bogoliubov modes. Ali et al. [14] investigated the excitation of electrostatic wake fields in metallic nanowires due to the propagation of a short electron pulse. To this end, they considered a nonlocal dielectric response of the system and discussed the stability conditions of wake fields. Moreover, they showed that the underling mechanism can be useful to investigate new sources of radiation in the extreme-ultraviolet range. Bordag et al. [15] provided a review of both new experimental and theoretical developments in the Casimir effect. They demonstrated that the Casimir force strongly depends on the shape, size, geometry and topology of the boundaries. Since then, many investigations have been conducted to compute the Casimir attraction for different geometries including parallel plates [16–18], plate-sphere [19], parallel cylinders [20] and plate-cylinder [21]. Several investigations have investigated the instability characteristics and nonlinear analysis of micro/nano-scale structures by employing different assumptions and theories such as nonlocal elasticity [22–24] modified couple stress theory [25–28], strain gradient theory [29, 30], modified strain gradient theory [31], strain-inertia gradient elasticity [32], etc. A nano-scale device might adhere to its substrate due to Casimir force if the minimum gap between the flexible beam and the substrate is not considered. Besides interfering with the stability of freestanding nanostructures, the Casimir force can also induce undesired adhesion during the fabrication stages. Therefore, the investigation on the stability behavior of suspended nanowires is very crucial for precise designing and mounting of these structures. All the published works have focused on the instability analysis of small-sized structures with planar or rectangular cross-section. However, the dynamic instability characteristics of size-dependent nano-beams with circular cross-section with the consideration of Casimir force by incorporating the surface effects have not been addressed so far.

Owing to the high surface/volume ratio of nano-sized structures [33], it was experimentally demonstrated that the surface layer plays an important role in the static and dynamic behavior of such devices. Atoms at a free surface of nano-structures experience a different local environment with respect to the atoms in the bulk material. Consequently, the energy associated with these atoms is different from that of the atoms in the bulk. The excess energy associated with surface atoms is called surface free energy [34]. In the classical continuum mechanics, the effect of surface layer is ignored. However, for nano-size devices, due to the high surface-to-volume ratios, the influence of the surface layer on the overall dynamic behavior of nano-structure becomes highlighted. A surface elasticity theory was presented by Gurtin and Murdoch [35] to model the surface layer of a solid as a membrane with negligible thickness. The dynamic pull-in behavior of an electrically actuated nano-bridge with rectangular cross-section incorporating the surface and small-size effects was studied by Sedighi [36]. Eltaher et al. [37] examined the vibration characteristics of nano-beams using the nonlocal finite element model with the consideration of surface layer effects. The pull-in behavior of an electrically actuated nano-beam by incorporating surface elasticity was studied by Fu and Zhang [38]. They solved the complex mathematical problem by the analog equation method (AEM) and discussed the effects of the surface energies on the static and dynamic responses, pull-in voltage and pull-in time. The influence of surface effect on the static instability behavior of cantilever nano-actuator in the presence of van der Waals force (vdW) was investigated by Koochi et al. [39].

As mentioned earlier, the Casimir force can induce instability and adhesion in suspended nanostructures. Based on the available published literature, previous investigations in this area have focused on modeling instability in structures with planar or rectangular cross-section and the Casimir-induced instability and dynamic behavior of nanosystems with circular cross-section (such as nanowires and nanotubes) have not been explored yet. Therefore, the main objective of this study was to examine the influence of Casimir attraction on the instability/adhesion characteristics of nano-bridges incorporating the size-dependency and surface layer effects. To this end, the nonlocal elasticity together with the Euler–Bernoulli beam theory is adopted to derive the vibrational governing equation of nanowires with the consideration of vacuum fluctuations and surface energy. To solve the nonlinear governing equation a stepwise numerical method is introduced. Finally, the effect of different parameters on the instability behavior and adhesion time of Casimir-induced suspended nanowires is addressed.

2 Mathematical modeling

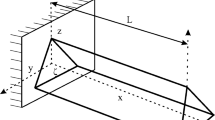
The schematic view and SEM image of suspended doubly clamped nanowire above a flat plate substrate is depicted in Fig. 1. The flexible cylinder can deform towards the fixed ground plane due to the influence of Casimir attractive force. The nanowire has the initial gap D, length L and radius R. In the following subsections, based on two different approaches, e.g. PFA (small separation approximation) and Dirichlet mode (large separation approximation), the governing equation of Casimir-induced nanowires are extracted.

Fig. 1
figure 1

a Schematics view b side view and c SEM image of doubly clamped cylinder-plate

Full size image

Figure 2 shows the schematic representation of a doubly clamped nanowire suspended on three substrates. When the interface force that originates from Casimir attraction between two surfaces is smaller than the critical value, the nanowire deflected toward the fixed substrate. As the Casimir force increases and approaches the critical value, the nanowire cannot tolerate the attractive load and suddenly collapses on the lower plate and the stiction/adhesion phenomena occurs [40].

Fig. 2
figure 2

Adhesion phenomena of suspended doubly clamped nanowire under Casimir attraction

Full size image

2.1 Equation of motion

The configuration of a doubly clamped nanowire with consideration of surface layer is shown in Fig. 3a. Based on the Gurtin–Murdoch method [35], it is assumed that the nanowire has an elastic surface with zero thickness with specific material characteristics which accounts for the surface energy effects. Moreover, Fig. 3b shows the free-body diagram of an infinitely small nano-beam element. The governing equation for transverse vibration of nanowire is expressed as follows [38]:

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} - \frac{\partial }{\partial x}\int\limits_{S} {T_{z} {\text{d}}s} - q\left( {x,t} \right) - \frac{\partial }{\partial x}\left( {N\frac{\partial w}{\partial x}} \right) + \left( {\rho A} \right)_{\text{eff}} \frac{{\partial^{2} w}}{{\partial t^{2} }} = 0,$$
(1)

where T x and T z refer to the contact tractions between the surface layer and bulk material, respectively. M is the bending moment, N is the axial force, S is the perimeter of the cross-section and q(x, t), that is derived in the subsequent section, denotes the Casimir force per unit length of the nanowire.

Fig. 3
figure 3

a Schematic representation of a doubly clamped nanowire and b nano-beam element

Full size image

The relation between the contact traction and the surface layer stresses is written as

$$\frac{{\partial \tau_{ix} }}{\partial x} - T_{i} = \rho_{0} \frac{{\partial^{2} u_{i}^{s} }}{{\partial t^{2} }},$$
(2)

where i = x, z, ρ 0 represents the mass density of surface layer and u s i is the deflection of the surface layer in the i direction. The constitutive equations for the surface layer and the governing equations for the axial force and bending moment are given by

$$N = \frac{EA}{2L}\int\limits_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} {\text{d}}x} + N_{0}$$
(3)
$$M = \left( {EI} \right)_{\text{eff}} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{2vI}{2R}\left( {\tau_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)$$
(4)
$$\tau_{xx} = \tau_{0} + E_{0} \left( {\frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(5)
$$\tau_{zx} = \tau_{0} \frac{\partial w}{\partial x}$$
(6)

Substituting of Eq. (2) into Eq. (1) and using the above-mentioned relations results in

$$\left[ {EI + E_{0} I_{0} - \frac{{2vI\tau_{0} }}{2R}} \right]\frac{{\partial^{4} w}}{{\partial x^{4} }} + \left[ {\rho A + \rho_{0} S_{0} } \right]\frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{{vI\rho_{0} }}{R}\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} = q\left( {x,t} \right) + \left[ {\tau_{0} S_{0} + \frac{EA}{2L}\int\limits_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} {\text{d}}x} + N_{0} } \right]\frac{{\partial^{2} w}}{{\partial x^{2} }},$$
(7)

where E 0 is the elasticity of surface layer, \(I_{0} = \int_{S} {z^{2} {\text{d}}s}\) represents the perimeter moment of inertia, τ 0 is the initial residual surface stress and v is the Poisson’s ratio of the bulk material. The nonlocal constitutive equations for the nanowire are given by

$$\left( {1 - e_{0}^{2} a^{2} \varDelta^{2} } \right)M^{\text{nl}} = M^{l}$$
(8)
$$\left( {1 - e_{0}^{2} a^{2} \varDelta^{2} } \right)\tau_{xx}^{\text{nl}} = \tau_{xx}^{l}$$
(9)
$$\left( {1 - e_{0}^{2} a^{2} \varDelta^{2} } \right)\tau_{zx}^{\text{nl}} = \tau_{zx}^{l} ,$$
(10)

where \(\varDelta^{2} = {{\partial^{2} } \mathord{\left/ {\vphantom {{\partial^{2} } {\partial x^{2} }}} \right. \kern-0pt} {\partial x^{2} }}\), e 0 and a represent the nonlocal effects dependent on material and an internal characteristic length nanoscale. Rewriting the governing equation described in Eq. (1) in the nonlocal form and multiplied by the nonlocal operator (1 − e 20 a 2Δ2), the governing equation for the Casimir-induced nonlocal nanowires is obtained as

$$\begin{aligned} \left[ {EI + E_{0} I_{0} - \frac{{2vI\tau_{0} }}{2R}} \right]\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{vI\rho_{0} }}{R}\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} - \tau_{0} S_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} = \hfill \\ \left( {1 - e_{0}^{2} a^{2} \varDelta^{2} } \right)\left[ {q\left( {x,t} \right) + \left( {N_{0} + \frac{EA}{2L}\int\limits_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} {\text{d}}x} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} - \left( {\rho A + \rho_{0} S_{0} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right] \hfill \\ \end{aligned}$$
(11)

Equation (11) is subjected to the boundary conditions as follows:

$$w\left( {0,t} \right) = 0,\,\,w^{\prime}\left( {0,t} \right) = 0,\,\,w\left( {L,t} \right) = 0,\,\,w^{\prime}\left( {L,t} \right) = 0,\,$$
(12)

In addition, the initial conditions of nano-structure are defined as

$$w\left( {x,0} \right) = 0,\,\,\dot{w}\left( {x,0} \right) = 0,\,\,$$
(13)

2.2 Casimir force for the cylinder-plate geometry

For the case of conducting parallel flat plates, the Casimir energy per unit area separated by a distance D is [41]

$$E_{\text{pp}} (D )= - \frac{{\pi^{2} \overline{h} c}}{{ 7 2 0D^{3} }},$$
(14)

where c is the light speed and \(\bar{h}\) is Planck’s constant. It should be noted that this formula can be obtained with the consideration of the electromagnetic mode structure between the two plates in comparison with the free space by assigning a zero-point energy to each electromagnetic mode [42]. Proximity force approximation (PFA) fundamentally uses the relation described in Eq. (14) to predict the Casimir force in the case of small separation. Based on PFA approach, the interaction between any other surfaces is modeled through a summation of infinitesimal parallel plates [41]. For small separations, the correct zeroth order approximation for the Casimir energy is given by [10]

$$E^{\text{PFA}} = \int\limits_{s} {E_{\text{PP}} (D ) {\text{d}}S} = - \frac{{\pi^{2} \overline{h} C}}{ 7 2 0}\iint {\frac{{{\text{d}}S}}{{D^{3} }}},$$
(15)

in which S is one of the two surfaces restricting a gap. It should be emphasized that for large separation as well as non-smooth surfaces the PFA cannot be used. Therefore, another approach should be employed to model the Casimir attraction force for the case of larger separations. To model the Casimir energy in large separations, a path integral representation [43] is used and the electrodynamic Casimir energy of two disconnected metallic surfaces using Dirichlet mode definition at zero temperature is determined [44, 45]. The Casimir energy of this mode at zero temperature is expressed as

$$E^{D} = \frac{{\bar{h}c}}{ 2\pi }\mathop \int \limits_{0}^{\infty } Tr\,{\text{ln(}}MM_{\infty }^{ - 1} ) {\text{d}}q_{0} ,$$
(16-a)

in which

$$M_{12} \left( {u\text{,} u^{\prime}\text{;}q_{0} } \right) = G_{0} \left( {s_{1} \left( u \right) - s_{2} \left( {u^{\prime}} \right)\text{;} q_{0} } \right)\text{,}$$
(16-b)
$$G_{0} \left( {x\text{, }x^{'} \text{;}q_{0} } \right) = \frac{{e^{{ - q_{0} \left| {x - x'} \right|}} }}{{ 4\pi \left| {x - x'} \right|}},$$

where matrix M 12 represents the geometry of the surfaces 1 and 2, M −1∞ is the functional inverse of matrix M at infinite surface separation, s i (u) is a vector referring to the ith surface parameterized by the surface vector u and G 0 denotes the free space Green function [46]. Based on the PFA (for small separations), the Casimir energy can be obtained as [10]

$$E^{\text{PFA}} = - \frac{{\pi^{3} \bar{h}cL}}{ 9 6 0}\sqrt {\frac{R}{{ 2D^{5} }}} ,$$
(17)

where R denotes the radius of nanowire and D is the gap distance. Thus, the Casimir force for small separation approximation (SSA) can be obtained by differentiating the energy with respect to D as

$$f_{\text{cas}} = - \frac{\partial E\left( D \right)}{\partial D} = \frac{ 1}{ 7 6 8}\pi^{3} \bar{h}cL\sqrt {\frac{ 2R}{{D^{7} }}}$$
(18)

Otherwise, for the case of cylinder-plate geometry with large separation gap, i.e. D ≫ R, the approximate expression for the attractive Casimir energy is stated as [47]

$$E^{D} = - \frac{{\bar{h}cL}}{{D^{2} }}\frac{ 1}{{ 1 6\pi { \ln }\left( {\frac{D}{R}} \right)}};$$
(19)

therefore, the Casimir force for large separation approximation (LSA) can be expressed as follows:

$$f_{\text{cas}} = \frac{{\bar{h}cL}}{{D^{3} }}\frac{ 1}{{ 8\pi { \ln }\left( {\frac{D}{R}} \right)}} + \frac{{\bar{h}cL}}{{D^{3} }}\frac{ 1}{{ 1 6\pi { \ln }^{ 2} \left( {\frac{D}{R}} \right)}}$$
(20)

2.3 Nondimensionalization of governing equation

In order to express the governing equation in the non-dimensional from, the following variables are defined:

$$\begin{aligned} \tau = \sqrt {\frac{EI}{{\rho bhL^{4} }}\,} \,t,\,\,\,W = \frac{w}{D},\,\,\,\xi = \frac{x}{L},\,\,\alpha = \frac{{EAD^{2} }}{2EI},\,\,k = \frac{D}{R},\,\,\,\mu = \frac{{E_{0} I_{0} }}{EI}, \hfill \\ \sigma_{1} = \frac{{v\tau_{0} }}{ER},\,\,\sigma_{2} = \frac{{\tau_{0} S_{0} L^{2} }}{EI},\,\,\gamma = \frac{{\bar{h}cL^{4} }}{{ 8\pi D^{4} EI}},\,\,\,f_{i} = \frac{{N_{0} L^{2} }}{EI},\,\,\varepsilon_{0} = \frac{{e_{0} a}}{L},\,\,\kappa_{1} = \frac{{v\rho_{0} R}}{{3\rho L^{2} }},\,\,\kappa_{2} = \frac{{\rho_{0} S_{0} }}{\rho A} \hfill \\ \end{aligned}$$
(21)

Thereby, the non-dimensional equation of motion for nonlocal nanowires considering the surface effects and Casimir force can be written as

$$\begin{aligned} \left( {1 + \mu - \sigma_{1} } \right)\frac{{\partial^{4} W}}{{\partial \xi^{4} }} + \kappa_{1} \frac{{\partial^{4} W}}{{\partial \xi^{2} \partial \bar{\tau }^{2} }} - \sigma_{2} \frac{{\partial^{2} W}}{{\partial \xi^{2} }} \hfill \\ = \left( {1 - \varepsilon_{0}^{2} \frac{{\partial^{2} }}{{\partial \xi^{2} }}} \right)\left[ {\frac{{\pi^{4} \gamma }}{ 9 6}\sqrt {\frac{ 2}{{k\left( {1 - W} \right)^{7} }}} \, + \left( {f_{i} + \alpha \int\limits_{0}^{1} {\left( {\frac{\partial W}{\partial \xi }} \right)^{2} d\xi } } \right)\frac{{\partial^{2} W}}{{\partial \xi^{2} }} - \left( {1 + \kappa_{2} } \right)\frac{{\partial^{2} W}}{{\partial \bar{\tau }^{2} }}} \right] \hfill \\ \end{aligned}$$
(22-a)

for SSA approximation and

$$\begin{aligned} \left( {1 + \mu - \sigma_{1} } \right)\frac{{\partial^{4} W}}{{\partial \xi^{4} }} + \kappa_{1} \frac{{\partial^{4} W}}{{\partial \xi^{2} \partial \bar{\tau }^{2} }} - \sigma_{2} \frac{{\partial^{2} W}}{{\partial \xi^{2} }} \hfill \\ = \left( {1 - \varepsilon_{0}^{2} \frac{{\partial^{2} }}{{\partial \xi^{2} }}} \right)\left[ {\frac{\gamma }{{ (1 - W )^{3} }}\frac{1}{{{ \ln }\left( {k (1 - W )} \right)}} + \frac{\gamma }{{ (1 - W )^{3} }}\frac{1}{{2\left( {\ln \left( {k (1 - W )} \right)} \right)^{2} }}} \right. \hfill \\ \,\,\, + \left. {\left( {f_{i} + \alpha \int\limits_{0}^{1} {\left( {\frac{\partial W}{\partial \xi }} \right)^{2} d\xi } } \right)\frac{{\partial^{2} W}}{{\partial \xi^{2} }} - \left( {1 + \kappa_{2} } \right)\frac{{\partial^{2} W}}{{\partial \bar{\tau }^{2} }}} \right] \hfill \\ \end{aligned}$$
(22-b)

for LSA approximation.

It is worth pointing out that due to the nano-beam deflection, the distance D presented in the Casimir force is replaced by D − w and for the case of large separation gap, it is assumed that D + R ≈ D.

3 Numerical approach for the non-linear problem

In order to numerically investigate the instability/adhesion properties and dynamic behavior of nanowires, the governing equation of motions (22-a) and (22-b) should be integrated over the time domain. In each time step of integration, the nonlinear terms on the right-hand side of Eq. (22) are assumed to be a function of the values in the previous step [48]. Accurate results can then be obtained if the time steps are selected reasonably small. The reduced order model eliminates the spatial dependency in the PDEs using the Galerkin-based methods. In this method, the displacements are described as a linear combination of independent eigenmodes which must satisfy the kinematic boundary conditions. By defining the orthogonality condition of the residue to every basis function, the second-order time-dependent ODEs in terms of the generalized coordinates corresponding to the each basis function are obtained.

To find an approximate reduced-order-model (ROM), the non-dimensional deflection are assumed as \(W\left( {\xi ,\tau } \right) = \sum\limits_{j = 1}^{N} {q_{j} \left( \tau \right)\phi_{j} \left( \xi \right)} ,\), where N denotes the number of considered modes, q j (τ) denotes the time-dependent generalized coordinate of the system and ϕ j (ξ) is the jth mode shape of nano-bridge which is given by

$$\phi_{j} \left( \xi \right) = \cosh \left( {\lambda_{j} \xi } \right) - \cos \left( {\lambda_{j} \xi } \right) - \frac{{\cosh \left( {\lambda_{j} } \right) - \cos \left( {\lambda_{j} } \right)}}{{\sinh \left( {\lambda_{j} } \right) - \sinh \left( {\lambda_{j} } \right)}}\left( {\sinh \left( {\lambda_{j} \xi } \right) - \sinh \left( {\lambda_{j} \xi } \right)} \right),$$
(23)

where λ j is the root of characteristic equation for jth eigenmode. By substituting Eq. (23) into Eqs. (22-a) and (22-b), multiplying by ϕ j (ξ) and integrating from ξ = 0 to μ mc, the approximate Reduced-Order-Model on the basis of Bubnov–Galerkin decomposition method can be simplified as

$$\sum\limits_{j = 1}^{N} {M_{ij} \textit{\"{q}}_{j} \left( \tau \right)} + \sum\limits_{j = 1}^{N} {K_{ij} q_{j} \left( \tau \right)} = F_{i} ,$$
(24)

where

$$M_{ij} = \left( {1 + \kappa_{2} } \right)\int_{0}^{1} {\varphi_{i} \varphi_{j} {\text{d}}\xi } + \left[ {\kappa_{1} - \varepsilon_{0} \left( {1 + \kappa_{2} } \right)} \right]\int_{0}^{1} {\varphi_{i} \varphi^{\prime\prime}_{j} {\text{d}}\xi }$$
(25)
$$K_{ij} = \left( {1 + \mu - \sigma_{1} } \right)\int_{0}^{1} {\varphi_{i} \varphi_{j}^{(iv)} {\text{d}}\xi } - \left( {f_{i} + \sigma_{2} } \right)\int_{0}^{1} {\varphi_{i} \varphi^{\prime\prime}_{j} {\text{d}}\xi } + \varepsilon_{0} f_{0} \int_{0}^{1} {\varphi_{i} \varphi_{j}^{(iv)} {\text{d}}\xi }$$
(26)
$$\begin{aligned} F_{i} & = \alpha \int_{0}^{1} {\varphi_{i} \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)\left( {\int_{0}^{1} {\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} {\text{d}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } } \right){\text{d}}\xi } - \varepsilon_{0} \alpha \int_{0}^{1} {\varphi_{i} \left( {\sum\limits_{j = 1}^{N} {\varphi_{j}^{(iv)} q_{j} } } \right)\left( {\int_{0}^{1} {\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} {\text{d}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } } \right){\text{d}}\xi } \, \\ & + \frac{{\pi^{4} \gamma }}{ 9 6}\int_{0}^{1} {\varphi_{i} \sqrt {\frac{ 2}{{k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{7} }}} {\text{d}}\xi } + \frac{{49\pi^{4} \varepsilon_{0} \gamma }}{ 3 8 4}\int_{0}^{1} {\varphi_{i} \frac{{\sqrt 2 \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} }}{{k^{2} \sqrt {\left( {\frac{ 1}{{k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{7} }}} \right)^{3} } \left( {\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{16} } \right)}}{\text{d}}\xi } \\ & - \frac{{28\pi^{4} \varepsilon_{0} \gamma }}{ 9 6}\int_{0}^{1} {\varphi_{i} \frac{{\sqrt 2 \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} }}{{k\sqrt {\left( {\frac{ 1}{{k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{7} }}} \right)^{3} } \left( {\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{9} } \right)}}{\text{d}}\xi } - \frac{{7\pi^{4} \varepsilon_{0} \gamma }}{192}\int_{0}^{1} {\varphi_{i} \frac{{\sqrt 2 \sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } }}{{k\sqrt {\left( {\frac{ 1}{{k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{7} }}} \right)^{3} } \left( {\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{8} } \right)}}{\text{d}}\xi } \\ \end{aligned}$$
(27-a)

for SSA approximation and

$$\begin{aligned} F_{i} & = \alpha \int_{0}^{1} {\varphi_{i} \left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } } \right)\left( {\int_{0}^{1} {\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} {\text{d}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } } \right){\text{d}}\xi } - \varepsilon_{0} \alpha \int_{0}^{1} {\varphi_{i} \left( {\sum\limits_{j = 1}^{N} {\varphi_{j}^{(iv)} q_{j} } } \right)\left( {\int_{0}^{1} {\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} {\text{d}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } } \right){\text{d}}\xi } \, \\ & + \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{1}{{\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{3} }}\left[ {\frac{1}{{{ \ln }\left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)}} + \frac{1}{{2\left( {\ln \left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)} \right)^{2} }}} \right]} \right){\text{d}}\xi } \\ & - 12\varepsilon_{0} \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{{\left[ {\frac{1}{{{ \ln }\left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)}} + \frac{1}{{2\left( {\ln \left( {k (1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } )} \right)} \right)^{2} }}} \right]\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} }}{{\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{5} }}} \right){\text{d}}\xi } \\ & - 6\varepsilon_{0} \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{{\left[ {\frac{1}{{{ \ln }\left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)^{2} \left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)}} + \frac{1}{{\left( {\ln \left( {k (1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } )} \right)} \right)^{3} \left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)}}} \right]\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} }}{{\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{4} }}} \right){\text{d}}\xi } \\ & - 3\varepsilon_{0} \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{{\left[ {\frac{1}{{{ \ln }\left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)}} + \frac{1}{{2\left( {\ln \left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)} \right)^{2} }}} \right]^{{}} \sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } }}{{\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{4} }}} \right){\text{d}}\xi } \\ & - \varepsilon_{0} \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{{\left[ {\frac{{3\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} }}{{{ \ln }\left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)^{3} \left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{2} }} + \frac{{\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime}_{j} q_{j} } }}{{\left( {\ln \left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)} \right)^{2} \left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)}}} \right]^{{}} }}{{\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{3} }}} \right){\text{d}}\xi } \\ \end{aligned}$$
$$\begin{aligned} & - \varepsilon_{0} \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{{\left[ {\frac{{\left( {W^{\prime}} \right)^{2} }}{{{ \ln }\left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)^{2} \left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{2} }} + \frac{{3\left( {\sum\limits_{j = 1}^{N} {\varphi^{\prime}_{j} q_{j} } } \right)^{2} }}{{\left( {\ln \left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)} \right)^{4} \left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{2} }}} \right]^{{}} }}{{\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{3} }}} \right){\text{d}}\xi } \\ & - \varepsilon_{0} \gamma \int_{0}^{1} {\varphi_{i} \left( {\frac{{\left[ {\frac{{\sum\limits_{j = 1}^{N} {\varphi^{\prime\prime\prime}_{j} q_{j} } }}{{\left( {\ln \left( {k\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)} \right)} \right)^{3} \left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)}}} \right]^{{}} }}{{\left( {1 - \sum\limits_{j = 1}^{N} {\varphi_{j} q_{j} } } \right)^{3} }}} \right){\text{d}}\xi } \\ \end{aligned}$$
(27-b)

for LSA approximation. In the recent equations, F i describes the nonlinear terms. By integrating Eq. (24) over the time domain, the dynamic behavior of the system can be described.

4 Results and discussion

The Casimir force has an important role in the design and fabrication of nano-devices. To assess the influences of vacuum fluctuations on the dynamics and instability characteristics of nano-systems, the variations of non-dimensional gap (1 − W) versus the Casimir parameter are drawn for SSA and LSA models. Figure 4 shows the non-dimensional gap as a function of Casimir force parameter γ for some values of geometry parameter k. Any increase in the Casimir parameter can decrease the initial gap between the flexible nanowire and bottom plate. According to the illustrated results, it is inferred that any increase in the Casimir parameter leads to increase in the dynamic deflection of nano-beam. In addition, when the Casimir parameter approaches to the critical value γ cr, the nano-beam loses its stability and adheres to the fixed substrate. On the other hand, one can clearly observe that for both SSA and LSA approximations, the significant effect of geometry parameter k is to increase γ cr. In addition, it is shown that the effect of parameter k in the case of small separations is more significant than large separations. Finally, one can see that for small separation gaps the nanowire may collapse into contact with the bottom plate at lower values of Casimir parameter in comparison with large separation gaps. It should be noted that if the nanowire length is greater than the critical length (i.e. detachment length) any disturbance in the fabrication process can result in the instability of the structure even in the absence of any actuation voltages.

Fig. 4
figure 4

Non-dimensional gap versus the Casimir parameter: investigating the effect of geometry parameter k for a SSA b LSA approaches

Full size image

Figure 5a, b shows the non-dimensional gap (1 − W) versus the Casmir parameter γ for different values of the nonlocal parameter ɛ 0 considering the SSA and LSA models, respectively. It is observed that by increasing the nonlocal parameter, the mid-point of the nano-bridge diverges to the bottom substrate at lower values of Casimir parameter ɛ 0 which means that the dynamic instability of nano-structure happens at lower values of nanowire length as the size-effect parameter ɛ 0 increases.

Fig. 5
figure 5

Non-dimensional gap versus the Casimir parameter: investigating the effect of nonlocal parameter ɛ 0 for a SSA b LSA approaches

Full size image

The influence of the non-dimensional parameter μ, i.e. the effect of the surface elasticity in the dynamic instability of nonlocal nanowires, is shown in Fig. 6a, b. It is seen that the predicted critical values for Casimir parameter increases as the parameter μ increases, for both SSA and LSA models.

Fig. 6
figure 6

Non-dimensional gap versus the Casimir parameter: investigating the effect of surface effect parameter μ for a SSA b LSA approaches

Full size image

The time responses of vibrating nanowires for various values of geometry parameter k at the corresponding adhesion time are illustrated in Fig. 7. According to this figure, for both SSA and LSA approaches, the adhesion time of the nano-beam is increased by increasing the geometry parameter and the dynamic instability occurs at higher values of Casimir force parameter γ.

Fig. 7
figure 7

Time responses of nanowires at corresponding instability state: investigating the effect of geometry parameter k for a SSA b LSA approaches

Full size image

Figures 8 and 9 illustrate the time histories and phase portraits of Casimir-induced nanowires at the corresponding adhesion times for some given values of non-dimensional surface parameter μ. According to the obtained results, it is clearly inferred that for both small and large separation gaps, by increasing the parameter μ, the adhesion time decreases. Moreover, by increasing the parameter μ, the dynamic instability occurs at higher values of Casimir force. In addition, one can see that as the surface effect parameter μ increases, the corresponding deflection slightly decreases and instability happens at lower values of nano-beam deflection.

Fig. 8
figure 8

a Time history and b phase diagram of vibrating Casimir-induced nanowire for different values of μ at corresponding adhesion time for SSA model

Full size image
Fig. 9
figure 9

a Time history and b phase diagram of vibrating Casimir-induced nanowire for different values of μ at corresponding adhesion time for LSA model

Full size image

The effect of the nonlocal parameter ɛ 0 which accounts for the size dependency of nanowire on the critical values of Casimir force is illustrated in Fig. 10a, b. The obtained results elucidate that γ cr decreases by increasing the nonlocal parameter. Furthermore, it is concluded from this figure that the positive μ, which stands for the surface elasticity, can increase the critical Casimir value of nanowires while the negative one will decrease it.

Fig. 10
figure 10

The relation between γ cr and nonlocal parameter ɛ 0: investigating the effect of surface parameter μ for a SSA and b LSA models

Full size image

The plot of time responses and phase portraits of the Casimir-induced nanowires may be of interest. To this end, the influence of Casimir force on the instability characteristics of nanowires is investigated through Figs. 11 and 12 for the case of SSA and LSA models, respectively. According to illustrated results in Figs. 11a and 12a, one can observe that the nano-beam deflection and time period of vibrating nanowires under the influence of Casimir force is increased by increasing parameter γ up to the adhesion time. On the other hand, in the vicinity of adhesion state, any increase in the Casimir parameter changes the dynamic behavior of the system and causes the nanowire to drop to the fixed plate.

Fig. 11
figure 11

Effect of Casimir parameter on the instability characteristics of nanowires for SSA model, a time history b phase portrait

Full size image
Fig. 12
figure 12

Effect of Casimir parameter on the instability characteristics of nanowires for LSA model, a time history b phase portrait

Full size image

It is observed from Figs. 11b and 12b that at lower values of Casimir parameter, the system exhibits the periodic motions around the stable center point. When the dynamic instability occurs at critical Casimir value (γ cr = 67.0171 for SSA and γ cr = 137.0981 for LSA models), a homoclinic orbit appears in the phase plane which separates periodic solutions from the unbounded non-periodic trajectories around an unstable saddle node. The homoclinic orbit starts from the unstable branch of saddle node and returns to it via the stable one. In addition, one can conclude that the Casimir-induced nanowire collapses to the bottom plate beyond the unstable saddle node.

5 Conclusions

In this research work, the significant effects of Casimir force, nonlocal and surface effects on instability/adhesion properties of suspended nanowires were investigated. For this purpose, considering both small and large separation regimes, the non-linear governing equation of vibrating nanowires was extracted and solved using a step-by-step numerical approach. Based on the results, the effect of geometry parameter k was to increase the critical Casimir value of nanowires for both SSA and LSA models. It was also observed that the critical Casimir value decreases as the nonlocal parameter increases. In addition, the effect of surface elasticity parameter was to increase the critical Casimir value and to decrease the adhesion time. Finally, it was found that at lower values of Casimir force, the nanowire showed periodic motions around the stable center point. By increasing the Casimir force, the nano-system experiences unbounded non-periodic motions in the vicinity of unstable saddle node.