Two-Dimensional Stationary Thermocapillary Flow of Two Liquids in a Plane Channel

Abstract

The problem of two-dimensional stationary flow of two immiscible liquids in a plane channel with rigid walls is studied. On the one of walls a temperature distribution is imposed and the another wall is heat-insulated. On the common interface the interfacial energy change is taken into account. The temperature in the liquids is distributed according to a quadratic law. It agrees with velocities field of the Hiemenz type. The conjugate boundary value problem is nonlinear and inverse for pressure gradients along the channel. The tau-method is used for the solution of problem. Three different solutions are obtained in results. It is established numerically that the obtained solutions converge to the solutions of the slowly flow problem with a decrease the Marangoni number. For each of the solutions the characteristic flow structures are constructed.

1 INTRODUCTION

In case of the non-stationary motion of liquid media with the interface $\Gamma$ in an inhomogeneous temperature field, the difference of the heat flux is not equal to zero [1, 2]

$${{k}_{2}}\frac{{\partial {{\theta }_{2}}}}{{\partial n}} - {{k}_{1}}\frac{{\partial {{\theta }_{1}}}}{{\partial n}} = \text{æ} \theta {{\operatorname{div} }_{\Gamma }}{\mathbf{u}} + \omega ({{\theta }_{t}} + {\mathbf{u}} \cdot {{\nabla }_{\Gamma }}\theta ),$$

(1.1)

where $\text{æ} = - \partial \sigma {\text{/}}\partial \theta$, $\omega = \partial (\sigma (\theta ) + \text{æ} (\theta )){\text{/}}\partial \theta$, $\sigma (\theta )$ is the surface tension coefficient. In equality (1.1) ${{k}_{j}}$ are coefficients of thermal conductivity and ${{\theta }_{j}}$ are temperature of liquids, $j = 1,2$; $\theta = {{\theta }_{1}} = {{\theta }_{2}}$, ${\mathbf{u}} = {{{\mathbf{u}}}_{1}} = {{{\mathbf{u}}}_{2}}$ are the general values of temperatures and velocity vectors at the interface $\Gamma$, n is the normal to $\Gamma$ directed to the second liquid. Condition (1.1) can be called the energy condition at the interface $\Gamma$ of two liquids [3]. It means that the heat flux jump in the direction of the normal to $\Gamma$ is compensated by a change in the internal energy of this surface. In turn, this change is associated with both a change in temperature and the area of the interface.

For many liquid media, $\sigma (\theta )$ is well approximated by the linear function

$$\sigma (\theta ) = {{\sigma }_{0}} - \text{æ} (\theta - {{\theta }_{0}}),$$

(1.2)

with positive constants ${{\sigma }_{0}}$, $\text{æ}$, ${{\theta }_{0}}$. Then energy equality (1.1) is simplified and has the form

$${{k}_{2}}\frac{{\partial {{\theta }_{2}}}}{{\partial n}} - {{k}_{1}}\frac{{\partial {{\theta }_{1}}}}{{\partial n}} = \text{æ} \theta {{\operatorname{div} }_{\Gamma }}{\mathbf{u}}.$$

(1.3)

The relation order of equation right-hand side (1.3) to the first term of its left-hand side is estimated by the parameter ${\text{E}} = \text{æ} \theta {\text{*/}}{{\mu }_{2}}{{k}_{2}}$ (for the second term it is necessary to assume ${{\mu }_{1}}{{k}_{1}}$, ${{\mu }_{j}}$ are dynamic viscosities). It determines the influence of interphase energy on the dynamics of liquids motion inside the layers; $\theta {\text{*}}$ is the characteristic temperature on the interface. These parameters are small for ordinary liquids at room temperature [2, 4, 5]. For example, we have ${\text{E}} \sim 5 \times {{10}^{{ - 4}}}$ for the air – ethyl alcohol system at $\theta {\text{*}} = 15^\circ {\text{C}}$. Therefore, the right-hand side in (1.1) is often omitted and we have the equalities of the heat flux across the interface. However, for low-viscosity liquids, these terms must be taken into account. In paper [5], motion of bubbles in various liquids is considered. It is established, that the value ${\text{E}} = O(1)$ is achieved at sufficiently high temperatures. It means that the viscosity decreases rapidly with increasing temperature. This fact is also true for some cryogenic liquids, for example, liquid ${\text{C}}{{{\text{O}}}_{2}}$. The maximum values of ${\text{E}}$ are reached near the critical points. So, for water we have ${\text{E}} \sim 0.02$ at $\theta = 303.15$ К; ${\text{E}} \sim 0.6$ at $\theta = 573.15$ К; ${\text{E}} \sim 0.7$ at $\theta = 623.15$ К (critical point for water is ${{\theta }_{{{\text{cr}}}}} = 647.30$ К).

In book [2], simple examples of two-layer systems are considered, when the main state is rest or unidirectional steady flow. It is established, that the heat absorbed or released during local hanges in the interface area influence on the formation of Marangoni stresses and weakly linear wave regimes at the interface of liquids with small viscosity. In [6], the condition (1.3) was used for perturbations and the effect of a change in the interfacial surface energy on the nature and type of instabilities of the basic unidirectional flow is studied. It is shown, when the right-hand side vanishes in (1.3), the significant difference in the perturbations behavior is observed in the region of short waves. Namely, in a problem with a full condition, a flow crisis is caused by a thermal oscillatory mode and is accompanied by the formation of transverse traveling waves that propagate in the direction opposite to the basic flow. In the problem with the classical condition the instability manifests itself in the form of transverse standing waves. Taking into account additional term in the energy condition the result is obtained that agrees qualitatively with the experimental data for the FC-72 – nitrogen system.

In the problems mentioned above, the basic stationary two-layer flow was independent of the interfacial energy change. In the present paper, we research such dependence for two-dimensional two-layer stationary flow with the velocities field of the Hiemenz type.

2 THE PROBLEM STATEMENT

We consider a plane two-layer stationary flow of viscous heat-conducting liquids in layers bounded by rigid walls $y = 0$, $y = h$ with a common interface $y = l < h$. The gravitational effects are ignored.

Suppose the interface is a flat. For this it is enough that the capillary number ${\text{Ca}} = {{\mu }_{1}}{{\chi }_{1}}{\text{/}}{{\sigma }_{0}}l \ll 1$ [7], $\chi$ is the coefficient of thermal diffusivity. The velocity and temperature field of the system of a viscous heat-conducting fluid equations in the layers are sought in the form

$$u_{j}^{1}(x,y) = {{w}_{j}}(y)x,u_{j}^{2}(x,y) = {{v}_{j}}(y),\quad {{\theta }_{j}}(x,y) = {{a}_{j}}(y){{x}^{2}} + {{b}_{j}}(y),$$

(2.1)

where $0 < y < l$ at $j = 1$, $l < y < h$ at $j = 2$ and ${{\operatorname{div} }_{\Gamma }}{\mathbf{u}} = {{w}_{1}}(l)$. Such representation of the velocity field corresponds to the well-known Hiemenz solution [8]. The substitution of expression (2.1) into the equations of motion and heat transfer and their compatibility analysis leads to the fact that the functions ${{w}_{j}}(y)$, ${{v}_{j}}(y)$, ${{a}_{j}}(y)$ and ${{b}_{j}}(y)$ are solutions of the system

$$\begin{gathered} {{v}_{j}}{{w}_{{jy}}} + w_{j}^{2} = {{\nu }_{j}}{{w}_{{jyy}}} + {{f}_{j}},\quad {{w}_{j}} + {{v}_{{jy}}} = 0, \\ 2{{w}_{j}}{{a}_{j}} + {{v}_{j}}{{a}_{{jy}}} = {{\chi }_{j}}{{a}_{{jyy}}},\quad {{v}_{j}}{{b}_{{jy}}} = {{\chi }_{j}}{{b}_{{jyy}}} + 2{{\chi }_{j}}{{a}_{j}}, \\ \end{gathered} $$

(2.2)

where ${{\nu }_{j}}$ are the kinematic viscosities, ${{\rho }_{j}} = {{\mu }_{j}}{\text{/}}{{\nu }_{j}}$ are the densities, ${{f}_{j}}$ are the constants. The pressures in liquids are distributed according to the laws

$$\frac{1}{{{{\rho }_{j}}}}{{p}_{j}}(x,y) = {{\nu }_{j}}{{v}_{{jy}}} - \frac{{v_{j}^{2}}}{2} - {{f}_{j}}\frac{{{{x}^{2}}}}{2} + {{d}_{{0j}}},\quad {{d}_{{0j}}} = {\text{const}},$$

(2.3)

so the values of ${{f}_{j}}$ characterize pressure gradients along the $x$ axis.

Suppose the temperature distribution ${{\theta }_{1}}(x,0) = {{a}_{{10}}}{{x}^{2}} + {{b}_{{10}}}$ with constants ${{a}_{{10}}}$, ${{b}_{{10}}}$ is set on the rigid wall $y = 0$. At ${{a}_{{10}}} > 0$, the temperature has a minimum value at the point $x = 0$, and at ${{a}_{{10}}} < 0$ the temperature is maximal. The upper wall is thermally insulated, i.e., ${{\theta }_{{2y}}}(x,h) = 0$. Thus, on the rigid walls, the conditions for the unknowns have form

$$\begin{gathered} {{w}_{1}}(0) = {{v}_{1}}(0) = 0,\quad {{a}_{1}}(0) = {{a}_{{10}}},\quad {{b}_{1}}(0) = {{b}_{{10}}}, \\ {{w}_{2}}(h) = {{v}_{2}}(h) = 0,\quad {{a}_{{2y}}}(h) = {{b}_{{2y}}}(h) = 0. \\ \end{gathered} $$

(2.4)

The relations are satisfied on the interface $y = l$

$$\begin{gathered} {{w}_{1}}(l) = {{w}_{2}}(l),\quad {{v}_{1}}(l) = {{v}_{2}}(l) = 0,\quad {{a}_{1}}(l) = {{a}_{2}}(l),\quad {{b}_{1}}(l) = {{b}_{2}}(l), \\ {{\mu }_{2}}{{w}_{{2y}}}(l) - {{\mu }_{1}}{{w}_{{1y}}}(l) = - 2\text{æ} {{a}_{1}}(l),\quad {{k}_{2}}{{a}_{{2y}}}(l) - {{k}_{1}}{{a}_{{1y}}}(l) = \text{æ} {{a}_{1}}(l){{w}_{1}}(l), \\ {{k}_{2}}{{b}_{{2y}}}(l) - {{k}_{1}}{{b}_{{1y}}}(l) = \text{æ} {{b}_{1}}(l){{w}_{1}}(l). \\ \end{gathered} $$

(2.5)

The first four conditions in (2.5) are consequences of the velocity and temperature fields continuity on the interface and the fifth condition is the dynamic condition. The last two conditions are obtained taking into account the dependence of the surface tension coefficient (1.2) and the relation (1.3).

Remark 1. This problem is inverse, because, along with the functions ${{w}_{j}}$, ${{v}_{j}}$, ${{a}_{j}}$, ${{b}_{j}}$, the constants ${{f}_{j}}$ (the pressure gradients along the layers) are also unknown. Using known functions ${{v}_{j}}$ and ${{f}_{j}}$ pressures gradients are determined by the formulas (2.3).

The vertical velocities ${{v}_{j}}(y)$ are excluded from the continuity equations taking into account the no-slip conditions on the walls (2.4)

$${{v}_{1}}(y) = - \int\limits_0^y \,{{w}_{1}}(z)dz,\quad 0 \leqslant y \leqslant l;\quad {{v}_{2}}(y) = - \int\limits_h^y \,{{w}_{2}}(z)dz,\quad l \leqslant y \leqslant h.$$

(2.6)

Then we obtain inverse conjugate boundary value problem

$${{\nu }_{1}}{{w}_{{1yy}}} = w_{1}^{2} - {{f}_{1}} - {{w}_{{1y}}}\int\limits_0^y \,{{w}_{1}}(z)dz,\quad {{\chi }_{1}}{{a}_{{1yy}}} = 2{{a}_{1}}{{w}_{1}} - {{a}_{{1y}}}\int\limits_0^y \,{{w}_{1}}(z)dz,$$

$$\begin{gathered} {{\chi }_{1}}{{b}_{{1yy}}} = - 2{{\chi }_{1}}{{a}_{1}} - {{b}_{{1y}}}\int\limits_0^y \,{{w}_{1}}(z)dz,\quad 0 < y < l, \\ {{\nu }_{2}}{{w}_{{2yy}}} = w_{2}^{2} - {{f}_{2}} - {{w}_{{2y}}}\int\limits_h^y \,{{w}_{2}}(z)dz,\quad {{\chi }_{2}}{{a}_{{2yy}}} = 2{{a}_{2}}{{w}_{2}} - {{a}_{{2y}}}\int\limits_h^y \,{{w}_{2}}(z)dz, \\ \end{gathered} $$

(2.7)

$${{\chi }_{2}}{{b}_{{2yy}}} = - 2{{\chi }_{2}}{{a}_{2}} - {{b}_{{2y}}}\int\limits_h^y \,{{w}_{2}}(z)dz,\quad l < y < h.$$

The boundary conditions follow from expressions (2.4), (2.5) and (2.6)

$$\begin{gathered} {{w}_{1}}(0) = 0,\quad {{w}_{2}}(h) = 0,\quad {{a}_{1}}(0) = {{a}_{{10}}},\quad {{a}_{{2y}}}(h) = 0,\quad {{b}_{1}}(0) = {{b}_{{10}}},\quad {{b}_{{2y}}}(h) = 0, \\ \int\limits_0^l \,{{w}_{1}}(z)dz = 0,\quad \int\limits_l^h \,{{w}_{2}}(z)dz = 0,\quad {{\mu }_{2}}{{w}_{{2y}}}(l) - {{\mu }_{1}}{{w}_{{1y}}}(l) = - 2\text{æ} {{a}_{1}}(l),\quad {{w}_{1}}(l) = {{w}_{2}}(l), \\ {{a}_{1}}(l) = {{a}_{2}}(l),\quad {{k}_{2}}{{a}_{{2y}}}(l) - {{k}_{1}}{{a}_{{1y}}}(l) = \text{æ} {{a}_{1}}(l){{w}_{1}}(l),\quad {{b}_{1}}(l) = {{b}_{2}}(l),\quad {{k}_{2}}{{b}_{{2y}}}(l) - {{k}_{1}}{{b}_{{1y}}}(l) = \text{æ} {{b}_{1}}(l){{w}_{1}}(l). \\ \end{gathered} $$

(2.8)

The problem for the functions ${{b}_{j}}(y)$ is separated. The function ${{b}_{j}}(y)$ are found after the solution of the problem for functions ${{w}_{j}}(y),\;{{a}_{j}}(y)$ and it does not affect the velocity field in layers.

The following dimensionless variables and parameters are introduced

$$\begin{gathered} {{W}_{j}}(\xi ) = \frac{{{{l}^{2}}}}{{{\text{M}}{{\chi }_{1}}}}{{w}_{j}}(y),\quad {{A}_{j}}(\xi ) = \frac{{{{a}_{j}}(y)}}{{{{a}_{{10}}}}},\quad {{B}_{j}}(\xi ) = \frac{{{{b}_{j}}(y)}}{{{{a}_{{10}}}{{l}^{2}}}},\quad {{F}_{j}} = \frac{{{{l}^{4}}}}{{{\text{M}}\chi _{1}^{2}}}{{f}_{j}}, \\ \xi = \frac{y}{h},\quad {{{\text{P}}}_{j}} = \frac{{{{\nu }_{j}}}}{{{{\chi }_{j}}}},\quad {\text{M}} = \frac{{\text{æ} {{a}_{{10}}}{{l}^{3}}}}{{{{\chi }_{1}}{{\mu }_{2}}}},\quad {\text{E}} = \frac{{{{\text{æ} }^{2}}{{a}_{{10}}}{{l}^{2}}}}{{{{\mu }_{2}}{{k}_{2}}}}, \\ \end{gathered} $$

(2.9)

where ${{{\text{P}}}_{j}}$ are the Prandtl numbers, ${\text{M}}$ is the Marangoni number, $\theta {\text{*}} = {\text{|}}{{a}_{{10}}}{\text{|}}{{l}^{2}}$ is the characteristic temperature along interface; the parameters ${\text{M}}$, ${\text{E}}$ can be either positive or negative. Then, the nonlinear conjugate boundary problem in non-dimensional variables takes the form

$${{\gamma }^{2}}{{{\text{P}}}_{1}}{{W}_{{1\xi \xi }}} = {\text{M}}\left[ {W_{1}^{2} - {{W}_{{1\xi }}}\int\limits_0^\xi \,{{W}_{1}}(z)dz} \right] - {{F}_{1}},\quad {{A}_{{1\xi \xi }}} = \frac{{\text{M}}}{{{{\gamma }^{2}}}}\left[ {2{{A}_{1}}{{W}_{1}} - {{A}_{{1\xi }}}\int\limits_0^\xi \,{{W}_{1}}(z)dz} \right],$$

$$\begin{gathered} {{\gamma }^{2}}{{B}_{{1\xi \xi }}} = - 2{{A}_{1}} - {\text{M}}{{B}_{{1\xi }}}\int\limits_0^\xi \,{{W}_{1}}(z)dz,\quad 0 < \xi < \gamma , \\ \frac{{{{\gamma }^{2}}{{{\text{P}}}_{2}}}}{\chi }{{W}_{{2\xi \xi }}} = {\text{M}}\left[ {W_{2}^{2} - {{W}_{{2\xi }}}\int\limits_1^\xi \,{{W}_{2}}(z)dz} \right] - {{F}_{2}},\quad {{A}_{{2\xi \xi }}} = \frac{{\chi {\text{M}}}}{{{{\gamma }^{2}}}}\left[ {2{{A}_{2}}{{W}_{2}} - {{A}_{{2\xi }}}\int\limits_1^\xi \,{{W}_{2}}(z)dz} \right], \\ \end{gathered} $$

(2.10)

$${{\gamma }^{2}}{{B}_{{2\xi \xi }}} = - 2{{A}_{2}} - \chi {\text{M}}{{B}_{{2\xi }}}\int\limits_1^\xi \,{{W}_{2}}(z)dz,\quad \gamma < \xi < 1,$$

$$\begin{gathered} {{W}_{1}}(0) = 0,\quad {{W}_{2}}(1) = 0,\quad {{A}_{1}}(0) = 1,\quad {{A}_{{2\xi }}}(1) = 0,\quad {{B}_{1}}(0) = {{B}_{{10}}},\quad {{B}_{{2\xi }}}(1) = 0, \\ {{W}_{1}}(\gamma ) = {{W}_{2}}(\gamma ),\quad {{W}_{{2\xi }}}(\gamma ) - \mu {{W}_{{1\xi }}}(\gamma ) = - 2{{\gamma }^{{ - 1}}}{{A}_{1}}(\gamma ),\quad {{A}_{1}}(\gamma ) = {{A}_{2}}(\gamma ), \\ {{A}_{{2\xi }}}(\gamma ) - k{{A}_{{1\xi }}}(\gamma ) = {{\gamma }^{{ - 1}}}{\text{E}}{{A}_{1}}(\gamma ){{W}_{1}}(\gamma ),\quad {{B}_{1}}(\gamma ) = {{B}_{2}}(\gamma ),\quad {{B}_{{2\xi }}}(\gamma ) - k{{B}_{{1\xi }}}(\gamma ) = {{\gamma }^{{ - 1}}}{\text{E}}{{B}_{1}}(\gamma ){{W}_{1}}(\gamma ), \\ \end{gathered} $$

(2.11)

where $\gamma = l{\text{/}}h < 1$, $\mu = {{\mu }_{1}}{\text{/}}{{\mu }_{2}}$, $\chi = {{\chi }_{1}}{\text{/}}{{\chi }_{2}}$, $k = {{k}_{1}}{\text{/}}{{k}_{2}}$. To the boundary conditions (2.11) it is necessary to add the integral redefinition conditions

$$\int\limits_0^\gamma \,{{W}_{1}}(z)dz = 0,\quad \int\limits_\gamma ^1 \,{{W}_{2}}(z)dz = 0,$$

(2.12)

that allow you to find unknown constants (pressure gradients along the layers) ${{F}_{j}}$, $j = 1,2$.

3 SOLUTION OF THE MODEL PROBLEM—CREEPING FLOWS

It is known that for small Reynolds numbers, the momentum and energy equations are simplified by discarding convective acceleration. Such movements are called creeping. Creeping flows occur in many structural elements of machines, mechanisms, equipment and devices, if the transverse dimensions of the channels or flow rates are small or the viscosity of the flowing liquid is high. In our case, the role of the Reynolds number is played by the Marangoni number, which can be small both due to the physical parameters of the liquid and the thickness of the channel [9, 10].

Suppose that $\left| {\text{M}} \right| \ll 1$ and we seek the solution of problem (2.10)–(2.12) in the form ${{W}_{j}} = W_{j}^{0} + {\text{M}}W_{j}^{1} + ...$, ${{F}_{j}} = F_{j}^{0} + {\text{M}}F_{j}^{1} + ...$, ${{A}_{j}} = A_{j}^{0} + {\text{M}}A_{j}^{1} + ...$, then, for the zeroth approximation, the solution has the form [11]

$$\begin{gathered} W_{1}^{0}(\xi ) = - \frac{{F_{1}^{0}}}{{6{{\gamma }^{2}}{{{\text{P}}}_{1}}}}(3{{\xi }^{2}} - 2\gamma \xi ),\quad A_{1}^{0}(\xi ) = 1 + {{C}_{1}}\xi , \\ B_{1}^{0}(\xi ) = - \frac{1}{{{{\gamma }^{2}}}}({{\xi }^{2}} + {{C}_{1}}{{\xi }^{3}}) + {{d}_{1}}\xi + {{B}_{{10}}},\quad 0 \leqslant \xi \leqslant \gamma , \\ \end{gathered} $$

(3.1)

$$\begin{gathered} W_{2}^{0}(\xi ) = - \frac{{\chi F_{2}^{0}}}{{6{{\gamma }^{2}}{{{\text{P}}}_{2}}}}(3{{\xi }^{2}} + 2\delta (\xi - 1) - 3),\quad A_{2}^{0}(\xi ) = 1 + \gamma {{C}_{1}} \equiv {{C}_{2}}, \\ B_{2}^{0}(\xi ) = - \frac{{{{C}_{2}}}}{{{{\gamma }^{2}}}}({{\xi }^{2}} - 2\xi ) + {{d}_{2}},\quad \gamma \leqslant \xi \leqslant 1, \\ \end{gathered} $$

(3.2)

and

$$\begin{gathered} F_{1}^{0} = - 6{{{\text{P}}}_{1}}{{C}_{2}}{{\delta }_{1}},\quad F_{2}^{0} = \frac{{{{\gamma }^{2}}F_{1}^{0}}}{{\nu {{{(1 - \gamma )}}^{2}}}}, \\ \delta = \frac{{{{\gamma }^{2}} + \gamma - 2}}{{1 - \gamma }},\quad {{\delta }_{1}} = \frac{{1 - \gamma }}{{2(\gamma + \mu (1 - \gamma ))}},\quad {{d}_{2}} = - \frac{{2{{C}_{2}}}}{\gamma } + {{d}_{1}}\gamma + {{B}_{{10}}}, \\ {{d}_{1}} = \frac{{{\text{E}}{{\delta }_{1}}C_{2}^{2} - {{C}_{2}}({\text{E}}{{B}_{{10}}}{{\delta }_{1}} + 2(\gamma - 1)) + k(2 + 3{{C}_{1}}\gamma )}}{{\gamma ({\text{E}}{{C}_{2}}{{\delta }_{1}} + k)}} \\ \end{gathered} $$

(3.3)

at the same time ${{C}_{2}}$ is the solution of the quadratic equation

$${\text{E}}{{\delta }_{1}}C_{2}^{2} + k({{C}_{2}} - 1) = 0,$$

(3.4)

with discriminant

$$D = 1 + \frac{{2{{\gamma }^{2}}(1 - \gamma ){\text{E}}}}{{k[\gamma + \mu (1 - \gamma )]}}.$$

Therefore, when

$${\text{E}} > - \frac{{k[\gamma + \mu (1 - \gamma )]}}{{2{{\gamma }^{2}}(1 - \gamma )}} = {\text{E*}}{\text{,}}$$

there are two solutions (it’s always true for ${{a}_{{10}}} > 0$). At ${\text{E}} = {\text{E*}}$ there is one solution and at ${\text{E}} < {\text{E*}}$ solutions does not exist. The last two cases are realized only for ${{a}_{{10}}} < 0$, when the temperature on the bottom wall has a maximum at the point $x = 0$. Expressions for dimensionless vertical velocities are determined by the formula (2.6) and it has the form

$$\begin{gathered} V_{1}^{0}(\xi ) = \frac{{F_{2}^{0}}}{{6{{\gamma }^{2}}{{{\text{P}}}_{1}}}}({{\xi }^{3}} - \gamma {{\xi }^{2}}),\quad 0 \leqslant \xi \leqslant \gamma , \\ V_{2}^{0}(\xi ) = \frac{{\chi F_{2}^{0}}}{{6{{\gamma }^{2}}{{{\text{P}}}_{2}}}}({{\xi }^{3}} + \delta ({{\xi }^{2}} - 1) - (2\delta + 3)(\xi - 1) - 1),\quad \gamma \leqslant \xi \leqslant 1. \\ \end{gathered} $$

(3.5)

Remark 2. Simple calculations show that for ${\text{E}} = 0$ we obtain the unique solution of the problem (1.10)–(1.16) for small Marangoni numbers

$$W_{1}^{0}(\xi ) = \frac{{{{\delta }_{1}}}}{{6{{\gamma }^{2}}}}(3{{\xi }^{2}} - 2\gamma \xi ),\quad A_{1}^{0}(\xi ) = 1,\quad F_{1}^{0} = - 6{{{\text{P}}}_{1}}{{\delta }_{1}},$$

$$\begin{gathered} B_{1}^{0}(\xi ) = - \frac{1}{{{{\gamma }^{2}}}}{{\xi }^{2}} + \frac{{2(k + \gamma - 1)}}{{\gamma k}}\xi + {{B}_{{10}}},\quad 0 \leqslant \xi \leqslant \gamma , \\ W_{2}^{0}(\xi ) = \frac{{{{\delta }_{1}}}}{{{{{(1 - \gamma )}}^{2}}}}(3{{\xi }^{2}} + 2\delta (\xi - 1) - 3),\quad A_{2}^{0}(\xi ) = 1,\quad F_{2}^{0} = \frac{{{{\gamma }^{2}}F_{1}^{0}}}{{\nu {{{(1 - \gamma )}}^{2}}}}, \\ \end{gathered} $$

(3.6)

$$B_{2}^{0}(\xi ) = - \frac{1}{{{{\gamma }^{2}}}}({{\xi }^{2}} - 2\xi ) + \frac{{2(\gamma - 1)(k + \gamma )}}{{k\gamma }} + {{B}_{{10}}},\quad \gamma \leqslant \xi \leqslant 1.$$

The obtained solution differs significantly from solution (3.1)–(3.4).

4 NUMERICAL SOLUTION METHOD AND CALCULATION RESULTS

To solve the problem (2.10)–(2.12) the tau-method is used. This method is a modification of the Galerkin method [12]. We make the change of variables: $\xi ' = \xi {\text{/}}\gamma$ for $j = 1$ and $\xi ' = (1 - \xi ){\text{/}}(1 - \gamma )$ for $j = 2$. Then problem (2.10)–(2.12) can be rewritten in the form (the primes are omitted)

$${{L}_{1}}({{W}_{1}},{{F}_{1}}) \equiv {{{\text{P}}}_{1}}{{W}_{{1\xi \xi }}} - {\text{M}}\left[ {W_{1}^{2} - {{W}_{{1\xi }}}\int\limits_0^\xi \,{{W}_{1}}(z)dz} \right] + {{F}_{1}} = 0,$$

$${{N}_{1}}({{W}_{1}},{{A}_{1}}) \equiv {{A}_{{1\xi \xi }}} - {\text{M}}\left[ {2{{A}_{1}}{{W}_{1}} - {{A}_{{1\xi }}}\int\limits_0^\xi \,{{W}_{1}}(z)dz} \right] = 0,$$

(4.1)

$${{K}_{1}}({{W}_{1}},{{A}_{1}},{{B}_{1}}) \equiv {{B}_{{1\xi \xi }}} + 2{{A}_{1}} + {\text{M}}{{B}_{{1\xi }}}\int\limits_0^\xi \,{{W}_{1}}(z)dz = 0,\quad 0 < \xi < 1,$$

$${{L}_{2}}({{W}_{2}},{{F}_{2}}) \equiv \frac{{{{\gamma }^{2}}{{{\text{P}}}_{2}}}}{{\chi {{{(1 - \gamma )}}^{2}}}}{{W}_{{2\xi \xi }}} - {\text{M}}\left[ {W_{2}^{2} - {{W}_{{2\xi }}}\int\limits_0^\xi \,{{W}_{2}}(z)dz} \right] + {{F}_{2}} = 0,$$

$${{N}_{2}}({{W}_{2}},{{A}_{2}}) \equiv \frac{{{{\gamma }^{2}}}}{{\chi {{{(1 - \gamma )}}^{2}}}}{{A}_{{2\xi \xi }}} - {\text{M}}\left[ {2{{A}_{2}}{{W}_{2}} - {{A}_{{2\xi }}}\int\limits_0^\xi \,{{W}_{2}}(z)dz} \right] = 0,$$

(4.2)

$${{K}_{2}}({{W}_{2}},{{A}_{2}},{{B}_{2}}) \equiv \frac{{{{\gamma }^{2}}}}{{\chi {{{(1 - \gamma )}}^{2}}}}{{B}_{{2\xi \xi }}} + 2{{A}_{2}} + {\text{M}}\chi {{B}_{{2\xi }}}\int\limits_0^\xi \,{{W}_{2}}(z)dz = 0,\quad 0 < \xi < 1,$$

$$\begin{gathered} {{W}_{1}}(0) = 0,\quad {{W}_{2}}(0) = 0,\quad {{A}_{1}}(0) = 1,\quad {{A}_{{2\xi }}}(0) = 0,\quad {{B}_{1}}(0) = {{B}_{{10}}},\quad {{B}_{{2\xi }}}(0) = 0, \\ {{W}_{1}}(1) = {{W}_{2}}(1),\quad \frac{\gamma }{{1 - \gamma }}{{W}_{{2\xi }}}(1) + \mu {{W}_{{1\xi }}}(1) = 2{{A}_{1}}(1), \\ {{A}_{1}}(1) = {{A}_{2}}(1),\quad \frac{\gamma }{{1 - \gamma }}{{A}_{{2\xi }}}(1) + k{{A}_{{1\xi }}}(1) = - {\text{E}}{{A}_{1}}(1){{W}_{1}}(1), \\ {{B}_{1}}(1) = {{B}_{2}}(1),\quad \frac{\gamma }{{1 - \gamma }}{{B}_{{2\xi }}}(1) + k{{B}_{{1\xi }}}(1) = - {\text{E}}{{B}_{1}}(1){{W}_{1}}(1), \\ \end{gathered} $$

(4.3)

$$\int\limits_0^1 \,{{W}_{1}}(z)dz = 0,\quad \int\limits_0^1 \,{{W}_{2}}(z)dz = 0.$$

(4.4)

An approximate solution of problem (4.1)–(4.4) is sought in the form of sums

$${{W}_{{jn}}}(\xi ) = \sum\limits_{k = 1}^n \,W_{j}^{k}{{R}_{k}}(\xi ),\quad {{A}_{{jn}}}(\xi ) = \sum\limits_{k = 0}^n \,A_{j}^{k}{{R}_{k}}(\xi ),\quad {{B}_{{jn}}}(\xi ) = \sum\limits_{k = 0}^n \,B_{j}^{k}{{R}_{k}}(\xi ),$$

(4.5)

where ${{R}_{k}}(z) = {{P}_{k}}(2z - 1)$ are shifted Legendre polynomials [13], $z \in [0,1]$, ${{P}_{k}}(z)$ are usual Legendre polynomials. The orthogonality of the Legendre polynomials ${{R}_{k}}(z)$ is taken into account on the interval $[0,1]$

$$\int\limits_0^1 \,{{R}_{k}}(z){{R}_{m}}(z)dz = {{\delta }_{{km}}}{{h}_{m}},\quad {{h}_{m}} = \frac{1}{{2m + 1}},\quad {{\delta }_{{km}}} = \left\{ \begin{gathered} 1,\quad k = m, \hfill \\ 0,\quad k \ne m. \hfill \\ \end{gathered} \right.$$

Then, from the integral conditions (4.4), we obtain that $W_{1}^{0} = W_{2}^{0} = 0$. The other coefficients $W_{j}^{k},\;A_{j}^{k},\;B_{j}^{k}$ and constants ${{F}_{{1n}}},\;{{F}_{{2n}}}$ are found from the system of Galerkin approximations

$$\begin{gathered} \int\limits_0^1 \,{{L}_{j}}({{W}_{{jn}}},{{F}_{j}}){{R}_{m}}(\xi )d\xi = 0,\quad \int\limits_0^1 \,{{N}_{j}}({{W}_{{jn}}},{{A}_{{jn}}}){{R}_{m}}(\xi )d\xi = 0, \\ \int\limits_0^1 \,{{K}_{j}}({{W}_{{jn}}},{{A}_{{jn}}}){{R}_{m}}(\xi )d\xi = 0,\quad m = 0,...,n - 2,\quad j = 1,2, \\ \end{gathered} $$

(4.6)

and transformed boundary conditions (4.3)

$$\begin{gathered} \sum\limits_{k = 1}^n \,{{( - 1)}^{k}}W_{1}^{k} = 0,\quad \sum\limits_{k = 1}^n \,{{( - 1)}^{k}}W_{2}^{k} = 0,\quad \sum\limits_{k = 1}^n \,W_{1}^{k} = \sum\limits_{k = 1}^n \,W_{2}^{k}, \\ \sum\limits_{k = 0}^n \,{{( - 1)}^{k}}A_{1}^{k} = 1,\quad \sum\limits_{k = 0}^n \,A_{2}^{k}R_{k}^{'}(0) = 0,\quad \sum\limits_{k = 0}^n \,A_{1}^{k} = \sum\limits_{k = 0}^n \,A_{2}^{k}, \\ \end{gathered} $$

$$\begin{gathered} \sum\limits_{k = 0}^n \,{{( - 1)}^{k}}B_{1}^{k} = {{B}_{{10}}},\quad \sum\limits_{k = 0}^n \,B_{2}^{k}R_{k}^{'}(0) = 0,\quad \sum\limits_{k = 0}^n \,B_{1}^{k} = \sum\limits_{k = 0}^n \,B_{2}^{k}, \\ \frac{\gamma }{{1 - \gamma }}\sum\limits_{k = 1}^n \,W_{2}^{k}R_{k}^{'}(1) + \mu \sum\limits_{k = 1}^n \,W_{1}^{k}R_{k}^{'}(1) = 2\sum\limits_{k = 0}^n \,A_{1}^{k}, \\ \end{gathered} $$

(4.7)

$$\begin{gathered} \frac{\gamma }{{1 - \gamma }}\sum\limits_{k = 0}^n \,A_{2}^{k}R_{k}^{'}(1) + k\sum\limits_{k = 0}^n \,A_{1}^{k}R_{k}^{'}(1) = - {\text{E}}\sum\limits_{k = 0}^n \,A_{1}^{k}\sum\limits_{k = 1}^n \,W_{1}^{k}, \\ \frac{\gamma }{{1 - \gamma }}\sum\limits_{k = 0}^n \,B_{2}^{k}R_{k}^{'}(1) + k\sum\limits_{k = 0}^n \,B_{1}^{k}R_{k}^{'}(1) = - {\text{E}}\sum\limits_{k = 0}^n \,B_{1}^{k}\sum\limits_{k = 1}^n \,W_{1}^{k}. \\ \end{gathered} $$

In particular, unknown constants ${{F}_{{1n}}},\;{{F}_{{2n}}}$ are defined by known ${{W}_{{jn}}}$ and ${{A}_{{jn}}}$, from the equations $\int_0^1 {{{L}_{j}}({{W}_{{jn}}},{{F}_{{jn}}}){{R}_{0}}(\xi )d\xi = 0}$, $j = 1,2$. When obtaining the system (4.7) we also taken into account that ${{R}_{k}}(1) = 1$, ${{R}_{k}}(0) = {{( - 1)}^{k}}$. Thus, equations (4.6), (4.7) form a closed system of algebraic nonlinear equations for the coefficients $W_{j}^{k},\;A_{j}^{k}$ and constants ${{F}_{{jn}}},\;j = 1,2$.

To solve the nonlinear system of equations (4.6), (4.7) the Newton method was used. As a zero approximation for the unknown coefficients $W_{j}^{k}$, $A_{j}^{k}$, $B_{j}^{k}$ and constants ${{F}_{{1n}}}$, ${{F}_{{2n}}}$ we take values that satisfy the conditions (4.7) and equalities

$$\begin{gathered} 2{{A}_{{1n}}}(1){{W}_{{1n}}}(1) - \mu \int\limits_0^1 \,W_{{1n}}^{{'2}}d\xi - \frac{\gamma }{{1 - \gamma }}\int\limits_0^1 \,W_{{2n}}^{{'2}}d\xi - \frac{{3{\text{M}}}}{{2{{{\text{P}}}_{1}}}}\left( {\mu \int\limits_0^1 \,W_{{1n}}^{3}d\xi + \frac{{\nu (1 - \gamma )}}{\gamma }\int\limits_0^1 \,W_{{2n}}^{3}d\xi } \right) = 0, \\ - {\text{E}}{{A}_{{1n}}}(1){{W}_{{1n}}}(1) - kA_{{1n}}^{'}(0) - 3{\text{M}}\left( {k\int\limits_0^1 \,{{A}_{{1n}}}{{W}_{{1n}}}d\xi + \frac{{\chi (1 - \gamma )}}{\gamma }\int\limits_0^1 \,{{A}_{{2n}}}{{W}_{{2n}}}d\xi } \right) = 0, \\ \end{gathered} $$

$${{F}_{{1n}}} = 2{\text{M}}\int\limits_0^1 \,W_{{1n}}^{2}d\xi - {{{\text{P}}}_{1}}(W_{{1n}}^{'}(1) - W_{{1n}}^{'}(0)),\quad {{F}_{{2n}}} = 2{\text{M}}\int\limits_0^1 \,W_{{2n}}^{2}d\xi - \frac{{{{\gamma }^{2}}{{{\text{P}}}_{2}}}}{{\chi (1 - \gamma )}}(W_{{2n}}^{'}(1) - W_{{2n}}^{'}(0)),$$

(4.8)

$$\begin{gathered} - {\text{E}}{{B}_{{1n}}}(1){{W}_{{1n}}}(1) - kB_{n}^{'}(0) + 2\left( {k\int\limits_0^1 \,{{A}_{{1n}}}d\xi + \frac{{(1 - \gamma )}}{\gamma }\int\limits_0^1 \,{{A}_{{2n}}}d\xi } \right) \\ \, - {\text{M}}\left( {k\int\limits_0^1 \,{{B}_{{1n}}}{{W}_{{1n}}}d\xi + \tfrac{{\chi (1 - \gamma )}}{\gamma }\int\limits_0^1 \,{{B}_{{2n}}}{{W}_{{2n}}}d\xi } \right) = 0. \\ \end{gathered} $$

Integral equalities (4.8) follow from equations (4.1), (4.2), taking into account the boundary conditions (4.3) and the form of solutions (4.5).

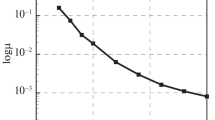
The calculations were carried out for parameters of water ($j = 1$) and water vapor ($j = 2$) system on the saturation line at temperature ${{300}^{{^{ \circ }}}}{\text{C}}$ [14]: ${\text{E}} = 0.6$, ${\text{M}} = 11.5$, $h = 1 \times {{10}^{{ - 6}}}$ m, $l = 0.5 \times {{10}^{{ - 6}}}$ m and $n = 15$ (then the lower index $n$ will be omitted). Two different values of dimensionless constants ${{F}_{1}}$, ${{F}_{2}}$ were obtained: $\{ F_{1}^{1} = - 0.434,\;F_{2}^{1} = - 1.506\}$, $\{ F_{1}^{2} = 2.446,\;F_{2}^{2} = 7.366\}$ (the upper index indicates the solution number). The obtained values at $n = 15$ and at $n = 16$ differ by ${{10}^{{ - 15}}}$ and ${{10}^{{ - 10}}}$ for ${{F}^{1}}$ and ${{F}^{2}}$, respectively. It means good convergence of the tau-method in solving this boundary value problem. Fig. 1 shows the profiles of the dimensionless functions ${{W}_{j}}(\xi )$ and transverse velocities ${{V}_{j}}(\xi )$ for values ${{F}^{1}}$ and ${{F}^{2}}$, respectively. Here the functions $W(\xi )$ and $V(\xi )$ coincide with the functions ${{W}_{j}}(\xi )$ and ${{V}_{j}}(\xi )$, $j = 1,2$, on their fields of definition. It is also worth noting that with decreasing Marangoni number the obtained solutions $F_{1}^{1},\;F_{2}^{1}$ and $F_{1}^{2},\;F_{2}^{2}$ tend to solutions of the model problem $F_{1}^{{01}} = - 0.515$, $F_{2}^{{01}} = - 1.743$ and $F_{1}^{{02}} = 72.615$, $F_{2}^{{02}} = 245.712$, respectively (see (3.3)). For example, at ${\text{M}} = 0.001$ we obtain ${\text{|}}F_{j}^{{01}} - F_{j}^{1}{\text{|}} \approx {\text{1}}{{{\text{0}}}^{{ - 15}}}$ and ${\text{|}}F_{j}^{{02}} - F_{j}^{2}{\text{|}} \approx {{10}^{{ - 10}}}$, $j = 1,2$.

Fig. 1.

Profiles of dimensionless function $W(\xi )$ (– – –) and transverse velocity $V(\xi )$ (– –) for ${{F}^{1}}$ (a) and ${{F}^{2}}$(b).

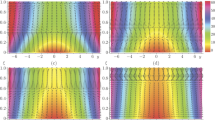
Figures 2, 3 shows velocity and temperature fields in layers for ${{F}^{1}}$ and ${{F}^{2}}$, respectively. In both cases, there are zones of return flow: in the first case, near the interface (Fig. 2), and in the second, near solid walls (Fig. 3). In addition to the surface tension gradient, there is another movement mechanism that occurs when the lower wall is heated.This mechanism is the pressure gradient in the layers. Calculations show that the pressure gradient in the first layer significantly exceeds the surface tension gradient in absolute value and acts in the opposite direction. Therefore, in both cases, the flow near the interface is directed in the direction of increasing temperature, that is, in the direction opposite to the direction of action of thermocapillary forces.

Fig. 2.

The field of velocities (a) and temperatures (b) in the layers for ${{F}^{1}}$.

Fig. 3.

The field of velocities (a) and temperatures (b) in the layers for ${{F}^{2}}$.

For the case where there is no effect of changes in the internal interfacial energy (${\text{E}} = 0$), there is one solution ${{F}_{1}} = - 0.438$, ${{F}_{2}} = - 1.518$. This solution with decreasing Marangoni number tends to a unique solution of the model problem (3.6) $F_{1}^{0} = - 0.519$, $F_{2}^{0} = - 1.756$, and at ${\text{M}} = 0.001$ we obtain ${\text{|}}F_{j}^{0} - {{F}_{j}}{\text{|}} \approx {{10}^{{ - 15}}}$, $j = 1,2$.

It is also worth mentioning about the influence of dimensionless parameters on occurring flows: as the dimensionless parameters ${\text{M}}$ and ${\text{E}}$ increase the values of the dimensionless function $W(\xi )$ and the transverse velocity $V(\xi )$ decrease. As the thickness of the second layer increases (decrease $\gamma$) the dimensionless pressure gradient in the second liquid decreases in absolute value, while in the first one it practically does not change. So, at $E = 0,\;\gamma = 0.2$ (the thickness of the second layer is 4 times greater than the first) we obtain ${{F}_{1}} = - 0.431$, ${{F}_{2}} = - 0.081$. The dimensionless parameter $\gamma$ does not affect the intensity of flows.