TWO-LAYER STEADY CREEPING THERMOCAPILLARY FLOW IN A THREE-DIMENSIONAL CHANNEL

Abstract

We study the problem of three-dimensional steady creeping flow of two immiscible liquids in a channel with solid parallel walls, one of which a given temperature distribution is maintained and the other is hear-insulated. Thermocapillary forces act on the flat interface. Temperature in the liquids depends quadratically on the horizontal coordinates, and the velocity field has a special form. The resulting conjugate problem for the Oberbeck–Boussinesq model is inverse and reduces to the system of ten integro-differential equations. The total energy condition on the interface is taken into account. The problem has up to two solutions, and if the heat fluxes are equal, it has one solution. Characteristic flow structures are constructed for each of the solutions. The influence of dimensionless physical and geometric parameters on the flows is investigated.

INTRODUCTION AND FORMULATION OF THE PROBLEM

Hiemenz [1] flows can be observed both on a macroscale (hydraulic fracturing in the oil industry) and a microscale (liquid biochips in medicine). Such flows, also known as flows near the critical point, are characterized by the presence of zones in which the pressure and temperature are higher than in the surrounding area. Studying the characteristics of these flows is required to evaluate the technological parameters and predict the dynamics and evolution of the liquid layer. The most effective way to study processes in liquids and evaluate their characteristics is to obtain exact solutions of constitutive equations. In the literature, one can find solutions of problems describing Hiemenz flows in various geometries: axisymmetric [2] and three-dimensional [3, 4] analogs of the Hiemenz solution, including flows in cylindrical geometry [5, 6]. A brief review of exact solutions close to the Hiemenz solution is given in [7]. In the present paper, three-dimensional flow of two viscous incompressible heat-conducting liquids with a Hiemenz type velocity field is considered within the framework of a model problem. At the inner interface, the energy balance condition taking into account the change in the internal energy of the interface is specified. As shown in [8], accounting for energy consumption for surface deformation can have a significant effect on the characteristics of liquid flows with low viscosities or under microconvection conditions. In this work, to evaluate this effect on emerging flows, we study a model linear problem in which the only nonlinear term is the term in the energy balance condition at the interface.

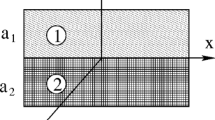
Consider three-dimensional plane steady flow of two viscous heat-conducting liquids in a layer where $|x|<\infty$, $|y|<\infty$, and $0<z<l_2$. The liquids are in contact through a common interface $z=l_1<l_2$ ($l_j$ are constants). Liquid 1 occupies a layer $0<z<l_1$, and liquid 2 occupies a layer $l_1<z<l_2$. The planes $z=0$ and $z=l_2$ are solid fixed walls, and the gravity is normal to the layers. As a mathematical model of liquid motion we use the Oberbeck–Boussinesq equations, whose solutions are sought in the following form (here and below $j=1,2$):

$$u_j(x,z)=(f_j(z)+h_j(z))x, \quad v_j(y,z)=(f_j(z)-h_j(z))y, \quad w_j(z)=-2\int\limits_{z_0}^z f_j(\xi)\,d\xi,$$

$$ \frac{1}{\rho_j}\,p_j(x,y,z)=b_j(z)x^2+d_j(z)y^2+q_j(z), \quad T_j(x,y,z)=a_j(z)x^2+c_j(z)y^2+\theta_j(z).$$

(1)

Here $u_j(x,z)$, $v_j(y,z)$, and $w_j(z)$ are the projections of the velocity vectors onto the $x$, $y$, and $z$ axes, respectively, $p_j(x,y,z)$ are the pressures, $T_j(x,y,z)$ are the absolute temperatures, and $\rho_j$ are the constant densities. Studying flows (including unsteady ones) with such a velocity field for the Navier–Stokes system was proposed in [9, 10]. However, Lin [11] was apparently the first to advance the idea of searching for exact solutions of the Navier–Stokes equations with a linear dependence of the velocity components on two spatial variables.

Substituting solution (1) into the Oberbeck–Boussinesq system of equations, we write the resulting equations in the dimensionless form

$$ \mathop{\mathrm{ Mn}}\nolimits\Big(F_j^2+H_j^2-2F_{j\xi}\int\limits_{z_0/l_2}^{\xi}F_j(\zeta)\,d\zeta\Big) +\mathrm{Gr}_j\int\limits_{z_0/l_2}^{\xi}(A_j(\zeta)+C_j(\zeta))\,d\zeta =\mathrm{Pr}_jl^2\varepsilon_jF_{j\xi\xi}+N_{j1};$$

(2)

$$ 2\mathop{\mathrm{ Mn}}\nolimits\Big(F_jH_j-H_{j\xi}\int\limits_{z_0/l_2}^{\xi}F_j(\zeta)\,d\zeta\Big) +\mathrm{Gr}_j\int\limits_{z_0/l_2}^{\xi}(A_j(\zeta)-C_j(\zeta))\,d\zeta =\mathrm{Pr}_jl^2\varepsilon_jH_{j\xi\xi}+N_{j2};$$

(3)

$$ 2\mathop{\mathrm{ Mn}}\nolimits\Big(A_j(F_j+H_j)-A_{j\xi}\int\limits_{z_0/l_2}^{\xi}F_j(\zeta)\,d\zeta\Big) =l^2\varepsilon_jA_{j\xi\xi};$$

(4)

$$ 2\mathop{\mathrm{ Mn}}\nolimits\Big(C_j(F_j-H_j)-C_{j\xi}\int\limits_{z_0/l_2}^{\xi}F_j(\zeta)\,d\zeta\Big) =l^2\varepsilon_jC_{j\xi\xi};$$

(5)

$$ -2\mathop{\mathrm{ Mn}}\nolimits Q_{j\xi}\int\limits_{z_0/l_2}^{\xi}F_j(\zeta)\,d\zeta =l^2\varepsilon_jQ_{j\xi\xi}+2\varepsilon_j(A_j+C_j),$$

(6)

where $\mathrm{Pr}_j$, $\mathrm{Gr}_j$, and $\mathop{\mathrm{ Mn}}\nolimits$ are the Prandtl, Grashof, and Marangoni numbers, respectively. In the integral expressions, we have $z_0=0$ for $j=1$ and $z_0=l_1$ for $j=2$, and hence $0<\xi<l$ in the first layer and $l<\xi<1$ in the second layer. In Eqs. (2) and (3), $N_{j1}$ and $N_{j2}$ are arbitrary constants.

On the solid boundaries, the no-slip conditions for velocities are imposed; as a result, we obtain the equalities

$$ F_1(0)=H_1(0)=0, \qquad F_2(1)=H_2(1)=\int\limits_l^1 F_2(\xi)\,d\xi=0.$$

(7)

Temperature is specified on the lower solid wall, and the upper solid wall is heat-insulated:

$$ A_1(0)=A_1^s, \quad C_1(0)=C_1^s, \quad Q_1(0)=Q_1^s,\quad A_{2\xi}(1)=C_{2\xi}(1)=Q_{2\xi}(1)=0.$$

(8)

At the interface $z=l$, the velocities and temperatures are equal:

$$ F_1(l)=F_2(l), \quad H_1(l)=H_2(l), \quad Q_1(l)=Q_2(l), \quad A_1(l)=A_2(l), \quad C_1(l)=C_2(l).$$

(9)

We assume that the surface tension depends linearly on temperature: $\sigma(T)=\sigma_0-\varkappa(T-T_0)$ [$\sigma_0$, $\varkappa$, and $T_0$ are given positive constants, and $T(x,y,l_1)$ is the temperature at this boundary]. Then, the condition for tangential stresses reduces to two relations:

$$ F_{2\xi}(l)-\mu F_{1\xi}(l)=-\mathop{\mathrm{ Mn}}\nolimits\,(A_1(l)+C_1(l)), \quad H_{2\xi}(l)-\mu H_{1\xi}(l)=-\mathop{\mathrm{ Mn}}\nolimits\,(A_1(l)-C_1(l)).$$

(10)

The kinematic condition for the fixed non-deformable interface is equivalent to the integral equality

$$ \int\limits_0^l F_1(\xi)\,d\xi=0.$$

(11)

The complete energy condition taking into account (1) reduces to the relations

$$A_{2\xi}(l)-k A_{1\xi}(l)=2EA_1(l)F_1(l),\qquad C_{2\xi}(l)-k C_{1\xi}(l)=2EC_1(l)F_1(l),$$

$$ Q_{2\xi}(l)-k Q_{1\xi}(l)=2EQ_1(l)F_1(l).$$

(12)

In Eqs. (2)–(6) and boundary conditions (7)–(12), the following dimensionless variables and parameters are introduced:

$$\xi=\frac{z}{l_2}, \quad \chi=\frac{\chi_1}{\chi_2}, \quad \mu=\frac{\mu_1}{\mu_2}, \quad k=\frac{k_1}{k_2}, \quad l=\frac{l_1}{l_2}<1, \quad \varepsilon_j=\frac{\chi_j}{\chi_1}, \quad \mathrm{Pr}_j=\frac{\nu_j}{\chi_j},$$

$$N_{jk}=\frac{l_1^4n_{jk}}{\chi_1^2\mathop{\mathrm{ Mn}}\nolimits}, \quad F_j(\xi)=\frac{l_1^2}{\chi_1\mathop{\mathrm{ Mn}}\nolimits}\,f_j(z), \quad H_j(\xi)=\frac{l_1^2}{\chi_1\mathop{\mathrm{ Mn}}\nolimits}\,h_j(z), \quad A_j(\xi)=\frac{a_j(z)}{a^*\mathop{\mathrm{ Mn}}\nolimits},$$

$$C_j(\xi)=\frac{c_j(z)}{a^*\mathop{\mathrm{ Mn}}\nolimits}, \quad Q_j(\xi)=\frac{\theta_j(z)}{a^*l_1^2\mathop{\mathrm{ Mn}}\nolimits}, \quad \mathrm{Gr}_j=\frac{a^*l_2l_1^4g\beta_j}{\chi_1^2}, \quad \mathop{\mathrm{ Mn}}\nolimits=\frac{\varkappa a^*l_1^2l_2}{\mu_2\chi_1}, \quad E=\frac{\varkappa^2 a^*l_2^2}{\mu_2k_2}.$$

Here $\nu_j$, $\mu_j$, $\chi_j$, $k_j$, and $\beta_j$ are the constant kinematic and dynamic viscosities, thermal diffusivities, heat conductivities, and the volume expansion coefficient, respectively, $N_{jk}$ are the dimensionless pressure gradients along the horizontal coordinates ($j=1,2$ and $k=1,2$), and $E$ is the energy parameter that characterizes the energy expended for deformation of the interface by thermocapillary forces. Under the assumption that $a^*=\max\,\{|a_1(0)|,|c_1(0)|\}>0$ and the characteristic temperature at the interface is $\theta^*=a^*l_1^2$, the values $\mathrm{Gr}_j$, $\mathop{\mathrm{ Mn}}\nolimits$, and $E$ are positive numbers. Note that a local change in the internal energy of the interface due to absorption (release) of heat generates inhomogeneity of the temperature field (thermocapillary effect). The influence of the heat of formation of the interface on the occurrence of temperature gradients and additional heat flows in the problem of bubble motion was found in [8].

Remark 1. The formulated initial-boundary value problem (2)–(12) is inverse since the constants $N_{j1}$ and $N_{j2}$ should be found along with its solution. To completely define this problem, we should specify two more conditions:

$$ \int\limits_0^l H_1(\xi)\,d\xi=0, \qquad \int\limits_l^1 H_2(\xi)\,d\xi=0,$$

(13)

which, along with the integral equalities (7) and (11), imply that the flows in the layers are closed [12].

Remark 2. Using the well-known dimensional functions $a_j$ and $c_j$, the functions $b_j$ and $d_j$ are given by the quadratures

$$b_j(z)=g\beta_j\int\limits_{z_0}^za_j(\xi)\,d\xi-n_{j1}, \qquad d_j(z)=g\beta_j\int\limits_{z_0}^zc_j(\xi)\,d\xi-n_{j2},$$

and the pressures in the liquids are defined as

$$\frac{1}{\rho_j}\,p_j=\Big(g\beta_j\int\limits_{z_0}^z a_j(\xi)\,d\xi-n_{j1}\Big)x^2 +\Big(g\beta_j\int\limits_{z_0}^z c_j(\xi)\,d\xi-n_{j2}\Big)y^2 -2\nu_jf_j-gz{}$$

$${}+g\beta_j\int\limits_{z_0}^z\theta_j(\xi)\,d\xi -2\Big(\int\limits_{z_0}^zf(\xi,t)\,d\xi\Big)^2+q_{j0}$$

($q_{j0}$ are arbitrary constants).

SOLUTION OF THE MODEL PROBLEM FOR CREEPING FLOWS

Flows at small Marangoni numbers are usually called creeping. The smallness of the parameter can be achieved due to the physical parameters of the liquid as well as due to the channel thickness [13, 14]. Let $\mathop{\mathrm{ Mn}}\nolimits\rightarrow 0$, then, Eqs. (2)–(6) are linear, and the right sides of boundary conditions (10) are equal to zero. However, relations (12) remain nonlinear. Performing simple but rather cumbersome transformations, we obtain

$$A_1^0(\xi)=\alpha_1\xi+A_1^s, \qquad A_2^0(\xi)=\alpha_2\equiv\alpha_1 l+A_1^s,$$

$$C_1^0(\xi)=\gamma_1\xi+C_1^s, \qquad C_2^0(\xi)=\gamma_2\equiv\gamma_1 l+C_1^s,$$

$$ Q_1^0(\xi)=-\frac{2}{l^2}\Big(\frac{\alpha_1+\gamma_1}{6}\,\xi^3 +\frac{A_1^s+C_1^s}{2}\,\xi^2\Big)+R_1\xi+Q_1^s,$$

(14)

$$Q_2^0(\xi)=-(\alpha_2+\gamma_2)l^{-2}\xi^2+R_2\xi+R_3;$$

$$F_1^0(\xi)=\frac{1}{\mathrm{Pr}_1l^2}\Big[\mathrm{Gr}_1\Big(\frac{\alpha_1+\gamma_1}{24}\,\xi^4 +\frac{A_1^s+C_1^s}{6}\,\xi^3\Big)-\frac{N_{11}\xi^2}{2}\Big]+D_1\xi,$$

$$F_2^0(\xi)=\frac{\chi}{\mathrm{Pr}_2l^2}\Big[\mathrm{Gr}_2\,(\alpha_2+\gamma_2) \Big(\frac{\xi^3-1}{6}-\frac{l}{2}\,(\xi^2-1)\Big) -\frac{N_{21}}{2}\,(\xi^2-1)\Big]+D_2(\xi-1),$$

$$ H_1^0(\xi)=\frac{1}{\mathrm{Pr}_1l^2}\,\Big[\mathrm{Gr}_1\Big(\frac{\alpha_1-\gamma_1}{24}\,\xi^4 +\frac{A_1^s-C_1^s}{6}\,\xi^3\Big)-\frac{N_{12}\xi^2}{2}\Big]+D_3\xi,$$

(15)

$$H_2^0(\xi)=\frac{\chi}{\mathrm{Pr}_2l^2}\,\Big[\mathrm{Gr}_2\,(\alpha_2-\gamma_2) \Big(\frac{\xi^3-1}{6}-\frac{l}{2}\,(\xi^2-1)\Big) -\frac{N_{22}}{2}\,(\xi^2-1)\Big]+D_4(\xi-1).$$

The constants $D_1,\dots,D_4$ are found from the integral equalities (7), (11), and (13). In strength (14), we have $\alpha_2+\gamma_2=(\alpha_1+\gamma_1)l+A_1^s+C_1^s$ and $\alpha_2-\gamma_2=(\alpha_1-\gamma_1)l+A_1^s-C_1^s$. To determine the unknowns $\alpha_1$, $\gamma_1$, $R_1$, $R_2$, $R_3$, $N_{11}$, $N_{21}$, $N_{12}$, and $N_{22}$, we use the last condition of (8), the first three conditions of Eqs. (9), and conditions (10) and (12). The form of the constants $\alpha_1$, $\gamma_1$, $R_1$, $R_2$, $R_3$, $N_{11}$, $N_{21}$, $N_{12}$, and $N_{22}$ is not given due to their cumbersomeness. Note that the unknown parameter $\alpha_1$ satisfies the quadratic equation. Therefore, the creeping flow problem can have two solutions. Obviously, for $E=0$, there is a unique solution. Analysis of the obtained solutions (14) and (15) leads to the following conclusions: for $A_1^s=C_1^s=0$, the only solution of the problem is the solution corresponding to the state of rest; $N_{12}=N_{22}=0$, $N_{11}\neq 0$, and $N_{21}\neq 0$ for $A_1^s=C_1^s$; $N_{12}=-N_{11}$ and $N_{22}=-N_{21}$ for $A_1^s=0$ and $C_1^s\neq 0$; $N_{12}=N_{11}$ and $N_{22}=N_{21}$ for $A_1^s\neq0$ and $C_1^s=0$.

Fig. 1

Temperature and velocity fields in the layers at different thicknesses: $l=0.4$ (a), 0.5 (b), 0.6 (c), and 0.75 (d).

Fig. 2

Velocity profiles $W(\xi)$ in the layers for $A_1^s=0.1$ and different values of $C_1^s$: $C_1^s=0$ (1), $-0.05$ (2), $-0.1$ (3), and $-0.15$ (4).

The calculations were carried out for the transformer oil–formic acid system with six dimensionless parameters $\mu=11.4$, $\chi=0.71$, $k=0.41$, $\beta=\beta_1\beta_2^{-1}=1.46$, $\mathrm{Pr}_1=308.2$, and $\mathrm{Pr}_2=14.2$. Figures 1 and 2 show the results of calculations for $E=0$, i.e., for the case where there is no influence of a change in the interfacial energy and there is a unique solution of the creeping flow problem. Figure 1 shows the temperature and velocity fields in layers of different thicknesses in the plane $(y,\xi)$ ($y$, $\xi$, and $T$ are dimensionless variables). For $l\le 0.4$, one vortex occurs in each layer, and in the second layer, there is reverse flow (the liquid moves opposite to the $z$ direction). At $l=0.5$, the flow in the first layer becomes two-vortex, and with an increase in $l$, it becomes fully reverse. In the second layer, the flow structure also changes: at $l>0.8$, one vortex occurs (the liquid moves in the positive $z$ direction). With a change in the thickness of the layers, the temperature field also changes: at $l=0.4$, a thermocline is formed in the lower layer, and at $l>0.8$, the temperature is equally distributed in the layers.

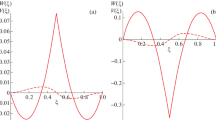
Figure 2 shows the velocity profiles $W(\xi)$ in the layers for different values of $C_1^s$ (the situation for $A_1^s$ is similar). Here and below, the function $W(\xi)$ coincides with the functions $W_j(\xi)$ ($j=1,2$) in their domains of definition. Note that for the case $A_1^s=-C_1^s$, the only solution of the problem is the solution corresponding to the state of rest. We also studied the influence of Grashof numbers ($\mathrm{Gr}_j$) on the emerging flow: as $\mathrm{Gr}_j$ increases, the modulus of the dimensionless velocity $W(\xi)$ increases.

Fig. 3

Velocity profiles $W^1(\xi)$ (curve 1) and $W^2(\xi)$ (curve 2) in the layers for $E=0.5$.

Fig. 4

Velocity profiles $W^2(\xi)$ in the layers for $E=0.3$ (1), $0.5$ (2), and $0.7$ (3).

For the case $E\neq 0$, two solutions are found. Figure 3 shows the velocity profiles $W^1(\xi)$ and $W^2(\xi)$ corresponding to each solution for $E=0.5$ (superscript denotes the solution number). The velocity profile $W^1(\xi)$ is similar to the velocity profile $W(\xi)$ for $E=0$, $\big|\max\limits_{\xi\in[0,1]}|W^1(\xi)|-\max\limits_{\xi\in[0,1]}|W(\xi)|\big| \approx 10^{-5}$, and the influence of the parameter $E$ on the emerging flow corresponding to the first solution is negligible. The velocity profiles $W^2(\xi)$ in the layers for different values of the dimensionless parameter $E$ are given in Fig. 4. It can be seen that as $E$ increases, the dimensionless velocity $W^2(\xi)$ decreases.

CONCLUSIONS

The problem of three-dimensional two-layer motion with a special velocity field was solved by reducing it to a conjugate problem for a system of one-dimensional integro-differential equations. The resulting problem is inverse with respect to pressure gradients along horizontal coordinates. In the case of steady flow at low Marangoni numbers, the solution is found in analytical form. It is shown that, depending on the values of physical parameters, there can be up to two steady modes. For the transformer oil–formic acid system, the influence of dimensionless physical and geometric parameters on emerging flows was investigated.

This work was supported by the Russian Foundation for Basic Research (Grant No. 20-01-00234) and the Krasnoyarsk Mathematical Center financed by the Ministry of Education and Science of the Russian Federation under the project for the creation and development of regional scientific and educational mathematical centers (Agreement No. 075-02-2020-1631).