1 INTRODUCTION

The Supernova Cosmology Project collaboration [1], the Supernova Search Team collaboration [2], the WMAP collaboration [3, 4], the Planck Collaboration [5], and recent observational predictions suggest that our Universe is going through an accelerated phase of expansion which assigns a new boulevard in modern cosmology. These results suggest that our universe is dominated by dark energy (DE), or extraterrestrial cosmic fluid with heavy negative pressure, which accounts for \(\simeq 3/4\) of the critical density. Moreover, information from the Cosmic microwave background (CMB) [6] indicates that the Universe appears to be shaped like a flat surface on a huge scale. The flatness of the cosmos cannot be explained by conventional matter or dark matter alone; instead, a “dark energy” must be the cause of the discrepancy. The same dark energy also accelerates the expansion of the universe.

Einstein’s general theory of relativity (GR) is the most successful theory of gravity. This theory, however, is incompatible with Mach’s principle and the recent finding of the universe’s late-time acceleration of expansion. Numerous observations [7–9] indicate that the \(\Lambda\)CDM DE model is the best fit to the current observable universe that is speeding up in the present and was slowing down in the past. The simplest way to explain the DE behavior of the universe in the context of GR is to use the cosmological constant \(\Lambda\), which has a negative and constant equation of state and makes the most sense for late-time accelerating expanded universes [10–13]. Although this cosmological term \(\Lambda\) accurately describes the current behavior of the universe and makes best fits to modern observational evidence, it suffers from two main fundamental issues: its fine-tuning problem and its derivation in the field equations [14, 15].

Cosmologists believe that the late-time acceleration of the cosmos could be better explained by a modified theory of gravitation. Many ways to tweak Einstein’s initial concepts have been found by researchers to improve the theory of gravity: \(f(R)\) gravity [16], \(f(G)\) gravity [17], \(f(T)\) gravity [18], \(f(R,T)\) gravity [19], and \(f(Q)\) gravity [20] etc. are well-known modified theories of gravitation. With these updated theories, the DE problem was better understood, and other gravity theories that may account for the Universe’s late-time fast expansion were constructed.

A research on the intriguing concept of gravitational interaction mediated by non-metricity when torsion and curvature vanish has recently been conducted [21–29]. This method can be highly significant for a fundamental understanding of gravity since gravity can be interpreted as a gauge theory without explicitly stating the existence of the Equivalence Principle. Examining \(f(Q)\) theories, where \(Q\) is the nonmetricity scalar, offers new perspectives on the cosmic speed-up that arises from the inherent effects of a geometry different from Riemannian. A power-law function is assumed in the analysis of the connecting matter in \(f(Q)\) gravity in [30]; cosmological aspects were recently studied in [31] using a model-independent reconstruction technique, and [32] provides a covariant formulation of \(f(Q)\) theory. In recent times, [33] reviewed a number of cosmological models in \(f(Q)\) gravity, and [34] used a tachyon field to study the Tsallis holographic dark energy in viscous \(f(Q)\) gravity. Reference [35] presents a dynamical system analysis in \(f(Q)\) gravity with perturbations, whereas [36–38] have examined string-fluid cosmological models in \(f(Q)\) gravity. A holographic Ricci dark energy model in \(f(T)\) gravity is described in [39], and some \(\Lambda\)CDM cosmological models were recently rebuilt in \(f(T)\) gravity in [39–41]. References [42–44] examine a few accelerating cosmic viscous fluid models in \(f(T)\) gravity. Recently, [45] suggested an extension of \(f(Q)\) gravity to \(f(Q,T)\) theory, and some transit phase accelerating cosmological models with observational constraints were recently examined in \(f(Q,T)\) gravity in [46–50].

Though there are parallels between the modified theories at the equation level, the previously mentioned novel classes of modified gravity arise in curvature, torsional, and nonmetricity conditions. This is because, the conventional Levi-Civita Ricci scalar \(\mathring{R}\), the torsion scalar \(T\), and the nonmetricity scalar \(Q\) there are arbitrary functions \(f(\mathring{R})\), \(f(T)\), and \(f(Q)\) no more differ by a complete derivative. The boundary terms \(C=\mathring{R}-Q\) were recently added to the \(f(Q)\) gravity theory to generate the \(f(Q,C)\) theory [51], a new extended theory of gravity. They proposed a particular form of the \(f(Q,C)\) function as \(f(Q,C)=Qe^{\lambda\frac{Q_{0}}{Q}}+\beta C^{2}\), with a prediction that the boundary term could function as a dark energy term. A recent detailed study of the role of boundary terms in the \(f(Q)\) theory was conducted by [52]. Recently, an accelerating cosmological model was investigated in \(f(Q,C)\) gravity in [53] with the arbitrary function \(f(Q,C)\) chosen as \(Q+\alpha C^{2}\), and we have investigated a DE accelerating in late-time universe with an function \(f(Q,C)=\alpha Q^{2}+\beta C^{2}\) in [54]. According to these preliminary investigations, the boundary term might function as a DE factor. We will investigate the behavior of DE cosmological models in \(f(Q,C)\) gravity with a perfect fluid in this study, motivated by the recently suggested theory described earlier.

To assess the properties of the DE component of the cosmos using observational data, current research aims at determining the equation-of-state (EoS) parameter \(\omega\). This parameter is defined as \(\omega(t)=p/\rho\), the ratio of fluid pressure to energy density. The most straightforward explanation for DE is the vacuum energy with EoS \(\omega=-1\), also referred to as the “cosmological constant,” or the \(\Lambda\)-term. Quintom (\(\omega<-1\)) and quintessence (\(\omega>-1\)) are described by minimally coupled scalar fields and as alternatives to vacuum energy with time-dependent EoS features. Consciousness may go from the phantom realm to the quintessence zone as it grows. In [55] and [56] it is stated that \(-1.67<\omega<-0.62\), and \(-1.33<\omega<-0.79\), respectively, are some observational constraints on the EoS parameter \(\omega\). The most recent results on the limits of the EoS were obtained in 2009 in [57, 58], and were \(-1.44<\omega<-0.92\) at \(68\%\) confidence level. We are unable to utilize a constant value for \(\omega\) since we do not yet have observational data that distinguish between constant and variable \(\omega\). The EoS parameter was considered to be a constant with phase values of \(-1\), \(0,+\frac{1}{3}\), and \(+1\) for a vacuum fluid, dust, radiation, and stiff fluid dominated worlds, respectively, according to [59, 60]. That being said, \(\omega\) is usually a function of time or redshift (mu-reference [61, 62]).

Motivated by the preceding debate, we study in this work an isotropic and homogeneous flat universe model in \(f(Q,C)=Q+\lambda C^{m}\) gravity theory, where \(\lambda,m\) are model parameters. To find the best fit model, we compare our findings with \(H(z)\) datasets.

The present paper is organized as follows: a brief introduction was given in Section 1, some basic concepts of \(f(Q,C)\) gravity are mentioned in Section 2. Section 3 contains the modified field equations, and in Section 4 we obtain some cosmological solutions. In Section 5 we obtain some observational constraints on the model using \(\chi^{2}\)-test with contour plots, and the resulting analysis and discussion are presented in Section 6. Finally, the conclusions are given in the last Section 7.

2 BRIEF CONCEPTS OF \(f(Q,C)\) GRAVITY

Let us start with the affine connection’s most basic version in order to analyze the cosmological characteristics of nonmetric gravity [63],

$${\Gamma^{k}}_{ij}={\mathring{\Gamma}^{k}}_{ij}+{K^{k}}_{ij}+{L^{k}}_{ij}.$$
(1)

The metric tensor \(g_{ij}\)’s Levi-Civita connection is provided here by

$${\mathring{\Gamma}^{k}}_{ij}\equiv\frac{1}{2}g^{k\beta}(\partial_{i}g_{\beta j}+\partial_{j}g_{\beta i}-\partial_{\beta}g_{ij}),$$
(2)

whereas

$${K^{k}}_{ij}\equiv\frac{1}{2}g^{k\beta}(\mathcal{T}_{i\beta j}+\mathcal{T}_{j\beta i}+\mathcal{T}\beta ij),$$
(3)
$${L^{k}}_{ij}\equiv\frac{1}{2}g^{k\beta}(-Q_{i\beta j}-Q_{j\beta i}+Q_{\beta ij}),$$
(4)

are, respectively, the disformation and contortion tensors. The torsion tensor is \({\mathcal{T}^{k}}_{ij}\equiv{\Gamma^{k}}_{ij}-{\Gamma^{k}}_{ji}\), and the nonmetricity tensor is given by

$$Q_{\rho ij}\equiv\nabla_{\rho}g_{ij}=\partial_{\rho}g_{ij}-{\Gamma^{\beta}}_{\rho i}g_{\beta j}-{\Gamma^{\beta}}_{\rho j}g_{i\beta}.$$
(5)

The characteristics of the metric-affine space-time will thus depend on some choices made regarding the links. In our study, it is presumable that the torsion and curvature will vanish, leaving the nonmetricity as the source of geometry. Depending on the contraction order, there are two distinct traces of the nonmetricity tensor: \({Q_{i}={Q_{i}}^{\alpha}}_{\alpha}\) and \(\tilde{Q}^{i}={Q_{\alpha}}^{i\alpha}\). Therefore, it is possible to define the nonmetricity scalar as [20]

$$Q=-\frac{1}{4}Q_{\alpha\beta i}Q^{\alpha\beta i}+\frac{1}{2}Q_{\alpha\beta i}Q^{\beta i\alpha}$$
$${}+\frac{1}{4}Q_{\alpha}Q^{\alpha}-\frac{1}{2}Q_{\alpha}\tilde{Q}^{\alpha},$$
(6)

which, for general diffeomorphisms, is an invariant quadratic combination.

Last but not least, the constraints on curvature and torsion can be used to further obtain the relationships (all values with a \(\mathring{()}\) are calculated with respect to the Levi-Civita connection \(\mathring{\Gamma}\))

$$\mathring{R}_{ij}+\mathring{\nabla}_{\alpha}{L^{\alpha}}_{ij}-\mathring{\nabla}_{j}\tilde{L}_{i}+\tilde{L}_{\alpha}{L^{\alpha}}_{ij}$$
$${}-L_{\alpha\beta j}{L^{\alpha\beta}}_{i}=0,$$
(7)
$$\mathring{R}+\mathring{\nabla}_{\alpha}(L^{\alpha}-\tilde{L}^{\alpha})-Q=0.$$
(8)

Thus it is evident that since \(Q^{\alpha}-\tilde{Q}^{\alpha}=L^{\alpha}-\tilde{L}^{\alpha}\), we consider the boundary term from the previous relation [30, 31].

$$C=\mathring{R}-Q=-\mathring{\nabla}_{\alpha}(Q^{\alpha}-\tilde{Q}^{\alpha})$$
$${}=-\frac{1}{\sqrt{-g}}\partial_{\alpha}[\sqrt{-g}(Q^{\alpha}-\tilde{Q}^{\alpha})].$$
(9)

Now, we consider the following action for \(f(Q,C)\) gravity theory [51, 52]:

$$S=\int{\frac{1}{16\pi}[f(Q,C)+16\pi\mathcal{L}_{m}]\sqrt{-g}\,d^{4}x},$$
(10)

where \(f(Q,C)\) is an arbitrary function of the nonmetricity scalar \(Q\), \(C\) is the boundary term, \(L_{m}\) denotes the matter Lagrangian, and \(g\) is the determinant of the metric tensor \(g_{ij}\).

The field equations emerge from variations in the action with respect to the metric as follows:

$$\frac{2}{\sqrt{-g}}\partial_{k}(\sqrt{-g}f_{Q}{P^{k}}_{ij})$$
$${}+(P_{i\alpha\beta}{Q_{j}}^{\alpha\beta}-2P_{\alpha\beta j}{Q^{\alpha\beta}}_{i})f_{Q}$$
$${}-\frac{f}{2}g_{ij}+\bigg{(}\frac{C}{2}g_{ij}-\mathring{\nabla}_{i}\mathring{\nabla}_{j}+g_{ij}\mathring{\nabla}^{\alpha}\mathring{\nabla}_{\alpha}$$
$${}-2{P^{k}}_{ij}\partial_{k}\bigg{)}f_{C}\ =\ 8\pi T_{ij},$$
(11)

where \(f_{Q}=\partial{f}/\partial{Q}\), \(f_{C}=\partial{f}/\partial{C}\), and where \(T_{ij}\) is the matter energy momentum tensor. We observe here that by varying the action with respect to the affine connection, we may obtain the connection field equation because the affine connection is independent from the metric tensor [51]

$$(\nabla_{i}-\tilde{L}_{i})(\nabla_{j}-\tilde{L}_{j})\big{[}4(f_{Q}-f_{C}){P^{ij}}_{k}$$
$${}+{\Delta_{k}}^{ij}\big{]}=0,$$
(12)

where

$${\Delta_{k}}^{ij}=-\frac{2}{\sqrt{-g}}\frac{\delta(\sqrt{-g}\mathcal{L}_{m})}{\delta{\Gamma^{k}}_{ij}}$$

is the hyper momentum tensor [45]. As

$$\partial_{j}\sqrt{-g}=-\sqrt{-g}\tilde{L}_{j},$$
(13)

the previous connection field equation can be reexpressed while taking the coincident gauge as

$$\partial_{i}\partial_{j}(\sqrt{-g}[4(f_{Q}-f_{C}){P^{ij}}_{k}+{\Delta_{k}}^{ij}])=0.$$
(14)

If this is the case, the field equation that is equivalent to the \(f(Q)\) gravity equation will be found [30]. The second and third terms on the right-hand side make up the \(f(Q)\) theory, as we can see from the field equation (11). Following the conventional computation (for an example, see [32, 45]), we arrive at

$$\frac{2}{\sqrt{-g}}\partial_{k}(\sqrt{-g}f_{Q}{P^{k}}_{ij})$$
$${}+(P_{i\alpha\beta}{Q_{j}}^{\alpha\beta}-2P_{\alpha\beta j}{Q^{\alpha\beta}}_{i})f_{Q}$$
$${}=\left(\frac{Q}{2}g_{ij}+\mathring{G}_{ij}+2{P^{k}}_{ij}\partial_{k}\right)f_{Q},$$
(15)

where the Einstein tensor associated with the Levi-Civita link is \(\mathring{G}_{ij}\). Consequently, e may covariantly rewrite the metric field equation as

$$-\frac{f}{2}g_{ij}+2{P^{k}}_{ij}\nabla_{k}(f_{Q}-f_{C})+\Big{(}\frac{Q}{2}g_{ij}+\mathring{G}_{ij}\Big{)}f_{Q}$$
$${}+\Big{(}\frac{C}{2}g_{ij}-\mathring{\nabla}_{i}\mathring{\nabla}_{j}+g_{ij}\mathring{\nabla}^{\alpha}\mathring{\nabla}_{\alpha}\Big{)}f_{C}=8\pi T_{ij}.$$
(16)

The effective stress energy tensor is defined as follows:

$$T^{\textrm{eff}}_{ij}=T_{ij}$$
$${}+\frac{1}{8\pi}\bigg{[}\frac{f}{2}g_{ij}-2{P^{k}}_{ij}\nabla_{k}(f_{Q}-f_{C})-\frac{Qf_{Q}}{2}g_{ij}$$
$${}-\Big{(}\frac{C}{2}g_{ij}-\mathring{\nabla}_{i}\mathring{\nabla}_{j}+g_{ij}\mathring{\nabla}^{\alpha}\mathring{\nabla}_{\alpha}\Big{)}f_{C}\bigg{]},$$
(17)

and as a result, we get

$$\mathring{G}_{ij}=\frac{8\pi}{f_{Q}}T^{\textrm{eff}}_{ij}.$$
(18)

As a result, we acquire an additional, effective sector of geometric origin within the context of \(f(Q,C)\) gravity.

If the function \(f\) is linear in \(C\), then (16) reduces to the standard field equation for \(f(Q)\) gravity: \(f(Q)=f(Q)+\beta C\):

$$-\frac{f}{2}g_{ij}+2{P^{k}}_{ij}\nabla_{k}f_{Q}+\left(\frac{Q}{2}g_{ij}+\mathring{G}_{ij}\right)f_{Q}$$
$${}=8\pi T_{ij}.$$
(19)

3 MODIFIED FIELD EQUATIONS

This section introduces \(f(Q,C)\) cosmology and applies \(f(Q,C)\) gravity to a cosmological framework. We investigate the flat Friedmann-Robertson-Walker (FRW) space-time, which is homogeneous and isotropic and is represented by the line element in Cartesian coordinates

$$ds^{2}=-dt^{2}+a^{2}(t)[dx^{2}+dy^{2}+dz^{2}],$$
(20)

where \(a(t)\) is called a scale factor, which is a function of only cosmic time \(t\). The corresponding stress-energy momentum tensor is given by

$$T_{ij}=(\rho_{m}+p_{m})u_{i}u_{j}+p_{m}g_{ij},$$
(21)

where \(\rho_{m}\) amd \(p_{m}\) are the matter fluid energy density and pressure, respectively, \(u_{i}u^{i}=-1\), and \(u^{i}=(0,0,0,-1)\) is the four-velocity vector, and \(g_{ij}\) is the metric tensor.

The framework of \(f(Q,C)\) gravity allows us to acquire an additional, helpful sector of geometric origin, as indicated in (17), as we said in the preceding section. As a result, this phrase will be analogous to an efficient dark-energy sector with an energy-momentum tensor in a cosmic context,

$$T^{\textrm{(de)}}_{ij}=\frac{1}{f_{Q}}\bigg{[}\frac{f}{2}g_{ij}-2{P^{k}}_{ij}\nabla_{k}(f_{Q}-f_{C})-\frac{Qf_{Q}}{2}g_{ij}$$
$${}-\left(\frac{C}{2}g_{ij}-\mathring{\nabla}_{i}\mathring{\nabla}_{j}+g_{ij}\mathring{\nabla}^{\alpha}\mathring{\nabla}_{\alpha}\right)f_{C}\bigg{]}.$$
(22)

In this paper, we consider a nonvanishing affine connection \(\Gamma\) whose nontrivial coefficients are given by \((i=1,2,3)\)

$$\Gamma^{t}_{tt}=\frac{\gamma_{0}}{a^{3}(t)}-3H(t),$$
$$\Gamma^{i}_{it}=\frac{\gamma_{0}}{a^{3}(t)},\quad\Gamma^{i}_{ti}=\frac{\gamma_{0}}{a^{3}(t)},$$
(23)

which, as mentioned above, leads to vanishing torsion and Riemann tensor components, whereas the nonmetricity tensor components are not all zero, giving rise to the same nonmetricity scalar and boundary term as in the coincident gauge, namely,

$$Q=-6H^{2},\quad C=\mathring{R}-Q=6(3H^{2}+\dot{H}).$$
(24)

We get the Friedmann-like equations by incorporating these into the general field equations (11) as

$$3H^{2}=8\pi(\rho_{m}+\rho_{\textrm{de}})$$
(25)
$$-(2\dot{H}+3H^{2})=8\pi(p_{m}+p_{\textrm{de}}),$$
(26)

where \(\rho_{m}\) and \(p_{m}\) are the energy density and pressure of the matter sector considered as a perfect fluid, and where we have defined the effective dark energy density and pressure as

$$\rho_{\textrm{de}}=\frac{1}{8\pi}\left[-3H^{2}f_{Q}-\frac{f}{2}-\frac{3\gamma_{0}}{2a^{3}}\dot{f}_{Q}\right.$$
$${}\left.+(9H^{2}+3\dot{H})f_{C}-3H\dot{f}_{C}+\frac{3\gamma_{0}}{2a^{3}}\dot{f}_{C}\right],$$
(27)
$$p_{\textrm{de}}=\frac{1}{8\pi}\left[\frac{f}{2}+3H^{2}f_{Q}+\left(2H-\frac{3\gamma_{0}}{2a^{3}}\right)\dot{f}_{Q}\right.$$
$${}\left.-(9H^{2}+3\dot{H})f_{C}+\frac{3\gamma_{0}}{2a^{3}}\dot{f}_{C}+\ddot{f}_{C}\right].$$
(28)

Now, we define the energy conservation equation as

$$\dot{\rho}_{m}+3H[\rho_{m}+p_{m}]\\ \displaystyle=\frac{3\gamma_{0}}{16\pi a^{3}}\left[3H(\dot{f}_{Q}-\dot{f}_{C})+(\ddot{f}_{Q}-\ddot{f}_{C})\right],$$

and from the Friedmann like equations (25) and (26), we can write the effective energy conservation equation as

$$\dot{\rho}_{e}+3H[\rho_{e}+p_{e}]=0,$$
(30)

where \(\rho_{e}=\rho_{m}+\rho_{\textrm{de}}\), and \(p_{e}=p_{m}+p_{\textrm{de}}\).

4 COSMOLOGICAL SOLUTIONS

We have two linearly independent field equations (25) and (26) in five unknowns \(H,\rho_{m},p_{m},\gamma_{0},f\), and hence to find exact solutions of the field equations, we require at least three constraints on these unknowns. First, we consider the arbitrary \(f(Q,C)\) gravity function, as

$$f(Q,C)=Q+\lambda C^{m},$$
(31)

where \(\lambda\) and \(m\) are arbitrary constants, \(Q\) is the nonmetricity scalar, and \(C\) is the boundary term given by \(C=\mathring{R}-Q\).

To study the dynamical behavior of the dark energy models in \(f(Q,C)\) gravity, and due to the nonlinear complexity of its field equations, we need to adopt a parametrization of either the scale factor \(a(t)\) or the Hubble function \(H(t)\). This technique is called a model-independent way to explore dark energy properties of expanding universe models. We consider the time-dependent deceleration parameter (DP) \(q(t)=-a\ddot{a}/\dot{a}^{2}\), which gives such a scale factor, called the hyperbolic expansion law [64], and this type of technique has been also used in several studies [65–70] to explore the cosmological properties in transit phase universe models. Therefore, motivated by above studies, we consider the scale factor

$$a(t)=[\sinh(k_{0}t)]^{1/n},$$
(32)

where \(n\) and \(k_{0}\) are arbitrary constants.

The universe has an accelerated expansion at the moment, as seen in recent observations of SNe Ia and CMB anisotropies [1–3, 71, 72], and a decelerated expansion in the past [73–75]. This has motivated us to choose such a time-dependent DP. Now, the DP must exhibit signature flipping for a universe that was decelerating in the past and accelerating in the present [76–78]. Therefore, the DP is generally a time variable rather than a constant.

Now, we define the Hubble function as \(H=\frac{\dot{a}}{a}\) and obtain it as

$$H(t)=\frac{k_{0}}{n}\coth(k_{0}t).$$
(33)

Now, we express the Hubble function \(H\) in terms of the redshift \(z\) using the relation [13, 79]

$$\frac{a_{0}}{a}=1+z,$$
(34)

with the standard convention \(a_{0}=1\), as given below

$$H(z)=\frac{k_{0}}{n}\sqrt{[(1+z)^{2n}+1]},$$
(35)

or

$$H(z)=\frac{H_{0}}{\sqrt{2}}\sqrt{[(1+z)^{2n}+1]},$$
(36)

where \(H_{0}=k_{0}\sqrt{2}/n\).

Now, we put the second constraint on the energy conservation, Eq. (29), we take the interaction of matter and dark energy as

$$\dot{\rho}_{m}+3H[\rho_{m}+p_{m}]=K,$$
(37)

and

$$\frac{3\gamma_{0}}{16\pi a^{3}}\left[3H(\dot{f}_{Q}-\dot{f}_{C})+(\ddot{f}_{Q}-\ddot{f}_{C})\right]=K,$$
(38)

where \(K\) is a coupling constant. Solving Eq. (38), we get the matter energy density \(\rho_{m}\) as

$$\rho_{m}=\rho_{m0}(1+z)^{3}-K(1+z)^{3}\int\limits_{0}^{z}\frac{dz}{H(z)}.$$
(39)

In our model \(f_{Q}=1\implies\dot{f}_{Q}=0\), \(\ddot{f}_{Q}=0\), hence, Eq. (39) reduces to

$$\ddot{f}_{C}=-\frac{16\pi Ka^{3}}{3\gamma_{0}}-3H\dot{f}_{C}.$$
(40)

Now, using Eqs. (31), (32), (34), and (35) in Eq. (27), we get the dark energy density as

$$\rho_{\textrm{de}}=\frac{(m-1)\lambda 6^{m}k_{0}^{2m}}{8\pi n^{2m}}[(3-n)(1+z)^{2n}+3]^{m}$$
$${}\times\bigg{[}\frac{1}{2}+\frac{m(n-3)n^{2}}{k_{0}}\bigg{(}\frac{\gamma_{0}}{2}(1+z)^{3}$$
$${}-\frac{k_{0}}{n}\sqrt{(1+z)^{2n}+1}\bigg{)}$$
$${}\times.\frac{(1+z)^{2n}\sqrt{(1+z)^{2n}+1}}{[(3-n)(1+z)^{2n}+3]^{2}}\bigg{]}.$$
(41)

Again using Eqs. (31), (32), (34), (35), and (40) in Eq. (28), we get the dark energy pressure as

$$p_{\textrm{de}}=-\frac{(m-1)\lambda 6^{m}k_{0}^{2m}}{8\pi n^{2m}}[(3-n)(1+z)^{2n}+3]^{m}$$
$${}\times\bigg{[}\frac{1}{2}-\frac{m(n-3)n^{2}}{k_{0}}\bigg{(}\frac{\gamma_{0}}{2}(1+z)^{3}$$
$${}-\frac{k_{0}}{n}\sqrt{(1+z)^{2n}+1}\bigg{)}\frac{(1+z)^{2n}\sqrt{(1+z)^{2n}+1}}{[(3-n)(1+z)^{2n}+3]^{2}}\bigg{]}$$
$${}-\frac{2K}{3\gamma_{0}(1+z)^{3}}.$$
(42)

5 OBSERVATIONAL CONSTRAINTS

5.1 The Hubble Function

To compare the model with observational datasets, we use the publicly available emcee software, which can be found at [80], to generate an MCMC (Monte Carlo Markov Chain) analysis for our model and dataset combination. By adjusting the parameter values throughout a range of cautious priors and looking at the parameter space posteriors, the MCMC sampler constrains the model and cosmological parameters. Thus we obtain one-dimensional and two-dimensional distributions for each parameter: a one-dimensional distribution represents the posterior distribution of the parameter, whilst a two-dimensional distribution shows the covariance between two different values.

Table 1 The observed values of \(H(z)\)
Full size table
Table 2 MCMC results with \(H(z)\) datasets
Full size table

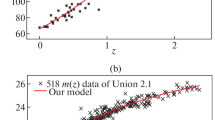
We have taken into account \(46\) Hubble constant datasets of \(H(z)\) over redshift \(z\) with errors in \(H(z)\) that are observed in [81–96] by the method of differential age (DA) time to time (see Table 1), for the best fit values of model parameters in \(H(z)\). We have used the \(\chi^{2}\)-test formula listed below for this analysis:

$$\chi^{2}(n,H_{0})=\sum_{i=1}^{i=N}\frac{[(H_{\textrm{ob}})_{i}-(H_{\textrm{th}})_{i}]^{2}}{\sigma_{i}^{2}},$$

where \(N\) denotes the total amount of data, \(H_{\textrm{ob}},H_{\textrm{th}}\), respectively, the observed and hypothesized datasets of \(H(z)\) and standard deviations are displayed by \(\sigma_{i}\).

The expression for the Hubble parameter is shown in Eq. (36) containing the parameters \(n,H_{0}\), and the contour plots of these parameters obtained from likelihood analysis is shown in Fig. 1. The MCMC results are shown in Table 2. We have found the best fit values of the model parameters \(n\) and \(H_{0}\) as \(n=1.3^{+0.018}_{-0.018}\), and \(H_{0}=66^{+0.91}_{-0.90}\) km/s/Mpc for the Hubble datasets \(H(z)\). From Eq. (35), we can find the present value of the Hubble parameter at \(z=0\) as \(H_{0}=k_{0}\sqrt{2}/n\), and for our analysis

$$k_{0}=\frac{nH_{0}}{\sqrt{2}}=60.6697.$$

From Eq. (35) we see that as \(z\to-1\), \(H\to k_{0}/n\) with \(k_{0}>0,\ n>0\), and hence, \(H>0\) for all z. Also, as \(z\to\infty\), \(H\to\infty\).

6 ANALYSIS AND DISCUSSIONS

The deceleration parameter is defined as

$$q=-\frac{\ddot{a}}{aH^{2}}=-1+n\,{\textrm{sech}}^{2}(k_{0}t),$$

and in terms of the redshift \(z\) it can be obtained as

$$q(z)=-1+\frac{n(1+z)^{2n}}{[(1+z)^{2n}+1]}.$$
(43)
Figure 1
figure 1

The contour plots of the parameters \((n,H_{0})\) for the model with \(1-\sigma\) and \(2-\sigma\) errors obtained from datasets.

Full size image
Figure 2
figure 2

The deceleration parameter \(q(z)\) versus \(z\).

Full size image
Figure 3
figure 3

Contour plots of the cosmological parameters \((m,\lambda,\gamma_{0},K)\) for the model, with \(1-\sigma\) and \(2-\sigma\) errors obtained from the datasets.

Full size image

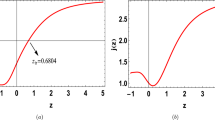
The geometric evolution of \(q(z)\) is depicted in Fig. 2, and Eq. (43) represents its mathematical expression. We can see that \(q(z)\) is an increasing function of \(z\) with a signature-flipping point (transition point) over the redshift \(-1\leq z\leq 3\). We can find that as \(z\to-1\), \(q\to-1\), and at \(z=0\), \(q=-1+n/2\), and this reveals that the model is decelerating (\(q>0\)) at present for \(n>2\) and accelerating (\(q<0\)) at present for \(n<2\). We can also see that as \(z\to\infty\), \(q\to-1\), which reveals that the late-time universe is in an accelerating phase. We have estimated the present value of the deceleration parameter \(q_{0}=-0.35\), which reveals the accelerated expanding phase of the universe at present. We can derive the transition redshift \(z_{t}\) as

$$z_{t}=\left[\frac{1}{n-1}\right]^{1/(2n)}-1,\quad n>1.$$
(44)

We have estimated the transition redshift \(z_{t}=0.589\), and this reveals that our universe begins accelerating its expansion from \(z<z_{t}\), and it was in a decelerating phase of expansion for \(z>z_{t}\). Here, the universe’s past evolution is revealed by a positive value of \(z>0\), its present state is indicated by \(z=0\), and its predicted future evolution is shown by a negative redshift, \(z<0\). As a result, we may express the cosmic redshift as \(0<z<\infty\) for cosmic time \(0<t<t_{0}\), the present age of the universe at \(z=0\) as \(t=t_{0}\), and the cosmic redshift \(-1\leq z<0\) for the cosmic time \(t_{0}<t<\infty\) (the future universe).

Now, from the Friedmann-like equations (25) and (26), we can obtain the LHS effective EoS parameter as

$$\omega^{\textrm{eff}}_{\textrm{lhs}}=-1+\frac{2}{3}\frac{n(1+z)^{2n}}{[(1+z)^{2n}+1]}.$$
(45)

Using the best fit values of the model parameters from Table 2, in Eq. (45), we obtain

$$\omega^{\textrm{eff}}_{\textrm{lhs}}=-\frac{2}{15}-\frac{13}{150[(1+z)^{2.6}+1]}.$$
(46)

Again, we define the RHS effective EoS parameter \(\omega^{\textrm{eff}}_{\textrm{rhs}}\) as

$$\omega^{\textrm{eff}}_{\textrm{rhs}}=\frac{p_{m}+p_{\textrm{de}}}{\rho_{m}+\rho_{m}}=F(\lambda,m,\gamma_{0},K,z)$$
(47)

where \(F(\lambda,m,\gamma_{0},K,z)={p_{e}}/{\rho_{e}}\).

Now, taking non-relativistic pressure \(p_{m}\approx 0\), and using Eqs. (39), (41), and (42) in (47), we obtain the expression for the RHS effective EoS parameter \(\omega_{\textrm{rhs}}^{\textrm{eff}}\) as

$$\omega_{\textrm{rhs}}^{\textrm{eff}}=\bigg{\{}-\frac{(m{-}1)\lambda 6^{m}k_{0}^{2m}}{8\pi n^{2m}}[(3-n)(1+z)^{2n}+3]^{m}$$
$${}\times\bigg{[}\frac{1}{2}-\frac{m(n-3)n^{2}}{k_{0}}\bigg{(}\frac{\gamma_{0}}{2}(1+z)^{3}$$
$${}-\frac{k_{0}}{n}\sqrt{(1+z)^{2n}+1}\bigg{)}\frac{(1+z)^{2n}\sqrt{(1+z)^{2n}+1}}{[(3-n)(1+z)^{2n}+3]^{2}}\bigg{]}$$
$${}-\frac{2K}{3\gamma_{0}(1+z)^{3}}\bigg{\}}$$
$${}\times\bigg{\{}\rho_{m0}(1+z)^{3}-K(1+z)^{3}\int\limits_{0}^{z}\frac{dz}{H(z)}$$
$${}+\frac{(m-1)\lambda 6^{m}k_{0}^{2m}}{8\pi n^{2m}}[(3-n)(1+z)^{2n}+3]^{m}$$
$${}\times\bigg{[}\frac{1}{2}+\frac{m(n-3)n^{2}}{k_{0}}\bigg{(}\frac{\gamma_{0}}{2}(1+z)^{3}$$
$${}-\frac{k_{0}}{n}\sqrt{(1+z)^{2n}+1}\bigg{)}$$
$${}\times\frac{(1+z)^{2n}\sqrt{(1+z)^{2n}+1}}{[(3-n)(1+z)^{2n}+3]^{2}}\bigg{]}\bigg{\}}^{-1},$$
(48)

where \(n\) and \(k_{0}\) are known from the observational constraints in the above Section 5. Therefore, now, we have to constrain only \(m\), \(\lambda\), \(\gamma_{0}\), and \(K\), the unknown model parameters.

The next step is to compare the effective EoS parameters \(\omega_{\textrm{lhs}}^{\textrm{eff}}\) and \(\omega_{\textrm{rhs}}^{\textrm{eff}}\) with observational datasets in order to determine the best fit values of cosmological parameters \((m,\lambda,\gamma_{0},K)\). To do that, we use Eq. (46) to produce \(100\) datasets of the EoS parameter \(\omega_{\textrm{lhs}}^{\textrm{eff}}\) across \(0\leq z\leq 3\). Using these datasets, we use likelihood analysis to estimate the values of the parameters \((m,\lambda,\gamma_{0},K)\) in Eq. (48). The \(\chi^{2}\) test formula was utilized in this case, as indicated below:

$$\chi^{2}((m,\lambda,\gamma_{0},K))=\sum_{i=1}^{100}\frac{[(\omega_{\textrm{lhs}}^{\textrm{eff}})_{i}-(\omega_{\textrm{rhs}}^{\textrm{eff}})_{i}]^{2}}{\sigma_{i}^{2}},$$

where \(\omega_{\textrm{lhs}}^{\textrm{eff}}\) is the \(100\) datasets generated values of \(\omega_{\textrm{lhs}}^{\textrm{eff}}\) from Eq. (46), \(\omega_{\textrm{rhs}}^{\textrm{eff}}\) is the theoretical value of \(\omega_{\textrm{rhs}}^{\textrm{eff}}\) obtained from Eq. (47), the corresponding values of \(z\), and \(\sigma_{i}\) denotes standard deviations.

Figure 4
figure 4

The energy densities \(\rho_{m}\), \(\rho_{\textrm{de}}\), and \(\rho_{e}\) versus redshift \(z\).

Full size image
Figure 5
figure 5

Variations of the effective EoS parameters \(\omega_{\textrm{lhs}}^{\textrm{eff}}\), \(\omega^{\textrm{(de)}}\), and \(\omega_{\textrm{rhs}}^{\textrm{eff}}\) versus redshift for the best fit values of the model parameters.

Full size image

Figure 3 depicts the contour plots of four model parameters for their best fit values, and the MCMC results are presented in Table 3. We found that \(m=0.52^{+0.00016}_{-0.00016}\), \(\lambda=-0.005^{+0.00016}_{-0.00016}\), \(\gamma_{0}=0.003^{+0.00016}_{-0.00016}\), and \(K=0.0007^{+0.00016}_{-0.00016}\). We have used these best fit values of the model parameters in our rest analysis of the model.

The expressions for the matter energy density \(\rho_{m}\) and the dark energy density \(\rho_{\textrm{de}}\) are shown in Eqs. (39) and (41), respectively. The geometric evolution of the matter energy density \(\rho_{m}\), the dark energy density \(\rho_{\textrm{de}}\), and the effective energy density \(\rho^{(\textrm{eff})}\) over the redshift \(z\) are presented in Fig. 4. From this figure, we can see that as \(z\to\infty\), \(\rho_{m}\to\infty\), and as \(z\to-1\), \(\rho_{m}\to 0\), while the dark energy density behaves as

$$\rho_{\textrm{de}}\to\frac{(m-1)\lambda 18^{m}(k_{0}k_{1})^{2m}}{16\pi}$$

as \(z\to-1\), while as \(z\to\infty\), \(\rho_{\textrm{de}}\to-\infty\). Also, one can see that as \(z\to-1\), the dark energy pressure \(p_{\textrm{de}}\to-\infty\). Thus the effective energy density of the universe is an increasing function of the redshift \(z\), or a decreasing function of cosmic time \(t\) in good agreement with the expanding universe.

The mathematical expressions for the effective EoS parameter \(\omega_{\textrm{lhs}}^{\textrm{eff}}\) and \(\omega_{\textrm{rhs}}^{\textrm{eff}}\) are given in (46) and (47), respectively, and their geometric evolution is shown in Fig. 5. From the figure, we see that the EoS parameters varies as \(-1\leq\omega_{\textrm{lhs}}^{\textrm{eff}}<0\) and \(-1.2\leq\omega_{\textrm{rhs}}^{\textrm{eff}}\leq-0.4\) over the redshift \(-1\leq z\leq 3\). The present values of the effective EoS parameters are estimated as \(\omega_{\textrm{lhs}}^{\textrm{eff}}=-0.5667\), \(\omega_{\textrm{rhs}}^{\textrm{eff}}=-0.6714\), and the dark energy EoS parameter is estimated as \(\omega^{\textrm{(de)}}=-0.6714\) at \(z=0\), which are consistent with the recent observational limits obtained in [55–58]. Thus we can say that our derived model is evolving from a matter-dominated state passing through quintessence, cosmological constant, phantom, and tends to the \(\Lambda\)CDM model in a late-time universe, which shows viability of the model [59, 60].

Table 3 MCMC results with \(\omega_{\textrm{lhs}}^{\textrm{eff}}(z)\) datasets
Full size table

6.1 Energy Conditions

The energy-momentum tensor \((T_{ij})\) needs to be subject to specific constraints, also known as the energy conditions, in order to reflect a realistic matter distribution. The Raychaudhuri equations provided the idea of energy conditions, the prerequisite that the energy density should be positive in addition to gravity being attracting [97]. The energy conditions are expressed primarily in terms of the isotropic pressure \(p\) and matter energy density \(\rho\) since \((T_{ij})\) is defined in these terms. The four basic energy conditions are null (NEC), weak (WEC), dominant (DEC), and strong (SEC). They are essential to the research of singularity and black hole thermodynamics theorems. Since the Big-Rip singularity of the universe results from breaking of the second rule of black hole thermodynamics, the NEC is crucial to discuss [98]. While SEC is helpful for understanding the Hawking-Penrose singularity theory [99], the DEC is the foundation for proving the positive mass theorem [100].

For a perfect fluid matter distribution, the inequalities providing the energy conditions are:

Null Energy Condition (NEC): \(\rho+p\geq 0\).

Weak Energy Conditions (WEC): \(\rho\geq 0\), \(\rho+p\geq 0\).

Dominant Energy Conditions (DEC): \(\rho\geq\lvert p\rvert\), i.e., \(\rho\pm p\geq 0\).

Strong Energy Conditions (SEC): \(\rho+p\geq 0\), \(\rho+3p\geq 0\).

Figure 6
figure 6

Evolution of the energy conditions over the redshift \(z\).

Full size image
Figure 7
figure 7

Evolution of the Om diagnostic function.

Full size image

From Fig. 6 we observe that all energy conditions, viz., NEC, WEC, DEC, and SEC, are satisfied in most of the evolution history. The violation of SEC at late time reveals the accelerating scenarios of the model.

6.2 Analysis of Om Diagnostic

The behavior of the Om diagnostic function can be used to categorize the cosmic dark energy models [101]. Given a spatially flat world, the simplest diagnostic is provided by

$${\textrm{Om}}\,(z)=\frac{\left(\dfrac{H(z)}{H_{0}}\right)^{2}-1}{(1+z)^{3}-1},$$
(49)

where \(H_{0}\) is the Hubble parameter’s current value, and \(H(z)\) is the Hubble parameter, as stated in Eq. (36). The Pith motion is represented by a negative slope of \({\textrm{Om}}(z)\), whereas phantom motion is represented by a positive slope. The \(\Lambda\)CDM model is represented by \({\textrm{Om}}(z)=\textrm{const}\).

The mathematical expression for the Om diagnostic function \({\textrm{Om}}(z)\) is provided in Eq. (49), which illustrates its geometric behavior over redshift \(z\) in Fig. 7. Figure 7 illustrates the quintessential behavior of our model by showing that the \({\textrm{Om}}(z)\) function has a negative slope. The resulting model within \(f(Q,C)=Q+\lambda C^{m}\) gravity thus exhibits a behavior identical to the quintessence dark energy concept. It is evident from [102] that a quintessence dark energy model can be equivalently transferred to a generalized holographic dark energy model given an appropriate cut-off selection. Because of its fundamental behavior, our derived model may be equivalently transferred to the generalized holographic dark energy model by selecting an appropriate cut-off, demonstrating the model’s viability.

6.3 Age of the Universe

We can calculate the age of the universe as

$$t_{0}-t=\int\limits_{0}^{z}\frac{dz}{(1+z)H(z)},$$
(50)

where \(H(z)\) is given by Eq. (36). Using Eq. (36) in (50), we have

$$H_{0}(t_{0}-t)$$
$${}=\lim_{z\to\infty}\int\limits_{0}^{z}\frac{\sqrt{2}dz}{(1+z)\sqrt{[(1+z)^{2n}+1]}}.$$
(51)

It is evident that as \(z\to\infty\), \(H_{0}(t_{0}-t)\) tends to a constant value, \(H_{0}(t_{0}-t)\to H_{0}t_{0}=0.9588080615\), which is the cosmic age of the universe. The estimated age of the universe at this time is \(t_{0}=14.20\) Gyrs, which is quite similar to the estimates derived from observations.

7 CONCLUSIONS

The current study investigates dark energy cosmological models using a boundary term and a non-coincident gauge formulation of nonmetricity gravity. To obtain the modified field equations from the action, we have considered the arbitrary function as \(f(Q,C)=Q+\lambda C^{m}\), where \(Q\) is the nonmetricity scalar, \(C\) is the boundary term given by \(C=\mathring{R}-Q\), and \(\lambda,m\) are model parameters. The scale factor that we acquired, \(a(t)=[\sinh(k_{0}t)]^{1/n}\), is determined by taking into account the time-dependent deceleration parameter. The constants \(n\) and \(k_{0}\) are used in this calculation. By comparing the Hubble function with \(H(z)\) datasets, we were able to use likelihood analysis to determine the model parameters that best fit the data. We have performed our result analysis and discussion using cosmological parameters, including the effective equation-of-state parameter, the energy density, energy conditions, the deceleration parameter, Om diagnostic analysis, and age of the universe, using these best match values of the model parameters. The main features of the model are as follows:

  • We have found the value of the model parameters \(m=0.52^{+0.00016}_{-0.00016}\), \(\lambda=-0.005^{+0.00016}_{-0.00016}\), which confirms the presence of a boundary term that behaves just like a dark energy candidate in this theory of gravity.

  • We have found the present value of the deceleration parameter \(q_{0}=-0.35\), which shows that the model is in an accelerating phase of expansion. The value of the deceleration parameter evolves with a transition point at \(z_{t}=0.589\) from deceleration to acceleration.

  • We have found that the effective EoS parameter varies as \(-1.2<\omega^{\textrm{eff}}<0\) over redshifts \(-1<z<3\), which is a good feature of our derived model.

  • We have found that all energy conditions are satisfied, except the Strong Energy Conditions (SEC), which causes acceleration in the expansion of the universe.

  • We have found that \(\rho_{e}=\rho_{m}+\rho_{\textrm{de}}\), and as at late times \(\rho_{m}\to 0\) with \(\rho_{e}\to\rho_{\textrm{de}}\), which means that at late times the matter energy density is converted into dark energy density that causes the universe’s acceleration.

  • Our Om diagnostic analysis suggests that the present model is a quintessence dark energy model, which is equivalent to a holographic dark energy model.

  • We have found the present age of the universe as \(t_{0}=14.20\) Gyrs, which is in good agreement with the recently observed values.