1 Introduction

The study of origin, evolution, and the large-scale structure of the universe is the subject matter of cosmology. It is a well-established fact that our universe is spatially homogeneous and isotropic (SHI) at large scale in the units of Megaparsecs and \(Giga\,yrs\). A veteran Friedman-Lemaitre-Robertson-Walker (FLRW) space-time represents the SHI universe. The solution of the Einstein Field Equations for FLRW space-time results in a universe that is both expanding and decelerating, indicating that the galaxies within it are gradually moving away from us at a diminishing rate over time. The present-day surveys and observations [1,2,3,4,5] suggest different types of scenario which tells us that the various galaxies are moving away from us at a relatively increasing pace with time. The literature tells us that cold dark matter of gravitating origin and dark energy of repulsive anti-gravitating origin are present in abundance in our universe which is responsible for the change in the mode of the universe.

The cosmological constant once introduced by Einstein in his field equations to describe a physical static universe was resurrected in order to explain the acceleration in it known as \(\Lambda\)CDM model, which fits best on observational ground [6,7,8,9,10,11]. Despite this, it fails in explaining fine-tuning that vacuum energy is very small compared to typical particle physics scales [12]. Cosmological tracking solutions [13, 14] were proposed to overcome the issues against the \(\Lambda\)CDM. By that time, a different way of thinking was developed. It was thought that Dark energy must arise from the gravitational origin and some nonlinear term of Ricci scalar R in the form of an arbitrary function f(R) in the Einstein Hilbert Action to arrive at an alternative to Einstein’s theory. The name was given f(R) gravity. In this theory, acceleration is obtained spontaneously from the gravitational sector.

In 2003, the \(f(R)= R + \frac{a}{R} + {b}{R^2}\) formalism was first enunciated by Nojiri and Odintsov [15] to explain the early inflation and the acceleration in late times. Starobinsky [16] used a different form of f(R) and developed a cosmology without a cosmological constant. Sotiriou and Liberati [17, 18] presented a Palatini Metric-affine formalism of f(R) gravity. It is noteworthy to mention the work of Srivastava [19] who has developed a model in f(R) gravity, which represents both early (inflation) and late acceleration in the Universe. Some remarkable work on f(R) and other modified  gravity have also been carried out by many authors, which are stated in [20,21,22,23,24,25,26,27,28,29,30]

In this paper, we have developed a model filled with perfect fluid in f(R) gravity by taking \(R + \alpha R^2 + \beta R^3\) as a particular form of f(R) . In the background of FLRW space-time, we have considered two field equations that resemble Einstein field equations (EFE). The additional terms which arise due to the nonlinear f(R) function are shifted to the right-hand side of field equations that are treated as energy expressions due to curvature-inspired geometry. As a result, they bring acceleration in the universe and put anti-gravitating negative pressure in it. The paper is presented in the following sequence. In section II, we have developed f(R) field equations for FLRW space-time, then taking a particular case \(f(R)= R + \alpha R^2 +\beta R^3\), we have found numerical solutions for Hubble, deceleration, and jerk parameters. In section III, we have used a data set of 46 Hubble points to estimate the present value of matter-energy parameter \((\Omega _m)\), density \((\rho _m)\) and equation of state (EoS) parameter for curvature \((\omega _k)\). On the basis of these estimated values, we present Error plots for Hubble parameter and distance modulus. The graphs show that our theoretical plots fit well with the observed Hubble and Pantheon data. Moreover, the plots match at par with the \(\Lambda\)CDM model. The deceleration parameter q versus redshift z plot describes the accelerating universe at the present epoch. The transition of red shift for our model is obtained at \(z_{{{\text{tr}}}} \simeq 0.6843\) causing transient acceleration in the early and late times, which is in good agreement with \(\Lambda\)CDM. In section III, we have also carried out the state finder analysis for our model. The analysis confirms that our model lies near \(\Lambda\)CDM and it fits well on the observational ground. In the last section, we interpret our work for our obtained curvature dominated model.

2 Einstein field equations in f(R) -formalism

The general action for f(R) gravity [15] coupled with the action of a matter field with matter Lagrangian \(S_m\) reads

$$\begin{aligned} S= \int \Big (\frac{1}{16\pi G} f(R)+S_m\Big )\sqrt{-g} \textrm{d}x^4, \end{aligned}$$
(1)

where f(R) is the function of the Ricci scalar R. Here, the function \(f(R) = R+\alpha R^2+\beta R^3\) is considered for inflation, which was first proposed by Starobinsky [16]. The function f(R) can be seen as the origin of the quantum correction on Friedmann equations. The term \(R^2\) of function f(R) is the natural correction in GR, which provides an inflationary scenario in the early Universe. Also, the Starobinsky model shows the best compatibility according to the latest observations of the Universe [31] and this model serves as a possible substitute for the scalar field models describing inflation [30]. Clearly, the function f(R) with negative exponents of the curvature term is capable of explaining the current accelerating expansion.

The Einstein Field Equations in f(R) -gravity are given as:

$$\begin{aligned} {} f'(R)R_{ij}-\frac{1}{2}f(R)g_{ij}= T_{ij} -g_{ij}\square f'(R)+\nabla _i\nabla _jf'(R), \end{aligned}$$
(2)

where we have taken \(8 \pi G\) and velocity of light c as unity. In this equation, \(f'(R)\) is the differentiation of f(R) with respect to R and other mathematical symbols have their usual meaning.

We consider FLRW flat space-time, which is a SHI filled with perfect fluid given by,

$$\begin{aligned} {} \textrm{d}s^2=\textrm{d}t^2-a^2(t)(\textrm{d}x^2+\textrm{d}y^2+\textrm{d}z^2). \end{aligned}$$
(3)

The energy-momentum tensor of a perfect fluid is as follows:

$$\begin{aligned} T_{ij}=(\rho _m +p_m)u_{i}u_{j}-p_m g_{ij}, \end{aligned}$$
(4)

where \(\rho _m\) and \(p_m\) are the matter density and the pressure of a perfect fluid. In co-moving coordinates, the four-velocity vector \(u^i\) satisfies \(u^i u_i = 1\).

The field equations given by Eq. (2) are solved for metric Eq. (3) and energy-momentum tensor given by Eq. (4) are obtained as,

$$\begin{aligned} {} G^0_0 = 3\frac{\dot{a}^2}{a^2}= \frac{\rho _m}{f'}+\frac{1}{f'} \bigg [\frac{1}{2}(f-f'R)-3\frac{\dot{a}}{a}\dot{R}f'' \bigg ] \end{aligned}$$
(5)

and

$$\begin{aligned} {} G^1_1= & {} G^2_2 = G^3_3 = 2\frac{\ddot{a}}{a}+\frac{\dot{a}^2}{a^2}=\nonumber \\{} & {} -\frac{1}{f'} \bigg [3\frac{\dot{a}}{a}f''\dot{R}+f'''\dot{R}^2+f''\ddot{R}+\frac{Rf'}{2}-\frac{f}{2} \bigg ], \end{aligned}$$
(6)

where prime and dot stand for differentiation with respect to R and proper time t respectively. At present, we take pressure-less fluid as \(p_m = 0\).

The field Eqs. (5) and (6) become Einstein field equations for FLRW space-time when \(f(R)= R\). The equations of motion (5) and (6) describe the expansion of the universe, as observed by the negative value of the deceleration parameter. These equations must also explain the acceleration of the universe, which is achieved by considering an arbitrary function of the Ricci scalar in f(R) gravity theory. This results in additional energy density and pressure terms, labeled as \(\rho _k\) and \(p_k\), respectively, on the right-hand side of the equations, which are a result of curvature dominance. These terms are assumed to arise from the additional terms in the \(G_0^0\), \(G_1^1\), \(G_2^2\), and \(G_3^3\) equations.

The curvature energy  \(\rho_k\) and curvature pressure \(p _k\) are given as follows:

$$\begin{aligned} {} \rho _{k}=\frac{1}{2}(f-R f')-3\frac{\dot{a}}{a}\dot{R}f'', \end{aligned}$$
(7)

and

$$\begin{aligned} {} p_k=3\frac{\dot{a}}{a}f''\dot{R}+f'''\dot{R}^2+f''\ddot{R}+\frac{Rf'}{2}-\frac{f}{2}. \end{aligned}$$
(8)

More specifically, we can express field Eqs. (5) and (6) in terms of the Hubble parameter \(H=\frac{\dot{a}}{a}\) and its derivative \(\dot{H}\) as follows:

$$\begin{aligned} {} 3H^2 = \frac{\rho _m +\rho _k}{f'}, \end{aligned}$$
(9)

and

$$\begin{aligned} {} 2\dot{H}+3H^2=-\frac{p_k}{f'}. \end{aligned}$$
(10)

The purpose of this work is to form a cosmological model of the universe which fits best on the observational ground. At present, we have two types of data sets which are described as follows:

  • Hubble observational data set (OHD) There is a data set of 46 H(z) observational Hubble points in the range of \(0\le z\le 2.36\), which are obtained from cosmic chronometric technique [32,33,34].

  • Pantheon data Set There is a data set of 1048 SNIa apparent magnitude measurements which are known as the Pantheon compilation [35]. This includes 276 SNIa data set of the Pan-STARRS1 Medium Deep Survey in the range \((0.03< z < 0.65)\) along with SNIa data set from SDSS, SNLS, and low-z HST samples.

So we express the field Eqs. (9) and (10) in terms of derivatives of the Hubble parameter with respect to redshift z instead of time. For this, we use the following transformation formula for redshift, \(1+z=\frac{a_0}{a}\), where \(a_0\) is the present value of the scale factor taken as 1. We obtain the following field Eqs. as per our requirement.

$$\begin{aligned}{} & {} 3 f' H^2 + 0.5 \bigg (f +6 f'(2 H^2 -(1+z) H \frac{\textrm{d} H}{\textrm{d}z} \bigg ) +\nonumber \\{} & {} 18 (1+z) f'' H^2 \bigg (3 H \frac{\textrm{d} H}{\textrm{d}z}-(1+z) \bigg (\frac{\textrm{d} H}{\textrm{d}z}\bigg )^2 - (1+z) H \frac{\textrm{d}^2 H}{\textrm{d}z^2} \bigg )=\rho _m, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \frac{\textrm{d}^3 H}{\textrm{d} z^3}=\frac{3Hf' - 0.5 f - 6 f'H^2}{6(1 + z)^3 f'' H^3} +\nonumber \\{} & {} \frac{\textrm{d}H}{\textrm{d}z} \bigg (\frac{f' + 36 f''H^2 - 6(1 + z) f'' H^2}{6(1 + z)^2 f'' H^2} \bigg ) +\nonumber \\{} & {} \left( \frac{\textrm{d}H}{\textrm{d}z} \right) ^2 \bigg (\frac{1}{(1 + z)H} + \frac{54f'''H}{(1 + z) f''} \bigg )+ \nonumber \\{} & {} \left( \frac{\textrm{d}H}{\textrm{d}z} \right) ^3 \bigg (\frac{-36 f'''}{f''} + \frac{1}{H^2} \bigg ) +\nonumber \\{} & {} \bigg (\frac{\textrm{d}H}{\textrm{d}z} \bigg )^4 \bigg (\frac{6(1 + z) f'''}{f''H} \bigg ) + \frac{d^2 H}{\textrm{d} z^2} \bigg (\frac{-3 -(1+z)}{ (1 + z)^2} \bigg ) +\nonumber \\{} & {} \bigg (\frac{\textrm{d}^2 H}{\textrm{d} z^2} \bigg )^2 \bigg (\frac{ 6(1 + z) f''' H}{ f''} \bigg )+\nonumber \\{} & {} \frac{\textrm{d}H}{\textrm{d}z} \frac{\textrm{d}^2 H}{\textrm{d}z^2} \bigg (\frac{ -36f''' H^2 + 4f''}{f'' H} \bigg ) + \bigg (\frac{\textrm{d}H}{\textrm{d}z}\bigg )^2 \frac{\textrm{d}^2 H}{\textrm{d} z^2} \bigg (\frac{6(1 + z) f'''}{ f''} \bigg ), \end{aligned}$$
(12)

In obtaining Eqs. (11) and (12), we required the following expressions for the Ricci scalar R and its time derivative \(\dot{R}\) in terms of the Hubble parameter H and its derivative with respect to redshift z,

$$\begin{aligned} R&= -6(\dot{H}+ 2 H^2)\end{aligned}$$
(13)
$$\begin{aligned}&=6H\left( \frac{\textrm{d}H}{\textrm{d}z}(1+z)-2H\right) ,\end{aligned}$$
(14)
$$\begin{aligned} \dot{R}&= -6( \ddot{H} +4 H\dot{H})\end{aligned}$$
(15)
$$\begin{aligned}&= -6\left( -3H^2(1+z)\frac{\textrm{d}H}{\textrm{d}z}+(1+z)^2H\left( \frac{\textrm{d}H}{\textrm{d}z}\right) ^2+H^2(1+z)^2\frac{\textrm{d}^2H}{\textrm{d}z^2}\right) , \end{aligned}$$
(16)

and

$$\begin{aligned} \ddot{R}= & {} -24 (1+z)^2 H^2 \bigg (\frac{\textrm{d} H}{\textrm{d} z} \bigg )^2 \nonumber \\{} & {} -18 (1+z) H^3 \frac{\textrm{d} H}{\textrm{d} z} -6 (1+z)^2 H^3 \frac{\textrm{d}^2 H}{\textrm{d} z^2}\nonumber \\{} & {} -24 (1+z)^3 H^2 \bigg ( \frac{\textrm{d} H}{\textrm{d} z} \bigg ) \bigg ( \frac{\textrm{d}^2 H}{\textrm{d} z^2} \bigg ) + 6 (1+z)^3 H \bigg ( \frac{\textrm{d} H}{\textrm{d}z} \bigg )^3 \nonumber \\{} & {} + 6 (1+z)^3 H^3 \frac{\textrm{d}^3 H}{\textrm{d} z^3}. \end{aligned}$$
(17)

3 Numerical solutions and the dynamics of the model

As stated earlier, we want to develop a model which provides an acceleration in the universe at present. For this purpose, we consider a particular form \(f(R)= R + \alpha R^2 +\beta R^3\). Previously, some authors [15, 16] have used second-order nonlinear Ricci scalar to develop an accelerating universe model. Thus, we were inspired from the earlier work [19, 20] who have used f(R) -gravity in developing their model. So, for the given form of f(R), \(f'(R)=1+2\alpha R+3\beta R^2\), \(f''(R)= 2\alpha + 6\beta R\) and \(f'''(R)= 6\beta\).

3.1 The deceleration and jerk parameters

The analysis of the model in any theory of gravity is greatly influenced by the geometrical parameters. Jerk parameter (j) and deceleration parameter (q) are available in addition to the Hubble parameter [36, 37]. The rate of change of acceleration is determined by the jerk parameter. The sign of j is crucial to determine if the behavior of the Universe has changed during evolution because the deceleration parameter is insufficient to account for the full cosmic dynamics. For models with positive values of \(j_0\) and negative values of \(q_0\), there is a shift from deceleration to acceleration. Flat \(\Lambda\)CDM models have a constant jerk \(j=1\). The accelerating and decelerating behavior of the universe are shown by the negative and positive signs of the deceleration parameter, respectively.

The deceleration and jerk parameters q and j are related to the second and third order of scale factor a respectively and are defined as:

$$\begin{aligned} q&= -\frac{\ddot{a}}{aH^2} \\&= -1 + (1+z) \frac{1}{H} \frac{\textrm{d}H}{\textrm{d}z}, \end{aligned}$$

and

$$\begin{aligned} j&=\frac{\dddot{a}}{aH^3}\\&=1+3\frac{\dot{H}}{H^2}+\frac{\ddot{H}}{H^3}\\&=1-2\frac{(1+z)}{H} \frac{\textrm{d}H}{\textrm{d}z}+ \frac{(1+z)^2}{H^2} \left( \frac{\textrm{d}H}{\textrm{d}z}\right) ^2 + \frac{(1+z)^2}{H}\frac{\textrm{d}^2 H}{\textrm{d}z^2}. \end{aligned}$$

The \(\Lambda\)CDM model fits best on the observational ground, which provides us the present value of the deceleration and jerk parameters as \(q_0 = -0.55\) and \(j_0 = 1\) [37, 38]. Planck’s latest survey [32] provides us with the present value of Hubble constant as \(H_0\simeq 67.32\, \textrm{Km}/\textrm{sec}/\textrm{Mpc} \simeq 0.07 \, \textrm{Gyr}^{-1}\) [39]. From these values, we can estimate the present values of the first and second derivatives of the Hubble parameter as \((\frac{\textrm{d}H}{\textrm{d}z})_0 = 0.0315\) and \((\frac{\textrm{d}^2\,H}{\textrm{d}z^2})_0 = 0.48825\).

The energy parameter \(\Omega _m\) is defined as \(\Omega _m=\frac{\rho _m}{\rho _c}\), where \(\rho _c= \frac{8\pi G}{3\,H^2}\) is the critical density. Its present value is given as \(\rho _{c0} = 1.88 \times 10^{-29}h_0^2 \, \textrm{gm}/\textrm{cm}^3\), where \(0.5<h_0<1\) [40]. The equation of state (EoS) parameter for curvature-inspired pressure and density may be defined as \(\omega _k=\frac{p_k}{{\rho }_k}\). If we put the present values of the Hubble parameter and its derivatives in Eqs. (7), (8) and (11), we get the following relations among the parameters \(\alpha\), \(\beta\), \(\Omega _{m0}\) and \(\omega _{k0}\) as:

$$\begin{aligned} {} \beta =261.437+1.55647~\alpha -17784.8~ \Omega _{m0} \end{aligned}$$
(18)
$$\begin{aligned} {} \alpha = \frac{22.5937+32.2766~\omega _{k0} -952.293~ \Omega _{m0}-2195.69~ \omega _{k0} ~\Omega _{m0}}{0.7+ \omega _{k0}} \end{aligned}$$
(19)
Fig. 1
figure 1

Plots of deceleration parameter q and jerk parameter j versus red shift z, respectively, for fixed value of \(\alpha = 1.0027\) and \(\beta = -5074.44\)

Full size image

In Fig. 1, we see that the deceleration parameter is negative at present. This shows that we are living in an accelerating universe. At approximately \(z_{{{\text{tr}}}} \simeq 0.6843\), the red shift transitions from positive to negative, indicating a shift from a decelerating universe in the past to an accelerating universe in present time. As \(z\rightarrow 0\) the value of j tends toward 1, indicating that the jerk parameter is currently converging toward \(\Lambda\)CDM.

3.2 Statistical analysis of the parameter

      As stated earlier in Section(II), Hubble data set of 46 points indicated as \(H_{{{\text{obs}}}}\) is used. Since Eq. (12) is a nonlinear third-order differential equation it is not possible to find its analytical solution. Therefore, we opt to obtain its numerical solution by providing the initial values of the first and second derivatives of H. The corresponding values of the Hubble parameter obtained from Eq. (12) are referred to as \(H_{\text{th}}\). To obtain more accurate estimates for the parameters \(\Omega _{m0}\) and \(\omega _{k0}\), we employ the Chi-square test. The Chi-square test is a method employed to achieve greater accuracy in estimations and is defined as

$$\begin{aligned} \chi ^{2}=\sum \limits _{i=1}^{46}\frac{[H_{obs}(z_{i})-H_{th}(z_{i})]^{2}}{err {(z_{i})}^{2}}, \end{aligned}$$
(20)

where \(err{(z_{i})}\) denotes the standard error in OHD.

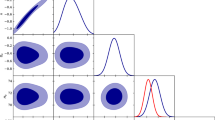
The minimum value of Chi-square is found to be \(\chi ^2 =19.348\) for \(\omega _{k0} = -0.44\) and \(\Omega _{m0} = 0.25\). From the Eqs. (18) and (19), we get \(\alpha =1.0027\) and \(\beta =-5074.44\). The process is shown in Fig. 2. in which blue dot is the estimated point \((-0.44, 0.25, 19.348)\) for minimum Chi-square.

Fig. 2
figure 2

Blue and Red dots indicate the present values of \(\Omega _{m0}\) and \(\omega _{k0}\) of our model in the Chi-square and Region plots with \(1\sigma\) error respectively

Full size image

3.3 Distance modulus and apparent magnitude for SNIa observations:

In this expanding Universe, there are different ways to measure the distance between two co-moving objects. Hogg [41] explains the distance measurements in cosmology in detail. The distance modulus \(\mu (z)\) is defined as [8, 38]

$$\begin{aligned} \mu (z)= m-M = 5 \textrm{Log} D_l(z)+\mu _{0}, \end{aligned}$$
(21)

where m and M are the apparent and absolute magnitude of the standard candle respectively. The luminosity distance \(D_l(z)\) and nuisance parameter \(\mu _0\) are defined as

$$\begin{aligned} \mu _0= 25+5 \textrm{Log} \big (\frac{c}{H_0} \big ), \end{aligned}$$
(22)

and

$$\begin{aligned} D_l(z)=(1+z)H_0 \int _0^z{\frac{1}{H(z*)} dz*}, \end{aligned}$$
(23)

respectively.

By carrying numerical integration of tabulated values of the Hubble parameter, we have been able to find a plot of distance modulus versus redshift for our model. We have an error bar plot for 620 supernova data sets which include 580 SNIa union compilation plus 40 binned data from [21, 42]. It is interesting to see that our theoretical plot coincides with the corresponding \(\Lambda\)CDM plot, which is displayed in Fig 3b.

We have plotted the errors related to the Hubble parameter and the distance modulus parameter in Fig. 3. We observed that our model is consistent with \(\Lambda\)CDM.

Fig. 3
figure 3

Plots (a) and (b) show the deviations of our model from \(\Lambda\)CDM by blue color error bars of observational dataset H(z) and SNIa data respectively. Red and black lines represent our obtained model and the \(\Lambda\)CDM, respectively

Full size image

3.4 EoS-parameter and Matter energy density

      Equation of state (EoS) parameter, \(\omega _k\), for curvature dominated energy is defined as \(\omega _k = \frac{p_k}{{\rho }_k}\), where \(\rho _k\) and \(p_k\) are given by Eqs. (7) and (8) respectively. In \(\omega _k \sim z\) plot, \(\omega _k\) is negative and is equal to \(-0.44\) at present (see Fig. 3). The curvature-dominated pressure \(p_k\) becomes negative from positive at the red-shift transition \(z \simeq 1.65\). The EoS behaves in a certain manner that is if \(\omega _k \in (0,1)\), it will be called the perfect fluid model. If \(\omega _k =1\), then \(p = \rho\) and is called a stiff matter field. If \(\omega _k = 0\), then a pressure-less universe is called as dust field universe but the energy density is not equal to zero \((\rho \ne 0)\). If \(\omega _k <0\), it will be called dark energy, i.e., negative pressure created. It is also called the dark energy universe. If \(\omega _k = -1\), it is said to be Lambda cosmology, i.e., \(\Lambda\)-CDM, i.e., Lambda cold dark matter model which shows standard dark energy model. If \(\omega _k \in (0,-1)\), it is called the Quintessence model [43, 44]. If \(\omega _k < -1\), it is called Ghost Model or Phantom Model. If \(\omega _k =\frac{1}{3}\), it is a radiation state model.

Therefore, from that, it can be concluded that the accelerated dark energy model is developed due to negative pressure.

Fig. 4
figure 4

Plots of matter density \(\rho _m\) and EoS-parameter \(\omega _k\) versus red-shift, respectively, for fixed value of \(\alpha = 1.0027\) and \(\beta = -5074.44\)

Full size image

The numerical values of H, \(\frac{\textrm{d}H}{\textrm{d}z}\) and \(\frac{\textrm{d}^2\,H}{\textrm{d}z^2}\) for red-shift z are calculated from Eq. (12) and then using Eq. (11), we evaluate matter density \(\rho _m\). The related plot of \(\rho _m\sim z\) can be seen in Fig. 4. As per observations, the value of matter-energy density should be \(\rho _{m0}= \Omega _{m0} \times \rho _{c0}\) at present. So putting \(\Omega _{m0}\simeq 0.3\), \(\rho _{c0}= 1.88 \times 10^{-29}\times h_0^2 \, gm/cm^3\) and \(h_0\simeq 0.68\) we get \(\rho _{m0}\simeq 0.27744\times 10^{-29}\) \(gm/cm^3\), which is consistent with recent observations. The unit for \(\rho _m\) is \(\textrm{gm}/\textrm{cm}^3\).

3.5 Statefinder Analysis

      A large number of dark energy cosmological models have been proposed since it is found that our universe is accelerating. Based on EoS-parameter \(\omega _{de}\) for dark energy, the most eminent models \(\Lambda\)CDM (\(\omega _{de}\)=1), QCDM (\(\omega _{de} \ge -1/3 \le -1\)), KCDM (\(\omega _{de}\) is negative and variable), Chaplygin gas energy model and Brain world model etc. are proposed so far. The references related to these models can be seen in [45,46,47]. In the year 2003, Sahni et al. [25, 30] proposed an analysis to examine the different categories of established dark energy models. This analysis is based on deceleration parameter q, jerk parameter r and snap parameter s, which are defined as

$$\begin{aligned} r=\frac{\dddot{a}}{a H^3} ,\quad s=\frac{r-1}{3(q-1/2)} \end{aligned}$$
(24)

where \(q \ne 1/2\) and focused on two-dimensional \(s \sim r\) and \(q\sim r\) plots. The temporal evolution of several dark energy models is defined in this configuration by distinct trajectories in the \(r-s\) and \(r-q\) planes. The statefinder pair for \(\Lambda\)CDM and standard cold dark matter(SCDM) in a spatially flat FLRW backdrop are \(\{r,s\} = \{1, 0\}\) and \(\{1,1\}\) respectively. \((r>1,s<0)\) corresponds to Chaplygin gas model while \((r<1,s>0)\) represents quintessence model.

We have presented the plots for our model (see Fig. 5). It is interesting to see that our model approaches to \(\Lambda\)CDM from both ends, i.e., from Chaplygin gas to \(\Lambda\)CDM and from quintessence to \(\Lambda\)CDM in \(s \sim r\) plot. In \(q\sim r\) plot, our model passes nearby \(\Lambda\)CDM and also passes by the point (\(r = 1\), \(q = -1\)) which corresponds to the steady-state model (SS). So we can say that our model lies near \(\Lambda\)CDM.

Fig. 5
figure 5

Plots of \(s-r\) and \(q-r\) for state finder analysis for fixed value of \(\alpha = 1.0027\) and \(\beta = -5074.44\)

Full size image

4 Conclusions

      We have probed a cosmological model with the perfect fluid-filled universe in f(R) -gravity by taking \(R + \alpha R^2 + \beta R^3\) as a particular form of f(R) function. The field equations in f(R) gravity are solved for FLRW spatially homogeneous and isotropic space-time. The terms which arise due to the nonlinear f(R) function are shifted to the right-hand side of the field equations that are treated as energy due to curvature-inspired geometry. As a result, it produces acceleration and anti-gravitating negative pressure in the universe. The plots show that our theoretical plots fit well with the observational Hubble and Pantheon data. Moreover, the plots match at par with the \(\Lambda\)CDM model. The deceleration parameter q versus redshift z plot describes the accelerating universe at the present epoch. The transition redshift for our model is obtained at \(z_{tr} \simeq 0.6843\), which is in good agreement with \(\Lambda\)CDM. We have also carried out the state finder analysis for our model, which confirms that our model lies near \(\Lambda\)CDM and it fits well on the observational ground.