1 INTRODUCTION

Different astronomical observation like SN Ia [1, 2], redshift survey [3], cosmic microwave background radiation data [4, 5] almost suggest that the universe is at present expanding with acceleration and thereby the equation-of-state (EoS) parameter \(\omega=p/\rho\) (where \(p\) is pressure and \(\rho\) is the density) shows \(p+\rho=0\) i.e., \(\omega=-1\), indicating the simplest dark energy term as the vacuum energy which is mathematically equivalent to a cosmological constant \(\Lambda\). The recent detection of Integrated Sachs-Wolfe effect [6] also gives a strong and independent support to dark energy. Principally, any physical field with positive energy density along with negative pressure, violating the strong energy conditions, may cause dark energy as an effect of repulsive gravitation. The paramount characteristic of dark energy is a constant very slowly changing energy density with the expansion of the universe, but its actual value is yet unknown [7–14]. In 2006, Caldwell et al. [15] and later on Yadav [16] suggested the idea of a transition of the universe from a decelerating phase to an accelerating one. Though the actual cause of such a sudden transition and the source responsible for the accelerated expansion is still not known, but it lies in the detection of a kind of repulsive force which is called dark energy. Which, on detection, might be a disclosure to the gravitational effect of zero point energies of particles and fields. Other simplest alternatives of dark energy are:

(i) quintessence (\(\omega\geq-1\) or \(p+\rho\geq 0\) ),

(ii) phantom energy (\(\omega\leq-1\) or \(p+\rho\leq 0\) ),

(iii) quintom (crossing from a phantom region to a quintessence region).

All the above are described by minimally coupled scalar fields.

In anisotropic models, the generalization of the EoS parameter of dark energy is characterized by the EoS parameters taken separately on each spatial axis consistent with the considered metric. Unlike the Robertson-Walker metric, Bianchi-type metrics can consider the anisotropy of the EoS parameter according to their characteristics. The large-scale structures data [17] and type Ia supernovae [18, 19] observations do not rule out the possibility of an anisotropic dark energy [20, 21]. Koivisto and Mota [22] have shown that the accelerated expansion of the universe driven by a field with an anisotropic equation of state leads to introduction of three skewness parameters quantifying the deviation of pressure from isotropy. But such studies are based on the assumption that the anisotropy in expansion is caused by an anisotropic fluid in Bianchi type I space-time.

However, an anisotropic fluid must not essentially promote the anisotropy in the expansion. Even such energy sources may support making the expansion isotropic, as earlier mentioned by Akarsu and Kilinc [23] and also shown within a Bianchi type III model [24, 25]. Thus even observing an isotropic expansion of the present universe, the possibility of dark energy with an anisotropic EoS cannot be ruled out.

While FRW models are spatially homogeneous and isotropic in nature, which establishes the isotropic, homogeneous and expanding nature of the physical universe, the early universe is not believed to be exactly uniform, and it has been sufficiently confirmed through inferences of the CMB experiments, about the spherical symmetry of the present evolving universe whose interior is entirely isotropic and homogeneous, but near the Big Bang singularity it had an anisotropic structure. The WMAP data analysis supports the fact that the universe has a preferred direction, and it should reach a slightly anisotropic geometry. Therefore, in view of the background anisotropy, the models with anisotropic background are more suitable to describe the early stages of the universe.

Bianchi type I models are among the simplest models of an anisotropic universe that describe the existence of anisotropy in its early stage. Kumar and Singh [26] studied the minimal interaction of a perfect fluid and anisotropic dark energy by applying the special law of variation of Hubble’s parameter that yields a constant value of the deceleration parameter. Various authors studied Bianchi cosmic models in different contexts like \(f(R,T)\) gravity, bulk viscosity, etc. [27–31].

In this paper we undertake a search for a transitioning model in Bianchi-III space-time within the framework of Lyra’s manifold. Akarsu et al. in 2014 [32] proposed a hybrid expansion law that provides an elegant explanation of a transition of the universe from deceleration to acceleration. Lyra in 1951 [33] first proposed a scalar-tensor theory which gives some important modifications of the Riemann geometry by introducing a time-varying gauge function. Lyra’s modified theory becomes more useful and attractive due its similar effects to Einstein’s theory. Harfold in 1970 and 1972 [34, 35] found that the time-varying vector field \(\beta(t)\) behaves similarly to the cosmological constant \(\Lambda(t)\) in general relativity. Recently, various authors (Sen and Vanstone, Bhamra, Singh and Singh; Rahaman et al., Pradhan et al., Yadav, Yadav and Haque, Yadav and Bhardwaj, Bali et al., Sahoo et al. [36–46] studied different cosmological models based on Lyra’s geometry in various physical contexts.

Here we take a generalized form of the hybrid expansion law for the scale factors in Bianchi III space-time with anisotropic dark energy, which is caused by variability of the EoS parameters on account of three skewness parameters \(\delta,\gamma\), and \(\eta\) along the \(x,y\), and \(z\) directions, respectively, and a perfect fluid by using an approach similar to that of Kumar and Singh [26]. The so obtained explicit expressions for the cosmological parameters are new and different.

The paper is organized as follows: in Section 2, the field equations are developed for Bianchi-III space-time within Lyra’s manifold. In Section 3, the generalized hybrid expansion law is considered for solution of the field equations. In Section 4, we determine the cosmological parameters and describe the consequences of energy conditions and cosmological parameters with graphic analysis. In Section 5, we discuss the stability condition and validation of the derived model. In Sections 6, we discussed our results with make conclusions.

2 FIELD EQUATIONS

The anisotropic line element described by the Bianchi type III metric is

$$ds^{2}=-dt^{2}+A^{2}(t)dx^{2}+e^{-2\alpha x}B^{2}(t)dy^{2}$$
$${}+C^{2}(t)dz^{2}.$$
(1)

Here, \(A(t),B(t),C(t)\) are the metric functions describing scales along the \(x,y\), and \(z\) directions, respectively, and \(\alpha\) is a nonzero constant.

We define \(a=(ABC)^{1/3}\) as the scale factor for the space-time described by (1). Hence, the average Hubble parameter is expressed as

$$H=\frac{\dot{a}}{a}=\frac{1}{3}\left(\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right).$$
(2)

An overdot denotes the derivative with respect to cosmic time \(t\).

For the perfect fluid and anisotropic dark energy components, the Einstein’s field equations in gravitational units are

$$R^{j}_{i}-\frac{1}{2}g^{j}_{i}R+\frac{3}{2}\phi_{i}\phi^{j}-\frac{3}{4}g^{j}_{i}\phi_{k}\phi^{k}$$
$${}=-T^{(\textrm{m})i}_{j}-T^{\textrm{{(de)}i}}_{j},$$
(3)

where \(T^{(\textrm{m})i}_{j}\) and \(T^{{\textrm{(de)}}i}_{j}\) stand for the energy momentum tensors of the fluid and and dark energy, respectively:

$$T^{\textrm{(m)}}_{ij}=\textrm{diag}{[-\rho^{\textrm{(m)}},p^{\textrm{(m)}},p^{\textrm{(m)}},p^{\textrm{(m)}}]},$$
(4)
$$T^{\textrm{{(de)}}}_{ij}=\textrm{diag}{[-\rho^{\textrm{{(de)}}},p^{\textrm{{(de)}}}_{x},p^{\textrm{{(de)}}}_{y},p^{\textrm{{(de)}}}_{z}]}$$
$${}=\textrm{diag}{[-1,\omega_{x},\omega_{y},\omega_{z}]\rho^{\textrm{{(de)}}}}$$
$${}=\textrm{diag}{[-1,\omega+\delta,\omega+\gamma,\omega+\eta]\rho^{\textrm{{(de)}}}},$$
(5)

where \(p^{\textrm{(m)}},\rho^{\textrm{(m)}},\rho^{\textrm{{(de)}}}\) are the pressure, and energy densities of the perfect fluid and dark energy,. respectively; \(p_{x}=(\omega+\delta(t))\rho^{\textrm{{(de)}}}\), \(p_{y}=(\omega+\gamma(t))\rho^{\textrm{{(de)}}}\), and \(p_{z}=(\omega+\eta(t))\rho^{\textrm{{(de)}}}\) are the EoS parameters along the spatial directions; \(\delta(t),\gamma(t)\), and \(\eta(t)\) are skewness parameters which are introduced to modify the EoS parameters of the DE components, that quantifies an anisotropic nature of DE. In Eq. (3), \(\phi_{i}\) is the displacement vector defined by

$$\phi_{i}=\left(0,0,0,\beta(t)\right).$$
(6)

In a comoving coordinate system, the field equations (3) for the anisotropic Bianchi-III space-time (1), along with Eqs. (4) and (5), can be written as

$$\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{B}\dot{C}}{BC}-\frac{3}{4}\beta^{2}$$
$${}=-p^{\textrm{(m)}}-{(\omega+\delta)\rho^{\textrm{{(de)}}}},$$
(7)
$$\frac{\ddot{C}}{C}+\frac{\ddot{A}}{A}+\frac{\dot{C}\dot{A}}{CA}-\frac{3}{4}\beta^{2}$$
$${}=-p^{\textrm{(m)}}-{(\omega+\gamma)\rho^{\textrm{{(de)}}}},$$
(8)
$$\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{AB}-\frac{\alpha^{2}}{A^{2}}-\frac{3}{4}\beta^{2}$$
$${}=-p^{\textrm{(m)}}-{(\omega+\eta)\rho^{\textrm{{(de)}}}},$$
(9)
$$\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}\dot{C}}{BC}+\frac{\dot{C}\dot{A}}{CA}-\frac{\alpha^{2}}{A^{2}}+\frac{3}{4}\beta^{2}$$
$${}=\rho^{\textrm{(m)}}+\rho^{\textrm{{(de)}}},$$
(10)
$$\alpha\left(\frac{\dot{A}}{A}-\frac{\dot{B}}{B}\right)=0.$$
(11)

We have assumed that the perfect fluid and dark energy components interact minimally [23, 47, 48]. Hence, the energy conservation equations for the perfect fluid and the dark energy component can hold independently.

The energy conservation equation \(T^{(\textrm{m})i}_{j}=0\) for the perfect fluid leads to

$$\dot{\rho}^{\textrm{(m)}}+3\left(p^{\textrm{(m)}}+\rho^{\textrm{(m)}}\right)H=0,$$
(12)

while the energy conservation equation \(T^{{\textrm{(de)}}i}_{j}=0\) for dark energy yields

$$\dot{\rho}^{\textrm{{(de)}}}+3\rho^{\textrm{{(de)}}}(\omega+1)H$$
$${}+\rho^{\textrm{{(de)}}}(\delta H_{x}+\gamma H_{y}+\eta H_{z})=0,$$
(13)

and conservation of the right-hand side of Eq. (3) leads to

$$\left(R^{j}_{i}-\frac{1}{2}g^{j}_{i}R\right)_{;j}+\frac{3}{2}\left(\phi_{i}\phi^{j}\right)_{;j}$$
$${}-\frac{3}{4}\left(g^{j}_{i}\phi_{k}\phi^{k}\right)_{;j}=0.$$
(14)

Equation (14) reduces to

$$\frac{3}{2}\phi_{i}\left[\frac{\partial\phi^{j}}{\partial x^{j}}+\phi^{l}\Gamma^{j}_{lj}\right]+\frac{3}{2}\left[\frac{\partial\phi_{i}}{\partial x^{j}}-\phi_{l}\Gamma^{l}_{ij}\right]$$
$${}-\frac{3}{4}g^{j}_{i}\phi_{k}\left[\frac{\partial\phi^{k}}{\partial x^{j}}+\phi^{l}\Gamma^{k}_{lj}\right]$$
$${}-\frac{3}{4}g^{j}_{i}\phi^{k}\left[\frac{\partial\phi_{k}}{\partial x^{j}}-\phi_{l}\Gamma^{l}_{kj}\right]=0.$$
(15)

Equation (15) is identically satisfied for \(i=1,2,3\). For \(i=4\), Eq. (15) reduces to

$$\frac{3}{2}\beta\left[\frac{\partial(g^{44}\phi_{4})}{\partial x^{4}}+\phi^{4}\Gamma^{4}_{44}\right]+\frac{3}{2}g^{44}\phi_{4}\left[\frac{\partial\phi_{4}}{\partial t}-\phi_{4}\Gamma^{4}_{44}\right]$$
$${}-\frac{3}{4}g^{4}_{4}\phi_{4}\left[\frac{\partial\phi^{4}}{\partial x^{4}}+\phi^{4}\Gamma^{4}_{44}\right]$$
$${}-\frac{3}{4}g^{4}_{4}g^{44}\phi^{4}\left[\frac{\partial\phi_{4}}{\partial t}-\phi^{4}\Gamma^{4}_{44}\right]=0.$$
(16)

Equation (16) leads to

$$\frac{3}{2}\beta\dot{\beta}+\frac{3}{2}\beta^{2}\left(\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right)=0.$$
(17)

3 THE GENERALIZED HYBRID EXPANSION LAW

We assume the generalized hybrid expansion law [32, 43, 47, 49, 50] for the scale factor as follows:

$$a=\left(t^{m}e^{\lambda t}\right)^{1/n},$$
(18)

where \(m\geq 0,\lambda\geq 0\), and \(n>0\) are constants.

The DE conservation equation can be split into two parts, one is the deviation-free part and the other for deviations of the EoS parameter of \(T^{\textrm{{(de)}}}_{ij}=0\),

$$\dot{\rho}^{\textrm{{(de)}}}+3p^{\textrm{{(de)}}}\left(\omega+1\right)H=0,$$
(19)
$$\rho^{\textrm{{(de)}}}(\delta H_{x}+\gamma H_{y}+\eta H_{z})=0.$$
(20)

The dynamics of skewness parameters on \(x,y,z\) axes are considered as

$$\eta(t)=\alpha_{1}\left(H_{x}+H_{y}\right),$$
(21)
$$\delta(t)=\gamma(t)=-\alpha_{1}H_{z},$$
(22)

where \(\alpha_{1}\) is a proportionality constant. In view of Eqs. (21)–(22), the solution of Eq. (19) is read as

$$\rho^{\textrm{{(de)}}}=\rho^{\textrm{{(de)}}}_{0}a^{-3(\omega+1)},$$
(23)

where \(\rho^{\textrm{{(de)}}}_{0}\) is a positive constant.

4 SOLUTION OF THE FIELD EQUATION AND ITS PHYSICAL SIGNIFICANCE

Integrating (11) and omitting the integration constant, we obtain

$$B=A.$$
(24)

Solving Eqs. (7)–(10) together with (18), we get

$$A=l_{1}\left(t^{m}e^{\lambda t}\right)^{\frac{1}{n}}\ \exp\bigg{[}s_{1}\int{\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}dt}$$
$${}+\frac{\alpha\rho^{\textrm{{(de)}}}_{0}}{3\omega}\int{\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}dt}\bigg{]},$$
(25)
$$B=l_{2}\left(t^{m}e^{\lambda t}\right)^{\frac{1}{n}}\ \exp\bigg{[}s_{2}\int{\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}dt}$$
$${}+\frac{\alpha\rho^{\textrm{{(de)}}}_{0}}{3\omega}\int{\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}dt}\bigg{]},$$
(26)
$$C=l_{3}\left(t^{m}e^{\lambda t}\right)^{\frac{1}{n}}\ \exp\bigg{[}s_{3}\int{\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}dt}$$
$${}-\frac{2\alpha\rho^{\textrm{{(de)}}}_{0}}{3\omega}\int{\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}dt}\bigg{]}.$$
(27)

Here \(l_{1},l_{2},l_{3}\) and \(s_{1},s_{2},s_{3}\) are constants satisfying the conditions \(l_{1}l_{2}l_{3}=1\) and \(s_{1}+s_{2}+s_{3}=0\).

The deceleration parameter (DP) in the derived model is given by

$$q=\frac{d}{dt}\left(\frac{1}{H}\right)-1=\frac{mn}{(m+\lambda t)^{2}}-1.$$
(28)

The expressions for directional Hubble parameters are

$$H_{x}=\frac{1}{n}\left(\frac{m}{t}+\lambda\right)+s_{1}\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}$$
$${}+\frac{\alpha\rho^{\textrm{{(de)}}}_{0}}{3\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}},$$
(29)
$$H_{y}=\frac{1}{n}\left(\frac{m}{t}+\lambda\right)+s_{2}\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}$$
$${}+\frac{\alpha\rho^{\textrm{{(de)}}}_{0}}{3\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}},$$
(30)
$$H_{z}=\frac{1}{n}\left(\frac{m}{t}+\lambda\right)+s_{3}\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}$$
$${}-\frac{2\alpha\rho^{\textrm{{(de)}}}_{0}}{3\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}.$$
(31)

The mean Hubble parameter for the model is found as

$$H=\frac{1}{n}\left(\frac{m}{t}+\lambda\right).$$
(32)

The mean anisotropy parameter \((\Delta)\) and the shear scalar \((\sigma^{2})\) are defined as [51, 52]

$$\Delta=\frac{1}{3}\bigg{[}\left(\frac{H_{x}{-}H}{H}\right)^{2}+\left(\frac{H_{y}{-}H}{H}\right)^{2}+\left(\frac{H_{z}{-}H}{H}\right)^{2}\bigg{]}$$
$${}=\frac{2n^{2}}{3(m/t+\lambda)^{2}}\bigg{[}\zeta\left(t^{m}e^{\lambda t}\right)^{\frac{-6}{n}}$$
$${}+\frac{\alpha^{2}{\rho^{\textrm{{(de)}}}_{0}}^{2}}{3\omega^{2}}\left(t^{m}e^{\lambda t}\right)^{\frac{-6(\omega+1)}{n}}\bigg{]}$$
$${}-\frac{2n^{2}}{3(m/t+\lambda)^{2}}\left[\frac{s_{3}\alpha\rho^{\textrm{{(de)}}}_{0}}{\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+2)}{n}}\right],$$
(33)

where \(\zeta=s^{2}_{2}+s^{2}_{3}+s_{2}s_{3}\), and

$$\sigma^{2}=\frac{1}{2}\left[H^{2}_{x}+H^{2}_{y}+H^{2}_{z}-3H^{2}\right]$$
$${}=\zeta\left(t^{m}e^{\lambda t}\right)^{\frac{-6}{n}}+\frac{\alpha^{2}{\rho^{\textrm{{(de)}}}_{0}}^{2}}{3\omega^{2}}\left(t^{m}e^{\lambda t}\right)^{\frac{-6(\omega+1)}{n}}$$
$${}-\frac{s_{3}\alpha\rho^{\textrm{{(de)}}}_{0}}{\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+2)}{n}}.$$
(34)

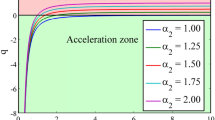
From Eq. (28), it has been found that the range of \(t\) is \(\left(0,\frac{1}{\lambda}(\sqrt{mn}-m)\right)\). At \(t<\frac{1}{\lambda}(\sqrt{mn}-m)\)\(q\) is positive, and the universe is decelerating. The phase transition take place at the value \(t=\frac{1}{\lambda}(\sqrt{mn}-m)\), but at \(t>\frac{1}{\lambda}(\sqrt{mn}-m)\)\(q\) is negative, and the universe is expanding with acceleration. This phase transition of the model is evident from the graphic behavior of \(q\), as shown in Fig. 1. Figure 2 exhibits the dynamics of the DP \(q\) as a function of the redshift \(z\). It is evident that at present time, i.e., at \(z=0\), the DP is negative, which is consistent with the recent observations.

Fig. 1
figure 1

Variation of the deceleration parameter \(q\) versus time \(t\) for \(n=3\).

Full size image
Fig. 2
figure 2

Variation of the deceleration parameter \(q\) versus redshift \(z\) for \(n=3\).

Full size image

From Eq. (33) we observe that at late times, as \(t\to\infty\), \(\Delta\to 0\) for \(\omega=-0.7\). Thus our model has a transition from an initial anisotropy to isotropy at the present epoch, which is in good harmony with current observations. The plot in Fig. 3 of the anisotropy parameter \(\Delta\) versus cosmic time shows a decreasing anisotropy parameter, tending to zero with the passage of time for \(\omega=-0.7\) i.e., for quintessence, whereas for \(\omega=-1.3\) (phantom) it seems to have a finite value indicating the nonremoval of anisotropy, which match the realistic properties of universe. Thus anisotropy is retained in the phantom model whereas in the quintessence model the universe seems to be isotropized with the passage of time.

Fig. 3
figure 3

Plot of the anisotropy parameter \(\Delta\) versus time \(t\) for \(n=3\), \(m=1.5\), \(\lambda=0.75\), \(\alpha=0.5\), \(s_{2}=0.7\), \(s_{3}=-1\).

Full size image

Solving Eq. (17), we find

$$\beta=\mu\left(t^{m}e^{\lambda t}\right)^{-3/n},$$
(35)

where \(\mu\) is an integration constant.

The skewness parameters are given by

$$\eta(t)=\alpha_{1}\left[\frac{2}{n}\left(\frac{m}{t}+\lambda\right)-s_{3}\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}\right]$$
$${}+\frac{2\alpha\alpha_{1}\rho^{\textrm{{(de)}}}_{0}}{3\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}},$$
(36)
$$\delta(t)=-\alpha_{1}\left[\frac{2}{n}\left(\frac{m}{t}+\lambda\right)+s_{3}\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}\right]$$
$${}+\frac{2\alpha\alpha_{1}\rho^{\textrm{{(de)}}}_{0}}{3\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}=\gamma(t).$$
(37)

The directional EoS parameters of DE are

$$\omega_{z}=\omega+\eta(t)=\omega+\alpha_{1}\bigg{[}\frac{2}{n}\left(\frac{m}{t}+\lambda\right)$$
$${}-s_{3}\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}\bigg{]}$$
$${}+\frac{2\alpha\alpha_{1}\rho^{\textrm{{(de)}}}_{0}}{3\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}},$$
(38)
$$\omega_{x}=\omega_{y}=\omega$$
$${}-\alpha_{1}\left[\frac{2}{n}\left(\frac{m}{t}+\lambda\right)+s_{3}\left(t^{m}e^{\lambda t}\right)^{\frac{-3}{n}}\right]$$
$${}+\frac{2\alpha\alpha_{1}\rho^{\textrm{{(de)}}}_{0}}{3\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}.$$
(39)

The energy density and pressure of the DE component read

$$\rho^{\textrm{{(de)}}}=\rho^{\textrm{{(de)}}}_{0}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}},$$
(40)
$$p^{\textrm{{(de)}}}=\omega\rho^{\textrm{{(de)}}}_{0}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}.$$
(41)

The corresponding Fig. 4 with energy density against time shows that the dark energy density of the quintessence model decreases with time while for the phantom model it increases; the spatial volume (\(V\)) is an increasing function of time, which shows the expansion of the universe.

Fig. 4
figure 4

Dark energy density versus time \(t\) for \(n=3\), \(m=1.5,\lambda=0.75\), \(\rho^{\textrm{{(de)}}}_{0}=0.75\).

Full size image

The EoS parameters depicted show that the earlier universe was highly anisotropic in dark energy, and later it is isotropized, especially as \(t\to\infty\).

The pressure and energy density of the perfect fluid are obtained as

$$p^{\textrm{(m)}}=\frac{2m}{nt^{2}}-\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}-\beta\left(t^{m}e^{\lambda t}\right)^{\frac{-6}{n}}$$
$${}-\frac{(2\omega+1)}{3\omega^{2}}\alpha^{2}{\rho^{\textrm{{(de)}}}_{0}}^{2}\left(t^{m}e^{\lambda t}\right)^{\frac{-6(\omega+1)}{n}}$$
$${}+\frac{(3\omega+1)}{3\omega}s_{3}\alpha\rho^{\textrm{{(de)}}}_{0}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+2)}{n}}$$
$${}-\omega\rho^{\textrm{{(de)}}}_{0}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}$$
$${}-\frac{(9\omega+1)}{3n\omega}\alpha\rho^{\textrm{{(de)}}}_{0}\left(m/t+\lambda\right)\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}},$$
(42)
$$\rho^{\textrm{(m)}}=\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}-\beta\left(t^{m}e^{\lambda t}\right)^{\frac{-6}{n}}$$
$${}-\frac{\alpha^{2}{\rho^{\textrm{{(de)}}}_{0}}^{2}}{3\omega^{2}}\left(t^{m}e^{\lambda t}\right)^{\frac{-6(\omega+1)}{n}}$$
$${}+\frac{s_{3}\alpha\rho^{\textrm{{(de)}}}_{0}}{\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+2)}{n}}$$
$${}-\rho^{\textrm{{(de)}}}_{0}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}.$$
(43)

The spatial scale factors \(A(t),B(t),C(t)\) vanish at \(t=0\), which means that the model has a point-type singularity at \(t=0\). However, for \(m=0\) the model has \(q=-1\) and \(dH/dt=0\). which shows a singularity-free universe with the fastest rate of expansion. This explains the future dynamics of the universe.

The perfect fluid density parameter \((\Omega^{\textrm{(m)}})\) and the DE density parameter \((\Omega^{\textrm{{(de)}}})\) are expressed as

$$\Omega^{\textrm{(m)}}=1$$
$${}+\frac{1}{\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}}\left[\frac{s_{3}\alpha\rho^{\textrm{{(de)}}}_{0}}{\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+2)}{n}}\right]$$
$${}-\frac{1}{\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}}\left[\frac{\alpha^{2}{\rho^{\textrm{{(de)}}}_{0}}^{2}}{3\omega^{2}}\left(t^{m}e^{\lambda t}\right)^{\frac{-6(\omega+1)}{n}}\right]$$
$${}-\frac{\rho^{\textrm{{(de)}}}_{0}}{\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}$$
$${}-\frac{1}{\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}}\beta\left(t^{m}e^{\lambda t}\right)^{\frac{-6}{n}},$$
(44)
$$\Omega^{\textrm{{(de)}}}=\frac{\rho^{\textrm{{(de)}}}_{0}}{\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+1)}{n}}.$$
(45)

Thus the overall density parameter \((\Omega)\) is obtained as

$$\Omega=1+\frac{1}{\frac{3}{n^{2}}\!\left(m/t+\lambda\right)^{2}}\left[\frac{s_{3}\alpha\rho^{\textrm{{(de)}}}_{0}}{\omega}\left(t^{m}e^{\lambda t}\right)^{\frac{-3(\omega+2)}{n}}\right]$$
$${}-\frac{1}{\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}}\left[\frac{\alpha^{2}{\rho^{\textrm{{(de)}}}_{0}}^{2}}{3\omega^{2}}\left(t^{m}e^{\lambda t}\right)^{\frac{-6(\omega+1)}{n}}\right]$$
$${}-\frac{1}{\frac{3}{n^{2}}\left(m/t+\lambda\right)^{2}}\beta\left(t^{m}e^{\lambda t}\right)^{\frac{-6}{n}}.$$
(46)

From Eq. (46), as \(t\to\infty\), the overall density parameter \(\Omega\to 1\), which satisfies the astrophysical observations [1, 2].

Both Figs. 6 and 7 show that the null energy condition (NEC) and dominant energy condition (DEC) are satisfied for the quintessence and phantom model, but they do not satisfy the strong energy condition (SEC). Instead of inflation, the ellipsoidal expansion of the universe is shown by the time-dependent skewness parameters.

Fig. 5
figure 5

The EoS parameters versus time \(t\) for \(n=3\), \(\mu=0.015\).

Full size image
Fig. 6
figure 6

Energy conditions versus time \(t\) for \(n=3\), \(m=1.5\), \(\lambda=0.75\), \(\rho^{\textrm{{(de)}}}_{0}=0.75\), \(\omega=-0.7\).

Full size image
Fig. 7
figure 7

Energy conditions versus time \(t\) for \(n=3\), \(m=1.5\), \(\lambda=0.75\), \(\rho^{\textrm{{(de)}}}_{0}=0.75\), \(\omega=-1.3\).

Full size image

5 STABILITY CONDITION

To check the stability of the present solution with respect to perturbation of the metric [53] the considered perturbations in three expansion factors \(a_{i}\) are

$$a_{i}\longrightarrow a_{B_{i}}+\delta a_{i}=a_{B_{i}}(1+\delta b_{i}).$$
(47)

With reference to Eq. (47), the relations representing perturbations of the volume scalar, the directional Hubble factors and the mean Hubble factor are

$$V\longrightarrow V_{B}+V_{B}\sum_{i}\delta b_{i},$$
$$\theta_{i}\longrightarrow\theta_{B_{i}}+\sum_{i}\delta b_{i},$$
$$\theta\longrightarrow\theta_{B}+\frac{1}{3}\sum_{i}\delta b_{i}.$$
(48)

For metric perturbation \(\delta b_{i}\) to be linear, the following equations must be satisfied:

$$\sum_{i}{\ddot{\delta b_{i}}}+2\sum_{i}\theta_{B_{i}}\dot{\delta b_{i}}=0,$$
(49)
$$\ddot{\delta b_{i}}+\frac{\dot{V_{B}}}{V_{B}}\dot{\delta b_{i}}+\sum_{j}\dot{\delta b_{j}}\theta_{B_{i}}=0,$$
(50)
$$\sum\dot{\delta b_{i}}=0.$$
(51)

From Eqs. (47)–(51) it follows

$$\ddot{\delta b_{i}}+\frac{\dot{V_{B}}}{V_{B}}\dot{\delta b_{i}}=0,$$
(52)

where the background volume scalar \(V_{B}\) leads to

$$V_{B}=t^{\frac{3m}{n}}\exp\left(\frac{3\lambda t}{n}\right).$$
(53)

From Eqs. (52) and (53), the metric perturbation becomes

$$\delta b_{i}=c_{2}-c_{1}\left(\frac{3\lambda}{n}\right)^{-1+\frac{3m}{n}}\Gamma\left[1-\frac{3m}{n},\frac{3\lambda t}{n}\right],$$
(54)

where \(c_{1}\) and \(c_{2}\) are integration constants.

Thus the actual fluctuation for each expansion factor \(\delta a_{i}=a_{B_{i}}\delta b_{i}\) are expressed as

$$\delta a_{i}=c_{2}t^{\frac{-3m}{n}}\exp\left(-\frac{3\lambda t}{n}\right)$$
$${}-c_{1}\left(\frac{3\lambda}{n}\right)^{-1+\frac{3m}{n}}t^{\frac{-3m}{n}}$$
$${}\times\exp\left(-\frac{3\lambda t}{n}\right)\Gamma\left[1-\frac{3m}{n},\frac{3\lambda t}{n}\right].$$
(55)

Figure 8 for \(\delta a_{i}\) versus cosmic time \(t\) shows a smaller value of \(\delta a_{i}\) at time very close to zero, which indicates a very little perturbation in the scale factor and means a negligible but significant instability. But this sharply decreases and soon becomes zero in a very short span of time with the evaluation of the universe, making further the stability of the model. Thus, in view of large-scale measurement, the solution of the present problem is stable against perturbation of the gravitation field.

Fig. 8
figure 8

Plot of \(\delta{a_{i}}\) versus cosmic time for \(n=3\), \(c_{1}=2.5\times 10^{-7}\), \(c_{2}=10^{-5}\).

Full size image

6 CONCLUDING REMARKS

In this paper, we have studied the existence of Lyra’s cosmology in a singularity-free hybrid universe within Bianchi-III space-time with the least interaction of a perfect fluid and an anisotropic dark energy. Using the generalized hybrid scale factor for the solution of the field equations, the conclusions are summarized as follows:

(i) Though the solutions to the differential equations are similar to those of Kumar and Singh [26], the obtained expressions for the cosmological parameters are different. The anisotropic dark energy has a dynamical energy density which shows a decreasing trend for the quintessence model and an increasing trend for the phantom model. From Eq. (18), for \(\lambda=0\), corresponding to power-law expansion, the dynamics of the universe seems to be described from the Big Bang to the present era, whereas \(n=0\) reasonably project a singularity-free universe. At \(t=0\), the model shows a point type singularity because both scale factors and the volume vanish.

(ii) As \(t\to\infty\), the scale factors and the volume both become large enough, and, on the other hand, dark energy pressure and pressure of perfect fluid become negligible.

(iii) The present model violates the strong energy condition, while the null and dominant energy conditions are preserved in the quintessence model. From the Big Bang, the expansion of the universe is never ceased, but te model analysis reflects that earlier its expansion was slowing down and then suddenly changes into acceleration. This change in the expansion of the universe from deceleration to acceleration is very interesting but is yet to be justified for a valid reason.

(iv) The plot of the anisotropy parameter \(\Delta\) vs. cosmic time clearly indicates that the anisotropy of dark energy is retained in the phantom model (for \(\omega=-1.3\)), while the quintessence model (\(\omega=-0.7\)) shows a transition from initial anisotropy to isotropy at the present epoch, which is in good harmony with recent observations.

(v) The behavior of the displacement vector \(\beta(t)\) is similar to that of the cosmological constant \(\Lambda(t)\), as is clear from Fig. 5, the displacement vector \(\beta(t)\) decreases with time and finally approaches zero as \(t\to\infty\).

(vi) The present model under various conditions reduces to those studied earlier by Akarsu et al. (2010) [43], Yadav et al. (2011) [48], Samanta (2013) [54], and Adhav et al. (2014) [55].

(vii) It is observed that the present hybrid cosmic model is more general. For \(\lambda=0\), the model reproduces power law expansion [46], for \(m=0\) it shows an exponential law, and for \(\lambda=0,n=1,m=1\) it turns into a linear expansion law [45]. Thus the above results are special cases of the present hybrid model.

(viii) The solution of the present model is almost perturbation=free, which has been verified for the condition of stability [53]. The fluctuations (\(\delta a_{i}\)) in the scale factor are found to start with a minimum value which in a very short time, with the evolution of the universe, approach zero, signifying almost stability of the model. Thus the present study reveals that the quintessence model is suitably describing the accelerated nature of the universe with anisotropic dark energy and is consistent with the observations. In the absence of dark energy and for some particular values of the parameters, the model possibly indicates the accelerating universe with positive pressure, which should be tested by other models.

(ix) As a final comment, we note that the derived model shows the possibility of incorporating both features of the universe, the decelerated and accelerated phases, depending on the values of the parameters under consideration. It can also be noted that for some values of the problem parameters, the derived model describes an accelerating universe with nonnegative pressure of its matter/energy constituent, which needs to be tested by other theories.

7 ACKNOWLEDGMENTS

We are grateful to the reviewers and the editor for illuminating suggestions that have significantly improved our work in terms of research quality and presentation.