1 Introduction

The analysis of observational data shows that our Universe for later stages of evolution indicates accelerated expansion. This conclusion is based on the observations of high redshift type SN Ia supernovae [1–3]. The best solution of this problem based on an assumptions and carries phenomenological character. It is confirmed that in the Universe, one of the main component is the dark energy and its negative pressure (positive energy density) has enough power to work against gravity and provide accelerated expansion of the Universe. The another component of universe is dark matter, which is considered to explain the other phenomenon known as structure formation. According to different estimations, dark energy (DE) occupies 73 % of the energy of the universe, while dark matter, about 23 % and usual baryonic matter occupy about 4 %. In physical cosmology, the simplest candidate for dark energy is the cosmological constant (Λ), but it needs to be extremely fine-tuned to satisfy a current value of the DE density, which is a serious problem. Alternatively, to explain the decay of the density, the different forms of dynamically changing DE with an effective equation of state (EoS) ω (de) = p (de)/ρ (de) < −1/3, were proposed instead of a constant vacuum energy density. Other possible forms of DE include quintessence (ω (de))>−1 [4], phantom (ω<−1) [5] etc while the possibility ω (de) < < −1 is ruled out by current cosmological data from SN Ia [6].

Harko et al. [7] proposed f(R,T) gravity theory by taking into account the gravitational Lagrangian as the function of Ricci scalar R and of the trace of energy-stress tensor T. They have obtained the equation of motion of test particle and the gravitational field equation in metric formalism both. Myrzakulov [8] presented point like Lagrangian’s for f(R,T) gravity. The f(R,T) gravity model that satisfy the local tests and transition of matter from dominated era to accelerated phase was considered by Houndjo [9]. Recently Yadav [10], Naidu et al. [11] and Ahmad and Pradhan [12] have investigated anisotropic cosmological model in f(R,T) gravity. Jamil et al [13] have reconstructed some cosmological models in f(R,T). In this paper, our aim is to study hybrid expansion of scale factor for dark energy dominated universe in f(R,T) gravity and LRS Bianchi-I space time. In the recent years, Bianchi universe have been gaining an increasing interest and tremendous impetus of observational cosmology. In connection to WMAP data [14], it is now revealed that the standard cosmological model requires a positive and dynamic cosmological parameters that resembles the Bianchi morphology [15]. According to this, the Universe should achieve the following features: a non-trivial isotropization history of Universe due to the presence of an anisotropic energy source, and ii) a slightly anisotropic special geometry in spite of the inflation. The anomalies found in the cosmic microwave background (CMB) and large scale structure observations stimulated a growing interest in anisotropic cosmological model of Universe. Here, we confine ourselves to LRS Bianchi-I model whose spatial sections are flat but the expansion or contraction rate are direction dependent.

In this paper, we search the existence of LRS Bianchi-I DE model in f(R,T) gravity and examine a cosmological scenario by proposing hybrid expansion law for scale factor. We observe that the hybrid expansion law gives time dependent DP, representing a transitioning Universe from early decelerating phase to current accelerating phase. The paper is organized as follows: the metric and field equations are presented in Section 2. Section 3 deals the cosmology for hybrid expansion law. Finally the conclusions are given in Section 4.

2 The Metric and Field Equations

We consider the space-time metric of LRS Bianchi type I as

$$ ds^{2}=-dt^{2}+A^{2}(t)dx^{2}+B^{2}(dy^{2}+dz^{2}) $$
(1)

where A(t) and B(t) are directional scale factor.

The action of f(R,T) gravity is given by

$$ S=\frac{1}{16\pi}\int{f(R,T)\sqrt{-g}d^{4}x}+\int{L_{m}\sqrt{-g}d^{4}x} $$
(2)

Where R, T and L m are the Ricci scalar, the trace of the stress-energy tensor of matter and the matter Lagrangian density respectively.

The stress-energy tensor of matter is given by

$$ T_{ij}=-\frac{2}{\sqrt{-g}}\frac{\delta \sqrt{-g}L_{m}}{\delta g^{ij}} $$
(3)

The gravitational field equation of f(R,T) gravity is given by

$$\begin{array}{@{}rcl@{}} &&f_{R}(R,T)R_{ij}-\frac{1}{2}f(R,T)g_{ij}+\left(g_{ij}\triangledown^{i}\triangledown_{i}- \triangledown_{i}\triangledown_{j}\right)f_{R}(R,T)\\ &&\quad= 8\pi T_{ij}-f_{T}(R,T)T_{ij}-f_{T}(R,T){\Theta}_{ij} \end{array} $$
(4)

where \(f_{R}(R,T) = \frac {\partial f(R,T)}{\partial R}\), \(f_{T} = \frac {\partial f(R,T)}{\partial T}\), Θ ij =−2T ij −p g ij and \(\triangledown _{i}\) denotes the covariant derivative.

The stress-energy tensor is given by

$$ T_{ij}= T^{(m)}_{ij} + T^{(de)}_{ij} $$
(5)

where \(T^{(m)i}_{j}\) and \(T^{(de)i}_{j}\) are energy momentum tensor of perfect fluid and dark energy respectively. These are given by

$$ T^{(m)i}_{j} = diag[-\rho^{(m)}, p^{(m)}, p^{(m)}, p^{(m)}] $$
(6)

and

$$ T^{(de)i}_{j}=diag\left[-\rho^{(de)}, p^{(de)}_{x}, p^{(de)}_{y}, p^{(de)}_{z}\right] = diag[-1, \omega^{(de)}\rho^{(de)}, \omega^{(de)}\rho^{(de)}, \omega^{(de)\rho^{(de)}}] $$
(7)

where p (m) and ρ (de) are, respectively the pressure and energy density of the perfect fluid component; ρ (de) is the energy density of the DE components.

In general, the field equations depend through the tensor Θ ij , on the physical nature of the matter field. Hence we obtain several theoretical models for different choice of f(R,T) depending on the nature of the matter source. In the literature, Reddy et al. [16], Naidu et al. [11] and Sahoo et al. [17] have been studied the cosmological models, assuming f(R,T) = R + 2f(T). Recently Ahmad & Pradhan [12] have studied consequence of Bianchi-V cosmological model in f(R,T) gravity by considering f(R,T) = f 1(R)+f 2(T). They have assumed perfect fluid as source of matter while in this paper, we assumed the dark energy as source of matter to describe the late time acceleration of universe. Thus our paper is all together different from the paper of Ahmad and Pradhan [12]. Assuming f 1(R)=μR and f 2(T) = μT where μ is arbitrary parameter.

Now (4) can be rewritten as

$$ R_{ij}-\frac{1}{2}g_{ij}R = \left(\frac{8\pi +\mu}{\mu}\right)T_{ij}+\left(p+\frac{1}{2}T\right)g_{ij} $$
(8)

Throughout the paper, we use units c = G = 1.

The expansion scalar (θ) and shear scalar (σ) have the form

$$ \theta = 3H = \frac{\dot A}{A} + \frac{\dot B}{B} + \frac{\dot C}{C} $$
(9)
$$ 2\sigma^{2} = \left[\frac{\dot A^{2}}{A^{2}}+\frac{\dot B^{2}}{B^{2}}+\frac{\dot C^{2}}{C^{2}}\right] - \frac{\theta^{2}}{3} $$
(10)

From (8), it is clear that in the framework of f(R,T) gravity, one obtain and additional term \(\left (p+\frac {1}{2}T\right )\) where p is the isotropic pressure and T is the trace of energy-momentum tensor. The physical interpretation of these term has been given by Paplawski [18, 19]. According to [19], the trace of energy-momentum tensor is function of isotropic pressure and energy density i.e. T = ρ − 3p = (1−3γ)ρ. Here (0 ≤ γ ≤ 1) is the equation of state parameter.

The Einstein’s field (8) for the line-element (1) leads to the following system of equations

$$ 2\frac{\ddot{B}}{B}+\frac{\dot{B}^{2}}{B^{2}} = -\left(\frac{8\pi+\lambda}{\lambda}\right) (p^{(m)}+\omega^{(de)}\rho^{(de)})-\frac{1}{2}(\rho^{(m)}-p^{(m)}) $$
(11)
$$ \frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{AB}=-\left(\frac{8\pi+\lambda}{\lambda}\right) (p^{(m)}+\omega^{(de)}\rho^{(de)})-\frac{1}{2}(\rho^{(m)}-p^{(m)}) $$
(12)
$$ 2\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}^{2}}{B^{2}}=\left(\frac{8\pi+\lambda}{\lambda}\right) (\rho^{(m)}+\rho^{(de)})+\frac{1}{2}(\rho^{(m)}-p^{(m)}) $$
(13)

The above equations can also be written in the terms of H, q and σ

$$ H^{2}(2q - 1)-\sigma^{2} = \left(\frac{8\pi+\lambda}{\lambda} \right)(p^{(m)}+\omega^{(de)}\rho^{(de)})-\frac{1}{2}(\rho^{(m)}-p^{(m)}) $$
(14)
$$ 3H^{2} - \sigma^{2} = \left(\frac{8\pi+\lambda}{\lambda}\right) (\rho^{(m)}+\rho^{(de)})+\frac{1}{2}(\rho^{(m)}-p^{(m)}) $$
(15)

Here, we assume that the universe is dominated by dark energy (DE) components and these DE components interect minimally with perfect fluid. Therefore, the energy momentum tensor for perfect fluid and DE sources may be conserved separately.

$$ \dot{\rho}^{(m)}+3(\rho^{(m)}+p^{(m)})H+\frac{(1+\omega^{(m)})}{2}\dot{\rho}^{(m)} = 0 $$
(16)
$$ \dot{\rho}^{(de)}+3(\omega^{(de)}+1)\rho^{(de)}H = 0 $$
(17)

Equations (16) and (17) represent the energy conservation equations for perfect fluid and DE component respectively.

The EoS parameter of perfect fluid is constant i. e. \(\omega ^{(m)} = \frac {p^{(m)}}{\rho ^{(m)}} = constant\), while the current cosmological data from SNIa, CMB and large scale structures mildly favour the time dependent EoS parameter for DE components.

Hence, the (16) leads to

$$ \left(\frac{3-\omega^{(m)}}{2}\right)\dot{\rho}^{(m)}+3(\omega^{(m)}+1)\rho^{(m)}H = 0 $$
(18)

3 Cosmology for Hybrid Expansion Law

Following, Pradhan and Amirhashchi [20], Yadav [21] and Yadav and Sharma [22], we consider the generalized hybrid expansion law for scale factor as following

$$ a = (t^{n}e^{kt})^{1/m} $$
(19)

where, m, n and k are non negative constant. The proposed law gives the time dependent deceleration parameter (DP) which describes the transitioning universe.

The spatial volume is given by

$$ V = a^{3} = AB^{2} $$
(20)

Equations (11) and (12) lead to

$$ \frac{A}{B} = d_{1}\;exp\left[x_{1}\int a^{-3}dt\right] $$
(21)

Here, x 1 and d 1 are constants of integration.

From (19)–(21), the metric functions can be explicitly written as

$$ A=a_{1}a\;exp\left[b_{1}\int (t^{n}e^{kt})^{\frac{1}{m}}dt\right] $$
(22)
$$ B=a_{2}a\;exp\left[b_{2}\int (t^{n}e^{kt})^{\frac{1}{m}}dt\right] $$
(23)

where

$$a_{1} = d_{1}^{\frac{1}{3}}, a_{2} = d_{1}^{\frac{4}{3}}, b_{1} = \frac{2x_{1}}{3}, b_{2} = -\frac{x_{1}}{3}$$

It deserves to mention that these constants must satisfy the following relation

$$a_{1}{a_{2}^{2}} = 1, b_{1} + 2b_{2} = 0$$

The deceleration parameter (DP) for HEL in the derived model is given by

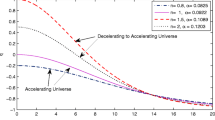
$$ q=\frac{d}{dt}\left(\frac{1}{H}\right)-1=\frac{mn}{(n+kt)^{2}}-1 $$
(24)

From (24), we see that DP is time-dependent. A negative sign of q corresponds to accelerating model of universe while positive q indicates the deceleration. The transition of universe from decelerating phase to accelerating phase takes place at \(t=\frac {\sqrt {mn}-n}{k}\). This imposes the restriction on the values of n i. e. all the values of n are not possible only certain values of n, satisfying m > n, is possible for derived model.

The present value of DP of derived model is obtained as

$$ q_{0}=-1+\frac{n}{m{H_{0}^{2}}{t_{0}^{2}}} $$
(25)

where, H 0 and t 0 are present value of Hubble’s parameter and present age of universe respectively.

In the particular cases, by choosing n = 0 and k = 0, one can obviously obtains the exponential expansion and power-law cosmology respectively. In the literature, the power-law cosmology resembles with the dynamics of universe from primordinal nucleosynthesis era to present epoch while exponential law project the dynamics of future universe. In the early universe, the power-law terms dominates over the exponential term. Thus at the time scale of primordinal nucleosynthesis (t ∼ 102 s), the cosmological parameters are given by choosing k = 0 as

$$a\sim t^{n/m}, H\sim \frac{n}{mt} \;\text{and}\; q = -1+\frac{m}{n}$$

At late times the cosmological parameters are given by

$$a\sim e^{kt/m}, H\sim \frac{k}{m} \;\text{and}\; q\sim -1$$

The directional Hubble’s parameters are given by

$$ H_{x} = \frac{1}{m}\left(\frac{n}{t}+k\right)+b_{1}(t^{n}e^{kt})^{\frac{1}{m}} $$
(26)
$$ H_{y} = H_{z} = \frac{1}{m}\left(\frac{n}{t}+k\right)+b_{2}(t^{n}e^{kt})^{\frac{1}{m}} $$
(27)

The physical parameters such as average Hubble’s parameters, expansion scalar, shear scalar and anisotropy parameter are, respectively, given by

$$ H = \frac{1}{m}\left(\frac{n}{t}+k\right) $$
(28)
$$ \theta = \frac{3}{m}\left(\frac{n}{t}+k\right) $$
(29)
$$ \sigma^{2} = \left({b_{1}^{2}}+2{b_{2}^{2}}\right)(t^{n}e^{kt})^{\frac{2}{m}} $$
(30)
$$ A_{m} = \frac{m^{2}\left({b_{1}^{2}}+2{b_{2}^{2}}\right)(t^{n}e^{kt})^{\frac{1}{m}}}{3\left(\frac{n}{t}+k\right)^{2}} $$
(31)

The energy density (ρ (m)) and pressure (p (m)) of perfect fluid are obtained as

$$ \rho^{(m)} = \rho_{0}(t^{n}e^{kt})^{-\frac{6(\omega^{(m)}+1)}{m(3-\omega^{{m}})}} $$
(32)
$$ p^{(m)} = \omega^{(m)}\rho_{0}(t^{n}e^{kt})^{-\frac{6(\omega^{(m)}+1)}{m(3-\omega^{(m)})}} $$
(33)

Here, ρ 0 is constant of integration.

The pressure (p (de)) and energy density (ρ (de)) of DE components are given by

$$\begin{array}{@{}rcl@{}} p^{(de)} &=& \left(\frac{\lambda}{8\pi+\lambda}\right)\left[\frac{1}{m^{2}}\left(\frac{n}{t}+k\right)^{2} \left(\frac{2mn}{(n+kt)^{2}}-2\right)-({b_{1}^{2}}+2{b_{2}^{2}})(t^{n}e^{kt})^{\frac{2}{m}}\right]\\ &&- \omega^{(m)}\rho_{0}(t^{n}e^{kt})^{-\frac{6(\omega^{(m)}+1)}{(3-\omega^{(m)})m}} \end{array} $$
(34)
$$ \rho^{(de)} = \left(\frac{\lambda}{8\pi+\lambda}\right)\left[\frac{1}{m^{2}}\left(\frac{n}{t}+k\right)^{2} -({b_{1}^{2}}+2{b_{2}^{2}})(t^{n}e^{kt})^{\frac{2}{m}}\right]- \rho_{0}(t^{n}e^{kt})^{-\frac{6(\omega^{(m)}+1)}{(3-\omega^{(m)})m}} $$
(35)

The EoS parameter of DE is obtained as

$$ \omega^{(de)} \,=\, \frac{\left(\frac{\lambda}{8\pi+\lambda}\right)\left[\frac{1}{m^{2}}\left(\frac{n}{t}\,+\,k\right)^{2} \left(\frac{2mn}{(n+kt)^{2}}\,-\,2\right)\,-\,({b_{1}^{2}}\,+\,2{b_{2}^{2}})(t^{n}e^{kt})^{\frac{2}{m}}\right]\,-\, \omega^{(m)}\rho_{0}(t^{n}e^{kt})^{\,-\,\frac{6(\omega^{(m)}+1)}{(3-\omega^{(m)})m}}} {\left(\frac{\lambda}{8\pi+\lambda}\right)\left[\frac{1}{m^{2}}\left(\frac{n}{t}+k\right)^{2} -({b_{1}^{2}}+2{b_{2}^{2}})(t^{n}e^{kt})^{\frac{2}{m}}\right]- \rho_{0}(t^{n}e^{kt})^{-\frac{6(\omega^{(m)}+1)}{(3-\omega^{(m)})m}}} $$
(36)

The overall density parameter (Ω) is given by

$$ {\Omega} = {\Omega}^{(de)}+{\Omega}^{(m)} = \left(\frac{\lambda}{8\pi+\lambda}\right) \left[1 -\frac{\left({b_{1}^{2}}+2{b_{2}^{2}}\right)(t^{n}e^{kt})^{\frac{2}{m}}}{\frac{1}{m^{2}}\left(\frac{n}{t}+k\right)^{2}}\right] $$
(37)

It is observe that expansion scalar is infinite at t = 0. For t → ∞, we obtain \(\theta \rightarrow \frac {3k}{m}\), q=−1 and \(\frac {dH}{dt} = 0\) which implies the greatest value of Hubble’s parameter. The behaviour of DP has been depicted in Fig. 1. It is also evident that at late times DP grows with negative sign which gives the accelerated expansion of universe at present epoch. The negative value of q will also increase the age of universe. Thus in our analysis, the model presented in this paper is turning out as a suitable model for describing the present evolution of universe.

Fig. 1
figure 1

a The variation of Hubble’s parameter (H) with respect to time. b Anisotropy parameter (A m ) versus time. c The behaviour of DP (q) with age of universe. d The variation of dark energy density with respect to time. e Pressure of DE components versus time. f The grow of EOS parameter of DE component with respect to time. g Single plot of energy conditions

Full size image

From Fig. 1, we observe that

  • ρ (de) > 0

  • ρ (de) + p (de) > 0

  • ρ (de) − p (de) > 0

  • ρ (de) +3 p (de) < 0

Thus in the derived model, the weak energy condition (WEC), null energy condition (NEC) and dominant energy condition (DEC) have been satisfied but it violates the strong energy condition (SEC). The same is suggested by numerous authors (Caldwell [5]; Srivastava [23]; Yadav [24]).

From Fig. 1, it is evident that Hubble’s parameter (H) and anisotropy parameter A m start off with extremely large value and continue to decrease with time. Further ρ (de) decreases with expansion of universe and finally approaches to a small positive value. The EOS parameter of DE components (ω (de)) also shows the transitioning nature. At late times, ω (de) evolves with negative sign and it’s range is in good agreement with recent astrophysical observations [25].

4 Concluding Remarks

In this paper, we have considered f (R, T) gravity model with an arbitrary coupling between matter and geometry in LRS Bianchi-I space-time. In f (R, T) gravity, the cosmic acceleration depends not only on geometric contribution but also on matter contents of universe. In this gravity, an extra acceleration is always present due to coupling between matter and geometry. We observed that the hybrid expansion law gives time dependent DP, representing a model which generates a transition of universe from an early decelerating phase to a recent accelerating phase. The spatial scale factor and volume scalar vanish at t = 0. The energy density and pressure are infinite at this initial moment. As t → ∞, the scale factor diverse and ρ (de) and p (de) both tend to zero. The anisotropy parameter A m is very large at the initial moment but decreases with time and vanish at t → ∞. Thus the model shows an isotropic state at the later time of its evolution. For n ≠ 0, all matter and radiation is concentrated at the big bang epoch and the cosmic expansion is driven by the big bang impulse. The derived model violates the strong energy condition (SEC) at late times while WEC, NEC and DEC may be preserved which can be acceptable in present time.