The initial-boundary value for the combined Schrödinger and Gerdjikov–Ivanov equation on the half-line via the Riemann–Hilbert approach

Abstract

The Fokas method is used to study the initial-boundary value problem for the combined Schrödinger and Gerdjikov–Ivanov equation on the half-line. Assuming that the solution $u(x,t)$ exists, it can be represented by the unique solution of a matrix Riemann–Hilbert problem formulated on the plane of the complex spectral parameter $\xi$. The jump matrices are given on the basis of the spectral functions, which are not independent, but are related by a global relation.

1. Introduction

The Riemann–Hilbert approach is a powerful tool to solve integrable nonlinear evolution equations. In 1851, the Riemann problem was first posed by Riemann. Then, Hilbert presented the famous 23 questions at the International Mathematical Conference in Paris [1]. The 21st problem was the proof of the existence of solutions of linear differential equations with order groups, commonly known as Riemann–Hilbert problem. The core issue is to find an analytic function on the complex plane such that it has a particular jump on a given curve. Subsequently, Fokas and others established a connection between the orthogonal multivariate and the Riemann–Hilbert problems. A new transformation method named the Fokas method was proposed to solve two-dimensional initial boundary value (IBV) problems. Many equations were discussed, such as the nonlinear Schrödinger equation [2], [3], the sine-Gordon equation [4], the KdV equation [5], [6], and the Gerdjikov–Ivanov equation [7]–[11]. The nonlinear Schrödinger equation takes the form

$$ iu_t+u_{xx}+|u|^2u=0,$$

(1.1)

which is a second-order partial differential equation obtained by combining the concept of a matter wave and the wave equation. The IBV problem for the nonlinear Schrödinger equation on the half-line was discussed in [12]–[21]. The derivative nonlinear Schrödinger equation on the half-line was studied in [22]–[25]. Furthermore, the IBV problem for the derivative nonlinear Schrödinger equation was considered in detail in [26].

The Gerdjikov–Ivanov equation has the form

$$ iu_t+u_{xx}-iu^2u_x^*+\frac{1}{2}u^3u^{*2}=0,$$

(1.2)

which has been studied from the standpoints of different types of Liouville integrability [27], exact solutions [28], rogue wave and breather solution [29], separation of variables and algebro-geometric solutions [30], bifurcations and new exact traveling wave solutions [31], and higher-order rogue wave solutions [32].

In this paper, we discuss the combined nonlinear Schrödinger and Gerdjikov–Ivanov (NLS–GI) equation by using the Riemann–Hilbert method. The system can be written as

$$ u_t=iu_{xx}-2i|u|^2u+u^2u_x^*+\frac{i}{2}|u|^4 u,$$

(1.3)

where $u(x,t)$ is a complex smooth envelop function, and $t$, $x$, and $\ast$ denote the respective temporal, spatial variables, and complex conjugations. The Riemann–Hilbert method for the combined NLS–GI equation and its $n$-soliton solutions have been discussed in [33]. In this paper, we aim to study the IBV problem for the combined NLS–GI equation on the half-line via the Riemann–Hilbert approach. The solution of the combined NLS–GI equation is obtained by analyzing the spectral function and jump matrices. We extend the IBV problem to an infinite interval following the Fokas method.

This paper is organized as follows. In Sec. 2, we study the direct scattering problems of the combined NLS–GI equation. In Sec. 3, the spectral functions are further investigated and the Riemann–Hilbert problem of the combined NLS–GI equation is presented. In Sec. 4, a brief summary of this paper is given.

2. Spectral analysis for the NLS–GI equation

2.1. Transformed Lax pair

The Lax pair of Eq. (1.3) can be written as

$$ \begin{aligned} \, &\phi_x=U_1\phi, \\ &\phi_t=U_2\phi, \end{aligned}$$

(2.1)

where $\phi=\phi(x,t;\xi)$ is a matrix function and

$$ \begin{aligned} \, &U_1=\begin{pmatrix} i\biggl(\kappa+\dfrac{1}{2}uu^*\biggr) & (1+\kappa)u \\ u^* & -i\biggl(\kappa+\dfrac{1}{2}uu^*\biggr) \end{pmatrix},\\ &U_2=\begin{pmatrix} A & (1+\kappa)(-2u\kappa+iu_x) \\ -2u^*\kappa-iu_x^* & -A \end{pmatrix},\\ &A=-2i\kappa^2-i\kappa uu^*-\frac{1}{2}(u_xu^*-u u_x^*)+\frac{i}{4}u^2u^{*2}-iuu^*, \end{aligned}$$

(2.2)

with $\kappa$ being a constant parameter. We make a gauge transformation

$$ \tilde{\phi}=T\phi,\qquad T=\begin{pmatrix} 1 & 0 \\ 0 & 1-i\xi \end{pmatrix}, \qquad \xi\neq -i,$$

(2.3)

where $\kappa=\xi^2$. Then Eq. (2.1) can be written in the equivalent form

$$ \begin{aligned} \, \tilde{\phi}_x=\tilde{U}_1\phi, \\ \tilde{\phi}_t=\tilde{U}_2\phi, \end{aligned}$$

(2.4)

where

$$ \begin{aligned} \, &\tilde{U}_1=\begin{pmatrix} i\biggl(\xi^2+\dfrac{1}{2}uu^*\biggr) & (1+i\xi)u \\ (1-i\xi)u^* & -i\biggl(\xi^2+\dfrac{1}{2}uu^*\biggr) \end{pmatrix},\\ &\tilde{U}_2=\begin{pmatrix} B & -2iu\xi^{3}-2u\xi^2-u_x\xi+iu_x \\ 2iu^*\xi^{3}-2u^*\xi^2-u_x^*\xi-iu_x^* & -B \end{pmatrix},\\ &B=-2i\xi^4-iuu^*\xi^2-\frac{1}{2}(u_xu^*-u u_x^*)+\frac{i}{4}u^2u^{*2}-iuu^*. \end{aligned}$$

(2.5)

Next, we define a matrix function $\psi=\psi(x,t;\xi)$ as

$$ \tilde{\phi}=\psi e^{i(\xi^2x-2\xi^4t)\sigma_3}.$$

(2.6)

According to transformation (2.6), Lax pair (2.4) can be rewritten as

$$ \begin{aligned} \, &\psi_x-i\xi^2[\sigma_3,\psi]=V_1\psi,\\ &\psi_t+2i\xi^4[\sigma_3,\psi]=V_2\psi, \end{aligned}$$

(2.7)

where

$$ \begin{aligned} \, &V_1=\begin{pmatrix} \dfrac{i}{2}uu^* & (1+i\xi)u \\ (1-i\xi)u^* & -\dfrac{i}{2}uu^* \end{pmatrix}, \qquad \sigma_3=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}, \qquad Q=\begin{pmatrix} 0 & u \\ u^* & 0 \end{pmatrix},\\ &V_2=\begin{pmatrix} -iuu^*\xi^2-\dfrac{1}{2}(u_xu^*-u u_x^*)+ & -2iu\xi^3-2u\xi^2-u_x\xi+iu_x\\ +\dfrac{i}{4}u^2u^{*2}-iuu^* & \\ 2iu^*\xi^3-2u^*\xi^2-u_x^*\xi-iu_x^* & iuu^*\xi^2+\dfrac{1}{2}(u_xu^*-u u_x^*)-\\ & -\dfrac{i}{4}u^2u^{*2}+iuu^* \end{pmatrix}. \end{aligned}$$

(2.8)

Equation (2.7) can be written in the full derivative form

$$ d(e^{-i(\xi^2x-2\xi^4t)\widehat{\sigma}_3}\psi(x,t;\xi))=W, \qquad 0<x<\infty,\, 0<t<T,$$

(2.9)

with

$$ W=e^{-i(\xi^2x-2\xi^4t)\widehat{\sigma}_3}(V_1\,dx+V_2\,dt)\psi(x,t;\xi).$$

(2.10)

We introduce a new function $\mu(x,t;\xi)$ such that

$$ \mu=I+O\biggl(\frac{1}{\xi}\biggr),\qquad \xi\to\infty.$$

(2.11)

Then Eq. (2.9) becomes

$$ d(e^{-i(\xi^2x-2\xi^4 t)\widehat{\sigma}_3}\mu(x,t;\xi))=W, \qquad 0<x<\infty,\,0<t<T,$$

(2.12)

where

$$ W=e^{-i(\xi^2x-2\xi^4t)\widehat{\sigma}_3}(V_1\,dx+V_2\,dt)\mu(x,t;\xi).$$

(2.13)

Equation (2.12) can now be written as

$$ \begin{aligned} \, &\mu_x-i\xi^2[\sigma_3,\mu]=V_1\mu,\\ &\mu_t+2i\xi^4[\sigma_3,\mu]=V_2\mu. \end{aligned}$$

(2.14)

2.2. Eigenfunctions and their relations

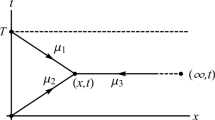
Following [34], we assume that $u(x,t)$ is sufficiently smooth in $\Upsilon=\{0<x<\infty, 0<t<T, T>0\}$. The solutions $\mu_j(x,t;\xi)$, $j=1,2,3$ of Eq. (2.14) can be constructed as

$$ \mu_j(x,t;\xi)=\mathrm{I}+\int_{(x_j,t_j)}^{(x,t)}e^{i(\xi^2 x-4\xi^4t)\widehat{\sigma}_3}W(\zeta,\tau,\xi),\qquad 0<x<\infty,\, 0<t<T,$$

(2.15)

where $(x_1,t_1)=(0,T)$, $(x_2,t_2)=(0,0)$, and $(x_3,t_3)=(\infty,t)$, as can be seen in Fig. 1.

Fig. 1.

Integration paths $\gamma_1\!:(0,T)\to (x,t)$, $\gamma_2\!:(0,0)\to (x,t)$, and $\gamma_3\!: (\infty,t)\to (x,t)$.

Because the integration of Eq. (2.15) is independent of the paths, the specific straight paths are chosen in Fig. 1:

$$ \begin{aligned} \, \mu_1(x,t;\xi)={}&\mathrm{I}+\int_0^x e^{i\xi^2 (x-\zeta)\widehat{\sigma}_3}(V_1\mu_1)(\zeta,t,\xi)\,d\zeta-{}\\ &-e^{i\xi^2 x\widehat{\sigma}_3}\int_t^T e^{2i\xi^4(\tau-t)\widehat{\sigma}_3}(V_2\mu_1)(0,\tau,\xi)\,d\tau,\\ \mu_2(x,t;\xi)={}&\mathrm{I}+\int_0^x e^{i\xi^2 (x-\zeta)\widehat{\sigma}_3}(V_1\mu_2)(\zeta,t,\xi)\,d\zeta+{}\\ &+e^{i\xi^2 x\widehat{\sigma}_3}\int_0^t e^{2i\xi^4(\tau-t)\widehat{\sigma}_3}(V_2\mu_2)(0,\tau,\xi)\,d\tau,\\ \mu_3(x,t;\xi)={}&\mathrm{I}-\int_x^\infty e^{i\xi^2 (x-\zeta)\widehat{\sigma}_3}(V_1\mu_3)(\zeta,t,\xi)\,d\zeta. \end{aligned}$$

(2.16)

The inequality on the contours can then be expressed as

$$ \begin{aligned} \, &(x_1,t_1)\to (x,t)\!: 0<\zeta<x,\, t<\tau<T,\\ &(x_2,t_2)\to (x,t)\!: 0<\zeta<x,\, 0<\tau<t,\\ &(\infty,t_3)\to (x,t\!): 0<x<\infty. \end{aligned}$$

(2.17)

The first column of the matrix in Eq. (2.15) involves $e^{-2i[\xi^2 (x-\zeta)-2\xi^4(t-\tau)]}$. By inequality (2.17), the functions $\mu_j(x,t;\xi)$, $j=1,2,3$, are bounded and analytic for $\xi \in \mathbb{C}$, which is constrained as

$$ \begin{aligned} \, &\mu_1^{(1)}(x,t;\xi)\!: \{\operatorname{Im}\xi^2 \leq 0\}\cap\{\operatorname{Im}\xi^4\leq 0\},\\ &\mu_2^{(1)}(x,t;\xi)\!: \{\operatorname{Im}\xi^2 \leq 0\}\cap\{\operatorname{Im}\xi^4\geq 0\},\\ &\mu_3^{(1)}(x,t;\xi)\!: \{\operatorname{Im}\xi^2 \geq 0\}. \end{aligned}$$

(2.18)

Similarly, the second column of the matrix in Eq. (2.15) involves $e^{2i[\xi^2(x-\zeta)-2\xi^4(t-\tau)]}$; the regions of the complex $\xi$ can be written as

$$ \begin{aligned} \, &\mu_1^{(2)}(x,t;\xi)\!: \{\operatorname{Im}\xi^2 \geq 0\}\cap\{\operatorname{Im}\xi^4\geq 0\},\\ &\mu_2^{(2)}(x,t;\xi)\!: \{\operatorname{Im}\xi^2 \geq 0\}\cap\{\operatorname{Im}\xi^4\leq 0\},\\ &\mu_3^{(2)}(x,t;\xi)\!: \{\operatorname{Im}\xi^2 \leq 0\}. \end{aligned}$$

(2.19)

As a result, we obtain

$$ \begin{aligned} \, &\mu_1(x,t;\xi)=(\mu_1^{D_4}(x,t;\xi),\mu_1^{D_1}(x,t;\xi)),\\ &\mu_2(x,t;\xi)=(\mu_2^{D_3}(x,t;\xi),\mu_2^{D_2}(x,t;\xi)),\\ &\mu_3(x,t;\xi)=(\mu_3^{D_1\cup D_2}(x,t;\xi),\mu_3^{D_3\cup D_4}(x,t;\xi)), \end{aligned}$$

(2.20)

where $\mu_{j}^{D_i}$ expresses that $\mu_j$ is bounded and analytic for $\xi \in D_i$,

$$\begin{aligned} \, &D_i=\biggl\{\omega\in\mathbb{C}|2l\pi+\frac{i-1}{4}\pi<\operatorname{Arg} \omega<2l\pi +\frac{i}{4}\pi\biggr\}, \\ &j=1,2,3,\, i=1,2,3,\, l=0,\pm1,\pm2,\dots, \end{aligned}$$

and $\operatorname{Arg} \omega$ means the argument of the complex $\xi$ (see Fig. 2).

Fig. 2.

The domains $D_i$, $i=1,2,3$, into which the complex $\xi$-plane decomposes.

We construct the Riemann–Hilbert problem to obtain the solution of the combined NLS–GI equation. First, the jumps matrices across the boundaries of the $D_i$, $i=1,2,3$, are uniquely determined by the two $2\times2$ matrix-valued spectral functions $s(\xi)$ and $S(\xi)$ that satisfy

$$ \begin{aligned} \, &\mu_3(x,t;\xi)=\mu_2(x,t;\xi)e^{i(\xi^2 x-2\xi^4t)\widehat{\sigma}_3}s(\xi),\\ &\mu_1(x,t;\xi)=\mu_2(x,t;\xi)e^{i(\xi^2 x-2\xi^4t)\widehat{\sigma}_3}S(\xi). \end{aligned}$$

(2.21)

Taking $(x,t)=(0,0)$ in the first equation in (2.21), and setting $(x,t)=(0,0)$ and $(x,t)=(0,T)$ in the second equation in (2.21), we have

$$ s(\xi)=\mu_3(0,0;\xi),\qquad S(\xi)=\mu_1(0,0;\xi),\qquad S(\xi)=(e^{2i\xi^4 T\widehat{\sigma}_3}\mu_2(0,T;\xi))^{-1}.$$

(2.22)

It follows from Eqs. (2.21) and (2.22) that

$$ \mu_1(x,t;\xi)=\mu_3(x,t;\xi)e^{i(\xi^2 x-2\xi^4t)\widehat{\sigma}_3}(s(\xi))^{-1}S(\xi).$$

(2.23)

Because $\mu_1(0,T,\xi)=\mathrm{I}$, a global relation can be obtained from Eq. (2.23) at $(x,t)=(0,T)$:

$$S^{-1}(\xi)s(\xi)=e^{2i\xi^4T\widehat\sigma_3}\mu_3(0,T;\xi).$$

Therefore, the matrix functions $\mu_j(x,t;\lambda)$, $j=1,2,3$, satisfy the linear integral equations

$$\begin{aligned} \, &\mu_1(0,t;\xi)=\mathrm{I}-\int_t^T e^{2i\xi^4(\tau-t)\widehat{\sigma}_3}(V_2\mu_1)(0,\tau,\xi)\,d\tau,\\ &\mu_2(0,t;\xi)=\mathrm{I}+\int_0^t e^{2i\xi^4(\tau-t)\widehat{\sigma}_3}(V_2\mu_2)(0,\tau,\xi)\,d\tau,\\ &\mu_3(x,0;\xi)=\mathrm{I}-\int_x^\infty e^{i\xi^2 (x-\zeta)\widehat{\sigma}_3}(V_1\mu_3)(\zeta,0,\xi)\,d\zeta,\\ &\mu_2(x,0;\xi)=\mathrm{I}+\int_0^x e^{i\xi^2 (x-\zeta)\widehat{\sigma}_3}(V_1\mu_2)(\zeta,0;\xi)\,d\zeta. \end{aligned}$$

Then, taking $x=0$ and $t=0$ in Eq. (2.8), we obtain

$$ \begin{aligned} \, &V_1(x,0;\xi)=\begin{pmatrix} \dfrac{i}{2}|u_0|^2 & (1+i\xi)u_0 \\ (1-i\xi)\bar{u}_0 & -\dfrac{i}{2}|u_0|^2 \end{pmatrix},\\ &V_2(0,t;\xi)=\begin{pmatrix} C & -2i\xi^3g_0-2\xi^2g_0-\xi g_1+ig_1 \\ 2i\xi^3\bar{g}_0-2\xi^2\bar{g}_0-\xi \bar{g}_1-i\bar{g}_1 & -C \end{pmatrix}, \end{aligned}$$

(2.24)

where $u_0(x)=u(x,0)$, $g_0(t)=u(0,t)$, $g_1(t)=u_x(0,t)$, and

$$C=-i\xi^2|g_0|^2-\frac{1}{2}(g_1\bar{g}_0-g_0\bar{g}_1)+\frac{i}{4}|g_0|^4-i|g_0|^2.$$

Because $\mu_j(x,t;\xi)$, $j=1,2,3$, defined by Eq. (2.15) are $2\times2$ matrices, their first and second columns can be respectively written as $\mu_j^{(1)}(x,t;\xi)$ and $\mu_j^{(2)}(x,t;\xi)$. We set

$$\mu_j(x,t;\xi)=(\mu_j^{(1)}(x,t;\xi),\mu_j^{(2)}(x,t;\xi)) =\begin{pmatrix} \mu_j^{11} & \mu_j^{12} \\ \mu_j^{21} & \mu_j^{22} \\ \end{pmatrix}, \qquad j=1,2,3.$$

Proposition 1.

The above matrices $\mu_j(x,t;\xi)$ have the following properties:

• • $\operatorname{det}\mu_1(x,t;\xi)=\operatorname{det}\mu_2(x,t;\xi)=\operatorname{det}\mu_3(x,t;\xi)=1;$

• • each component of $\mu_j(x,t;\xi)$ , $j=1,2,3$ , is analytic;

• • $\lim_{\xi\to\infty}\mu_1^{(1)}(x,t;\xi)=(1,0)^\mathrm{T}$ , $\xi\in D_4$ , $\lim_{\xi\to\infty}\mu_1^{(2)}(x,t;\xi)=(0,1)^\mathrm{T}$ , $\xi\in D_1;$

• • $\lim_{\xi\to\infty}\mu_2^{(1)}(x,t;\xi)=(1,0)^\mathrm{T}$ , $\xi\in D_3$ , $\lim_{\xi\to\infty}\mu_2^{(2)}(x,t;\xi)=(0,1)^\mathrm{T}$ , $\xi\in D_2;$

• • $\lim_{\xi\to\infty}\mu_3^{(1)}(x,t;\xi)=(1,0)^\mathrm{T}$ , $\xi\in D_1\cup D_2$ , $\lim_{\xi\to\infty}\mu_3^{(2)}(x,t;\xi)=(0,1)^\mathrm{T}$ , $\xi\in D_3\cup D_4$ .

Proposition 2.

Relations (2.21) and (2.22) can be written as

$$ \begin{aligned} \, &s(\xi)=\mu_3(0,0,\xi)=\mathrm{I}-\int_0^\infty e^{-i\xi^2 \zeta \widehat{\sigma}_3}(V_1\mu_3)(\zeta,0;\xi)\,d\zeta,\\ &S(\xi)=\biggl(e^{2i\xi^4T\widehat{\sigma}_3}\biggl(\mathrm{I}+\int_0^T e^{2i\xi^4(\tau-T)\tau\widehat{\sigma}_3}(V_2\mu_2)(0,\tau;\xi)\,d\tau\biggr)\biggr)^{-1}={}\\ &\hphantom{S(\xi)}=\biggl(e^{2i\xi^4T\widehat{\sigma}_3}+\int_0^T e^{2i\xi^4\tau\widehat{\sigma}_3}(V_2\mu_2)(0,\tau;\xi)\,d\tau\biggr)^{-1}. \end{aligned}$$

(2.25)

Because $s(\xi)$ and $S(\xi)$ are $2\times2$ matrix functions, we can set

$$ s(\xi)=\begin{pmatrix} \,\overline{a(\bar{\xi})} & b(\xi)\\[1mm] \,\overline{b(\bar{\xi})}& a(\xi) \end{pmatrix}, \qquad S(\xi)=\begin{pmatrix} \,\overline{A(\bar{\xi})} & B(\xi)\\[1mm] \,\overline{B(\bar{\xi})}& A(\xi)\\ \end{pmatrix}.$$

(2.26)

The following formulas follow from Eqs. (2.22) and (2.25):

$$\begin{aligned} \, &\begin{pmatrix} b(\xi) \\ a(\xi) \\ \end{pmatrix} =\mu_3^{(2)}(0,0;\xi)= \begin{pmatrix} \mu_3^{12}(0,0;\xi) \\ \mu_3^{22}(0,0;\xi) \\ \end{pmatrix}, \\[2mm] &\begin{pmatrix} -e^{-4i\xi^4T}B(\xi) \\ \overline{A(\bar{\xi})} \\ \end{pmatrix}=\mu_2^{(2)}(0,T;\xi) =\begin{pmatrix} \mu_2^{12}(0,T;\xi) \\ \mu_2^{22}(0,T;\xi) \\ \end{pmatrix}; \\[2mm] &\begin{alignedat}{2} a(-\xi)&=a(\xi),&\qquad b(-\xi)&=-b(\xi),\\ A(-\xi)&=A(\xi),&\qquad B(-\xi)&=-B(\xi); \end{alignedat} \\[2mm] &\det s(\xi)=\det S(\xi)=1; \\[2mm] &\begin{alignedat}{4} &a(\xi)=1+O\biggl(\frac{1}{\xi}\biggr)&\qquad &b(\xi)=O\biggl(\frac{1}{\xi}\biggr), &\qquad \xi\to\infty, \; &\xi\in D_3\cup D_4,\\ &A(\xi)=1+O\biggl(\frac{1}{\xi}\biggr),&\qquad &B(\xi)=O\biggl(\frac{1}{\xi}\biggr),&\qquad \xi\to\infty, \; &\xi\in D_1\cup D_3. \end{alignedat} \end{aligned}$$

2.3. The jump conditions

The matrix $M(x,t;\xi)$ is defined by

$$ \begin{aligned} \, &M_{+}(x,t,\xi)=\biggl(\mu_2^{D_3}(x,t,\xi),\frac{\mu_3^{D_3\cup D_4}(x,t,\xi)}{a(\xi)}\biggr), \qquad \xi\in D_3,\\[1mm] &M_{-}(x,t,\xi)=\biggl(\frac{\mu_3^{D_1\cup D_2}(x,t,\xi)}{\overline{\alpha(\bar{\xi})}},\mu_2^{D_2}(x,t,\xi)\biggr), \qquad \xi\in D_2,\\[1mm] &M_{+}(x,t,\xi)=\biggl(\frac{\mu_3^{D_1\cup D_2}(x,t,\xi)}{\alpha(\xi)},\mu_1^{D_1}(x,t,\xi)\biggr), \qquad \xi\in D_1,\\[1mm] &M_{-}(x,t,\xi)=\biggl(\mu_1^{D_4}(x,t,\xi),\frac{\mu_3^{D_3\cup D_4}(x,t,\xi)}{\overline{\alpha(\bar{\xi})}}\biggr), \qquad \xi\in D_4. \end{aligned}$$

(2.27)

where the scalars $o(\xi)$, $\alpha(\xi)$, $\beta(\xi)$, and $\gamma(\xi)$ are

$$ \begin{aligned} \, &o(\xi)=-\xi^2x+2\xi^4t,\\[1mm] &\alpha(\xi)=\overline{a(\bar{\xi})}A(\xi)-\overline{b(\bar{\xi})}B(\xi),\\[1mm] &\beta(\xi)=a(\xi)B(\xi)-b(\xi)A(\xi),\\[1mm] &\gamma(\xi)=\overline{a(\bar{\xi})}\beta(\xi)+b(\xi)\alpha(\xi). \end{aligned}$$

(2.28)

It follows from these definitions that

$$ \det M(x,t;\xi)=1,\qquad M(x,t;\xi)=\mathrm{I}+O\biggl(\frac{1}{\xi}\biggr), \quad \xi\to\infty.$$

(2.29)

Theorem 1.

Let $M(x,t;\xi)$ and $\mu_j(x,t,\xi)$, $j=1,2,3$, be defined by Eq. (2.27) and Eq. (2.15), and $u(x,t)$ be a smooth function. Then $M(x,t;\xi)$ satisfies the jump condition on $\bar D_h\cap\bar D_l$, $h,l=1,2,3$,

$$ M_+(x,t,\xi)=M_-(x,t,\xi)J(x,t,\xi),\qquad \xi \in \bar D_h\cap\bar D_l,\,h,l=1,2,3,\, h\neq l,$$

(2.30)

where

$$ J(x,t,\xi)=\begin{cases} J_1(x,t,\xi), \qquad \operatorname{Arg} \xi =k\pi+\pi/2, \\ J_2(x,t,\xi), \qquad \operatorname{Arg} \xi =k\pi+3\pi/4, \\ J_3(x,t,\xi), \qquad \operatorname{Arg} \xi =k\pi, \\ J_4(x,t,\xi), \qquad \operatorname{Arg} \xi =k\pi+\pi/4, \end{cases}$$

(2.31)

and

$$\begin{alignedat}{2} J_1(x,t,\xi)&=\begin{pmatrix} 1 & \dfrac{b(\xi)}{a(\xi)}e^{-2io(\xi)} \\ -\dfrac{\overline{b(\bar{\xi})}}{\overline{a(\bar{\xi})}}e^{2io(\xi)} & \dfrac{1}{a(\xi)\overline{a(\bar{\xi})}} \end{pmatrix},\quad &J_2(x,t,\xi)&=\begin{pmatrix} \dfrac{a(\xi)}{\overline{\xi(\bar{\xi})}} & 0 \\ -\overline{\gamma(\bar{\xi})} e^{2io(\xi)}& \dfrac{\overline{\alpha(\bar{\xi})}}{a(\xi)} \end{pmatrix}, \\ J_3(x,t,\xi)&=\begin{pmatrix} \dfrac{1}{\alpha(\xi)\overline{\alpha(\bar{\xi})}} & \dfrac{\beta(\xi)}{\overline{\alpha(\bar{\xi})}}e^{-2io(\xi)} \\ -\dfrac{\overline{\beta(\bar{\xi})}}{\alpha(\xi)}e^{2io(\xi)} & 1 \end{pmatrix},\quad &J_4(x,t,\xi)&=\begin{pmatrix} \dfrac{\overline{a(\bar{\xi})}}{\alpha(\xi)} & \gamma(\xi)e^{-2io(\xi)} \\ 0 & \dfrac{\alpha(\xi)}{\overline{a(\bar{\xi})}} \end{pmatrix}. \end{alignedat}$$

The proof of the theorem is similar to that given in Ref. [14]. We substitute Eqs. (2.26) in (2.21):

$$ \begin{aligned} \, &\begin{cases} \overline{a(\bar{\xi})}\mu_2^{D_3}+\overline{b(\bar{\xi})}e^{2io(\xi)}\mu_2^{D_2}=\mu_3^{D_1\cup D_2}, \\ b(\xi)e^{-2io(\xi)}\mu_2^{D_3}+a(\xi)\mu_2^{D_2}=\mu_3^{D_3\cup D_4}, \end{cases}\\ &\begin{cases} \overline{A(\bar{\xi})}\mu_2^{D_3}+\overline{B(\bar{\xi})}e^{2io(\xi)}\mu_2^{D_2}=\mu_1^{D_4}, \\ B(\xi)e^{-2io(\xi)}\mu_2^{D_3}+A(\xi)\mu_2^{D_2}=\mu_1^{D_1}, \end{cases}\\ &\begin{cases} \overline{\alpha(\bar{\xi})}\mu_3^{D_1\cup D_2}+\overline{\beta(\bar{\xi})}e^{2io(\xi)}\mu_2^{D_3\cup D_4}=\mu_1^{D_4}, \\ \beta(\xi)e^{-2io(\xi)}\mu_3^{D_1\cup D_2}+\alpha(\xi)\mu_2^{D_3\cup D_4}=\mu_1^{D_1}. \end{cases} \end{aligned}$$

(2.32)

By transforming Eqs. (2.32), we can write the jump matrices $J_i(x,t;\lambda)$, $i=1,2,3$, as

$$ \begin{aligned} \, \biggl(\mu_2^{D_3}(x,t,\xi),\frac{\mu_3^{D_3\cup D_4}(x,t,\xi)}{a(\xi)}\biggr)&=\biggl(\frac{\mu_3^{D_1\cup D_2}(x,t,\xi)}{\overline{a(\bar{\xi})}},\mu_2^{D_2}(x,t,\xi)\biggr)J_1(x,t;\xi),\\ \biggl(\mu_2^{D_3}(x,t,\xi),\frac{\mu_3^{D_3\cup D_4}(x,t,\xi)}{a(\xi)}\biggr)&=\biggl(\mu_1^{D_4}(x,t,\xi),\frac{\mu_3^{D_3\cup D_4}(x,t,\xi)}{\overline{\alpha(\bar{\xi})}}\biggr)J_2(x,t;\xi),\\ \biggl(\frac{\mu_3^{D_1\cup D_2}(x,t,\xi)}{\alpha(\xi)},\mu_1^{D_1}(x,t,\xi)\biggr)&=\biggl(\mu_1^{D_4}(x,t,\xi),\frac{\mu_3^{D_3\cup D_4}(x,t,\xi)}{\overline{\alpha(\bar{\xi})}}\biggr)J_3(x,t;\xi),\\ \biggl(\frac{\mu_3^{D_1\cup D_2}(x,t,\xi)}{\alpha(\xi)},\mu_1^{D_1}(x,t,\xi)\biggr)&=\biggl(\frac{\mu_3^{D_1\cup D_2}(x,t,\xi)}{\overline{a(\bar{\xi})}},\mu_2^{D_2}(x,t,\xi)\biggr)J_4(x,t;\xi). \end{aligned}$$

(2.33)

The matrix $M(x,t;\xi)$ is a sectionally meromorphic function. In terms of the zeros of $a(\xi), \alpha(\xi)$, and their complex conjugates, the possible poles of $M(x,t;\xi)$ can be obtained. Because $a(\xi)$ and $\alpha(\xi)$ are even functions, each of them has an even number of zeros.

Statement 1.

Let

• • $a(\xi)$ have $2h$ simple zeros $\{\epsilon_j\}_{j=1}^{2h}$ , $2h=2h_1+2h_2$ , such that $\epsilon_j$ , $j=1,2,\dots,2h_1$ , are located in $D_3$ and $\bar{\epsilon}_j$ , $j=1,2,\dots,2h_2$ , are located in $D_2$ .

• • $\alpha(\xi)$ has $2H$ simple zeros $\{\delta_j\}_{j=1}^{2H}$ , $2H=2H_1+2H_2$ , such that $\delta_j$ , $j=1,2,\dots,2H_1$ , are located in $D_1$ and $\bar{\delta}_j$ , $j=1,2,\dots,2H_2$ , are located in $D_4$ .

• • The zeros of $\alpha(\xi)$ does not coincide with the zeros of $a(\xi)$ .

Proposition 3.

Using Statement 1 , we can calculate the residues of the function $M(x,t;\xi)$ . We set

$$ M(x,t,\xi)=([M(x,t;\xi)]_1,[M(x,t;\xi)]_2),\qquad \xi\in D_3,\, \dot{a}(\xi)=\frac{da}{d\xi}.$$

(2.34)

We then have the residue conditions

$$\begin{aligned} \, &\operatorname{Res}\{[M(x,t;\xi)]_2, \epsilon_j\}=\frac{e^{-2io(\epsilon_j)}b(\epsilon_j)}{\dot{a}(\epsilon_j)} [M(x,t;\epsilon_j)]_1,\qquad j=1,2,\dots,2h_1,\\ &\operatorname{Res}\{[M(x,t;\xi)]_1, \bar{\epsilon}_j \}=\frac{e^{2io(\bar{\epsilon}_j)} \overline{b(\bar{\epsilon}_j)}}{\overline{\dot{a}(\bar{\epsilon}_j)}}[M(x,t;\bar{\epsilon}_j)]_2,\qquad j=1,2,\dots,2h_2,\\ &\operatorname{Res}\{[M(x,t;\xi)]_1, \delta_j \}=\frac{e^{2io(\delta_j)}}{\dot{\alpha}(\delta_j)\beta(\delta_j)} [M(x,t;\delta_j)]_2,\qquad j=1,2,\dots,2H_1,\\ &\operatorname{Res}\{[M(x,t;\xi)]_2, \ \bar{\delta}_j \}= \frac{e^{-2io(\bar{\delta}_j)}}{\overline{\dot{\alpha}(\bar{\delta}_j)}\overline{\beta(\bar{\delta_j})}} [M(x,t;\bar{\delta_j})]_1,\qquad j=1,2,\dots,2H_2. \end{aligned}$$

2.4. The inverse problem

We fix the jump condition

$$ M_+(x,t;\xi)-M_{-}(x,t;\xi)=M_-\tilde{J}(x,t;\xi),$$

(2.35)

where $\tilde{J}(x,t;\xi)=J(x,t;\xi)-\mathrm{I}$. By using Lax pair (2.14), we obtain

$$u_x(x,t)-iu_t(x,t)=2(\overline{M(x,t;\xi)})_{21}=2\lim_{\xi\to\infty}(\xi M(x,t;\xi))_{21}.$$

The inverse problem is to derive the potential $u(x,t)$ from the spectral functions $\mu_j$, $j=1,2,3$, such that

$$ u(x,t)=2im(x,t).$$

(2.36)

Then the inverse problem can be stated as follows:

• 1) calculate $m(x,t)$ in terms of

  $$m(x,t)=\lim_{\xi\to\infty}(\xi\mu_j(x,t;\xi))_{12}$$

  by the spectral functions $\mu_j$, $j=1,2,3$;

• 2) reconstruct $u(x,t)$ by Eq. (2.36).

3. The spectral functions and the Riemann–Hilbert problem

3.1. The spectral functions

Definition 1 (the spectral functions $a(\xi)$ and $b(\xi)$).

Given a smooth function $u_0(x)=u(x,0)$, we can define a map

$$\mathbb{S}\!: \{u_0(x)\}\rightarrow \{a(\xi),b(\xi) \},$$

with

$$\begin{pmatrix} b(\xi) \\ a(\xi) \end{pmatrix} =\mu_3^{(2)}(x,0;\xi)=\begin{pmatrix} \mu_3^{12}(x,0;\xi) \\ \mu_3^{22}(x,0;\xi) \end{pmatrix},\qquad \operatorname{Im}\xi^2 \leq 0,$$

where $\mu_3(x,0;\xi)$ is a unique solution of the Volterra linear integral equation

$$\mu_3(x,0;\xi)=\mathrm{I}-\int_x^\infty e^{i\xi^2 (x-\zeta)\widehat{\sigma}_3}(V_1\mu_3)(\zeta,0;\xi)\,d\zeta,$$

and $V_1(x, 0;\xi)$ is determined by $u(x,0;\xi)$ in Eq. (2.24).

Proposition 4.

The functions $a(\xi)$ and $b(\xi)$ have the following properties:

• (i) they are analytic and bounded for $\operatorname{Im}\xi^2<0;$

• (ii) $a(\xi)=1+O(1/\xi)$ , $b(\xi)=O(1/\xi)$ , $\xi\rightarrow\infty$ , $\operatorname{Im}\xi^2 \leq 0;$

• (iii) $a(\xi)\overline{a(\bar{\xi})}-b(\xi)\overline{b(\bar{\xi})}=1$ , $\xi^2 \in \mathbb{R};$

• (iv) $a(-\xi)=a(\xi)$ , $b(-\xi)=-b(\xi)$ , $\operatorname{Im}\xi^2 \leq 0$ .

Remark 1.

The map

$$\mathbb{S}\!: \{u_0(x)\}\to \{a(\xi),b(\xi) \}$$

is given by Definition 1. The inverse of $\mathbb{S}$,

$$\mathbb{Q}\!: \{a(\xi),b(\xi) \}\to \{u_0(x)\}$$

can be obtained from

$$ u_0(x)=2im(x),\qquad m(x)=\lim_{\xi\to\infty}(\xi M^{(x)}(x,\xi))_{12},$$

(3.1)

where $M^{(x)}(x,\xi)$ is a unique solution of the Riemann–Hilbert problem.

The function $M^{(x)}(x,\xi)$ has the following properties.

• • $M^{(x)}(x,\xi)=\begin{cases} M_-^{(x)} (x,\xi), & \operatorname{Im}\xi^2 \geq 0, \\ M_+^{(x)} (x,\xi), & \operatorname{Im}\xi^2 \leq 0, \end{cases}$ is a partly meromorphic function.

• • $M_+^{(x)} (x,\xi)=M_-^{(x)} (x,\xi)J^{(x)} (x,\xi)$, $\xi^2\in \mathbb{R}$, and

  $$ J^{(x)} (x,\xi)=\begin{pmatrix} 1 & \dfrac{b(\xi)}{a(\xi)}e^{-2i\xi^2 x} \\ -\dfrac{\overline{b(\bar{\xi})}}{\overline{a(\bar{\xi})}}e^{2i\xi^2 x} & \dfrac{1}{a(\xi)\overline{a(\bar{\xi})}} \end{pmatrix}.$$

  (3.2)

• • $M^{(x)} (x,\xi)=\mathrm{I}+O(1/\xi)$ as $\xi\to\infty$.

• • $a(\xi)$ has $2h$ simple zeros $\{\epsilon_j\}_1^{2h}$, $2h=2h_1+2h_2$, such that $\epsilon_j$, $j=1,2,\dots,2h_1$, are located in $D_3\cup D_4$ and $\bar{\epsilon}_j$, $j=1,2,\dots,2h_2$, are located in $D_1\cup D_2$.

• • The first column of $M_-^{(x)}(x,\xi)$ has simple poles at $\xi=\bar{\epsilon}_j$, $j=1,2,\dots,2h_2$. The second column of $M_{+}^{(x)}(x,\xi)$ has simple poles at $\xi=\epsilon_j$, $j=1,2,\dots,2h_1$. The corresponding residues are

  $$ \begin{alignedat}{2} &\operatorname{Res} \{[M^{(x)}(x,\xi)]_1 , \bar{\epsilon}_j \}=\frac{e^{-2i\bar{\epsilon_j}^2x}\overline{b(\bar{\epsilon}_j)}}{\overline{\dot{a} (\bar{\epsilon}_j)}}[M^{(x)}(x,\bar{\epsilon}_j)]_2,&\qquad &j=1,2,\dots,2h_2,\\ &\operatorname{Res} \{[M^{(x)}(x,\xi)]_2 , \epsilon_j \}=\frac{e^{2i\epsilon_j^2 x}b(\epsilon_j)}{\dot{a}(\epsilon_j)}[M^{(x)}(x,\epsilon_j)]_1,&\qquad &j=1,2,\dots,2h_1. \end{alignedat}$$

  (3.3)

Definition 2 (spectral functions $A(\xi)$ and $B(\xi)$).

Let $g_0(t)$ and $g_1(t)$ be smooth functions. We define a map

$$\mathbb{\bar{S}}\!: \{g_0(t),g_1(t)\}\to \{A(\xi),B(\xi)\},$$

with

$$\begin{pmatrix} B(\xi) \\ A(\xi) \end{pmatrix} =\mu_1^{(2)}(0,t,\xi)=\begin{pmatrix} \mu_1^{12}(0,t,\xi) \\ \mu_1^{22}(0,t,\xi) \end{pmatrix},\qquad \operatorname{Im}\xi^4\geq 0,$$

where $\mu_1(0,t,\xi)$ is a unique solution of the Volterra linear integral equation

$$\mu_1(0,t,\xi)=\mathrm{I}-\int_t^T e^{2i\xi^4(\tau-t)\widehat{\sigma}_3}(V_2\mu_1)(0,\tau,\xi)\,d\tau,$$

and $V_2(0, T;\xi)$ is determined by Eq. (2.24).

Proposition 5.

The functions $A(\xi)$ and $B(\xi)$ have the following properties:

• (i) they are analytic for $\operatorname{Im}\xi^4>0$ and bounded for $\operatorname{Im}\xi^4\geq 0;$

• (ii) $A(\xi)=1+O(1/\xi)$ , $B(\xi)=O(1/\xi)$ , $\xi\to\infty$ , $\operatorname{Im}\xi^4 \geq 0;$

• (iii) $A(\xi)\overline{A(\bar{\xi})}-B(\xi)\overline{B(\bar{\xi})}=1$ , $\xi^4 \in \mathbb{R};$

• (iv) $A(-\xi)=A(\xi)$ , $B(-\xi)=-B(\xi)$ , $\operatorname{Im}\xi^4 \geq 0;$

• (v) $\mathbb{\bar{Q}}=\mathbb{\bar{S}}^{-1}\!: \{A(\xi),B(\xi) \}\to \{g_0(t),g_1(t)\}$ $\mathbb{\bar{Q}}$ is given by

  $$ \begin{aligned} \, &g_0(t)=2im_{12}^{(1)}(t),\\ &g_1(t)=(4m_{12}^{(1)}(t)-2|g_0(t)|^2)+ig_0(t)(4m_{12}^{(1)}(t)+|g_0(t)|^2), \end{aligned}$$

  (3.4)

  where $M^{(t)}(t,\xi)$ is a unique solution of the Riemann–Hilbert problem (see Remark 2 ).

Remark 2.

We set

• • $M^{(t)}(t,\xi)=\begin{cases} M_-^{(t)} (t,\xi), & \operatorname{Im} \xi^4\leq 0, \\ M_+^{(t)} (t,\xi), & \operatorname{Im} \xi^4\geq 0, \end{cases}$ which is a sectionally meromorphic function.

• • $M_+^{(t)} (t,\xi)=M_-^{(t)}(t,\xi)J^{(t)}(t,\xi)$, $\xi^4 \in \mathbb{R}$, and

  $$ J^{(t)} (t,\xi)= \begin{pmatrix} \dfrac{1}{A(\xi)\overline{A(\bar{\xi})}} & \dfrac{B(\xi)}{\overline{A(\bar{\xi})}}e^{-4i\xi^4 t} \\ -\dfrac{\overline{B(\bar{\xi})}}{A(\xi)}e^{4i\xi^4 t} & 1 \\ \end{pmatrix};$$

  (3.5)

• • $M^{(t)}(T,\xi)=\mathrm{I}+O(1/\xi)$ as $\xi\to\infty$;

• • $A(\xi)$ has $2l$ simple zeros $\{\eta_j\}_1^{2l}$, $2l=2l_1+2l_2$, such that $\eta_j$, $j=1,2,\dots,2l_1$, are located in $D_1\cup D_3$, and $\bar{\eta}_j$, $j=2l_1+1,2l_1+2,\dots,2l$, are located in $D_2\cup D_4$;

• • The first column of $M_+^{(t)}(t,\xi)$ has simple poles at $\xi=\eta_j$, $j=1,2,\dots,2l_1$. The second column of $M_-^{(t)}(t,\xi)$ has simple poles at $\xi=\bar{\eta}_j$, $j=1,2,\dots,2l_2$. The associated residues are

  $$ \begin{aligned} \, &\operatorname{Res} \{[M^{(t)}(t,\xi)]_1 , \eta_j \}=\frac{e^{4i\eta_j^4t}}{\dot{A}(\eta_j)B(\eta_j)} [M^{(t)}(t,\eta_j)]_2,\qquad j=1,2,\dots,2l_1,\\ &\operatorname{Res} \{[M^{(t)}(t,\xi)]_2 , \bar{\eta}_j \}=\frac{e^{-4i\eta_j^4t}}{\overline{\dot{A}(\bar{\eta}_j) B(\bar{\eta}_j)}}[M^{(t)}(t,\bar{\eta}_j)]_1,\qquad j=1,2,\dots,2l_2. \end{aligned}$$

  (3.6)

Definition 3 (spectral functions $\alpha(\xi)$ and $\beta(\xi)$).

Given the spectral functions

$$\alpha(\xi)=\overline{a(\bar{\xi})}A(\xi)-\overline{b(\bar{\xi})}B(\xi),\qquad \beta(\xi)=a(\xi)B(\xi)-b(\xi)A(\xi)$$

and a smooth function $h_T(x)=u(x,T)$, we can construct a map

$$\mathbb{\bar{\bar{S}}}\!: \{h_T(x)\}\to \{\alpha(\xi),\beta(\xi) \},$$

with

$$\begin{pmatrix} \beta(\xi) \\ \alpha(\xi) \\ \end{pmatrix} =\mu_1^{(2)}(0,T;\xi)=\begin{pmatrix} \mu_1^{12}(0,T;\xi) \\ \mu_1^{22}(0,T;\xi) \\ \end{pmatrix}, \qquad \operatorname{Im}\xi^2\geq 0,$$

where $\mu_1(x,T;\xi)$ is a unique solution of the Volterra linear integral equation

$$\mu_1(x,T;\xi)=\mathrm{I}+\int_0^x e^{i\xi^2(x-\zeta)\widehat{\sigma}_3}(V_1\mu_1)(\zeta,T;\xi)\,d\zeta.$$

Proposition 6.

The functions $\alpha(\xi)$ and $\beta(\xi)$ have the following properties :

• (i) $\alpha(\xi)$ and $\beta(\xi)$ are analytic for $\operatorname{Im}\xi^2 >0$ and bounded for $\operatorname{Im}\xi^2 \geq 0;$

• (ii) $\alpha(\xi)=1+O(1/\xi)$, $\beta(\xi)=O(1/\xi)$, $\xi\to\infty$, $\operatorname{Im}\xi^2 \geq 0;$

• (iii) $\alpha(\xi)\overline{\alpha(\bar{\xi})}-\beta(\xi)\overline{\beta(\bar{\xi})}=1$, $\xi^2 \in \mathbb{R};$

• (iv) $\alpha(-\xi)=\alpha(\xi)$, $\beta(-\xi)=-\beta(\xi)$, $\operatorname{Im}\xi^2 \geq 0;$

• (v) $\mathbb{\bar{\bar{Q}}}=\mathbb{\bar{\bar{S}}}^{-1}\!: \{\alpha(\xi),\beta(\xi) \}\to \{h_T(x)\}$, $\mathbb{\bar{\bar{Q}}}$ is given by

  $$ h_T(x)=2im_{T}(x),\qquad m_T(x)=\lim_{\xi\to\infty}(\xi M^{(T)}(x,\xi))_{12},$$

  (3.17)

  where $M^{(T)}(x,\xi)$ is a unique solution of the Riemann–Hilbert problem (see Remark 3).

Remark 3.

We set

• • $M^{(t)}(t,\xi)=\begin{cases} M_-^{(T)} (x,\xi), & \operatorname{Im}\xi^2 \leq 0, \\ M_+^{(T)} (x,\xi), & \operatorname{Im}\xi^2 \geq 0, \end{cases}$ which is a partly meromorphic function.

• • $M_+^{(T)}(x,\xi)=M_{-}^{(T)}(x,\xi)J^{(T)}(x,\xi)$, $\xi^2 \in \mathbb{R}$, and

  $$ J^{(T)}(x,\xi)=\begin{pmatrix} \dfrac{1}{\alpha(\xi)\overline{\alpha(\bar{\xi})}} & \dfrac{\beta(\xi)}{\overline{\alpha(\bar{\xi})}}e^{2i(\xi^2 x-2\xi^4T)} \\ -\dfrac{\overline{\beta(\bar{\xi})}}{\alpha(\xi)}e^{-2i(\xi^2 x-2\xi^4T)} & 1 \end{pmatrix},\qquad \xi^2 \in \mathbb{R};$$

  (3.8)

• • $M^{(T)}(x,\xi)=\mathrm{I}+O(1/\xi)$ as $\xi\to\infty$.

• • $\alpha(\xi)$ has $2H$ simple zeros $\{\delta_j\}_1^{2H}$, $2H=2H_1+2H_2$, such that $\delta_j$, $j=1,2,\dots,2H_1$, are located in $D_1\cup D_2$ and $\bar{\delta}_j$, $j=2H_1+1,2H_1+2,\dots,2H$, are located in $D_3\cup D_4$.

• • The first column of $M_+^{(T)}(x,\xi)$ has simple poles at $\xi=\delta_j$, $j=1,2,\dots,2H_1$. The second column of $M_-^{(T)}(x,\xi)$ has simple poles at $\xi=\bar{\delta}_j$, $j=1,2,\dots,2H_2$. The associated residues are

  $$ \begin{aligned} \, &\operatorname{Res} \{[M^{(T)}(x,\xi)]_1 , \delta_j \}=\frac{e^{-2i(\delta_j^2x-2\delta_j^4t)}}{\dot{\alpha}(\delta_j)\beta(\delta_j)} M^{(T)}(x,\delta_j)]_2,\quad j=1,2,\dots,2H_1,\\ &\operatorname{Res} \{[M^{(T)}(x,\xi)]_2 , \bar{\delta}_j\} =\frac{e^{2i(\delta_j^2x-4\delta_j^4t)}}{\overline{\dot{\alpha}(\bar{\delta}_j)}\overline{\beta(\bar{\delta}_j)}} [M^{(T)}(x,\bar{\delta}_j)]_1,\quad j=1,2,\dots,2H_2. \end{aligned}$$

  (3.9)

3.2. The Riemann–Hilbert problem

The following theorem is the main result in this paper.

Theorem 2.

Let $u_0(x)$ be a smooth function. We assume that the functions $g_0(t)$ and $g_1(t)$ are acceptable with $u_0(t)$. We define the spectral functions $s(\xi)$ and $S(\xi)$ for which $a(\xi)$, $b(\xi)$, $A(\xi)$, and $B(\xi)$ are determined by $u_0(x)$, $g_0(t)$, and $g_1(t)$ in Definitions 1 and 2. Then there is the global relation

$$S^{-1}(\xi)s(\xi)=e^{2i\xi^4T\widehat\sigma_3}\mu_3(0,t;\xi),$$

where $s(\xi)=\mu_3(0,0;\xi)$ and $S(\xi)=(e^{2i\xi^2T\widehat\sigma_3}\mu_2(0,T;\xi))^{-1}$ are given by Eq. (2.22). We suppose that the possible zeros $\{\epsilon_j\}_{j=1}^{2h}$ of $a(\xi)$ and $\{\delta_j\}_{j=1}^{2H}$ of $\alpha(\xi)$ and $M(x,t,\xi)$ are defined as solutions of the Riemann–Hilbert problem.

• • $M(x,t;\xi)$ is partly meromorphic on the Riemann $\xi$-sphere of jumps across the contours on $\bar D_l\cap\bar D_m$, $l,m=1,2,3$ (see Figure 2).

• • $M(x,t;\xi)$ satisfies the jump condition

  $$ M_+(x,t;\xi)=M_-(x,t;\xi)J(x,t;\xi),\qquad \xi \in \bar D_l\cap\bar D_m,\,l,m=1,2,3,\, l\neq m;$$

  (3.10)

• • $M(x,t;\xi)=\mathrm{I}+O(1/\xi)$ as $\xi\to\infty$.

• • The residue condition for $M(x,t;\xi)$ is given by Proposition 3.

Then $M(x,t;\xi)$ exists and is unique, and $u(x,t)$ can be obtained from $M(x,t;\xi)$ as

$$ u(x,t)=2im(x,t),\qquad m(x,t)=\lim \limits_{\xi\to\infty}(\xi M(x,t;\xi))_{12}.$$

(3.11)

Given the initial value $u(x,0)=u_0(x)$ and boundary values $u(0,t)=g_0(t)$ and $u_x(0,t)=g_1(t)$ that belong to the Schwartz space, the function $u(x,t)$ is a solution of the combined NLS–GI equation (1.3).

4. Conclusions

In this paper, we have studied the IBV for the combined NLS–GI equation on the half-line by using the Riemann–Hilbert approach. If the solution $u(x,t)$ of the NLS–GI equation exists, then a solution can be proved to exist for the Riemann–Hilbert problem formulated in the plane of the complex spectral parameter $\xi$. Is it possible to construct Riemann–Hilbert problems and determine their solutions by the same way for other integrable equations? Can other methods be used to find the solution of those problems? We hope to address these issues in the future.