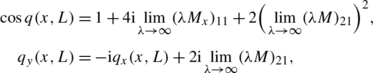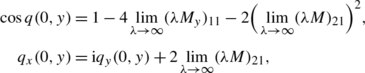1 Introduction

A method for solving initial-boundary value problems for linear and integrable nonlinear PDEs was introduced in Fokas (1997, 2000) and developed by several authors, see the survey Fokas (2008) and the references therein. This method has already been used for:

  1. (a)

    linear and integrable nonlinear evolution PDEs formulated on the half line and on a finite interval (Bona and Fokas 2008; Boutet de Monvel et al. 2004; Dujardin 2009; Flyer and Fokas 2008; Fokas 2002a, 2002b; Fokas and Its 1996, 2004; Fokas et al. 2005; Fokas and Lenells 2010; Fokas and Pelloni 2005; Pelloni 2005a, 2004; Treharne and Fokas 2008);

  2. (b)

    linear and integrable nonlinear hyperbolic PDEs (Fokas and Menyuk 1999; Pelloni 2005b; Pelloni and Pinotsis 2008);

  3. (c)

    linear elliptic PDEs (Antipov and Fokas 2005; ben Avraham and Fokas 2001; Crowdy and Fokas 2004; Dassios and Fokas 2005; Fokas 2001; Fokas and Spence 2009; Fokas and Zyskin 2002; Smitheman et al. 2010; Spence and Fokas 2010a, 2010b).

The aim of this paper is to implement this method in the case of the prototypical integrable nonlinear elliptic PDE, namely the celebrated elliptic sine-Gordon equation. This equation was first analysed in Lipovskii and Nikulichev (1988) (see also Borisov and Kiseliev 1989; Gutshabash and Lipovskii 1994); simple boundary value problems for this equation, using the method of Fokas (1997), have been considered in Pelloni (2009), Pelloni and Pinotsis (2010). For the case of nonlinear elliptic PDEs in cylindrical coordinates, see Lenells (2011), Lenells and Fokas (2011).

We will consider the sine-Gordon equation in the form

$$ q_{xx}+q_{yy}=\sin q,\quad q=q(x,y), $$
(1.1)

and we will analyse boundary value problems posed in the semi-infinite strip

(1.2)

where L is a positive finite constant. The sides {y=L,0<x<∞}, {x=0,0<y<L} and {y=0,0<x<∞} will be referred to as side (1), (2) and (3), respectively, see Fig. 1.

Fig. 1
figure 1

The semistrip \(\mathcal{S}\)

Full size image

Suppose that (1.1) is supplemented with appropriate, compatible boundary conditions on the boundary of the semistrip \(\mathcal{S}\), so that there exists a unique solution q(x,y). It will be shown in Sect. 2 that this solution can be expressed in terms of the solution of a 2×2 matrix Riemann–Hilbert (RH) problem with a jump on the union of the real and imaginary axis of the λ complex plane. The “jump matrix” is expressed in terms of certain functions, called spectral functions, which will be denoted by {a j (λ),b j (λ)}, j=1,2,3. These functions can be uniquely characterised via the solution of certain linear Volterra integral equations, in terms of the Dirichlet and Neumann boundary values. Namely, {a 1,b 1}, {a 2,b 2} and {a 3,b 3} are uniquely determined in terms of {q(x,L),q y (x,L)}, {q(0,y),q x (0,y)} and {q(x,0),q y (x,0)} respectively. However, for a well posed problem only a subset of these boundary values are prescribed as boundary conditions. Thus, in order to compute the spectral functions in terms of the given boundary conditions, one must first determine the unknown boundary values, i.e. one must characterise the Dirichlet to Neumann map. The solution of this problem, which makes crucial use of the so-called global relation, yields in general a nonlinear map, see Boutet de Monvel et al. (2003), Fokas (2005), Fokas and Lenells (2012), Lenells and Fokas (2012a, 2012b).

In the case of integrable nonlinear evolution PDEs, it has been shown in Fokas (2002a, 2004), Fokas et al. (2005), Fokas and Lenells (2010), Lenells and Fokas (2009) that there exists a particular class of boundary conditions, called linearisable, for which it is possible to avoid the above nonlinear map. The main result of the present paper is the analysis of a particular case of linearisable boundary conditions for the sine-Gordon equation on the semi-infinite strip. In particular, the following boundary conditions will be investigated in detail:

$$ q(x,L)=q(x,0)=0,\quad 0<x<\infty;\qquad q(0,y)=d,\quad 0<y<L, $$
(1.3)

where d is a finite constant. We assume that 0<d<π. These boundary conditions are discontinuous at the corners (0,0) and (0,L) of the domain. This implies that q y (x,y) has a non-integrable singularity at the two corners of the semistrip. Using an appropriate gauge transformation, which is motivated by the recent solution of the analogous problem for the modified Helmholtz equation (Ashton and Fokas 2012, see also Appendix), we are able to overcome this difficulty and introduce well-defined spectral functions. Furthermore, we show that the basic Riemann–Hilbert problem can be mapped to a simpler Riemann–Hilbert problem whose jump matrix, instead of depending on the six unknown spectral functions \(\{a_{j}(\lambda), b_{j}(\lambda)\}_{1}^{3}\), depends explicitly on the given constant d, on the width L of the semistrip, and on the residues at the given poles of a certain spectral function, denoted by h(λ). The rigorous analysis for the determination of h remains open.

This result, as well as the analogous result valid for the elliptic version of the Ernst equation (Lenells 2011; Lenells and Fokas 2011), imply that the method of Fokas (1997) provides a powerful tool for analysing effectively a large class of interesting boundary conditions.

2 Spectral Analysis Under the Assumption of Existence

In what follows we assume that (1.1) is supplemented with appropriate boundary conditions on the boundary of the semistrip \(\mathcal{S}\), compatible at the corners of the domain, so that the existence of a unique, smooth solution q(x,y) can be assumed. Furthermore, we assume the following:

(2.1)

The sine-Gordon equation is the compatibility condition of the following Lax pair (Lax 1968) for the 2×2 matrix-valued function Ψ(x,y,λ), λ∈ℂ:

(2.2)
(2.3)

where

(2.4)
(2.5)

Equations (2.2) and (2.3) can be written as the single equation

$$ \mathrm{d} \bigl({\rm e}^{(\varOmega(\lambda)x+\omega(\lambda)y)\frac{\widehat {\sigma_3}}{2}}\varPsi(x,y,\lambda) \bigr)=W(x,y,\lambda), $$
(2.6)

where the differential form W is given by

(2.7)

and \(\widehat{\sigma_{3}}\) acts on a 2×2 matrix A by

$$\widehat{\sigma_3}A=[\sigma_3,A]. $$

Remark 2.1

Note that

$$\overline{\varOmega(\bar{{\lambda }})}=-\varOmega({\lambda })=\varOmega \biggl(\frac{1}{{\lambda }}\biggr),\qquad \overline{\omega(\bar{{\lambda }})}=\omega({\lambda })=\omega \biggl(\frac{1}{{\lambda }}\biggr). $$

2.1 Bounded and Analytic Eigenfunctions

We define three solutions Ψ j (x,y,λ), j=1,2,3, of (2.6) by

$$ \varPsi_j(x,y,\lambda)=I+\int_{(x_j,y_j)}^{(x,y)} {\rm e}^{-(\varOmega (\lambda)x+\omega(\lambda)y)\frac{\widehat{\sigma_3}}{2}}W(\xi ,\eta,\lambda), $$
(2.8)

where

$$ (x_1,y_1)=(\infty,y),\qquad(x_2,y_2)=(0,L), \qquad(x_3,y_3)=(0,0). $$
(2.9)

Since the differential form W is exact, the integral on the right-hand side of (2.8) is independent of the path of integration. We choose the particular contours shown in Fig. 2. This choice implies the following inequalities on the contours:

The first inequality above implies that the exponential appearing in the second (first) column of the right-hand side of the equation defining Ψ 1 is bounded and analytic for Im(λ)<0 (Im(λ)>0). Similar considerations are valid for Ψ 2 and Ψ 3. Hence we denote the matrices Ψ j as follows:

$$\varPsi_{1}=\bigl(\varPsi_{1}^{(12)}, \varPsi_{1}^{(34)}\bigr),\qquad \varPsi_{2}=\bigl( \varPsi_{2}^{(4)}, \varPsi_{2}^{(2)} \bigr),\qquad \varPsi_{3}=\bigl(\varPsi_{3}^{(3)}, \varPsi_{3}^{(1)}\bigr), $$

where the superscript (12) denotes the union of the first and second quadrants of the λ complex plane, and similarly for the other superscripts. The function \(\varPsi_{1}^{(12)}\) is analytic for Im(λ)>0 and it has essential singularities at λ=∞ and λ=0; furthermore,

$$ \varPsi_1^{(12)}=\left ( \begin{array}{c} 1\\0 \end{array} \right )+\mathrm{O} \biggl(\frac{1}{\lambda}\biggr),\quad\lambda\to\infty ,\ \mathrm{Im}( \lambda)\geq0. $$
(2.10)

Similar considerations are valid for the column vectors \(\varPsi_{1}^{(34)}\), \(\varPsi_{3}^{(3)}\) and \(\varPsi_{3}^{(1)}\). The function Ψ 2 is an analytic function in the entire complex plane, except at λ=∞ and λ=0, where it has essential singularities. In addition,

(2.11)
Fig. 2
figure 2

The functions Ψ 1, Ψ 2 and Ψ 3

Full size image

2.2 Spectral Functions

Any two solutions Ψ, \(\tilde{\varPsi}\) of (2.6) are related by an equation of the form

$$ \varPsi(x,y,{\lambda })=\tilde{\varPsi}(x,y,{\lambda }){\rm e}^{-(\varOmega(\lambda)x+\omega (\lambda)y)\frac{\widehat{\sigma_3}}{2}}C(\lambda). $$
(2.12)

We introduce the notations

$$ S_1(\lambda)=\varPsi_1(0,L,\lambda),\qquad S_2(\lambda)=\varPsi_2(0,0,\lambda),\qquad S_3(\lambda)=\varPsi_1(0,0,\lambda). $$
(2.13)

Then (2.12) implies the following equations:

(2.14)
(2.15)
(2.16)

The notation λ∈(ℝ−,ℝ+) means that the equation for the first column vector in (2.16) is valid for λ∈ℝ−, while the equation for the second vector is valid for ℝ+.

Equations (2.13)–(2.16) suggest the following definitions:

(2.17)
(2.18)
(2.19)

The matrix Q satisfies the symmetry properties

$$ Q(\lambda)_{22}=Q(-\lambda)_{11}, \qquad Q( \lambda)_{12}=Q(-\lambda)_{21}. $$
(2.20)

Hence the matrices Φ i , i=1,…,3, can be represented in the form

and therefore

$$S_i(\lambda)=\left ( \begin{array}{c@{\quad}c} a_{i}(\lambda)&b_{i}(-\lambda) \\ b_{i}(\lambda)&a_{i}(-\lambda) \end{array} \right ), \quad i=1,2,3. $$

The spectral functions {a 1(λ),b 1(λ)}, {a 2(λ),b 2(λ)} and {a 3(λ),b 3(λ)} are defined in terms of {q(x,L),q y (x,L)}, {q(0,y),q x (0,y)} and {q(x,0),q y (x,0)}, respectively, through (2.17)–(2.19).

These functions have the following properties:

  • a 1(λ), b 1(λ) are analytic and bounded in ℂ+.

    a 1(λ)a 1(−λ)−b 1(λ)b 1(−λ)=1, λ∈ℝ.

    \(a_{1}(\lambda)=1+\mathrm{O} (\frac{1}{\lambda})\), \(b_{1}(\lambda )=\mathrm{O} (\frac{1}{\lambda})\) as λ→∞,Im(λ)≥0.

  • a 2(λ), b 2(λ) are analytic functions of λ for all λ∈ℂ, except for essential singularities at λ=∞ and λ=0.

    a 2(λ)a 2(−λ)−b 2(λ)b 2(−λ)=1, λ∈ℂ∖{0}.

    \(a_{2}(\lambda)=1+\mathrm{O} (\frac{1}{\lambda})\), \(b_{2}(\lambda )=\mathrm{O} (\frac{1}{\lambda})\) as \(\lambda\to\infty, \frac{3\pi}{2}\leq \mathrm{arg}(\lambda)\leq2\pi\).

  • a 3(λ), b 3(λ) are analytic and bounded in ℂ+.

    a 3(λ)a 3(−λ)−b 3(λ)b 3(−λ)=1, λ∈ℝ.

    \(a_{3}(\lambda)=1+\mathrm{O} (\frac{1}{\lambda})\), \(b_{3}(\lambda )=\mathrm{O} (\frac{1}{\lambda})\) as λ→∞,Im(λ)≥0.

These properties follow from the analogous properties of the matrix-valued functions Φ j , j=1,2,3, from the condition of unit determinant, and from the large λ asymptotics of these functions.

2.3 The Global Relation

Evaluating (2.15) and (2.16) at x=0, y=L, we find

$$I=\varPsi_3(0,L,\lambda){\rm e}^{-\frac{\omega(\lambda)}{2}L\widehat {\sigma_{3}}} S_2(\lambda) $$

and

$$S_{1}(\lambda)=\varPsi_{3}(0,L,\lambda) {\rm e}^{-\frac{\omega(\lambda )}{2}L\widehat{\sigma_{3}}} S_3(\lambda). $$

Eliminating Ψ 3(0,L,λ) we obtain

$$ {\rm e}^{\frac{\omega(\lambda)}{2}L\widehat{\sigma_{3}}}S_{1}(\lambda )=S_2( \lambda)^{-1}S_3(\lambda). $$
(2.21)

The first column vector of this equation yields the following global relations:

(2.22a)
(2.22b)

2.4 The Riemann–Hilbert Problem

Equations (2.14)–(2.16), relating the various analytic eigenfunctions, can be rewritten in a form that determines the jump conditions of a 2×2 RH problem, with unitary jump matrices on the real and imaginary axes. This involves tedious but straightforward algebraic manipulations. The final form is

$$ M_{-}(x,y,\lambda)=M_{+}(x,y,\lambda)J(x,y,\lambda), \quad \lambda \in {\mathbb{R}}\cup \mathrm{i}{\mathbb{R}}, $$
(2.23)

where the matrices M ± and J are defined as follows (see Fig. 3):

(2.24)
(2.25)

where, using the global relations (2.22a), (2.22b) we find

and

$$ J^{\pi}= J^{3\pi/2}\bigl(J^{0} \bigr)^{-1}J^{\pi/2}, $$
(2.26)

where

$$ \theta(x,y,\lambda)=\varOmega(\lambda)x+\omega(\lambda)y. $$
(2.27)

All the matrices J α have unit determinant: for J π/2 and J 3π/2 this is immediate, whereas for J 0 we find

$$\det\bigl(J^0\bigr)=\frac{a_2(\lambda)+{\rm e}^{-\omega(\lambda)L}b_1(\lambda )b_3(-\lambda)}{a_1(-\lambda)a_3(\lambda)}= \frac{a_1(-\lambda)a_3(\lambda)}{a_1(-\lambda)a_3(\lambda)}=1, $$

where we have used the equation

$$ a_2(\lambda)=a_1(-{\lambda })a_3( {\lambda })-b_3(-{\lambda })b_1({\lambda }){\rm e}^{-\omega (\lambda)L},\quad {\lambda }\in {\mathbb{R}}, $$
(2.28)

which is a consequence of the global relations (2.22a), (2.22b).

Fig. 3
figure 3

The bounded eigenfunctions and the Riemann–Hilbert problem

Full size image

The solution M(x,y,λ) of this RH problem is a sectionally meromorphic function of λ. The possible poles of this function are generated by the zeros of the function a 1(λ) in the region \(\{ \mathrm{arg}({\lambda })\in[\frac{\pi}{2},\pi]\}\), by the zeros of a 3(λ) in the region \(\{\mathrm{arg}({\lambda })\in[0,\frac{\pi}{2}]\}\), and by the corresponding zeros of a 1(−λ), a 3(−λ).

We assume

$$ \begin{array}{@{}l@{\ \ }l} \bullet & \mbox{The possible zeros of $a_{1}$ in the region $\{\mathrm{arg}({\lambda })\in(\frac{\pi }{2},\pi)\}$ are simple;}\hspace{22pt}\\[4pt] & \mbox{these zeros are denoted ${\lambda }_{j}$, $j=1,\ldots,N_{1}$}\\[4pt] \bullet & \mbox{The possible zeros of $a_{3}$ in the region $\{\mathrm{arg}({\lambda })\in(0,\frac{\pi}{2})\}$ are simple;}\\[4pt] & \mbox{these zeros are denoted $\zeta_{j}$, $j=1,\ldots,N_{3}$} \end{array} $$
(2.29)

The residues of the function M at the corresponding poles can be computed using (2.14)–(2.16). Indeed, (2.16) yields

$$\varPsi_1^{(12)}=a_3\varPsi_3^{(3)}+b_3 {\rm e}^{\theta(x,y,{\lambda })}\varPsi_3^{(1)}, $$

hence

$$ \mathrm{Res}_{\zeta_j} \frac{\varPsi_3^{(1)}}{a_3}=\frac{\varPsi_3^{(1)}(\zeta_j)}{\dot{a}_3(\zeta_j)}=\frac{\varPsi_1^{(12)}(\zeta_j)}{\dot{a}_3(\zeta_j)b_3(\zeta_j)} {\rm e}^{-\theta(x,y,\zeta_j)}, $$
(2.30)

where \(\dot{a}_{3}({\lambda })\) denotes the derivative of a 3 with respect to λ.

Similarly, using (2.14),

$$ \mathrm{Res}_{{\lambda }_j} \frac{\varPsi_2^{(2)}}{a_1}=\frac{\varPsi_2^{(2)}({\lambda }_j)}{\dot{a}_1({\lambda }_j)}=\frac{\varPsi_1^{(12)}({\lambda }_j)}{\dot{a}_1({\lambda }_j)b_1({\lambda }_j){\rm e}^{-\omega({\lambda }_j)L}} {\rm e}^{-\theta(x,y,{\lambda }_j)}. $$
(2.31)

Using the notation [M]1 for the first column and [M]2 for the second column of the solution M of the RH problem (2.23), (2.30) and (2.31) imply the following residue conditions:

(2.32)

Similar residue conditions are obtained in ℂ− by letting λ→−λ.

2.4.1 The Inverse Problem

Rewriting the jump condition, we obtain

$$ M_{+}-M_{-}=M_{+}-M_{+}J=M_{+}(I-J) \Rightarrow M_{+}-M_{-}=M_{+}\tilde{J}, $$
(2.33)

where \(\tilde{J}=I-J\). The asymptotic conditions (2.10)–(2.11) imply

$$ M(x,y,{\lambda })=I+\frac{M^{*}(x,y)}{\lambda}+ \mathrm{O} \biggl(\frac{1}{\lambda^{2}} \biggr),\quad| \lambda|\to\infty ,\ \lambda\in {\mathbb{C}}\setminus({\mathbb{R}}\cup \mathrm{i}{\mathbb{R}}). $$
(2.34)

Equation (2.33) and the condition (2.34) yield the following integral representation for the function M:

$$ M(x,y,\lambda)=I+\frac{1}{2\pi \mathrm{i}}\int_{\varGamma} \frac {M_{+}(x,y,\lambda')\tilde{J}(x,y,\lambda')}{\lambda'-\lambda}\,\mathrm{d}\lambda',\quad\lambda\in {\mathbb{C}}\setminus\varGamma, $$
(2.35)

where

$$\varGamma={\mathbb{R}}\cup \mathrm{i}{\mathbb{R}}. $$

Equations (2.34) and (2.35) imply

$$ M^{*}=-\frac{1}{2\pi \mathrm{i}}\int_{\varGamma}M_{+}(x,y, \lambda)\tilde{J}(x,y,\lambda)\,\mathrm{d}\lambda. $$
(2.36)

Using (2.34) in the first ODE in the Lax pair (2.2), we find

$$ -\frac{\mathrm{i}}{4}\bigl[\sigma_{3},M^{*}\bigr]=\mathrm{i} \frac{q_{x}-\mathrm{i}q_y}{4}\sigma_{1}\Rightarrow q_{x}-\mathrm{i}q_y=2 \bigl(M^{*}\bigr)_{21}=2\lim_{\lambda\to\infty}(\lambda M_{21}), $$
(2.37)

where σ 1, σ 3 denote the usual Pauli matrices.

In order to obtain an expression in terms of q rather than its derivatives, we consider the coefficient in (2.2) of the term λ −1. The (1, 1) element of this coefficient yields

$$ \cos q(x,y)=1+4\mathrm{i}\bigl(M^*_x\bigr)_{11}+2\bigl(M^* \bigr)^2_{21}. $$
(2.38)

3 Spectral Theory Assuming the Validity of the Global Relation

3.1 The Spectral Functions

The above analysis motivates the following definitions for the spectral functions.

3.1.1 The Spectral Functions at the y=0 and y=L Boundaries

Definition 3.1

Given the functions q(x,L), q y (x,L) satisfying conditions (2.1), define the map

$$\mathbb{S}_1:\bigl\{q(x,L),q_y(x,L)\bigr\}\to\bigl \{a_1(\lambda),b_1(\lambda)\bigr\} $$

by

$$\left ( \begin{array}{c} a_1(\lambda)\\b_1(\lambda) \end{array} \right )=\bigl[ \varPhi_1(0,{\lambda })\bigr]_1,\quad\lambda\in {\mathbb{C}}^+, $$

where [Φ 1(x,λ)]1 denotes the first column vector of the unique solution Φ 1(x,λ) of the Volterra linear integral equation

$$ \varPhi(x,\lambda)=I-\int_x^{\infty} {\rm e}^{\varOmega(\lambda)(\xi -x)\frac{\widehat{\sigma_3}}{2}} Q(\xi,L,\lambda)\varPhi(\xi,\lambda)\,\mathrm{d}\xi, $$
(3.1)

and Q(x,L,λ) is given in terms of q(x,L) and q y (x,L) by (2.5).

In what follows, we also assume that the function a 1(λ) may have N 1 simple poles λ j in ℂ+. Similarly for a 3(λ).

Proposition 3.1

The spectral functions a 1(λ), b 1(λ) have the following properties.

  1. (i)

    a 1(λ), b 1(λ) are continuous and bounded for Im(λ)≥0, and analytic for Im(λ)>0.

  2. (ii)

    \(a_{1}(\lambda)=1+\mathrm{O} (\frac{1}{\lambda})\), \(b_{1}(\lambda )=\mathrm{O} (\frac{1}{\lambda})\) as λ→∞,Im(λ)≥0.

  3. (iii)

    \(a_{1}(\lambda)=\cos\frac{q(0,L)}{2}+\mathrm{O} ( \lambda )\), \(b_{1}(\lambda)=\mathrm{i}\sin\frac{q(0,L)}{2}+\mathrm{O} (\lambda )\) as λ→0,Im(λ)≥0.

  4. (iv)

    a 1(λ)a 1(−λ)−b 1(λ)b 1(−λ)=1, λ∈ℝ.

  5. (v)

    The map ℚ1:{a 1, b 1}→{q(x,L) q y (x,L)}, inverse to \(\mathbb{S}_{1}\), is given

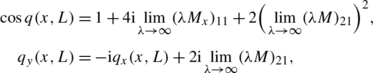
    where M is the solution of the following Riemann–Hilbert problem:

    • The function

      $$M(x,{\lambda })=\left \{ \begin{array}{l@{\quad}l} M_+(x,{\lambda }),&{\lambda }\in {\mathbb{C}}^+,\\[4pt] M_-(x,{\lambda }),&{\lambda }\in {\mathbb{C}}^- \end{array} \right . $$

      is a sectionally meromorphic function of λ∈ℂ.

    • \(M=I+\mathrm{O} (\frac{1}{{\lambda }})\) as λ→∞, and

      $$M_-(x,{\lambda })=M_+(x,{\lambda })J_1(x,{\lambda }),\quad {\lambda }\in {\mathbb{R}}, $$

      where

      $$ J_1(x,{\lambda })=\left ( \begin{array}{l@{\quad}l} 1&-\frac{b_1(-{\lambda })}{a_1({\lambda })}{\rm e}^{-\varOmega({\lambda })x} \\[7pt] \frac{b_1({\lambda })}{a_1(-{\lambda })}{\rm e}^{\varOmega({\lambda })x}&\frac{1}{a_1({\lambda })a_1(-{\lambda })} \end{array} \right ), \quad {\lambda }\in {\mathbb{R}}. $$
      (3.2)

    • Let [M] i denote the ith column vector of M, 1=1,2. The possible poles of M + occur at λ j , and the possible poles of M − occur at −λ j in ℂ−, and the associated residues are given by

      (3.3)

The spectral functions {a 3,b 3} are defined similarly:

Definition 3.2

Given the functions q(x,0), q y (x,0), satisfying conditions (2.1), define the map

$$\mathbb{S}_3:\bigl\{q(x,0),q_y(x,0)\bigr\}\to\bigl \{a_3(\lambda),b_3(\lambda)\bigr\} $$

by

$$\left ( \begin{array}{c} a_3(\lambda)\\b_3(\lambda) \end{array} \right )=\bigl[ \varPhi_3(0,0)\bigr]_1,\quad\lambda\in {\mathbb{C}}^+, $$

where [Φ 3(x,0)]1 denotes the first column vector of the unique solution Φ 3(x,0) of the Volterra linear integral equation

$$ \varPhi(x,\lambda)=I-\int_x^{\infty} {\rm e}^{\varOmega(\lambda)(\xi -x)\frac{\widehat{\sigma_3}}{2}} Q(\xi,0,\lambda)\varPhi(\xi,\lambda)\,\mathrm{d}\xi, $$
(3.4)

and Q(x,0,λ) is given in terms of q(x,0) and q y (x,0) by (2.5).

Proposition 3.2

The spectral functions a 3(λ), b 3(λ) have the properties (i)–(v) of Proposition 3.1, provided a 1 is replaced by a 3, b 1 is replaced by b 3, \(\mathbb{S}_{1}\) is replaced by \(\mathbb{S}_{3}\) and L is replaced by 0 in all expressions.

3.1.2 The Spectral Functions at the x=0 Boundary

Definition 3.3

Given the functions q(0,y), q x (0,y), satisfying conditions (2.1), define the map

$$\mathbb{S}_2:\bigl\{q(0,y),q_x(0,y)\bigr\}\to\bigl \{a_2(\lambda),b_2(\lambda)\bigr\} $$

by

$$\left ( \begin{array}{cc} a_2(\lambda)\\b_2(\lambda) \end{array} \right )=\bigl[ \varPhi_2(0,0)\bigr]_1,\quad\lambda\in {\mathbb{C}}^+, $$

where [Φ 2(0,y)]1 denotes the first column vector of the unique solution Φ 2(0,y) of the Volterra linear integral equation

$$ \varPhi(y,\lambda)=I-\mathrm{i}\int_y^L {\rm e}^{\omega(\lambda)(\eta-y)\frac {\widehat{\sigma_3}}{2}} Q(0,\eta,-\lambda)\varPhi(\eta,\lambda)\,\mathrm{d}\eta, $$
(3.5)

and Q(0,y,λ) is given in terms of q(0,y) and q x (0,y) by (2.5).

Proposition 3.3

The spectral functions a 2(λ), b 2(λ) have the following properties.

  1. (i)

    a 2(λ), b 2(λ) are analytic functions of λ, except for essential singularities at λ=0 and λ=∞, bounded for Re(λ)≥0.

  2. (ii)

    \(a_{2}(\lambda)=1+\mathrm{O} (\frac{1}{\lambda})\), \(b_{2}(\lambda )=\mathrm{O} (\frac{1}{\lambda})\) as λ→∞,Re(λ)≥0.

  3. (iii)

    \(a_{2}(\lambda)=\cos\frac{q(0,0)}{2}+\mathrm{O} ( \lambda )\), \(b_{2}(\lambda)=\mathrm{i}\sin\frac{q(0,0)}{2}+\mathrm{O} (\lambda )\) as λ→0,Re(λ)≥0.

  4. (iv)

    a 2(λ)a 2(−λ)−b 2(λ)b 2(−λ)=1, λ∈ℂ.

  5. (v)

    The map ℚ2:{a 2, b 2}→{q(0,y) q y (0,y)}, inverse to \(\mathbb{S}_{2}\), is given by

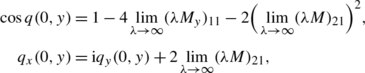
    where M is the solution of the following Riemann–Hilbert problem:

    • The function

      $$M(y,{\lambda })=\left \{ \begin{array}{l@{\quad}l} M_+(y,{\lambda }),&\mathrm{Re}\,{\lambda }\geq0, \\[2pt] M_-(y,{\lambda }),&\mathrm{Re}\,{\lambda }\leq0 \end{array} \right . $$

      is a sectionally meromorphic function of λ∈ℂ.

    • \(M=I+\mathrm{O} (\frac{1}{{\lambda }})\) as λ→∞, and

      $$M_-(y,{\lambda })=M_+(y,{\lambda })J_2(y,{\lambda }),\quad {\lambda }\in \mathrm{i}{\mathbb{R}}, $$

      where

      $$J_2(y,{\lambda })=\left ( \begin{array}{c@{\quad}c} 1&-\frac{b_2(-{\lambda })}{a_2({\lambda })}{\rm e}^{-\omega({\lambda })x} \\[4pt] \frac{b_2({\lambda })}{a_2(-{\lambda })}{\rm e}^{\omega({\lambda })x}&\frac{1}{a_2({\lambda })a_2(-{\lambda })} \end{array} \right ), \quad {\lambda }\in \mathrm{i}{\mathbb{R}}. $$

    • M satisfies appropriate residue conditions at the zeros of a 2(λ).

3.1.3 Proof of Propositions 3.1–3.3

The proof of properties (i)–(iv) follows from the discussion in Sect. 2.2. In particular, property (iii) follows from the asymptotic behaviour at λ→0, which can be derived by analyzing equations (2.2)–(2.3) (see Pelloni 2009), and is given by

$$ \varPsi=\varPsi_{0}+\mathrm{O} (\lambda ),\quad |\lambda|\to0,\qquad \varPsi_0(x,y)= \left ( \begin{array}{l@{\quad}l} \cos\frac{q(x,y)}{2}&\mathrm{i}\sin\frac{q(x,y)}{2} \\[4pt] \mathrm{i}\sin\frac{q(x,y)}{2}&\cos\frac{q(x,y)}{2} \end{array} \right ). $$
(3.6)

To prove (v), we note that the function Φ 1(x,λ) given by (2.17) is the unique solution of the ODE

Furthermore, Φ 3(x,λ) given by (2.19) is the solution of the same ODE problem, with Q(x,L,λ) replaced by Q(x,0,λ).

Similarly, Φ 2(y,λ) given by (2.18) is the unique solution of the ODE

The spectral analysis of the above ODEs yields the desired result.

Regarding the rigorous derivation of the above results, we note the following: If {q(x,L),q y (x,L)}, {q(x,0),q y (x,0)} and {q(y,0),q x (y,0)} are in \({\bf L}^{1}\), then the Volterra integral equations (3.1), (3.4) and (3.5), respectively, have a unique solution, and hence the spectral functions {a j ,b j }, j=1,…,3, are well defined. Moreover, under the assumption (2.1) the spectral functions belong to \({\bf H}^{1}({\mathbb{R}})\), hence the Riemann–Hilbert problems that determine the inverse maps can be characterised through the solutions of a Fredholm integral equation, see Deift (2000) and Zhou (1989).

3.2 The Riemann–Hilbert Problem

Theorem 3.1

Suppose that a subset of the boundary values {q(x,L),q y (x,L)}, {q(x,0),q y (x,0)}, 0<x<∞, and {q(y,0),q x (y,0)}, 0<y<L, satisfying (2.1), are prescribed as boundary conditions. Suppose that these prescribed boundary conditions are such that the global relations (2.22a), (2.22b) can be used to characterise the remaining boundary values.

Define the spectral functions {a j ,b j }, j=1,…,3, by definitions (3.1)–(3.3). Assume that the possible zeros \(\{{\lambda }_{j}\}_{j=1}^{N_{1}}\) of a 1(λ) and \(\{\zeta_{j}\}_{j=1}^{N_{3}}\) of a 3(λ) are as in assumption (2.29).

Define M(x,y,λ) as the solution of the following 2×2 matrix Riemann–Hilbert problem:

  • The function M(x,y,λ) is a sectionally meromorphic function of λ away from ℝ∪iℝ.

  • The possible poles of the second column of M occur at λ=ζ j , j=1,…,N 3, in the first quadrant and at λ=λ j , j=1,…,N 1, in the second quadrant of the complex λ plane.

    The possible poles of the first column of M occur at λ=−λ j (j=1,…,N 1) and λ=−ζ j (j=1,…,N 3).

    The associated residue conditions satisfy the relations (2.32).

  • \(M=I+\mathrm{O} (\frac{1}{{\lambda }})\) as λ→∞, and

    $$M_-(x,y,{\lambda })=M_+(x,y,{\lambda })J(x,y,{\lambda }),\quad {\lambda }\in {\mathbb{R}}\cup \mathrm{i}{\mathbb{R}}, $$

    where M=M + for λ in the first or third quadrant, and M=M − for λ in the second or fourth quadrant of the complex λ plane, and J is defined in terms of {a j ,b j } by (2.26).

Then M exists and is unique, provided that the \({\bf H}^{1}\) norm of the spectral functions is sufficiently small.

Define q(x,y) is terms of M(x,y,λ) by

(3.7)
(3.8)

Then q(x,y) solves (1.1). Furthermore, q(x,y) evaluated at the boundary, yields the functions used for the computation of the spectral functions.

Proof

Under the assumptions (2.1), the spectral functions are in \({\bf H}^{1}\).

In the case when a 1(λ) and a 3(λ) have no zeros, the Riemann–Hilbert problem is regular and it is equivalent to a Fredholm integral equation. However, we have not been able to establish a vanishing lemma, hence we require a small norm assumption for solvability.

If a 1(λ) and a 3(λ) have zeros, the singular RH problem can be mapped to a regular one coupled with a system of algebraic equations (Fokas and Its 1996). Moreover, it follows from standard arguments, using the dressing method (Zakharov and Shabat 1974, 1979), that if M solves the above RH problem and q(x,y) is defined by (3.7)–(3.8), then q(x,y) solves (1.1). The proof that q evaluated at the boundary yields the functions used for the computation of the spectral functions follows arguments similar to the ones used in Fokas et al. (2005). □

4 Linearisable Boundary Conditions

We now concentrate on the particular boundary conditions (1.3). We note that these boundary conditions are symmetric with respect to the line \(y=\frac{L}{2}\). Hence, if q(x,y) is a solution, so is q(x,L−y). Assuming that the solution is unique, we can conclude that

$$ q(x,y)=q(x,L-y), \quad0<x<\infty, 0<y<L. $$
(4.1)

These boundary conditions are not compatible at the corners of the domain, and therefore introduce a discontinuity at each corner. It turns out that these discontinuities imply that if q(x,y) is the solution of the resulting boundary value problem, then the function q y (x,0)=−q y (x,L) is not integrable near x=0. Similarly, q x (0,y) is not integrable near y=0 and y=L. Hence we cannot guarantee that the results of Propositions 3.1–3.3 hold. In particular, the spectral functions as given by (2.17)–(2.19) and the resulting Riemann–Hilbert problem are not well defined.

To overcome this lack of regularity, we will employ a gauge transformation to define a modified Lax pair. This transformation is motivated by the recent analysis of the linearised problem (Ashton and Fokas 2012), which we summarise in Appendix. For the linear case, it can be shown that the behaviour of the boundary function q y (x,0) as x→0 is given by \(q_{y}(x,0)\sim\frac{2d}{\pi x}\). The contribution of this term can be eliminated by an appropriate gauge transformation. The advantage of the new Lax pair we define below by adapting the linear gauge transformation to the nonlinear setting, is that the spectral functions and the Riemann–Hilbert problem are well defined, indicating that in the nonlinear case, as in the linear, the singular behaviour introduced by the terms q y (x,0) and q x (0,y) is eliminated.

4.1 A New Lax Pair

The linearised version of the elliptic sine-Gordon equation, namely the modified Helmholtz equation, with the boundary conditions (1.3), is discussed in Appendix, where we show how, by incorporating appropriately in the differential form associated with the linear equation the term

$$ \kappa(x,y)=-\frac{1}{4}\int_x^\infty q_y(\xi,y)\,\mathrm{d}\xi, $$
(4.2)

the spectral problem is regularised.

Motivated by the linear analysis, we now introduce a new eigenfunction Φ via the gauge transformation

$$ g\varPhi=\varPsi,\qquad g(x,y) := \mathrm{e}^{\kappa(x,y)\sigma_1} = \left ( \begin{array}{c@{\quad}c} \cosh\kappa(x,y)&\sinh\kappa(x,y) \\[4pt] \sinh\kappa(x,y)&\cosh\kappa(x,y) \end{array} \right ), $$
(4.3)

where Ψ denotes the solution of the Lax pair (2.2)–(2.3) and κ(x,y) is given by (4.2). Note that

$$\kappa_x(x,y)=\frac{1}{4} q_y(x,y),\qquad \kappa_y(x,y)=-\frac{1}{4} \int_x^\infty \sin q(\xi,y)\,\mathrm{d}\xi-\frac{1}{4} q_x(x,y). $$

The transformation matrix g(x,y) has unit determinant, and is chosen to satisfy the property

$$g^{-1}g_x=g_xg^{-1}=\frac{1}{4} \left ( \begin{array}{c@{\quad}c} 0&q_y(x,y)\\ q_y(x,y)&0 \end{array} \right ). $$

Let the function Φ satisfy the Lax pair

(4.4)
(4.5)

with

(4.6)
(4.7)

We now use the eigenfunctions determined by the Lax pair (4.4)–(4.5) to define new spectral functions. Namely, in analogy with (2.17)–(2.19), we define

(4.8)
(4.9)
(4.10)

Note that V 1 does not involve q y (x,y), and V 2 does not involve q x (x,y), the terms, respectively, responsible, at least in the linear case, for the non-integrable behaviour.

Note also that, since the symmetry relation (2.20) holds for V 1, V 2 in place of Q, we can represent the matrices φ i in the form

(4.11)

and set

$$ S_i(\lambda)=\left ( \begin{array}{c@{\quad}c} a_{i}(\lambda)&b_{i}(-\lambda) \\ b_{i}(\lambda)&a_{i}(-\lambda) \end{array} \right ), \quad i=1,2,3. $$
(4.12)

The rest of the general construction of Sects. 2.3–3.2 is formally valid with the spectral functions a j (λ), b j (λ), j=1,2,3 as defined by (4.12), except for the statement (i)–(iii) and (v) of Propositions 3.1–3.3.

4.1.1 Symmetry Conditions

Given the boundary conditions (1.3), (4.8)–(4.10) are written explicitly as follows:

(4.13)
(4.14)
(4.15)

Using that κ(x,0)=−κ(x,L), we can immediately conclude that

$$ \left ( \begin{array}{c}A_1(x,{\lambda })\\B_1(x,{\lambda }) \end{array} \right )= \left ( \begin{array}{c}A_3(x,{\lambda })\\-B_3(x,{\lambda }) \end{array} \right ) \quad \Longrightarrow\quad a_1( {\lambda })=a_3({\lambda }),\quad b_1({\lambda })=-b_3({\lambda }), $$
(4.16)

where A i , B 1, a i , b i are as in (4.11)–(4.12).

In (4.13) and (4.15), the only dependence on λ is through Ω(λ). Thus, since \(\varOmega(-\frac{1}{\lambda})=\varOmega(\lambda)\), it follows that the vector functions (A 1,B 1) and (A 3,B 3) satisfy the same symmetry properties. Hence,

$$ a_j \biggl(-\frac{1}{{\lambda }}\biggr)=a_j({\lambda }),\qquad b_j \biggl(-\frac{1}{{\lambda }}\biggr)=b_j({\lambda }),\quad j=1,3, \ \mathrm{Im}(\lambda)\geq0. $$
(4.17)

It turns out that the vector function (A 2,B 2) also satisfies a certain symmetry condition, as stated in the following proposition.

Proposition 4.1

Let q x (0,y) be a sufficiently smooth function. Then the vector solution of the linear Volterra integral equation (4.14) satisfies the following symmetry conditions:

(4.18)

where the function F(λ) is defined by

$$ F({\lambda })=\mathrm{i}\frac{1-{\lambda }^2}{1+{\lambda }^2}\tan\frac{d}{2}. $$
(4.19)

Proof

Define a function ϕ 2(y,λ) by

$$ \varphi_2(y,{\lambda })=\phi_2(y,{\lambda }){\rm e}^{\frac{\omega({\lambda })}{2}\sigma_3(y-L)}, $$
(4.20)

where φ 2 is defined by (4.14). It follows that ϕ 2 satisfies the ODE

(4.21)

where

$$ V(y,{\lambda })=V_2(0,y,{\lambda })-\frac{\omega(0,y,{\lambda })}{2}\sigma_3. $$
(4.22)

We seek a nonsingular matrix R(λ), independent of y, such that

$$ V \biggl(y,\frac{1}{{\lambda }}\biggr)=R({\lambda })V(y,{\lambda })R({\lambda })^{-1}. $$
(4.23)

It can be verified that such a matrix is given by

$$ R({\lambda })=\left ( \begin{array}{c@{\quad}c} 1&-F({\lambda }) \\ -F({\lambda })&1 \end{array} \right ), $$
(4.24)

where F is defined by (4.19).

Replacing in (4.21) λ by \(\frac{1}{{\lambda }}\), and using (4.23), we find the following equation:

$$\biggl(R({\lambda })^{-1}\phi_2 \biggl(y,\frac{1}{{\lambda }}\biggr) \biggr)_y =V(y,{\lambda }) \biggl(R({\lambda })^{-1}\phi_2 \biggl(y,\frac{1}{{\lambda }}\biggr) \biggr), $$

hence

$$R({\lambda })^{-1}\phi_2 \biggl(y,\frac{1}{{\lambda }}\biggr)= \phi_2(y,{\lambda })C({\lambda }), $$

where C is a y-independent matrix. Using the second of (4.21), it follows that C=R −1, and therefore

$$\phi_2 \biggl(y,\frac{1}{{\lambda }}\biggr)=R({\lambda })\phi_2(y,{\lambda })R( {\lambda })^{-1}. $$

This equation and (4.20) imply

$$ \varphi_2 \biggl(y,\frac{1}{{\lambda }}\biggr)=R({\lambda })\varphi_2(y, {\lambda }) \bigl({\rm e}^{-\omega({\lambda })\frac{\widehat{\sigma_3}}{2}(y-L)}R({\lambda })^{-1} \bigr). $$
(4.25)

The first column vector of this equation implies (4.18). □

Remark 4.1

Recalling that a 2(λ)=A 2(0,λ), and b 2(λ)=B 2(0,λ), equations (4.18) immediately imply the following important relations:

(4.26)

In summary, the basic equations characterizing the spectral functions are:

  1. (a)

    the symmetry relations (4.16), (4.17) and (4.26);

  2. (b)

    the global relations (2.22a), (2.22b);

  3. (c)

    the conditions of unit determinant.

In the next lemma, we collect some important consequences of these conditions. For simplicity, we will use the notations

$$f := f(\lambda), \qquad\hat{f} := f(-\lambda). $$

Lemma 4.1

The spectral functions satisfy the following relations:

(4.27)
(4.28)
(4.29)

where the function G(λ) is defined by

(4.30)

Proof

Equation (4.27) is just the condition of unit determinant.

Using the symmetry condition (4.16) to eliminate a 1 and b 1 from the global relations (2.22a), (2.22b), we find

(4.31a)
(4.31b)

Equations (4.31a), (4.31b) together with the equations obtained by letting λ→−λ in (4.31a), (4.31b) are four equations which can be solved for the four functions \(\{a_{2}, b_{2}, \hat{a}_{2}, \hat{b}_{2}\}\) with the result that

(4.32a)
(4.32b)

This proves (4.29).

Replacing λ by −1/λ in (4.31a), (4.31b) and using the symmetry (4.17), we find

(4.33a)
(4.33b)

Consider the two equations (4.33a), (4.33b) together with the two equations obtained by letting λ→−λ in (4.33a), (4.33b). We can eliminate \(a_{2} (\pm\frac {1}{\lambda} )\) and \(b_{2} (\pm\frac{1}{\lambda} )\) from these four equations by using the symmetry relations (4.26) as well as the symmetry relations obtained by letting λ→−λ in (4.26). The resulting four equations can then be solved for the four functions \(\{a_{2}, b_{2}, \hat{a}_{2}, \hat{b}_{2}\}\) with the result that

(4.34a)
(4.34b)

Comparing (4.32a) with (4.34a), we find (4.28). □

The functions a 3(λ) and b 3(λ) are defined by (4.12) only for λ in the upper half-plane. However, (4.29) implies that a 3(λ) and b 3(λ) can be analytically extended to the whole complex plane. Indeed, (4.29) provides the analytic continuation of a 3(λ) into ℂ−:

(4.35)

Similarly, (4.29) with λ replaced with −λ provides the analytic continuation of b 3(λ) into ℂ−:

(4.36)

Adopting these extended definitions of a 3(λ) and b 3(λ), analytic continuation implies that the relations (4.27)–(4.29) and the global relations (4.31a), (4.31b) are valid in the whole complex plane.

Proposition 4.2

The spectral functions satisfy the equations

(4.37)
(4.38)
(4.39)

as well as the global relations

(4.40a)
(4.40b)

where the known function G(λ) is given by (4.30).

5 Spectral Theory in the Linearisable Case

In Appendix we give the solution of the linear case. In this case, the dependence on the unknown spectral function B(λ) is resolved by mapping the basic Riemann–Hilbert problem to an equivalent but simpler one. To define this mapping, in the linear case, it is convenient to employ the two equations (A.19) and (A.20).

For the nonlinear problem, we will use the following equations, which provide the nonlinear analogues of (A.19) and (A.20):

$$ \frac{b_3({\lambda })}{a_3({\lambda })h({\lambda })}-\frac{b_3(-{\lambda })}{a_3({\lambda })}=\frac {G({\lambda })}{h({\lambda })},\quad {\lambda }\in {\mathbb{C}}, $$
(5.1)

and

$$ \frac{b_2({\lambda })}{a_3(-{\lambda })^2}-\bigl(1+{\rm e}^{-\omega({\lambda })L}\bigr)\frac {b_3(-{\lambda })}{a_3(-{\lambda })h(-{\lambda })}=\bigl(1+ {\rm e}^{-\omega({\lambda })L}\bigr)\frac{G({\lambda })}{h(-{\lambda })},\quad {\lambda }\in {\mathbb{C}}, $$
(5.2)

where the unknown function h(λ) is defined by

$$ h({\lambda })=a_3({\lambda })^2-b_3({\lambda })^2, \quad {\lambda }\in {\mathbb{C}}, $$
(5.3)

and the known function G(λ) is defined by (4.30). Note that from the above properties it follows that \(\frac{b_{3}(-{\lambda })}{a_{3}({\lambda })}\) is well defined at the zeros of the function h(λ). Moreover, in the linear limit,

$$b_3({\lambda })\to B_3({\lambda }), \qquad a_3({\lambda })\to1, \qquad h({\lambda })\to1, \qquad\tan\frac{d}{2} \to\frac{d}{2}, $$

and (5.1) and (5.2) become (A.19) and (A.20).

Equations (5.1) and (5.2) are a direct consequence of (4.37)–(4.39). Indeed,

which is equivalent to (5.1) (in the first and second equations above we have used (4.38) and (4.37), respectively). Furthermore,

$$\frac{b_2({\lambda })}{a_3(-{\lambda })^2}= \bigl(1+{\rm e}^{-\omega({\lambda })L} \bigr)\frac{b_3({\lambda })}{a_3(-{\lambda })}= \bigl(1+{\rm e}^{-\omega({\lambda })L} \bigr) \biggl[ \frac{b_3(-{\lambda })}{a_3(-{\lambda })h(-{\lambda })}-\frac{G(-{\lambda })}{h(-{\lambda })} \biggr], $$

which, using G(−λ)=−G(λ), becomes (5.2) (in the first and second equations above we have used the relation (4.39) and (5.1) with λ replaced by −λ).

The Properties of the Functions G(λ) and h(λ)

We give a summary of some of the properties of the function G(λ) given by (4.30) and of the unknown function h given by (5.3).

The set of poles of G(λ), denoted by P G ⊂ℂ, is given by

(5.4)

Note that G(λ) has no poles at λ=±i since the term eωL−1 vanishes at these points.

Proposition 5.1

The following statements hold:

  1. (a)

    G(λ) admits the symmetries G(λ)=−G(−λ)=−G(1/λ), λ∈ℂ.

  2. (b)

    G(λ) has essential singularities at ∞ and at 0 and a countable number of simple poles on the imaginary axis accumulating at ±i∞ and at 0. G(λ) has no other singularities.

  3. (c)

    Each of the functions 1±G(λ) has a countable number of zeros. All these zeros lie on the imaginary axis and they accumulate only at ±i∞ and at 0.

  4. (d)

    The set of zeros of the function 1−G(λ) is the disjoint union of the set of zeros of a 3(λ)−b 3(λ) and the set of zeros of a 3(−λ)+b 3(−λ).

  5. (e)

    The set of zeros of the function 1+G(λ) is the disjoint union of the set of zeros of a 3(λ)+b 3(λ) and the set of zeros of a 3(−λ)+b 3(−λ).

  6. (f)

    The set of zeros of the function 1−G 2(λ) is the disjoint union of the set of zeros of h(λ) and the set of zeros of h(−λ).

  7. (g)

    The function h(λ) has a double pole at each point in the set P G ∩ℂ−. The function h(−λ) has a double pole at each point in the set P G ∩ℂ+. The functions h(λ) and h(−λ) do not have any other poles.

Proof

The proof of (a) follows from the definition (4.30). The proof of (b) follows from the same definition and from (5.4).

In order to prove (c), we note that the function G is purely real for λ∈iℝ:

$$G(\mathrm{i}{\lambda }_I) = -\frac{1 + {\lambda }_I^2}{1 - {\lambda }_I^2}\tan \biggl(\frac {d}{2} \biggr) \tan \biggl(L\frac{{\lambda }_I^2 -1}{4{\lambda }_I} \biggr), \quad {\lambda }_I \in {\mathbb{R}}. $$

As λ I increases from 0 to +∞, the argument \(L\frac{{\lambda }_{I}^{2} -1}{4{\lambda }_{I}}\) increases from −∞ to ∞. It follows that each of the functions 1+G(λ) and 1−G(λ) has an infinite number of zeros on the imaginary axis, see Fig. 4. More precisely, if ip 1 and ip 2 are two consecutive poles of G on the positive imaginary axis, then, unless p 1<1<p 2, there is exactly one zero of 1−G(λ) and one zero of 1+G(λ) belonging to the interval (ip 1,ip 2). If p 1<1<p 2, then there are no zeros of 1+G(λ) in the interval (ip 1,ip 2) and there are two (counted with multiplicity) or no zeros of 1−G(λ) in this interval depending on whether \(G(\mathrm{i}) = \frac{L}{2}\tan(d/2)\) is ≤1 or >1. Since the poles of G(λ) accumulate at 0 and at ±i∞, the same is true for the zeros of 1±G(λ). This proves (c).

Fig. 4
figure 4

(a) The graph of G(λ) for λ on the imaginary axis when L=10 and d=1. (b) The corresponding picture of the poles of G(λ) and the zeros of G(λ)±1. The poles and zeros accumulate at the origin and at infinity

Full size image

Taking the sum and difference of (4.37) and (4.38) we find

(5.5)

It follows that

$$ h({\lambda })h(-{\lambda })=1-G^2({\lambda }),\quad {\lambda }\in {\mathbb{C}}. $$
(5.6)

Equation (5.5) implies that either a 3−b 3 or \(\hat {a}_{3} + \hat{b}_{3}\) vanishes whenever 1−G=0. Since all zeros of 1−G are simple, the functions a 3−b 3 and \(\hat{a}_{3} + \hat {b}_{3}\) cannot simultaneously vanish at one of these zeros. In order to prove (d), it only remains to show that 1−G vanishes whenever a 3−b 3 or \(\hat{a}_{3} + \hat{b}_{3}\) does. Equation (5.5) suggests that this is true; however, it is conceivable that a zero (pole) of a 3−b 3 could coincide with a pole (zero) of \(\hat {a}_{3} + \hat{b}_{3}\) in such a way that the product \((a_{3} - b_{3})(\hat {a}_{3} + \hat{b}_{3}) = 1 - G\) remains nonzero. We show now that this cannot occur.

Suppose λ 0 is a zero of a 3(λ)−b 3(λ). The unit determinant condition (4.37) implies that a 3(λ) and b 3(λ) cannot simultaneously vanish. Thus,

$$a_3(\lambda_0) = b_3(\lambda_0) \neq0. $$

The global relations (4.40a), (4.40b) yield

(5.7)

Using these equations to eliminate b 2(λ) and b 2(−λ) from the determinant condition

$$a_2({\lambda }_0)a_2(-{\lambda }_0) - b_2({\lambda }_0) b_2(-{\lambda }_0) = 1, $$

we find

(5.8)

If λ 0 is a zero of a 3(λ)−b 3(λ), then, by (4.17), so is −1/λ 0, and hence we also have

(5.9)

On the other hand, the symmetry condition (4.26) for a 2(λ) implies that

(5.10)

Indeed, if we use (4.26) to eliminate a 2(±1/λ) from the left-hand side of (5.10) and then simplify, we find the right-hand side of (5.10). Evaluating (5.10) at λ=λ 0 and using (5.8) and (5.9) to eliminate a 2(−1/λ 0) and a 2(−λ 0) from the resulting equation, we find

(5.11)

In view of (5.7), (5.8), and (5.11), the symmetry equation (4.26) for a 2(λ) evaluated at λ=λ 0 reduces to

$$0 = -1 - \mathrm{e}^{-\omega({\lambda }_0)L} + F({\lambda }_0) \bigl(1 - \mathrm{e}^{-\omega({\lambda }_0)L} \bigr), \quad\text{i.e.} \quad G({\lambda }_0) = 1. $$

This shows that 1−G(λ)=0 whenever a 3(λ)−b 3(λ)=0. A similar argument shows that 1−G(λ)=0 also whenever a 3(−λ)+b 3(−λ)=0. This proves (d). The proof of (e) is similar.

The statement (f) follows from (d) and (e) since h=(a 3−b 3)(a 3+b 3).

Since h(λ) is analytic in ℂ+ and h(λ) does not vanish at any point λ∈P G by (f), (5.6) implies that h(−λ) has a double pole at each point in the set P G ∩ℂ+. This proves (g). □

5.1 An Equivalent Riemann–Hilbert Problem

Using the relations (4.16) and (4.32a), the jump matrices (2.26) become

$$J^{0}(x,y,{\lambda })=\left ( \begin{array}{c@{\quad}c} 1+\frac{b_3({\lambda })b_3(-\lambda)}{a_3({\lambda })a_3(-\lambda)}{\rm e}^{-\omega ({\lambda })L}& \frac{b_3(-\lambda)}{a_3(\lambda)}{\rm e}^{-\theta (x,y,\lambda)} \\[7pt] \frac{b_3(\lambda)}{a_3(-\lambda)}{\rm e}^{-\omega(\lambda)L}{\rm e}^{\theta(x,y,\lambda)}& 1 \end{array} \right ), $$

and

$$ J^{\pi}= J^{3\pi/2}\bigl(J^{0} \bigr)^{-1}J^{\pi/2}, \quad {\rm e}^{\theta(x,y,\lambda )}= {\rm e}^{\varOmega({\lambda })x+\omega({\lambda })y}. $$
(5.12)

Let M(x,y,λ) be defined by (2.24) with Ψ j replaced with Φ j , j=1,2,3. Let D j denote the jth quadrant of the complex plane,

$$D_j = \biggl\{\lambda\in {\mathbb{C}}\bigg| (j-1)\frac{\pi}{2}< \mathrm{arg}( {\lambda })<j\frac{\pi}{2} \biggr\},\quad j=1,\ldots,4, $$

and let M j denote the restriction of M to D j .

The jump matrices (5.12) involve the unknown spectral functions b 2(λ),a 3(λ), and b 3(λ). We therefore seek matrices A j (x,y,λ), j=1,…,4, defined for λ∈D j , such that the functions \(\{\tilde{M}_{j}(x,y,{\lambda })\}_{1}^{4}\) by

$$ \tilde{M}_j(x,y,{\lambda })=M_j(x,y,{\lambda })A_j(x,y, {\lambda }),\quad\lambda\in D_j,\ j=1,\ldots,4, $$
(5.13)

satisfy a modified Riemann–Hilbert problem whose jump matrices involve only known functions. We would like A j to be bounded and analytic (or at least meromorphic) for λ∈D j .

The requirement that A j is bounded in the jth quadrant implies that A 1 and A 2 are upper triangular, while A 3 and A 4 are lower triangular. The requirement that A j has unit determinant implies that the diagonal elements of A j are d j and \(\frac{1}{d_{j}}\). The (2,2) components of (5.18) imply that

$$d_1=d_2=d_3=d_4. $$

On the other hand, the four exponential factors

(5.14)

are bounded in the first, second, third and fourth quadrant of the complex λ-plane, respectively.

This suggests choosing the matrices A j in the following form:

(5.15a)
(5.15b)
(5.15c)
(5.15d)

where α j (λ), j=1,…,4, is a scalar valued function of λ∈D j .

Substituting (5.13) into the jump relations

$$ M_4= M_1J^{0},\qquad M_2= M_1J^{\pi/2},\qquad M_4= M_3J^{3\pi/2}, $$
(5.16)

we find the equations

$$ \tilde{M}_4= \tilde{M}_1\tilde{J}^{0},\qquad \tilde{M}_2= \tilde {M}_1\tilde{J}^{\pi/2},\qquad \tilde{M}_4= \tilde{M}_3\tilde{J}^{3\pi/2}, $$
(5.17)

provided that the matrices \(\tilde{J}^{0}\), \(\tilde{J}^{\pi/2}\), \(\tilde{J}^{3\pi/2}\) satisfy the following equations:

$$ J^{0}A_4=A_1\tilde{J}^{0},\qquad J^{\pi/2}A_2=A_1\tilde{J}^{\pi/2}, \qquad J^{3\pi/2}A_4=A_3\tilde{J}^{3\pi/2}. $$
(5.18)

We analyse the first of (5.18). The (2,2) element of this equation is satisfied identically and the (1,1) element is a consequence of the (1,2) and (2,1) elements, as well as of the requirement that all matrices in (5.18) have unit determinant. Denoting the (1,2) and (2,1) components of \(\tilde{J}^{0}\) by \({\rm e}^{-\theta(x,y,\lambda)}\tilde{U}^{0}({\lambda })\) and \({\rm e}^{\theta(x,y,\lambda)}{\rm e}^{-\omega({\lambda })L}\tilde{V}^{0}({\lambda })\), respectively, we find that the (1,2) and (2,1) elements of the first of equations (5.18) yield

$$ \frac{b_3(-{\lambda })}{a_3({\lambda })}-\alpha_1({\lambda })=\tilde{U}^0({\lambda }) $$
(5.19)

and

$$ \frac{b_3({\lambda })}{a_3(-{\lambda })}+\alpha_4({\lambda })=\tilde{V}^0({\lambda }). $$
(5.20)

Comparing (5.19) with the identity (5.1) we find that a simple choice for the function α 1 (and hence for \(\tilde{U}^{0}\)) is \(\alpha_{1}({\lambda })=\frac{b_{3}({\lambda })}{a_{3}({\lambda })h({\lambda })}\) and \(\tilde{U}^{0}({\lambda })=-\frac{G({\lambda })}{h({\lambda })}\). Note that these functions are well defined on ℝ since h does not have any real zero. However, with these choices the functions α 1(λ) and \(\tilde{U}^{0}({\lambda })\) have (i) poles at the (unknown) zeros of h(λ) along the imaginary axis and (ii) poles at the (known) poles of G(λ) along the imaginary axis. To ensure that the poles in (i) are removable singularities we define the function \(\tilde{G}({\lambda })\) as follows:

$$ \tilde{G}({\lambda })=G({\lambda }) \bigl(h({\lambda })+1\bigr). $$
(5.21)

This function takes values 1 and −1 exactly where G(λ) does. Indeed, if h(λ)=0, then a 3(λ)=±b 3(λ) and correspondingly, in view of (5.5), \(G({\lambda })=\tilde{G}({\lambda })=\pm1\).

The above discussion suggests that a suitable choice for the functions α 1(λ) and \(\tilde{U}^{0}({\lambda })\) is

$$ \alpha_1({\lambda })= \frac{b_3({\lambda })}{a_3({\lambda })h({\lambda })}-\frac{\tilde{G}({\lambda })}{h({\lambda })},\qquad\tilde{U}^0({\lambda })=-\frac{G({\lambda })-\tilde{G}({\lambda })}{h({\lambda })}=G({\lambda }). $$
(5.22)

Similarly, (5.20) suggests

$$ \alpha_4({\lambda })=-\frac{b_3(-{\lambda })}{a_3(-{\lambda })h(-{\lambda })}+\frac{\tilde{G}(-{\lambda })}{h(-{\lambda })}, \qquad\tilde{V}^0({\lambda })=-\frac{G(-{\lambda })-\tilde{G}(-{\lambda })}{h(-{\lambda })}=-G({\lambda }). $$
(5.23)

We next analyse the second of equations (5.18). The (1,2) element of this equation yields

$$\alpha_2({\lambda }){\rm e}^{\omega({\lambda })L}+\frac{b_2(-{\lambda })}{a_3({\lambda })^2}= \frac{b_3({\lambda })}{a_3({\lambda })h({\lambda })}-\frac{\tilde{G}({\lambda })}{h({\lambda })}+\tilde{U}^{\pi/2}({\lambda }), $$

where \(\tilde{U}^{\pi/2}({\lambda }){\rm e}^{-\theta(x,y,\lambda)}\) denotes the (1,2) component of \(\tilde{J}^{\pi/2}\). Using the identity (5.2), we find

$$\alpha_2{\rm e}^{\omega({\lambda })L}+{\rm e}^{\omega({\lambda })L} \frac{b_3({\lambda })}{a_3({\lambda })h({\lambda })}- \bigl(1+{\rm e}^{\omega({\lambda })L}\bigr)\frac {G({\lambda })}{h({\lambda })}+\frac{\tilde{G}({\lambda })}{h({\lambda })}=\tilde{U}^{\pi /2}({\lambda }). $$

This suggests that we define

$$ \alpha_2({\lambda })=- \frac{b_3({\lambda })}{a_3({\lambda })h({\lambda })}+\frac{\tilde{G}({\lambda })}{h({\lambda })}, \qquad \tilde{U}^{\pi/2}({\lambda })= \bigl(1+{\rm e}^{\omega({\lambda })L}\bigr)G({\lambda }). $$
(5.24)

A similar analysis of the third of equations (5.18) yields

$$ \alpha_3({\lambda })= \frac{b_3(-{\lambda })}{a_3(-{\lambda })h(-{\lambda })}- \frac{\tilde{G}(-{\lambda })}{h(-{\lambda })},\qquad\tilde{V}^{3\pi/2}({\lambda })=\bigl(1+{\rm e}^{-\omega({\lambda })L}\bigr)G(-{\lambda }), $$
(5.25)

where \(V^{3\pi/2}({\lambda }){\rm e}^{\theta(x,y,\lambda)}\) denotes the (2,1) component of \(\tilde{J}^{\frac{3\pi}{2}}\). Note that the relations α 2(λ)=α 4(−λ) and α 3(λ)=α 1(−λ) are consistent with the symmetry (2.20).

We define the matrices A j , j=1,…,4, by (5.15a)–(5.15d) and (5.22)–(5.25). Henceforth, we assume that (x,y) lies in the interior of the semistrip (1.2) so that x>0 and 0<y<L. Then the jth exponential factor in (5.14) has exponential decay as λ→∞ and λ→0 for \({\lambda }\in\bar{I}_{j}\). Thus, although the analysis of the linear problem suggests that the spectral functions a j (λ),b j (λ) could have some minor growth as λ→∞ and λ→0 caused by the jumps in the boundary data at the corners of the semistrip (in the linear case this growth is logarithmic, see Appendix), this ensures that the A j ’s are bounded as λ→∞ and as λ→0 in the corresponding domains D j .

In fact, since the A j ’s have removable singularities at the zeros of the function h(λ) along the imaginary axis, the only remaining difficulty is that the A j ’s have singularities at the known poles of G(λ). To deal with these singularities, we add small indentations to the jump contour along the imaginary axis so that it passes to the right of the poles of G. Thus, instead of the four quadrants D j of the complex plane, we consider the deformed domains \(\tilde{D}_{j}\) defined in such a way that all λ∈P G ∩ℂ+ lie in \(\tilde{D}_{1}\) and all λ∈P G ∩ℂ− lie in \(\tilde {D}_{3}\), see Fig. 5.

Fig. 5
figure 5

The contour for the modified Riemann–Hilbert problem satisfied by \(\tilde{M}\). The contour has small indentations bypassing the poles of G(λ)

Full size image

We next determine the residue conditions at these poles. Let λ ∗∈P G ∩ℂ+ be a pole of α 1 in \(\tilde{D}_{1}\). In what follows, we use the notation M(x,y,λ)=([M(x,y,λ)]1,[M(x,y,λ)]2) to denote the first and second column vector of a given matrix M(x,y,λ). Then the relation \(\tilde{M}_{1} = M_{1} A_{1}\) implies that

Taking the residue of the second of these equations at λ ∗, we find

where the residue of G(λ) at λ ∗ is known from the definition (4.30) whereas the number h(λ ∗) remains unknown.

Similarly, the relation \(\tilde{M}_{3} = M_{3} A_{3}\) implies that

Taking the residue of the first of these equations at λ ∗∈P G ∩ℂ−, we find

In summary, we have derived the following result.

Theorem 5.1

The RH problem defined in Theorem 3.1 and characterised by the jump matrices {J π/2,J 3π/2,J 0,J π} defined in (5.12), can be mapped to a new RH problem with the following jump matrices:

(5.26)

where the known function G(λ) is defined in (4.30). This is achieved by using the matrices (5.15a)–(5.15d), with

(5.27)

where the functions h(λ) and \(\tilde{G}({\lambda })\) are defined by (5.3) and (5.21), respectively. The solution \(\tilde {M}\) of the new RH problem is a sectionally meromorphic function with simple poles at each point in the set P G given in (5.4). At these points the following residue conditions are valid:

(5.28)
(5.29)

The solution q(x,y), x>0, 0<y<L, of the boundary value problem determined by the boundary conditions (1.3) is given by

(5.30)
(5.31)

Proof

We only need to show how to represent the solution q(x,y) of the boundary value problem in terms of the solution of the RH problem characterised by the jump matrices given by (5.26). Recall that if M(x,y,λ) denotes the solution of the RH problem defined in Theorem 3.1 then q(x,y) is defined in terms of M by (3.7)–(3.8). Using \(\tilde{M}_{j}=A_{j}M_{j}\) in the jth quadrant, j=1,…,4, by choosing λ in the first quadrant we obtain

Since \({\rm e}^{-\theta(x,y,\lambda)}\) decays exponentially as λ→∞ in the first quadrant, the term involving the unknown coefficient α 1 does not contribute to the limit and we find (5.30)–(5.31). □

6 Conclusions and Open Problems

We have analysed the elliptic sine-Gordon equation in a semistrip for general boundary data (Sects. 2 and 3) and in the particular case of a linearisable boundary value problem (Sects. 4 and 5). The linearisable problem has the novelty that the function q y (x,0) possesses a non-integrable singularity as x→0 while the function q x (0,y) possesses a non-integrable singularity as y→0. Motivated by the recent solution of an analogous problem for the modified Helmholtz equation presented in Ashton and Fokas (2012), we have been able to bypass this problem by employing a suitable gauge transformation. Furthermore, we have shown that the RH problem characterizing the solution q(x,y) can be mapped to a modified RH problem whose “jump matrix” is determined only by the width L of the semistrip and the given constant value d of the boundary condition prescribed at x=0 (see Theorem 5.1). However, the modified RH problem also includes residue conditions at the points λ∈P G , where the set P G consists of a countable number of points on the imaginary axis. The formulation of these residue conditions requires the knowledge of h(λ) for λ∈P G , where h(λ) is an unknown meromorphic function defined in terms of the spectral functions. It remains an open problem to characterise the values of h(λ) for λ∈P G in terms of L and d alone; progress in this direction is likely to rely on the analyticity properties of h(λ) as well as on relations derived from the symmetry properties of the spectral functions, such as the relation (5.6), and the known structure of the poles of h.