Thermodynamics and Crystallization Kinetics of Solid Solutions GaS_xSe_1 – x (0 ≤ х ≤ 1)

Abstract

The results on the study of phase equilibria and crystallization of GaS_xSe_1 – x (0 ≤ х ≤ 1) solid solution in the GaS–GaSe system are presented. Using DTA, XRD, and the approximation of regular solutions, the physico-chemical and thermodynamic laws of the T – x phase diagram of GaS–GaSe, where a continuous series of solid solutions are formed, are determined. The temperature–concentration dependences of the change in the Gibbs free energy of the system are calculated. For nucleation and crystallization of GaS_xSe_1 – x solid solutions, a model based on a Fokker–Planck type equation in the size space has been tested.

INTRODUCTION

Interest in 2D semiconductor materials based on A^IIIB^VI compounds, which are characterized by quantum effects, is due to the potential for their use in nanoscale devices. Data on the crystal and electronic structure of GaS and GaSe compounds are given in [1–3]. GaS and GaSe crystals belong to hexagonal syngony, characterized by a layered structure and space group $D_{{3h}}^{1}$—$P\bar {6}m2$ [1]. They have several polymorphic modifications. For example, GaSe has four modifications (β-, ε-, γ-, and δ-GaSe). At room temperature, β-GaS and ε-GaSe are more thermodynamically stable modifications.

In A^IIIB^VI 2D crystals covalent bonds are in the layers, and a weak Van der Waals bond exists between the layers. Due to this, the anisotropic properties manifest in A^IIIB^VI. By their optical and electrical properties A^IIIB^VI crystals (GaS [4–8], GaSe [9–19]) are close to promising nanotechnology materials, such as graphene and topological insulators. GaS and GaSe are wide-gap semiconductors and at room temperature have a band gap of 2.53 and 1.98 eV, respectively. They have several advantages over other 2D materials: a large range of operating temperatures, the ability to create light-emitting devices on their basis in the visible spectrum, high values of the critical field of electrical breakdown, radiation resistance.

GaS and GaSe form a continuous series of GaS_xSe_1 – x (0 ≤ х ≤ 1) solid solutions between each other [20, 21]. However, the formed poly- and single crystals of GaS_xSe_1 – x solid solutions often have an inhomogeneous distribution of dislocation density, which leads to mechanical stresses and the formation of intrinsic point defects [22–25]. As a result, such a material has irreproducible electrical, optical, photoelectric, luminescent, and other physical characteristics.

The reasons for the nonuniform distribution of structural defects over the volume of the formed GaS_xSe_1 – x crystals are determined by several processes. The main ones are crystallization (edge and screw dislocations, grain boundaries, pores can form) and heat treatment of crystals (point defects intrinsic and impurity can be created or eliminated), as a result of which concentration and temperature gradients appear. However, the parameters affecting the structure formation and physical properties of GaS_xSe_1 – x have not yet been considered from the standpoint of thermodynamic modeling and the theory of phase crystallization.

In the present work, the crystallization of GaS_xSe_1 – x solid solutions is considered taking into account metastable phases, which are formed by fluctuations. The results of studying the crystallization of GaS_xSe_1 – x from a solution in a closed system are presented. Nonlinear crystallization processes of GaS_xSe_1 – x are considered in the framework of the Fokker–Planck type equation [26, 27] in the size space. The Fokker–Planck equation characterizes diffusion with the presence of a drifting force field. It describes the evolution in time of the probability density function of the particle’s position, which follows the stochastic differential equation. In this case, sample particle trajectories are continuous functions of time.

EXPERIMENTAL

Ga-5 N gallium, B5 sulfur and OSCh-17-3 selenium with impurity content no higher than 5 × 10^‒4 wt % were used in the synthesis of GaS and GaSe binary compounds. The compounds were synthesized by melting from elements taken in stoichiometric ratios in evacuated (10^–3 Pa) quartz ampules. The ampules with the corresponding components were placed in an electric furnace. The ampules were held for 6–8 h at a temperature above the melting temperature by 25–30 K (melting points of GaS and GaSe are 1288 and 1211 K, respectively) and then left to cool down to room temperature. At temperatures above the melting point of GaS and GaSe, ampules may be destroyed due to high vapor pressure of chalcogens. Synthesized GaS and GaSe compounds were identified by differential thermal analysis (DTA; a heating/cooling rate of 10 K min^–1) and powder X-ray diffraction (XRD). The above method is performed in quartz ampules by fusion of GaS and GaSe compounds obtained from GaS_xSe_1 – x (x = 0–1.0 mole fraction) solid solutions. DTA of GaS and GaSe compounds and alloys was carried out using a NETZSCH 404 F1 Pegasus system. The accuracy of measurements was ±0.5–1 K. The XRD analysis of the obtained samples was performed on a Bruker D8 ADVANCE diffractometer with CuK_α radiation [21–25]. GaS_xSe_1 – x single crystals were grown by the Bridgman method [25, 28, 29]. The ampule was moved in the furnace at a rate of 0.5–1.1 mm h^–1, and the temperature gradient near the crystallization front was 25 ± 3 K.

Band gap and dielectric coefficients of the solid solutions GaS_xSe_1 – x single-crystal samples were determined by physical methods. The dielectric coefficients of single crystals samples were measured by the resonance method [26] in the frequency range from $f~$ = 5 $\times$ 10⁴ to 3.5 $\times$ 10⁷ Hz. Samples of the GaS_1 – хSe_х for electrical measurements on alternating current (ac-conductivity–${{{{\sigma }}}_{{{\text{ac}}}}}$) were fabricated in the form of plane capacitors, the plane of which was perpendicular to the crystallographic c-axis of single crystals. Silver paste was used to fabricate Ohmic contacts. The thickness of the studied single-crystal samples was 200–700 μm, and the plate area was 7 × 10^–2 cm². All of the ac-measurements were performed at 300 K in electric fields corresponding to Ohmic current-voltage behavior. The accuracy in determining the sample capacitance and the merit factor Q = 1/tanδ of the measuring circuit was limited by reading errors. The capacitors were calibrated with an accuracy of ±0.1 pF. The reproducibility in the resonance position was ±0.2 pF in terms of capacitance and ±1.0–1.5 scale divisions in terms of Q. The largest deviations were 3–4% in ε and 7% in tanδ.

Thermodynamic Properties

T – x phase equilibrium in the binary system 1–2 with an unlimited range of solid solutions is calculated from thermodynamic data using Gibbs energies for relevant phases. For calculation of T – x phase diagram of binary system 1–2, we used a method including ratios between the concentrations of initial components and their thermodynamic enthalpies of melting [30, 31]. Thus, the liquidus and solidus lines of the binary system 1–2 with continuous series of liquid and solid solutions can be analytically described by the formulae:

$$x_{1}^{l} = \frac{{1 - {{F}_{2}}}}{{{{F}_{1}} - {{F}_{2}}}},$$

$$x_{1}^{s} = {{F}_{1}}x_{1}^{l},$$

(1)

$${{F}_{i}} = {\text{exp}}\left[ {\frac{{\Delta H_{i}^{{0,{\text{m}}}}({{T}^{{ - 1}}}T_{i}^{{ - 1,{\kern 1pt} {\text{m}}}})}}{R}} \right],$$

where $x_{1}^{l}$ and $x_{1}^{s}$ are the mole fractions of the compound in the equilibrium liquid and solid solutions, respectively, $T_{i}^{{\text{m}}}$ and $\Delta H_{i}^{{0,{\text{m}}}}$—the melting temperature and melting enthalpy of the $i$th component, and $R$ = 8.314 J K^–1 mol^–1—universal gas constant.

To build T–x phase diagram for GaS–GaSe, for each particular $T_{i}^{{\text{m}}}$, ${{F}_{1}}$, and ${{F}_{2}}$ values were calculated and then $x_{1}^{l}$ and $x_{1}^{s}$ values were approximated from formula (1).

Concentration–temperature dependences of Gibbs free energy of formation ($\Delta G_{T}^{0}$ = $f(x,~T)$) of GaS_xSe_1 – x (0 ≤ $x$ ≤ 1) solid solutions were calculated using a solution model which included non-molecular compounds [32]. Equation for the $\Delta G_{T}^{0}$ of solid solutions from their constituent components at p, T = const:

$${{\Delta }_{{\text{f}}}}G_{T}^{0}({\text{J mo}}{{{\text{l}}}^{{ - 1}}}) = (1 - x){{\Delta }_{{\text{f}}}}H_{{298~}}^{0}({\text{GaSe}})~$$

$$ + x{{\Delta }_{{\text{f}}}}H_{{298}}^{0}({\text{GaS}}) - ~(1 - x)T{{\Delta }_{{\text{f}}}}S_{{298~}}^{0}({\text{GaSe}})$$

$$ - x~T{{\Delta }_{{\text{f}}}}S_{{298~}}^{0}({\text{GaS}})$$

(2)

$$ - T\Delta C_{{p,298~}}^{0}~\left[ {\ln \left( {\frac{T}{{298}}} \right) + \left( {\frac{{298}}{T}} \right) - 1} \right]~$$

$$ + ~ 8.314~T\left[ {(1 - x)\ln (1 - x) + x\ln (x)} \right] + ~{{\Delta }_{{\text{f}}}}G_{T}^{{0,{\text{mix}}}},$$

where $x$ is the mole fraction of GaS; $1-x$ is the mole fraction of GaSe; $\Delta H_{{298}}^{0}$ and $\Delta S_{{298}}^{0}$ are the enthalpy and entropy of formation of GaSe and GaS compounds; $\Delta C_{{p,298~}}^{0}$ is the difference between the heat capacities of the GaS_xSe_1 – x solid solutions and GaSe and GaS compounds, respectively; and $\Delta G_{T}^{{0,{\text{mix}}}}$ is the excess molar Gibbs free energy of mixing. The temperature dependence of the heat capacity $\Delta C_{{p~}}^{0} = f(T)~$was estimated using the second Ulich approximation [33]:

$$T\Delta C_{{p,298~}}^{0}\left[ {\ln \left( {\frac{T}{{298}}} \right) + \left( {\frac{{298}}{T}} \right) - 1} \right].$$

Nucleation

The evolution of the dispersed phase in crystallization experiments in a closed system occurs by a complex mechanism. In this case, the formation of metastable intermediate solid phases and the evolution of dispersed particles of the solid phase at the end of the process are possible. The mechanisms of such phase transformations and the crystallization kinetics are described using nonlinear models [34, 35]. Nonlinear properties of the crystallization process are determined taking into account the boundary conditions and coefficients of the kinetic equations, and also depend on the crystallization prehistory. Kinetic coefficients are calculated based on the theory of diffusion growth and dissolution of second-phase precipitates. These coefficients determine the probability of attachment and ejection of one particle per unit time, respectively.

A homogenized solid solution quenched in the concentration region of the T–x phase diagram of the GaS–GaSe system may remain in the metastable state for some time. Ultimately, it reaches thermodynamic equilibrium. At one of the equilibrium concentrations, some micro clusters can form in the matrix GaS_xSe_1 – x [36, 37].

Using Fokker–Planck Equation

Nucleation kinetics, taking into account the walk in the size space, can be described by an equation of the Fokker–Planck type [26, 27]. This equation allows to describe the dynamics of changes in certain crystallization properties, considering the properties to be random walk. The equation allows to consider the evolution of the size distribution function and to describe the walk of nuclei in the size space. Such a model is used in this work.

Suppose that crystallization of solid solutions occurs from a uniformly supersaturated solution in a closed system. Solution has a limited volume $V$ at time $t$ = 0. If the concentration of the dispersed phase Q exceeds the solubility of the components of the system, then the nucleation and growth of the solid phase occurs. With such crystallization, the formation of various modifications of the solid phase is possible. Assume that during crystallization a chemical reaction does not occur and a constant temperature of the solution is maintained. Mixing the solution does not lead to cracking and aggregation. Mass crystallization occurs by spontaneous nucleation, i.e., nucleation of crystallization centers, crystal growth and dissolution of particles of the dispersed phase.

Nucleation involves the formation and growth of clusters from molecules of the initial solution. Cluster formation occurs up to the size at which it is possible to distinguish a crystal face as a structural element responsible for growth. The nucleation rate, crystal growth rate and dissolution of the particles of the dispersed phase are determined with the degree of supersaturation of the solution and the size of the crystal face [38, 39]. Within the framework of this model, we assume that crystallization is described by an equation based on the evolution of the function ${{\varphi }_{k}}$ of the crystal size distribution ($L$) in time ($t$). In the entire volume of the solution, the temperature and concentration are constant. Then the Fokker–Planck kinetic equation for the distribution density is written as [26, 27]:

$$\frac{{\partial \varphi }}{{\partial t}} = - \frac{{\partial (\varphi G)}}{{\partial L}} + \frac{\partial }{{\partial L}}\left( {p\frac{{\partial (\varphi G)}}{{\partial L}}} \right),$$

(3)

where $L \geqslant {{L}_{0}}$, ${{L}_{0}}$ is the minimum crystal size, $G$ is the linear growth rate of the crystal face, and $p$ is the fluctuation coefficient of the growth rate. The supersaturation of a solution is determined as follows: $\gamma (t) = {{C}_{k}}(t){\text{/}}C_{k}^{\infty }$, where ${{C}_{k}}$(t) is the concentration in time $t$, $C_{k}^{\infty }$ is the concentration of the saturated solution. Here the linear velocity is $G = {{\beta }}(\gamma - 1)$, where ${{\beta }}$ is the kinetic coefficient of the growth rate. Since the formed crystals have a limited size, it is necessary to choose the boundary conditions for the equation of distribution density. After that, the kinetic equation is supplemented by the initial condition and the balance equation. Thus, we obtain a system of nonlinear equations that are solved by the difference method [40].

The system of nonlinear equations was solved numerically, where a uniform grid was used with a step $h$ in size and $t$ in time. The solution was transferred from the $j$th layer to the ($j + 1$)st layer by a purely implicit difference scheme, after this the function $G$ was recalculated. The differencing scheme for Eq. (3) has the form:

$$\begin{gathered} \frac{{\varphi _{i}^{{j + 1}} - \varphi _{i}^{j}}}{\tau } = - \frac{{{{G}^{j}}}}{{2h}}(\varphi _{{i + 1}}^{{j + 1}} - \varphi _{{i - 1}}^{{j + 1}}) \\ + \;\frac{{p{{G}^{j}}}}{{{{h}^{2}}}}(\varphi _{{i + 1}}^{{j + 1}} - 2\varphi _{i}^{{j + 1}} + \varphi _{{i - 1}}^{{j + 1}}). \\ \end{gathered} $$

(4)

Equation (4) has order of approximation $O(\tau + {{h}^{2}})$. The difference equation for the left boundary condition has the form:

$$\varphi _{0}^{{j + 1}}{{G}^{j}} - p{{G}^{j}}\frac{{\varphi _{1}^{{j + 1}} - \varphi _{0}^{{j + 1}}}}{h} + p{{G}^{j}}\frac{{\varphi _{0}^{j}2\varphi _{1}^{j} + \varphi _{2}^{j}}}{{{{h}^{2}}}} = {{\eta }^{j}}.$$

(5)

The equation has order of approximation $O(\tau + \tau h + {{h}^{2}})$. Difference equations were solved by the sweep method, which is applicable due to diagonal prevalence. The differencing schemes (4) and (5) are stable on the right-hand side. After transferring the solution to the ($j + 1$-st layer, a new value of the concentration ${{C}_{k}}$ was calculated, as well as parameters G and $\eta$. The integral was calculated by the trapezoidal rule—its accuracy is of the order of $O({{h}^{2}})$, which corresponds to the approximation of the differencing scheme. The obtained concentration value ${{C}_{k}}$ was reused to find the solution on the ($j + 1$)st layer. This procedure was repeated a fixed number of times. Thus, the crystallization of a multicomponent system is considered as a combination of physico-chemical and mathematical models. Such a model allows for the numerical implementation of nonlinear equations by a differencing scheme. Numerical experiments to study the crystallization of GaS_xSe_1 – x were carried out using programs developed in Delphi.

RESULTS AND DISCUSSION

Figure 1 shows X-ray powder diffraction patterns of GaS_xSe_1 – x solid solutions and β-GaS and β-GaSe pure compounds, which crystallize in hexagonal syngony with the space group $P{{6}_{3}}{\text{/}}mmc$ and have the following lattice parameters: β-GaS (a = 4.002 ± 0.002 Å and c = 15.447 ± 0.005 Å) and β-GaSe (a = 3.755 ± 0.002 Å and c = 15.475 ± 0.005 Å) at room temperature. These values of lattice parameters of for polytypes β-GaS and β-GaSe compounds are consistent with the literature data [21, 23] and the JCPDS-ICDD Powder Diffraction File (PDF) card file data: β-GaS (JCPDS no. 30-0576; a = 3.587 Å and c = 15.492 Å), β-GaSe (JCPDS no. 03-65-3508; a = 3.7555 and c = 15.94 Å). The values of lattice constants of GaS_xSe_1 – x solid solutions are also consistent with the data of [23].

Fig. 1.

XRD patterns of β-GaS (top), β-GaSe (bottom) and solid solutions GaS_1 – xSe_x at 298 K.

According to the XRD data (Fig. 1) and DTA (Fig. 2), the components of GaS and GaSe unlimitedly dissolve in each other both in the liquid and in the solid state. Unlimited component solubility in GaS–GaSe occurs because both GaSe and GaS have the same crystal structure, and Se and S have similar radii, electronegativity and valence. In GaSe–GaS system melting occurs over a relatively narrow temperature range, between the solidus and liquidus lines. In other words, solid and liquid phases are at equilibrium in a narrow temperature range.

Fig. 2.

Differential thermal analysis (DTA) curves of solid solutions GaS_1 – xSe_x crystals; (a) x = 0 (1), 0.8 (2), 0.7 (3), and 1.0 (4); (b) x = 0.4, where 1220 K—solidus and 1241 K—liquidus.

According to DTA data for components GaSe and GaS, the following melting parameters were chosen: ${{\Delta }}{{H}^{{\text{m}}}}$(GaSe) = 30 300 ± 200 J mol^–1, ${{T}^{{\text{m}}}}$(GaSe) = 1211 ± 3 K, ${{\Delta }}{{H}^{{\text{m}}}}$(GaS) = 34 800 ± 200 J mol^–1, and ${{T}^{{\text{m}}}}$ (GaS) = 1288 ± 3 K. Comparison of these data with experimental data [21] indicates their correspondence. The calculation of the liquidus (${{T}^{{\text{l}}}}$) and solidus (${{T}^{{\text{s}}}}$) lines of the GaS–GaSe system was carried out taking into account these data and using Eq. (1).

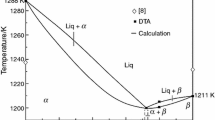
Our studied and calculated phase diagram for GaS–GaSe is shown in Fig. 3. The phase diagram of the GaS–GaSe system is a third type of the Roseboome classification. The calculations of solidus and liquidus were carried out using Eq. (1). Calculated solidus and liquidus temperatures differ slightly from the experimental data (solidus difference was ∼5 K and liquidus ∼10 K). Phase diagram of the state for GaS–GaSe system is characterized by the minimum (0.7 ± 0.05 mol fraction GaSe and 1200 ± 1 K) and presence of unlimited mutual solubility of the components in the system. Our calculation and experimental DTA data on the temperatures of liquidus, solidus and the coordinates of the invariant equilibria in the GaS–GaSe system (Figs. 3, 4) are very different from the data given in [20].

Fig. 3.

Calculated according to Eq. (1) (the curves) and constructed by us T–x phase diagram of the GaS–GaSe system (points: DTA data).

Fig. 4.

Concentration–temperature dependence of the Gibbs free energy of mixing calculated by Eq. (2) for GaS_1 – xSe_x solid solutions using our data for GaS and GaSe; (1) 298, (2) 800, and (3) 1200 K.

As can be seen from Fig. 3, our data for the melting point of GaS and GaSe are 1288 and 1211 K, respectively. In [20] it was shown that for GaS and GaSe, the melting points are 1238 and 1233 K, respectively. This DTA data [20] are also very different from the other literature data. For example, according to [15], the melting point of GaSe is 1210 K, which exactly ±1 K matches our data (Fig. 3).

When compositions of two equilibrium phases are equal (x ≈ 0.7), the GaS–GaSe system degenerates into a quasi-single-component system. Thus, the composition corresponding to the minimum point (x ≈ 0.7) on the phase equilibrium on GaS–GaSe curves can be considered as an individual component. Calculation of the temperature dependence of the free energy of mixing of components in GaS–GaSe system was performed using Eq. (2) in the 300–1200 K range. The calculated concentration–temperature dependences of the free energy of component mixing (Fig. 4) are consistent with the GaS–GaSe phase diagram.

A study of the relief of GaS_1 – xSe_x crystals grown of various compositions indicates the formation of various 2D nanostructures on the surface [36, 37]. Two main types of heterogeneities can be distinguished: extended structures and local 2D nano-objects.

GaS_xSe_1 – x solid solutions melt without decomposition and have no phase transitions. Depending on the composition of GaS_xSe_1 – x, the physical properties of solid solutions differ noticeably. As an example, we give below the studied concentration dependence of the conductivity of GaS_xSe_1 – x single crystals solid solutions (x = 0–1).

Figure 5 shows the results of studying the frequency-dependent ac conductivity (${{{{\sigma }}}_{{{\text{ac}}}}}$) of GaS_1 – xSe_x single crystals at 298 K. GaS_xSe_1 – x (x = 0–1) single crystals, as indicated above in the experimental part, were grown by the Bridgman method. An increase in the selenium concentration in GaS_1 – xSe_x leads to an increase in ac conductivity, for example, at 5 × 10⁴ Hz, the conductivity of a GaS_0.2Se_0.8 single crystal with the highest selenium content is almost two orders of magnitude higher than the ${{{{\sigma }}}_{{{\text{ac}}}}}$ of the GaS single crystal. With increasing frequency, the difference in the values of σ_ac GaS_1 – xSe_х decreases.

Fig. 5.

Dependence of ac-conductivity in the frequency range 5 × 10⁴–3.5 × 10⁷ Hz on the single crystal composition of solid solutions of the GaS–GaSe system: GaS (1), GaS_0.5Se_0.5 (2), GaS_0.3Se_0.7 (3), and GaS_0.2Se_0.8 (4) at 300 K.

In the entire studied frequency range, the ac-conductivity of GaS_1 – хSe_х changed according to the power law ${{{{\sigma }}}_{{{\text{ac\;}}}}}\sim {{f}^{n}}$, where n ≤ 1. In GaS, the dispersion curve ${{{{\sigma }}}_{{{\text{ac}}}}}\sim {{f}^{n}}~$ obeyed the ${{{{\sigma }}}_{{{\text{ac}}}}}\sim {{f}^{{0.8}}}$ law, and in GaS_0.5Se_0.5 after the ${{{{\sigma }}}_{{{\text{ac}}}}}\sim {{f}^{{0.8}}}$ at high frequencies ($f$ ≥ 6 × 10⁶ Hz), a linear dependence ${{{{\sigma }}}_{{{\text{ac}}}}}\sim f$ was observed. In GaS_0.3Se_0.7 and GaS_0.2Se_0.8 crystals, the dependence ${{{{\sigma }}}_{{{\text{ac}}}}}\sim {{f}^{{0.5}}}$ was observed in the entire frequency range.

The experimental dependence ${{{{\sigma }}}_{{{\text{ac}}}}}\sim {{f}^{{0.8}}}$ in GaS and GaS_0.5Se_0.5 observed by us indicates that it is due to jumps of charge carriers over states localized near the Fermi level. The formula for such conductivity has the form [41]:

$${{\sigma }_{{{\text{ac}}}}}(f) = \frac{{{{\pi }^{3}}}}{{96}}~{{e}^{2}}kTN_{{\text{F}}}^{2}{{a}^{5}}f{{\left[ {\ln \left( {\frac{{{{\nu }_{{{\text{ph}}}}}}}{f}} \right)} \right]}^{4}},$$

(6)

where $e$ is the elementary charge; $k$ is the Boltzmann constant; ${{N}_{{\text{F}}}}$ is the density of states near the Fermi level; $a = 1{\text{/}\alpha }$ is the radius of localization; $\alpha$ is the decay constant for the wave function of the localized charge carrier ${{\psi }}\sim {{e}^{{ - \alpha r}}}$; ${{\nu }_{{{\text{ph}}}}}$ is the phonon frequency. Using formula (6), the density of states at the Fermi level was calculated from the experimentally found ${{{{\sigma }}}_{{{\text{ac}}}}}\sim {{f}^{{0.8}}}$ values of the GaS and GaS_0.5Se_0.5 samples: ${{N}_{{\text{F}}}}$ = 8.8 × 10¹⁸ and 2 × 10¹⁹ eV^–1 cm^–3, respectively. In the calculations of ${{N}_{{\text{F}}}}$ for the localization radius, the value of $a$ = 14 Å was taken, which was obtained experimentally for a GaS single crystal [42]. And the ${{\nu }_{{{\text{ph}}}}}$ value for GaS is about 10¹² Hz.

Thus, it was found that the conductivity naturally changes with a change in the composition of solid solutions GaS_xSe_1 – x single crystals (Figs. 5, 6). In particular, as the concentration of selenium in solid solutions increases, their conductivity gradually increases by about two orders of magnitude at 298 K (Fig. 6).

Fig. 6.

Dependence of conductivity on changes in the composition of GaS_xSe_1 – x solid solutions at 298 K.

Taking into account the 2D nucleation mechanism [35], the growth of GaS_xSe_1 – x single crystals can be represented as follows. Crystal faces grow due to the formation of two-dimensional nuclei of critical size in the absence of screw dislocations ending on the surface. 2D nuclei are formed when individual growth units (for example, atoms, molecules, dimers) are adsorbed on the surface of a crystal, diffuse and agglomerate. After a 2D nucleus becomes larger than its critical size, it becomes thermodynamically advantageous for attaching growth units to this nucleus. In a supersaturated solution, a 2D nucleus larger than the critical one propagates across the face until it reaches the crystal boundary. These boundaries can be either the edge of the crystal layer, or the front of the layer below it or the growth front from another nucleus.

The nucleation rate, $J(t)$, approaches a stable state according to an equation of the form [43]:

$$\begin{gathered} J(t) = ~{{J}_{s}}\left[ {1 - {\text{exp}}( - t{\text{/}}{{t}_{{{\text{lag}}}}})} \right], \\ \frac{1}{{(6.3a({{L}_{c}}){{Z}^{2}})}} \geqslant {{t}_{{{\text{lag}}}}} \geqslant \frac{1}{{(12a({{L}_{c}}){{Z}^{2}})}}, \\ \end{gathered} $$

(7)

where ${{J}_{s}}$ is the stationary nucleation rate, Z is the Zeldovich factor, $a({{L}_{c}})$ is the rate at which monomers are absorbed by a cluster with a critical size ${{L}_{c}}$, ${{t}_{{{\text{lag}}}}}$ is time lag. Expression (7) describes the asymptotic behavior of the Fokker–Planck equation and is in qualitative agreement with the numerical calculation for the dependence of the nucleation frequency of GaS_xSe_1 – x on time. Since the gradient $(L)$ in the region |$~L$ − ${{L}_{c}}$| < 1/2Z is small, then the cluster will move in this region by random walk with a jump frequency $a({{L}_{c}})$. The time required for the cluster to disperse the 1/Z distance by random walk is determined by the time lag, which is estimated as ${{t}_{{{\text{lag}}}}} = 1{\text{/}}2a({{L}_{c}}){{Z}^{2}}$.

The Fokker–Planck equation approximates distribution density of GaS_xSe_1 – x crystals by size (Fig. 7). It was assumed that the temperature dependence on particle size is described by the relation:

$$T = {{T}_{{0~}}}{\text{exp}}\left( {\frac{{{{R}^{2}}}}{{R_{0}^{2}}}} \right),$$

(8)

R is the particle radius; ${{R}_{0}}$ is the initial particle radius.

Fig. 7.

Evolution of distribution function of GaS_xSe_1 – x (х = 0.7) crystals by size in nucleation time t: (1) 0.005, (2) 0.001 s; $\gamma$ = 5 and β = 1 (Eq. (3)).

Comparison results of the calculation (curve) and experiment (points) of the dynamics of the mass change (∆m) of GaS_xSe_1 – x nanocrystals with respect to the initial arithmetic mean mass of particles ${{m}_{0}}$ diameter ∼30 nm are shown in Fig. 8. Numerical experiments indicate that the concentration of crystals of a given composition varies from the initial supersaturation to equilibrium concentration in a very short time. From the concentration dependence of the formed GaS_xSe_1 – x crystals on the formation time, it follows that the bulk of the crystals is formed within 2 × 10^–3 s from the moment of crystallization initiation.

Fig. 8.

Concentration dependence of GaS_xSe_1 – x (x = 0.7) nanocrystals on time; $m$ is particle mass with diameter $d \approx 25 \; {\text{nm}}$, ${{m}_{0}}$ is arithmetic mean mass of particles.

During the same time, the crystal concentration of a given composition decreases from the initial supersaturation to the equilibrium concentration. This process is accompanied by a decrease in the oversaturation of the solution. The supersaturation ends with a constant number of nuclei and then the crystals grow with a further increase in crystal size. Thus, when using the Fokker–Planck equation, the concentration of the crystallizing phase was taken into account, as well as data on the supersaturation and crystal size.

CONCLUSIONS

On the basis of DTA, XRD and thermodynamic calculation, the equilibrium Т–x phase diagram of the GaS–GaSe quasibinary system with unlimited component solubility is described and modeled. Model takes into account our experimental thermodynamic data on the initial GaS and GaSe components. The concentration–temperature dependence of the Gibbs free energy of mixing of GaS_xSe_1 – x solid solutions, calculated taking into account the rule of mixing components, well approximates the T–x phase diagram of the GaS–GaSe system. Conductivity smoothly changes with a change in the composition of solid solutions GaS_xSe_1 – x (x = 0–1) single crystals. As the concentration of selenium in solid solutions increases, their conductivity gradually increases by about two orders of magnitude at 298 K.

Model of kinetics of GaS_xSe_1 – x nucleation using the Fokker–Planck equation, takes into account compositional fluctuations due to the initial state of solid solutions. It is established that taking into account random walks into the size space during crystallization allows to describe the dynamics of changes in the GaS_xSe_1 – x properties. By numerically solving the equation, the evolution of the size distribution function of the GaS_xSe_1 – x crystal nuclei in nucleation time is approximated. For calculations, a purely implicit differencing scheme is used, which involves splitting the extended volume of the solution into independent fragments. It follows from the time dependence of the concentration of GaS_xSe_1 – x crystals (x ≈ 0.7) that the bulk of the crystals form within 2 × 10^–3 s from the moment of crystallization initiation.