INTRODUCTION

High-energy electrons are produced and accelerated toward the target during interaction of a high-power short laser pulse and a solid target [1–6]. One of the most significant applications of such laser-generated electron beams is inertial confinement fusion [2, 3].

In the concept of fast ignition, a high-intensity (\(10^{24}\) W/m2) high-energy (\(10^5\) J) short (\(10^{- 11}\) s) laser pulse irradiates pellets containing a deuterium-tritium (DT) mixture. This method is more effective than conventional ignition [3]. Relativistic electrons can be produced in this approach at the edge of the pellets (usually \(50\cdot 10^{- 6}\) m away from the dense core) through various mechanisms. These energetic electrons can propagate through a bulk solid and transfer their energy to a dense core [2, 3]. When a fast electron beam (FEB) propagates through a dense plasma, the beam current is neutralized by the electron return current of the background plasma generated by large electric fields of fast electron beams [7].

One of the most significant mechanisms is produced by the return current Ohmic heating [5]. The effective coupling of the short-pulse energy to the compressed core is critical in this scenario.

The transverse angular distribution of an FEB was studied in [8]. The possibility of collimating the relativistic electron beam with a compressed core of the target is the main reason for successful ignition. Various methods and targets with a variety of geometries and structures are applied to reduce the transverse angular distribution of the FEB (in order to control its divergence). Some studies were performed in this field, namely, self-generated magnetic field at the resistivity boundary in a sandwich target [9], target with a high-resistivity core and low-resistivity cladding [10], switchyard target [11], double cone target [12], imposed axial magnetic field [13], applying an external magnetic field [14], target with a low-density core and high-density cladding with planner design [15], the use of two consecutive laser pulses [16], etc. It is shown that all these methods allow FEB collimation.

Another approach is using cylindrical targets that have a density gradient. Cylindrical targets are essential, more practical, and desirable options for experimental research [17, 18]. Djaoui [19] proposed an analytical model for calculating the self-generated magnetic field at the cylindrical target structure (low-density core and high-density cladding) for the first time. In the present study, we consider a cylindrical target and an annular laser beam and compare the self-generated magnetic fields of planar and cylindrical targets.

1. ANALYTICAL MODEL

In this model, an annular high-intensity laser beam irradiates an un-magnetized target (the beam axis coincides with the target axis). The target is assumed to be a plasma structure with a density gradient (low-density core and high-density cladding). A homogeneous FEB is generated during the laser-plasma interaction. This homogeneous FEB propagates through the target and generates electric fields, which will drive a return current.

Numerical and analytical simulations show that the target whose structure consists of a low-density core and high-density cladding can generate a megagauss interface magnetic field, which collimates fast electrons [15, 20]. The self-generated magnetic field is calculated using a “rigid beam" approach (used for laser-driven electron beam transportation in solid /plasma matter) [21, 22]. The model implies that cylindrical beam has a fixed current density and moves with an average velocity \(\boldsymbol {v}_0\) along the \(z\) axis. The ions, in this paper, are assumed to be immobile, and they form a charge-neutralizing background. As all we need is just a short time to produce and develop the interface magnetic field, the focus is put on this early stage, where we neglect the collision term.

As the plasma density is higher than the FEB density (\(n_p>n_b\)), the background plasma flow is non-relativistic with a tiny thermal spread compared to the fast electron beam.

Assuming cold plasma electrons, however, the electron thermal effects are disregarded. This approach has been widely applied to laser-plasma interaction studies [23]. Thus, the background electrons can be treated as a single non-relativistic cold collisionless fluid.

The electron fluid equations, together with the Maxwell equations, comprise a complete system of equations describing the system response to FEB propagation [24]. The continuity equation and electron fluid equation are written as

$$ \frac{\partial n}{\partial t}+\nabla \cdot (n\boldsymbol {v}_e)=0;$$
(1)
$$ \Big(\frac{\partial\boldsymbol {p}_e}{\partial t} +(\boldsymbol {v}_e\cdot \nabla)\boldsymbol {p}_e\Big) =-e\Big(\boldsymbol {E}+\frac{1}{c}\,\boldsymbol {v}_e\times \boldsymbol {B}\Big),$$
(2)

where \(-e\) is the electron charge, \(\boldsymbol {v}_e\) is the flow velocity of the background electrons, \(\boldsymbol E\) and \(\boldsymbol B\) are the electric and magnetic fields, \(\boldsymbol {p}_e=m\gamma_e \boldsymbol {v}_e\) is the momentum of the background electrons, \(m\) is the electron rest mass, and \(\gamma_e=1/\sqrt{(1-\boldsymbol {v}_e^2/c^2)}\) is the relativistic mass factor.

As we can see, the electron pressure and collisional terms in Eq. (2) are neglected (according to the explanation given above).

Introducing the vector potential \(\boldsymbol {A}\) and the scalar potential \(\varphi\), which satisfy the Coulomb gauge \(\nabla \cdot \boldsymbol {A}=0\), we can rewrite Eq. (2) as

$$ \frac{\partial}{\partial t}\,\Big(\boldsymbol {p}_e-\frac{e}{c}\,\boldsymbol {A}\Big) -\boldsymbol {v}_e\times \nabla \times \Big(\boldsymbol {p}_e-\frac{e}{c}\,\boldsymbol {A}\Big) =-\nabla \Big(\gamma_e\,\frac{\boldsymbol {v}_e\cdot \boldsymbol {v}_e}{2}\Big) +e\nabla \varphi.$$
(3)

We introduce the vorticity \(\boldsymbol \Omega\) defined as

$$\boldsymbol {\Omega}=\nabla \times \Big(\boldsymbol {p}_e-\frac{e\boldsymbol {A}}{c}\Big).$$

Multiplying Eq. (3) by \(\nabla\times\), we obtain the generalized vorticity conservation law [24]

$$\frac{\partial \boldsymbol {\Omega}}{\partial t} -\nabla \times (\boldsymbol {v}_e\times \boldsymbol {\Omega})=0\quad\Longrightarrow\quad \frac{\partial \boldsymbol {\Omega}}{\partial t}+(\boldsymbol v_e\cdot\nabla)\boldsymbol \Omega =-\boldsymbol \Omega(\nabla\cdot\boldsymbol v_e)+(\boldsymbol \Omega\cdot\nabla)\boldsymbol v_e.$$

If \(\boldsymbol {B}\) and \(\nabla \times\boldsymbol {p}_e\) are equal to zero before FEB arrival, the vector \(\boldsymbol \Omega\) is also equal to zero; therefore, we have

$$\boldsymbol {B}=\frac{c}{e}\,\nabla \times \boldsymbol {p}_e.$$

In this case, the electron flow velocity is non-relativistic. Therefore, the relativistic effects are negligible, and

$$ B_{\theta }(r)=-\frac{c}{e}\,\frac{\partial p_{e_z}(r)}{\partial r}.$$
(4)

The Maxwell equation for the self-generated electric and magnetic fields has the form

$$ \nabla \times \boldsymbol {B}=\frac{4\pi }{c}\,\Big(-\frac{en}{m\gamma_e}\,\boldsymbol {p}_e +\boldsymbol {J}_0\Big)+\frac{1}{c}\,\frac{\partial \boldsymbol {E}}{\partial t}.$$
(5)

For long beams (\(l_b\gg v_0/\omega_{pe}\)), the displacement current \(c^{-1}\,\partial \boldsymbol {E}/\partial t\) is of the order of \((\boldsymbol {v}_0/(\omega_pl_b))^2\ll 1\). Here \(\boldsymbol {v}_0\) and \(\omega_p\) are the FEB and background plasma frequencies, respectively. Therefore, the displacement current term at the left-hand side of Eq. (5) can be neglected [24]:

$$ \nabla \times \boldsymbol {B}=\frac{4\pi }{c}\, \Big(-\frac{en}{m\gamma_e}\,\boldsymbol {p}_e+\boldsymbol {J}_0\Big).$$
(6)

Using Eqs. (4) and (6), we obtain the self-generated magnetic field for the collisionless case:

$$ \frac{mc^2}{4\pi e^2}\,\nabla \times \Big(\frac{\gamma_e}{n}\, \nabla \times \boldsymbol {B}\Big)+\boldsymbol {B} =\frac{mc\gamma_e}{e^2}\Big(\frac{1}{n}\,\nabla \times \boldsymbol {J}_0 -\frac{1}{n^2}\,\nabla n\times \boldsymbol {J}_0\Big).$$
(7)

Equation (7) clearly shows that such a structure with a density gradient in the transverse direction to the FEB flow velocity should produce strong magnetic fields at the interface of a low-density core and high-density cladding, which collimate the FEB flow.

2. ANALYTICAL STUDY OF A MAGNETIC FIELD GENERATED IN A CYLINDRICAL GEOMETRY FOR HOMOGENEOUS FAST ELECTRON BEAMS

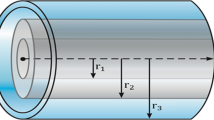
In this section, the self-generated magnetic field is calculated for a cylindrical target at the interface of the low-density core and high-density cladding. In this model, three layers are considered for the target structure, and the core is regarded as annular with the inner \(r_1\) and outer \(r_2\) radii, radial distance from the annulus center \(r\), and characteristic width of the annular core \(r_2-r_1\) (Fig. 1). The background plasma densities in three regions indicated in Fig. 1 are \(n_{i1}\) for \(0<r<r_1\), \(n_{i2}\) \(r_1\le r\le r_2\), and \(n_{i3}\) for \(r>r_2\).

Fig. 1
figure 1

Target structure: (1) low-density core; (2) high-density cladding.

Full size image

It is assumed that the FEB densities in regions 1, 2, and 3 are \(n_{01}\), \(n_{02}\), \(n_{03}\), respectively. The quasi-neutrality condition for each region is

$$n_j=z_jn_{ij}-n_{0j},\qquad j=1,2,3,$$

where \(n_j\) is the background thermal electron density, and \(z_j\) is the charge state for the \(j\)-th region.

[3] Equations (4) and (6) yield

$$ \frac{mc^2}{4\pi e^2}\Big(\frac{d^2v_{ez}(r)}{dr^2} +\frac{1}{r}\,\frac{dv_{ez}(r)}{dr}\Big)=nv_{ez}(r)+n_0v_0,$$
(8)

which can be written as

$$\begin{array}{cl} \displaystyle\delta^2_1\Big(\frac{d^2v_{ez}(r)}{dr^2}+\frac{1}{r}\, \frac{dv_{ez}(r)}{dr}\Big)-\Big(v_{ez}(r)+\frac{v_{01}n_{01}}{n_1}\Big)=0, & 0<r<r_1,\\[4mm] \displaystyle\delta^2_2\Big(\frac{d^2v_{ez}(r)}{dr^2}+\frac{1}{r}\,\frac{dv_{ez}(r)}{dr}\Big) -\Big(v_{ez}(r)+\frac{v_{02}n_{02}}{n_2}\Big)=0, & r_1\le r\le r_2,\\[4mm] \displaystyle\delta^2_3\Big(\frac{d^2v_{ez}(r)}{dr^2}+\frac{1}{r}\,\frac{dv_{ez}(r)}{dr}\Big) -\Big(v_{ez}(r)+\frac{v_{03}n_{03}}{n_3}\Big)=0, & r>r_2,\end{array}$$

where \(\delta_j=c/\omega_{pj}\) is the collisionless electron skin depth, and \(\omega_{pj}=\sqrt{4\pi n_je^2/m}\) (\(j=1,2,3\)) is the electron plasma frequency for the background plasma in the \(j\)-th region.

These equations are called the modified Bessel equations, and their solutions have the form

$$ v_{ez}(r)=\left\{ \begin{array}{cl} c_1I_0(r/\delta_1)-v_{01}n_{01}/n_1, & 0<r<r_1 \\[2mm] c_2I_0(r/\delta_2)+c_3K_0(r/\delta_2) -v_{02}n_{02}/n_2, & r_1\le r\le r_2, \\[2mm] c_4K_0(r/\delta_3)-v_{03}n_{03}/n_3, & r>r_2, \end{array}\right.$$
(9)

where \(I_0(r/\delta_2)\) and \(K_0(r/\delta_2)\) are the modified Bessel functions of the zeroth order. The constants \(c_1\), \(c_2\), \(c_3\), and \(c_4\) are determined from the boundary conditions:

$$C_1=\frac{\delta_1}{\delta_2}\Big[c_2I_1\Big(\frac{r_1}{\delta_2}\Big) -c_3K_1\Big(\frac{r_1}{\delta_2}\Big)\Big]\;\Big/\; I_1\Big(\frac{r_1}{\delta_1}\Big),$$
$$C_2=\Big\{C_3\Big[K_0\Big(\frac{r_1}{\delta_2}\Big) +\frac{\delta_1}{\delta_2}\,\frac{I_0(r_1/\delta_1)} {I_1(r_1/\delta_1)}\,K_1\Big(\frac{r_1}{\delta_2}\Big)\Big] -\frac{v_{02}n_{02}}{n_2} +\frac{v_{01}n_{01}}{n_1}\Big\}\;\Big/ \;\Big[\frac{\delta_1}{\delta_2}\, \frac{I_0(r_1/\delta_1)}{I_1(r_1/\delta_1)}\, I_1\Big(\frac{r_1}{\delta_2}\Big)-I_0\Big(\frac{r_1}{\delta_2}\Big)\Big],$$
$$C_3=\Big\{\Big[\frac{\delta_1}{\delta_2}\, \frac{I_0(r_1/\delta_1)}{I_1(r_1/\delta_1)}\, I_1\Big(\frac{r_1}{\delta_2}\Big) -I_0\Big(\frac{r_1}{\delta_2}\Big)\Big] \Big(\frac{v_{02}n_{02}}{n_2}-\frac{v_{03}n_{03}}{n_3}\Big)-{}$$
$${}-\Big[\frac{\delta_3}{\delta_2}\, \frac{K_0(r_2/\delta_3)}{K_1(r_2/\delta_3)}\, I_1\Big(\frac{r_2}{\delta_2}\Big) +I_0\Big(\frac{r_2}{\delta_2}\Big)\Big] \Big(-\frac{v_{02}n_{02}}{n_2}+\frac{v_{01}n_{01}}{n_1}\Big)\Big\}\;\Big/{}$$
$${}\;\Big/\;\Big\{ \Big[\frac{\delta_1}{\delta_2}\,\frac{I_0(r_1/\delta_1)}{I_1(r_1/\delta_1)}\, K_1\Big(\frac{r_1}{\delta_2}\Big) +K_0\Big(\frac{r_1}{\delta_2}\Big)\Big] \Big[\frac{\delta_3}{\delta_2}\,\frac{K_0(r_2/\delta_3)}{K_1(r_2/\delta_3)}\, I_1\Big(\frac{r_2}{\delta_2}\Big) +I_0\Big(\frac{r_2}{\delta_2}\Big)\Big]-{}$$
$${}-\Big[\frac{\delta_3}{\delta_2}\, \frac{K_0(r_2/\delta_3)}{K_1(r_2/\delta_3)}\, K_1\Big(\frac{r_2}{\delta_2}\Big) -K_0\Big(\frac{r_2}{\delta_2}\Big)\Big] \Big[\frac{\delta_1}{\delta_2}\, \frac{I_0(r_1/\delta_1)}{I_1(r_1/\delta_1)}\, I_1\Big(\frac{r_1}{\delta_2}\Big) -I_0\Big(\frac{r_1}{\delta_2}\Big)\Big]\Big\},$$
$$C_4=-\frac{\delta_3}{\delta_2}\, \Big[c_2I_1\Big(\frac{r_2}{\delta_2}\Big) -c_3K_1\Big(\frac{r_2}{\delta_2}\Big)\Big]\;\Big/\; K_1\Big(\frac{r_2}{\delta_3}\Big).$$

The magnetic field can be obtained by substituting Eq. (9) into Eq. (4):

$$ \frac{eB_{\theta }(r)}{mc}=\left\{\begin{array}{cl} \displaystyle-\frac{C_1}{\delta_1}\,I_1\Big(\frac{r}{\delta_1}\Big), & 0<r<r_1,\\[4mm] \displaystyle-\frac{c_2}{\delta_2}\,I_1\Big(\frac{r}{\delta_2}\Big) +\frac{c_3}{\delta_2}\,K_1\Big(\frac{r}{\delta_2}\Big), & r_1\le r\le r_2,\\[4mm] \displaystyle\frac{c_4}{\delta_3}\,K_1\Big(\frac{r}{\delta_3}\Big), & r>r_2,\end{array}\right.$$
(10)

where \(I_1(r/\delta_2)\) and \(K_1(r/\delta_2)\) are the modified Bessel functions of the first kind.

3. RESULTS AND DISCUSSION

The results reported and discussed below were obtained for the values of the constants taken from [15]: \(v_{02}\sim c\), \(n_{01}=n_{03}\approx 0\), \(n_{02}/n_2\approx 3/10\), \(n_1=n_3\approx 36n_2\), and \(\delta_2\approx 0.7\cdot 10^{-6}\) m.

Fig. 2
figure 2

Radial distributions of the magnetic field: a) \(r_1=2\cdot 10^{-6}\) m and \(r_2=12\cdot 10^{-6}\) m; (b) \(r_1=4\cdot 10^{-6}\) m and \(r_2=14\cdot 10^{-6}\) m; (c) \(r_1=20\cdot 10^{-6}\) m and \(r_2=30\cdot 10^{-6}\) m.

Full size image

Figure 2 shows the radial distributions of the normalized self-generated magnetic fields for \(r_1=2\cdot 10^{-6}\), \(4\cdot 10^{-6}\), and \(20\cdot 10^{-6}\) m. For all three cases, the thickness of the inner layer is assumed to be \(10^{-5}\) m. These cylindrical targets with the density gradient also provide a possibility of electric charge and electron beam current neutralization everywhere except for the boundaries of different density regions over a characteristic transverse distance \(\Delta r=\delta_j\) [25]. It is seen from Fig. 2 that the spontaneous magnetic field produced in these target structures reaches its maximum value at the boundaries. These spontaneous interface magnetic fields tend to bend the fast electrons toward the main core by means of generating the \(v_0/B\) force when the electron beam approaches the interface. The self-generated magnetic field penetrates into the inner region, which is greater than the characteristic skin depth. The spontaneous magnetic field is normalized to

$$B_0=\frac{m_e\omega_{p2}c}{e},$$

whose value is as high as several tens of megagauss (because the order of the electron plasma frequency in the over-dense plasma is large: \(\omega_{p2}\) is of the order of \(10^{14}\) s\(^{-1}\)), which can be understood as the order of magnitude of the self-generated magnetic field in such structures. According to the above-mentioned equations, the density jump at the boundaries of different layers leads to abrupt and rapid changes in the flow velocity of the background electrons in the transverse direction to the flow and to generation of a spontaneous interface magnetic field. A stronger magnetic field is generated at the inner interface, due to the creation of a larger density gradient in structures having a smaller internal radius. It is found that selecting an appropriate thickness for different regions leads to production of strong spontaneous magnetic fields at the interfaces, which, in turn, leads to better preservation of fast electrons in the inner layer to transfer energy more efficiently.

Though the self-generated magnetic field tends to collimate the fast electrons, it disperses the returned background electrons and expels some of them from the low-density core region to retain charge neutralization.

In order to keep the current neutralized, the self-generated magnetic field accelerates the background electrons to a higher velocity. Next, we performed a comparison between the resulting spontaneous interface magnetic field for a cylindrical target and a target structure (planar target) considered in [15] to study the impact of geometry of these kinds of targets.

In the first investigation, we assumed a situation where the widths of all three regions in the two target structures were identical: \(v_{02}\sim c\), \(n_{01}=n_{03}\approx 0\), \(n_{02}/n_2\approx 3/10\), \(n_1=n_3\approx 36n_2\), \(\delta_2\approx 0.7\cdot 10^{-6}\) m, \(r_1=2\cdot 10^{-6}\) m, and \(r_2=12\times {10}^{-6}\) m.

Fig. 3
figure 3

Radial distributions of the background electron flow velocity (a) and self-generated magnetic field (b) for \(r_1=2\cdot 10^{-6}\) m and \(r_2=12\cdot 10^{-6}\) m: the solid and dot-and-dashed curves show the results for the cylindrical and planar target, respectively.

Full size image

It is clear from Fig. 3a that neutralization of the electric current of the fast electron beam is more effective in the cylindrical target as compared to the planar target if the thickness of the first layer is small. The background electron flow velocity is normalized to the speed of light. The self-generated magnetic field is larger at the inner interface of the cylindrical target than that in the planar target, which can lead to conservation of a higher fraction of fast electrons in the main target (Fig. 3b). However, the magnetic field in the cylindrical target with a large radius is approximately the same in both geometries.

Fig. 4
figure 4

Radial distributions of the background electron flow velocity (a) and self-generated magnetic field (b) for \(r_1=10^{-5}\) m and \(r_2=25\cdot 10^{-6}\) m: the solid and dot-and-dashed curves show the results for the cylindrical and planar target, respectively.

Full size image

The results presented in Fig. 4 were obtained for \(r_1=10^{-5}\) m and \(r_2=25\cdot 10^{-6}\) m. The other parameters were the same as those in the previous case.

As is seen from Fig. 4, the greater the radius, the better the correspondence between the two geometries. The self-generated magnetic fields are almost identical. In the ranges considered in the present study, the type of geometry is insignificant. In small and compact dimensions, however, the type of geometry is quite conspicuous, and cylindrical geometry is superior as compared to planar geometry. If \(B_0\) is large, minor differences in the diagrams lead to production of self-generated magnetic fields of different orders.

Furthermore, in order to gain a better insight into the effect of the target geometry on collimating the fast electron beam during the interactions, we tried to quantify the maximum spontaneous interface magnetic fields for different geometries.

The expression for the self-generated magnetic field in the inner region for the planar target can be written as follows [15]:

$$ \frac{eB(r)}{mc}=-\frac{1}{\delta_2} \big(c_5\mathrm{e}^{r/\delta_2}-c_6\mathrm{e}^{-r/\delta_2}\big).$$
(11)

Here

$$C_5=\Big\{C_6\Big[\Big(1+\frac{\delta_1}{\delta_2}\Big)\mathrm{e}^{-r_1/\delta_2}\Big] -\frac{v_{02}n_{02}}{n_2}+\frac{v_{01}n_{01}}{n_1}\Big\}\;\Big/\; \Big[\Big(\frac{\delta_1}{\delta_2}-1\Big)\mathrm{e}^{r_1/\delta_2}\Big],$$
$$\quad C_6=\Big\{\Big[\Big(\frac{\delta_1}{\delta_2}-1\Big)\mathrm{e}^{r_1/\delta_2}\Big] \Big(\frac{v_{03}n_{03}}{n_3}-\frac{v_{02}n_{02}}{n_2}\Big)+{}$$
$${}+\Big[\Big(1+\frac{\delta_3}{\delta_2}\Big)\mathrm{e}^{r_2/\delta_2}\Big] \Big(-\frac{v_{02}n_{02}}{n_2}+\frac{v_{01}n_{01}}{n_1}\Big)\Big\}\;\Big/\;{}$$
$$\Big\{\Big[\Big(\frac{\delta_1}{\delta_2}-1\Big)\mathrm{e}^{r_1/\delta_2}\Big] \Big[\Big(\frac{\delta_3}{\delta_2}-1\Big)\mathrm{e}^{-r_2/\delta_2}\Big] -\Big[\Big(\frac{\delta_3}{\delta_2}+1\Big)\mathrm{e}^{r_2/\delta_2}\Big] \Big[\Big(\frac{\delta_1}{\delta_2}+1\Big)\mathrm{e}^{-r_1/\delta_2}\Big]\Big\}.\quad$$

According to Eqs. (10) and (11), the maximum spontaneous magnetic fields generated at the interfaces are calculated by using the above-mentioned data. The results of Fig. 3 were obtained for the first interface radius \(r=2\cdot 10^{-6}\) m. For this value of \(r\), we have \(B_p/B_0\approx 0.33\), \(B_c/B_0\approx 0.41\), \(B_0\approx 200\) MGs, and \(B_c-B_p\approx 16~\mbox{MGs} =1600\) T. The subscripts \(p\) and \(c\) are used to mark the self-generated magnetic fields in the planar and cylindrical targets, respectively. For the first interface radius \(r=10^{-5}\) m, we obtain \(B_p/B_0\approx 0.33\), \(B_c/B_0\approx 0.37\), \(B_0\approx 200\) MGs, and \(B_c-B_p\approx 8~\mbox{MGs}=800\) T.

For the above-considered values of the first interface radius, the magnetic induction is seen to be almost at the same level. For \(r=12\cdot10^{-6}\) and \(25\cdot10^{-6}\) m, we have \(B_p/B_0\approx B_c/B_0\approx -0.36\).

Fig. 5
figure 5

Radial distribution of the self-generated magnetic field in the cylindrical (solid curve) and planar (dot-and-dashed curve) targets for \(r_1=10^{-6}\) m and \(r_2=5\cdot 10^{-6}\) m.

Full size image

Figure 5 shows the radial distributions of the dimensionless self-generated magnetic field for the cylindrical and planar targets for \(r_1=10^{-6}\) m and \(r_2=5\cdot 10^{-6}\) m. It is seen that the magnetic field is stronger at the interface with a smaller radius in cylindrical targets. In this way, the magnetic field can better converge and preserve fast electrons in the target core.

Eventually, if the value of \(r\) is very large, the magnetic field in the cylindrical target coincides with the magnetic field in the planar target.

It is found that excitation of magnetic fields due to rapid changing in the flow velocity of background electrons in the transverse direction to the flow velocity caused by the density jump in specially engineered targets (exhibiting a low-density core and high-density cladding) can collimate fast electrons. The laser-generated incident fast electrons enter with a wide distribution of angles and a vast variety of velocities. Some fast electrons with higher velocities may be affected by these improved collimating magnetic fields and accumulate a higher FEB density in the target core.

Increasing the generation of interface magnetic fields, which depends on the target configuration, is valuable, especially if utilizing an external strong magnetic field is expensive.

CONCLUSIONS

In this paper, a pioneering theoretical investigation of the plasma with a low-density core and high-density cladding irradiated by an annular laser beam is proposed in cylindrical geometry. The analytical results indicate that cylindrical targets with the density gradient nonparallel to the flow velocity of the fast electron beam change the flow velocity of the background plasma electrons in the transverse direction to the FEB flow velocity. As a result, a spontaneous interface magnetic field is produced, which guides and collimates fast electrons.

It is shown that the maximum spontaneous magnetic field appears at the interface, and the self-generated magnetic field penetrates into the inner region over the characteristic skin depth.

The self-generated magnetic fields of cylindrical structures having three different radii were compared. The results reveal that the magnitude of the self-generated magnetic field at the interface is large if the first layer thickness is small. The self-generated magnetic fields of cylindrical and planar structures are compared to each other. As it is observed, the smaller the target size, the more distinct the relative advantages of cylindrical structures. Thus, they can be used for fast ignition.