Effects of the inhomogeneous fast electron beam on the self-generated magnetic fields in cylindrical targets

Abstract

The evolution of the self-generated magnetic fields during the transportation of inhomogeneous fast electron beams with Gaussian and super-Gaussian density profiles in cylindrical specially engineered targets is studied. The analysis is based on a fluid model for electron beam, and we consider the low-density core with a high-density cladding structure for cylindrical targets. Gaussian and super-Gaussian density distributions of the electron beam generate the spatial extent of magnetic fields, while their magnitude decreases greatly at the boundaries, compared to the homogeneous distributions.

1 Introduction

Fast electron beam with an inhomogeneous density profile generated by the laser-over-dense target interaction. One of the most attractive applications of the high-energy electrons produced and accelerated during the interaction between a high power short laser pulse and a solid target is related to the fast ignition scenarios (FIS) [1, 2]. A fast ignition is an alternative form to inertial confinement fusion (ICF). In this scheme, the pre-compressed fuel ignites using a high-power laser. This array can lead to higher gains than that conventional ignition [3]. Fast ignition (FI) inertial confinement fusion is a variant of inertial fusion in which a DT fuel pellet (∼10–20 $\mu$ m at its core) is first compressed to a high density and then ignited by a fast electron beam (FEB). This FEB is generated by an ultra-intense laser pulse at the edge of the pellet (which is usually ∼50 μm away from the dense core), through some different mechanisms [4]. These energetic relativistic electrons can propagate through a bulk solid and transfer their energy to a dense core during various mechanisms [1, 2]. When FEB propagates through dense plasma, it will drive a background plasma electron return current which coincides spatially with the fast electron current and cancels the fast electron current to a good approximation [5]. The physics of the fast electron generation and transportation through over-dense plasmas and the coupling efficiency of short-pulse energy into the compressed core are an important issue for FIS. A wide range of experimental results has confirmed the characteristic fast electron divergence angles [6]. Therefore, the possibility of collimating a relativistic electron beam (REB) with the compressed core size to overcome the limitations of the coupling efficiency imposed by the transverse angular distribution of a fast electron beam, is a fundamental demand for a FI-viable point design.

Investigating how to control fast electron transportation and improve the coupling into the compressed core has attracted great attention. Various ideas and considerable works have been presented, which results include: fast electron self-collimation by resistively generated magnetic fields (due to beam profile or resistivity gradients) [7], electrostatic confinement by a vacuum gap (double-cone target) [8], imposed axial magnetic fields [9], the use of two consecutive laser pulses [10], and so on.

Theoretical and numerical calculations, to the best of our knowledge, revealed that a structure with a density gradient (a target of a low-density core–high-density-cladding structure) in a transverse direction to the flow velocity of a fast electron beam is able to produce a spontaneous interface magnetic field that can reach as high as hundreds of mega-Gauss. This method was first developed by Hong-bo-Cai et al. [11]. The results of studies have indicated that this scheme (applying a target structure with a density gradient in a transverse direction to the flow velocity of a fast electron beam) can collimate the fast electron beams as well as more effectively couple the fast electron energy to the compressed core [12].

In previous studies, the magnetic field generation in such a structure has been analyzed in the case of transportation of fast electrons with homogeneous density profile [11, 13]. We will now, however, investigate the more general cases where the inhomogeneous density distributions for fast electron beams are considered since these distributions fit well the profile obtained in simulations and experimental works [14,15,16].

This paper is structured as follows: The theoretical model (coupled Maxwell and electron fluid equations) and governing equations of the evolution of a beam-plasma system are presented in Section 2. Section 3 is dedicated to the calculations of self-generated magnetic fields for transporting fast electrons with Gaussian and super-Gaussian density profiles. Section 4 provides the results as well as a comparison between the self-generated magnetic field for fast electron beams with Gaussian and homogeneous density profiles. This section continues through a detailed discussion on the inhomogeneous density profiles propagating through the structured targets. Finally, a brief conclusion is given in Section 5.

2 Analytical model

Passing the fast electron beam through the plasma generates electric fields and a return current of background electrons. The self-generated magnetic field is calculated using a "rigid beam" approach proposed by Davies et al [14, 15].

The cylindrical beam with radial heterogeneity propagates with an average velocity ${{\varvec{v}}}_{0}$ along the ${\varvec{z}}$ axis. The ions are supposed to be immobile and form a charge-neutralizing background. Assumptions are since a spontaneous generated magnetic field can develop in a very short time, we neglect the collision term, the plasma density is much higher than the electron beam (${n}_{p}\gg {n}_{b}$), background plasma flow is non-relativistic, the plasma electrons are cold (the flow velocity is much higher than the electron thermal velocity; then, the energy transfer from the flow to the background plasma is weak, i.e., the electron thermal temperature of the background plasma is hard to increase in such a short time (~ pulse duration of the flow, e.g., ~100fs[17])), the background electrons can be treated as a single non-relativistic cold collision-less fluid.

The electron fluid equations, together with the Maxwell equations, comprise a complete system of equations describing the system response to the fast electron beam propagation [11, 13, 18]. The continuity equation and the non-relativistic electron fluid equation are written as:

$$ \frac{\partial n}{{\partial t}} + \nabla \times \left( {nv_{e} } \right) = o $$

(1)

$$ \left[ {\frac{{\partial {\varvec{p}}_{e} }}{\partial t} + \left( {v_{e} \cdot {\mathbf{\nabla }}} \right)p_{e} } \right] = - e\left( {{\varvec{E}} + \frac{1}{c}v_{e} \times {\varvec{B}}} \right) $$

(2)

where $- e, v_{e} , p_{e} = mv_{e} , m, E and B$ are the electron charge, the flow velocity of the background electrons, the momentum of the background electrons, the electron rest mass, the electric and magnetic fields, respectively.

Maxwell’s equations for the self-generated electric and magnetic fields, ${\varvec{E}}$ and ${\varvec{B}}$, are given by

$$ \nabla \times {\varvec{B}} = \frac{4\pi }{c}\left( {{-}en{\varvec{p}}_{{\varvec{e}}} /m + {\varvec{J}}_{0} } \right) $$

(3)

$$ \nabla \times {\varvec{E}} = - \frac{1}{c}\frac{{\partial {\varvec{B}}}}{\partial t} $$

(4)

where ${{\varvec{J}}}_{0}$ is the fast electron current. For long beams, with a pulse length of ${l}_{b}\gg {{\varvec{v}}}_{0}/{\omega }_{p}$, the displacement current ( $\frac{1}{c}\frac{\partial {\varvec{E}}}{\partial t}$) is much less than the electron current (of the order ${\left({{\varvec{v}}}_{0}/{\omega }_{p}{l}_{b}\right)}^{2}\ll 1$), so the displacement current term is neglected[19], and ${{{\varvec{v}}}_{0}\boldsymbol{ }\text{and }\omega }_{p}$ are the fast electron beam velocity and background plasma frequency. By the curl of Eq. (2) and using Eq. (4) we have

$$ \frac{{\partial{\varvec{\varOmega}}}}{\partial t} - \nabla \times \left( {{\varvec{v}}_{{\varvec{e}}} \times{\varvec{\varOmega}}} \right) = 0 $$

which can be rewritten in the form:

$$ \frac{\partial \Omega }{{\partial t}} + \left( {v_{e} \cdot {\mathbf{\nabla }}} \right)\Omega = - \Omega \left( {\nabla \cdot v_{e} } \right) + \left( {\Omega \cdot \nabla } \right)v_{e} $$

(5)

where ${\varvec{\varOmega}}= \nabla \times {\varvec{p}}_{{\varvec{e}}} - {\text{e}}{\varvec{B}}/{\text{c}}$ is the generalized vorticity. Equation (5) governs the evolution of generalized vorticity in plasma. The equation shows that the generalized vorticity is transported with the electrons, also if at initial times ${\varvec{\varOmega}}= 0$, then it will be zero at all times[18]. Thus the self-generated magnetic fields $\user2{ B}$ related to curl of the electron flow momentum ${\varvec{p}}_{{\varvec{e}}}$[13, 18]:

$$ {\varvec{B}} = \frac{c}{e}\nabla \times {\varvec{p}}_{{\varvec{e}}} $$

(6)

Equation (6) can be expressed as follows:

$$ B_{\varphi } \left( r \right) = - \frac{c}{e}\frac{{\partial p_{ez} \left( r \right)}}{\partial r} $$

(7)

Using Eqs. (6) and (3), we obtain the self-generated magnetic field for the collision-less plasmas:

$$ {\varvec{B}} = \frac{mc}{{e^{2} }}\left( {\frac{1}{n}\nabla \times {\varvec{J}}_{0} - \frac{1}{{n^{2} }}\nabla n \times {\varvec{J}}_{0} } \right) - \frac{{mc^{2} }}{{4\pi e^{2} }}\nabla \times \left( {\frac{1}{n}\nabla \times {\varvec{B}}} \right) $$

(8)

The first term of Eq. (8) generates a magnetic field that pushes the fast electrons toward regions of higher fast electron current density, and the second term guides the fast electrons toward regions of lower density. The third term describes the interaction of the self-generated magnetic field with the plasmas of the multilayered target. In the present case, in which the fast electron beam is transported to the engineered structure target with an inhomogeneous current density profile, two mechanisms can generate a magnetic field, which are as follows:

• (1) A structure with a density gradient in a transverse direction (perpendicular) to the flow velocity of a fast electron beam $(\nabla n\times {{\varvec{J}}}_{0})$.

• (2) A spatial variation in the density of propagating fast electron current $(\nabla \times {{\varvec{J}}}_{0})$.

3 Magnetic fields generating by fast electron beams with Gaussian and super-Gaussian density profiles in cylindrical targets

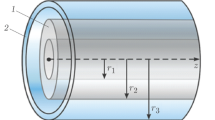
The self-generated magnetic field is calculated for a cylindrical target structure with a low-density core and high-density cladding. Figure 1 shows three regions of the target. The core of the target is regarded as annular with inner radius $r_{1}$ and outer radius $r_{2}$. The plasma electron densities ${ }n_{1}$,${ }n_{2} { , }n_{3}$ and ion densities of the background plasma for three different regions are:

$$ \left\{ {\begin{array}{*{20}c} {n_{i1} } & { o < r < r_{1} } \\ {n_{i2} } & { r_{1} < r < r_{2} } \\ {n_{i3} } & { r_{2} < r < r_{3} } \\ \end{array} } \right. $$

(9)

Fig. 1

The sketch of the low-density core–high-density-cladding target structure in cylindrical geometry.

Also, the densities of the fast electron beam for three regions are $n_{b1} {,} n_{b2}$, and $n_{b3}$, respectively. The quasi-neutrality condition is satisfied for each region as follows:

$$ n_{j} = z_{j} n_{ij} - n_{bj} \left( {j = 1{,} 2{,} 3} \right) $$

(10)

where $n_{j}$ is the background electron density and $z_{j}$ is the charge state for the j-th region.

In cylindrical geometry, the flow velocity of the background electrons is obtained from Eqs. (2-8). The velocity just depends on r.

$$ \frac{{mc^{2} }}{{4\pi e^{2} }}\left[ {\frac{{d^{2} v_{ez} \left( r \right)}}{{dr^{2} }} + \frac{1}{r}\frac{{dv_{ez} \left( r \right)}}{dr}} \right] = nv_{ez} \left( r \right) + n_{b} v_{0} $$

(11)

Consider the propagation of a fast electron beam with inhomogeneous density profile in the low-density core (the main core) along the z-axis. The density distribution of the fast electron beam is assumed to be Gaussian for $l = 1$ or super-Gaussian for $l > 1$ that is given by:

$$ n_{b2} = n_{0} {\text{exp}}\left[ { - \left[ {2\left( {\frac{{r - \lambda_{1} }}{{r_{2} - r_{1} }}} \right)} \right]^{2l} } \right] $$

(12)

where ${\lambda }_{1}=\left({r}_{2}+{r}_{1}\right)/2$, and r is the radial distance. The maximum value of the density is defined ${n}_{0}$. The tail of the density function affects the first and third regions. In fact, in this section, beams with more realistic distributions are considered. This density function is a better description of reality.

We can rewrite Eq. (11) as:

$$ \begin{gathered} \begin{array}{*{20}c} {\delta_{1}^{2} \left[ {\frac{{d^{2} v_{ez} \left( r \right)}}{{dr^{2} }} + \frac{1}{r}\frac{{dv_{ez} \left( r \right)}}{dr}} \right] - \left[ {v_{ez} \left( r \right) + \frac{{v_{01} n_{b1} }}{{n_{1} }}} \right] = 0} & {o < r < r_{1} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\delta_{2}^{2} \left[ {\frac{{d^{2} v_{ez} \left( r \right)}}{{dr^{2} }} + \frac{1}{r}\frac{{dv_{ez} \left( r \right)}}{dr}} \right] - \left[ {v_{ez} \left( r \right)} \right] = \frac{{v_{02} n_{0} }}{{n_{2} }}\exp \left[ { - \left[ {\frac{{\left( {r - \lambda_{1} } \right)}}{{\left( {\frac{{r_{2} - r_{1} }}{2}} \right)}}} \right]^{2l} } \right]} & {r_{1} \le r \le r_{2} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\delta_{3}^{2} \left[ {\frac{{d^{2} v_{ez} \left( r \right)}}{{dr^{2} }} + \frac{1}{r}\frac{{dv_{ez} \left( r \right)}}{dr}} \right] - \left[ {v_{ez} \left( r \right) + \frac{{v_{03} n_{b3} }}{{n_{3} }}} \right] = 0} & {r > r_{2} } \\ \end{array} \hfill \\ \end{gathered} $$

(13)

where $\delta_{j} = c/\omega_{pj}$ is the collisionless electron skin depth and $\omega_{pj} = \sqrt {4\pi n_{j} e^{2} /m} \left( {j{ } = { }1{, }2{,}3} \right)$ is the electron plasma frequency for the background plasma in the j-th region.

Equation (13) is homogeneous modified Bessel equations (for the first and third regions) and the inhomogeneous modified Bessel equation for the second region which their solutions are as follows [20]:

$$ v_{ez} \left( r \right) = \left\{ {\begin{array}{*{20}c} {c_{1} I_{o} \left( {\frac{r}{{\delta_{1} }}} \right) - \frac{{v_{01} n_{b1} }}{{n_{1} }}} & { o < r < r_{1} } \\ {c_{2} u_{1} \left( r \right)I_{o} \left( {\frac{r}{{\delta_{2} }}} \right) + c_{3} u_{2} \left( r \right)K_{o} \left( {\frac{r}{{\delta_{2} }}} \right)} & {r_{1} \le r \le r_{2} } \\ {c_{4} K_{o} \left( {\frac{r}{{\delta_{3} }}} \right) - \frac{{v_{03} n_{b3} }}{{n_{3} }}} & { r > r_{2} } \\ \end{array} } \right. $$

(14)

where $I_{o} \left( {r/\delta_{j} } \right)$ and $K_{o} \left( {r/\delta_{j} } \right)$ are the zero order of the modified Bessel functions. The constants ${c}_{1}$,${c}_{2}$,${c}_{3}$,${c }_{4}$ and functions ${u}_{1}\left(r\right)$,${u}_{2}\left(r\right)$ are reported in Appendix. The constants ${c}_{i}$ are determined from the boundary conditions.

A spontaneous magnetic field will be obtained by substituting Eq. (14) into Eq. (7),

$$ B_{\varphi } \left( r \right) = \frac{{mc}}{e}\left\{ {\begin{array}{*{20}l} { - \frac{{C_{1} }}{{\delta _{1} }}I_{1} \left( {\frac{r}{{\delta _{1} }}} \right)} \hfill & {o < r < r_{1} } \hfill \\ { - c_{2} \left[ {u_{1}^{\prime } \left( r \right)I_{o} \left( {\frac{r}{{\delta _{2} }}} \right) + \frac{{u_{1} \left( r \right)I_{1} \left( {\frac{r}{{\delta _{2} }}} \right)}}{{\delta _{2} }}} \right] - c_{3} [u_{2}^{\prime } \left( r \right)K_{o} \left( {\frac{r}{{\delta _{2} }}} \right) - \frac{{u_{2} \left( r \right)K_{1} \left( {\frac{r}{{\delta _{2} }}} \right)}}{{\delta _{2} }}]} \hfill & {r_{1} \le r \le r_{2} } \hfill \\ {\frac{{c_{4} }}{{\delta _{3} }}K_{1} \left( {\frac{r}{{\delta _{3} }}} \right)} \hfill & {r > r_{2} } \hfill \\ \end{array} } \right. $$

(15)

where the prime on the function $u\left(r\right)$ is derivative relative to r.

4 4-Effects of the electron beam density distribution on magnetic fields

Figure 2 depicts the density profile of a fast electron beam with Gaussian density distribution vs. radius (the Gaussian profile was chosen because it is the most probable shape of the distribution for generated fast electrons [21]). The density profile is normalized by the critical density $n_{c}$, with the order of $\left( {n_{c} \sim 10^{19} cm^{ - 3} } \right)$.

Fig. 2

The Gaussian electron beam density of the middle layer for ${r}_{1}=8\times {10}^{-6}m\text{,}{r}_{2}=15\times {10}^{-6}$, and ${n}_{0}\approx 1{n}_{c}$.

Figure (3a)and (b) shows the normalized magnetic fields by $B_{o} = m_{e} c\omega_{p2} /e$. The quantity of $B_{o}$ can be as high as several tens of mega-Gauss. The numerical parameters used for collimating magnetic field calculations in this model based on the simulation parameters [19] are:

$$ v_{02} \sim c , n_{b1} = n_{b3} \approx \frac{{0 ,n_{b2} }}{{n_{2} }} \approx 0.5, n_{1} = n_{3} \approx 40n_{2} , \delta_{2} \sim 0.5 \times 10^{ - 6} m , $$

Fig. 3

The normalized self-generated magnetic field as a function of the radius, for the propagation of a fast electron beam with a) homogeneous density profile and b) Gaussian density profile.

$r_{1} = 8 \times 10^{ - 6} m {,} r_{2} = 15 \times 10^{ - 6} m$.

Figs. 3 The magnetic field generated by the homogeneous fast electron beam has a maximum magnitude at the interfaces and then decreases rapidly. Numerical comparison of the magnetic fields at interfaces for the homogeneous beam density ${B}_{h}$ and the Gaussian beam density ${B}_{G}$ shows that ${B}_{G}$ is 60-100 times smaller than ${B}_{h}$. However, the magnetic fields ${B}_{G}$ act over longer distances and extend throughout the main core. In fact, the width of the collimating magnetic field increases. Electron beams with the homogeneous density generate strong azimuthal magnetic fields with steep gradients form at the interfaces of the layers and penetrate the inner region, which is over a characteristic skin depth [11]. In the Gaussian electron beam, two terms of density jump and inhomogeneous propagation of fast electrons contribute to the generation of magnetic field.

As mentioned, when the fast electron beam with a Gaussian density distribution in radius flows into the target structure, the self-generated fields at interfaces are very smaller than that produced by the transportation of electron beams with homogeneous density profile in the dense core. This is because, during the transportation of a beam with Gaussian density distribution, very few fast electrons are located at the boundary regions compared to the homogeneous distribution. This leads to reducing the fast electron current density in the vicinity of the interfaces. Since the non-parallel density gradient term to the flow velocity of a fast electron beam $(\nabla n\times {{\varvec{J}}}_{0})$ plays a dominant role in generating the magnetic field at the boundary regions, the effect of the mentioned term on the production of the magnetic field decreases significantly. The effect of non-parallel density gradient on the generation of magnetic field and the guidance of fast electrons only present at the interfaces of a low-density core with a high-density cladding. The gradient in the fast electron current density, however, results in the magnetic field inside the inner layer.

Collimation of the fast electrons is affected by the extended magnetic field. This is because the ability of a guiding structure to confine fast electrons depends on the ratio of the fast electron Larmor radius $\left( { r_{L} = \gamma v_{f} m_{e} /eB_{\varphi } } \right)$ to the generated azimuthal magnetic field width $L_{r}$. The confinement condition of the fast electrons along the guiding structure is expressed as [22, 23]:

$$ B_{\varphi } L_{r} \ge \frac{{\gamma v_{f} m_{e} }}{e}\left( {1 - cos\theta_{d} } \right) $$

(16)

where $B_{\varphi }$ is the azimuthal magnetic flux density, $v_{f}$ is the fast electron velocity, $\gamma$ is the Lorentz factor, $m_{e}$ is the electron rest mass, and $\theta_{d }$ is the fast electron divergence angle (the angle between the fast electron and the target axis). This confirms that the product of ${B}_{\mathrm{\varphi }}{L}_{r}$ must be larger than that the fast electron momentum to reflect the fast electrons back toward the guiding structure axis[22, 24]. Whereas the laser-generated incident fast electrons enter the core with a wide distribution of angles, they may be affected by these extended magnetic fields at the different radii and some fast electrons are concentrated at distances far from the interfaces. So, only a part of fast electrons with sufficiently high angles can escape through the boundary areas and feel magnetic fields with higher intensity. Therefore, the electron transportation pattern can be more beneficial to improve the energy coupling efficiency and heating the dense core.

Figure 4 shows the comparison of the Gaussian and super-Gaussian densities [25]. Increasing the power of inhomogeneous density profile for the fast electron beam that was introduced in Eq. (12) causes larger values of the self-generated extended magnetic fields in the boundary regions. It happens, because the higher the power of fast electron current density profiles, the sharper they are around the boundary areas. In fact, by increasing the power of the function, the amount of density variations ($\frac{{\Delta j_{b2} }}{\Delta r}$), in these radial intervals, increases and the impact of gradient term on the fast electron current density becomes more pronounced. Figure 5 shows the comparison of the magnetic fields generated by the Gaussian and super-Gaussian fast electron beams in specially engineered multilayer targets vs. radius. In summary, we have observed that as we move closer to the center of the fast electron beam distributions, the trend of the beam density profiles influences the magnetic field direction and magnitude.

Fig. 4

The normalized electron beam density for Gaussian and super-Gaussian profiles.

Fig.5

Comparison of normalized self-generated magnetic fields generated by the Gaussian and super-Gaussian electron beams.

Additionally, the sharper density increases the magnetic field in the dense core. Figure 4 shows that the Gaussian shape at some intervals, for example $11< r<13$, has the most changes, which leads to the production of a greater magnetic field.

5 Conclusions

We developed a theoretical model for the propagation of a fast electron beam with inhomogeneous density profiles in a radial direction through a cylindrical specially engineered multilayer target. The analytical solutions for the magnetic field generated by an inhomogeneous fast electron beam have been determined in the Gaussian and super-Gaussian cases. In this situation the generation of magnetic field is due to two different mechanisms: (1) non-parallel density gradient to the flow velocity of a fast electron beam and (2) the gradient of the fast electron current density propagating into the target structure. Then, we compared the self-generated magnetic fields due to the propagation of fast electron beams with Gaussian density distributions and the homogeneous fast electron beams in cylindrical structures of the same density. The results show that as the Gaussian (or super-Gaussian) beams propagate through a target structure, the magnitude of the self-generated magnetic field at the interfaces reduces enormously and significantly as compared to homogeneous density beams. It is because of the lower accumulation of fast electrons at the boundaries. But the Gaussian and super-Gaussian beams extend the length of the resulting magnetic field and reduce the magnetic field gradient at the interfaces.

Also, a comparative study on the extended magnetic field result from the fast electron beams with the Gaussian and super-Gaussian density profiles shows that the beam distribution shape and the trend of density changes, influence the magnetic field. The above calculations indicate that, when fast electrons with Gaussian and super-Gaussian density profiles propagate in cylindrical specially engineered multilayer targets, although tend to broaden the magnetic fields throughout the core region and may affect the electron transportation pattern, they are no longer able to produce the magnetic fields with magnitudes of the order of tens of mega-Gauss at interfaces.

Here for the first time we study the transportation of a relativistic electron beam through a cylindrical specially engineered multilayer target with more realistic density distributions through a theoretical model. Important aspects of this paper, as mentioned before, are the prominent reduction of the self-generated magnetic fields at the interfaces of the layers as well as the increase in the width of the resulting magnetic fields. Consequently, these results can be useful and notable for future investigations and experimental studies. Having considered them, it is possible to take place promising progress in this area.

It should be noted that this simple analytical model is only used to gain insight into the generation of a spontaneous magnetic field when a fast electron beam with inhomogeneous density profile in a radial direction propagates in a cylindrical specially engineered multilayer target and the effects of different instabilities (such as filamentation and two-stream instabilities) in fast electron beam–plasma interactions in this suggested model and our equations are not taken into account. In fact, a proper analysis of these physical processes needs more complex and accurate models that are not the purpose of our study. Since the self-generated magnetic field can develop in a very short time (of the order of a hundred femtoseconds), in this investigation, the focus is put on this early stage.

However, such considerations are ignored in our simple model, but this kind of process during fast electron beam–plasma interactions in a fast ignition scenario needs further study.

Appendix

The functions $u_{1} \left( r \right)$ and $u_{2} \left( r \right)$ introduced in Eqs. (14) are calculated as follows:

$$ u_{1} \left( r \right) = \mathop \smallint \limits_{r}^{{r_{2} }} \frac{{v_{02} n_{0} }}{{n_{2} }}exp\left[ { - 4\left( {\frac{{r - \lambda_{1} }}{{r_{2} - r_{1} }}} \right)^{2} } \right]K_{o} \left( {\frac{r}{{\delta_{2} }}} \right)r dr $$

$$ u_{2} \left( r \right) = - \mathop \smallint \limits_{{r_{1} }}^{r} \frac{{v_{02} n_{0} }}{{n_{2} }}exp\left[ { - 4\left( {\frac{{r - \lambda_{1} }}{{r_{2} - r_{1} }}} \right)^{2} } \right]I_{o} \left( {\frac{r}{{\delta_{2} }}} \right)r dr $$

Also, the constants $c_{1}$,$c_{2}$, $c_{3}$, and $c_{4 } are$ derived as follows:

$$ c_{1} = c_{2} u_{1} \left( {r_{1} } \right) + \frac{{v_{01} n_{b1} }}{{n_{1} I_{o} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}} $$

$$ c_{2} = \frac{{ - \delta_{2} c_{3} \mathop {u_{2} }\limits^{\prime } \left( {r_{1} } \right)K_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right) + \frac{{v_{01} n_{b1} }}{{n_{1} }}\frac{{\delta_{2} I_{1} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}{{\delta_{1} I_{o} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}}}{{\left[ {\mathop {u_{1} }\limits^{\prime } \left( {r_{1} } \right)\delta_{2} I_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right) + u_{1} \left( {r_{1} } \right)I_{1} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right) - \frac{{\delta_{2} u_{1} \left( {r_{1} } \right)I_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right)I_{1} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}{{\delta_{1} I_{o} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}} \right]}} $$

$$ A_{1} = \left( {\mathop {u_{1} }\limits^{\rm{\prime }} \left( {r_{2} } \right)I_{o} \left( {\frac{{r_{2} }}{{\delta_{2} }}} \right)} \right)\left( {\frac{{v_{01} n_{b1} }}{{n_{1} }}\frac{{I_{1} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}{{\delta_{1} I_{o} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}} \right) $$

$$ A_{2} = \left[ {\frac{{v_{03} n_{b3} }}{{n_{3} }}\frac{{K_{1} \left( {\frac{{r_{2} }}{{\delta_{3} }}} \right)}}{{\delta_{3} K_{o} \left( {\frac{{r_{2} }}{{\delta_{3} }}} \right)}}\left[ {\mathop {u_{1} }\limits^{\prime } \left( {r_{1} } \right)I_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right) + \frac{{u_{1} \left( {r_{1} } \right)I_{1} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right)}}{{\delta_{2} }} - \frac{{u_{1} \left( {r_{1} } \right)I_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right)I_{1} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}{{\delta_{1} I_{o} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}} \right]} \right] $$

$$ A_{3} = \left[ {\mathop {u_{2} }\limits^{\prime } \left( {r_{2} } \right)K_{o} \left( {\frac{{r_{2} }}{{\delta_{2} }}} \right) - \frac{{u_{2} \left( {r_{2} } \right)K_{1} \left( {\frac{{r_{2} }}{{\delta_{2} }}} \right)}}{{\delta_{2} }} + \frac{{u_{2} \left( {r_{2} } \right)K_{o} \left( {\frac{{r_{2} }}{{\delta_{2} }}} \right)K_{1} \left( {\frac{{r_{2} }}{{\delta_{3} }}} \right)}}{{\delta_{3} K_{o} \left( {\frac{{r_{2} }}{{\delta_{3} }}} \right)}}} \right] $$

$$ A_{4 } = \left[ {\mathop {u_{1} }\limits^{\prime } \left( {r_{1} } \right)I_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right) + \frac{{u_{1} \left( {r_{1} } \right)I_{1} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right)}}{{\delta_{2} }} - \frac{{u_{1} \left( {r_{1} } \right)I_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right)I_{1} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}{{\delta_{1} I_{o} \left( {\frac{{r_{1} }}{{\delta_{1} }}} \right)}}} \right] $$

$$ A_{5} = \left[ {\left( {\mathop {u_{2} }\limits^{\rm{\prime }} \left( {r_{1} } \right)K_{o} \left( {\frac{{r_{1} }}{{\delta_{2} }}} \right)} \right)\mathop {u_{1} }\limits^{\rm{\prime }} \left( {r_{2} } \right)I_{o} \left( {\frac{{r_{2} }}{{\delta_{2} }}} \right)} \right] $$

$$ c_{3} = \frac{{A_{1} + A_{2} }}{{ - A_{3} A_{4} + A_{5} }} $$

$$ c_{4 } = \frac{{c_{3} u_{2} \left( {r_{2} } \right)K_{o} \left( {\frac{{r_{2} }}{{\delta_{2} }}} \right) + \frac{{v_{03} n_{b3} }}{{n_{3} }}}}{{K_{o} \left( {\frac{{r_{2} }}{{\delta_{3} }}} \right)}} $$