Two Phases of the 11-Year Cycle and Parameterization of Its Shape

Abstract

Evolution of the 11-year cycle of solar activity in time can be divided into two different phases. In the first phase the activity increases rather rapidly, and in the second one it decreases more slowly. An additional property of the second phase is that the shape of the curve describing it is practically independent on the power of the cycle. We present an approximation of the 11-yr cycle shape that takes into account these features of the cycle and described by a system of simple differential equations.

1 INTRODUCTION

The search for empirical relations describing the 11-yr cycle of solar activity started as early as in the 19th century, and over the past 150 yr numerous attempts have been made to approximate the cycle shape (see, e.g., Vitinskii et al., 1986; Hathaway et al., 1994; Du, 2011; Li et al., 2017 and references within). As a rule, such attempts are of a formal mathematical character: functions with a minimum number of parameters are sought that describe the behavior of a sunspot index.

Any realistic approximation has to take into account that the shape of 11-yr cycle is asymmetric. In the ascending (“explosive”) phase of the cycle solar activity rapidly increases to a maximum, and in the descending phase (as seen below, it can be also called “the diffusive phase”) its gradually decreases. Then the next 11-yr cycle begins, and with increase of the number of sunspot of the new cycle, that of the previous one gradually tends to zero.

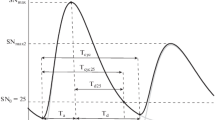
As many authors have shown (e.g. Eigenson et al., 1948; Gnevyshev and Gnevysheva, 1949; Ivanov and Miletsky, 2014; Cameron and Schüssler, 2016), the curve describing the sunspot index on the descending phase of the 11-yr cycle has an almost universal shape that weakly depends on the power of the cycle. This universality is illustrated in Fig. 1, where each of the curves corresponds to a certain cycle and shifted by time Δt_i relative to the minimum of the cycle. (Hereafter we will use the monthly averages of the recalibrated sunspot number S_N (Clette et al., 2014) for 1749–2021 smoothed by a Gaussian filter with σ = 12 months). Ivanov and Miletsky (2014) and Ivanov, (2018) demonstrated that the shifts Δt_i can be chosen in such a way that the descending parts of the curves almost merge into one.

Fig. 1.

The smoothed activity index for cycles 1–22. Time t = 0 for each cycle corresponds to its minimum. Shifts Δt_i are chosen to minimize the RMS differences between second halves of the descending branches of individual cycles.

Cameron and Schüssler (2016) showed that such behavior can be described by a simple model. The model is based on assumption that no new magnetic fields are generated on the descending phase of the cycle, while the old ones dissipate via diffusion towards the solar equator and mutual annihilation. Thus, the dynamics of the system is simplified and can be represented by a single first-order nonlinear differential equation (Cameron and Schüssler, 2016; Ivanov, 2018),

$$\frac{{dS}}{{dt}} = - \frac{A}{{{{{(S + \alpha )}}^{2}}}}S,$$

(1)

where S(t) is a sunspot index, A and α are parameters of the system. It is readily follows from the form of the equation that if S₀(t) is its solution then S₀(t – t₀) for arbitrary t₀ is also its solution. Therefore, (1) defines a family of curves of the same shape shifted along the time axis, which is consistent with behavior of the observed index.

Equation (1), which describes the evolution of the sunspot index in the descending phase of the cycle, is based on a simple model of magnetic fields diffusion. Developing this approach, it is interesting to find an approximation of the shape of the entire 11-yr cycle that reproduce its specific behavior in the two phases and is described by differential equations, which can be interpreted, at least in part, from a physical point of view. In this paper, we propose a way to implement this approach.

2 MODEL DESCRIPTION OF THE SOLAR CYCLE SHAPE

We start from a simplest lumped-parameter model that can be obtained by averaging of αω-dynamo equations over the zone of magnetic field generation (see, e.g. Priest, 1985):

$$\begin{gathered} \frac{{d{{B}_{{{\varphi }}}}}}{{dt}} = \Omega {\kern 1pt} '{{B}_{p}} - \frac{{{{B}_{{{\varphi }}}}}}{{{{\tau }_{d}}}}, \\ \frac{{d{{B}_{p}}}}{{dt}} = - \frac{{{\alpha }}}{L}{{B}_{{{\varphi }}}} - \frac{{{{B}_{p}}}}{{{{\tau }_{d}}}}, \\ \end{gathered} $$

(2)

where B_φ(t) and B_p(t) are the averaged strengths of the toroidal and poloidal magnetic fields (in arbitrary units), $\Omega {\kern 1pt} '$, α, τ_d и L are characteristic values of the differential rotation (or the difference of angular velocities of the Sun at low and high latitudes, that is the same by order of magnitude), alpha-effect, ohmic diffusion time and radial size of the generation zone correspondingly. We also set initial conditions at the moment of the start of the cycle t = 0 as

$${{B}_{\varphi }}\left( 0 \right){\text{ }} = {\text{ }}0,\,\,\,\,{{B}_{p}}\left( 0 \right){\text{ }} = {{B}_{p}}_{0}.$$

(2a)

The solutions of linear system (2) are the equations of damped oscillations of the field components with the period $T = 2\pi \sqrt {\frac{L}{{\alpha \Omega {\kern 1pt} '}}} .$

To describe both phases of the cycle one can insert into Eq. (2) functions h_i(t) that will suppress certain terms of equations at a proper time. Introducing a new parameter $\beta = \sqrt {\frac{{\Omega {\kern 1pt} 'L}}{\alpha },}$ we obtain

$$\begin{gathered} \frac{{d{{B}_{{{\varphi }}}}}}{{dt}} = {{h}_{\omega }}(t)\frac{{2\pi \beta }}{T}{{B}_{p}} - {{h}_{{\tau \phi }}}(t)\frac{{{{B}_{{{\varphi }}}}}}{{{{\tau }_{d}}}}, \hfill \\ \frac{{d{{B}_{p}}}}{{dt}} = - {{h}_{\alpha }}(t)\frac{{2\pi }}{{\beta T}}{{B}_{{{\varphi }}}} - {{h}_{{\tau p}}}(t)\frac{{{{B}_{p}}}}{{{{\tau }_{d}}}}. \hfill \\ \end{gathered} $$

(3)

To describe the two regimes of the system it is suffices to set h_ω ≈ 1 and h_τφ ≈ 0 in the ascending phase and h_ω ≈ 0 and h_τφ ≈ 1 in the descending one. To do this, we define “the supression function” $h(t;c,n) = \frac{1}{{1 + {{{(ct)}}^{n}}}}$ (where we will assume that n is integer) and set h_ω(t) = 1 – h_τφ(t) = h(t; c, n), where parameters c and n will be found below. In the general case function h_α и h_τp can also be introduced, but here we will assume that they are equal to unit.

Therefore, we have defined a set of solutions of Eqs. (3) with initial conditions (2a) and six free parameters n, τ_d, c, β, T and B_p0. It is easily seen that after substitution b_p = β B_p (3) is transformed to a form that does not contain β. Thus, for solutions of (3) the following scaling relation is valid:

$${{B}_{{{\varphi }}}}(t;n,{{\tau }_{d}},c,\beta ,T,{{B}_{p}}_{0}) = {{B}_{{{\varphi }}}}(t;n,{{\tau }_{d}},c,\beta k,T,{{B}_{p}}_{0}{\text{/}}k)$$

for any k. Therefore, we can set β to unit without loss of generality, arriving at five independent parameters n, τ_d, c, T and B_p0.

We must also choose a relation that binds the toroidal field to the observed sunspot index. The absolute value function is not good for our purpose, since we would like to obtain smooth solutions. Hence we assume that the observed sunspot index is proportional to the squared magnetic field (B_φ)². Since we do not have fixed the magnetic field units yet, here we can set the proportionality factor equal to one, so S_N = (B_φ)².

We also imply that parameters n, and τ_d, characterize the system as a whole and do not change from cycle to cycle. Therefore, the ith cycle is described by two individual parameters B_p0,i and T_i.

In Figure 2 phase diagrams and families of modeled curves are shown that describe shapes of the cycles for various sets of parameters. Plots (a) and (c) show that in the descending phase (i.e. for d(B_φ)²/dt < 0) the phase curves “clump together”, and, as expected, the dynamics of the system simplifies. The same can be seen in plots (b) and (d), where curves that describe the 11-yr cycle in the descending phase, with a certain selection of shifts Δt_i, almost coincide, i.e. have shapes that do depends upon parameters of individual cycles (compare with Fig. 1 for the observed index).

Fig. 2.

The sets of curves described by Eqs. (3) and (2a). (а) The phase diagram for variables (B_φ)² и d(B_φ)²/dt and parameters n = 4, c = 0.5 yr^–1, τ_d = 11 yr, T = 11 yr and B_p0,i = 100, 110, …, 150; (b) The corresponding shapes of cycles for shifts Δt_i = 0, 0.75, …, 4.5 yr; (c) The phase diagram for the same n, c, τ_d and T_i = 10, 11, …, 15 yr, B_p0,i = 100; (d) the corresponding shapes of cycles for shifts Δt_i = 0, (1/3)², …,(5/3)² yr.

To estimate quality of our approximation we introduce (Δ_i)²—the mean squared difference between the observed index in the ith cycle and our model. To get rid of the cycles overlapping effect, we will use a slightly modified observed index, subtracting from it the parts that correspond to residual activity of descending branches of cycles (Fig. 3).

Fig. 3.

Taking into account the overlapping effect of two successive cycles. The thin line corresponds to the asymptotics S_a(t) of the descending branch of the first cycle described by Eq. (1). The thick dashed line is the sunspot index without subtraction of S_a(t), the thick solid line—after such subtraction for the second cycle.

The problem of finding of parameters of the system can be divided into two steps. Firstly, one looks for parameters n, τ_d, c that minimize the sum of (Δ_i)² over all cycles. Secondly, one looks for B_p0,i и T_i that minimize (Δ_i)² for the ith cycle. The results of minimization (for solar cycles 2–24) are n = 4, τ_d = 5.4 yr, c = 0.13 yr^–1 and parameters for individual cycles are listed in Table 1. The observed index S_N is compared with the model one in Fig. 4.

Table 1. Parameters of individual solar cycles. S_N,max are amplitudes of cycles (for the smoothed index), T_mm are their lengths (from minimum to minimum), T and B_p0 are the best-fit parameters of the approximation, Δ and Δ_std are the RMS differences between the observed index and its approximation by our model and by the standard one correspondingly. The cycle numbers for which Δ > Δ_std are marked by asterisks

Fig. 4.

The observed index S_N (thin dotted line) and its approximation by our model (thick gray line). The digits above the cycles correspond to their numbers.

3 DISCUSSION AND CONCLUSION

It is illustrative to compare quality of our parameterization of the cycle with another two-parameter one that is commonly used for description of 11-yr cycles. As an example, we choose the parameterization by the Pearson type III distribution $A{{t}^{3}}{{e}^{{ - bt}}}$ (Vitinskii et al., 1986). The RMS differences Δ_std,i for it are also listed in Table 1. Numbers of cycles for which Δ_i > Δ_std,i is marked by asterisk. One can see that in most cases our parameterization describe the shape of the cycle better than the common one (for 18 cycles out of 23), especially in the epoch of Greenwich observations that starts from cycle 11 (for 13 cycles out of 14).

The squares of the best-fit parameters B_p0 are highly correlated with the cycle amplitudes, with the only exception of cycle 7 (Fig. 5). Slightly lower correlation is observed between cycle lengths from minimum to minimum T_mm and parameters T, again with the exception of cycles 6 and 7 (Fig. 6). Probably, the problem with cycles 6 and 7 is related to the general fact that pre-Greenwich cycles have more shape anomalies then later ones, because of greater errors in the reconstructed part of the series (Ivanov, 2020).

Fig. 5.

Relation between amplitudes of cycles S_N,max and the best-fit parameters (B_p0)². The empty circle corresponds to cycle 7. The linear correlation coefficient for all point r = 0.55, without cycle 7 r = 0.89.

Fig. 6.

Relation between the cycle lengths T_mm and the best-fit parameters T. The empty circles corresponds to cycles 6 and 7. The linear correlation coefficient for all point r = 0.27, without cycles 6 and 7 r = 0.67.

Therefore, we have built a parameterization of the 11-yr cycle shape that, being of approximately the same accuracy as other two-parameter ones, has some advantages over them. First, it naturally reproduces the division of the cycle onto “explosive” and “diffusive” phases, as well as the universal shape of the latter. Secondly, it is represented by a system of differential equations that is derived from a simple αω-dynamo model, which structure can be interpreted from physical point of view.

Dynamics of the magnetic fields B_φ and B_p in the proposed model are described by differential equations. However, it is not the case for the suppression function h_ω and h_τφ, which modulate correspondingly the processes of generation and decay of the toroidal field. They are not dynamic variables, but are given as explicit functions of time, and rather arbitrary ones. It can be regarded as a weak point of the model. One of the possible directions for its development is inclusion of a dynamic description for the suppression functions h, but it will require a clearer understanding of their physical background.