The Second Waldmeier Rule and the Form of the 11-Year Cycle

Abstract

It is known that the form of the 11-year solar-activity cycle can be approximately described by its amplitude A and the arrangement of three characteristic moments: the moment of the minimum (T_min), maximum (T_max), and the subsequent minimum (T_min2). According to the classical Waldmeier rule, there is an anticorrelation between the maximum activity value (amplitude) of cycle A and the duration of its ascending branch T_max – T_min, while the correlation between A and the length of the downward branch of the cycle T_min2 – T_max is much lower. Following Waldmeier, the moment T_V can be entered near the end of the downward branch of the cycle, in which the activity falls within a certain (low) specified level V. The relationship between the length of the corresponding phase of cycle T_V – T_max and the amplitude of this cycle is quite strong. We demonstrate that this connection, which can be called the “second Waldmeier rule,” agrees well with the fact that the downward branch of the cycle has a universal appearance. Thus, one parameter, its value is at the maximum, is enough for an approximate qualitative description of the form of a single 11-year cycle that takes into account the two Waldmeier rules.

1 INTRODUCTION

It is known that the shape of the curve describing the development of solar activity during the 11-year cycle is asymmetric. It is usually assumed that the cycle begins at the moment of minimal activity T_min; the activity quickly increases to the maximum value of A at time T_max and then decreases at a slower rate, reaching the next minimum at T_min2. Of course, sunspots of this 11-year cycle are also observed outside the range T_min – T_min2, which coexists with spots of adjacent cycles; however, this fact can usually be disregarded in the description of activity with traditional solar indices. In some approximation, the shape of the cycle is described by three parameters: its amplitude A, the length of the growth phase T_a = T_max – T_min, and the phases of decline T_d = T_min2 – T_max (Fig. 1).

Fig. 1.

Characteristic moments in the development of the 11-year solar cycle for the spot index SN. Gray curves correspond to spots of individual cycles, and black curves correspond to their sum.

These parameters, however, are not completely independent. One of the most famous connections between them is called the Waldmeier’s rule (WR) (Waldmeier, 1935), according to which the length of the growth phase of the cycle T_a anticorrelates with its amplitude A. In this paper, we analyze this and other, less well-known relations between the parameters of the 11-year cycle that determine its shape.

2 DATA

We consider four rows of average monthly spot indices: W is the traditional Wolf number (1749–2015b http://www.sidc.be/silso/DATA/ARCHIVE/V1.0/ monthssn.dat), SN is the alternative recalibrated index of the sunspot number according to WDC-SILSO (1749–2018) (http://www.sidc.be/silso/DATA/SN_ m_tot_V2.0.txt), G is the number of groups in the extended Greenwich catalog (1874–2016) (http://solarscience.msfc.nasa.gov/greenwch.shtml), and GSN is the Group Sunspot Number index (1750–1995) (Hoyt and Schatten, 1998).

3 EXPRESSION OF WALDMEIER’S RULE IN VARIOUS INDICES

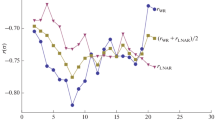
As a measure of WR expression, it is convenient to use the correlation coefficient between the length of the growth phase and the amplitude of the cycle r_wr = r (T_a, A). This coefficient varies for different indices and types of averaging. Figure 2 shows the dependence of r_wr on the scale of averaging L for the series of monthly spot indices W, SN, G and GSN smoothed by the running average for L months. With annual smoothing, the WR expression in the W and SN indices is high (r ≈ –0.8), while it is significantly lower in the indices related to the number of G and GSN groups. Interestingly, with increasing L, the WR expression decreases. It increases again with a smoothing scale of 40–50 months (r < –0.7), while it is most pronounced for the G index.

Fig. 2.

Expression of the Waldmeier rule r_wr = r(T_a, A) for different indices and averaging scales L.

4 RELATIONSHIP OF CYCLE AMPLITUDE WITH ITS BRANCH LENGTHS

Figure 2 shows that, from the point of view of the WR expression, the W and SN series differ only slightly; for a more detailed study, we choose the monthly SN index for 1749–2018 and the near-year smoothing scale L = 13 months, which approximately correspond to the first minimum r_wr on the corresponding curve (Fig. 2). For this scale, r_wr = ‒0.77, and the amplitude of the cycle is related to the length of the growth phase by linear regression

$${\text{S}}{{{\text{N}}}_{{{\text{max}}}}} = 347 - 38.1{\kern 1pt} {{{\text{T}}}_{{\text{a}}}}$$

((1))

(Fig. 3a).

Fig. 3.

Relationship between the lengths of the phases of the 11-year cycle and its amplitude for the smoothed monthly mean SN index. Charts (a) and (e) comply with the first and second Waldmeier rules.

It is known (e.g., Vitinsky et al., 1986) that the length of the decay phase and the full length of the cycle T_cyc = T_a + T_d with respect to the amplitude is much weaker than for WR. Indeed, r(T_dSN_max) = +0.39 (Fig. 3b) and r (T_cycSN_max) = ‒0.30 (Fig. 3c).

Such a difference in the strength of the relationship of the lengths of different phases of a cycle with its amplitude fits well with Waldmeier’s “eruptive hypothesis” (Waldmeier, 1935). According to Waldmeier, the sequence of 11-year cycles is a series of relatively independent activity “eruptions.” The activity index in each of them increases rapidly and then gradually decreases to zero. Thus, it makes sense to talk about the beginning of a given activity eruption (near T_min) and its maximum T_max, but its second minimum is obviously at infinity. The moments of the activity-index minima are determined via the superposition of the descending branch of the old and ascending branches of the new cycle and may be, generally speaking, related to the characteristics of both eruptions.

Following Waldmeier (1935), the moment at which the activity level falls to the threshold value of the average monthly Wolf number W = 7.5 (let us denote this moment T_7.5) can be used as a characteristic of the decay branch that is not related to the properties of neighboring cycles. Waldmeier drew attention to the fact that the value of T_7.5 – T_max correlates well with the cycle length. Using the smoothed average monthly SN index, choosing the threshold SN₀ = 25, and designating the corresponding time T₂₅ for the interval T_d25 = T₂₅ – T_max, we get the correlation r(T_d25SN_max) = +0.72 and regression

$${\text{S}}{{{\text{N}}}_{{{\text{max}}}}} = 32.8 + 28.4{{{\text{T}}}_{{{\text{d}}25}}}$$

((2))

(Fig. 3e).

Since moment T₂₅ is located near the cycle minimum T_min2 (although it does not coincide with it: on average, T₂₅ is at least 1.4 ± 1.0 years ahead of the minimum), the value of T_d25 can be considered an alternative “end-of-cycle marker.” The relationship between the “alternative length of the branch decay” T_d25 = T₂₅ – T_max and the cycle amplitude will be referred to below as the “second Waldmeier rule” (PW2).

Table 1 shows the correlations between the lengths of the various phases of the cycle and its amplitude. In addition to the already introduced notation, the amplitude of the next cycle SN_max2, the cycle length T_cyc = T_min2 – T_min = T_a + T_d, and the “alternate cycle length” T_cyc25 = T₂₅ – T_min = T_a + T_d25 are used (Fig. 1). Strong bonds are highlighted (r > 0.65) in bold type in Table 1. In addition to WR and WR2, these include the anticorrelation between the length of a given cycle and the amplitude of the following: r(T_cycSN_max2) = ‒0.69 (Fig. 3d). The corresponding regression is

$${\text{S}}{{{\text{N}}}_{{{\text{max}}}}} = 530 - 31.7{{{\text{T}}}_{{{\text{cyc}}}}}.$$

((3))

Apparently, this curious correlation was clearly noted for the first time only in the 1990s (Hathaway et al, 1994). As expected, the connections between the interval lengths T_d and T_d25, as well as T_cyc and T_cyc25, are also strong. Note also that, due to the different sign of the correlations T_a and T_d25 with the amplitude of the cycle, the sum of these lengths T_cyc25 = T₂₅ – T_min correlates with the latter very weakly: r(T_cyc25SN_max) = +0.17 (Fig. 3f).

Table 1.   Correlations between the various parameters of the 11-year cycle (see notation in Fig. 1)

5 SECOND WALDMEYER RULE AND UNIVERSAL FORM OF THE DESCENDING BRANCH OF A CYCLE

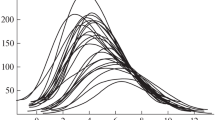
It was shown (Cameron and Schüssler, 2016; Ivanov, 2018) that the descending branches of the 11-year cycle are well approximated by a curve with a shape that does not depend on the cycle height, and the entire dependence on the latter consists of the individual shift of this curve along the time axis. This fact is illustrated in Fig. 4, in which the cyclic curves (thin lines) are shifted so that the parts of the curves corresponding to their decay phase overlap each other and the universal curve (bold line) is given by the equation (Ivanov, 2018)

$$A({{t}_{0}} - t) = {{\alpha }^{2}}\log {\text{SN}} + 2\alpha {\text{SN}} + {{{\text{S}}{{{\text{N}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{\text{S}}{{{\text{N}}}^{{\text{2}}}}} 2}} \right. \kern-0em} 2},$$

((4))

where A = 4.17 × 10⁴ year^–1, α = 248, and t₀ = 14.8 years.

Fig. 4.

Universality of the form of the downstream branch of the 11-year cycle for the SN index (1749–2018). Thin lines correspond to individual cycles, each of which is shifted along the time axis so that its descending branch is close to the universal curve (bold line) given by equation (4).

Note that any point can be selected as a measure of branch decline on that part of the descending branch, which is universal for all cycles (it starts about two to three years from the maximum). If we chose as a threshold not SN₀ = 25 but another value related to the area common for all cycles, it would shift all points T_SN0 approximately the same distance and would have almost no effect on the magnitude of the correlations shown in Table 1.

It is easy to understand that WR2 follows directly from the universality of the shape of the declining branch. In fact, the higher the cycle is, the higher is the activity at which the universal part of the decay branch begins (Fig. 4) and the longer is the period between the maximum and the moment at which the activity falls to a predetermined value. Note that, if the shape of the decay branch strongly depended on the cycle amplitude, then the relationship described by WR2 would, in general, be destroyed.

6 CONCLUSIONS

As shown above, three characteristic points can be identified in the development of the 11-year cycle: the minimum T_min, the maximum T_max, and the “end-of-cycle marker” T₂₅—the moment of a reduction of activity to the level of SN₀ = 25. The intervals between these moments are strongly associated with the cycle amplitude: the length of the growth branch T_a = T_max – T_min anticorrelates with the maximum cycle value (the first WR, r(T_aSN_max) = –0.77 for monthly values, smoothed with an annual scale), and the length of the “alternative branch of decline” T_d25 = T_max – T₂₅ correlates with this value (the second WR, r (T_d25SN_max) = +0.72). Moment T₂₅ is close to the moment of the second minimum T_min2, but, unlike the latter, it is determined only by the properties of this cycle and not by the details of its imposition on the subsequent one. Such properties of moment T₂₅ is associated with the universality of the form of the descending branch of the 11-year cycle.

Thus, for a rough description of the form of a single 11-year cycle, it is sufficient to know its amplitude SN_max, while the length of the cycle branches T_a and T_d25 is approximately reconstructed by the two Waldmeier rules with regressions (1) and (2).

The position of T_min2 between the given cycle and the next one and the cycle length defined by this moment T_cyc is more closely related to the characteristics of the next cycle than the current one. This picture fits well with Waldmeier’s “eruptive hypothesis,” according to which solar cyclicity is considered to be a sequence of relatively independent eruptions.