Asymmetric Self-Similar Viscous Gas Flows in a Wedge

Abstract

The flow of a viscous compressible gas from the apex of a flat wedge is considered. It is shown that an asymmetric self-similar flow is possible and is realized when special boundary conditions for the temperature of the channel walls are specified. For the case of low subsonic gas-flow velocities at constant but different temperatures of the wedge walls, an asymptotic solution is found. In the general case, the resulting system of ordinary differential equations is solved numerically.

1 INTRODUCTION

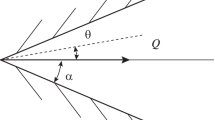
The well-known Jeffery–Hamel exact solution of the Navier–Stokes equations for the case of a viscous incompressible fluid describes a self-similar flow in a flat wedge-shaped diffuser from a source/sink located at the apex of the wedge [1, 2]. In the case of a confusor flow (sink), the solution exists for any Reynolds numbers $\operatorname{Re}$ and an arbitrary wedge-opening angle $2\alpha < \pi$ and is symmetric with respect to the plane θ = 0 (Fig. 1). In the case of a diffuser flow, the velocity profile in the transverse direction upon reaching a certain critical number $\operatorname{Re} = {{\operatorname{Re} }_{{\max }}}$ turns out to be nonmonotonic. With increasing number $\operatorname{Re} > {{\operatorname{Re} }_{{\max }}}$, reverse flow regions appear and the velocity profile can become asymmetrical. With a further increase in Re, a symmetric solution with one minimum and two velocity maxima arises. In all these solutions, there are alternating outflow and inflow regions. As $\operatorname{Re} \to \infty$, an increase in the number of local minima and maxima is observed; therefore, there is no definite limiting solution, which, apparently, is due to the fact that, with an increase in $\operatorname{Re}$, the steady diffuser flow of the described type, soon after reaching a certain critical value, becomes unstable and, in fact, unsteady turbulent motion takes place [3].

Fig. 1.

Scheme of a flow in a flat wedge.

For incompressible flows, in [4], a wide class of known and new exact solutions of the Navier–Stokes equations are described, in particular, the well-known Jeffery–Hamel solution for the flow of a viscous incompressible fluid in a flat diffuser.

The possibility of constructing Jeffery–Hamel-type self-similar flows of a viscous compressible gas is discussed in [5–13]. In [5], the problem of a viscous gas flow in a conical diffuser with slip boundary conditions on the walls was considered. In [6, 7], the problem of gas flow in a conical diffuser in the presence of an internal volume source/sink of energy inside the flow was also considered. Other axisymmetric self-similar solutions of the Navier–Stokes equations for viscous gas flows were obtained in [8, 9].

In [10, 11], a class of self-similar solutions for a gas flow in a flat wedge is considered. In particular, [10] considers the flow of a gas of hard spheres and Maxwellian molecules with dynamic viscosity coefficients $\eta \sim {{T}^{{0.5}}}$ and $\eta \sim T$, respectively. In [11], an analytical solution was found for an arbitrary power-law temperature dependence of the transport coefficients, $\eta \sim {{T}^{k}}$ (the Frost law). In [12], an analogous self-similar flow of a viscous compressible gas from a jet (impulse source) flowing into the region between two divergent walls was considered. The exact solution of the Navier–Stokes equations for Couette and Poiseuille flows of hot gas with a viscosity coefficient depending on temperature according to Sutherland’s law was obtained in [13, 14].

In recent paper [15], it was established that a self-similar solution also exists for a viscous gas flow for which the transport coefficients depend arbitrarily on temperature, $\eta = \eta (T)$. In all the above-cited works devoted to self-similar flows of a viscous gas, only symmetric-flow regimes are considered.

In this paper, we study analytically and numerically the possibility of constructing Jeffery–Hamel-type asymmetric self-similar solutions for flows of a viscous compressible heat-conducting gas in a flat diffuser.

2 JEFFERY–HAMEL-TYPE SELF-SIMILAR FLOWS

We consider the flow of a viscous gas from the apex of a flat wedge at different wall temperatures $T_{w}^{ + }$ and $T_{w}^{ - }$ (Fig. 1).

The Navier–Stokes equations in polar coordinates (r, θ) (Fig. 1), written in dimensionless variables, have the form [16]:

$$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\rho u} \right) = 0,$$

(2.1)

$$\rho u\frac{{\partial u}}{{\partial r}} = - \frac{{\partial p}}{{\partial r}} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{rr}}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{r\theta }}}}}{{\partial \theta }} - \frac{{{{\sigma }_{{\theta \theta }}}}}{r}} \right],$$

(2.2)

$$0 = - \frac{1}{r}\frac{{\partial p}}{{\partial \theta }} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{r\theta }}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{\theta \theta }}}}}{{\partial \theta }} + \frac{{{{\sigma }_{{r\theta }}}}}{r}} \right],$$

(2.3)

$$\begin{gathered} \frac{{\rho u}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}}}\frac{{\partial T}}{{\partial r}} = u\frac{{\partial p}}{{\partial r}} + \frac{{\nabla \cdot \left( {\varkappa \nabla T} \right)}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr {{{\operatorname{Re} }}_{0}}}} \\ + \;\frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {2\eta (\varepsilon _{{rr}}^{2} + \varepsilon _{{\theta \theta }}^{2}) + 4\eta \varepsilon _{{r\theta }}^{2} - \frac{2}{3}\eta {{{\left( {\nabla \cdot {\mathbf{V}}} \right)}}^{2}}} \right]. \\ \end{gathered} $$

(2.4)

The flow is assumed to be radial, ${\mathbf{V}} = (u,\,0)$. The components of the viscous stress tensor σ and strain rate tensor ε have the form

$${{\sigma }_{{rr}}} = \eta {{\varepsilon }_{{rr}}} - \frac{2}{3}\eta \frac{1}{r}\frac{\partial }{{\partial r}}\left( {ru} \right),\quad {{\sigma }_{{\theta \theta }}} = \eta {{\varepsilon }_{{\theta \theta }}} - \frac{2}{3}\eta \frac{1}{r}\frac{\partial }{{\partial r}}\left( {ru} \right),\quad {{\sigma }_{{r\theta }}} = \eta {{\varepsilon }_{{r\theta }}},$$

$${{\varepsilon }_{{rr}}} = 2\frac{{\partial u}}{{\partial r}},\quad {{\varepsilon }_{{r\theta }}} = \frac{1}{r}\frac{{\partial u}}{{\partial \theta }},\quad {{\varepsilon }_{{\theta \theta }}} = \frac{{2u}}{r}.$$

In Eqs. (2.1)–(2.4), the dimensionless variables are related to the dimensional gas-dynamic parameters, marked with an asterisk, as follows:

$$\rho = \frac{{\rho {\text{*}}}}{{{{\rho }_{0}}}},\quad p = \frac{{p{\text{*}}}}{{{{\rho }_{0}}u_{0}^{2}}},\quad T = \frac{{T{\text{*}}}}{{{{T}_{0}}}},\quad u = \frac{{u{\text{*}}}}{{{{u}_{0}}}},\quad \eta = \frac{{\eta {\text{*}}}}{{{{\eta }_{0}}}},\quad \kappa = \frac{{\kappa {\text{*}}}}{{{{\kappa }_{0}}}},$$

where ${{\rho }_{0}}$, ${{u}_{0}}$, ${{T}_{0}}$, ${{\eta }_{0}}$, and ${{\kappa }_{0}}$ are, respectively, the density, velocity, temperature, viscosity coefficient, and thermal conductivity at some point $({{r}_{0}},\,0)$ on the axis of the wedge. The gas is considered ideal, so that $\gamma {\text{M}}_{0}^{2}p = \rho T$. The Mach number M₀, the Reynolds number Re₀, and the Prandtl number Pr are calculated according to the rules:

$${{\operatorname{Re} }_{0}} = \frac{{{{\rho }_{0}}{{u}_{0}}{{r}_{0}}}}{{{{\eta }_{0}}}},\quad {{{\text{M}}}_{0}} = \frac{{{{u}_{0}}}}{{\sqrt {\gamma R{{T}_{0}}} }},\quad \Pr = \frac{{{{c}_{p}}{{\eta }_{0}}}}{{{{\kappa }_{0}}}}.$$

Energy equation (2.4) takes into account the terms responsible for the dissipation of energy due to viscosity. As will be shown below, at moderate M₀, the Reynolds number in the self-similar solution turns out to be small, i.e., the viscosity and energy dissipation affect the entire flow field inside the wedge.

The self-similar solution of Eqs. (2.1)–(2.4) is sought in the form:

$$u{\kern 1pt} \; = \frac{{u(\theta )}}{{{{r}^{m}}}},\quad \rho = {{r}^{{m - 1}}}\rho (\theta ),\quad p = \frac{{p(\theta )}}{{{{r}^{{m + 1}}}}},\quad T = \frac{{T(\theta )}}{{{{r}^{{2m}}}}},\quad \eta = {{\left( {\frac{{T(\theta )}}{{{{r}^{{2m}}}}}} \right)}^{k}},\quad \varkappa = {{\left( {\frac{{T(\theta )}}{{{{r}^{{2m}}}}}} \right)}^{k}}.$$

(2.5)

The exponent m will be called the self-similarity parameter. As shown earlier in [9–11], the existence of planar self-similar solutions necessitates the following condition:

$$mk = 0.$$

The existence of self-similar solutions for k = 0 and different m, depending on the defining parameters of the problem for the case of symmetric plane flows, was studied in [9]. Gas flows for m ≠ 0 are more difficult to study. The solution in this case reduces to the analysis of a system of nonlinear differential equations with a previously unknown self-similarity parameter m, which must be determined in the course of numerical solution of the problem.

In this paper, we consider another case: namely, of $k \ne 0$ and m = 0. It was found in [15] that, in this case, a self-similar solution can be constructed for an arbitrary temperature dependence of the transfer coefficients. Below, when studying asymmetrical solutions, for definiteness, we assume a power dependence $\eta \sim {{T}^{k}}$.

3 SELF-SIMILAR GAS FLOW IN A WEDGE AT DIFFERENT WALL TEMPERATURES

To obtain asymmetric solutions, the temperatures of the wedge walls will be considered different, but constant. Substituting (2.5) into (2.1)–(2.4), it is easy to check that continuity equation (2.1) is fulfilled automatically and Eqs. (2.2)–(2.4) can be rewritten in the form of a system of ordinary differential equations (ODEs):

$${{\operatorname{Re} }_{0}}p - \frac{4}{3}u\eta + \frac{d}{{d\theta }}\left( {\eta \frac{{du}}{{d\theta }}} \right) = 0,$$

(3.1)

$${{\operatorname{Re} }_{0}}\frac{{dp}}{{d\theta }} = \eta \frac{{du}}{{d\theta }} + \frac{4}{3}\frac{d}{{d\theta }}\left( {\eta u} \right),$$

(3.2)

$${{\operatorname{Re} }_{0}}up = \frac{1}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr }}\frac{d}{{d\theta }}\left( {\eta \frac{{dT}}{{d\theta }}} \right) + \eta \left[ {\frac{4}{3}{{u}^{2}} + {{{\left( {\frac{{du}}{{d\theta }}} \right)}}^{2}}} \right],$$

(3.3)

with no-slip boundary conditions for velocity and a given temperature on the wedge walls:

$${{\left. u \right|}_{{\theta = \pm \alpha }}} = 0,\quad {{\left. T \right|}_{{\theta = \pm \alpha }}} = T_{w}^{ \pm }.$$

From the normalization condition for the flow parameters on the wedge axis, at θ = 0, we have:

$$u(0) = 1,\quad T(0) = 1,\quad p(0) = \frac{1}{{\gamma {\text{M}}_{0}^{2}}}.$$

(3.4)

We differentiate Eq. (3.1) with respect to θ and subtract it from (3.2). As a result, we get the following equation:

$$\eta \frac{{du}}{{d\theta }} + \frac{{{{d}^{2}}}}{{d{{\theta }^{2}}}}\left( {\eta \frac{{du}}{{d\theta }}} \right) = 0,$$

the solution of which has the form

$$\eta \frac{{du}}{{d\theta }} = a\sin \theta + b\cos \theta ,$$

(3.5)

where a and b are some constants. Replacing in (3.1) the expression $\eta du{\text{/}}d\theta$ by the right side of Eq. (3.5), we obtain

$${{\operatorname{Re} }_{0}}p = \frac{4}{3}\eta u - a\cos \theta + b\sin \theta .$$

(3.6)

Using normalization conditions (3.4), we relate the constant a to the numbers M₀ and Re₀:

$$a = \frac{4}{3} - \frac{{{{{\operatorname{Re} }}_{0}}}}{{\gamma {\text{M}}_{0}^{2}}}$$

We substitute (3.5) and (3.6) into energy equation (3.3) and integrate once with respect to θ. As a result, we get the following expression:

$$\frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\eta \frac{{dT}}{{d\theta }} + au\sin \theta + bu\cos \theta = Q,$$

which, taking into account (3.5), can be rewritten as

$$\frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\eta \frac{{dT}}{{d\theta }} + \eta u\frac{{du}}{{d\theta }} = Q,$$

(3.7)

where Q is some constant.

Using expression (3.7), it is possible to determine the specific heat flux through the channel walls in the azimuthal direction:

$${{\left. {q_{\theta }^{ * } = - \frac{{\kappa {\text{*}}}}{{r{\text{*}}}}\frac{{dT{\text{*}}}}{{d\theta }}} \right|}_{{\theta = \pm \alpha }}}.$$

(3.8)

We introduce the dimensionless heat flux ${{q}_{\theta }} = q_{\theta }^{ * }{{r}_{0}}{\text{/}}{{\kappa }_{0}}{{T}_{0}}$ and rewrite (3.8) in the following form:

$${{\left. {{{q}_{\theta }} = - \frac{\kappa }{r}\frac{{dT}}{{d\theta }}} \right|}_{{\theta = \pm \alpha }}}.$$

Then, using (3.7) and taking into account that, in the dimensionless variables $\eta = \kappa$, we obtain

$${{q}_{\theta }} = - \frac{Q}{r}{\text{M}}_{0}^{2}\Pr (\gamma - 1),$$

(3.9)

where e_θ is the unit azimuthal vector. It can be seen from relation (3.9) that the constant Q is proportional to the heat flux through the wedge walls. It also follows from (3.9) that the absolute value of the heat flux through the lower and upper wedge walls is the same. In this case, if $Q > 0$, then heat is supplied to the upper wall and removed from the lower wall.

The equality of the values of the heat fluxes through the wedge walls is explained by the fact that, in a self-similar flow, the energy flux in the radial direction is absent, since, for m = 0, as follows from (2.5), the temperature does not depend on $r$: $T = T(\theta )$. Thus, in the solution obtained, the transfer of thermal energy is observed only in the azimuthal direction. We note that, since there is no transfer of another type of energy in the azimuthal direction, the equality of heat fluxes is due to the energy-conservation law.

4 ANALYTICAL SOLUTION FOR THE CASE OF LOW SUBSONIC GAS-FLOW VEOCITIES IN A WEDGE

Let us introduce the dimensionless parameter $\chi = {\text{M}}_{0}^{2}\Pr \left( {\gamma - 1} \right)$ and consider the limiting case $\chi \ll 1$, corresponding to low subsonic gas-flow velocities in a wedge. Obviously, the solution of the problem depends on the value of the heat flux Q. To obtain a clear result on the effect of the temperature difference of the wedge walls on the symmetry of the solution, we consider the case of a strong heat flux, $Q \sim 1{\text{/}}\chi \gg 1$.

The solution of Eqs. (3.5) and (3.7) will be sought in the form of power series in the small parameter χ:

$$u = {{u}^{0}} + \chi {{u}^{1}} + ...,\quad T = {{T}^{0}} + \chi {{T}^{1}} + ....$$

In what follows, we will assume that the derivatives $du{\text{/}}d\theta$ and $dT{\text{/}}d\theta$ are bounded everywhere in the flow region. Then, in the zero approximation, we obtain the following system of equations:

$${{\eta }^{0}}\frac{{d{{u}^{0}}}}{{d\theta }} = a\sin \theta + b\cos \theta ,$$

(4.1)

$${{\eta }^{0}}\frac{{d{{T}^{0}}}}{{d\theta }} = {\rm X},$$

(4.2)

where ${\rm X} = Q\chi \sim O(1)$. For a given dependence ${{\eta }^{0}} = {{\eta }^{0}}({{T}^{0}})$, the solution of Eq. (4.2) under normalization conditions (3.4) takes the form:

$${\rm N}({{T}^{0}}) = \theta {\rm X},\quad {\rm N}({{T}^{0}}) = \int\limits_1^{{{T}^{0}}} {{{\eta }^{0}}\left( T \right)dT} .$$

(4.3)

Hence, the temperatures $T_{w}^{ + }$ and $T_{w}^{ - }$ on the wedge walls, the half-opening angle α, and the heat flux ${\rm X}$ in the zero approximation are related as

$${\rm N}(T_{w}^{ + }) = \alpha {\rm X},\quad {\rm N}(T_{w}^{ - }) = - \alpha {\rm X}.$$

From Eqs. (4.1) and (4.2), taking into account relations (4.3), we obtain the following differential equation:

$$\frac{{d{{u}^{0}}}}{{d{{T}^{0}}}} = \frac{a}{{\rm X}}\sin \left( {\frac{{{\rm N}\left( {{{T}^{0}}} \right)}}{{\rm X}}} \right) + \frac{b}{{\rm X}}\cos \left( {\frac{{{\rm N}\left( {{{T}^{0}}} \right)}}{{\rm X}}} \right),$$

the solution of which under normalization conditions (3.4) takes the form

$${{u}^{0}}({{T}^{0}}) = \frac{a}{{\rm X}}\int\limits_1^{{{T}^{0}}} {\sin \left( {\frac{{{\rm N}\left( T \right)}}{{\rm X}}} \right)dT} + \frac{b}{{\rm X}}\int\limits_1^{{{T}^{0}}} {\cos \left( {\frac{{{\rm N}\left( T \right)}}{{\rm X}}} \right)dT} + 1.$$

The constants a and b are determined from the no-slip boundary conditions on the wedge walls. Using the wall temperatures $T_{w}^{ + }$ and $T_{w}^{ - }$, these conditions can be written as:

$$\begin{array}{*{20}{c}} {\frac{a}{{\rm X}}\int\limits_1^{T_{w}^{ + }} {\sin \left( {\frac{{{\rm N}\left( T \right)}}{{\rm X}}} \right)dT} + \frac{b}{{\rm X}}\int\limits_1^{T_{w}^{ + }} {\cos \left( {\frac{{{\rm N}\left( T \right)}}{{\rm X}}} \right)dT} = - 1,} \\ {\frac{a}{{\rm X}}\int\limits_{T_{w}^{ - }}^1 {\sin \left( {\frac{{{\rm N}\left( T \right)}}{{\rm X}}} \right)dT} + \frac{b}{{\rm X}}\int\limits_{T_{w}^{ - }}^1 {\cos \left( {\frac{{{\rm N}\left( T \right)}}{{\rm X}}} \right)dT} = 1.} \end{array}$$

Let us consider the case of the power dependence ${{\eta }^{0}} = {{({{T}^{0}})}^{k}}$. Then, integral (4.3) takes the form:

$${{T}^{0}} = {{\left( {1 + \left( {k + 1} \right){\rm X}\theta } \right)}^{{\frac{1}{{k + 1}}}}}.$$

(4.4)

Using this expression, we can find the solution of Eq. (4.1) in quadratures:

$${{u}^{0}}(\theta ) = a\int\limits_0^\theta {\frac{{\sin \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } + b\int\limits_0^\theta {\frac{{\cos \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } + 1.$$

(4.5)

Here, we took into account normalization conditions (4.3). The constants a and b are determined from the following relations:

$$\begin{array}{*{20}{c}} {a\int\limits_0^\alpha {\frac{{\sin \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } + b\int\limits_0^\alpha {\frac{{\cos \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } = - 1,} \\ {a\int\limits_{ - \alpha }^0 {\frac{{\sin \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } + b\int\limits_{ - \alpha }^0 {\frac{{\cos \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } = 1.} \end{array}$$

In a special case of the model of a gas of super-hard particles (k = 0), solutions (4.4) and (4.5) take a simple form:

$${{T}^{0}} = 1 + {\rm X}\theta ,\quad {{u}^{0}} = \frac{{\cos \alpha - \cos \theta }}{{\cos \alpha - 1}},$$

(4.6)

which implies that the velocity profile is symmetrical. The resulting expression coincides with the solution found earlier in [11, 15], where, in particular, the case of a symmetrical gas flow with constant transfer coefficients, k = 0, was considered. The model of a gas of super-hard particles was encountered in works on kinetic theory (see [17]). This model is based on the assumption that the differential scattering cross section increases in direct proportion to the relative velocity of the colliding particles. Despite the indicated nonphysical behavior of the scattering cross section, this model proved to be extremely useful in constructing exact solutions of the Boltzmann equation [18–20].

A comparison of the symmetrical (4.6) and asymmetrical velocity profiles in the zero approximation for the flow of a monatomic gas of Maxwellian molecules (k = 1) [21] in a wedge with a half-opening angle α = 0.4 rad at X = 1 is shown in Fig. 2.

Fig. 2.

Comparison of self-similar solutions: (solid line) asymmetric velocity profile and (dashed line) symmetric velocity profile.

5 NUMERICAL STUDY OF ASYMMETRIC SOLUTIONS AT DIFFERENT MACH NUMBERS OF A GAS FLOW ON THE WEDGE AXIS

For an arbitrary Mach number, the system of equations (3.5) and (3.7) cannot be studied analytically; therefore, to obtain solutions, a numerical study of the problem is required. For convenience and simplicity of the numerical calculation, instead of solving the boundary-value problem with given parameters (angle α, wall temperatures $T_{w}^{ + }$ and $T_{w}^{ - }$, and numbers M₀ and Re₀), the Cauchy problem is solved with initial conditions on the wedge axis for velocity, $u(0) = 1$, and temperature, $T(0) = 1$, in the regions $\theta > 0$ and $\theta < 0$; the numbers M₀, Re₀, and Q are assumed to be given. In the course of numerical integration, the opening angle $2\alpha$ is found from the condition that the velocity on the channel walls is zero: $u(\theta _{w}^{ + }) = u(\theta _{w}^{ - })$ = 0, $2\alpha = \theta _{w}^{ + } - \theta _{w}^{ - }$, where $\theta _{w}^{ + }$ and $\theta _{w}^{ - }$ are the azimuthal coordinates on the upper and lower walls, respectively. The wall temperature is determined as a result of numerical integration at a given value of the heat flux Q: $T_{w}^{ \pm } = T(\theta _{w}^{ \pm })$.

Below are the results of numerical calculations for the flow of monatomic helium at γ = 5/3 and Pr = 2/3 with k = 1. A comparison of the velocity and temperature profiles at ${{{\text{M}}}_{0}} = 1.5$ and ${{\operatorname{Re} }_{0}} = 1000$ for Q = 8 in the asymmetric case and Q = 0 in the symmetric case is shown in Figs. 3 and 4. We note that a noticeable difference from the symmetry of the flow manifests itself at a sufficiently large temperature difference on the channel walls.

Fig. 3.

Velocity profiles: (solid line) symmetric profile and (dashed line) asymmetric profile.

Fig. 4.

Temperature profiles: (solid line) symmetric profile and (dashed line) asymmetric profile.

Based on the systematic calculations carried out, it can be concluded that a self-similar asymmetric flow exists only in a limited range of Q. It turns out that, at a certain limiting value Q_max, the temperature on one of the wedge walls is zero. The dependence of the quantity ${{{\rm X}}_{{\max }}} = {{Q}_{{\max }}}{\text{M}}_{0}^{2}\Pr (\gamma - 1)$, which is proportional to the dimensionless heat flux through the wedge walls, on the Mach number M₀ on the axis is shown in Fig. 5 for different opening angles $2\alpha = 0.2$, $0.4$, and 0.6 rad.

Fig. 5.

X_max vs. M₀: (1) $\alpha \approx 0.1$, (2) $0.2$, and (3) $0.3$ rad.

As can be seen from Fig. 5, with an increase in M₀, the maximum possible heat flux increases. This is explained by the fact that, with increasing M₀, the temperature increases on one of the channel walls and, therefore, the temperature difference increases. With an increase in the opening angle, the temperature difference decreases.

CONCLUSIONS

Within the framework of the Navier–Stokes equations, the possibility of constructing asymmetric Jeffery–Hamel-type exact solutions for a viscous compressible gas flow in a flat wedge has been established. For the power-law temperature dependence of the transfer coefficients, it has been shown that an asymmetric self-similar flow is realized at different temperatures of the lower and upper walls of the wedge. In the solution obtained, the transfer of thermal energy takes place only in the azimuthal direction and the total heat flux through the wedge walls turns out to be zero. An analytical solution has been found for the case of low subsonic gas-flow velocities.

The resulting solution has a very special form: the flow velocity turns out to be radial and constant for the stream lines θ = const, the temperature is also constant for the stream lines, and the density and pressure decrease in inverse proportion to the distance from the apex of the wedge. A similar behavior of the solution was observed earlier in [10, 11, 15] when constructing self-similar solutions of the stationary Navier–Stokes equations for a viscous heat-conducting gas for a mass source and in [12] for an impulse source.

It is known [22] that self-similar solutions describe not only the behavior of physical systems under certain special conditions, but also the intermediate asymptotic behavior of solutions to broader classes of problems in the region where these solutions cease to depend on the details of the initial and/or boundary conditions, but the system is still far from the limit state. This means that the solution obtained describes not only the physically unrealizable flow field from a point source into infinite space. It also describes the real flow field that arises in a finite region of size D if outflow with a given flow rate issues not from a point, but from a finite region $d \ll D$. In this case, the self-similar solution will be valid at distances much larger than d and, at the same time, much smaller than D.