1 INTRODUCTION

Since the second half of the 20th century, increased interest has been observed worldwide in investigations of flows of fluids and gases in the “microdevices” used in various technical wares, for example, in ink-jet printers [1–3], as well as in some medical and chemical technological processes, such as gas chromatography [4–6]. Flow sensors, pressure control valves, separators, chemical sensors, etc., are such microdevices. Flows in micronozzles have been studied experimentally on the basis of the engineering approach [7, 8].

The self-similar solutions of the Navier–Stokes equations for the flow of a viscous compressible gas from a mass source in flat and axisymmetric divergent conical diffusers were studied theoretically for the first time in [9–12]. Axisymmetric flows in a cone with impermeable walls with slipping conditions for the velocity and temperature at the wall were studied in [9]. Flows in the axisymmetric and flat channels with the gas mass outlet at the wall were studied in [10–12].

For incompressible flows [13], a description has been presented for a wide class of known and new exact solutions of the Navier–Stokes equations, in particular, for the known Jeffry–Gamel solution for the flow of a viscous incompressible fluid in a flat diffuser.

The flow in the wedge has been considered under the condition of an adiabatic wall [14, 15], and it was shown that the self-similar solutions satisfying the condition of continuum are realized in the channels with small opening angles. The Reynolds number at the wedge axis proves to be not large, which corresponds to the flows of a strongly rarefied gas or gas flows in the microchannels under normal conditions. Analytical solutions are found [15] for the flow in a flat channel with the coefficients of dynamic viscosity η and heat conductivity \(\kappa \) depending on temperature according to the Frost power law (\(\eta ,\;\kappa \propto {{T}^{k}}\)). An analogous self-similar flow of a viscous compressible gas from a stream (the momentum source) that flows to the region between two splay walls was considered in [16].

In this work, an exact self-similar solution was obtained to the equations of motion of a viscous heat-conducting gas in a flat wedge-shaped channel at an arbitrary dependence of the transfer coefficients on temperature. The analytical solutions obtained are compared with those obtained earlier for the power dependence of the transfer coefficients on temperature. For the gas flows in the micronozzles, the self-similar solutions obtained in this work were compared with the results of experiments performed by other authors.

2 SELF-SIMILAR FLOWS

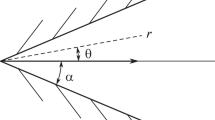
Let us consider the flow of a viscous gas from the apex of a flat wedge (Fig. 1).

Fig. 1.
figure 1

Scheme of flow in the flat wedge.

Full size image

The equations of motion in polar coordinates (r, θ) have the form [17]

$$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\rho u} \right) = 0,$$
(2.1)
$$\rho u\frac{{\partial u}}{{\partial r}} = - \frac{{\partial p}}{{\partial r}} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{rr}}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{r\theta }}}}}{{\partial \theta }} - \frac{{{{\sigma }_{{\theta \theta }}}}}{r}} \right],$$
(2.2)
$$0 = - \frac{1}{r}\frac{{\partial p}}{{\partial \theta }} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{r\theta }}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{\theta \theta }}}}}{{\partial \theta }} + \frac{{{{\sigma }_{{r\theta }}}}}{r}} \right],$$
(2.3)
$$\frac{{\rho u}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}}}\frac{{\partial T}}{{\partial r}} = u\frac{{\partial p}}{{\partial r}} + \frac{{\nabla \cdot \left( {\kappa \nabla T} \right)}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr {{{\operatorname{Re} }}_{0}}}} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{{1\eta }}{2}(\varepsilon _{{rr}}^{2} + \varepsilon _{{\theta \theta }}^{2}) + \varepsilon _{{r\theta }}^{2}\eta - \frac{2}{3}\eta {{{\left( {\nabla \cdot {\mathbf{V}}} \right)}}^{2}}} \right].$$
(2.4)

The flow is assumed to be radial; i.e., \({\mathbf{V}} = (u,\,0)\). In Eqs. (2.1)–(2.4), the dimensionless variables are linked with the dimension gas-dynamic parameters marked with an asterisk as follows:

$$\rho = \frac{{\rho \text{*}}}{{{{\rho }_{0}}}},\quad p = \frac{{p\text{*}}}{{{{\rho }_{0}}u_{0}^{2}}},\quad T = \frac{{T\text{*}}}{{{{T}_{0}}}},\quad u = \frac{{u\text{*}}}{{{{u}_{0}}}},\quad \eta = \frac{{\eta \text{*}}}{{{{\eta }_{0}}}},$$

where \({{\rho }_{0}}\), \({{u}_{0}}\), and \({{T}_{0}}\) are the density, velocity, and temperature, respectively, at some point \(({{r}_{0}},\,0)\) located at the wedge axis. The gas is assumed to be perfect, so that \(\gamma {\text{M}}_{0}^{2}p = \rho T\). The channel walls are assumed to be heat-insulated.

The components of viscous-stress tensor \(\boldsymbol\sigma\) and strain-rate tensor \(\boldsymbol\epsilon\) have the form

$${{\sigma }_{{rr}}} = \eta {{\varepsilon }_{{rr}}} - \frac{2}{3}\eta \nabla \cdot {\mathbf{V}},\quad {{\sigma }_{{\theta \theta }}} = \eta {{\varepsilon }_{{\theta \theta }}} - \frac{2}{3}\eta \nabla \cdot {\mathbf{V}},\quad {{\sigma }_{{r\theta }}} = \eta {{\varepsilon }_{{r\theta }}};$$
$${{\varepsilon }_{{rr}}} = 2\frac{{\partial u}}{{\partial r}},\quad {{\varepsilon }_{{r\theta }}} = \frac{1}{r}\frac{{\partial u}}{{\partial \theta }},\quad {{\varepsilon }_{{\theta \theta }}} = \frac{{2u}}{r}.$$

Equations (2.1)–(2.4) contain the following similarity parameters: Mach number M0, Reynolds number Re0, and Prandtl number Pr, which are calculated as follows:

$${{\operatorname{Re} }_{0}} = \frac{{{{\rho }_{0}}{{u}_{0}}{{r}_{0}}}}{{{{\eta }_{0}}}},\quad {{{\text{M}}}_{0}} = \frac{{{{u}_{0}}}}{{\sqrt {\gamma R{{T}_{0}}} }},\quad \Pr = \frac{{{{c}_{p}}{{\eta }_{0}}}}{{{{\kappa }_{0}}}}.$$

We search for the self-similar solution to Eqs. (2.1)–(2.4) in the form

$$\rho = \frac{{\rho (\theta )}}{r},\quad p = \frac{{p(\theta )}}{r},\quad u = u(\theta ),\quad T = T(\theta ),\quad \eta = \eta (\theta ),\quad \kappa = \kappa (\theta ).$$
(2.5)

Then, continuity equation (2.1) is satisfied automatically; determining equations (2.2)–(2.4) can be rewritten as

$${{\operatorname{Re} }_{0}}p - \frac{4}{3}u\eta + \frac{d}{{d\theta }}\left( {\eta \frac{{du}}{{d\theta }}} \right) = 0,$$
(2.6)
$${{\operatorname{Re} }_{0}}\frac{{dp}}{{d\theta }} = \eta \frac{{du}}{{d\theta }} + \frac{4}{3}\frac{d}{{d\theta }}\left( {\eta u} \right),$$
(2.7)
$${{\operatorname{Re} }_{0}}up = \frac{1}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr }}\frac{d}{{d\theta }}\left( {\eta \frac{{dT}}{{d\theta }}} \right) + \eta \left[ {\frac{4}{3}{{u}^{2}} + {{{\left( {\frac{{du}}{{d\theta }}} \right)}}^{2}}} \right].$$
(2.8)

with the following boundary conditions of adhesion at the heat-insulated wall:

$$u( \pm \alpha ) = 0,\quad {{\left. {\frac{{dT}}{{d\theta }}} \right|}_{{\theta = \pm \alpha }}} = 0.$$
(2.9)

We assume that the flow is symmetric with respect to the wedge axis:

$${{\left. {\frac{{du}}{{d\theta }}} \right|}_{{\theta = 0}}} = 0,\quad {{\left. {\frac{{dT}}{{d\theta }}} \right|}_{{\theta = 0}}} = 0.$$
(2.10)

From the normalization condition for the flow parameters at the wedge axis at \(\theta = 0\), we obtain

$$u(0) = 1,\quad T(0) = 1,\quad p(0) = \frac{1}{{\gamma {\text{M}}_{0}^{2}}}.$$
(2.11)

Let us differentiate Eq. (2.6) with respect to \(\theta \) and subtract the expression obtained from Eq. (2.7). As a result, we arrive at the following ordinary differential equation:

$$\frac{{{{d}^{2}}}}{{d{{\theta }^{2}}}}\left( {\eta \frac{{du}}{{d\theta }}} \right) + \eta \frac{{du}}{{d\theta }} = 0,$$

the solution of which, with symmetry conditions (2.10) taken into account, has the form

$$\eta \frac{{du}}{{d\theta }} = {{\tau }_{0}}{\text{sin}}\theta ,$$
(2.12)

where \({{\tau }_{0}}\) is some constant. From Eqs. (2.6) and (2.12), we find the expression for the pressure:

$${{\operatorname{Re} }_{0}}p = \frac{4}{3}\eta u - {{\tau }_{0}}\cos \theta ,$$
(2.13)

from which, using conditions (2.11), we find unknown constant \({{\tau }_{0}}\):

$${{\tau }_{0}} = \frac{4}{3} - \frac{{{{{\operatorname{Re} }}_{0}}}}{{\gamma {\text{M}}_{0}^{2}}}.$$
(2.14)

Substituting (2.13) into energy equation (2.8), we obtain

$$0 = \frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\frac{d}{{d\theta }}\left( {\eta \frac{{dT}}{{d\theta }}} \right) + \frac{{du}}{{d\theta }}{{\tau }_{0}}\sin \theta + {{\tau }_{0}}u\cos \theta .$$

Integrating the expression obtained with respect to \(\theta \), with the symmetry condition taken into account, we obtain

$$0 = \frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\eta \frac{{dT}}{{d\theta }} + u{{\tau }_{0}}\sin \theta .$$

Replacing the expression \({{\tau }_{0}}\sin \theta \) with the corresponding expression from formula (2.12), we obtain the following ordinary differential equation with respect to the velocity and temperature:

$$0 = \frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\eta \frac{{dT}}{{d\theta }} + \eta \frac{{du}}{{d\theta }}u,$$

which can be easily integrated with boundary conditions (2.9) taken into account:

$$T = 1 + \frac{{1 - {{u}^{2}}}}{2}{\text{M}}_{0}^{2}\Pr (\gamma - 1).$$
(2.15)

Formula (2.15) gives the dependence of temperature on velocity, \(T = T(u)\). Then, with (2.14) taken into account, Eq. (2.14) can be solved in quadratures. Finally, we obtain

$$\int\limits_0^u {\eta (U)dU} = \left( {\frac{4}{3} - \frac{{{{{\operatorname{Re} }}_{0}}}}{{\gamma {\text{M}}_{0}^{2}}}} \right)\left( {\cos \alpha - \cos \theta } \right).$$
(2.16)

It should be noted that, by virtue of the normalization conditions (2.11), the following condition must be satisfied:

$$\int\limits_0^1 {\eta (U)dU} = \left( {\frac{4}{3} - \frac{{{{{\operatorname{Re} }}_{0}}}}{{\gamma {\text{M}}_{0}^{2}}}} \right)\left( {\cos \alpha - 1} \right).$$
(2.17)

From this condition, we can find the relationship for dimensionless parameters \({{\operatorname{Re} }_{0}}\) and M0:

$${{\operatorname{Re} }_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}\int\limits_0^1 {\eta (U)dU} } \right).$$
(2.18)

In the case in which \(\eta = \operatorname{const} \), formula (2.18) takes the form of a finite relationship:

$${{\operatorname{Re} }_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}} \right).$$
(2.19)

In the case of arbitrary power dependence \(\eta = {{T}^{k}}\), it takes the following form:

$${{\operatorname{Re} }_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}\int\limits_0^1 {{{{\left( {1 + \frac{{1 - {{U}^{2}}}}{2}{\text{M}}_{0}^{2}\Pr (\gamma - 1)} \right)}}^{k}}dU} } \right).$$
(2.20)

It should be noted that formulas (2.19) and (2.20) coincide with the corresponding formulas obtained earlier in [15], where it was assumed that there is a power dependence of the transfer coefficients on temperature [18, 19]. We note also that it follows from formula (2.18) that Knudsen number \({\text{Kn}} = {{{\text{M}}}_{{\text{0}}}}{\text{/R}}{{{\text{e}}}_{{\text{0}}}}\) has the order \({\text{Kn}} \propto 1{\text{/}}\gamma {{{\text{M}}}_{{\text{0}}}}f(\alpha )\), where \(f(\alpha )\) varies from some finite value \(4{\text{/}}3 + \int_0^1 {\eta (U)dU} \) at \(\alpha = \pi {\text{/}}2\) to infinity at \(\alpha \to 0\). So, we can come to the conclusion that, for flows in nozzles at moderate numbers M0, continuum condition \({\text{Kn}} \ll 1\) is satisfied.

3 RESULTS OF CALCULATION OF THE PARAMETERS OF GAS FLOW IN A FLAT CHANNEL FOR VARIOUS DEPENDENCES OF TRANSFER COEFFICIENTS ON TEMPERATURE

Let us consider the flow of air for which Prandtl number Pr under normal conditions is approximately 0.71. Let us compare the self-similar solutions we obtained for two different models of gas.

1. The model of gas with constant transfer coefficients: \(\eta ,\;\kappa = \operatorname{const} \).

2. The model of gas with transfer coefficients the dependence on temperature of which is described by the Sutherland law [20], which is closer to reality.

The exact solution of the Navier–Stokes equations for the Couette and Poiseuille flows of a hot gas with a viscosity coefficient the temperature dependence of which is described by the Sutherland law has been obtained in recently published works [21, 22].

As was noted above, in the first case, the problem allows the analytical solution obtained earlier in [15]. Below, we investigate the self-similar solution for the Sutherland law used in practice, which can be written in dimensionless form at η0 = 18.27 × 10–6 Pa s and T0 = 291.15 K as follows:

$$\eta (T) = \frac{{1 + 120{\text{/}}291.15}}{{T + 120{\text{/}}291.15}}{{T}^{{3/2}}}.$$
(3.1)

The calculations performed by using formulas (2.16) and (2.17) for flows of air in micronozzles have shown that, at small and moderate numbers M0, the self-similar solutions for different dependences \(\eta = \eta (T)\) nearly coincide with each other. Noticeable discrepancies are observed at \({{{\text{M}}}_{0}} > 2\). Comparisons of profiles of velocity \(u = u(\theta )\) and temperature \(T = T(\theta )\) at \({{{\text{M}}}_{0}} = 4\) for different dependences \(\eta = \eta (T)\) are shown in Figs. 2a and 2b.

Fig. 2.
figure 2

Profiles of (a) velocity and (b) temperature. The solid line refers to the Sutherland formula. The dotted line refers to \(\eta = 1\).

Full size image

The value of opening semiangle of the wedge \(\alpha = 0.074\) rad was chosen to be the same as that in [23], where the air flow in the microchannel was studied experimentally.

Figure 3 shows the dependence of number \({{\operatorname{Re} }_{0}}\) on number M0 at the wedge symmetry axis for different laws \(\eta = \eta (T)\).

Fig. 3.
figure 3

Dependence of number \({{\operatorname{Re} }_{0}}\) on number \({{{\text{M}}}_{0}}\) at the symmetry axis. The solid line refers to the Sutherland formula. The dotted line refers to \(\eta = 1\).

Full size image

It is seen from the dependences presented in Fig. 3 that, for the wedge with opening semiangle \(\alpha = 0.074\) rad, self-similar flow regimes at \({{{\text{M}}}_{0}} \propto 1\) are realized at \({\text{R}}{{{\text{e}}}_{0}} \propto 500\) for both the gas with constant transfer coefficient and for the “Sutherland” gas. It follows from the definition of Reynolds number \({{\operatorname{Re} }_{0}} = {{\rho }_{0}}{{u}_{0}}{{r}_{0}}{\text{/}}{{\eta }_{0}}\) that, under normal conditions (\(T \propto 300\) K, \(p \propto 100\) kPa), the self-similar flow is realized in the wedge with the length \({{r}_{0}} \propto {{10}^{{ - 4}}}\), which is characteristic for microchannels [23].

Earlier [7, 8, 23], flows in the flat and axisymmetrical microchannels were considered. In particular [23], the flows in the flat micronozzles were studied experimentally and numerically at various values of the pressure in the output cross section of the channel. The scheme of the channel is shown in Fig. 4; the sizes are presented in micrometers. The channel walls are made of a polymeric material with a low heat conductivity; therefore, in the numerical calculation based on solving the Navier–Stokes equations, the condition of adhesion and the condition of heat-insulated wall were used at the channel boundaries.

Fig. 4.
figure 4

Scheme of flow inside the microchannel.

Full size image

According to the calculation and experimental data [23], the pressure and temperature in the narrowest part of the channel (see Fig. 4) had the following values: \(p \simeq 40\) kPa and \(T \simeq 245\;\operatorname{K} \).

Let us represent Reynolds number \({{\operatorname{Re} }_{0}} = {{\rho }_{0}}{{u}_{0}}{{r}_{0}}{\text{/}}{{\eta }_{0}}\) in the following form:

$${{\operatorname{Re} }_{0}} = \frac{{{{\rho }_{0}}{{u}_{0}}{{r}_{0}}}}{{{{\eta }_{0}}}} = \frac{{{{\rho }_{0}}{{a}_{0}}{{r}_{0}}}}{{{{\eta }_{0}}}}{{{\text{M}}}_{0}} \simeq 1500{{{\text{M}}}_{0}}.$$
(3.2)

Then, with formula (2.18) taken into account, this expression takes the form:

$$1500{{{\text{M}}}_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}\int\limits_0^1 {\eta (U)dU} } \right).$$

Solving the derived equation with dependence \(\eta = \eta (T)\) calculated by using the Sutherland formula (3.1), we find from relationship (3.2) the value of Reynolds number \({{\operatorname{Re} }_{0}} \simeq 3300\). Let us estimate gas-flow rate Q with the formula

$$Q = {{r}_{0}}D{{\rho }_{0}}{{u}_{0}}\int\limits_{ - \alpha }^\alpha {\rho (\theta )u(\theta )d\theta } = D{{\mu }_{0}}{{\operatorname{Re} }_{0}}\int\limits_{ - \alpha }^\alpha {\rho (\theta )u(\theta )d\theta } ,$$
(3.3)

where D is the width of the channel cross section. At values \({{\operatorname{Re} }_{0}} \simeq 3300\) and \(D = 120\) μm, we obtain \(Q \simeq \) 2.5 × 10–4 g/s; the order of magnitude of this value agrees with the experimental value [23] \(Q \approx 3.8 \times {{10}^{{ - 4}}}\) g/s. Some discrepancy between the gas-flow rate calculated with the help of the self-similar solution obtained in our work and the experimental value can be explained by the fact that in [23] the gas is coming to the nozzle of finite length from the input cross section of finite size, while, in the case of a self-similar solution, the gas outflows from a point source to a channel of infinite length.

CONCLUSIONS

The possibility of constructing self-similar solutions for the flow of a viscous compressible gas in a flat channel at an arbitrary dependence of transfer coefficients on temperature is established. At \(\eta = \operatorname{const} \) and \(\eta = {{T}^{k}}\), the found analytical solutions agree with those obtained earlier [15].

For the gas flow in the microchannel, we compared the self-similar solutions for two different dependences of the viscosity coefficient on temperature, namely, \(\eta = \operatorname{const} \) and η calculated by using the Sutherland formula. It proves to be the case that significant discrepancies start to appear at the values of Mach number at the wedge axis \({{{\text{M}}}_{0}} > 2\).

The performed numerical calculations of the self-similar solutions are compared with the experimental data [23]. It is shown that gas-flow rate \(Q\) in the microchannel calculated by using formula (3.3) agrees satisfactorily with the experimental data.