From both scientific and applied points of view, it is of importance to describe adequately the mixing processes in the upper ocean layer. This is testified by the enormous number of studies in this direction, starting from studies by Kitaigorodskii and Lumley [1], their further development in [2–6], and ending with publications in the last years [7–9]. The scientific interest in the problem is determined by natural tendency of investigators to clarify the physics of mixing processes in the upper ocean layer. The practical significance of solving the problem is caused by the purposes of improvement of simulation of ocean circulation and of forecasting the weather and climate variability. In [7–9] particular geophysical applications of such solutions were described in detail; therefore, in what follows, we will consider only the physical aspect of this problem.

The traditional theoretical approach to the problem is based on using the multilevel schemes of closure of statistical moments for the fluctuating components of the velocity field. For the problems of upper ocean dynamics these schemes were systematized in the general form in [4]. In such an approach the full Navier–Stokes equations which contain the motions of various variability scales are considered, the chains of equations for moments of different orders are constructed, and the closures of the higher-order moments are made in terms of the lower-order moments on the basis of some or other hypotheses. Taking into account the great number of details of multiscale variability leads to necessity of introducing various turbulent variables (kinetic turbulence energy generation, diffusion, dissipation rates and etc.). This is characteristic of the entire turbulence theory [10]. In this direction, the obvious progress is reached and numerous models of the upper ocean layer dynamics are constructed (see, e.g., [6–14]). However, so general approach contains numerous physical assumptions, hypotheses, and simplifications. All these uncertainties lead to underestimation of the vertical mixing in the upper layer and of the depth of the mixed layer [2, 3, 7, 13].

These limitations of simulation can be removed by taking into account the effect of surface waves on the processes of vertical mixing. This concept was implemented in many studies (see, e.g., [1, 3, 5, 11–13] and the literature cited in these papers) in which the authors attempted to use various forms of involving the wave processes on the air–water interface into the traditional turbulence schemes. As a result, it was shown that the surface waves can significantly strengthen the mixing in the upper ocean layer [7–9]. However, so far the description of the mixing processes and their effective parametrization are far from to be done.

One of the successful results of solving the problem of mixing was obtained in [5] in which the turbulence induced by surface waves was investigated by means of direct closure of the Reynolds stresses. This approach is based on the idea of existence of the wave-induced turbulence in the upper water layer that has been justified and confirmed in numerous experimental [15–21] and theoretical [6, 22] studies. The analytical approach [5] seems to be the very simple, direct, and fairly effective solution of the problem under consideration.

In [5] the problem of wave mixing was considered by closing directly the Reynolds stresses appearing in the Navier–Stokes equations after averaging them over the scales of turbulent flow fluctuations [10]. Decomposing the flow velocity fluctuations into the background turbulent fluctuations \(u_{i}^{'}\) and the wave-induced fluctuations \(\tilde {u}_{i}^{'}\), the authors of [5] investigated the question of closure of the stress \(\langle \tilde {u}_{i}^{'}u_{j}^{'}\rangle \) (the angular brackets \(\left\langle \ldots \right\rangle \) denote statistical averaging) in the very simple case of one-dimensional and homogeneous mean flow U = (U(z), 0, 0). For the stress of vertical mixing the following closure was used:

$$\langle u_{1}^{'}\tilde {u}_{3}^{'}\rangle = {{B}_{v}}\frac{{dU}}{{d{{x}_{3}}}}.$$
(0.1)

Here, the subscripts (1, 2, 3) denote the x, y, and z components of flow and the value of the coefficient \({{B}_{v}}\) is treated as the turbulent diffusivity (viscosity) or the function of wave-induced vertical mixing.

Then in [5] it was taken parametrization of the quantity \({{B}_{v}}\) represented in the form:

$${{B}_{v}} = \langle \tilde {\lambda }_{3}^{'}\tilde {u}_{3}^{'}\rangle .$$
(0.2)

Here, the Prandtl mixing length \(\lambda _{3}^{'}\) inherent in background turbulence (introduced implicitly in the closure (0.1)) is taken to be equal to the scale of the mixing length \(\lambda _{3}^{'}\) which relates to wave-induced turbulence. Then, the wave-induced turbulent flow fluctuations \(\tilde {u}_{3}^{'}\) can be expressed in terms of the orbital velocities of wave motions \(\tilde {u}_{1}^{{}}\) by means of the same Prandtl approximation: \(\tilde {u}_{3}^{'} = \tilde {\lambda }_{3}^{'}(d{{\tilde {u}}_{1}}{\text{/}}dz)\). As a result, the expression for the vertical mixing coefficient \({{B}_{v}}\) gains the form that takes into account only the wave motions:

$${{B}_{v}} = \langle {{(\tilde {\lambda }_{3}^{'})}^{2}}(d{{\tilde {u}}_{1}}{\text{/}}d{{x}_{3}})\rangle .$$
(0.3)

The quantities \(\tilde {\lambda }_{3}^{'}\) and \({{\tilde {u}}_{1}}\) in (0.3) can be expressed with the use of formulas for the potential approximation for surface waves in terms of the wave number spectrum \(S({\mathbf{k}})\) and the wave-induced mixing functions \({{B}_{v}}\) is defined in the form [5]:

$${{B}_{v}}(S,z) = \alpha \int {S({\mathbf{k}})\exp (2kz)d{\mathbf{k}}} \frac{{d{{{(\int {{{\omega }^{2}}({\mathbf{k}})S({\mathbf{k}})\exp (2kz)d{\mathbf{k}}} )}}^{{1/2}}}}}{{dz}}.$$
(0.4)

In (0.4) α is the dimensionless fitting coefficient, ω2(k) = g|k| is the wave frequency which corresponds to the wave vector k for the gravity waves, g is the acceleration of gravity, and the exponential functions denote the dependence of the surface wave spectrum on the depth z reckoned from the middle interface between the media (the z axis is directed upward).

The main feature of Eq. (0.4) consists in cubic dependence of the function \({{B}_{v}}\) on the wave amplitude \({{a}_{0}} = {{\left( {2\int {S({\mathbf{k}})d{\mathbf{k}}} } \right)}^{{1/2}}}\) on the surface. This leads a fairly strong damping of \({{B}_{v}}\) with increase in the depth: \({{B}_{v}}(S,z) \propto {{({{a}_{0}})}^{3}}\exp (3{{k}_{p}}z)\), where kp is the wave number corresponding to the spectrum peak. Despite of the so strong dependence on the depth, in [5] it was noted that “adding \({{B}_{v}}\) to the vertical diffusivity in a global ocean circulation model yields a temperature structure in the upper 100 m that is closer to the observed climatology than a model without the wave-induced mixing.” Later, the fact of significant impact of the wave-induced mixing on the global circulation was confirmed in a large series of studies [7–9, 19, 23, 24].

In accordance with the above, the outlined approach seems to be a perspective semi-phenomenological solution of the problem of mixing induced by the presence of waves on the sea surface. However, taking into account several vulnerable assumptions in the proposed version of the wave-induced mixing model (Eqs. (0.2) and (0.3)), this approach requires a certain modification.

The present study is directed to creation of a new version of the wind-wave-induced mixing model. Note that the new version of the model under consideration leads to the significantly stronger impact of waves on vertical mixing as compared with that yielded by Eq. (0.4).

1. CONSTRUCTION OF A MODIFIED MODEL

1.1. Theoretical Prerequisites

We will reproduce certain well-known analytical insights entering into solution of the problem under consideration. These insights clarify certain assumptions not discussed in [5] when postulating its governing equations. Note that the motions (flows) in the upper water layer located below the deepest troughs of wind waves on the fluid surface will be considered. It is also assumed that in the upper water layer there is a certain background fluid current which exists regardless of surface waves.

Following the well-known approach of turbulence theory [10, 11], we can write the governing Navier-Stokes equations in the tensor form:

$$\frac{{\partial {{U}_{i}}}}{{\partial t}} + {{U}_{j}}\frac{{\partial {{U}_{i}}}}{{\partial {{x}_{j}}}} = - \frac{1}{\rho }\frac{{\partial {{P}_{{}}}}}{{\partial {{x}_{i}}}} + \nu \frac{{{{\partial }^{2}}{{U}_{i}}}}{{\partial x_{j}^{2}}}.$$
(1.1)

Here, as before, the quantities Ui (i = 1, 2, 3) represent the x–y–z-components of fluid flow in the upper layer below the wave troughs, ρ is the water density; P is the pressure, and ν is the kinematic viscosity of water; repeating indices mean summation over them. Following the approaches adopted in [5, 11], in (1.1) the effect of the Coriolis forces is neglected by reason of small scales of the motions considered.

In this problem, it is of first importance to distinguish different forms of motion before performing statistical averaging. For this purpose, we represent the expansion of the total fluid velocity in the presence of wind waves in the following form:

$${{U}_{i}} = \left\langle {{{U}_{i}}} \right\rangle + {{u}_{i}} = ({{\bar {U}}_{i}} + \tilde {U}{{\delta }_{{i,1}}}) + \tilde {u}{}_{i}\; + \;\tilde {u}_{i}^{'} + u_{i}^{'}.$$
(1.2)

Here, \(\left\langle {{{U}_{i}}} \right\rangle = ({{\bar {U}}_{i}} + \tilde {U}{{\delta }_{{i,1}}})\) is the general velocity (average over the ensemble of waves) in which \(\bar {U}_{i}^{{}}\) is the “background” average velocity and \(\tilde {U}{{\delta }_{{i,1}}}\) is the average velocity of wind-wave drift induced by the wind and wave motions directed along the Ox axis (this is reflected by the Kroneker delta \({{\delta }_{{i,1}}}\)), and the quantity \({{u}_{i}}\) is the total addition to the mean flow. The addition \({{u}_{i}}\) includes the following set of terms: the orbital wave motions \(\tilde {u}{}_{i}\), the wave-induced turbulent components \(\tilde {u}_{i}^{'}\), and the background turbulent fluctuations \(u_{i}^{'}\) which below will be called “background” turbulence. The Stokes drift induced by waves by virtue of their nonlinearity is included in the term \(\tilde {U}{{\delta }_{{i,1}}}\). (The situation of waves without wind when only the Stokes drift occurs requires individual consideration.) Here, it should be noted that in decomposition (1.2) the following conditions are fulfilled: 1) the orbital velocity \(\tilde {u}{}_{i}\) does not relates to turbulent velocity fluctuations; 2) by definition, the background turbulent motions \(u_{i}^{'}\) are independent of the wave-induced turbulent motions \(\tilde {u}_{i}^{'}\); 3) in accordance with their nature, both types of fluctuations can be statistically correlated with one another. The last remark is of first importance for the further consideration.

The decomposition similar to (1.2) is assumed to be also fulfilled for the pressure Р (without the term related to drift). However, in what follows, we will not consider the contribution of the terms related to the pressure in Eq. (1.1) assuming that the terms related to the pressure simply “correct” the fluctuations \(u_{i}^{'}\) and \(\tilde {u}_{i}^{'}\) introduced above in this version of our constructions. Since no explicit expressions for the fluctuations \(u_{i}^{'}\) and \(\tilde {u}_{i}^{'}\) are required in our model, this simplification of the system of equations seems to be fairly reasonable.

We adopt the following well-known statistical approximations [10, 11]:

1) All the wave, except for drift, and turbulent terms of flow in (1.2) are equal to zero in statistical averaging over the ensemble of waves

$$\left\langle {{{{\tilde {u}}}_{i}}} \right\rangle = 0;\quad \langle \tilde {u}_{i}^{'}\rangle = 0;\quad \langle u_{i}^{'}\rangle = 0.$$
(1.3a)

2) There are no correlations between the average, orbital, and turbulent motions

$$\left\langle {{{{\bar {U}}}_{i}}{{{\tilde {u}}}_{i}}} \right\rangle = 0,\quad \langle {{\bar {U}}_{i}}\tilde {u}_{i}^{'}\rangle = 0,\quad \langle {{\bar {U}}_{i}}u_{i}^{'}\rangle = 0.$$
(1.3b)

A similar statement is also valid for drift flow \(\tilde {U}{{\delta }_{{i,1}}}\).

3) There are no correlations between the orbital wave motions and the turbulent fluctuations of both types

$$\langle \tilde {u}{}_{i}\tilde {u}_{j}^{'}\rangle = 0,\quad \langle \tilde {u}{}_{i}u_{j}^{'}\rangle = 0.$$
(1.3c)

4) The wave-induced turbulent fluctuations and the background turbulent terms correlate

$$\langle \tilde {u}_{i}^{'}\tilde {u}_{j}^{'}\rangle \ne 0,\quad \langle \tilde {u}_{i}^{'}u_{j}^{'}\rangle \ne 0,\quad \langle u_{i}^{'}u_{j}^{'}\rangle \ne 0.$$
(1.3d)

Moreover, the continuity condition holds for each component in (1.2).

Substituting (1.2) in (1.1), averaging over the ensemble of waves, and taking into account relations (1.3a) and (1.3b) and the continuity conditions for u, we obtain the equations

$$\frac{{\partial \left\langle {{{U}_{i}}} \right\rangle }}{{\partial t}} + \left\langle {{{U}_{j}}} \right\rangle \frac{{\partial \left\langle {{{U}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} + \frac{{\partial \left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} = \left[ {pressure - terms} \right] + \nu \frac{{{{\partial }^{2}}\left\langle {{{U}_{i}}} \right\rangle }}{{\partial x_{j}^{2}}}.$$
(1.4)

Here, \(\left\langle {{{U}_{i}}} \right\rangle = {{\bar {U}}_{i}} + {{\tilde {U}}_{i}}{{\delta }_{{i,1}}}\) and the third term on the left-hand side contains the Reynolds stress Re = \(\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle \). In view of the adopted decomposition (1.2), the complete expression for the stress Re takes the form:

$$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = \left\langle {{{{\tilde {u}}}_{j}}{{{\tilde {u}}}_{i}}} \right\rangle + \langle {{\tilde {u}}_{j}}\tilde {u}_{i}^{'}\rangle + \langle {{\tilde {u}}_{j}}u_{i}^{'}\rangle + \langle \tilde {u}_{j}^{'}{{\tilde {u}}_{i}}\rangle + \langle \tilde {u}_{j}^{'}\tilde {u}_{i}^{'}\rangle + \langle \tilde {u}_{j}^{'}u_{i}^{'}\rangle + \langle u_{j}^{'}{{\tilde {u}}_{i}}\rangle + \langle {{u}_{j}}\tilde {u}_{i}^{'}\rangle + \langle u_{j}^{'}u_{i}^{'}\rangle .$$
(1.5)

From (1.5) with regard to relations (1.3c) and (1.3d) it follows that

$$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = \left\langle {{{{\tilde {u}}}_{j}}{{{\tilde {u}}}_{i}}} \right\rangle + \langle \tilde {u}_{j}^{'}\tilde {u}_{i}^{'}\rangle + \langle \tilde {u}_{j}^{'}u_{i}^{'}\rangle + \langle u_{j}^{'}\tilde {u}_{i}^{'}\rangle + \langle u_{j}^{'}u_{i}^{'}\rangle .$$
(1.6)

If there are no waves, then \({{\tilde {u}}_{i}} = 0\) and \(\tilde {u}_{i}^{'} = 0\) and the stress Re takes the standard form [10]:

$$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = \langle u_{j}^{'}u_{i}^{'}\rangle ,$$
(1.7)

which corresponds to background turbulence existing without waves.

When there are no waves in the approximation of first-level closure [10], from (1.7) it follows that

$$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = {{K}_{{ji}}}(\partial {{\bar {U}}_{i}}{\text{/}}\partial {{x}_{j}}),$$
(1.8)

where the coefficient Kji has the sense of the turbulent viscosity (diffusivity). In fact, at constant value of Kji = K0 the closure (1.8) leads the stress (1.7) to the standard form of the viscous term in Eq. (1.1):

$$\frac{{\partial \langle u_{j}^{'}u_{i}^{'}\rangle }}{{\partial {{x}_{j}}}} = \frac{\partial }{{\partial {{x}_{j}}}}{{K}_{{ji}}}(\partial {{\bar {U}}_{i}}{\text{/}}\partial {{x}_{j}}) = {{K}_{0}}\frac{{{{\partial }^{2}}{{{\bar {U}}}_{i}}}}{{{{{(\partial {{x}_{j}})}}^{2}}}}.$$

Thus, carrying out closure of the “wave” terms in the stress Re of form (1.6), we can obtain the unknown wave-induced vertical mixing function.

1.2. Initial Detailed Elaboration

For the sake of simplicity, we will consider the case of the constant and homogeneous mean flow \(\left\langle {\mathbf{U}} \right\rangle \) with regard to the drift \(\tilde {U}\) and the vertical shear directed along the OX axis, i.e., \(\left\langle {\mathbf{U}} \right\rangle = (U(z),0,0)\) and \(\partial U{\text{/}}\partial {{x}_{i}} = 0\) for i = 1, 2.

Restricting our attention only to vertical flows and setting, to be specific, j = 1 and i = 3 in Eq. (1.6), we obtain the following form of the stress to be analyzed:

$$\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle = \left\langle {{{{\tilde {u}}}_{1}}{{{\tilde {u}}}_{3}}} \right\rangle + \langle \tilde {u}_{1}^{'}\tilde {u}_{3}^{'}\rangle + \langle \tilde {u}_{1}^{'}u_{3}^{'}\rangle + \langle u_{1}^{'}\tilde {u}_{3}^{'}\rangle + \langle u_{1}^{'}u_{3}^{'}\rangle ,$$
(1.9)

for which it is necessary to find a final expression.

Firstly, we suppose that the orbital wave motion is potential. Then a monochromatic wave with the frequency ω, the wave number k, and the amplitude a0 (at z = 0), which propagates in deep water in two-dimensional (x, z)-space, can be described in the linear approximation by the following formulas [25].

The elevation on the water surface has the form:

$$\eta (x,t) = {{a}_{0}}\cos (kx - \omega t).$$
(1.10a)

The velocity potential is specified by the formula

$$\phi (x,z,t) = {{a}_{0}}\frac{\omega }{k}\exp (kz)\sin (kx - \omega t).$$
(1.10b)

The orbital velocities can be given by the relations

$${{\tilde {u}}_{1}} = {{u}_{x}} = {{a}_{0}}\omega \exp (kz)\cos (kx - \omega t)\quad {\text{and}}\quad {{\tilde {u}}_{3}} = {{u}_{z}} = {{a}_{0}}\omega \exp (kz)\sin (kx - \omega t),$$
(1.10c)

i.e., the amplitude of the wave motions damps with depth as \(a(k,z) = {{a}_{0}}\exp (kz)\).

Secondly, by reason of orthogonality of the oscillating functions, from (1.10c) it follows that

$$\left\langle {{{{\tilde {u}}}_{1}}{{{\tilde {u}}}_{3}}} \right\rangle = 0.$$
(1.11)

Using the Prandtl approximation for wave turbulent motions in the form:

$$\tilde {u}_{{1,3}}^{'} = \lambda _{{1,3}}^{'}\partial {{\tilde {u}}_{{1,3}}}{\text{/}}\partial {{x}_{3}},$$

similarly to (1.11) we can obtain

$$\langle \tilde {u}_{1}^{'}\tilde {u}_{3}^{'}\rangle = 0.$$
(1.12)

Thirdly, eliminating the “background” turbulence in (1.9) (the last term) and using relations (1.11) and (1.12), we obtain the following wave-induced stress:

$${{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}} = \langle \tilde {u}_{1}^{'}u_{3}^{'}\rangle + \langle u_{1}^{'}\tilde {u}_{3}^{'}\rangle .$$
(1.13)

The quantity \({{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}}\) is the wave stress which is additive to the background turbulent viscosity determined by the relation of form (1.8). In [5] an analog of Eq. (1.13) was first postulated and thereafter analyzed (see introduction). In what follows, we will present its final detailed elaboration.

1.3. Formulas of Closure

The new approach to closure of stress (1.11) includes the following steps.

1) Because of spatial homogeneity of wave-induced turbulence, we can assume that both terms in (1.13) have identical values. Then

$${{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}} \cong 2\langle \tilde {u}_{1}^{'}u_{3}^{'}\rangle .$$
(1.14)

2) We will now use the standard Prandtl approximation for the background turbulence fluctuations of the form:

$$u_{3}^{'} = \lambda _{3}^{'}\partial U{\text{/}}\partial {{x}_{3}},$$
(1.15)

where \(\lambda _{3}^{'}\) is the unknown stochastic mixing length of background turbulence which, by definition, is not related to wave motions since it is inherent in turbulence which exists when there are no waves. As a result, the basic expression for the further analysis takes the form:

$${{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}} \cong 2\langle \tilde {u}_{1}^{'}\lambda _{3}^{'}\rangle \partial U{\text{/}}\partial {{x}_{3}}.$$
(1.16)

3) By analogy with relation (1.8), from (1.16) there follows the implicit expression for the wave-induced turbulent viscosity \({{B}_{v}}\) of the form:

$${{B}_{v}} \approx 2\langle \tilde {u}_{1}^{'}\lambda _{3}^{'}\rangle .$$
(1.17)

It remains now to find closure of statistical averaging in (1.17).

4) We note that relation (1.17) for \({{B}_{v}}\) differs from formula (0.2) proposed in [5]. Here, the mixing length \(\lambda _{3}^{'}\) inherent in background turbulence is used. The mixing length cannot be expressed in terms of any part of the wave motions as discussed above.

The function \({{B}_{v}}\) has the following features:

—\({{B}_{v}}\) is the statistical moment whose finite value can be postulated; this is usually made in turbulence theory [10].

—\({{B}_{v}}\) is a linear function of the wave-induced turbulent fluctuation \(\tilde {u}_{1}^{'}\) which, in turn, in the Prandtl approximation, is also a linear function of the orbital wave velocity \((d\tilde {u}_{1}^{{}}{\text{/}}d{{x}_{3}})\), i.e., of the wave amplitude (see formula (1.10c)). It can be expected that at any fixed depth z the quantity \({{B}_{v}}\) must be a linear function of the local wave amplitude a(z) that depends on the depth z.

5) In what follows, we do not suggest to use the Prandtl approximation for the wave-induced turbulent fluctuation \(\tilde {u}_{1}^{'}\) of the type (1.15) in order that thereafter not to seek a parametrization for the arising moment \(\langle \tilde {\lambda }_{3}^{'}\lambda _{3}^{'}\rangle \), but to carry out closure for \({{B}_{v}}\) by means of indirect determination of the statistical moment in (1.17) on the basis of recent theory of wind-induced drift flow constructed in author’s study [26].

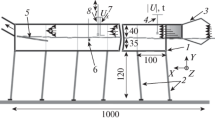
In accordance with this theory [26, 27] and empirical observations [28], the wavy air-water interface has the three-layer structure, namely, the near-water atmosphere layer, the wave zone in which air and water are alternatively present, and the upper (boundary) water layer (Fig. 1a). In [28] such a structure was obtained as a result of processing the empirical observations. The principal feature of the above three-layer structure of the wavy interface consists in the fact that in the wave zone the vertical profiles of both mean wind velocity W(z) and mean flow U(z) are linear functions of z. Outside the wave zone these profiles approach to logarithmic ones [27, 28].

Fig. 1.
figure 1

Generalized pattern of the motions in the neighborhood of the interface between the media. (a) Diagram of location of the boundary atmosphere layer, the wave zone, and the upper water layer; curves describe ensemble of the surface elevations \(\eta (t)\) at a fixed point in space. (b) Schematic view of the mean flow velocity profile U(z) (on the basis of the measurement data in [28]) and the mean wind velocity profile W(z) (on the basis of the calculations in [27]). The scale of height z is normalized by the wave length L corresponding to the peak frequency ωp and the mean velocities by the wind velocity W10 .

Full size image

The author has obtained theoretically [27], by processing the numerical experiments described in [29], the fact that the mean wind velocity profile W(z) is linear, as shown in Fig. 1. In Fig. 1b we have reproduced schematically the profile U(z) for the flow velocity in the wave zone. The exact results of measurements of U(z) are given in [28]. The presence of the linear profile for the mean fluxes (both of wind and flows) means [10] that the wave zone plays a role of the viscous layer located between the near-water atmosphere and upper water layers. Therefore, from the point of view of statistical hydrodynamics [10] the following conditions of steady-state viscous shear flow must be satisfied in the wave zone: the momentum flux τw induced by wind and directed downward is constant and the turbulent viscosity coefficient Ktw which maintains the linear flow profile \(U(z)\) is also constant.

In accordance with the classical turbulence theory [10], on the basis of the above consideration the following balance of the momentum flux must be fulfilled in the wave zone:

$${{\tau }_{w}}{\text{/}}{{\rho }_{w}} = {{K}_{{{\text{tw}}}}}\partial U(z){\text{/}}\partial z,$$

where on the left-hand side we have the vertical momentum flux in water \({{\tau }_{w}}\) divided by the water density \({{\rho }_{w}}\). Using this approach, in [26] the author established that in the wave zone the turbulent mixing (viscosity) coefficient Ktw has the form:

$${{K}_{{{\text{tw}}}}} = {{\left. {{{c}_{{{\text{tw}}}}}{{u}_{*}}a} \right|}_{{z = 0}}},$$
(1.18)

where ctw ~ 10–2 is a dimensionless coefficient and \({{u}_{*}}\) is the friction velocity in the near-water atmosphere layer (see details in Appendix). Equation (1.18) means that in the wave zone the wave-induced turbulent viscosity Ktw is a linear function of the wave amplitude a.

6) In admitting unity of the mixing mechanism in the wave zone and the upper water layer, we can suggest that the unknown turbulent viscosity \({{B}_{v}}\) which takes place in the upper water layer is the natural continuation of the turbulent viscosity Ktw existing in the wave zone. This hypothesis makes it possible to assume that parametrization of \({{B}_{v}}\) is the analytical continuations of the well-known parametrization of the quantity Ktw. On this basis we can assume that the following relation will be satisfied at an arbitrary depth z:

$${{B}_{{v}}}(z) \approx {{K}_{{{\text{tw}}}}}(z),$$
(1.19)

where Ktw(z) is the analytical continuation of the function Ktw given by relation (1.18) at the undisturbed water level z = 0. Evidently, this continuation is implemented in terms of the well-known exponential dependence on the depth z for the amplitude of orbital motions for each of the spectral components of the wave spectrum, i.e., in accordance with (1.10c), a(k, z) = a0exp(kz), where a0 is the wave amplitude at the level z = 0.

Thus, in the case of monochromatic surface wave the explicit expression for the function \({{B}_{v}}(a,{{u}_{*}},z)\), dependent on the wave amplitude, the friction velocity \({{u}_{*}}\), and the depth z, takes the form:

$${{B}_{v}}(a,{{u}_{*}},z) \approx {{K}_{w}}(z) \approx {{c}_{v}}{{u}_{*}}{{a}_{0}}\exp (kz),$$
(1.20)

where \({{c}_{v}}\) ~ 10–2 is a dimensionless fitting coefficient. Generalization of relation (1.20) to the case of the surface wave spectrum can be specified by the formula

$${{B}_{v}}(z) = {{c}_{B}}_{v}{{u}_{*}}{{\left( {\int {S({\mathbf{k}})\exp (2kz)d{\mathbf{k}}} } \right)}^{{1/2}}},$$
(1.21)

where \({{c}_{B}}_{v}\) ~ 10–2 is a fitting coefficient similar to the coefficient \({{c}_{v}}\) in (1.20).

1.4. Concluding Remarks

Relations (1.20) and (1.21) complete derivation of the unknown function for the vertical mixing \({{B}_{v}}\) induced by wind waves. As can be seen from these formulas, the main difference between (1.21) and the result (0.4) of [5] consists in the significantly stronger dependence of \({{B}_{v}}\) on the local wave amplitude by virtue of the lower degree of damping exponent in Eq. (1.21). This result testifies to the possibility of implementation of the significantly higher intensity of wave-induced vertical mixing at the depth z than that following from the result (0.4). In practice, the result obtained can lead to the greater effect of waves on the processes in the upper sea layer and in large-scale circulation as compared with the estimates obtained earlier [5–9].

For physical understanding of the processes in the upper water layer it is of interest to verify the obtained dependences of the form (1.20) and (1.21). The dependences \({{B}_{v}}({{a}_{0}})\) and \({{B}_{v}}({{u}_{*}})\) can be verified using the numerical simulation of the wavy air-water interface by analogy with [6, 29, 30] and also in the laboratory experiments similar to [16, 19]. The successful verification of these dependences would make it possible to give preference to one or another version of the model that describes the processes of wave-induced mixing. In principle, methods of analytical verification of the dependences \({{B}_{v}}({{a}_{0}})\) and \({{B}_{v}}({{u}_{*}})\) are also possible. Some variants of them will be discussed below.

2. DISCUSSION OF THE RESULTS

We will verify the correspondence of the result (1.20) to certain well-known empirical dependences. Since the author do not know any empirical data on direct measurement of the turbulent viscosity coefficient \({{B}_{v}}\) in the upper water layer, it is necessary to take suitable physical quantities which would make it possible to carry out verification of the dependences \({{B}_{v}}({{a}_{0}})\) and \({{B}_{v}}({{u}_{*}})\) on the basis of the available measurement data. The most convenient of such quantities is the dissipation rate of the turbulence kinetic energy ε whose value can be measured experimentally, see, for example, [11, 16, 17, 31].

For this purpose we can use the following relation between the wave-induced part of the dissipation rate of the turbulence kinetic energy εw and the viscosity \({{B}_{v}}\)written in the form [25]:

$${{\varepsilon }_{w}} \approx {{B}_{v}}{{\left( {\partial {{{\tilde {u}}}_{1}}{\text{/}}\partial {{x}_{3}}} \right)}^{2}}.$$
(2.1)

In relation (2.1) the vertical gradient of the velocity of orbital wave motions is used as an approximation suitable for qualitative estimates. Equation (2.1) makes it possible to carry out analytical verification of correspondence of relations (1.20) and (1.21) to the well-known empirical dependences of εw on the surface wave amplitude \({{a}_{0}}\) and the friction velocity \({{u}_{*}}\) in the atmosphere [11, 16, 31].

In accordance with the measurements [16], in the case of the presence of the monochromatic wave on the water surface the following dependence takes place:

$${{\varepsilon }_{w}} \propto a_{0}^{3}.$$
(2.2)

The correspondence between relations (1.20) and (2.2) becomes evident if we take into account that the wave velocity \({{\tilde {u}}_{1}}\) in (2.1) is linear with respect to the wave amplitude (see (1.10c)). Thus, the analytical verification of the dependence \({{\varepsilon }_{w}}({{a}_{0}})\) is quite successful.

In accordance with the measurements [11, 31], the well-known dependence of εw on \({{u}_{*}}\) in the upper water layer takes the form:

$${{\varepsilon }_{w}} \propto u_{*}^{3}.$$
(2.3)

Using relations (1.20), (1.21), and (1.10c), from formula (2.1) we can arrive at the relation

$${{\varepsilon }_{w}} \propto {{u}_{*}}a{{({{\omega }_{p}}{{k}_{p}}a)}^{2}} \propto {{u}_{*}}\omega _{p}^{6}{{a}^{3}},$$
(2.4)

where \(\omega _{p}^{{}}\) is wave spectrum peak frequency and the subscript “0” of the wave amplitude is omitted for simplicity of the further notation. In order to obtain the dependence \(\varepsilon ({{u}_{*}})\) from formula (2.4), the well-known dependences for the dimensionless wave energy \(\tilde {E}\) and the spectrum peak frequency \({{\tilde {\omega }}_{p}}\) on the dimensionless wave fetch \(\tilde {X}\) can be used in the case of steady-statewaving. In accordance with the numerous experimental data, these dependences are as follows [32]:

$$\tilde {E} \equiv \frac{{{{a}^{2}}g}}{{u_{*}^{4}}} \propto \tilde {X} \equiv \frac{{Xg}}{{u_{*}^{2}}}\quad {\text{and}}\quad {{\tilde {\omega }}_{p}} \equiv \frac{{{{\omega }_{p}}{{u}_{*}}}}{g} \propto {{\tilde {X}}^{{ - 1/3}}} \equiv {{\left( {\frac{{Xg}}{{u_{*}^{2}}}} \right)}^{{ - 1/3}}},$$
(2.5)

where X is the wave fetch in units of length and g is the acceleration of gravity. From the first of the equations (2.5) it follows that the dependence of the (mean) wave amplitude on the friction velocity takes the form \(a(u_{*}^{{}}) \propto u_{*}^{{}}\) and from the second we have \(\omega _{p}^{{}}(u_{*}^{{}}) \propto {{(u_{*}^{{}})}^{{ - 1/3}}}\). In this case, relation (2.4) takes the form:

$${{\varepsilon }_{w}} \propto {{u}_{*}}\omega _{p}^{6}{{a}^{3}} \propto u_{*}^{2}.$$

This corresponds to the empirical dependence (2.3) when taking into account the inevitable errors in estimates of the powers in Eqs. (2.2), (2.3), and (2.5).

Thus, the encouraging results of analytical verification of the correspondence of relations (1.20) and (1.21) to the well-known empirical dependences (2.2) and (2.3) raise the significance of their experimental verification. The latter can be implemented by estimating the empirical dependences \({{B}_{v}}({{a}_{0}})\) and \({{B}_{v}}({{u}_{*}})\) in the flume experiments similar to those described in [16, 19].

We also note that, in our opinion, the experimental verification of the dependences \({{B}_{v}}({{a}_{0}})\) and \({{B}_{v}}({{u}_{*}})\) can be made by two ways. The first (indirect) way is based on measurement of the dissipation rate of the turbulence kinetic energy εw as a function of the mean wave amplitude on the fluid surface \({{a}_{0}}\) and the friction velocity \({{u}_{*}}\) with the successive use of the right-hand side of relation (2.4) for comparison with the theory, as presented above. The second (direct) way can be implemented by calculating the wave-induced vertical mixing \({{B}_{v}}\) (as a function of \({{a}_{0}}\) and \({{u}_{*}}\)) found from the rate of spatial spreading of a small droplet of colored ink in the water layer below the deepest wave troughs. For this purpose, we can use the well-known Einstein formula (\({{B}_{v}}\sim {{\left\langle {\Delta z} \right\rangle }^{2}}{\text{/}}\Delta t\), where Δz is the ink-spot dimension and Δt is the ink-spot spreading time), bearing in mind the physical identity between the quantity \({{B}_{v}}\) and the passive-particle diffusion coefficient in water [10]. Naturally, the corresponding technique of carrying out the experiment is needed for the special detailed elaboration which can be developed in the case of necessity.

SUMMARY

The vertical turbulent mixing model is constructed. This model predicts the impact of wind waves on mixing in the upper fluid layer which is stronger as compared with the estimates [5]. The model is based on the following theoretical propositions.

In the Navier–Stokes equations the total flow velocity is decomposed into four components including the mean flow velocity, the wave orbital motions, the wave-induced turbulent flow fluctuations, and the background turbulent fluctuations. This makes it possible to separate the wave stress Rew from the background stress Reb and obtain the implicit expression for the wave-induced vertical mixing coefficient \({{B}_{v}}\).

The expression for \({{B}_{v}}\) is specified more strictly using author’s results [26] for the turbulent viscosity function Ktw in the wave zone located between the atmospheric boundary layer and the upper water layer. The unknown turbulent viscosity \({{B}_{v}}\) in the upper water layer is set to be equal to analytical continuation of the turbulent viscosity function Ktw in the wave zone. Finally, \({{B}_{v}}\) is specified as a linear function of the wave amplitude a(z) at the depth z and the friction velocity \({{u}_{*}}\) in air. This means the possibility of strengthening the wave impact on vertical mixing as compared with the well-known cubic dependence of \({{B}_{v}}(a)\) obtained earlier in [5].

The predicted analytic dependences \({{B}_{v}}({{a}_{0}})\) and \({{B}_{v}}({{u}_{*}})\) can be tested empirically by their determination from the data of measurements in the flume experiments of the type [16, 19].