1 Introduction

1.1 The System Under Consideration and the Aims

Airflow above a sea surface induces a wide variety of motions of different scales in the vicinity of an air–sea interface. Some of them, the wind waves and the mean drift current, affect human marine activity significantly, though many features related to these phenomena are still not completely clear. These circumstances determine both the practical and scientific interest in studying dynamics of the wavy air–water interface.Footnote 1

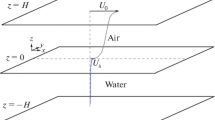
A schematic layout of motions at a wavy air–sea interface is shown in Fig. 1, illustrating the complexity of the system under consideration. The vertical profiles of the wind speed, W(z), and the drift velocity, Ud(z), together with the wind waves described by the surface elevation, η(x,t), form the certain vertical structure of the interface. This structure is provided by the turbulent momentum flux (the wind stress), τ, directed from the airflow to the wavy water surface and beneath. This turbulent flux determines the stochastic nature of the motions at the entire interface (Phillips 1977).

Fig. 1
figure 1

A schematic layout of the wavy air–sea interface. The spirals denote turbulent eddies

Full size image

A joint presence of shear flow, waves, and turbulent motions in the vicinity of a moving water surface (Fig. 1) provides a complicated hydrodynamics concerning the air–sea interface (Monin and Yaglom 1971; Phillips 1977). To simplify the system, we restrict our consideration to a case study of moderate wind speeds, when the wave-breaking intensity is rather small, and the water surface is well defined, allowing certain wind–wave parameters, e.g., height, period, length, to be fixed.

Below, in Sect. 2.2, it will be shown that, in the considered case study, the wavy interface can be conditionally partitioned into three constituents, each of which has its own features. These three constituents are: the air boundary layer (ABL), where the air is permanently present; the wave zone, where the air and water are alternate; and the water boundary layer (WBL), where the water is continuous. Dynamics of each part of the interface system depends significantly on a wind–wave state, as far as wind waves mediate all movements near the interface (Phillips 1977). However, here we consider the dynamic parameters of the ABL and the wave zone as given, and confine ourselves to a description of the wind-induced drift current Ud(z) above the WBL (simply, wind-drift) as a function of wind and wave parameters discussed below. Derivation of this function is the main aim of the present work.

1.2 Experimental Aspects of the Problem

In the problem under consideration, there are numerous experimental studies of the wind-drift phenomenon; early results can be found, for example, in Shemdin (1972), Wu (1975, 1983), Churchill and Csanady (1983), Bye (1988), and references therein. Since all contributions cannot be mentioned here, we restrict our attention to a small set that is relevant to our aims (Wu 1975, 1983; Churchill and Csanady 1983; Babanin 1988; Malinovsky et al. 2007; Kudryavtsev et al. 2008; Longo et al. 2012a, b; Zavadsky and Shemer 2017).

This abundance of earlier work is explained by the availability of the water surface under study and the evident simplicity of measurement. However, this simplicity, in fact, is only apparent, since accurate measurements at a wavy (oscillating) interface are not easy. Indeed, the measurement of drift velocity in the field has many sources of error (Churchill and Csanady 1983; Babanin 1988; Malinovsky et al. 2007; Kudryavtsev et al. 2008). They include the non-stationarity of the wind field, uncontrolled background currents Ub, stratification of air and water in situ, numerous technical difficulties in field measurements, and so on. At the same time, the field experiments have the advantage of providing a wide range for the wind- and wave-origin conditions (fetch, age, dominant frequency).

An alternative method for studying regularities of the drift-current formation is based on laboratory (tank) measurements, though there are also numerous drawbacks in this approach. Indeed, while conducting tank measurements, sources of errors include the influence of vertical and lateral boundaries of the tank, the presence of the reverse currents, short wind and wave fetches, and difficulties of equipment location in a tank (Wu 1975, 1983; Longo et al. 2012a; Zavadsky and Shemer 2017). All these limitations influence the wind and current profiles and the establishing of dependencies of wind-drift on wind and wave parameters of the interface. Besides, a small tank limits the range of the wave-state parameters, and decreasing the opportunity for finding the above-mentioned dependences. However, tank measurements have the evident advantage that all parameters in the wind–wave system are completely controlled during an experiment.

The listed and other sources of the errors impose significant limitations on the accuracy of measurement results. Therefore, all kinds of experiments require careful preparation both for measurements and for their analysis, which are well described in the cited references. Although accuracy estimates for the drift-velocity measurements are not always available, the analysis of scatter in the published values allows us to assume that the measurement errors for Ud are about 10% (Wu 1975; Churchill and Csanady 1983; Babanin 1988; Kudryavtsev et al. 2008; Longo et al. 2012a). These values are explicitly confirmed in Babanin (1988) and Malinovsky et al. (2007).

Before representing empirical data for the surface drift velocity, Ud, we note that in the absence of a background current Ub, the velocity vector of the surface current at a wavy surface, US, includes, in fact, two terms,

$$ {\mathbf{U}}_{S} = \alpha_{1} {\mathbf{U}}_{St} + \alpha_{2} {\mathbf{U}}_{d} , $$
(1)

where α1 and α2 are coefficients close to unity (Malinovsky et al. 2007), and USt is the Stokes-drift vector directed along the wavenumber vector, k, corresponding to the wave-propagation direction (Stokes 1847). As is known, the Stokes drift (sometimes referred to as the wave-induced drift, e.g., Wu 1983; Bye 1988) is created due to the unclosed orbits of non-linear waves, i.e., it is not directly related to the airflow. Therefore, the Stokes drift is an additive to the wind-drift current Ud, which vector coincides with the wind-stress vector, τ. In field experiments, the directions of τ and the wind-drift vector Ud may not coincide with the direction of the local wind W (Babanin 1988; Malinovsky et al. 2007; Kudryavtsev et al. 2008). This effect is due to the influence of the Coriolis force, associated with the rotation of the Earth.

The expression for the magnitude of the Stokes drift induced by a non-linear gravity wave with amplitude a, frequency ω, and wavenumber k, is well known (Phillips 1977),

$$ U_{St} = (\omega /k)(ka)^{2} = (\omega a)(ka), $$
(2)

where the first equality corresponds to scaling of USt by the phase velocity, \( \omega /k \), the second by the orbital one, \( \omega a \). The factor \( ka \) is the steepness of the wave (typically ~ 0.1, which determines the smallness of the Stokes drift with respect to the mentioned velocities. For the wave spectrum, S(ω), Eq. 2 for USt has the evident generalization. For potential gravity waves in deep water, the value of the Stokes drift can be estimated by (Churchill and Csanady 1983),

$$ U_{st} (z) = (2/g)\int\limits_{{\omega_{\text{min} } }}^{{\omega_{\text{max} } }} {\omega^{3} } S(\omega )\exp (2\omega^{2} z/g)d\omega , $$
(3)

where g is the acceleration due to gravity, [ωmin, ωmax] is the available frequency band of the wave spectrum S(ω), and z is the vertical coordinate directed positively upward. Equation 2 allows for a simple estimating of the Stokes drift at the surface, USt(0), for a given spectrum S(ω), to exclude it from the measured current when necessary. As shown (Wu 1975, 1983; Churchill and Csanady 1983; Longo et al. 2012a), the Stokes drift at the surface, USt(0), has a typical empirical value of about 10-15% of the wind-drift Ud. This indicates the necessity of taking USt into account in measurements and practical tasks, especially in the presence of intensive long waves that have high phase velocities (e.g., swell).

However, in the context of our task (see the end of Sect. 1.1), we do not consider the Stokes drift, keeping in mind its additive feature. The effect of the Earth’s rotation is also not taken into account below. This simplification, widely accepted in laboratory measurements (Wu 1975, 1983; Longo et al. 2012a; Zavadsky and Shemer 2017), requires adopting the approximation of the “spatial locality” for the air–sea interaction processes at the wavy water surface. Theoretical justification for applicability of this approach is discussed in the next section.

1.3 Main Theoretical Approaches to the Problem

Despite a long history of theoretical study of the dynamics of the WBL (e.g., Huang 1979; Kitaigorodskii et al. 1983; Lumley and Terray 1983; Anis and Moum 1995; Mellor 2001; Qiao et al. 2004; Babanin 2006; Rascle and Ardhuin 2009; Chalikov and Rainchik 2011; Babanin and Chalikov 2012; Benilov 2012; Teixeira 2018; and numerous references therein), at present there is no theoretical model that describes the wind-drift current at a wavy surface in a simple form that would be relevant to the known experimental data (e.g., Wu 1975, 1983; Babanin 2006; Longo et al. 2012a). Most of the mentioned studies deal with the modelling of turbulent motions or current profiles in the WBL rather than with the drift current at a wavy surface.

In particular, one may mention Shemdin (1972), Bye (1988), Kudryavtsev et al. (2008), Polnikov and Kabatchenko (2011), Teixeira (2018), among others, where these authors attempted to explain some features of the surface drift induced by the airflow. Shemdin (1972) fixed experimental values Ud(0) to about 3% of the wind speed at 10 m, W(10) (W10 is used for short hand), and found the logarithmic profile for Ud(z), then he attempted to derive theoretically this profile from the two-dimensional Navier–Stokes equations for an ideal fluid with a regular harmonic wave on the surface. His theoretical approach is not accurate enough, since he missed the averaging of the governing equations over the wave scales, without which it is impossible to obtain the mean drift current.

Bye (1988) attempted theoretically to explain the values of surface flows observed in open sea, but, in fact, based on the Toba spectrum for wind waves, he only found estimates for surface values of the Stokes drift rather than for the wind drift.

A more complex analysis in this direction was done by Teixeira (2018), based on a first-order turbulence closure for the momentum flux in the upper layer. He developed an analytical model for the current profile in the upper water layer, induced by the airflow and modified by wind waves at the surface. Combining the logarithmic profile for the drift current and the exponential profile for the Stokes drift, he considered “the effect of a vortex force representing the Stokes drift of the waves”. By means of partitioning the wind stress between the production of the shear current and the wave-induced drift, he found that, under the wavy layer, the apparent friction velocity is reduced and the roughness length is enhanced with respect to the values expected from the total stress. Finally, this result was applied to the detailed comparison with experimental data of Cheung and Street (1988) and Kudryavtsev et al. (2008), to describe the empirical features of the drift-current profiles.

The study of Kudryavtsev et al. (2008) was devoted to the peculiarities of the vertical structure for the wind-driven current in the open sea. In the experimental part, they measured the drift-current gradients at different levels below the mean surface and found that the velocity gradients beneath the surface are several times smaller than in the “wall” boundary layer. In the theoretical part, they attempted to explain the experimental results, and to this end, they constructed their own version of the WBL dynamics based on the balance equations for kinetic energy, written in the framework of the full Navier–Stokes equations without the Coriolis force, according to the formulation of Anis and Moum (1995). In this approach, as usual, they were required to introduce many physical assumptions on the sources and sinks of turbulence beneath a wavy surface, provided by the shear instability and wave breaking. This theory results in a system of complicated equations describing the vertical profile, though without a direct relation to the values of the current at the surface.

To our knowledge, the only attempt to derive an explicit relation for the surface-drift current, Ud(0), was made by Polnikov and Kabatchenko (2011). To this end, we applied the concept of the logarithmic profile for Ud(z), extending it down to the Ekman depth:\( d_{E} = u_{*w} /\varOmega \sin (\varphi ) \) (where \( u_{*w} \) is the friction velocity in water, Ω is the Coriolis frequency, and φ is the latitude of the location of the Earth under consideration). As of now, this approach seems vulnerable, because it includes rather arbitrary assumptions about the roughness length z0 for the logarithmic profile beneath a water surface, which are not based on the real structure of the air–sea interface.

In this regard, we should note that in a model for the drift current, it is not necessary to take into account the Earth’s rotation and the Coriolis terms in the equations of motion. Such a simplification can be justified by the fact that the wind-drift current is the local phenomenon that can arise even in a small laboratory tank. For this reason, all work dealing with the ocean-scale surface drift (or with the WBL dynamics) and accounting for the Earth’s rotation (e.g., Mellor 2001; Rascle and Ardhuin 2009; Janssen 2012) and the Langmuir circulation (e.g., Huang 1979; Grant and Belcher 2009) are not considered. The detailed analysis of the drift-current profiles, done by Kudryavtsev et al. (2008) or Teixeira (2018) without accounting for the Coriolis force, supports the applicability of the mentioned simplification.

Thus, at present, there is a need for constructing a theoretical model for the wind-induced drift current at a wavy surface, which would be simpler than the models mentioned above (e.g., Kudryavtsev et al. 2008; Teixeira 2018), though it should have both physical and practical significance. The physical interest is determined by the aspiration of clarifying the nature of this phenomenon. The practical aspect is important for solving the problems of navigation, safety of marine activity, and managing environmental tasks.

There is only one suitable theoretical model that provides an explicit estimate for value of the wind-induced drift current at the water surface (Polnikov and Kabatchenko 2011). However, the approach used herein is questionable, as noted above. This circumstance has its own reason, and in our mind, the relevant solution of this problem requires the use of detailed experimental data on the structure of a wavy air–sea interface. Such understanding of the problem was only recently achieved after the combined analysis of the results in Polnikov (2010, 2011) and in Longo et al. (2012a, b) (see below Sect. 2.2). This understanding provides an opportunity for constructing the aforementioned model.

2 Empirical Data and Analysis

In this topic there is much experimental data dealing with numerous parameters of the interface system, as mentioned in Sect. 1.2. To our aim, we refer to those that concern only the empirical relations for the surface wind-drift, Ud (hereafter, the zero-level index is omitted), and the velocity profiles, Ud(z), in the vicinity of the air–sea interface. Leaving description of the interface structure and the current profiles for the subsequent sub-section, we consider first the empirical relations for Ud. All these results are referred to the long-term averaged drift current, Ud, traditionally prescribed to the mean water surface.

2.1 Relations for U d, and the Questions to be Answered

We start from the measurements of the wind-induced drift velocity at a water surface Ud, performed in laboratory tanks under strictly controlled conditions (Wu 1975, 1983; Longo et al. 2012a, b; Zavadsky and Shemer 2017). In the classic work of Wu (1975), the following relation was found,

$$ U_{d} = c_{d} u_{*a}^{{}} , $$
(4)

where \( u_{*a}^{{}} \) is the friction velocity in the ABL, and cd ≈ 0.53. The value of \( u_{*a}^{{}} \) was estimated in Wu (1975) by measuring wind speed ​​W(z) at a number of horizons z and using the standard logarithmic law for the wind profile in the ABL,

$$ W(z) = (u_{*a} /\kappa )\ln (z/z_{0} ). $$
(5)

In Wu (1983) there was noted the non-monotonic behaviour of the ratio Ud/\( u_{*a} \) with a growing wind, though a regular variability of this ratio with changing \( u_{*a} \) was not fixed. Herewith, the expected dependence of \( u_{*a} \) on fetch (Donelan 1988; Drennan et al. 2003) was not noted in Wu (1975, 1983), apparently because of the short length of the tank. Besides, it is also important to note that no explicit dependence of Ud on wave parameters was fixed in Wu (1975, 1983).

Hereafter, we keep in mind the following wave parameters (at point x): the significant wave height, HS ≈ 4 h, where h is the standard deviation of the wave record η(t); the wave steepness, ε = kph, where kp is the wavenumber corresponding to the peak frequency, ωp, of the wind–wave spectrum, S(ω); and the wave age, A, defined as A = cph(ωp)/W10, where cph(ω) is the phase velocity at peak frequency ωp, and W10 is the wind speed at the standard reference height, z = 10 m. Values k(ω) and cph(ω) = ω/k(ω) are related to ω via the dispersion relation which for gravity waves has the form, k(ω) = ω2/g.

Relations for Ud, similar to Eq. 4, were obtained in all other experimental work, both in tanks (e.g., Bye 1988; Longo et al. 2012a; Zavadsky and Shemer 2017, and references therein) and in the field (Tsahalis 1979; Babanin 1988; Malinovsky et al. 2007; among others). These relations differ only by the coefficient cd, and no dependence of cd on the mentioned wave parameters was fixed.

For example, Longo et al. (2012a), using the most modern laboratory equipment, established a value cd ≈ 0.4. In this case, as expected, the steepness of waves decreases with the fetch (see Tables 1 and 3 in Longo 2012), though the growth of the friction velocity \( u_{*a}^{{}} \) with fetch (Table 4 in Longo 2012), accompanied by the proper growth of Ud, was also noted. In turn, Zavadsky and Shemer (2017) did not fix any dependence of Ud on fetch in their experiments, where they found cd ≈ 0.3 – 0.5.

All these differences in the laboratory measurements for Ud, obtained by different authors, are simply related to the geometry of the tanks in which the experiments were conducted. In view of the above remarks on the drawbacks of tank experiments, here we accept this interpretation for the results of the mentioned tank experiments and do not dwell on the reasons for variations of cd in such measurements.

For field measurements under a uniform wind (for example, Tsahalis 1979; Churchill and Csanady 1983; Babanin 1988; Malinovsky et al. 2007; Kudryavtsev et al. 2008), the same Eq. 4 was established for the drift velocity, though the valuesof cd vary within a wide range, from 0.24 in Babanin (1988) to 1.5 in Tsahalis (1979). (Here we do not consider more complicated cases, such as a mixed sea or wind directed opposite to the waves, but attempt to clarify the simplest situations). Such a wide scattering of cd values is due to both the natural variability of the wind–wave conditions and the technical difficulties of conducting accurate measurements in the field. The last reason, apparently, explains the lack of information regarding the explicit dependences of Ud on the wind–wave parameters, which could be realized under field conditions. However, it should be noted that both the significant scatter in the values of cd (Tsahalis 1979; Babanin 1988) and the non-monotonic dependence of the ratio Ud/\( u_{*a}^{{}} \) on W (Wu 1983) suggests a certain dependence of cd on wave parameters, which is still not established empirically.

It can be assumed that all possible dependences of drift velocity on a wave state are “hidden” in the direct proportionality between Ud and friction velocity \( u_{*a}^{{}} \), whilst the latter, as is well known, depends explicitly on the above-mentioned wave parameters: HS, ε, and A (Donelan 1988; Drennan et al. 2003; see also the data analysis in Polnikov et al. 2003 and Polnikov 2013).

The results presented above give rise to the following questions:

First, why does the drift current Ud have values on the order of the friction velocity in air, \( u_{*a}^{{}} \), when they are of the order of the friction velocity in water, \( u_{*w}^{{}} \approx 0.03u_{*a}^{{}} \), as should follow from the condition of the momentum-flux continuity at the interface (for details, see Sect. 3.1)? It is required to deduce a proper mechanism. Second, why does the empirical ratio, Ud/\( u_{*a}^{{}} \), not manifest itself in any dependence on wave parameters? The expected theoretical model has to specify the proper dependence, i.e., it should either predict a dependence of the ratio Ud/\( u_{*a}^{{}} \) on wave parameters or provide an interpretation of its absence. In Sect. 3 a model is constructed that attempts to clarify the posed questions.

2.2 The Structure of the Wavy Air–Sea Interface and the Wind-Drift Profile

Here we represent the facts confirming both the existence of the three-layer structure of the wavy air–water interface, mentioned in Sect. 1.1, and the physical expediency of accounting for such a structure in the further theoretical constructions.

For the first time, a theoretical suggestion on the three-layer structure of the wavy air–water interface (see Fig. 1) was proposed in Polnikov (2010, 2011). It was stated that this structure consists of the air boundary layer (ABL), where the air is permanently present; the wave zone, where the air and water alternate; and the water boundary layer (WBL), where the water is continuous. This conclusion was based on the results of processing the numerical simulation data obtained by Chalikov and Rainchik (2011). Polnikov (2010) showed that the wind speed, W(z), averaged over the wind–wave statistical ensemble, depends linearly on height z, from level z ≈ ─ h to level z ≈ (2–3)h, counted relative to the mean water level (here h is the standard deviation of a wavy surface).Footnote 2 This result was successfully applied for constructing the model of the ABL aimed at estimating the friction velocity in the ABL, \( u_{*a}^{{}} \), as a function of wind speed W10 and the frequency–angular wave spectrum, S(ω,θ) (Polnikov 2011, 2013).

Recently it was found (Longo et al. 2012b) that the mentioned partition is empirically confirmed in the tank measurements. This is clearly seen in Fig. 2, for a wide range of heights above the mean water level, and in the somewhat smaller range below the linear profiles for flows actually observed. Moreover, they take place both for the wind speed, W(z), and for the water current, U(z), for the range of levels corresponding to that stated above.

Fig. 2
figure 2

The general scheme for the mean-flow distribution in the interface system (from Longo et al. 2012b). The speed scales in the ABL (\( \bar{U} \)) and in the WBL (\( \bar{u} \)) are shown at the top and the bottom, respectively

Full size image

The water-current profiles, U(z), are explicitly shown in Fig. 3 for a series of points in the tank. This empirical fact, taken from Longo et al. (2012a), is presented here for clarity (with respect to the numerical results in Polnikov 2010), so far as it is relevant to the following constructions.

Fig. 3
figure 3

The measured mean current profiles \( \bar{u}(z) \) at different points in the tank (from Longo et al. 2012a)

Full size image

Note that the region between the ABL and the WBL where the linear profiles for wind speed W(z) and water current U(z) occur is, in fact, the wave zone proposed in Polnikov(2010). Below we accept that the width of this zone, Dwz, is proportional to the mean wave height,

$$ D_{wz} = c_{wz} h, $$
(6)

and according to the measurements in Longo et al. (2012a) and the numerical estimates in Polnikov (2010), cwz ≈ 3.

Outside of the wave zone, the profiles of wind speed W(z) in the ABL, and water current U(z) in the WBL, have shapes close to the wall-turbulence logarithmic law (5) with their own values for parameters \( u_{*}^{{}} \) and z0 in each boundary layer (for details, see Longo et al. 2012a, b; see also Shemdin 1972; Bye 1988; Teixeira 2018). Note that the interface structure containing the wave zone corresponds to the statistical averaging of the airflow and water flow in the vicinity of the wavy interface. Herewith, the water current at the upper boundary of the wave zone corresponds to the current at the mean water surface (Wu 1975; Longo et al. 2012a).

The physical expediency of extracting the wave zone as the constituent of the interface is stipulated by the fact that the mean wind speed and current have linear profiles in the wave zone. From the hydrodynamic point of view, the linear velocity profile is the genuine characteristic of the flow in the friction layer supported by a viscosity coefficient K that is independent of z. Due to the turbulent nature of the wave zone, the quantity K should be considered as the eddy (turbulent) viscosity, the effective relation for which (separately, in the air and in the water) is the object of the theoretical constructions.

Summarizing the facts presented here, one can draw the following conclusions: (i) the wavy interface has the three-layer structure, including the air boundary layer (ABL), the wave zone, and the water boundary layer (WBL); (ii) from the hydrodynamic point of view, the wave zone is the analogue of the friction layer located between the ABL and the WBL, where the linear velocity profiles for mean wind speed W(z) and drift current Ud(z) are realized; (iii) in the ABL and the WBL, the logarithmic profiles (5) take place for airflow W(z) and water current Ud(z), respectively, with parameters \( u_{*}^{{}} \) and z0 determined by the wind waves in the wave zone.

The first two items of these conclusions play a crucial role in the subsequent construction of the model.

3 A Model for the Wind-Induced Drift Current

3.1 Basic Grounds

While constructing the model for the wind-induced drift current, we need to keep in mind the following well-known physical features of the wavy air–sea interface system.

First of all, the phenomena and processes taking place in the system (shear air and water flows, wave motions, vertical momentum flux, effective eddy viscosity, energy transfer between waves, air and water flows) have the stochastic (turbulent) nature. Second, in practice, a major of the measured quantities are the mean values, averaged over the statistical wind–wave ensemble. Third, in theory, one should use the properly averaged motion equations to describe the mean values (as with the wind-induced drift under consideration). The latter is the main difficulty for the relevant theoretical constructions based on the exact Navier–Stokes equations (e.g., Mellor 2001; Kudryavtsev et al. 2008; Rascle and Ardhuin 2009; Janssen 2012; Teixeira 2018). Thus, there is need for an alternative approach.

In our case, the proper mean values are: the vertical momentum flux, \( \tau_{a} \), directed from the airflow to the air–sea interface (and the flux beneath a water surface, \( \tau_{w} \)); the wave parameters mentioned above (h, ε, ωp, and A); the shear wind speed, W(z), and the shear water drift, Ud(z). In addition, there is the rate of energy transfer from the airflow to the waves in the wave zone, and the back transfer from the waves to the mean and turbulent motions, taking place in the wave zone and in the WBL. The latter process is mainly realized due to wave breaking (Babanin 2009) and the wave-current interactions via the Reynolds stresses (Monin and Yaglom 1971; Phillips 1977; Polnikov 2012).

The direct energy-exchange process (from the airflow to the waves) is usually taken into consideration by means of partitioning the momentum transfer in the air, \( \tau_{a} \), into two parts (e.g. Janssen 1991; Makin and Kudryavtsev 1999; Polnikov 2011; Teixeira 2018). The first relates to the stochastic (turbulent) current production, the other to the wave-energy generation. The reverse energy-transfer process from the waves to water currents is much more complex, and is not completely known and is usually described through suitable parametrization (e.g., Kudryavtsev et al. 2008; Rascle and Ardhuin 2009; Janssen 2012; Polnikov 2012).

This means that the theoretical approach to the wind-drift problem should be considered in the framework of the turbulence theory for hydrodynamic values averaged over the wave scales. In theory, the mean values are referred to the wave-ensemble averaging, whilst for measurements this means the averaging over the scales of about several tens of the dominant wave period, 2π/ωp, and the proper number of wavelengths. Hereafter, we refer to a model as the semi-phenomenological model, if the certain theoretical relations and empirical data dealing with the mean quantities are only used for the model construction, instead of applying the exact Navier–Stokes equations and their consequences. Such a model for the wind-induced drift current is constructed below on the basis of the empirical data and theoretical results presented in Sect. 2.

3.2 The Model Initialization

We start from the wind-induced momentum flux,\( \tau_{a} \), formed in the ABL and directed to the wave zone, written in the form,

$$ \tau_{a} = - \rho_{a}^{{}} < w_{1} w_{3}^{{}} > = \rho_{a}^{{}} u_{*a}^{2} , $$
(7)

where \( \rho_{a}^{{}} \) is the air density, \( u_{*a}^{{}} \) is the friction velocity in the air, and w1 and w3 are, respectively, the x- and z-components of wind speed W far from the interface. Only one component, \( \tau_{t} \), of the total flux \( \tau_{a} \), and referred to as the “skin drag” (Donelan 1998), is consumed directly for creating surface wind drift. The remainder, \( \tau_{w} \) (the “form drag”), is supplied to the wave-energy growth (Janssen 1991; Makin and Kudryavtsev 1999; Teixeira 2018). Thus, one can write,

$$ \tau_{a} = \tau_{t} + \tau_{w} , $$
(8)

and according to the empirical estimates in Janssen (1991), Donelan (1998), Drennan et al. (2003), \( \tau_{t} \) ranges from 30 to 70% of the total flux \( \tau_{a} \). Numerical modelling of this process shows that this proportion depends on the wave state (Polnikov 2011, 2013).

The physics of the momentum-energy transformation in the air–sea interface is the following. A part of the energy acquired by the waves in the wave zone is carried away due to their progressive feature. Another part of the wave energy dissipates with the rate Ewd, transmitting the additional momentum flux to the drift current and turbulent motions both in the wave zone and in the WBL. The part of the dissipated energy, Ewd1, is consumed in the wave zone, and the remainder, Ewd2, is lost in the entire upper layer that extends down to the depth of a half of the dominant wave length (Phillips 1977). We assume that the second part of the dissipative flux, Ewd2, is completely transmitted to turbulence in the WBL.

The first part of the wave-energy dissipation rate, Ewd1, generates the turbulence in the wave zone and transmits some fraction of the momentum to the mean drift current (for example, due to wave-breaking processes). Consequently, the final value of the momentum flux transmitted to the currents in the wave zone, \( \tau_{t} \), should be higher than the value mentioned above.

Thus, we assume that the total skin drag at the upper boundary of the wave zone, \( \tau_{ta} \), can be written as

$$ \tau_{ta} \approx c_{a} \tau_{a} = c_{a} \rho_{a} u_{*a}^{2} , $$
(9)

where the value of ca ≈ 0.8–0.9 (note that the exact value of ca is not needed below).We state that it is the momentum given by Eq. 9 that forms the wind-drift in the wave zone.

The skin drag in water, \( \tau_{tw} \), should be normalized by the density of water, \( \rho_{w} \), and by virtue of the continuity of a skin drag at the entire interface, one may write,

$$ \tau_{tw} \equiv \rho_{w} u_{*w}^{2} = \tau_{ta} = c_{a} \rho_{a} u_{*a}^{2} . $$
(10)

This equation determines the friction velocity in the water, \( u_{*w}^{{}} \),

$$ u_{*w}^{2} = r_{o} \tau_{ta} \approx r_{o} c_{a} u_{*a}^{2} , $$

where \( r_{o} = \rho_{a} /\rho_{w} \)  ≈ 10−3 is the ratio of the air and water densities. It is evident that

$$ u_{*w}^{{}} \approx (r_{o} )^{1/2} u_{*a}^{{}} \approx 0.03u_{*a}^{{}} < < u_{*a}^{{}} , $$
(11)

i.e., the friction velocity in the water is much smaller than that in the air. Thus, \( u_{*w}^{{}} \) is of an order smaller than the measured surface wind-drift current, Ud, given by Eq. 4. Here we state that the friction velocity in the water is formed at the upper boundary of the WBL, i.e., at the lower boundary of the wave zone, located at level z ≤ − h. This implies that \( u_{*w}^{{}} \) should be the real scale of the drift current at the boundary between the wave zone and the WBL.

Now we may clarify the geometry of the vertical distribution of the drift current. On the basis of the observed results shown in Figs. 2, 3 (Longo et al. 2012a, b), one may assert that the drift current in the wave zone has a linear profile. In our model, we assume that the sought drift current at the surface, Ud0, is referred to the upper boundary of the wave zone. At the lower boundary of the wave zone, the drift current should be determined by the friction velocity in water, \( u_{*w}^{{}} \), as this is expected due to the momentum-flux continuity. Thus, in the layer corresponding to the wave zone, the drift current changes from a value Ud0 to a value of the order of \( u_{*w}^{{}} \).

To balance the momentum flux in the wave zone, we use first-level turbulence closure (Teixeira 2018); namely, we suppose that \( \tau_{tw} \) is balanced by the vertical gradient of the mean velocity (Monin and Yaglom 1971; Phillips 1977; Teixeira 2018). Thus, one may write

$$ \tau_{tw} /\rho_{w} = K_{t} \frac{{\partial U_{d} (z)}}{\partial z}, $$
(12)

where \( K_{t} \) is the unknown eddy (turbulent) viscosity in the wave zone, the value of which is provided by the turbulent hydrodynamics in this zone. Equation 12 plays the key role in the model under construction.

To finish the initial formulations of the model, it remains to add that in the wave zone the following conditions take place: (i) the vertical gradient of the current is constant; (ii) the value of \( K_{t} \) is also constant over the height. In the constructed model, the unknown turbulent viscosity function, \( K_{t} \), is the object of further specification.

3.3 Semi-phenomenological Approximation of the Model

The sought estimate of the velocity gradient in the wave zone is given by

$$ \frac{{\partial U_{d} (z)}}{\partial z} \approx (U_{d0} - u_{*w} )/D_{wz} \approx U_{d0} /c{}_{zw}h, $$
(13)

where Eqs. 6 and 11 are used.

The eddy viscosity function \( K_{t} \) could be parametrized by means of dimensional consideration, as is commonly used in the theory of turbulence (Monin and Yaglom 1971; Phillips 1977). To this aim, we use the following scaling parameters: (i) the characteristic length of the system is the mean wave amplitude, h; and (ii) the characteristic velocity is the drift-current value, Ud, referred to the upper boundary of the wave zone (subindex 0 is omitted for simplicity). In this case, one may write

$$ K_{t} = f_{t} (h,\varepsilon ,A, \ldots ) \cdot U_{d} h, $$
(14)

where \( f_{t} (h,\varepsilon ,A, \ldots ) \) is the unknown dimensionless function, depending only on the wave parameters. As a result, Eq. 13 gains the form of the equation that provides the drift velocity Ud at the upper boundary of the wave zone,

$$ r_oC_au_{*a}^2(.)=[f_tU_dh] (U_d/c_{zw}h)=f_t(.)U_d^2/c_{cw} $$
(15)

Here (.) is the symbolic sign added for completeness, to take into account the known dependences of friction velocity \( u_{*a}^{{}} \) on the wave spectrum S, wind speed W10, and wave parameters (Donelan 1998; Drennan et al. 2003), and the possible analogous dependences for the dimensionless function ft(.).

From Eq. 15 one can immediately find the solution to the sought drift velocity,

$$ U_{d} = \left[ {r_{o} c_{a} c_{zw} /f_{t} (.)} \right]^{1/2} u_{*a}^{{}} . $$
(16)

For values \( c_{a} \) = 0.8 and \( c_{zw} \) = 3, Eq. 16 yields the result that coincides with the measurements in the range of observed values, \( U_{d} \approx (0.3 - 0.5){u_{*a}^{{}}} \), if values of ft(.) vary within the range of 0.01 – 0.03.

Equation 16 provides the theoretical justification of empirical Eq. 4, so far as the model clarifies the reason why the values of Ud, are of an order greater than the friction velocity in the water, \( u_{*w}^{{}} \). This reason resides in the formation of the wave zone between the ABL and the WBL, in which the viscous turbulent flow of water is realized with a proper value of the eddy viscosity. Moreover, the presented model prompts the possible dependence of the drift current on wave parameters (via the function ft(.)), providing the answer to the second question posed in the task (see the end of Sect. 2.1).

The above finalizes our construction of the model for the wind-induced drift current.

4 Discussion

First of all, let us check the robustness of Eq. 16 to alternative parametrizations for the eddy viscosity function in Eq. 14. Consider two cases: (i) the scaling \( K_{t} \) via \( u_{*w}^{{}} \)(instead of Ud), and (ii) the case of no wind. In both cases, it is found that the functional form of Eq. 16 is fully preserved. Really, if in Eq. 14, one uses \( u_{*w}^{{}} \)(with coefficient \( f_{t2} (.) \)) instead of Ud, in view of Eq. 11, this leads to the following result,

$$ U_{d} = (r_{o} )^{1/2} \left[ {c_{a} c_{zw} /f_{t2} (.)} \right]u_{*a}^{{}} , $$
(17)

which is quite similar to Eq. 16, if a proper choice of the dimensionless function \( f_{t2} (.) \) is done. Again, if there is no wind then there are no momentum flux and no wave zone, and Eq. 12 degenerates to the zero identity. The considered cases confirm the robustness of the main Eq. 12 providing the model, and allow us to use Eq. 16 for further analysis.Footnote 3 Second, let us estimate the value of eddy viscosity \( K_{t} \) in the wave zone. For values \( c_{a} \) = 0.8 and \( c_{zw} \) = 3, we have the following estimate for \( K_{t} \),

$$ K_{t} \approx 10^{ - 2} (u_{*a} h). $$
(18)

For typical values, \( u_{*a} \) = 0.3 m s−1 and h = 1 m, Eq. 18 yields \( K_{t} \) ≈ 10−3 m2 s−1, what is of three orders greater than the kinematic viscosity of water, \( \nu_{w} \approx 10^{ - 6} \) m2 s−1 (Phillips 1977). In our mind, this is a reasonable estimate for the eddy viscosity in the turbulent wave zone.

Note that the above-mentioned estimate for the turbulence-intensity coefficient, ft(.) ≈ 0.01–0.03, is also quite reasonable. For example, the Phillips parameter, αPh, in the relation for the saturated wind–wave spectrum, \( S(\omega ) = \alpha_{Ph} g^{2} \omega^{ - 5} \), has the magnitude αPh ≈ 0.01 (Phillips 1977). Another example is the Charnock parameter, αCh, defined by the relation, \( \alpha_{Ch} = z_{0} /(u_{*a}^{2} /g) \), and has the same order (Phillips 1977). Moreover, the both dimensionless values are functions of the wave parameters and the wave-formation factors and vary within a wide range (Phillips 1977). The same property may be also assumed for the function ft(.), which leads to very interesting predictions.

Indeed, according to the observations (Sect. 2.1), the drift velocity Ud depends on the friction velocity in the air only. The explicit dependences of Ud on the wave parameters have not yet been established in the experiments. This can be caused either by the physics of the processes considered, resulting in the invariability of the function ft(.), or by the lack of proper experimental data. In this regard, Eq. 16 provides a more detailed description of the drift-current properties.

Following the model described by Eq. 12, all possible dependencies of the drift velocity on wave parameters, Ud (ε, A,…), are determined by the parametrization of drift-current gradient ∂Ud/∂z and eddy viscosity \( K_{t} \). Estimate (13) for the vertical gradient of the drift current in the wave zone is fully based on the measurements. Thus, this estimate does not allow any changes, and the same is valid for the dimension of value \( K_{t} \) in Eq. 14. So, the explicit inverse dependence of gradient ∂Ud/∂z on the wave height in Eq. 13 is compensated by the explicit linear dependence of eddy viscosity \( K_{t} \) on h in Eq. 14. Therefore, the only degree of freedom, leaving room for any additional dependence of \( K_{t} \) on the wave parameters, is the specification of a parametrization for the dimensionless function ft(.).

Since function ft(.) is responsible for the magnitude of the eddy viscosity, it is necessary to search for physical processes in the wave zone that might change the intensity of mixing processes in this zone and, thus, influence the magnitude of the eddy viscosity, i.e., on the value of ft(.). The most likely processes of such a kind can be: (i) the micro- and macro-breaking of wave crests (Longo et al. 2012a); (ii) the shear instability of orbital wave motions. The intensity of the first process, obviously, must grow with increase in wave steepness (Babanin 2009). In turn, the instability of wave motions may increase with increasing wave amplitude (including the process of wave-age growth and the peak-frequency downshifting) due to increasing the local Reynolds number, Re, referred to the orbital wave motions. According to Babanin (2006),

$$ Re \equiv h^{2} \omega_{p} /\nu_{w} = (hk_{p} )^{2} \omega_{p} /(k_{p}^{2} \nu_{w} ) \propto \varepsilon^{2} /(\omega_{p}^{3} \nu_{w} ), $$
(19)

and the wave-induced turbulence emerges when Re > 103, allowing an estimate of the wave parameters corresponding to growth in the wind-drift.

An increase in the breaking intensity is also possible for sharp wave crests, appearing with the wave-age growth due to the additional horizontal impact of the wind on the crests (Babanin 2009). Herewith, in any case, an increase of intensity of the vertical motions in the wave zone corresponds, obviously, to a decrease in eddy viscosity, i.e., to the decrease in the value of ft(.).

This discussion leads to the inference that the function ft(.) could decrease with increase in both the steepness of waves and their age. As a result, according to Eq. 16, one can expect an increase in Ud/\( u_{*a} \) with increasing wave steepness ε and age A.

It is impossible to predict theoretically the functional form of the dependences Ud (ε) and Ud(A) because of the stochastic nature of the instability processes forming these dependences. Besides, it needs to be kept in mind that with the growing wave age A, both wave steepness ε and friction velocity \( u_{*a} \) (depending on ε) tend to decrease (Drennan et al. 2003). Therefore, with increasing A, multidirectional trends occur, which can compensate each other to a large extent, canceling out the potential dependence of the drift velocity on age, Ud(A). Nevertheless, in future experiments, it seems reasonable to search for the possible empirical dependences of the ratio Ud/\( u_{*a} \) both on wave steepness ε and on age A, in addition to the explicit proportionality, Ud\( \propto \)\( u_{*a} \), already established.

5 Conclusions

The results presented above allow us to draw the following conclusions.

  1. 1.

    On the basis of the empirical facts (Longo et al. 2012a, b), the theoretical concept of the three-layer structure for the air–sea interface is justified. This states that the region between the air and water boundary layers, where air and water are present alternately, has its own statistical features. This region, having a depth of about three mean wave heights, is referred to as the wave zone.

  2. 2.

    The measured surface wind-induced drift current, Ud, is formed at the upper boundary of the wave zone. In the entire wave zone, the drift current has a linear profile, experimentally established in (Longo et al. 2012a, b) (Figs. 2, 3). This fact allows considering the wave zone as an analogue of the friction layer, where the vertical wind-induced momentum flux, \( \tau_{tw} \), and the eddy viscosity, \( K_{t} \), are constant.

  3. 3.

    The proposed model for the wind-induced drift current is based on the balance between the vertical momentum flux and the vertical gradient of the drift velocity multiplied by the eddy-viscosity function, \( K_{t} \) (Eq. 12). This function is parametrized by means of the dimensional consideration via Eq. 14.

  4. 4.

    This model provides the empirically found linear proportionality between the surface-drift current Ud and friction velocity in air, \( u_{*a} \) (Eq. 16). The modelled values of Ud become equal to empirical values \( U_{d} \approx (0.3 - 0.5)u_{*a}^{{}} \), if the dimensionless parameter for the eddy viscosity, ft, introduced in Eq. 14, varies within the range 0.01–0.03.

  5. 5.

    The concept of the turbulent wave zone, as the constituent of the air–sea interface, plays the key role in the theoretical justification of the observed values for the surface wind-induced drift current.

  6. 6.

    In the more general case, Eq. 16 predicts a possible increase in the ratio Ud/\( u_{*a} \) with an increase in mean wave steepness ε and age A. The physical basis for this effect is the increase in wave-breaking intensity with the growth of ε or A, resulting in the increase of the vertical mixing intensity. The latter corresponds to the decreasing eddy viscosity \( K_{t} \), which can only be implemented by the decreasing dimensionless function ft(ε, A…) (Eq. 14). Finally, this results in an increase in Ud/\( u_{*a} \).

  7. 7.

    Verification of existing explicit empirical dependences of Ud/\( u_{*a} \) on the wave parameters, ε, A and others, requires further experimental study accompanied with stern checking and reliable evidence of the results determined.