Probabilistic independence axiom

Abstract

One of the most well-known theories of decision making under risk is expected utility theory based on the independence axiom. The independence axiom postulates that decision maker’s preferences between two lotteries are not affected by mixing both lotteries with the same third lottery (in identical proportions). The probabilistic independence axiom (also known as the cancelation axiom) extends this classic independence axiom to situations when a decision maker chooses in a probabilistic manner (i.e., she does not necessarily prefer the same choice alternative when repeatedly presented with the same choice set). Probabilistic choice may occur for a variety of reasons such as unobserved attributes of choice alternatives, imprecision of preferences, random errors/noise in decisions. According to probabilistic independence axiom, the probability that a decision maker chooses one lottery over another does not change when both lotteries are mixed with the same third lottery (in identical proportions). This paper presents a model of probabilistic binary choice under risk based on this probabilistic independence axiom. The presented model generalizes an incremental expected utility advantage model of Fishburn (Int Econ Rev 19(3):633–646, 1978) and stronger utility model of Blavatskyy (Theory Decis 76(2):265–286, 2014).

Traditional theories of decision making under risk such as expected utility (von Neumann and Morgenstern 1947) are based on a binary preference relation as a primitive of choice. A decision maker with deterministic preferences generally¹ chooses the same choice alternative when repeatedly presented with the same choice set except for the special case of indifference between two or more most preferred choice alternatives. Yet, decision makers often choose in a probabilistic manner, i.e., they do not necessarily stick to the same choice alternative when repeatedly presented with the same choice set within a short period of time. For example, Camerer (1989, p. 81) reports that 31.6% of experimental subjects reverse their preferences over risky lotteries. Starmer and Sugden (1989, p. 170) report that 25.8% (28.3%) of experimental subjects reveal inconsistent preferences over risky lotteries with positive (negative) outcomes when presented with an identical binary choice within a short period of time. Hey and Orme (1994, p. 1296) find the average inconsistency rate of 25% for binary choice under risk. Ballinger and Wilcox (1997, p. 1100) report a median switching rate of 20.8% for binary choice under risk.

Probabilistic choice may occur for a variety of reasons such as unobserved attributes of choice alternatives (e.g., McFadden 1976), imprecision of preferences (Falmagne 1985; Butler and Loomes 2007, 2011), random errors/noise in decisions (e.g., Fechner 1860; Hey and Orme 1994). The main approaches to modeling probabilistic choice are random utility (also known as random preference or random parameter) approach (e.g., Falmagne 1985; Loomes and Sugden 1995), Fechner's (1860) model of random errors (also known as strong utility), Luce's (1959) choice model (also known as strict utility or multinomial logit), an incremental expected utility advantage model of Fishburn (1978), a constant error (tremble) model of Harless and Camerer (1994), the stronger utility model of Blavatskyy (2014), and the contextual utility model of Wilcox (2008, 2011).

One of the most well-known theories of decision making under risk is expected utility theory first proposed by Bernoulli (1738/1954) for resolving the St. Petersburg paradox. Expected utility theory gained momentum in microeconomics after von Neumann and Morgenstern (1947, Chapter 3 and Appendix) developed its first behavioral characterization. Von Neumann and Morgenstern (1947) imposed their behavioral assumptions (axioms) on a binary preference relation with a key assumption being the independence axiom. The independence axiom postulates that decision maker’s preferences between two lotteries are not affected by mixing both lotteries with the same third lottery (in identical proportions).

When decision makers choose in a probabilistic manner, a probabilistic analogue of this axiom is the probabilistic independence axiom (cf. Blavatskyy 2014, axiom 4, p. 277), which is also known as the cancelation axiom (cf. Fishburn 1978, axiom A3, p. 636) or linearity (cf. Gul and Pesendorfer 2006, p. 128). According to the probabilistic independence axiom, the probability that a decision maker chooses one lottery over another does not change when both lotteries are mixed with the same third lottery (in identical proportions). Existing models of probabilistic choice under risk that satisfy this axiom include the binary random expected utility (cf., Loomes 2005, p. 306), an incremental expected utility advantage model of Fishburn (1978), a constant error model of Harless and Camerer (1994), and the stronger utility model of Blavatskyy (2014).² These models, however, combine the probabilistic independence axiom with other assumptions that are arguably less intuitively appealing compared to the independence axiom. This paper considers a model of probabilistic choice that purely satisfies the probabilistic independence axiom (without any additional non-standard assumptions) and generalizes the above-mentioned models of probabilistic binary choice under risk.

The remainder is organized as follows. Section 1 presents our mathematical notation and formulates the probabilistic independence axiom. Section 2 presents our model of probabilistic choice derived purely from this axiom. Section 3 compares the goodness of fit of this model to that of other existing models using experimental data collected by Loomes and Sugden (1998). Section 4 presents an insurance example. Section 5 concludes.

1 Mathematical notation and probabilistic independence axiom

We work in the classic framework of von Neumann and Morgenstern (1947). Let X denote a finite non-empty set of $n \in {\mathbb{N}}$ outcomes. An outcome x ∈ X can be a consumption bundle, a portfolio of financial assets, a stream of intertemporal outcomes, a behavioral strategy, a health state, the afterlife (cf. Pascal 1670) etc. Choice alternatives are risky lotteries—probability distributions over the set of outcomes X. Let L(p₁,…,p_n) denote a (simple) lottery that yields outcome x_i ∈ X with probability p_i ∈ [0,1], i ∈ {1,…,n}, $\sum\nolimits_{i = 1}^{n} {p_{i} = 1.}$ The set of all lotteries is denoted by ${\mathcal{L}}$. For any two lotteries $L\left( {p_{ 1} , \ldots ,p_{n} } \right) \in {\mathcal{L}}\;{\text{and}}\;L^{{\prime }} \left( {q_{ 1} , \ldots ,q_{n} } \right) \in {\mathcal{L}}$ and probability α ∈ [0,1] let αL + (1 − α)L′ denote a compound lottery that yields outcome x_i ∈ X with probability αp_i + (1 − α) q_i, i ∈ {1,…,n}.

Finally, for any two distinct³ lotteries $L \in {\mathcal{L}}$ and $L^{{\prime }} \in {\mathcal{L}},L^{{\prime }} \, \ne \,L,$ let P(L,L′) ∈ [0,1] denote the probability that a decision maker chooses lottery L over lottery L′ in a direct binary choice. For example, P(L,L′) = 1 represents a strict preference for lottery L over lottery L′, i.e., a decision maker always chooses L over L′. Similarly, P(L,L′) = 0 represents a strict preference for lottery L′ over lottery L, i.e., a decision maker never chooses L over L′. Finally, P(L,L′) ∈ (0,1) represents a decision maker who sometimes chooses lottery L and sometimes lottery L′ when facing a binary choice between L and L′.

We assume that a binary choice probability function $P:{\mathcal{L}}\, \times \,{\mathcal{L}} \to \left[ {0, 1} \right]$ satisfies the probabilistic independence axiom (Axiom 1). This axiom appears as Axiom A3 (cancelation) in Fishburn (1978, p. 636) and axiom 4 in Blavatskyy (2014, p. 277). Gul and Pesendorfer (2006, p. 128) use a more general notion of linearity that is equivalent to Axiom 1 if we restrict their choice sets to binary choice sets considered in this paper. Note that Axiom 1 becomes the classic independence axiom of expected utility theory if P(L,L′) = 1 is interpreted as a strict preference for L over L′ and P(L,L′) ∈ (0,1) is interpreted as indifference between L and L′. Thus, Axiom 1 generalizes the classic independence axiom.

Axiom 1

(Probabilistic independence axiom) P(L,L′) = P(αL + (1 − α)L″, αL′ + (1 − α)L″) for any three lotteries $L,L^{{\prime }} ,L^{{\prime \prime }} \in {\mathcal{L}},L^{{\prime }} \, \ne \,L,$ and any probability α ∈ (0,1].

2 A model of probabilistic binary choice under risk

Let us consider any two distinct lotteries $L\left( {p_{ 1} , \ldots ,p_{n} } \right) \in {\mathcal{L}}$ and $L^{{\prime }} \left( {q_{ 1} , \ldots ,q_{n} } \right) \in {\mathcal{L}}.$ For convenience, we number outcomes so that p_i≥ q_i for all i ∈ {1,…,k} and q_j> p_j for all j ∈ {k + 1,…,n} for some k ∈ {1,…,n − 1}. Note that if lotteries L and L′ are distinct and probabilities of all possible outcomes in each lottery sum up to one then there is at least one outcome i ∈ {1,…,k} such that p_i> q_i and there is at least one outcome j ∈ {k + 1,…,n} such that q_j> p_j.

Proposition 1

Axiom 1 holds if and only if for any two distinct lotteries $L\left( {p_{ 1} , \ldots ,p_{n} } \right) \in {\mathcal{L}}{\text{ and}}\;L^{{\prime }} \left( {q_{ 1} , \ldots ,q_{n} } \right) \in {\mathcal{L}}.$

$$P\left( {L,L '} \right) = F\left( {\frac{{p_{1} - q_{1} }}{{\mathop \sum \nolimits_{i = 1}^{k} \left( {p_{i} - q_{i} } \right)}}, \ldots ,\frac{{p_{k - 1} - q_{k - 1} }}{{\mathop \sum \nolimits_{i = 1}^{k} \left( {p_{i} - q_{i} } \right)}},\frac{{q_{k + 1} - p_{k + 1} }}{{\mathop \sum \nolimits_{j = k + 1}^{n} \left( {q_{j} - p_{j} } \right)}}, \ldots ,\frac{{q_{n - 1} - p_{n - 1} }}{{\mathop \sum \nolimits_{j = k + 1}^{n} \left( {q_{j} - p_{j} } \right)}}} \right)$$

(1)

where $F:\left[ {0,1} \right]^{n - 2} \to \left[ {0,1} \right]$ is an arbitrary function.

The proof is presented in “Appendix”.

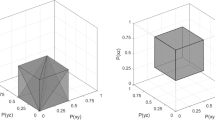
Any two distinct lotteries $L \in {\mathcal{L}}{\text{ and}}\;L^{{\prime }} \in {\mathcal{L}},L^{{\prime }} \, \ne \,L$ can be represented as a vector in the unit simplex in [0,1]ⁿ⁻¹. Consider pairs of lotteries that are represented by parallel vectors. When are choice probabilities in these pairs the same across all pairs? According to Proposition 1 this holds if and only if the choice probabilities satisfy the probabilistic independence Axiom 1. Figure 1 illustrates model (1) in the probability simplex for lotteries over n = 4 outcomes. Model (1) can be interpreted as a reduced-form econometric model where choice probabilities depend only on lotteries’ parameters (probabilities of various outcomes).

Fig. 1

Illustration of model (1) in the probability simplex for lotteries over n = 4 outcomes

3 Lotteries over three outcomes (n = 3)

The simplest non-trivial⁴ decision under risk is when lotteries have only three outcomes (n = 3). For a binary choice between a relatively riskier lottery L, which yields the least desirable outcome with probability p₁ and the most desirable outcome with probability p₂, and a relatively safer lottery L′, which yields the least desirable outcome with probability q₁ < p₁ and the most desirable outcome with probability q₂ < p₂, model (1) becomes

$$P\left( {L,L '} \right) = F\left( {\frac{{p_{1} - q_{1} }}{{p_{1} - q_{1} + p_{2} - q_{2} }}} \right)$$

(2)

where $F:\left[ {0,1} \right] \to \left[ {0,1} \right]$ is an arbitrary function. For example, the stronger utility model of Blavatskyy (2014) is a special case of Eq. (2) when function F takes the form

$$F(x) =\Phi \left( {\frac{1 - u - x}{{\sigma \left[ {1 - u - \left( {1 - 2u} \right)x} \right]}}} \right),$$

(3)

where Φ is the cumulative distribution function of the standard normal distribution,⁵σ > 0 is a free parameter that is interpreted as the variance of random errors and u ∈ [0,1] is a free parameter that is interpreted as the Bernoulli utility of the middle outcome (under conventional normalization⁶). On top of the probabilistic independence Axiom 1, the stronger utility model of Blavatskyy (2014) employs an additional assumption that binary choice probabilities depend only on the difference in contextual probability equivalents (Blavatskyy 2014, Axiom 5, p. 278).⁷ The intuition of this additional assumption is quite simple—the higher is the contextual probability equivalent of L compared to that of L′, the more L is likely to be chosen over L′. From an empirical point of view this additional assumption can be evaluated by eliciting contextual probability equivalents and testing whether binary choice probabilities are positively correlated with greater differences in contextual probability equivalents.

As another example, an incremental expected utility advantage model of Fishburn (1978) is a special case of Eq. (2) when function F takes the form

$$F\left( x \right) = \frac{{\left( {1 - u} \right)^{\rho } \left( {1 - x} \right)^{\rho } }}{{\left( {1 - u} \right)^{\rho } \left( {1 - x} \right)^{\rho } + u^{\rho } x^{\rho } }}$$

(4)

where ρ > 0 is a free noise parameter and u ∈ [0,1], as before, denotes the Bernoulli utility of the middle outcome (under conventional normalization). Model (4) also coincides with the model of probabilistic choice proposed by Blavatskyy (2011, 2012) with a power function φ. On top of the probabilistic independence Axiom 1, the incremental expected utility advantage model of Fishburn (1978) employs an additional assumption that the odds of binary choice probabilities depend only on the ratio of contextual probability equivalents. The intuition of this additional assumption is the following—the higher is the contextual probability equivalent of L compared to that of L′, the better are the odds that L is chosen over L′. From an empirical point of view this additional assumption can be evaluated by eliciting contextual probability equivalents and testing whether the odds of binary choice probabilities are positively correlated with greater ratios of contextual probability equivalents.

A constant error (tremble) model of Harless and Camerer (1994) is a special case of Eq. (2) when function F takes the form

$$F\left( x \right) = \frac{1}{2} + \left( {\frac{1}{2} - \tau } \right)sgn\left( {1 - u - x} \right)$$

(5)

where τ ∊ [0,0.5] denotes the probability of a tremble (constant error), u ∊ [0,1], as before, denotes the Bernoulli utility of the middle outcome and sgn(.) is the sign function. On top of the probabilistic independence Axiom 1, the constant error (tremble) model of Harless and Camerer (1994) restricts binary choice probabilities to only three values: τ, ½, and 1 − τ. The intuition of this additional restriction is the following—a decision maker generally chooses accordingly to a deterministic preference relation but there is a constant probability of a tremble (when a decision maker chooses in contradiction to his or her preference). This additional restriction can be tested via cluster analysis.

Random expected utility of Gul and Pesendorfer (2006) is a special case of Eq. (2) when function F is a decumulative distribution function of one minus the Bernoulli utility of the middle outcome (which is a random variable in the random utility/preference approach).

Additional axioms that are used in the literature (cf. Fishburn 1978; Gul and Pesendorfer 2006; Blavatskyy 2014) in conjunction with the probabilistic independence Axiom 1 essentially restrict the functional form of F(.) in model (2) to generate various models of probabilistic choice described above. Model (2) can be also interpreted as a reduced-form econometric model of the structural econometric models (3)–(5).

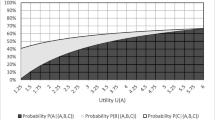
How much goodness of fit to the data is lost when a reduced-form econometric model (2) with a linear function F(.) is used instead of the non-linear structural econometric models (3)–(5)? The answer appears to be “not much” if we consider the data collected by Loomes and Sugden (1998).⁸ Figure 2 plots ratios $\left( {p_{1} - q_{1} } \right)/\left( {p_{1} - q_{1} + p_{2} - q_{2} } \right)$ on the horizontal axis and choice probabilities P(L,L′) on the vertical axis for 40 binary choice problems from Loomes and Sugden (1998), where one lottery does not first-order stochastically dominate the other lottery. Black unconnected dots represent experimental data (averaged over two repetitions and 46 subjects from the “£20 group”). The dotted line on Fig. 2 represents model (2) with the best fitting linear function F(x) = − 1.0997x + 0.6806, which results in R² = 0.678. The solid line on Fig. 2 represents model (3) with the best fitting parameters σ = 0.515 and u = 0.795, which results in R² = 0.689. The dashed line on Fig. 2 represents model (4) with the best fitting parameters ρ = 1.422 and u = 0.798, which results in R² = 0.696. Thus, model (2) with a linear function F(.) fits the experimental data almost as well as non-linear models (3) and (4).

Fig. 2

Goodness of fit to data collected by Loomes and Sugden (1998), the “£20 group”

Figure 3 mirrors Fig. 2 for experimental data collected by Loomes and Sugden (1998) from the “£30 group”. The dotted line on Fig. 3 represents model (2) with the best fitting linear function F(x) = − 1.236x + 0.9136, which results in R² = 0.534. The solid line on Fig. 3 represents model (3) with the best fitting parameters σ = 0.606 and u = 0.671, which results in R² = 0.529. The dashed line on Fig. 3 represents model (4) with the best fitting parameters ρ = 1.265 and u = 0.671, which results in R² = 0.531. Thus, model (2) with a linear function F(.) fits the data from the “£30 group” slightly better than non-linear structural models (3) and (4).

Fig. 3

Goodness of fit to data collected by Loomes and Sugden (1998), the “£30 group”

4 Example: insurance

This section shows how a probabilistic choice model based on the probabilistic independence Axiom 1 is applied to a decision problem of insurance coverage. Let us consider a decision maker with wealth w > 0 who faces a loss D ∊ (0,w) with probability π ∊ (0,1). This decision maker can buy actuarially fair insurance. If the decision maker decides to insure completely against the loss, he or she pays the insurance premium πD and receives compensation D when the loss happens.

If the decision maker stays uninsured, he or she faces a binary lottery that yields w − D with probability π and w with probability 1 − π. If the decision maker insures completely, he or she receives w − πD for certain (regardless of the state of the world). According to model (2) based on the probabilistic independence Axiom 1, the probability that the decision maker chooses no insurance coverage over full insurance is F(π). Special cases of model (2) are models (3)–(5), which specify the functional form of function F(.). According to models (3)–(5), the probability that the decision maker chooses to remain uninsured is greater than 50% if

$$1 - u - \pi > 0$$

(6)

where u is the normalized utility of the final wealth position in case of complete insurance. For a conventional Bernoulli utility function v, parameter u is given by Eq. (7):

$$u = \frac{{v\left( {w - \pi D} \right) - v\left( {w - D} \right)}}{{v\left( w \right) - v\left( {w - D} \right)}}$$

(7)

Plugging Eq. (7) into inequality (6) we obtain the following result. The decision maker is more likely to remain uninsured rather than fully insured if inequality (8) holds:

$$\left( {1 - \pi } \right)v\left( w \right) + \pi v\left( {w - D} \right) > v\left( {w - \pi D} \right)$$

(8)

Inequality (8) is known as Jensen’s inequality for a convex Bernoulli utility function v (Jensen 1906). Thus, a decision maker with a convex Bernoulli utility function is more likely to remain uninsured than fully insured. An analogous argument shows that a decision maker with a concave Bernoulli utility function is more likely to remain fully insured than uninsured.

5 Conclusion

Expected utility theory is based on an intuitively appealing independence axiom. For example, in a dynamic choice, where earlier decisions influence the outcomes of subsequent decisions, only a decision maker who satisfies the independence axiom is dynamically consistent. Von Neumann and Morgenstern (1947) formulated the classic independence axiom for a (deterministic) binary preference relation over lotteries. Yet, empirical evidence suggests that decision makers choose under risk in a probabilistic rather than deterministic manner (when there is no transparent first-order stochastic dominance between lotteries.⁹) The probabilistic independence axiom is the analogue of its classic counterpart for probabilistic choice under risk. This axiom is used as a building block (in conjunction with other axioms) in several models of probabilistic choice (cf. Fishburn 1978; Gul and Pesendorfer 2006; Blavatskyy 2014).

This paper considers implications of the probabilistic independence axiom without any additional behavioral assumptions (that are often less intuitively appealing than the principle of independence). The main theoretical result is that the probabilistic independence axiom is equivalent to a model of probabilistic choice where choice probabilities depend only on the ratios of differences in probabilities of various outcomes between two lotteries. This model of probabilistic choice generalizes several existing models such as an incremental expected utility advantage model of Fishburn (1978) and stronger utility model of Blavatskyy (2014). In this generalized model, a decision maker chooses with the same probabilities across all pairs of lotteries that are represented geometrically by parallel vectors in the probability simplex (parallel vectors have constant ratios of differences in probabilities/coordinates).

A model of choice probabilities as a simple linear function of the ratios of differences in probabilities of lottery outcomes fits experimental data collected by Loomes and Sugden (1998) equally well as non-linear structural models. This finding supports the methodology of a reduced-form linear econometric regression based on the probabilistic independence axiom.

Models of probabilistic choice have a comparative advantage over deterministic models when rationalizing the preference reversal phenomenon (Seidl 2002). A standard preference reversal is observed when a decision maker chooses the P-bet (a modest payoff with a high probability) over the $-bet (a large payoff with a small probability) in a direct binary choice but reveals a higher certainty equivalent for the $-bet than for the P-bet (e.g., Tversky et al. 1990). Models of binary (probabilistic) choice can be applied to valuations. Blavatskyy (2009, definition 1, p. 242) proposed the following definition of a probabilistic certainty equivalent. The probability that the certainty equivalent of a lottery L is less than or equal to x is the probability that a degenerate lottery that yields x for sure is chosen over L in a direct binary choice. If the P-bet and the $-bet yield the same expected utility, then a decision maker is equally likely to choose either of them in a direct binary choice. Median certainty equivalents of the P-bet and the $-bet are the same in this case. If the distribution of certainty equivalents is symmetric (as in Fechner's (1860) or Luce's (1959) choice model) then no systematic preference reversals occur. If the distribution of the certainty equivalent of the P-bet is negatively skewed and that of the $-bet positively skewed [as in models (3) and (4)], then there is a higher likelihood of standard preference reversals (Blavatskyy 2014, Sect. 4, pp. 274–276).

Appendix

Proof of Proposition 1

Consider any two distinct lotteries $L\left( {p_{ 1} , \ldots ,p_{n} } \right) \in {\mathcal{L}}{\text{ and}}\;L^{{\prime }} \left( {q_{ 1} , \ldots ,q_{n} } \right) \in {\mathcal{L}}$ such that p_i≥ q_i for all i ∊ {1,…,k} and q_j> p_j for all j ∊ {k + 1,…,n} for some k ∊ {1,…,n − 1}.

First, lottery L′(q₁,…,q_n) is a reduced-form of a compound lottery $q_{ 1} \varvec{x}_{{\mathbf{1}}} \, + \,\left( { 1 - q_{ 1} } \right)L_{1}^{{\prime }} ,$ where x₁ denotes a degenerate lottery that yields outcome x₁ for sure and $L_{1}^{{\prime }}$ denotes lottery

$$\left( {0,\frac{{q_{2} }}{{1 - q_{1} }}, \ldots ,\frac{{q_{n} }}{{1 - q_{1} }}} \right)$$

Similarly, lottery L(p₁,…,p_n) is a reduced-form of a compound lottery $q_{ 1} \varvec{x}_{{\mathbf{1}}} \, + \,\left( { 1- q_{ 1} } \right)L_{ 1} ,$ where L₁ denotes lottery

$$\left( {\frac{{p_{1} - q_{1} }}{{1 - q_{1} }},\frac{{p_{2} }}{{1 - q_{1} }}, \ldots ,\frac{{p_{n} }}{{1 - q_{1} }}} \right)$$

If Axiom 1 holds then $P\left( {L,L^{{\prime }} } \right)\, \equiv \,P\left( {q_{ 1} x_{{\mathbf{1}}} \, + \,\left( { 1- q_{ 1} } \right)L_{ 1} ,q_{ 1} x_{{\mathbf{1}}} \, + \,\left( { 1- q_{ 1} } \right)L_{1}^{{\prime }} } \right)\, = \,P\left( {L_{ 1} ,L_{1}^{{\prime }} } \right).$

Second, $L_{1}^{{\prime }}$ is a reduced-form of a compound lottery $\left[ {q_{ 2} /\left( { 1 - q_{ 1} } \right)} \right]\varvec{x}_{{\mathbf{2}}} \, + \,\left[ { 1 - q_{ 2} /\left( { 1 - q_{ 1} } \right)} \right]L_{2}^{{\prime }} ,$ where x₂ denotes a degenerate lottery that yields outcome x₂ for sure and $L_{2}^{{\prime }}$ denotes lottery

$$\left( {0,0,\frac{{q_{3} }}{{1 - q_{1} - q_{2} }}, \ldots ,\frac{{q_{n} }}{{1 - q_{1} - q_{2} }}} \right)$$

Similarly, lottery L₁ is a reduced-form of a compound lottery $\left[ {q_{ 2} /\left( { 1 - q_{ 1} } \right)} \right]\varvec{x}_{{\mathbf{2}}} \, + \,\left[ { 1 - q_{ 2} /\left( { 1 - q_{ 1} } \right)} \right]L_{2} ,$ where L₂ denotes lottery

$$\left( {\frac{{p_{1} - q_{1} }}{{1 - q_{1} - q_{2} }},\frac{{p_{2} - q_{2} }}{{1 - q_{1} - q_{2} }},\frac{{p_{3} }}{{1 - q_{1} - q_{2} }}, \ldots ,\frac{{p_{n} }}{{1 - q_{1} - q_{2} }}} \right)$$

If Axiom 1 holds then $P\left( {L_{ 1} ,L_{1}^{{\prime }} } \right)\, \equiv \,P\left( {\left[ {q_{ 2} /\left( { 1- q_{ 1} } \right)} \right]x_{{\mathbf{2}}} \, + \,\left[ { 1- q_{ 2} /\left( { 1- q_{ 1} } \right)} \right]L_{ 2} ,\left[ {q_{ 2} /\left( { 1- q_{ 1} } \right)} \right]x_{{\mathbf{2}}} \, + \,\left[ { 1- q_{ 2} /\left( { 1- q_{ 1} } \right)} \right]L_{2}^{{\prime }} } \right)\, = \,P\left( {L_{ 2} ,L_{2}^{{\prime }} } \right).$

Iterating such application of Axiom 1 for the first k outcomes we obtain that $P\left( {L,L^{{\prime }} } \right)\, = \,P\left( {L_{k} ,L_{k}^{{\prime }} } \right),$ where L_k denotes lottery

$$\left( {\frac{{p_{1} - q_{1} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }}, \ldots ,\frac{{p_{k} - q_{k} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }},\frac{{p_{k + 1} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }}, \ldots ,\frac{{p_{n} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }}} \right)$$

and $L_{k}^{{\prime }}$ denotes lottery

$$\left( {\underbrace {{0, \ldots ,0}}_{k},\frac{{q_{{k + 1}} }}{{1 - \sum\nolimits_{{i = 1}}^{k} {q_{i} } }}, \ldots ,\frac{{q_{n} }}{{1 - \sum\nolimits_{{i = 1}}^{k} {q_{i} } }}} \right)$$

Lottery L_k is a reduced form of a compound lottery

$$L_{k} \equiv \frac{{p_{k + 1} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }}\varvec{x}_{{\varvec{k} + 1}} + \left( {1 - \frac{{p_{k + 1} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }}} \right)L_{k + 1}$$

where x_k+1 denotes a degenerate lottery that yields outcome x_k+1 for sure and L_k+1 denotes lottery

$$\left( {\frac{{p_{1} - q_{1} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} - p_{k + 1} }}, \ldots ,\frac{{p_{k} - q_{k} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} - p_{k + 1} }},0,\frac{{p_{k + 2} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} - p_{k + 1} }}, \ldots ,\frac{{p_{n} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} - p_{k + 1} }}} \right)$$

Similarly, lottery $L_{k}^{{\prime }}$ is a reduced form of a compound lottery

$$L'_{k} \equiv \frac{{p_{k + 1} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }}\varvec{x}_{{\varvec{k} + 1}} + \left( {1 - \frac{{p_{k + 1} }}{{1 - \mathop \sum \nolimits_{i = 1}^{k} q_{i} }}} \right)L'_{k + 1}$$

where $L_{k + 1}^{{\prime }}$ denotes lottery

$$\left( {\underbrace {{0, \ldots ,0}}_{k},\frac{{q_{{k + 1}} - p_{{k + 1}} }}{{1 - \sum\nolimits_{{i = 1}}^{k} {q_{i} } - p_{{k + 1}} }},,\frac{{q_{{k + 2}} }}{{1 - \sum\nolimits_{{i = 1}}^{k} {q_{i} } - p_{{k + 1}} }} \ldots ,\frac{{q_{n} }}{{1 - \sum\nolimits_{{i = 1}}^{k} {q_{i} } - p_{{k + 1}} }}} \right)$$

Axiom 1 then implies $P\left( {L_{k} ,L_{k}^{{\prime }} } \right)\, = \,P\left( {L_{k + 1} ,L_{k + 1}^{{\prime }} } \right).$

Iterating such application of Axiom 1 for the remaining n − k − 1 outcomes we obtain that $P\left( {L,L^{{\prime }} } \right)\, = \,P\left( {L_{n} ,L_{n}^{{\prime }} } \right)$ where L_n denotes lottery

$$\left( {\frac{{p_{1} - q_{1} }}{{\sum\nolimits_{{i = 1}}^{k} {\left( {p_{i} - q_{i} } \right)} }}, \ldots ,\frac{{p_{k} - q_{k} }}{{\sum\nolimits_{{i = 1}}^{k} {\left( {p_{i} - q_{i} } \right)} }},\underbrace {{0, \ldots ,0}}_{{n - k}},} \right)$$

and $L_{n}^{{\prime }}$ denotes lottery

$$\left( {\underbrace {{0, \ldots ,0}}_{k},\frac{{q_{{k + 1}} - p_{{k + 1}} }}{{\sum\nolimits_{{j = k + 1}}^{n} {\left( {q_{j} - p_{j} } \right)} }}, \ldots ,\frac{{q_{n} - p_{n} }}{{\sum\nolimits_{{j = k + 1}}^{n} {\left( {q_{j} - p_{j} } \right)} }}} \right)$$

The last non-zero probability in lottery L_n is one minus the sum of the first k − 1 probabilities:

$$\frac{{p_{k} - q_{k} }}{{\mathop \sum \nolimits_{i = 1}^{k} \left( {p_{i} - q_{i} } \right)}} = 1 - \mathop \sum \limits_{r = 1}^{k - 1} \frac{{p_{r} - q_{r} }}{{\mathop \sum \nolimits_{i = 1}^{k} \left( {p_{i} - q_{i} } \right)}}$$

The last probability in lottery $L_{n}^{{\prime }}$ is one minus the sum of the proceeding n − k − 1 probabilities:

$$\frac{{q_{n} - p_{n} }}{{\mathop \sum \nolimits_{j = k + 1}^{n} \left( {q_{j} - p_{j} } \right)}} = 1 - \mathop \sum \limits_{s = k + 1}^{n - 1} \frac{{q_{s} - p_{s} }}{{\mathop \sum \nolimits_{j = k + 1}^{n} \left( {q_{j} - p_{j} } \right)}}$$

Thus, P(L,L′) can be written as function (1) of n − 2 probabilities, where function $F:\left[ {0,1} \right]^{n - 2} \to \left[ {0,1} \right]$ denotes the probability that a decision maker chooses lottery L_n over lottery $L_{n}^{{\prime }} .$****