Uncertainty and binary stochastic choice

Abstract

Experimental evidence suggests that decision-making has a stochastic element and is better described through choice probabilities than preference relations. Binary choice probabilities admit a strong utility representation if there exists a utility function u such that the probability of choosing a over b is a strictly increasing function of the utility difference $u(a) -u(b)$. Debreu (Econometrica 26(3):440–444, 1958) obtained a simple set of sufficient conditions for the existence of a strong utility representation when alternatives are drawn from a suitably rich domain. Dagsvik (Math Soc Sci 55:341–370, 2008) specialised Debreu’s result to the domain of lotteries (risky prospects) and provided axiomatic foundations for a strong utility representation in which the underlying utility function conforms to expected utility. This paper considers general mixture set domains. These include the domain of lotteries, but also the domain of Anscombe–Aumann acts: uncertain prospects in the form of state-contingent lotteries. For the risky domain, we show that one of Dagsvik’s axioms can be weakened. For the uncertain domain, we provide axiomatic foundations for a strong utility representation in which the utility function represents invariant biseparable preferences (Ghirardato et al. in J Econ Theory 118:133–173, 2004). The latter is a wide class that includes subjective expected utility, Choquet expected utility and maxmin expected utility preferences. We prove a specialised strong utility representation theorem for each of these special cases.

1 Introduction

Experiments provide robust evidence of randomness in choice behaviour, especially when choosing between risky or uncertain prospects (Loomes 2005; Wilcox 2008; Hey 2014; Hollard et al. 2016).¹ Subjects are often observed to make different choices in successive presentations of the same choice problem. Since the early 1990s increasing attention has been paid to this phenomenon, and to the way in which “noise” is modelled in the analysis of experimental data on choice behaviour.

Such lines of inquiry have prompted revisionist thinking about the descriptive merits of expected utility (EU). By 1995 John Hey was prepared to advance the following tentative hypothesis:

“[O]ne can explain experimental analyses of decision-making under risk better (and simpler) as EU plus noise – rather than through some higher level functional – as long as one specifies the noise appropriately.” (Hey 1995, p. 640)

Numerous subsequent papers have put Hey’s hypothesis to the test. Contributions such as Buschena and Zilberman (2000) and Schmidt and Neugebauer (2007) lend confirmatory evidence, though contrary evidence has also been found (e.g. Loomes and Sugden 1998; Loomes and Pogrebna 2014).

For uncertain prospects, the descriptive merits of subjective expected utility (SEU) have also become the subject of renewed debate. The experiments of Ellsberg (1961) originally discredited SEU by suggesting the prevalence of uncertainty (or ambiguity) aversion. The latter entails the possibility of a strict preference for betting on a given “risky” event—one with an objectively determined probability of occurrence—over betting on an alternative “uncertain” event—one of unknown probability—together with a strict preference for betting against the risky event over betting against the uncertain event. Various generalisations of SEU that can accommodate uncertainty aversion have been proposed, the best known of which are Choquet expected utility (Schmeidler 1989) and maxmin expected utility (Gilboa and Schmeidler 1989).

More recently, new experimental designs have cast doubt on the prevalence of uncertainty aversion and have restored some respectability to SEU. Halevy (2007), for example, found that evidence against SEU all but disappears when attention is restricted to subjects whose behaviour is consistent with the reduction of compound lotteries assumption. Approximately 18% of Halevy’s subjects behave in conformity with this assumption, and 96% of these exhibit behaviour that is consistent with SEU. Abdellaoui et al. (2016) obtain similar, though less dramatic, results. The experiments of Binmore et al. (2012) find substantial support for the principle of insufficient reason—that is, subjective expected utility maximisation with equal subjective probabilities assigned to each state—while “[t]heories that postulate a large level of ambiguity aversion all perform badly” (ibid. p. 233). The results in Hey et al. (2010) are more equivocal, but SEU still performs respectably in describing their aggregate data, and better, in the sense of minimising the prediction (i.e. out-of-sample) log-likelihood, than Choquet expected utility—see their Table 1.²

This recent experimental literature, which is ably surveyed by Hey (2014), has prompted experimentalists to think more carefully about the noise term when analysing their data. Amongst theorists, it has revived interest in probabilistic models of choice. These models characterise decision-makers through choice probabilities rather than preference relations. The theoretical challenge is to devise parsimonious, but descriptively accurate, representations for choice probabilities, validated by plausible sets of axioms.

For binary choices, Fechnerian representations are common. Consider pairs of alternatives drawn from a set A. Let P(a, b) denote the probability with which a particular decision-maker chooses a from the choice set $\left\{ a,b\right\} \subseteq A$. We call P the decision-maker’s binary choice probability function. The function P has a Fechner model, or Fechner representation, if there exists a utility function $u:A\rightarrow {\mathbb {R}}$ such that P(a, b) is a non-decreasing function of the utility difference, $u(a) -u(b)$. If P(a, b) is a strictly increasing function of this utility difference, we have a strong Fechner (or strong utility) model. In the latter case, we also say that u is a strong utility for P.

If P has a Fechner model, then binary choice behaviour can be described as “noisy” utility maximisation, with the probability of “error” being inversely related to the absolute utility difference between the two options.

There is a small literature on the axiomatic foundations of Fechner models for probabilistic choice between risky prospects, and an even smaller literature on Fechner models for choice under uncertainty.³ The relevant portions of this literature are briefly surveyed in Sect. 2. The present paper adds to this literature, with a particular focus on choice under uncertainty. Since our formal analysis requires that A has a mixture set structure (Herstein and Milnor 1953), we adopt the framework of Anscombe and Aumann (1963) to describe uncertain prospects. An Anscombe–Aumann act is a mapping from states to lotteries. We provide axiomatic foundations for strong utility models in which the utility function u may take (respectively) the subjective expected utility, Choquet expected utility (CEU) or maxmin expected utility (MEU) form. We also axiomatise a strong utility model in which u represents invariant biseparable preferences (Ghirardato et al. 2004, 2005). The latter is a rather broad class of utility functions, which contains SEU, MEU and CEU as special cases.

Our results expose the axiomatic foundations beneath “noisy” versions of the most popular models of choice under uncertainty. These are the models amongst which recent experimental work seeks to adjudicate. When assessing the descriptive accuracy of SEU, experiments such as those of Hey et al. (2010) are really assessing the descriptive credentials of SEU maximisation with Fechnerian noise. It is therefore important to understand the axioms that underpin “noisy” SEU maximisation, and those that underpin its noisy competitors. The present paper provides these axiomatic foundations.

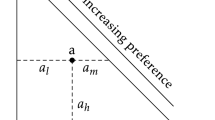
All of our representation theorems are corollaries of a more general result (Theorem 1) which, though somewhat abstract, may be of independent interest. We say that a is weakly stochastically preferred to b (denoted $a\succsim ^{P}b$) if the decision-maker is at least as likely to choose a as to choose b from the set $\left\{ a,b\right\}$. That is,

$$\begin{aligned} a\succsim ^{P}b\ \ \ \text {iff}\ \ \ P(a,b) \ge \frac{1}{2} \end{aligned}$$

(1)

Suppose $u:A\rightarrow {\mathbb {R}}$ is a utility function that represents $\succsim ^{P}$, in the usual sense that $a\succsim ^{P}b$ if and only if $u(a) \ge u(b)$. A natural question arises:

What are sufficient conditions for P to be a strictly increasing function of utility differences measured by u ?

Theorem 1 provides an answer to this question. The required conditions are joint restrictions on P and u. The restriction on u is a restricted form of linearity that we call M -linearity (Definition 3)⁴ and is partnered with a corresponding restriction on P called Strong M -Independence (Axiom 3). The latter is a weakened form of the Strong Independence axiom of Dagsvik (2008).

Many interesting classes of utility functions are M-linear (for suitable choice of M). In an Anscombe–Aumann environment, the SEU, MEU and CEU classes are all M-linear when M is the set of “constant” acts—constant mappings from states to lotteries—as we explain in Sect. 5.

To see the practical significance of Theorem 1, fix some M-linear class of utility functions, ${\mathcal {U}}$. For example, ${\mathcal {U}}$ might be the class of CEU functions in an Anscombe–Aumann environment. Theorem 1 provides a three-step “recipe” for assembling a set of conditions on P that are sufficient for the existence of a strong utility contained in ${\mathcal {U}}$:

Step 1.:

Identify axioms on preferences which are sufficient for a utility representation within the class ${\mathcal {U}}$. Such axioms will usually be available for utility classes of interest. (In the case of CEU, we could use the axioms of Schmeidler (1989), for example.)

Step 2.:

Impose these axioms on the weak stochastic preference relation, $\succsim ^{P}$, and identify the corresponding restrictions on P by using (1). The resulting restrictions on P ensure that $\succsim ^{P}$ has a utility representation $u\in {\mathcal {U}}$.

Step 3.:

Add the Strong M-Independence axiom (plus any further restrictions on P identified in Theorem 1).

This recipe allows us to leverage any axiomatically grounded model of deterministic choice, described by a family ${\mathcal {U}}$ of M-linear utility functions, into an axiomatically grounded model of stochastic choice in which a utility function from ${\mathcal {U}}$ is maximised with Fechnerian error.

The remainder of the paper is organised as follows. The next section reviews the related literature on Fechner representation theorems. Section 3 contains our main result (Theorem 1). The remaining sections present applications of Theorem 1. In Sect. 4, A is a set of lotteries (the domain of risk) and we axiomatise a strong Fechner model in which u has the EU form (Proposition 1). Dagsvik (2008, 2015) already provided axiomatic foundations for such a model, but our axioms differ from his. “Appendix 2” presents a variant of our representation theorem which shows that one of Dagsvik’s (2008) axioms can be significantly weakened without jeopardising the representation (Theorem 3). In Sect. 5, A is a set of Anscombe–Aumann acts (the domain of uncertainty). We provide four strong Fechner representation theorems for each of the following utility classes: invariant biseparable (Proposition 2),⁵ subjective expected utility (Proposition 3), maxmin expected utility (Proposition 4) and Choquet expected utility (Proposition 5). Section 6 provides some discussion of our results. “Appendix 1” contains proofs omitted from the text.

2 Related literature

There are few results on the axiomatics of Fechner, or Fechner-like, models for choice between risky or uncertain prospects. We review the key contributions here, as well as some related work on random utility models.

2.1 Risk

For the domain of risk, Blavatskyy (2008) provides sufficient conditions for the existence of a Fechner representation with u of the expected utility form.⁶ Dagsvik (2008, 2015) provides sufficient conditions for a strong Fechner representation with u of the expected utility form.⁷ In terms of axioms, the critical difference between the results of Dagsvik and Blavatskyy is the stochastic version of the independence property that is used: Strong Independence (Dagsvik 2008, Axiom 5)⁸ versus Common Consequence Independence (Blavatskyy 2008, Axiom 4).

We focus on strong Fechner models in the present paper. For the domain of risk, we obtain two sets of sufficient conditions for the existence of a strong Fechner model with u of the EU form—Proposition 1 and Theorem 3—each of which differs significantly from the axiomatisations of Dagsvik.

Following the lead of Wilcox (2008, 2011), recent experimental literature often employs “contextual” Fechner models, in which choice probabilities depend on utility differences that are “normalised” to reflect different choice contexts.⁹ In these models, the same utility difference may vary in its impact on choice depending on the particular alternatives being compared—that is, on the “context” in which the utilities arise. A standard Fechnerian logic applies within any fixed context.

For the domain of risk, Wilcox (2008, 2011) advocates a contextual model in which the relevant context consists of the best and worst possible outcomes across the two alternative lotteries under consideration. The term “contextual Fechner model” is often used to refer specifically to Wilcox’s model.

Blavatskyy (2011, 2012) suggests a different specification of context, one based on a dominance relation—first-order stochastic dominance for choice under risk (Blavatskyy 2011) or statewise dominance for choice under uncertainty (Blavatskyy 2012). If A is a set of lotteries with outcomes in ${\mathbb {R}}_{+}$ (a risky domain), with each lottery described by its associated distribution function, then the first-order stochastic dominance relation induces a lattice on A. Blavatskyy’s proposed “context” for a choice between a and b is the least upper bound and greatest lower bound for $\left\{ a,b\right\}$ within this lattice. Blavatskyy (2011) provides an axiomatic foundation for a contextual Fechner model of this sort.

All representation theorems in the present paper are for standard (i.e. context-independent) Fechner models. Our purpose is to describe a new approach to the construction of such theorems—one embodied in the “recipe” based on Theorem 1—and to use this approach to prove some new representation results, especially for the domain of uncertainty.

That said, the axiomatisation of contextual Fechner models is certainly an important task for future research, and the results of Blavatskyy (2011, 2012) are valuable first steps in this direction.

2.2 Uncertainty

For choice between uncertain prospects, the aforementioned paper by Blavatskyy (2012) is the only axiomatisation of a Fechner(-like) model of which we are aware. In Blavatskyy (2012), A is a set of Savage acts—functions from a given state space, ${\mathcal {S}}$, to an arbitrary outcome space, X (outcomes need not be lotteries)—and Blavatskyy axiomatises a model of SEU maximisation with “contextual” Fechnerian error. The context is based on a statewise dominance relation. Given a utility function $u:A\rightarrow {\mathbb {R}}$, one induces a utility function on X via the utilities of constant acts (i.e. acts that assign the same outcome to every state). We use u to denote this utility function on X also. Given Savage acts, a and b, let $a\vee b$ denote a Savage act that gives, in each state s, an outcome with utility

$$\begin{aligned} \max \left\{ u\left( a(s) \right) ,u\left( b(s) \right) \right\} \end{aligned}$$

and let $a\wedge b$ be a Savage act that gives, in each state s, an outcome with utility

$$\begin{aligned} \min \left\{ u\left( a(s) \right) ,u\left( b(s) \right) \right\} \text {.} \end{aligned}$$

Thus, a and b are mutually statewise dominated by $a\vee b$ and they mutually statewise dominate $a\wedge b$. The acts $a\vee b$ and $a\wedge b$ provide the “context” in which a and b are evaluated. In Blavatskyy’s (2012) representation, P(a, b) is a function of the normalised utility difference

$$\begin{aligned} \frac{u(a) -u(b)}{u\left( a\vee b\right) -u\left( a\wedge b\right) } \end{aligned}$$

(2)

where u has the SEU form. Blavatskyy provides a set of necessary and sufficient conditions for the existence of a representation of this form.

The present paper is complementary to Blavatskyy’s work. We consider Anscombe–Aumann acts, rather than Savage acts, and we obtain a conventional (i.e. context-independent) strong Fechner representation. In addition to providing an axiomatic foundation for a strong utility of the SEU form, we also axiomatise strong Fechner models in which u takes the CEU or MEU form, as well as a more general model in which u may represent any invariant biseparable preference ordering.

2.3 Random utility models

The main rivals to the Fechner models are the random utility models. In a random utility model, the decision-maker has a set of utility functions, one of which is randomly drawn according to a fixed probability measure whenever the decision-maker has a decision to make. The randomly selected utility function is then maximised without error. In a random utility model, P(a, b) is the probability that a utility function is selected for which the utility of a exceeds that of b.

Gul and Pesendorfer (2006) axiomatise a random expected utility model, which requires all possible utility functions to have the expected utility form. Lu (2014) provides axiomatic foundations for a random utility model for choice under uncertainty in an Anscombe–Aumann environment. In Lu’s model, utility functions are randomly selected from a subset of the MEU class.

Random utility models have the advantage that they exclude the possibility of dominated alternatives being chosen. They are also suitable for studying multinomial choice. However, they suffer from their own drawbacks. Most notably, they admit violations of Weak Stochastic Transitivity, which requires that the weak stochastic preference relation $\succsim ^{P}$ be transitive (see Luce and Suppes, 1965, Theorem 43).¹⁰ The preponderance of experimental evidence suggests that violations of Weak Stochastic Transitivity are rare (Rieskamp et al. 2006; Loomes et al. 2015).

3 A general result for mixture set domains

The basic object of analysis is a binary choice probability function (BCPF) defined over a set, A, of alternatives. This is a mapping

$$\begin{aligned} P:A\times A\rightarrow \left[ 0,1\right] \end{aligned}$$

that satisfies

$$\begin{aligned} P(a,b) =1-P\left( b,a\right) \end{aligned}$$

(3)

for all $a,b\in A$. The quantity P(a, b) is interpreted as the probability with which the decision-maker selects a when given the choice of a or b. Abstention is not an option—choices are “forced”—so BCPFs must satisfy the completeness (or balance) condition (3).

Our interpretation of P(a, b) is behaviourally meaningful only if $a\ne b$, but it is traditional to define P on the entire Cartesian product $A\times A$ for convenience. An immediate implication of (3) is that

$$\begin{aligned} P\left( a,a\right) =\ \frac{1}{2} \end{aligned}$$

for any $a\in A$.

Given a BCPF, P, we may construct the following binary relation on A: for any $a,b\in A$,

$$\begin{aligned} a\succsim ^{P}b~~~\Leftrightarrow ~~~P(a,b) \ge P\left( b,a\right) ~~~\Leftrightarrow ~~~P(a,b) \ge \frac{1}{2} \end{aligned}$$

(4)

where the second equivalence follows from (3). When $a\succsim ^{P}b$ we say that a is weakly stochastically preferred to b. That is, a decision-maker weakly stochastically prefers a over b if she is at least as likely to choose a from $\left\{ a,b\right\}$ as she is to choose b. It is natural to think of P as a “noisy” expression of these preferences. Note, however, that while $\succsim ^{P}$ is complete by construction, it need not be transitive. In particular, there may not exist any utility representation for $\succsim ^{P}$. The asymmetric and symmetric parts of $\succsim ^{P}$ are denoted $\succ ^{P}$ and $\sim ^{P}$, respectively:

$$\begin{aligned} a\succ ^{P}b~~~\Leftrightarrow ~~~P(a,b) >\frac{1}{2} \end{aligned}$$

and

$$\begin{aligned} a\sim ^{P}b~~~\Leftrightarrow ~~~P(a,b) =\frac{1}{2}\text {.} \end{aligned}$$

Following Marschak (1960) we introduce the following definitions:¹¹

Definition 1

We call $u:A\rightarrow {\mathbb {R}}$ a weak utility for P if u represents $\succsim ^{P}$; that is, if the following holds for any $a,b\in A$:

$$\begin{aligned} a\succsim ^{P}b~~~\text {iff}~~~u(a) \ge u(b) \end{aligned}$$

(5)

Definition 2

We call $u:A\rightarrow {\mathbb {R}}$ a strong utility for P if

$$\begin{aligned} P(a,b) \ge P\left( c,d\right) ~~~\text {iff}~~~u(a) -u(b) \ge u\left( c\right) -u(d) \end{aligned}$$

(6)

for any $a,b,c,d\in A$.

This terminology is motivated by the following observation.

Lemma 1

If u is a strong utility for P, then u is a weak utility for P.

Proof

If u is a strong utility for P, then

$$\begin{aligned} P(a,b) \ge P\left( b,a\right) ~~~\Leftrightarrow ~~~u(a) \ge u(b) \end{aligned}$$

for any $a,b\in A$. Hence, using (4), we see that u is a weak utility for P. $\square$

When P possesses a strong utility function, then choice probabilities are determined by utility differences in the Fechnerian tradition of psychophysics (Falmagne 2002).¹²

Suppose u is a strong utility for P and let

$$\begin{aligned} \varGamma _{u}=\left\{ u(a) -u(b) \ \left| \ a,b\in A\right. \right\} \end{aligned}$$

(7)

be the set of utility differences generated by u. Note that $\varGamma _{u}$ is symmetric about 0: if $x\in \varGamma _{u}$ then $-x\in \varGamma _{u}$. It follows that there exists a strictly increasing function $F:\varGamma _{u}\rightarrow \left[ 0,1\right]$ such that

$$\begin{aligned} P(a,b) =F\left( u(a) -u(b) \right) \end{aligned}$$

(8)

for any $a,b\in A$. The completeness condition (3) implies that F must also satisfy

$$\begin{aligned} F(x) +F\left( -x\right) =1 \end{aligned}$$

(9)

for any $x\in \varGamma _{u}$. Suppose F is continuous.¹³ Then we may interpret F as a distribution function—or rather, the restriction to $\varGamma _{u}$ of a distribution function—for some zero-mean, symmetrically distributed random variable, ${\tilde{\varepsilon }}$, so that

$$\begin{aligned} P(a,b) =F\left( u(a) -u(b) \right) =\Pr \left[ u(a) -u(b) \ge {\tilde{\varepsilon }}\right] \end{aligned}$$

(10)

for any $a,b\in A$. The representation (10) is the guise in which Fechnerian models are usually encountered by economists.

In this paper, we study conditions under which a BCPF has a strong utility representation within specific classes of utility functions. Throughout, we assume that A is a mixture set (Herstein and Milnor 1953). Mixture sets generalise the Euclidean notion of a convex set. Given $a,b\in A$ and $\lambda \in \left[ 0,1\right]$, we write $a\lambda b$ for the $\lambda$ -mixture of a and b. In particular, $a1b=a$ and $a0b=b$. For example, if A is a convex subset of ${\mathbb {R}}^{n}$ then

$$\begin{aligned} a\lambda b=\lambda a+\left( 1-\lambda \right) b \end{aligned}$$

under the standard mixture operation on ${\mathbb {R}}^{n}$.

Mixture sets are very familiar in the domain of risk. The unit simplex in ${\mathbb {R}}^{n}$, denoted by $\varDelta ^{n}$, may be used to describe the set of all lotteries over a fixed set of n possible outcomes. This is a mixture (indeed, convex) set under the usual mixing operation for ${\mathbb {R}}^{n}$. Similarly, spaces of distribution functions on a given interval are mixture sets under the usual mixing operation on real-valued functions. For the domain of uncertainty, mixture sets appear in the framework of Anscombe and Aumann (1963). Given a set ${\mathcal {S}}$ of states and a mixture set ${\mathcal {C}}$ of consequences, an Anscombe–Aumann act is a function from ${\mathcal {S}}$ to ${\mathcal {C}}$. Anscombe and Aumann (1963) assume that ${\mathcal {C}}$ is a set of lotteries but none of our formal results relies on this interpretation.¹⁴ If A is the set of Anscombe–Aumann acts, the mixture operation on ${\mathcal {C}}$ induces a mixture operation on A as follows: given $a,b\in A$ and $\lambda \in \left[ 0,1\right]$, $a\lambda b$ is the Anscombe–Aumann act that maps state $s\in {\mathcal {S}}$ to the consequence $a(s) \lambda b(s) \in {\mathcal {C}}$.

When A is a mixture set, we say that $u:A\rightarrow {\mathbb {R}}$ is mixture linear if

$$\begin{aligned} u\left( a\lambda b\right) =\lambda u(a) +\left( 1-\lambda \right) u(b) \end{aligned}$$

for any $a,b\in A$ and any $\lambda \in \left[ 0,1\right]$. For example, if $A=\varDelta ^{n}$ then EU functions are mixture linear. The following definition generalises the notion of mixture linearity:

Definition 3

Given some $M\subseteq A$ we say that $u:A\rightarrow {\mathbb {R}}$ is M -linear if $u\left( M\right) =u\left( A\right)$ and

$$\begin{aligned} u\left( a\lambda b\right) =\lambda u(a) +\left( 1-\lambda \right) u(b) \end{aligned}$$

for any $a\in A$, any $b\in M$ and any $\lambda \in \left[ 0,1\right]$.

When $M=A$ the notion of M-linearity coincides with ordinary mixture linearity. For future reference, it will be useful to note that the range of any M-linear function is convex.

Lemma 2

If u is M-linear, then $u\left( A\right)$ is an interval (i.e. a convex subset of ${\mathbb {R}}$).

Proof

Suppose $x,y\in u\left( A\right)$ and $\lambda \in \left[ 0,1\right]$. If u is M-linear, then there exist $a,b\in M$ such that $u(a) =x$ and $u(b) =y$. Moreover:

$$\begin{aligned} u\left( a\lambda b\right) =\lambda x+\left( 1-\lambda \right) y \end{aligned}$$

so $\lambda x+\left( 1-\lambda \right) y\in u\left( A\right)$. $\square$

To the best of our knowledge, the notion of M-linearity has not been defined elsewhere in the literature. We introduce it here for two reasons. First, because we can identify simple conditions on P which ensure that any M-linear weak utility for P is also a strong utility for P (Theorem 1). This is the central result of the paper. Second, many familiar classes of utility functions are M-linear for suitable choice of M. These include the SEU, MEU and CEU classes in the Anscombe–Aumann domain.

Example 1

Let A be the Anscombe–Aumann domain with finite state space ${\mathcal {S}}=\left\{ 1,\ldots ,S\right\}$ and consequence set ${\mathcal {C}}$. Let

$$\begin{aligned} \varTheta =\ \left\{ \theta :{\mathcal {S}}\rightarrow \left[ 0,1\right] \ \left| \ \sum _{s=1}^{S}\theta (s) =1\right. \right\} \end{aligned}$$

be the set of all probability distributions over states. A utility function $u:A\rightarrow {\mathbb {R}}$ has the maxmin expected utility form if there exists a non-empty, closed and convex set ${\mathcal {P}}\subseteq \varTheta$ and a mixture linear function $v:{\mathcal {C}}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} u(a) =\min _{\theta \in {\mathcal {P}}}\sum _{s\in {\mathcal {S}}}\theta (s) v\left( a(s) \right) \end{aligned}$$

(11)

for all $a\in A$. Let

$$\begin{aligned} {\overline{A}}=\left\{ a\in A\ \left| \ a(s) =a\left( s^{\prime } \right) \text { for each} s,s^{\prime } \in {\mathcal {S}}\right. \right\} \end{aligned}$$

be the set of constant acts. Since

$$\begin{aligned} u\left( A\right) \supseteq u\left( {\overline{A}}\right) =v\left( {\mathcal {C}} \right) \supseteq u\left( A\right) \end{aligned}$$

(where the final inclusion follows from the mixture linearity of v) we have $u\left( A\right) =u\left( {\overline{A}}\right)$. Moreover, if $a\in A$ and $b\in {\overline{A}}$ with $b(s) =x\in {\mathcal {C}}$ for every $s\in {\mathcal {S}}$, then

$$\begin{aligned} u\left( a\lambda b\right)= & {} \ \min _{\theta \in {\mathcal {P}}}\sum _{s\in {\mathcal {S}}}\theta (s) \left[ \lambda v\left( a(s) \right) +\left( 1-\lambda \right) v(x) \right] \\= & {} \ \lambda \left[ \min _{\theta \in {\mathcal {P}}}\sum _{s\in {\mathcal {S}}} \theta (s) v\left( a(s) \right) \right] \ +\ \left( 1-\lambda \right) v(x) \\= & {} \ \lambda u(a) +\left( 1-\lambda \right) u(b) \text {.} \end{aligned}$$

It follows that (11) is ${\overline{A}}$-linear.

In order to state our main result, we need three axioms.

Axiom 1

(Strong Stochastic Transitivity) For all $a,b,c\in A$, if

$$\begin{aligned} \min \left\{ P(a,b) ,\ P\left( b,c\right) \right\} \ \ge \ \frac{1}{2} \end{aligned}$$

then

$$\begin{aligned} P(a,c) \ \ge \ \max \left\{ P(a,b) ,\ P(b,c) \right\} \text {.} \end{aligned}$$

Strong Stochastic Transitivity is a standard assumption in the literature on binary stochastic choice. It implies (but is not implied by) the transitivity of $\succsim ^{P}$ (i.e. the Weak Stochastic Transitivity of P)—see Fishburn (1973).

Axiom 2

(Solvability) For all $a,b,c\in A$ and all $\rho \in \left( 0,1\right)$

$$\begin{aligned} P(a,b) \ge \rho \ge P\left( a,c\right) ~~~\Rightarrow ~~~P\left( a,e\right) =\rho ~~\text {for}\, \text {some}~\, e\in A \end{aligned}$$

This condition was introduced by Debreu (1958).¹⁵ One consequence of Axiom 2 is that A must be a sufficiently rich domain.

Our third axiom is actually a family of axioms, indexed by $M\subseteq A$. When interpreting references to “Axiom 3,” context must be used to determine which member of the family is intended.

Axiom 3

(Strong M-Independence) For any $a,b,c,d\in A$, any $e\in M$ and any $\lambda \in \left( 0,1\right)$,

$$\begin{aligned} P(a,b) \ge P\left( c,d\right) ~~~\Rightarrow ~~~P\left( a\lambda e,b\lambda e\right) \ge P\left( c\lambda e,d\lambda e\right) \end{aligned}$$

(12)

This notion generalises Dagsvik’s (2008) Strong Independence axiom, which is equivalent to Strong A-Independence. Note that if $M^{\prime } \subseteq M$, then Strong M-Independence implies Strong $M^{\prime }$ -Independence. In other words, Dagsvik’s axiom is the “strongest” member of this family of axioms. We will use the terms Strong Independence and Strong A-Independence interchangeably.¹⁶

Theorem 1

Let $M\subseteq A$ be given and let P satisfy Axioms 1–3. Suppose that $u:A\rightarrow {\mathbb {R}}$ is an M-linear weak utility for P. Then u is a strong utility for P.

Theorem 1 is our main result. The rest of the paper explores various applications of Theorem 1. To understand how this theorem may be applied, suppose we wish to establish sufficient conditions for the existence of a strong utility for P within a given M-linear class, ${\mathcal {U}}$. Suppose further that we know a set of sufficient conditions for preferences on A to have a utility representation in ${\mathcal {U}}$. Then we can use this knowledge, together with the three-step recipe from the Introduction, to obtain the desired conditions on P. (At Step 3, we add Strong Stochastic Transitivity and Solvability, in addition to Strong M-Independence.)¹⁷

We end this section by noting a useful corollary to Theorem 1.¹⁸

Corollary 1

Let $M\subseteq A$ be given and let P satisfy Axioms 1–3. Suppose that $u:A\rightarrow {\mathbb {R}}$ is an M-linear weak utility for P and let $I\subseteq {\mathbb {R}}$ be a closed interval that is symmetric about 0 and contains the set $\varGamma _{u}$ defined by (7). Then there exists a zero-mean, symmetrically and continuously distributed random variable, ${\tilde{\varepsilon }}$, with support contained in I, such that

$$\begin{aligned} P(a,b) =\Pr \left[ u(a) -u(b) \ge {\tilde{\varepsilon }}\right] \end{aligned}$$

for all $a,b\in A$.

It follows from Corollary 1 that all of the models presented in this paper can be re-expressed in the familiar form (10) for some zero-mean random variable, ${\tilde{\varepsilon }}$, with continuous and strictly increasing distribution function, F. When expressed in this form, the axioms in our various representation theorems are also necessary, as is easily verified.

4 Application I: choice between risky prospects

In this section, we prove a strong “expected utility” representation theorem (Proposition 1). That is, we obtain sufficient conditions for P to possess a strong utility that is mixture linear. Our result requires only that A is a mixture set, but the Strong Independence axiom (which underpins the result) is motivated by scenarios in which A is a set of lotteries—a risky domain.

To state our result, we first introduce a strengthening of Axiom 2:

Axiom 4

(Mixture Solvability) For all $a,b,c\in A$ and all $\rho \in \left( 0,1\right)$

$$\begin{aligned} P(a,b) \ge \rho \ge P\left( a,c\right) ~~~\Rightarrow ~~~P\left( a,b\lambda c\right) =\rho ~~\text {for}\,\text {some}~\,\lambda \in \left[ 0,1 \right] \end{aligned}$$

Proposition 1

Let A be a mixture set. If P satisfies Axioms 1, 4 and Strong Independence, then P has a strong utility that is mixture linear.

Proposition 1 is closely related to Theorem 4 in Dagsvik (2008), which also establishes sufficient conditions for a strong expected utility representation. Dagsvik’s result is less general, in the sense that he assumes $A=\varDelta ^{n}$, and also uses a different set of axioms. In place of Strong Stochastic Transitivity (Axiom 1), Dagsvik assumes the following:

Axiom 5

(Quadruple Condition) For all $a,b,a^{\prime } ,b^{\prime } \in A$:

$$\begin{aligned} P(a,b) \ge P\left( a^{\prime } ,b^{\prime } \right) ~~~\Rightarrow ~~ ~P\left( a,a^{\prime } \right) \ge P\left( b,b^{\prime } \right) \end{aligned}$$

(13)

Like Strong Stochastic Transitivity, the Quadruple Condition has a long history in the literature on stochastic choice. It appears in Debreu (1958), who attributes it to Davidson and Marschak (1959). It is well known that the Quadruple Condition implies Strong Stochastic Transitivity, but not conversely (Luce and Suppes 1965, Theorem 39). The extra strength of the Quadruple Condition comes at the cost of some intuitive appeal. Strong Stochastic Transitivity has a familiar and transparent logic,¹⁹ while the Quadruple Condition appears less compelling from a normative point of view.

In place of Mixture Solvability (Axiom 4), Dagsvik assumes two continuity conditions: Axiom 2 (Solvability) and the following:

Axiom 6

(Archimedean Property) For all $a,b,c\in A$, if

$$\begin{aligned} P(a,b) \>\ \frac{1}{2}\ >\ P\left( c,b\right) \end{aligned}$$

then there exist $\alpha ,\beta \in \left( 0,1\right)$ such that

$$\begin{aligned} P\left( a\alpha c,b\right) \>\ \frac{1}{2}\ >\ P\left( a\beta c,b\right) \text {.} \end{aligned}$$

Theorem 2

(Dagsvik 2008) Let $A=\varDelta ^{n}$. If P satisfies Axioms 2, 5, 6 and Strong Independence, then P has a strong utility that is mixture linear.

In a recent paper, Dagsvik (2015, Theorem 4) shows that some of the conditions in Theorem 2 can be relaxed without jeopardising the result: Solvability (Axiom 2) can be dropped and Strong Independence weakened by requiring that (12) holds only for degenerate lotteries (i.e. vertices of the simplex). In “Appendix 2” we establish that the axioms in Theorem 2 can be weakened in another direction, again without jeopardising the result (Theorem 3). We show that the Quadruple Condition (Axiom 5) can be replaced with the weaker (and more intuitively appealing) Strong Stochastic Transitivity condition. Of course, this raises the interesting question as to whether both sets of relaxations—those of our Theorem 3 and those of Dagsvik (2015, Theorem 4)—can be simultaneously made while preserving the existence of a mixture linear strong utility. The answer is obscured by the fact that the two theorems use very different proof strategies. The question remains open at this time.

5 Application II: choice between uncertain prospects

For this section (and its subsections), A will be a set of Anscombe–Aumann acts—a domain of uncertainty. For expositional convenience, we confine attention to a finite state space, ${\mathcal {S}}=\left\{ 1,\ldots ,S\right\}$, but our results generalise straightforwardly to richer state spaces. We use ${\overline{A}}$ to denote the set of constant acts (recall Example 1) and we take the usual notational liberty of identifying ${\overline{A}}$ with ${\mathcal {C}}$: if $x\in \mathcal {C }$ we also treat x as an element of ${\overline{A}}$, relying on context to indicate the intended meaning. Note, in particular, that ${\overline{A}}$ is a mixture set. As discussed in Sect. 3, it is conventional to choose ${\mathcal {C}}$ to be a space of lotteries (such as $\varDelta ^{n}$) but our formal results require only that ${\mathcal {C}}$ is a mixture set.

In Example 1 we showed that utility functions of the MEU form are ${\overline{A}}$-linear. This arises because of the Certainty independence (or C-independence) property of MEU preferences:²⁰ for any $a,b\in A$ , any $x\in {\overline{A}}$ and any $\lambda \in \left( 0,1\right)$,

$$\begin{aligned} a\succsim b\ \ \ \ \text {iff}\ \ \ \ a\lambda x\succsim b\lambda x\text {.} \end{aligned}$$

Preferences of the CEU variety also enjoy this property, as do SEU preferences, which are contained in the intersection of the MEU and CEU classes. All these classes are special cases of invariant biseparable preferences, which were introduced by Ghirardato et al. (2004). Invariant biseparable preferences are characterised by C-independence plus another four standard axioms (ibid., p. 141). Ghirardato, Maccheroni and Marinacci (2004, Theorem 11) describe the utility functions that represent such preferences. We say that a utility function is “invariant biseparable” if it represents invariant biseparable preferences.

We refer the reader to Ghirardato et al. (2004) for a detailed description of invariant biseparable utility functions, which is somewhat involved. For our purposes, invariant biseparable utilities are interesting because they are all ${\overline{A}}$-linear (ibid., Lemma 1) and they include many familiar classes of utility functions for the Anscombe–Aumann domain, such as SEU, MEU and CEU.

Proposition 2 (below) identifies sufficient conditions for a BCPF to possess a strong utility of the invariant biseparable form. In Sects. 5.1, 5.3 and 5.3 we refine this result to obtain sufficient conditions for a strong utility of the SEU, MEU and CEU form, respectively.

To state these representation theorems, it will be convenient to exclude the uninteresting case in which the decision-maker is stochastically indifferent between any two alternatives. We say that a BCPF is non-trivial if there exist $a,b\in A$ such that $P(a,b) \ne \frac{1}{2}$. The following axiom will also be needed for each representation theorem. (In reading the statement of this axiom, recall that we identify the consequence $x\in {\mathcal {C}}$ with the constant act that maps each state to x.)

Axiom 7

(Stochastic Monotonicity) For any $a,b\in A$, if

$$\begin{aligned} P\left( a(s) ,b(s) \right) \ \ge \ \frac{1}{2} \end{aligned}$$

for every $s\in {\mathcal {S}}$ then $P(a,b) \ge \frac{1}{2}$.

Proposition 2

If P is a non-trivial BCPF that satisfies Axioms 1, 4, 7 and Strong ${\overline{A}}$-Independence, then $\succsim ^{P}$ are invariant biseparable preferences and P has a strong utility of the invariant biseparable form.

5.1 Strong SEU

Defining

$$\begin{aligned} \varTheta =\ \left\{ \theta :{\mathcal {S}}\rightarrow \left[ 0,1\right] \ \left| \ \sum _{s=1}^{S}\theta (s) =1\right. \right\} \end{aligned}$$

to be the set of all probability distributions over states, the utility function $u:A\rightarrow {\mathbb {R}}$ has the SEU form if there exists a mixture linear function $v:{\mathcal {C}}\rightarrow {\mathbb {R}}$ and a probability $\theta \in \varTheta$ such that

$$\begin{aligned} u(a) =\ \sum _{s=1}^{S}\theta (s) v\left( a(s) \right) \end{aligned}$$

(14)

for all $a\in A$. Not surprisingly, a strong utility of the form (14) is obtained by strengthening Strong ${\overline{A}}$-Independence to Strong A-Independence in Proposition 2. This gives the following stochastic analogue of the Anscombe and Aumann (1963) representation theorem.

Proposition 3

If P is a non-trivial BCPF that satisfies Axioms 1, 4, 7 and Strong A-Independence, then P has a strong utility of the SEU form (14).

5.2 Strong MEU

Recall the MEU specification (11) from Example 1. To obtain this functional form, we need to add a stochastic analogue of Gilboa and Schmeidler’s (1989) uncertainty aversion axiom:

Axiom 8

(Stochastic Uncertainty Aversion) For any $a,b\in A$ and any $\lambda \in \left( 0,1\right)$,

$$\begin{aligned} P(a,b) =\frac{1}{2}~~~\Rightarrow ~~~P\left( a\lambda b,b\right) \ge \frac{1}{2}\text {.} \end{aligned}$$

Axiom 8 may be written

$$\begin{aligned} a\sim ^{P}b~~~\Rightarrow ~~~a\lambda b\succsim ^{P}b \end{aligned}$$

for any $a,b\in A$ and any $\lambda \in \left( 0,1\right)$. In other words, Stochastic Uncertainty Aversion is the property of P implied by the requirement that $\succsim ^{P}$ satisfy uncertainty aversion—Axiom A.5 in Gilboa and Schmeidler (1989).

Proposition 4

If P is a non-trivial BCPF that satisfies Axioms 1, 4, 7, 8 and Strong ${\overline{A}}$ -Independence, then P has a strong utility of the MEU form (11).

5.3 Strong CEU

For our final application, we develop a stochastic version of Choquet expected utility (Schmeidler 1989). CEU is arguably the most frequently applied alternative to SEU. Unlike MEU, the Choquet expected utility model does not impose uncertainty aversion—it can accommodate a wide variety of attitudes to uncertainty. However, it does require that preferences satisfy comonotonic independence (Schmeidler 1989, p. 575), which is a stronger independence property than C-independence.

Definition 4

Let $\succsim$ be a weak order (complete and transitive binary relation) on A. Acts $a,b\in A$ are $\succsim$ -comonotonic if there do not exist states $s,s^{\prime } \in {\mathcal {S}}$ with $a(s) \succ a\left( s^{\prime } \right)$ and $b\left( s^{\prime } \right) \succ b(s)$, where $\succ$ is the asymmetric part of $\succsim$ and we identify ${\mathcal {C}}$ with ${\overline{A}}$ in the usual manner.

Axiom 9

(Stochastic Comonotonic Independence) For any pairwise $\succsim ^{P}$-comonotonic $a,b,c\in A$ and any $\lambda \in \left( 0,1\right)$,

$$\begin{aligned} P(a,b)>\frac{1}{2}~~~\Rightarrow ~~~P\left( a\lambda c,b\lambda c\right) >\frac{1}{2}\text {.} \end{aligned}$$

Axiom 9 says that $\succsim ^{P}$ satisfies the comonotonic independence property (Schmeidler 1989) .

A utility of the CEU class has the same form as (14), but the probability $\theta$ is replaced by a capacity and summation by Choquet integration.

Definition 5

A capacity on ${\mathcal {S}}$ is a mapping $\omega :2^{{\mathcal {S}}} \rightarrow \left[ 0,1\right]$ that satisfies $\omega \left( \emptyset \right) =0$, $\omega \left( {\mathcal {S}}\right) =1$ and $\omega \left( A\right) \le \omega \left( B\right)$ whenever $A\subseteq B$.

Capacities are non-additive generalisations of probabilities. Choquet integration allows us to take expectations of real-valued functions with respect to capacities.²¹ Given a function $f:{\mathcal {S}}\rightarrow {\mathbb {R}}$, let

$$\begin{aligned} f\left( {\mathcal {S}}\right) =\left\{ x_{1},x_{2},\ldots ,x_{k}\right\} \end{aligned}$$

with $x_{1}>x_{2}>\cdots >x_{k}$ and let

$$\begin{aligned} E_{i}=\left\{ s\in {\mathcal {S}}\ |\ f(s) =x_{i}\right\} \text {.} \end{aligned}$$

Then

$$\begin{aligned} f =\ \sum _{i=1}^{k}x_{i}E_{i}^{*} \end{aligned}$$

(15)

where $E_{i}^{*} :{\mathcal {S}}\rightarrow \left\{ 0,1\right\}$ is the indicator function for $E_{i}$. If $\omega$ is a capacity on ${\mathcal {S}}$, the Choquet expectation of (15) with respect to $\omega$ is defined as follows:

$$\begin{aligned} \int f\ d\omega \ \equiv \ \sum _{i=1}^{k}\left( x_{i}-x_{i+1}\right) \omega \left( \bigcup \limits _{j=1}^{i}E_{j}\right) \end{aligned}$$

(16)

where $x_{k+1}=0$. When $\omega$ is additive—that is, a probability—( 16) is just the usual expected value of f with respect to $\omega$.

The utility function $u:A\rightarrow {\mathbb {R}}$ has the CEU form if there exists a mixture linear function $v:{\mathcal {C}}\rightarrow {\mathbb {R}}$ and a capacity $\omega$ on ${\mathcal {S}}$ such that

$$\begin{aligned} u(a) =\ \int \left( v\circ a\right) \ d\omega \end{aligned}$$

(17)

Proposition 5

If P is a non-trivial BCPF that satisfies Axioms 1, 4, 7, 9 and Strong ${\overline{A}}$ -Independence, then P has a strong utility of the CEU form (17).

6 Discussion

In their recent, and comprehensive, survey of Fechnerian representation theorems, Marley and Regenwetter (2015, p. 59) observe: “Clearly, much more research is needed in this area for uncertain (or ambiguous) gambles and representations other than expected utility”. Our paper fills some of this gap. It also provides theoretical background for recent experimental work on binary choice between uncertain prospects.

Hey et al. (2010) tested the “descriptive and predictive adequacy” of eight preference-based models of decision-making under uncertainty.²² These included SEU, MEU, CEU and three other models based on preferences within the invariant biseparable class. Each utility model was embedded in a strong utility structure (10), with Fechnerian errors drawn from a zero-mean Normal distribution.²³

In terms of aggregate predictive accuracy (summarised in Table 1 of Hey, Lotito and Maffioletti 2010), the strong SEU model out-performed the strong CEU model but was marginally inferior to the strong MEU model. The best performing models were those based on the “maximax” dual to MEU and on $\alpha$-MEU (Ghirardato et al. 2004). Both of these are within the invariant biseparable class; the latter is axiomatised in Section 6 of Ghirardato et al. (2004).

Our paper provides explicit axiomatic foundations for the strong SEU, strong CEU and strong MEU models, as well as a “recipe” for constructing axiomatisations of strong utility models based on maximax utility and $\alpha$-MEU. Corollary 1 shows that all of our strong utility representations can be re-expressed in the form (10).

Importantly, our results provide axiomatic demarcations between the various models. Proposition 2 reveals that Strong ${\overline{A}}$-Independence is a central pillar in the foundation of any strong utility model within the invariant biseparable class. It is a prime candidate for further testing. Propositions 4 and 5 indicate the additional axiomatic refinements necessary to confine strong utility to the MEU and CEU classes, respectively: Stochastic Uncertainty Aversion in the case of MEU and Stochastic Comonotonic Independence in the case of CEU. If both axiomatic restrictions are supported by the data, there exists a strong utility within the convex CEU class (Schmeidler 1989, Proposition), which is commonly encountered in applied work.

Theorem  1 could also be used to axiomatise strong utility models beyond those considered here, such as a probabilistic analogue of Jaffray’s (1989) linear utility theory for (the mixture set of) belief functions over a given set of outcomes.

Of course, one limitation of our models, like all Fechner models, is the restriction to binary choices. It is obviously desirable to have an extension to multinomial choice, and preferably an extension with an axiomatic foundation. One such extension is provided by Blavatskyy (2012, Sect. 4). Let P be a BCPF defined on an arbitrary domain of alternatives, A. Given a finite choice set $C\subseteq A$, let ${\mathbf {P}} \left( a|C\right)$ denote the probability of choosing $a\in C$ from C. Consider the following formula for constructing ${\mathbf {P}}\left( a|C\right)$ from P:

$$\begin{aligned} {\mathbf {P}}\left( a|C\right) =\ \frac{\prod \limits _{b\in C}P(a,b)}{\sum _{a^{\prime } \in C}\left[ \prod \limits _{b^{\prime }\in C}P\left( a^{\prime } ,b^{\prime } \right) \right] } \end{aligned}$$

(18)

Blavatskyy (2012, p. 49) provides an axiomatic foundation for (18). One may think of

$$\begin{aligned} \prod \limits _{b\in C}P(a,b) \end{aligned}$$

(19)

as the probability that $a\in C$ is a Condorcet winner amongst the “candidates” in C—the probability that a would be chosen over every other element of C in a sequence of binary choices. Let us therefore call (19) the Condorcet probability of choosing a from C. The expression (18) says that the relative choice probability

$$\begin{aligned} \frac{{\mathbf {P}}\left( a|C\right) }{{\mathbf {P}}\left( b|C\right) } \end{aligned}$$

(where $a,b\in C$) matches the relative Condorcet probability. This gives a rather natural extension of a binary choice probabilities to multinomial choice probabilities. In particular, it could be applied to any of the models in the present paper.²⁴

Appendices

Appendix 1: Proofs

1.1 Proof of Theorem 1

In what follows we will make frequent use of the following well-known result:

Lemma 3

(Davidson and Marschak 1959) Let P be a BCPF. Then P satisfies Strong Stochastic Transitivity (Axiom 1) iff it satisfies the the following condition:

$$\begin{aligned} P(a,b) \ge \frac{1}{2}~~~~\Rightarrow ~~~~P\left( a,c\right) \ge P\left( b,c\right) \end{aligned}$$

(20)

for any $a,b,c\in A$.

Property (20) is called weak substitutability. If we replace “$\Rightarrow$” with “$\Leftrightarrow$” in (20), we obtain the substitutability condition (Tversky and Russo 1969). Weak substitutability is obviously implied by substitutability, but the converse is false (Fishburn 1973).

The next result sets the foundation for our proof of Theorem 1.

Lemma 4

Let $M\subseteq A$ and let P satisfy Axioms 1–3. Suppose further that $\succsim ^{P}$ has an M-linear representation $u:A\rightarrow {\mathbb {R}}$ and let $\varSigma =u\left( A\right)$. Then there exists a function $\pi :\varSigma \times \varSigma \rightarrow [0,1]$ such that

$$\begin{aligned} P(a,b) =\pi \left( u(a) ,u(b) \right) \end{aligned}$$

(21)

for any $a,b\in A$. Moreover, $\pi$ satisfies the following conditions for any $\lambda \in [0,1]$ and any $x,y,x^{\prime },y^{\prime } ,z\in \varSigma _{u}$:

• (i) $\pi \left( x,y\right) =\frac{1}{2}$ iff $x=y$.

• (ii) $\pi \left( x,y\right) +\pi \left( y,x\right) =1$.

• (iii) $\pi \left( x,y\right) =\pi \left( x^{\prime } ,y^{\prime }\right)$ implies $\pi \left( x\lambda z,y\lambda z\right) =\pi \left( x^{\prime } \lambda z,y^{\prime } \lambda z\right)$.

• (iv) $\pi$ is continuous in each argument.

• (v) $\pi$ is strictly increasing (respectively, strictly decreasing) in its first (respectively, second) argument.

Proof

Since u is M-linear, $\varSigma$ is an interval in ${\mathbb {R}}$ (Lemma 2). The weak substitutability condition—which is implied by Axiom 1 (Lemma 3)—together with (3) gives

$$\begin{aligned} u(a)\! =\!u(b) ~~~\Leftrightarrow ~~~P(a,b) \!=\! \frac{1}{2}~~~\Rightarrow ~~~P\left( a,c\right) \!=\!P\left( b,c\right) ~~~\Leftrightarrow ~~~P\left( c,a\right) \!=\!P\left( c,b\right) \end{aligned}$$

for any $a,b,c\in A$. It follows that (21) determines a well-defined function $\pi :\varSigma \times \varSigma \rightarrow [0,1]$. It remains to show that $\pi$ satisfies properties (i)–(v).

Property (i) is immediate from the definition of u. Property (ii) follows from (3).

Strong M-Independence of P and the M-linearity of u imply

$$\begin{aligned} \pi \left( x,y\right) =\pi \left( x^{\prime } ,y^{\prime } \right) ~~~\Rightarrow ~~~\pi \left( x\lambda z,y\lambda z\right) =\pi \left( x^{\prime } \lambda z,y^{\prime } \lambda z\right) \end{aligned}$$

for any $x,y,x^{\prime } ,y^{\prime } \in \varSigma$ and any $z\in u\left( M\right)$. Since $u\left( M\right) =u\left( A\right) =\varSigma$, property (iii) holds.

To establish property (iv), note that $\pi$ inherits solvability with respect to its second argument: for any $x,y,z\in \varSigma$ and any $q\in \left[ 0,1\right]$, if $\pi \left( z,x\right) \ge q\ge \pi \left( z,y\right)$ then $\pi \left( z,w\right) =q$ for some $w\in \varSigma$. The weak substitutability property, together with (ii), implies that $\pi$ is also non-increasing in its second argument. It follows that $\pi$ is continuous in its second argument. Continuity in its first argument therefore follows from (ii).

As already noted, Strong Stochastic Transitivity (Axiom 1) implies that $\pi$ is non-increasing in its second argument. Suppose, contrary to what we need to show, that $\pi \left( x,y^{0}\right) =\pi \left( x,y^{1}\right)$ for some $y^{1}>y^{0}$. We can exclude the possibility that $x\in \left[ y^{0},y^{1}\right]$ since (i) and weak monotonicity would then imply $\pi \left( x,y^{0}\right) <\pi \left( x,y^{1}\right)$. Hence, either $x>y^{1}>y^{0}$ or $y^{1}>y^{0}>x$. We only consider the former case, since the latter may be handled similarly. Thus:

$$\begin{aligned} \pi \left( x,y^{0}\right) =\ \pi \left( x,y^{1}\right) \ >\ \frac{1}{2} \end{aligned}$$

(22)

Let $\lambda \in \left( 0,1\right)$ satisfy $y^{1}=y^{0}\lambda x$ and define $y^{n}=y^{n-1}\lambda x=y^{0}\lambda ^{n}x$ for each $n\in \left\{ 2,3,\ldots \right\}$. Since $\pi \left( x,y^{0}\right) =\pi \left( x,y^{1}\right)$, property (iii) gives $\pi \left( x,y^{0}\right) =\pi \left( x,y^{n}\right)$ for all n. By continuity

$$\begin{aligned} \lim _{n\rightarrow \infty } \ \pi \left( x,y^{n}\right) =\ \pi \left( x,x\right) =\ \frac{1}{2} \end{aligned}$$

which contradicts (22). This proves that $\pi$ is strictly decreasing in its second argument. Using (ii), we deduce that it is also strictly increasing in its first argument. $\square$

Corollary 2

Let $M\subseteq A$ and let P satisfy Axioms 1–3. If there is an M-linear utility representation for $\succsim ^{P}$, then P satisfies the substitutability property; that is,

$$\begin{aligned} P(a,b) \ge \frac{1}{2}~~~~\text {iff}~~~~P\left( a,c\right) \ge P\left( b,c\right) \end{aligned}$$

(23)

for any $a,b,c\in A$.

Proof

Strong Stochastic Transitivity (Axiom 1) implies the “only if” part of (23)—recall Lemma 3. The “if” part follows from property (v) in Lemma 4. $\square$

Before proving Theorem 1, let us outline the main obstacle to be overcome. Suppose P satisfies Axioms 1–2 and Strong M-Independence, and suppose further that u is an M-linear representation for $\succsim ^{P}$. Consider the weak order $\ge ^{*}$ on $\varSigma \times \varSigma$ represented by the function $\pi$ defined in Lemma 4:

$$\begin{aligned} \left( x,y\right) \ge ^{*} \left( x^{\prime } ,y^{\prime } \right) \ \ \ \Leftrightarrow \ \ \ \pi \left( x,y\right) \ge \pi \left( x^{\prime } ,y^{\prime } \right) \text {.} \end{aligned}$$

If we can show that $\ge ^{*}$ has a linear representation, then properties (i) and (v) in Lemma 1 imply that $\pi \left( x,y\right) =F\left( x-y\right)$ for some strictly increasing function F. This gives the desired strong utility representation for P. Establishing the existence of a linear representation for $\ge ^{*}$ is complicated by the fact that property (iii) is weaker than the usual (Anscombe–Aumann) independence condition on $\ge ^{*}$. Property (iii) ensures only the Certainty independence (or C-independence) of $\ge ^{*}$.²⁵ We must therefore use the other properties of $\pi$ to make up for this deficiency.

Proof of Theorem 1 Suppose $u:A\rightarrow {\mathbb {R}}$ is an M-linear representation for $\succsim ^{P}$ with $u\left( A\right) =u\left( M\right) =\varSigma$. Then $\varSigma$ is an interval (Lemma 2). The result is trivial if $\varSigma$ is a singleton so suppose otherwise. It is without loss of generality to assume that 0 is contained in the interior of $\varSigma$—if not, apply a suitable affine transformation to u.

Let $\pi$ be defined as in Lemma 4 and let

$$\begin{aligned} \varLambda =\left\{ \left( x,y\right) \in \varSigma \times \varSigma \ |\ x=y\right\} \text {.} \end{aligned}$$

Figure 1 illustrates. Lemma 4 implies that $\varLambda$ is the $\pi$-contour along which $\pi =\frac{1}{2}$. Lemma 4 further implies that $\pi$ is strictly increasing as we move southwards or eastwards in Fig. 1. We need to show that all the other contours of $\pi$ are parallel to $\varLambda$. Property (ii) ensures that these contours are symmetric about $\varLambda$ so it suffices to consider the contours with $\pi \left( x,y\right) <\frac{1}{2}$ (i.e. those lying above $\varLambda$ in Fig. 1).

Suppose, contrary to what we seek to show, that there exist $x,y,x^{\prime } ,y^{\prime } \in \varSigma$ with

$$\begin{aligned} x-y=x^{\prime } -y^{\prime } <0 \end{aligned}$$

but

$$\begin{aligned} \pi \left( x,y\right) >\pi \left( x^{\prime } ,y^{\prime } \right) . \end{aligned}$$

See Fig. 1 (which assumes $x^{\prime } >x$).

Fig. 1

Illustrating points (x, y) and $(x',y')$ in the proof of Theorem 1

Fig. 2

Constructing point $(x',y'')$ in the proof of Theorem 1

By properties (i), (iv) and (v) of $\pi$, there exists some $y^{\prime \prime } \in \varSigma$ such that $x^{\prime }<y^{\prime \prime } <y^{\prime }$ and $\pi \left( x,y\right) =\pi \left( x^{\prime } ,y^{\prime \prime } \right)$. Since $\left( x^{\prime },y^{\prime \prime } \right)$ lies below the line segment joining $\left( x,y\right)$ to $\left( x^{\prime } ,y^{\prime } \right)$, we must have

$$\begin{aligned} \left( x^{\prime } ,y^{\prime \prime } \right) =\ \lambda \left( x,y\right) +\left( 1-\lambda \right) \left( z,z\right) =\ \left( x\lambda z,y\lambda z\right) \end{aligned}$$

(24)

for some $z\in {\mathbb {R}}$ and some $\lambda \in \left( 0,1\right)$. Figure 2 illustrates (again for the case $x<x^{\prime }$). We may further assume that $z\in \varSigma$; otherwise, we can use property (iii) to contract $\left( x,y\right)$ and $\left( x^{\prime },y^{\prime \prime } \right)$ towards $\left( 0,0\right)$ until this condition is satisfied.²⁶

From (24) and the fact that

$$\begin{aligned} \frac{1}{2}>\pi \left( x,y\right) =\pi \left( x^{\prime } ,y^{\prime \prime } \right) =\left( x\lambda z,y\lambda z\right) \text {,} \end{aligned}$$

repeated applications of property (iii) give

$$\begin{aligned} \frac{1}{2}>\pi \left( x,y\right) =\pi \left( x\lambda ^{n}z,y\lambda ^{n}z\right) \ \ \ \ \ \text {for}\, \text {each}~\, n\in \left\{ 1,2,\ldots \right\} \end{aligned}$$

(25)

Since $\left( x\lambda ^{n}z,y\lambda ^{n}z\right) \rightarrow \left( z,z\right)$ as $n\rightarrow \infty$ and $\pi \left( z,z\right) =\frac{1}{2}$, we deduce a contradiction to the continuity property (iv). The contradiction is not quite immediate, as (iv) does not assert the joint continuity of $\pi$. However, for the scenario depicted in Fig. 2 we obtain the required contradiction by considering the sequence $\left\{ \left( x\lambda ^{n}z,\ z\right) \right\} _{n=1}^{\infty }$, which also converges to $\left( z,z\right)$ and satisfies

$$\begin{aligned} \pi \left( x\lambda ^{n}z,z\right) \ \le \ \pi \left( x\lambda ^{n}z,y\lambda ^{n}z\right) \end{aligned}$$

for all n by property (v). For the alternative scenario in which $x>x^{\prime }$, we may consider the sequence $\left\{ \left( z,y\lambda ^{n}z\right) \right\} _{n=1}^{\infty }$ instead.

This contradiction establishes that $\pi \left( x,y\right) =\pi \left( x^{\prime } ,y^{\prime } \right)$ whenever $x-y=x^{\prime }-y^{\prime }$. Since $\pi \left( x,y\right)$ is strictly increasing in $x-y$ by property (v), it follows that $\pi \left( x,y\right) =F\left( x-y\right)$ for some strictly increasing function F. $\square$

1.2 Proof of Corollary 1

The proof of Theorem 1 establishes that $P(a,b) =F\left( u(a) -u(b) \right)$ for some strictly increasing F—see the discussion following the proof of Lemma 4. Property (iv) in Lemma 4 ensures that F is continuous. We can obviously construct a continuous extension of F to I that is non-decreasing everywhere, satisfies $F(x) +F\left( -x\right) =1$ for all $x\in I$, and whose limit is 1 approaching the right-hand end of I. This will be the distribution function for a random variable with the required properties.

1.3 Proof of Proposition 1

Suppose P satisfies Axioms 1, 4 and Strong Independence. By Theorem 1, it suffices to prove that $\succsim ^{P}$ has a mixture linear (i.e. A-linear) representation. We do so by showing that it satisfies the conditions of Theorem 1 in Fishburn (Fisburn 1982, Chapter 2).

It is obvious that $\succsim ^{P}$ is complete. It is transitive by virtue of the Strong Stochastic Transitivity of P (Axiom 1). Setting $c=d$ in the definition of Strong A-Independence, we see that $\succsim ^{P}$ inherits the following independence property: for all $a,b,e\in A$ and all $\lambda \in \left( 0,1\right)$

$$\begin{aligned} a\succsim ^{P}b~~~\Rightarrow ~~~a\lambda e\succsim ^{P}b\lambda e \end{aligned}$$

(26)

The proof is completed by showing that

$$\begin{aligned} \left\{ \lambda \in \left[ 0,1\right] \ \left| \ a\lambda b\succsim ^{P}c\right. \right\} \end{aligned}$$

and

$$\begin{aligned} \left\{ \lambda \in \left[ 0,1\right] \ \left| \ c\succsim ^{P}a\lambda b\right. \right\} \end{aligned}$$

are closed for any $a,b,c\in A$.

Fix some $a,b,c\in A$ and consider the set

$$\begin{aligned} \left\{ \lambda \in \left[ 0,1\right] \ \left| \ c\succsim ^{P}a\lambda b\right. \right\} \end{aligned}$$

(27)

It is without loss of generality to assume $a\succsim ^{P}b$. Then $a\lambda b\succsim ^{P}b$ for any $\lambda \in \left( 0,1\right)$ by (26). Hence, applying (26) once more, we have:

$$\begin{aligned} a\lambda b\succsim ^{P}b\mu \left( a\lambda b\right) \end{aligned}$$

for any $\mu \in \left( 0,1\right)$. Since $b\mu \left( a\lambda b\right) =a \left[ \lambda \left( 1-\mu \right) \right] b$, it follows that if $\lambda$ is in (27) then so is any $\lambda ^{\prime } <\lambda$. It remains to exclude the possibility that (27) is of the form $\left[ 0,\zeta \right)$ for some $\zeta >0$.

Let $\left\{ \lambda _{m}\right\} _{m=1}^{\infty } \subseteq \left[ 0,\zeta \right)$ be a convergent sequence with limit $\zeta$. Suppose $a\lambda _{m}b\succsim ^{P}c$ for each m, while $c\succ ^{P}a\zeta b$. Then

$$\begin{aligned} P\left( c,a\zeta b\right) \ >\ \frac{1}{2}\ \ge \ P\left( c,a\lambda _{m}b\right) \end{aligned}$$

for each m. Let

$$\begin{aligned} \rho \in \left( P\left( c,a\zeta b\right) ,\frac{1}{2}\right) \text {.} \end{aligned}$$

Given some $m\in \left\{ 1,2,\ldots \right\}$, Mixture Solvability (Axiom 4) ensures that there exists $\mu \in \left( 0,1\right)$ such that

$$\begin{aligned} \rho =\ P\left( c,\left( a\zeta b\right) \mu \left( a\lambda _{m}b\right) \right) =\ P\left( c,a\left[ \mu \zeta +\left( 1-\mu \right) \lambda _{m} \right] b\right) \text {.} \end{aligned}$$

Since $\mu \zeta +\left( 1-\mu \right) \lambda _{m}\in \left[ 0,\zeta \right)$ and $\rho >\frac{1}{2}$ we have the desired contradiction.

The same argument (mutatis mutandis) shows that the set

$$\begin{aligned} \left\{ \lambda \in \left[ 0,1\right] \ \left| \ a\lambda b\succsim ^{P}c\right. \right\} \end{aligned}$$

is closed. This completes the proof of Proposition 1.

1.4 Proof of Proposition 2

Lemma 5

Suppose that P satisfies Axioms 1, 4 and 7. Then for every $a\in A$ there exists some ${\overline{a}}\in {\overline{A}}$ such that $a\sim ^{P}{\overline{a}}$.

Proof

Given Strong Stochastic Transitivity (Axiom 1), the binary relation $\succsim ^{P}$ weakly orders the elements of

$$\begin{aligned} \left\{ a(s) \in {\overline{A}}\ |\ s\in {\mathcal {S}}\right\} \text { .} \end{aligned}$$

Suppose that $s^{\prime } ,s^{\prime \prime } \in {\mathcal {S}}$ are such that $a\left( s^{\prime \prime } \right) \succsim ^{P}a(s) \succsim ^{P}a\left( s^{\prime } \right)$ for all $s\in {\mathcal {S}}$. Then Stochastic Monotonicity (Axiom 7) implies $a\left( s^{\prime \prime } \right) \succsim ^{P}a\succsim ^{P}a\left( s^{\prime } \right)$. That is:

$$\begin{aligned} P\left( a,a\left( s^{\prime } \right) \right) \ge \frac{1}{2}\ge P\left( a,a\left( s^{\prime \prime } \right) \right) \text {.} \end{aligned}$$

Hence, Mixture Solvability (Axiom 4) ensures that

$$\begin{aligned} a\sim ^{P}a\left( s^{\prime \prime } \right) \lambda a\left( s^{\prime } \right) \end{aligned}$$

for some $\lambda \in \left[ 0,1\right]$. $\square$

When P satisfies Axioms 1, 4 and 7, we may therefore associate each non-constant act $a\in A\diagdown {\overline{A}}$ with a specific (but arbitrarily chosen) certainty equivalent, denoted by ${\overline{a}}$. For every constant act $a\in {\overline{A}}$, we define ${\overline{a}}=a$. Hence, ${\overline{a}}\in {\overline{A}}$ and $a\sim ^{P}{\overline{a}}$ for every $a\in A$.

Proof of Proposition 2

The restriction of P to ${\overline{A}}\times {\overline{A}}$ satisfies Strong Stochastic Transitivity, Mixture Solvability and Strong ${\overline{A}}$-Independence. By Proposition 1, there exists a mixture linear function $v: {\overline{A}}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} P(a,b) \ge P\left( c,d\right) ~~~\Leftrightarrow ~~~v(a) -v(b) \ge v\left( c\right) -v(d) \ \ \ \ \text {for}\, \text {all}\, a,b,c,d\in {\overline{A}} \qquad \end{aligned}$$

(28)

In particular, v represents $\succsim ^{P}$ on ${\overline{A}}$. Let u extend v to A by using Lemma 5 to define $u(a) =v\left( {\overline{a}}\right)$ for all $a\in A\diagdown {\overline{A}}$. Then u represents $\succsim ^{P}$ by construction. We next show that u is ${\overline{A}}$-linear.

Suppose $a\in A, x\in {\overline{A}}$ and $\lambda \in \left( 0,1\right)$. Since $P\left( a,{\overline{a}}\right) =\frac{1}{2}$, Strong ${\overline{A}}$ -Independence implies that $P\left( a\lambda x,{\overline{a}}\lambda x\right) = \frac{1}{2}$. Thus:

$$\begin{aligned} u\left( a\lambda x\right) =\ u\left( {\overline{a}}\lambda x\right) =\ v\left( {\overline{a}}\lambda x\right) =\ \lambda v\left( {\overline{a}} \right) +\left( 1-\lambda \right) v(x) =\ \lambda u(a) +\left( 1-\lambda \right) u(x) \text {,} \end{aligned}$$

where the penultimate equality uses the fact that $v:{\overline{A}}\rightarrow {\mathbb {R}}$ is mixture linear. This proves that u is ${\overline{A}}$ -linear.

Applying Corollary 2 (with $M={\overline{A}}$), and making use of (3), it follows that

$$\begin{aligned} P(a,b) \ge P\left( c,d\right) ~~~\Leftrightarrow ~~~P\left( {\overline{a}},{\overline{b}}\right) \ge P\left( {\overline{c}},{\overline{d}} \right) \ \ \ \ \text {for all}\,a,b,c,d\in A \end{aligned}$$

(29)

Combining (28) and (29), we see that u is a strong utility for P.

It remains to show that u is of the invariant biseparable class.

Observe that v and u have the same range by Lemma 5. Call this common range $\varSigma$. Since v is mixture linear, $\varSigma$ is an interval in ${\mathbb {R}}$ (Lemma 2). Using Stochastic Monotonicity (Axiom 7), it is easy to see that there exists a well-defined function $h:\varSigma ^{S}\rightarrow \varSigma$ such that

$$\begin{aligned} u(a) =\ h\left( v\left( a\left( 1\right) \right) ,\ldots ,v\left( a\left( S\right) \right) \right) \end{aligned}$$

(30)

for all $a\in A$. That is, the utility of any act depends only on the v-utility obtained in each state and is uniquely determined by these v-utilities. We use h to denote the function that converts vectors of state-(v-)utilities into the (u-)utility of the corresponding act.

Let C denote the set of constant vectors in $\varSigma ^{S}$, and identify elements of C with elements of $\varSigma$ in the obvious fashion. We now observe that h has the following properties: (a) $h\left( c\right) =c$ for all $c\in \varSigma$; (b) h is non-decreasing in each argument by virtue of Stochastic Monotonicity; and (c) h is C-linear by virtue of the ${\overline{A}}$-linearity of u. In the language of Ghirardato et al. (2005), h is normalised, monotonic and constant affine. If P is non-trivial, then $\varSigma$ is a non-degenerate interval and it follows (ibid., p. 132) that h has a unique extension $h:{\mathbb {R}} ^{S}\rightarrow {\mathbb {R}}$ satisfying constant linearity: $h\left( ax+b\right) =ah(x) +b$ for all $x\in {\mathbb {R}}^{S}$ and all $a,b\in {\mathbb {R}}$ with $a\ge 0$. The desired result is now immediate from Ghirardato, Maccheroni and Marinacci (2004, Lemma 1 and Theorem 11). $\square$

1.5 Proof of Proposition 3

Let v and u be defined as in the proof of Proposition 2 and let h: $\varSigma ^{S}\rightarrow \varSigma$ be the function defined by (30). Non-triviality of P implies that $\varSigma$ is a non-degenerate interval (Lemma 2), which we assume, without loss of generality, to contain $\left[ -1,1\right]$.

We first show that Strong A-Independence of P implies A-linearity of u. Let $a,b\in A$ and $\lambda \in \left( 0,1\right)$. Since $P\left( a, {\overline{a}}\right) =\frac{1}{2}$ we deduce that $P\left( a\lambda b, {\overline{a}}\lambda b\right) =\frac{1}{2}$ from Strong A-Independence. Thus, $u\left( a\lambda b\right) =u\left( {\overline{a}}\lambda b\right)$. Using the ${\overline{A}}$-linearity of u, we have:

$$\begin{aligned} u\left( a\lambda b\right)= & {} \ u\left( {\overline{a}}\lambda b\right) \ \\= & {} \ \lambda u\left( {\overline{a}}\right) +\left( 1-\lambda \right) u(b) \\= & {} \ \lambda u(a) +\left( 1-\lambda \right) u(b) \end{aligned}$$

Hence, u is A-linear.²⁷

Next, we show that h is mixture linear. Let $a,b\in A$ and $\lambda \in \left[ 0,1\right]$. If $x_{s}=v\left( a(s) \right)$ and $y_{s}=v\left( b(s) \right)$, then $u(a) =h(x)$ and $u(b) =h\left( y\right)$. Using the ${\overline{A}}$-linearity of v and the A-linearity of u we have:

$$\begin{aligned} h\left( \lambda x+\left( 1-\lambda \right) y\right)= & {} \ u\left( a\lambda b\right) \\= & {} \ \lambda u(a) +\left( 1-\lambda \right) u(b) \\= & {} \ \lambda h(x) +\left( 1-\lambda \right) h\left( y\right) \text {.} \end{aligned}$$

Hence, h is mixture linear. It has a unique linear extension h: ${\mathbb {R}} ^{S}\rightarrow {\mathbb {R}}$ by standard arguments.²⁸ Stochastic Monotonicity (Axiom 7) implies that the coefficients of this linear function are non-negative. Since u is non-constant, at least one coefficient is strictly positive so the vector of coefficients can be positively scaled to lie in $\varTheta$. $\square$

1.6 Proof of Proposition 4

Once again, let v and u be defined as in the proof of Proposition 2 and let $h:\varSigma ^{S}\rightarrow \varSigma$ be the function defined by (30).

From Stochastic Uncertainty Aversion (Axiom 8) and the ${\overline{A}}$-linearity of v, we see that $h:\varSigma ^{S}\rightarrow \varSigma$ satisfies—in addition to the properties noted in the proof of Proposition 2—the following: for any $x,y\in \varSigma ^{S}$,

$$\begin{aligned} h(x) =h\left( y\right) \ \ \ \Rightarrow \ \ \ h\left( \lambda x+\left( 1-\lambda \right) y\right) \ge h\left( y\right) \end{aligned}$$

(31)

Its unique constant-linear extension h: ${\mathbb {R}}^{S}\rightarrow {\mathbb {R}}$ is therefore superadditive: that is,

$$\begin{aligned} h\left( x+y\right) \ \ge \ h(x) +h\left( y\right) \end{aligned}$$

(32)

for any $x,y\in {\mathbb {R}}^{S}$. To see why, let $x,y\in {\mathbb {R}}^{S}$, ${\overline{x}}=h(x)$, ${\overline{y}}=h\left( y\right)$ and $\varepsilon ={\overline{x}}-{\overline{y}}$. Then constant linearity and (31) give

$$\begin{aligned} \frac{1}{2}h\left( x+y\right) +\frac{1}{2}\varepsilon= & {} \ h\left( \frac{1}{2} \left( x+y\right) +\frac{1}{2}\varepsilon \right) \\\ge & {} \ \frac{1}{2} h(x) +\frac{1}{2}h\left( y+\varepsilon \right) \\= & {} \frac{1}{2} \left[ h(x) +h\left( y\right) \right] +\frac{1}{2}\varepsilon \end{aligned}$$

which implies (32).

The proof is completed by applying the following well-known result (see, for example, Lemma 3.5 in Gilboa and Schmeidler 1989):

Lemma 6

Let $h:{\mathbb {R}}^{S}\rightarrow {\mathbb {R}}$ be a superadditive, constant-linear function that is non-decreasing in each argument. Then there exists a closed and convex set ${\mathcal {P}}\subseteq \varTheta$ such that

$$\begin{aligned} h(x) =\ \min _{\theta \in {\mathcal {P}}}\sum _{s=1}^{S}\theta (s) x_{s} \end{aligned}$$

for every $x\in {\mathbb {R}}^{S}$.

1.7 Proof of Proposition 5

As usual, we let v and u be defined as in the proof of Proposition 2 and let $h:\varSigma ^{S}\rightarrow \varSigma$ be the function defined by (30). Since $\varSigma$ is a non-degenerate interval we may assume, without loss of generality, that it contains $\left[ -1,1\right]$.

Definition 6

Vectors $x,y\in \varSigma ^{S}$ are comonotonic if there do not exist $s,s^{\prime } \in {\mathcal {S}}$ with $x_{s}>x_{s^{\prime } }$ and $y_{s^{\prime } }>y_{s}$.

If P satisfies Stochastic Comonotonic Independence (Axiom 9), then $h:\varSigma ^{S}\rightarrow \varSigma$ satisfies

$$\begin{aligned} h(x)>h\left( y\right) ~~~\Rightarrow ~~~h\left( \lambda x+\left( 1-\lambda \right) z\right) >h\left( \lambda y+\left( 1-\lambda \right) z\right) \end{aligned}$$

(33)

for any pairwise comonotonic $x,y,z\in \varSigma ^{S}$ and any $\lambda \in \left( 0,1\right)$. The desired representation is now an immediate implication of the following result:²⁹

Lemma 7

(Schmeidler 1986, Corollary) Let $\varSigma \subseteq {\mathbb {R}}$ be a non-degenerate interval containing $\left[ -1,1\right]$ and let $h:\varSigma ^{S}\rightarrow \varSigma$ be a normalised, monotonic function that satisfies (33) for any for any pairwise comonotonic $x,y,z\in \varSigma ^{S}$ and any $\lambda \in \left( 0,1\right)$. Then there exists a capacity $\omega$ such that

$$\begin{aligned} h(x) =\ \int x\ d\omega \end{aligned}$$

(34)

for all x.³⁰

Appendix 2: Strengthening Theorem 2

The following strengthens Theorem 2 by replacing the Quadruple Condition (Axiom 5) with Strong Stochastic Transitivity (Axiom 1).

Theorem 3

Let $A=\varDelta ^{n}$. If P satisfies Axioms 1, 2, 6 and Strong Independence, then P has a strong utility that is mixture linear.

We use a similar argument to that for Proposition 1, except we can no longer appeal to Mixture Solvability to establish the continuity of $\succsim ^{P}$. Instead, we show that $\succsim ^{P}$ possesses a linear representation by an alternative route.

Proof of Theorem 3

As in the proof of Proposition 1, we may assume that $\succsim ^{P}$ is a weak order satisfying

$$\begin{aligned} a\succsim ^{P}b~~~\Rightarrow ~~~a\lambda c\succsim ^{P}b\lambda c \end{aligned}$$

(35)

for all $a,b,c\in A$ and all $\lambda \in \left( 0,1\right)$. Since the result is obvious if $\succsim ^{P}$ is trivial (i.e. $a\sim ^{P}b$ for all $a,b\in A$), let us assume otherwise. From Axiom 6, we also know that $\succsim ^{P}$ satisfies the following Archimedean property: for any $a,b,c\in A$

$$\begin{aligned} a\succ ^{P}b\succ ^{P}c~~~\Rightarrow ~~~a\lambda c\succ ^{P}b\succ ^{P}a\mu c \end{aligned}$$

(36)

for some $\lambda ,\mu \in \left( 0,1\right)$. It therefore suffices (Fisburn 1982, Chapter 2) to establish that

$$\begin{aligned} a\succ ^{P}b~~~\Rightarrow ~~~a\lambda c\succ ^{P}b\lambda c \end{aligned}$$

(37)

for all $a,b,c\in A$ and all $\lambda \in \left( 0,1\right)$.

Lemma 8

Condition (37) holds on the interior of A (that is, for any $a,b,c\in A\cap {\mathbb {R}}_{++}^{n}$).

Proof

Suppose $a,b,c\in A\cap {\mathbb {R}}_{++}^{n}$ with $a\succ ^{P}b$ and $a\lambda c\sim ^{P}b\lambda c$.³¹ That is,

$$\begin{aligned} P(a,b) >\frac{1}{2}~~~\text {and}~~~P\left( a\lambda c,b\lambda c\right) =\frac{1}{2} \end{aligned}$$

(38)

We claim that

$$\begin{aligned} P(a,b) \ge P\left( d,e\right) \ge \frac{1}{2}~~~\Rightarrow ~~~P\left( d\lambda c,e\lambda c\right) =\frac{1}{2} \end{aligned}$$

(39)

for any $d,e\in A$. To see why, observe that Strong Independence and

$$\begin{aligned} P\left( d,e\right) \ge \frac{1}{2}=P\left( c,c\right) \end{aligned}$$

give

$$\begin{aligned} P\left( d\lambda c,e\lambda c\right) \ge \frac{1}{2}\text {.} \end{aligned}$$

The reverse inequality follows by applying Strong Independence to $P(a,b) \ge P\left( d,e\right)$ and using (38).

We next show that $d=a\mu b$ and $e=b$ satisfy the antecedent in (39) for any $\mu \in \left[ 0,1\right]$. The cases $\mu \in \left\{ 0,1\right\}$ are trivial so we focus on $\mu \in \left( 0,1\right)$.

Since

$$\begin{aligned} P(a,b) >\frac{1}{2}=P\left( b,b\right) =P\left( a,a\right) \end{aligned}$$

we have

$$\begin{aligned} P\left( a\mu b,b\right) \ge \frac{1}{2} \end{aligned}$$

(40)

and

$$\begin{aligned} P\left( a,a\mu b\right) =P\left( a,b\left( 1-\mu \right) a\right) \ge \frac{ 1}{2} \end{aligned}$$

by Strong Independence. From the latter inequality and weak substitutability (which is implied by Strong Stochastic Transitivity—Lemma 3), we have

$$\begin{aligned} P(a,b) \ge P\left( a\mu b,b\right) \end{aligned}$$

(41)

Thus, from (39)–(41):

$$\begin{aligned} P\left( \left( a\mu b\right) \lambda c,b\lambda c\right) =\frac{1}{2} \end{aligned}$$

(42)

for any $\mu \in \left[ 0,1\right]$.

From (42) we obtain a linear segment of strictly positive length,³² parallel to the line joining a and b, which forms part of an indifference curve for $\succsim ^{P}$. Since a and b are in the interior of the simplex, we can use the existence of this linear segment, together with transitivity of $\succsim ^{P}$ and the independence property (35), to deduce that the line segment joining a and b must also be part of an indifference curve. Figure 3 illustrates the required construction (for the case $n=3$). By moving point z along the segment from x to y, we sweep out an indifference curve joining a to b.³³ This is the desired contradiction, since $a\succ ^{P}b$. $\square$

Since $A\cap {\mathbb {R}}_{++}^{n}$ is a mixture set (under the usual mixing operation for ${\mathbb {R}}^{n}$), it follows that $\succsim ^{P}$ possesses a linear representation on $A\cap {\mathbb {R}}_{++}^{n}$. Let u be such a representation.

Fig. 3

Illustrating the construction in the proof of Lemma 8

Observe that Axiom 6 is not required for the proof of Lemma 8—Strong Independence does all the work. We now use Axiom 6 to extend the linear representation to the boundary of the simplex.

First, u has a unique mixture linear extension to A. We use u to denote the extended function, as no confusion should arise. Let a be a boundary point of A. There are two possibilities: either (i) $u(a) =u(b)$ for some $b\in A\cap {\mathbb {R}}_{++}^{n}$ or else (ii) the face of the simplex containing a is part of a contour of u.

For case (i) we show that $a\sim ^{P}b$. (It follows that $a\sim ^{P}b$ for any boundary point a and any interior point b on the same utility contour as a.) If, for example, $a\succ ^{P}b$, then we can find some $c\in A\cap {\mathbb {R}}_{++}^{n}$ with $u\left( c\right) <u(b) =u(a)$. Hence $a\succ ^{P}b\succ ^{P}c$, but $u\left( a\lambda c\right) <u(b)$ for all $\lambda \in \left( 0,1\right)$ by the mixture linearity of u. Since $a\lambda c\in A\cap {\mathbb {R}}_{++}^{n}$ for any $\lambda \in \left( 0,1\right)$, we have $b\succ ^{P}a\lambda c$ for all $\lambda \in \left( 0,1\right)$, which contradicts the Archimedean property (36). Assuming $b\succ ^{P}a$ leads similarly to contradiction.

Now consider case (ii). Thus, u is constant on the face of the simplex containing a. Suppose, in particular, that $u(a) >u(b)$ for all $b\in A\cap {\mathbb {R}}_{++}^{n}$. The alternative scenario, in which $u(a) <u(b)$ for all $b\in A\cap {\mathbb {R}}_{++}^{n}$, may be handled similarly. We will show that $a\sim ^{P}b$ for any b on the same face as a, and $a\succ ^{P}b$ for any $b\in A$ not contained in the face containing a. Combined with case (i), this shows that $\succsim ^{P}$ is represented by u on all of A.

Suppose $b\in A$ with $u(a) =u(b)$, so b lies on the same face of the simplex as a. If $a\succ ^{P}b$ then $a\succ ^{P}b\succ ^{P}c$ for any $c\in A\cap {\mathbb {R}}_{++}^{n}$. Since $b\succ ^{P}a\lambda c\in A\cap {\mathbb {R}}_{++}^{n}$ for any $\lambda \in \left( 0,1\right)$, we deduce a contradiction to (36). Assuming $b\succ ^{P}a$ leads similarly to contradiction.

Finally, let $b\in A$ with $u(a) >u(b)$. Assume, contrary to what we seek to show, that $b\succsim ^{P}a$. Since $u(a) >u(b)$ we may choose some $c,d\in A\cap {\mathbb {R}} _{++}^{n}$ with

$$\begin{aligned} u(a)>u(d)>u\left( c\right) >u(b) \text { .} \end{aligned}$$

Therefore, $d\succ ^{P}c\succ ^{P}b\succsim ^{P}a$ and

$$\begin{aligned} u\left( d\lambda a\right) =\lambda u(d) +\left( 1-\lambda \right) u(a)>u(d) >u\left( c\right) \end{aligned}$$

It follows that $d\lambda a\succ ^{P}c$ for all $\lambda \in \left( 0,1\right)$. This contradicts the Archimedean property (36) and completes the proof of Theorem 3. $\square$