Development of coupled fluid-flow/geomechanics model considering storage and transport mechanism in shale gas reservoirs with complex fracture morphology

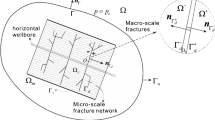
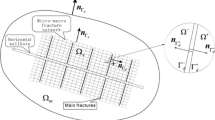
Abstract

Field observations frequently demonstrate stress fluctuations resulting from the reservoir depletion. The development of reservoirs, particularly the completion of infill wells and refracturing, can be significantly impacted by stress changes in and around drainage areas. Previous studies mainly focus on plane fractures and few studies consider the influence of complex transport and storage mechanism and irregular fracture geometry on stress evolution in shale gas reservoirs. Based on the embedded discrete fracture model (EDFM) and finite-volume method (FVM), a coupled geomechanics/fluid model has been successfully developed considering the adsorption, desorption, diffusion and slippage of shale gas. This model achieves coupling simulation of natural fractures, hydraulic fractures with complex geometry, storage and transport mechanism, reservoir stress, and pore-elastic effect. The open-source software OpenFOAM is used as the main solver for this model. The stress calculation and productivity simulation of the model are verified by the classical poroelasticity problem and the simulation results of published research and commercial simulator with EDFM respectively. The simulation results indicate that σ_xx, σ_yy, σ_xy and Δσ changes with time and space due to the time effect and anisotropy of formation pressure depletion; Due to the influence of different mechanisms on shale gas storage and transport, the reservoir pressure and stress distribution under different mechanisms are different; Among them, the stress with full mechanisms differs the most compared to the stress without any mechanism. The reservoir with stronger stress sensitivity (smaller Biot coefficient) is less sensitive to formation pressure depletion, and the stress variation range is smaller. For reservoirs with weak stress sensitivity, formation pressure depletion is more likely to lead to stress reversal. Under the influence of fracture geometry, the pressure depletion regions caused by the three types of fracture geometry are approximately rectangular, parallelogram and square, respectively. The corresponding σ_xx, σ_yy and Δσ also have great differences in spatial distribution and values. Therefore, the time effect, shale gas storage and transport mechanism and the influence of complex fracture geometry should be considered when predicting pressure depletion induced stress under the condition of simultaneous production. This study is of great significance for understanding the evolution law of stress induced by pressure consumption, as well as the design of infill wells and repeated fracturing.

Introduction

As the global economy recovers, oil and gas consumption will increase, but the amount of new reserves explored and developed each year is limited. In addition to developing new oil and gas plays, refracturing or infill well development in older fields is another important way to increase production. For example, over the past decade, the number of hydraulically fractured horizontal wells has increased rapidly globally, with infill or sub-wells exceeding the total number of parent wells in some unconventional reservoirs¹. Due to the influence of natural fractures, bedding, faults and other heterogeneous factors, the original in-situ stress of the reservoir will change greatly after the long-term drainage of the mother well, showing strong heterogeneity, and even the situation of in-situ stress reversal in some areas^2,3,4,5,6,7. As a result, the design of a refracturing or infill well is more challenging than the first development.

Due to the critical influence of reservoir stress distribution on fracture propagation in infill or subwell, it is necessary to accurately predict stress after pressure depletion before refracturing design to achieve an ideal fracture propagation trajectory^8,9. Gupta et al.¹⁰ believed that the variation of stress field was related to reservoir development, and proposed that the smaller the horizontal principal stress difference of reservoir, the more conducive to the generation of stress reversal. Roussel et al.² verified the stress reversal phenomenon by studying the evolution process of stress field around infill wells, suggesting that the principal stress direction around infill wells reverses by 90°, and the maximum horizontal principal stress direction gradually returns to the initial state as development progresses. Based on the porous elasticity theory, Hagemann et al.¹¹ established a fluid–solid coupling model of single-phase flow in fractured vertical wells in tight gas reservoirs, and analyzed the influence of reservoir boundary conditions and permeability on the change of stress field. Based on Hagemann’s research, Li et al.¹² considered the influence of gas reservoir outer boundary closure and permeability heterogeneity on the change of stress field, and believed that the stress reversal area first increased at a fast speed in the process of oil well production and development, then began to shrink and finally returned to the initial stress state after increasing to the limit value. Therefore, it is suggested that the time when the stress reversal zone reaches its maximum should be taken as the refracturing time. According to the study of Safari et al.¹³, due to stress reorientation of horizontal wells, hydraulic fractures may either bend or form straight fractures in the fracturing process of infill wells, which mainly depends on the diversion of horizontal principal stress. Sangnimnuan et al.¹⁴ developed a novel and efficient fluid-flow/geomechanical coupled model based on the embedded discrete fracture model (EDFM) to describe stress evolution induced by pressure depletion in unconventional reservoirs with complex fracture geometry. Pei et al.⁶ proposed a new integrated reservoir-geomechanical-fracture model to simulate the spatio-temporal evolution of stress during reservoir production. The potential effects of horizontal deviation, vertical deviation and infilling time on fracturing and stimulation of sub-wells are also studied. Yang et al.¹⁵ used the finite volume method to study the effect of fracture spacing on reservoir stress redirection. Wang et al.¹⁶ combined the discontinuous displacement method to optimize the optimal cluster location and number of fracture clusters in the fracturing stage, which greatly improved the fracturing effect and well performance. In addition, Safari et al.¹⁷ believed that interwell interference can be minimized by controlling fracture curvature, bottomhole pressure (BHP), infill well timing, and stimulation design. By studying fracture morphology parameters and how reservoir depletion affects in-situ stress evolution, we can minimize interwell communication and maximize secondary production¹⁸. Cui et al.¹⁹ devised a methodology to delineate fracture-controlled zones, thereby distinguishing the flow domains within the matrix of hydraulic fracture networks. This approach highlights the disparity in flow extents between the interior and exterior regions of the matrix system attributed to the network’s architecture. Their findings underscore that neglecting the variance in matrix flow areas between these zones leads to an overestimation of ultimate recovery rates and a premature manifestation of boundary-dominated flow phases in typical well test curves.

The study of reservoir pressure exhaustion induced stress is actually the study of the interaction between fluid flow and geomechanics. In the realm of fractured reservoir research, a diverse array of techniques exists for simulating and analyzing geological mechanics and fluid flow within fractured oil reservoirs. These methodologies encompass the Finite Volume Method (FVM), Boundary Element Method (BEM)^20,21, and the Extended Finite Element Method (XFEM)^22,23. Among them, FVM stands out for its capability to precisely model fluid flow and distribution within fractured reservoirs, as well as its adeptness in handling complex boundary conditions. This method divides the solution domain into a series of non-overlapping control volumes (or volumetric elements), simulating the overall flow process by computing the fluid flux within each control volume. It is precisely this technique that underpins the numerical simulation study conducted in this article. Based on the FVM, Hwang et al.²⁴ developed a simulator which considers the fluid-thermal-solid coupling and studies the evolution law of stress field in the process of water injection development of oil field. Tang et al.²⁵ developed a model for coupled poroelastoplasticity using the FVM and Manipulation (OpenFOAM) software. This model includes both material nonlinearity and strong coupling effects between the solid and fluid components that are obtained through implicit/explicit discretization methods.

There are two kinds of classification methods for solving the production induced stress field, which are divided into weak coupling and strong coupling according to the form of solving the equation, and are divided into one-way coupling and two-way coupling according to the order of solving the stress field and pressure field^26,27,28. Weak coupling is to solve the deformation equation of porous media and the fluid seepage equation separately, and exchange the data of two physical fields during the iteration. The displacement matrix obtained from the solid field is transmitted to the fluid field, and the fluid field transmits pressure data to the solid field^29,30,31. The one-way coupling means that the solution module 1 sends data to the solution module 2, and the module 2 does not return the solution result, while the two-way coupling means that both the solid solver and the fluid pressure solver send response data to each other. Carlos et al.³² put forward a strategy of weakly coupling to solve the fluid–solid coupling equation, and proposed that the solid strain module be solved by ABAQUS software, the fluid seepage module be solved by ECLIPSE, and the pressure, saturation and stress–strain data are alternately transmitted between the two modules. Full coupling is to unify the discrete equations of stress field and seepage field into a large matrix, and then directly solve this large matrix. This coupling calculation result has high accuracy. Because of the strong nonlinear coupling between seepage equation and stress equation, the time cost of solution is high, and the convergence is difficult, so it is also a good choice to adopt sequential coupling under the condition of ensuring engineering accuracy. Inoue et al.³³ developed a fully coupled numerical simulator based on the finite element method. On this basis, Segura et al.³⁴ coupled the model with the ECLIPSE black oil model, and analyzed the effects of reservoir physical parameters and fracture morphology on the permeability and productivity around the well.

Although a lot of researches have been done to simulate the evolution of reservoir stress induced by pressure depletion, there are still some deficiencies in the treatment of fluid–solid coupling problems with arbitrary fracture geometry and complex seepage mechanism. Previous studies mainly focused on the induced stress of reservoirs with plane cracks, but in actual production, the fracture form is not completely plane cracks, especially in unconventional reservoirs, non-plane cracks occupy the majority. At the same time, there is no fluid–solid coupling model considering the mechanism of adsorption, desorption, diffusion and slip of shale gas. Therefore, the establishment of a fluid flow/geomechanical coupling model considering the complex fracture geometry and shale gas storage and transport mechanism plays an important role in the accurate prediction of stress and production capacity. Considering the deficiency of current research, the purpose of this research is to accurately understand the stress evolution law caused by shale gas exploitation by considering the complex fracture geometry and multiple seepage mechanisms, to achieve the design optimization of infill wells and refracturing wells. Therefore, a coupled fluid-flow/geomechanics model is established by means of EDFM and FVM, which can consider adsorption desorption, diffusion and slip and complex fracture geometry. OpenFOAM is used as the main simulator. The main advantage of this model is that it can be simulated with high computational efficiency to consider the effects of complex seepage mechanisms and arbitrary fracture geometry on geomechanics/fluid flow coupling, which cannot be achieved by commercial software. The details of the model are described in the section “Governing equations”, the numerical discretization and validation of the model are further elaborated in sections “Numerical discretization” and “Validation”, respectively. Section “Case studies” provides an analysis and discussion of various case studies, while section “Conclusions” concludes the paper.

Governing equations

Coupled fluid flow/geomechanics

In our current work, we have assumed minimal temperature variation during deep shale development, thereby neglecting its influence on stress and focusing solely on the stress alterations arising from pressure reduction, coupled with multi-transport mechanisms and gas desorption processes. According to Biot’s^35,36 theory, the fluid flow/geomechanics coupling theory can be derived, which describes the pore elastic effect in isothermal linear isotropic porous elastic materials and can be used for reservoir modeling. The governing equations of the coupled system are derived from mass conservation and linear momentum balance. The stress equilibrium relationship can be expressed as

$$ \nabla \cdot \sigma + \rho_{r} \,{\text{g}}\,{ = }\,{0} $$

(1)

where $\sigma$ is the total stress tensor; $\rho_{r}$ represents the density of rocks, kg/m³; ${\text{g}}{\kern 1pt}$ is gravitational acceleration, m/s².

According to Biot’s theory of porous elastic medium, the poroelasticity equations take the following form^35,37:

$$ \sigma - \sigma_{0} = {\text{C}}_{dr} :\varepsilon - b\left( {p - p_{0} } \right)I $$

(2)

$$ \frac{1}{{\rho_{{\text{g}}} }}\left( {m - m_{0} } \right) = b\varepsilon_{v} + \frac{1}{M}\left( {p - p_{0} } \right) $$

(3)

where the subscript 0 represents the reference state; ${\mathbf{C}}_{{{\text{dr}}}}$ is the elastic tensor; ${\mathbf{I}}$ is the equivalent tensor;$p$ is the fluid pressure, MPa. $\rho_{{\text{g}}}$ indicates shale gas density, kg/m³; $m$ represents fluid mass per unit bulk volume, kg/m³; $\varepsilon_{{\text{v}}}$ is the volumetric strain, $\varepsilon_{{\text{v}}} = {\text{tr}}\left( \varepsilon \right)$; $b$ is the Biot coefficient, $b = 1 - \frac{{K_{{{\text{dr}}}} }}{{K_{{\text{s}}} }}$; $M$ represents the Biot modulus, and there is relationship of $\frac{{1}}{M} = \phi_{{\text{m}}} c_{{\text{g}}} + \frac{b - \phi }{{K_{s} }}$; $K_{{\text{s}}}$ is the bulk modulus of rock, MPa;

$K_{{{\text{dr}}}}$ is the drained bulk modulus of rock, which can be show as

$$ K_{{{\text{dr}}}} { = }\frac{{E\left( {1 - v} \right)}}{{\left( {1 + v} \right)\left( {1 - 2v} \right)}} $$

(4)

In Eq. (2), $\varepsilon$ is the strain tensor, which can be expressed as³⁸:

$$ {{\varvec{\upvarepsilon}}}{ = }\frac{{1}}{{2}}\left( {\nabla {\mathbf{u}} + \nabla^{T} {\mathbf{u}}} \right) $$

(5)

where ${\mathbf{u}}$ is the displacement vector; $v$ is the Poisson’s ratio, dimensionless; $E$ is the elastic modulus of rock, MPa.

By substituting the volume mean total stress into Eq. (2), a new stress–strain relationship can be obtained:

$$ \left( {{{\varvec{\upsigma}}}_{{\text{v}}} - {{\varvec{\upsigma}}}_{{\text{v,0}}} } \right) + b\left( {p - p_{0} } \right){ = }K_{{{\text{dr}}}} \varepsilon_{{\text{v}}} $$

(6)

where ${{\varvec{\upsigma}}}_{{\text{v}}}$ is one third of the trace of the stress tensor ${{\varvec{\upsigma}}}$, ${{\varvec{\upsigma}}}_{{\text{v}}} { = }\frac{{1}}{{3}}{\text{tr}}{{\varvec{\upsigma}}}$; By substituting Eqs. (2), (4), (5) and (6) into Eq. (1) and ignoring the influence of gravity term, the stress balance equation can be expressed as

$$ \nabla \cdot \left[ {\mu \nabla {\mathbf{u}} + \mu \nabla {\mathbf{u}}^{T} + \lambda Itr\left( {\nabla {\mathbf{u}}} \right)} \right] + \nabla \cdot {{\varvec{\upsigma}}}_{0} - b\nabla p + b\nabla p_{0} = 0 $$

(7)

where $\lambda$ and $\mu$ represent Lamé constants, $\mu { = }\frac{E}{{2\left( {1 + v} \right)}}$ and $\lambda { = }\frac{vE}{{\left( {1 + v} \right)\left( {1 - 2v} \right)}}$.

Assuming that the pore deformation is small, the mass conservation equation is expressed as³⁹

$$ \frac{{\partial {\text{m}}}}{\partial t} + \rho_{g} \nabla \cdot V = \rho_{g} q $$

(8)

where $q$ represents the source or sink item, ${{1} \mathord{\left/ {\vphantom {{1} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$; $V$ denotes fluid-flow rate, ${{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-0pt} {\text{s}}}$. By substituting Eq. (3) into Eq. (8), the mass conservation equation expressed by formation pressure and strain can be further obtained:

$$ \frac{{1}}{M}\frac{\partial p}{{\partial t}} + b\frac{{\partial \varepsilon_{{\text{v}}} }}{\partial t} + \nabla \cdot V = q $$

(9)

Considering the influence of shale gas adsorption and desorption mechanism on Biot modulus, the following equation can be obtained:

$$ \frac{{1}}{M} = \phi_{{\text{m}}} c_{{\text{g}}} + \frac{b - \phi }{{K_{s} }}\frac{{m_{{{\text{ad}}}} }}{{\rho_{g} }} $$

(10)

where $m_{{{\text{ad}}}}$ represents the adsorbed gas per unit matrix volume, ${{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}$.$c_{{\text{g}}}$ is fluid compressibility, MPa^-1; $\phi$ indicates shale porosity.

Considering various transport mechanisms of shale gas in matrix pores, it can be expressed as:

$$ V = - \frac{{\prod\limits_{i} {F_{app,i} } k}}{{\mu_{{\text{g}}} }}\left( {\nabla p} \right) $$

(11)

where $\mu_{{\text{g}}}$ denotes the viscosity of shale gas, mPa.s. $F_{app,i}$ represents the correction factor for shale gas permeability; $k$ represents absolute Darcy permeability. Substituting Eqs. (10) and (11) into Eq. (9), we can get:

$$ \left( {\phi_{{\text{m}}} c_{{\text{g}}} + \frac{b - \phi }{{K_{s} }}\frac{{m_{{{\text{ad}}}} }}{{\rho_{g} }}} \right)\frac{\partial p}{{\partial t}} + b\frac{{\partial \varepsilon_{{\text{v}}} }}{\partial t} + \nabla \cdot \left( { - \frac{{\prod\limits_{i} {F_{app,i} } k}}{{\mu_{{\text{g}}} }}\nabla p} \right) = q $$

(12)

Equations (2) and (12) are called fixed-strain split, in which the equations are solved in terms of strain. According to the research of Kim et al.⁴⁰, because Eq. (12) has a strong coupling term, it is easy to appear non-convergence in the calculation process, so the fixed stress segmentation method is used to rewrite Eq. (12) into the following form.

$$ \left( {\phi_{{\text{m}}} c_{{\text{g}}} + \frac{b - \phi }{{K_{s} }}\frac{{m_{{{\text{ad}}}} }}{{\rho_{g} }} + \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}} \right)\frac{\partial p}{{\partial t}} + \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}\frac{{\partial \sigma_{v} }}{\partial t} - \nabla \cdot \left( {\frac{{\prod\limits_{i} {F_{app,i} } k}}{{\mu_{{\text{g}}} }}\nabla p} \right) = q $$

(13)

Equation (13) is called the fixed-stress-split method and is unconditionally stable. Equation (13) is rewritten into a form containing displacement:

$$ \left( {\phi_{{\text{m}}} c_{{\text{g}}} + \frac{b - \phi }{{K_{s} }}\frac{{m_{{{\text{ad}}}} }}{{\rho_{g} }} + \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}} \right)\frac{{\partial p^{n} }}{\partial t} - \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}\frac{{\partial p^{n - 1} }}{\partial t} + b\frac{{\partial \left( {\nabla \cdot u} \right)}}{\partial t} - \nabla \cdot \left( {\frac{{\prod\limits_{i} {F_{app,i} } k}}{{\mu_{{\text{g}}} }}\nabla p^{n} } \right) = q $$

(14)

where n is the current timestep and n–1 is the previous timestep. Equations (7) and (14) are solved iteratively to obtain displacement and pressure. The details of discretization and how to solve each of the major equations are discussed in the section on Numerical Discretization.

Storage and transport mechanism

At present, the nonlinear gas storage function (m_ad) and apparent permeability correction factor (F_app) are mainly used to characterize the shale gas seepage mechanism^41,42. Generally, shale gas can be adsorbed on kerogen pore wall in single or multiple layers. The gas molecules adsorbed on the Kerogen pore wall of shale reservoir can be simulated by using single-layer Langmuir isotherm and multi-layer BET isotherm^43,44 (Yu et al., 2016 and 2017):

$$ m_{{\text{ad,L}}} = \rho_{s} \rho_{gsc} \frac{{pV_{L} }}{{p + P_{L} }} $$

(15)

$$ m_{{\text{ad,B}}} = \rho_{s} \rho_{gsc} \frac{{V_{m} Cp_{r} }}{{1 - P_{r} }}\left[ {\frac{{1 - \left( {d + 1} \right)p_{r}^{d} + dp_{r}^{d + 1} }}{{1 + \left( {C - 1} \right)p_{r} - Cp_{r}^{d + 1} }}} \right] $$

(16)

In the above equation,

$$ p_{r} = \frac{p}{{p_{s} }} $$

(17)

$$ p_{{\text{s}}} = \exp \left( {7.7437 - \frac{1306.5485}{{19.4362 + T}}} \right) $$

(18)

where $V_{L}$ is the Langmuir volume; $\rho_{s}$ is the density of rock bulk matrix; $\rho_{gsc}$ represents the density of shale gas in reservoir; $P_{L}$ is the Langmuir pressure.

The flow of shale gas in the matrix has slippage and diffusion effects, and the apparent permeability of the low-pressure area around the fracture will increase, and the permeability correction factor can be expressed as⁴⁵

$$ F_{app} = \left( {1 + \alpha K_{n} } \right)\left( {1 + \frac{{4K_{n} }}{{1 + K_{n} }}} \right) $$

(19)

In the above equation,

$$ K_{n} = \frac{{\mu_{g} }}{2.8284p}\sqrt {\frac{\pi RT}{{2M}}\frac{\phi }{k}} $$

(20)

$$ \alpha = \frac{128}{{15\pi^{2} }}\tan^{ - 1} \left( {4K_{n}^{0.4} } \right) $$

(21)

where $K_{n}$ is the Knudsen number, dimensionless.$\alpha$ is the rarefaction parameter, dimensionless.

Fully coupled fluid flow/geomechanics with EDFM

It is necessary to encrypt the local grids to construct complex fractures in unstructured grids, and the calculation cost is high. The EDFM can be used to simulate the reservoir with complex fracture morphology and arbitrary number of fractures. This method not only achieves the precision of discrete fracture model (DFM), but also has the high efficiency of structured grid⁴⁶. The core idea of this method is to establish matrix and fracture simulation domain independently by using structured mesh, and to establish the flow relationship between them by using non-adjacent conductivity. The fracture segment volume represented in the fracture domain can be calculated as⁴⁷:

$$ V_{f} = S_{seg} w_{f} $$

(22)

where $w_{f}$ is the fracture aperture;$S_{seg}$ represents the area of the fracture segment perpendicular to the fracture aperture. The porosity of fracture segment can be expressed by the following formula⁴⁸:

$$ \phi_{f} = \frac{{S_{seg} w_{f} }}{{V_{b} }} $$

(23)

where $V_{b}$ represents the total volume of matrix cell embedded in the fracture segment; In the simulation, it is necessary to establish the relationship of fluid transport between the fracture flow system and the matrix flow system through the conductivity. For any fracture cell and the corresponding matrix cell, the volume flow between them can be expressed as⁴⁹:

$$ q_{f - m} = \lambda_{{\text{t}}} \,T_{f - m} \,\Delta p $$

(24)

where $q_{f - m}$ represents the flow rate between the fracture cell and the corresponding matrix cell; $T_{f - m}$ is the conductivity between the fracture and the matrix cell; $\lambda_{{\text{t}}}$ denotes the relative mobility; $\Delta p$ represents the pressure difference between the matrix and the fracture cell. The transmissibility between the matrix and the fracture segment depends on the matrix permeability and the fracture geometry, can be expressed as³¹:

$$ T_{f - m} = \frac{{2A_{f} \left( {{\mathbf{k}} \cdot {\mathbf{n}}} \right) \cdot {\mathbf{n}}}}{{d_{f - m} }} $$

(25)

where $A_{f}$ denotes the area of the fracture segment on one side; ${\mathbf{k}}$ is the matrix permeability tensor and ${\mathbf{n}}$ is the normal vector of the fracture surface; $d_{f - m}$ represents the average normal distance between the matrix cell and the fracture plane, which can be expressed as:

$$ d_{f - m} = \frac{{\int\limits_{V} {x_{n}^{V} dV} }}{{V_{{\text{c}}} }} $$

(26)

where $x_{n}^{V}$ represents the distance from the volume element to the fracture plane, m;$V_{{\text{c}}}$ is the matrix cell volume, m³; $dV$ represents the volume element within a matrix cell. For two intersecting fractures, the conductivity between the intersecting fracture elements can be expressed as⁴⁷:

$$ T_{f - f} = \frac{{T_{1} T_{2} }}{{T_{1} + T_{2} }} $$

(27)

$$ T_{1} = \frac{{k_{f1} w_{f1} L_{{\text{int}}} }}{{d_{f1} }},T_{2} = \frac{{k_{f2} w_{f2} L_{{\text{int}}} }}{{d_{f2} }} $$

(28)

where $T_{f - f}$ is the conductivity between intersecting fracture elements; $T_{1}$ and $T_{2}$ represent the conductivity of fracture unit 1 and fracture unit 2, respectively; $k_{f1}$ and $k_{f2}$ are the permeability of fracture cells 1 and 2, respectively; $w_{f1}$ and $w_{f2}$ are the width of Fracture Cells 1 and 2, respectively; $d_{f1}$ and $d_{f2}$ represent the weighted average of the normal distances from the centroids of the subsegments (on both sides) to the intersection line; $L_{{\text{int}}}$ denotes the length of intersecting lines of intersecting fracture cells.

By substituting the flow exchange term (Eq. (24)) between matrix and fracture into Eq. (14), the in-matrix flow equation considering the influence of fracture system can be obtained:

$$ \begin{gathered} \left( {\phi_{{\text{m}}} c_{{\text{g}}} + \frac{b - \phi }{{K_{s} }}\frac{{m_{{{\text{ad}}}} }}{{\rho_{g} }} + \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}} \right)\frac{{\partial p^{n} }}{\partial t} - \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}\frac{{\partial p^{n - 1} }}{\partial t} + b\frac{{\partial \left( {\nabla \cdot u} \right)}}{\partial t} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - \nabla \cdot \left( {\frac{{\prod\limits_{i} {F_{app,i} } k}}{{\mu_{{\text{g}}} }}\nabla p^{n} } \right) + \lambda_{{\text{t}}} T_{f - m} \left( {p_{f}^{n} - p^{n} } \right) = 0 \hfill \\ \end{gathered} $$

(29)

Similarly, the flow equation in the fracture can be obtained

$$ \begin{gathered} \left( {\frac{1}{{M_{f} }} + \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}} \right)\frac{{\partial p_{f}^{n} }}{\partial t} - \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}\frac{{\partial p_{f}^{n - 1} }}{\partial t} - \nabla \cdot \left( {\frac{{\prod\limits_{i} {F_{app,i} } k_{f} }}{{\mu_{{\text{g}}} }}\nabla p_{f}^{n} } \right) \hfill \\ + \,\lambda_{{\text{t}}} T_{f - m} \left( {p^{n} - p_{f}^{n} } \right) + \lambda_{{\text{t}}} T_{f - f} \left( {p_{f1}^{n} - p_{f2}^{n} } \right) = q \hfill \\ \end{gathered} $$

(30)

where $M_{f}$ represents the Biot modulus inside the fracture domain calculated using modified porosity obtained from Eq. (23); $k_{f}$ is fracture permeability.

Numerical discretization

Equations (7), (29), and (30) are the main solving equations, and the finite volume method is used to discretize these three equations in space and time. The solution of discrete equations in time has implicit first-order accuracy, while discrete equations in space combine implicit and explicit methods with second-order accuracy. OpenFOAM is used as the solver for this fully coupled model. According to Tang’s research, the volume of each control cell is expressed in integral form and discrete details are provided. Stress balance Eq. (7) can be expressed as:

$$ \begin{aligned} \oint_{\partial V} {ds \cdot \left[ {\left( {2\mu + \lambda } \right)\nabla u} \right]} = & - \int_{\partial V} {ds \cdot \left[ {\mu \nabla u^{T} + \lambda Itr\left( {\nabla u} \right) - \left( {\mu + \lambda } \right)\nabla u} \right]} \\ & + \,\oint_{\partial V} {ds \cdot \left( {bpI} \right) - \oint_{\partial V} {ds \cdot \left( {bp_{0} I + \sigma_{0} } \right)} } \\ \end{aligned} $$

(31)

The left term of Eq. (31) equals sign is an implicit surface diffusion term, and the right term is followed by an explicit surface diffusion term, an explicit pressure coupling term, and an explicit constant term representing the initial state. Based on the finite volume method, discretizing the flow Eq. (29) in the matrix can obtain:

$$ \begin{gathered} \int_{V} {\left[ {\left( {\phi_{{\text{m}}} c_{{\text{g}}} + \frac{b - \phi }{{K_{s} }}\frac{{m_{{{\text{ad}}}} }}{{\rho_{g} }} + \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}} \right)\frac{{\partial p^{n} }}{\partial t}} \right]dV - \oint_{\partial V} {ds \cdot \left( {\frac{{\prod\limits_{i} {F_{app,i} } k}}{{\mu_{{\text{g}}} }}\nabla p^{n} } \right)} } \hfill \\ = \int_{V} {\left( {\frac{{b^{2} }}{{K_{{{\text{dr}}}} }}\frac{{\partial p^{n - 1} }}{\partial t}} \right)} \,dV - \oint_{\partial V} {ds \cdot \frac{\partial u}{{\partial t}} - \int_{V} {\left[ {\lambda_{t} T_{f - m} \left( {p_{f}^{n} - p^{n} } \right)} \right]dV} } \hfill \\ \end{gathered} $$

(32)

The first term to the left of the equal sign in the above equation represents the pressure term of the current time step, and the second term represents the implicit pressure flow term of the current time step. The first term to the right of the equal sign is the implicit pressure term of the previous time step, the second term is the explicit displacement coupling term, and the last term is the explicit source/sink term, representing the influence of cracks. The discretization method of fluid flow equation in fractures (Eq. (30)) is similar to Eq. (32):

$$ \begin{gathered} \int_{V} {\left[ {\left( {\frac{1}{{M_{f} }} + \frac{{b^{2} }}{{K_{{{\text{dr}}}} }}} \right)\frac{{\partial p_{n}^{f} }}{\partial t}} \right]dV - \oint_{\partial V} {ds \cdot \left( {\frac{{\prod\limits_{i} {F_{app,i} } k_{f} }}{{\mu_{{\text{g}}} }}\nabla p_{f}^{n} } \right)} } = \int_{V} {\left( {\frac{{b^{2} }}{{K_{{{\text{dr}}}} }}\frac{{\partial p_{f}^{n - 1} }}{\partial t}} \right)\,} dV \hfill \\ - \,\oint_{\partial V} {ds \cdot \frac{\partial u}{{\partial t}} - \int_{V} {\left[ {\lambda_{t} T_{f - m} \left( {p^{n} - p_{f}^{n} } \right)} \right]dV - } } \int_{V} {\left[ {\lambda_{{\text{t}}} T_{f - f} \left( {p_{f1}^{n} - p_{f2}^{n} } \right)} \right]dV} + \int_{V} {qdV} \hfill \\ \end{gathered} $$

(33)

After the discretization of the above three equations, the matrix with five unknowns (u_x, u_y, u_z, p, p_f) can be solved successively by the iterative method. It is a matrix composed of three displacement equations, coefficient matrices of fluid flow equations in matrix and cracks. After obtaining the displacement component and pressure, the effective stress and the total stress can be calculated. In this model, production is conducted by setting a fixed bottomhole flowing pressure, with a closed outer boundary and a pressure differential existing between the fractures and the matrix. The model incorporates varying initial loads along the three principal stress directions, facilitating subsequent stress analysis. Similarly, albeit the present model is formulated within a two-dimensional framework, the underlying algorithmic principles and mathematical derivations are inherently extensible to three-dimensional environments.

Validation

The fluid solid coupling model based on embedded discrete fracture model and considering shale gas storage and transport mechanism was verified by using the data in Jiang and Younis’s research and commercial simulator. Jiang et al.⁵⁰ uses the discrete fracture model to establish a shale gas production model with a storage and transport mechanism, and uses an in-house simulator to conduct simulation calculations. Similarly, an identical physical model was established using the embedded discrete fracture model, in which the fracture cluster spacing was 25 m, the number of fracture clusters was 5, and the fracture length was 60 m, as shown in Fig. 1. The main input parameters are shown in Table 1. In this case, we obtained the dynamic curves of productivity change considering the full mechanism, adsorption only, diffusion and slip only, and no mechanism respectively through simulation. The results are shown in Figs. 2 and 3. Figure 2 represents the comparison between the formation pressure distribution simulated by our model and that of Jiang and Younis considering all mechanisms, indicating good consistency between the two. Figure 3 shows that both adsorption effect and gas slippage and diffusion effect significantly improve gas production. In tight unconventional reservoirs, smaller pore throats and lower bottomhole pressure can result in higher production through gas slippage, diffusion flow, and release of adsorbed gas. Meanwhile, compared with the reference results, the productivity change data of our model with all mechanisms and without any mechanism is in high consistency with the results of commercial simulator and Jiang and Younis’s results, which verifies the accuracy of our model.

Figure 1

Hydraulic fracture distribution in the validation model.

Table 1 Main simulation parameters.

Figure 2

Comparison between the formation pore pressure obtained by our model and the result of Jiang and Younis’s study with full mechanisms. (a) Our model. (b) Jiang and Younis’s result.

Figure 3

Productivity dynamics considering different mechanisms and comparison with existing research and commercial simulators.

The Mandel problem addresses the two-dimensional consolidation of a fluid-saturated slab sandwich^51,52. Based on the model established by Mandel (1953), a two-dimensional plane verification model is established herein, as shown in Fig. 4. The length of the model (H) in the y-direction is 100 m, which is divided into 200 grids. the length (L) in the x-direction is 10 m, which is divided into 20 grids. A normal displacement cannot occur at the bottom and left of the model, and it is a closed boundary (the fluid cannot flow). At the left border $u_{{\text{x}}} = 0$ and bottom border, $u_{{\text{y}}}$ is zero. On the right edge of the model is the traction free boundary, and the fluid can flow. A uniform force is applied to the top of the model to maintain a consistent vertical displacement. A 4.2 MPa load (W) is applied uniformly on top of the domain. The pore pressure in the model of the initial value is 0. Other specific parameters are listed in Tab. 2. The stress along the y-direction obtained using our model were used to compare with the results obtained by the analytical solutions. Figure 5 shows the comparison between the numerical models (dots) and analytical models (lines) for stress in y-direction in x-direction at various times (t). By comparison, it can be seen that the numerical simulation results are consistent with the analytical solution results. Therefore, the numerical model and analytical model exhibit a high degree of matching (Table 2).

Figure 4

Validation model of porous medium (Mandel problem).

Table 2 Parameters used in calculation of the validation model.

Figure 5

Comparison between the calculation results of the numerical solution (dots) and the analytical solution (lines).

Case studies

Effect of drainage time on stress

The timing of discharge plays a significant role in the redistribution of reservoir stress. The optimal design of infill wells and refracturing requires a clear understanding of the distribution of stress at different drainage times to identify the most favorable timing for drilling or refracturing under the stress distribution after the first iteration of production. In this case, a single-stage shale gas production model with cluster spacing of 30 m and three fractures was established to simulate the distribution of formation pressure and reservoir stress under different production times. The results are shown in Figs. 6, 7. The main input parameters in the model are shown in Table 3, and the parameters about the storage and transport mechanism of shale gas are shown in Table 1. Figure 6a shows that with the increase of production time, shale gas is continuously produced, the formation pressure near the fracture gradually decreases, and the range of pressure depletion gradually expands, resulting in the anisotropy of formation pressure. It can be seen from Fig. 6b,c that the stress near the fracture are greatly reduced under the influence of the sharp reduction of formation pressure. On the upper and bottom of the simulated area, σ_xx (stress in x-axis direction, σ_xx = σ_xx,0 + Δσ_xx) increased by about 5 MPa in the x-axis direction to support pressure depletion, while on the left and right of the simulated area, σ_yy (stress in y-axis direction, σ_yy = σ_yy,0 + Δσ_yy) increased by about 3 MPa in the y-axis direction to support pressure depletion. Under the influence of the current stress anisotropy, the induced shear stress varies from − 3 to 3 MPa (Fig. 6d) and the horizontal stress difference Δσ (Δσ = σ_yy − σ_xx) is strongly heterogeneous (Fig. 6e). Compared with the initial horizontal stress difference Δσ₀ (Δσ₀ = σ_yy,0 − σ_xx,0) of 3 MPa, Δσ at the left and right sides of the hydraulic fracture increases to 7 MPa after 15 years of drainage, while Δσ at the upper and lower sides of the hydraulic fracture decreases to − 3 MPa, indicating that the local regional stress has been reversed. This change has great influence on the fracture propagation trajectory of refracturing in the future.

Figure 6

Distribution of pressure (a), σ_xx (b), σ_yy (c), σ_xy (d) and Δσ (e) at different production times.

Figure 7

Distribution of σ_xx along the hydraulic fracture direction (a), σyy along the horizontal well direction (b), σ_xy along the hydraulic fracture direction (c), Δσ along the horizontal well direction (d) and Δσ along the hydraulic fracture direction (e) at different production times.

Table 3 Main simulation parameters.

Further analysis of Fig. 7a shows that σ_xx, σ_yy, and Δσ do not change in a monotonous trend with the production time, but decrease or increase rapidly in the initial stage of drainage, and gradually change to the initial value after reaching the limit value. As shown in Fig. 7a, when the drainage reaches the fourth year, σ_xx decreases to the minimum value of 37 MPa near the fracture tip; when the drainage reaches the 15th year, σ_xx increases to 47 MPa in the upper and lower parts of the simulated area, while When the drainage reaches the 50th year, σ_xx is close to the initial value of 42 MPa. Similar trends can also be seen in Fig. 7b, d and e. The minimum values in Fig. 5d and 7b and the absolute value of the induced shear stress in Fig. 7c have a monotonous change trend with the production time. It can be seen from Fig. 7d,e that Δσ in the local area will be less than 0 in the early stage of drainage, indicating that stress reversal has occurred. As the drainage time gradually increased to 50 years, Δσ began to be greater than 0, and the horizontal principal stress began to return to the initial state. This change law of stress difference can provide theoretical guidance for the optimization of filling wells and refracturing opportunities in the future.

Effect of different mechanisms on stress

The seepage mechanism of shale gas generally includes adsorption and desorption slippage and diffusion. By integrating these complex mechanisms into the fluid–structure coupling model, shale gas productivity and formation stress can be accurately predicted. Using the data in Table 2, the variation law of formation pressure and stress was studied under the four conditions of considering all mechanisms, no mechanism, only adsorption, and only diffusion and slippage, as shown in Figs. 8 and 9. It can be found that compared with no any mechanism, the range of formation pressure consumption will be larger and the production flow rate will be larger with full mechanisms, resulting in a larger range of induced stress. The key reason for this result is that the corrected permeability and flow coefficient corresponding to different mechanisms are different. Figure 9 also shows that stress distribution with full mechanism is very close to stress distribution with only slippage and diffusion, while considering only adsorption and not considering any mechanism has close influence on stress, which indicates that diffusion and slippage have relatively greater influence on shale gas production and stress distribution. In general, there are certain differences in stress distribution under different mechanisms. In order to accurately predict the evolution of stress, it is necessary to consider the storage and transport mechanism of shale gas.

Figure 8

Comparison of pressure (a), σ_xx (b), σ_yy (c), σ_xy (d) and Δσ (e) after 10 years of production with full mechanism and no mechanism.

Figure 9

Distribution of σ_xx along the hydraulic fracture direction (a), σ_yy along the horizontal well direction (b), σ_xy along the horizontal well direction (c), Δσ along the hydraulic fracture direction (d) with different mechanism.

Effect of biot coefficient on stress

In general, the larger the rock porosity, the smaller the Biot coefficient, and the stronger the sensitivity of rock porosity and permeability; otherwise, the larger the Biot coefficient, the weaker the sensitivity. Therefore, the study of Biot coefficient is to indirectly study the stress redirection of different stress-sensitive reservoirs during production. In this case, based on the input parameters in Table 2, fluid–solid coupling models with Biot coefficients of 0.5, 0.7, and 0.9 were established respectively, and the influence of Biot coefficients on stress evolution was studied. The simulation results are shown in Figs. 10 and 11. It can be seen from the figure that as the Biot coefficient increases, σxx and σ_yy in the area away from the fracture gradually increase, while σxx and σ_yy near the fracture gradually decrease. In addition, Δσ also increases with the increase of the Biot coefficient. By calculating the difference (peak-valley value) between the maximum value (peak value) and the minimum value (valley value) of the stress in the simulated area, as the Biot coefficient increases, the peak-valley value becomes larger. This shows that the reservoir with stronger stress sensitivity (smaller Biot coefficient) is less sensitive to formation pressure depletion, and the stress variation range is smaller. For reservoirs with weak stress sensitivity, formation pressure depletion is more likely to lead to stress reversal.

Figure 10

Distribution of σ_xx (a), σ_yy (b) and Δσ (c) in shale gas reservoirs with different Biot coefficients after 10 years of production.

Figure 11

Distribution of σ_xx along the hydraulic fracture direction (a), σ_yy along the horizontal well direction (b), and Δσ along the hydraulic fracture direction (c) with different Biot coefficients.

Effect of fracture geometry on stress

In existing studies, hydraulic fractures are mostly assumed to be plane and vertical fractures, but the actual fracturing fractures are mostly inclined or non-planar fractures affected by factors such as natural fractures, stress interference, and perforation orientation. To study the influence of fracture geometry on stress evolution, three fracture geometries were set up in this section, namely vertical fractures, inclined fractures and non-planar fractures. The number of fractures was 4 clusters, and the cluster spacing was 30 m. The size of the model is 400 m(x) × 400 m(y), the number of unit grids divided in the x and y axis directions is 200, and the rest of the parameters are shown in Table 2. Figure 12a represents the distribution cloud map of formation pressure after 10 years of production under different fracture geometries. It can be seen that the shape of the pressure depleted region is greatly different due to the influence of the fracture geometry. The pressure depletion area formed by vertical fractures is approximately rectangular, and the pressure depletion area formed by inclined fractures is approximately parallelogram; the pressure depletion area formed by non-planar fractures is the largest, approximately a square. Figures 12b–d reveal significant differences in the spatial distribution of reservoir stress due to the shape of the pressure depleted area. The stress distribution in reservoirs with vertical hydraulic fractures and non-planar fractures is axisymmetric after 10 years of development, while the locations with significant stress changes in reservoirs with inclined fractures have shifted. As can be seen from Fig. 13, σ_xx in the direction of hydraulic fractures, σ_yy in the direction of horizontal wells, and Δσ in the direction of hydraulic fractures corresponding to the geometric shapes of the three kinds of fractures also differ greatly at the same position. It is further indicated that the stress evolution law with complex fracture geometry is different from that of simplified plane fracture under the same drainage conditions. To accurately predict the stress distribution of pressure depletion, it is necessary to consider the influence of complex fracture geometry.

Figure 12

Distribution of formation pressure (a), σ_xx (b), σ_yy (c) and Δσ (d) after 10 years of production under different hydraulic fracture geometry (vertical fracture, inclined fracture and non-plane fracture).

Figure 13

The distribution of σ_xx in the y-axis direction (a), σ_yy in the x-axis direction (b), and Δσ in the y-axis direction (c) under different hydraulic fracture geometry (vertical fractures, inclined fractures, and non-planar fractures) after 10 years of production.

Conclusions

Based on the EDFM and FVM, a simulation model of shale gas stress evolution coupled with geomechanics/fluid flow is successfully developed considering the adsorption, desorption, diffusion and slippage flow of shale gas. The model achieves the coupled simulation of natural fractures, complex hydraulic fractures, storage and transport mechanism, stress and pore-elastic effect, and can more accurately predict the shale gas capacity and stress distribution of pressure depletion. Then, the stress calculation part of the model is then verified by the classical pore elasticity problem, while the productivity simulation part of the model is verified by the simulation results against published research and commercial simulators. The following conclusions are obtained through simulation:

• 1. Due to the anisotropy caused by the depletion of formation pressure, the stress evolution changes with time and space. And the stress evolution in different spaces does not show a monotonic trend with time, but rapidly decreases or increases to a certain limit value in the early stage of pressure depletion, and then tends towards the initial stress value evolution. This evolutionary law provides optimization direction and theoretical support for optimizing the timing of infill wells and refracturing.

• 2. Due to the influence of different mechanisms (full mechanisms, no mechanism, only adsorption, and only diffusion and slippage) on shale gas storage and transmission, the formation pressure and stress distribution under different mechanisms are somewhat different, especially the stress without considering any mechanism is quite different from the stress considering full mechanisms. This result shows that considering the storage and transmission mechanism of shale gas is of great significance for accurate prediction of shale gas productivity and four-dimensional stress evolution.

• 3. As the Biot coefficient increases (0.5 ~ 0.9), σ_xx and σ_yy in the area away from the fracture gradually increase, while σ_xx and σ_yy near the fracture gradually decrease. In addition, Δσ also increases with the increase of the Biot coefficient. the reservoir with stronger stress sensitivity (smaller Biot coefficient) is less sensitive to formation pressure depletion, and the stress variation range is smaller. For reservoirs with weak stress sensitivity, formation pressure depletion is more likely to lead to stress reversal.

• 4. Under the influence of fracture geometry, the pressure depletion regions caused by the three types of fracture geometry are approximately rectangular, parallelogram and square, respectively. The corresponding σ_xx, σ_yy and Δσ also have great differences in spatial distribution and values. Therefore, it is necessary to consider the influence of complex fracture geometry to predict the induced stress under the same drainage conditions.

This study is of great significance for understanding the stress evolution induced by pressure consumption and the design of filling well or refracturing.