Introduction

Economic exploration for shale gas is highly dependent on the complexity of the fracture network caused by hydraulic fracturing technology as well as the coverage area. It is very important to accurately assess the effect of the fracture network on gas flow feature and productivity. However, due to the multiple flow regimes and the strong multi-scale behavior, modeling for multi-scale flow in the fractured shale reservoir is challenging but worthwhile, and many researchers have done some meaningful work on this issue.

Having multiple scales is a characteristic of the flows in a fractured shale reservoir which involves multiple mechanisms, including gas desorption from matrix, Knudson flow in nanoscale pores, Darcy flow in the porous media, Darcy flow in the fracture networks and fluid exchange between the matrix system and the fracture system. Researchers proposed a lot of models with the multi-scale problem to tackle based on various methods including the analytical method (Ozkan et al. 2011; Brown et al. 2011), the semi-analytical method (Medeiros 2007a; Medeiros et al. 2007b) and the numerical method (Dershowitz et al. 2000; Cipolla et al. 2010; Kristinof et al. 2010; Sheng et al. 2012).

Ozkan et al. (2011) and Brown et al. (2011) adopted the trilinear analytical model to couple the flow in three environments: a tight, homogeneous reservoir beyond the tips of the hydraulic fractures (outer reservoir), a naturally fractured reservoir between hydraulic fractures (inner reservoir) and hydraulic fractures distributed along the length of the horizontal well. Their studies highlighted the effect of the SRV consisting of the hydraulic and natural fractures and noted that the production beyond the stimulated reservoir volume can be negligible (Carratú 2013).

Medeiros (2007a) proposed a semi-analytical model to investigate the performances of horizontal wells with multiple fractures. They solved the diffusivity equation on the basis of Green’s function solution and utilized dual-porosity idealization to cope with the flow in the SRV. Medeiros et al. (2007b) further obtained several important conclusions in which the most important one is that the variation of stress distribution caused by hydraulic fracturing may significantly promote the formation of the fracture networks and the productivity. Based on the finite difference method, Cipolla et al. (2010) studied the impact of the conductivity of the hydraulic fractures on productivity. Cherubini et al. (2013) carried out a 3D finite element simulation to analyze the impact of single inclined faults on the fluid flow. Huang et al. (2014) coupled the discrete fracture model and the continuum model to simulate groundwater flow in fractured rocks, based on domain decomposition.

The XFEM was initially proposed to tackle the strong-discontinuity problem in relation to crack growth and was soon extended to other problems characterized by localization, complex geometries and multi-phase. The method has two main advantages over other numerical methods. The first is that the modeling of arbitrary geometric features can be independent of the mesh. The second is that the local field can be accurately reproduced based on the theory of partition of unity (Melenk and Babuška 1996). Belytschko and Black (1999) first presented the essential ideas of modeling crack growth by finite elements with minimal remeshing and adopting a discontinuous function to enrich the approximation. Moës et al. (1999) further improved Belytschko and Black’s work by introducing the Heaviside function and the near-tip asymptotic function to capture the strong-discontinuity behavior. Many researchers developed the XFEM to solve problems for weak discontinuity such as interface problems and fluid flow in fractured reservoir. Sukumar et al. (2001) combined the level set method with the XFEM to represent the weak discontinuity due to material interfaces in composite. Réthoré et al. (2007, 2008) adopted a two-scale approach to model fluid flow in fractured porous media, and at the fine scale, the flow in the fracture was modeled using Stokes equations. Mohammadnejad and Khoei (2013a, b) regarded the pressure gradient jump across the hydraulic fracture as the weak discontinuity and established a fully coupled extended finite element model for modeling hydraulic fracture propagation.

Lamb et al. (2010) first combined the DPM and the XFEM to analyze coupled deformation and fluid flow in fractured porous media and demonstrated the validity of the weak-discontinuity enrichment scheme. On the basis of Lamb’s work, Sheng et al. (2012) built an XFEM–DPM model for multi-scale flow in fractured shale gas reservoir which integrated multiple flow regimes including mass transfer between matrix and fractures, four kinds of flow regimes and pressure dependence. Both Lamb’s work and Sheng’s work are meaningful, but have some shortcomings. Firstly, all the fractures are treated as micro-mecro scale fractures, including the macroscale hydraulic fractures which dominate the main flow direction. Secondly, the domain of dual-permeability media is unreasonably confined in the small finite elements which are bisected by the fractures, so the coverage area of the fracture network characterized by the SRV is underestimated and should be enlarged. Thirdly, they usually located the wellbore on the outer boundary of the whole domain rather than its interior according to the assumption of symmetry which did not always make sense, because both the complex fracture network and the reservoir were usually asymmetrical.

This paper aims to improve Lamb’s and Sheng’s work. The complex fracture network is further subsumed under two scales (the micro-mecro scale fracture network and the macroscale hydraulic fractures) according to their different impact on gas flow, and the flow in the two scales of fractures is strongly coupled. The notion of SRV is highlighted to reflect the coverage area of the micro-mecro scale fracture network and its impact on draining shale gas. The dual-permeability method (DPM) is adopted to capture the flow behavior resulting from the micro-mecro scale fracture network in the SRV, and in the meantime, extended finite element method (XFEM) is used to tackle the strong-/weak-discontinuity problems in relation to the flow field variations of the fracture system and the matrix system across the macroscale fractures which dominate the main flow direction. Combined with the method of introducing the interior well boundary condition into the XFEM based on the theory of Lagrangian multiplier (Cheng 1999), the arbitrariness and the asymmetry of the model can be taken into account easily to represent the real flow behavior. This study improves the XFEM–DPM model for multi-scale flow in fractured shale gas reservoir and the corresponding solution scheme.

Governing equations

Descriptions of physical model

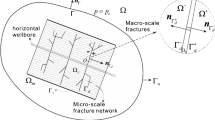
The whole domain Ω is divided into three adjacent parts, including matrix domain \(\varOmega_{m}\) (outer reservoir), SRV domain \(\varOmega_{s}\) (inner reservoir) and macroscale fracture domain \(\varOmega_{F}\) (see Fig. 1). \(\varOmega\) is bounded by the outer boundary \(\varGamma_{o}\), while \(\varOmega_{s}\) bounded by the exterior boundary \(\varGamma_{s}\) of the SRV and the interior boundary \(\varGamma_{d}^{ + } \cup \varGamma_{d}^{ - }\) which on the other side is the outer boundary of \(\varOmega_{F}\). A fractured horizontal well with several hydraulic fractures is located in the domain. The macroscale hydraulic fractures dominate the main flow direction in the reservoir, and due to their high permeability and conductivity, they are defined and dealt with explicitly. The SRV domain is regarded as the dual-permeability media which involves numerous micro-mecro scale fractures. Every flow regime in the model is an isothermal event and obeys Darcy’s law. The internal boundary conditions related to the wellbore include the Dirichlet boundary condition on \(\varGamma_{w}\) and the Neumann boundary condition on \(\varGamma_{\phi }\).

Fig. 1
figure 1

Fluid flow in a hydraulically multi-fractured reservoir

Full size image

\(\varvec{n}_{{\varGamma_{o} }}\) and \(\varvec{n}_{{\varGamma_{s} }}\) are the unit outward normal to \(\varOmega\) and \(\varOmega_{s}\), respectively. \(\varvec{n}_{{\varGamma_{d} }}\) is the unit normal vector to the discontinuity pointing to \(\varOmega^{ + }\) (\(\varvec{n}_{{\varGamma_{d} }} \varvec{ = n}_{{\varGamma_{d}^{ - } }} \varvec{ = } - \varvec{n}_{{\varGamma_{d}^{ + } }}\)).

Fluid flow in multi-fractured shale involves multiple scale flow regimes, including the gas desorption from the shale matrix, Knudsen flow in nanoscale pores, Darcy flow in the micro-mecro scale fracture network and Darcy flow in the macroscale hydraulic fractures. The last two kinds of flow regimes are coupled by considering mass transfer between the two scale fractures.

The impermeable boundary conditions are imposed on the external and the internal boundary of the matrix system as

$$\frac{{\partial p_{m} }}{{\partial \varvec{n}}} = 0 \quad{\text{on}}\;\varGamma_{o} \cup \varGamma_{d}^{ + } \cup \varGamma_{d}^{ - } ,$$
(1)

The impermeable boundary conditions are also imposed on the external boundary of the SRV domain as

$$\frac{{\partial p_{f} }}{{\partial \varvec{n}}} = 0 \quad{\text{on}}\,\varGamma_{s} .$$
(2)

In addition, mass transfer is considered to couple the fluid flow in the micro-mecro scale fracture network and the macroscale fractures. The complementary coupling condition is written as

$$\left[\kern-0.15em\left[ {\dot{W}_{f} } \right]\kern-0.15em\right]\varvec{n}_{{\varGamma_{d} }} = \left[\kern-0.15em\left[ {\dot{W}_{F} } \right]\kern-0.15em\right]\varvec{n}_{{\varGamma_{d} }} = q_{wd} \quad{\text{on}}\;\varGamma_{d}$$
(3)

\(\left[\kern-0.15em\left[ * \right]\kern-0.15em\right] = *^{ + } - *^{ - }\) represents the difference between the corresponding values at the two fracture faces.The Dirichlet boundary condition and the Neumann boundary condition can be imposed on the wellbore according to different production modes as

$$p_{f} = p_{wf} \;{\text{on}}\quad\varGamma_{\phi } .$$
(4)
$$\left. {\rho_{F} \frac{{k_{{x^{\prime } F}} }}{{\mu_{F} }}\frac{{\partial p_{f} }}{{\partial x^{\prime } }}} \right|_{w} = \bar{q}_{w} \quad{\text{on }}\varGamma_{w} .$$
(5)

Improvements and assumptions

Lamb et al. (2010) first combined the DPM and the XFEM to model the fluid flow in fractured porous media, and further Sheng et al. (2012) adopted the same approach to study multi-scale flow problem in a fractured shale reservoir. Their works are very meaningful, but should still be improved. In this paper, mistakes that exist in several equations given by Sheng have been corrected and some improvements have been made in several aspects as follows:

  1. (a)

    It is assumed that two scale fractures exist in hydraulically fractured shale. This kind of classification scheme is similar to the scheme proposed by Lee et al. (2000). The first scale refers to the numerous micro-mecro scale fractures which usually compose a network, while the second scale fractures are the hydraulic fractures in control of the main flow direction.

  2. (b)

    Many research findings revealed that economic exploration for shale gas is highly dependent on the complexity and the coverage area of the fracture network which can be characterized by the SRV. In comparison with the previous works, this paper enlarges the coverage area of SRV of the model in accordance with the popular opinion, rather than confining SRV in the elements which are bisected by the fractures. In this study, the DPM is adopted to capture the behavior of flow in the micro-mecro scale fracture network in the SRV (namely “inner reservoir” defined by Ozkan et al. 2011). On the other hand, the XFEM is used to tackle the weak-discontinuity problems involving the matrix system and the fracture system.

  3. (c)

    In the fractured shale reservoir, gas flows mainly from the porous matrix into the micro-mecro scale fracture network first, then into the macro-fractures and finally into the wellbore. In addition, the fracture pressure which falls quite faster and is weak discontinuous strongly affects the matrix pressure near the macro-fracture. So the direct fluid transfer between the matrix and the macro-fractures can be ignored, and both the matrix pressure field and the fracture pressure field are assumed to be weak discontinuous across the macroscale fractures.

  4. (d)

    The model is constructed on the basis of real gas, instead of ideal gas.

  5. (e)

    The fluid pressure within the fracture is assumed to be constant along the inward direction that is perpendicular to the fracture line, while the pressure gradient and the fluid flow are discontinuous.

Based on the above five main improvements, this paper uses the same mesh to approximate the fluid pressure in both the fracture and matrix systems.

Strong form

The flow in a hydraulically fractured shale reservoir involves two highly coupled systems, i.e., the multiple scale matrix and fracture systems.

The gas flow in the matrix is at nano-, micro- and macroscales due to the difference in pore diameter, molecular collisions and so on, while fractures can be classified into two scales (macro- and micro-mecro scales) according to their lengths and conductivities. Macroscale fractures denote the main fractures which can dominate the main flow direction. Micro-mecro scale fractures are numerous and usually compose fracture networks. First to be constituted are the strong-form equations corresponding to the matrix and the fracture systems.

The continuity equation for the porous flow in the shale matrix is written as

$$\begin{aligned} \left[ {\rho_{m} \varphi_{m} C_{tm} + (1 - \varphi_{m} )C_{a} \rho_{m} \beta_{\rho } - q_{L} \varphi_{m} \beta_{\phi m} } \right]\frac{{\partial p_{m} }}{\partial t} \hfill \\ - \nabla \left( {\rho_{m} \frac{{K_{m} }}{{\mu_{m} }}\nabla p_{m} } \right) + \alpha \frac{{\rho_{m} K_{m} }}{{\mu_{m} }}(p_{m} - p_{f} ) = 0. \hfill \\ \end{aligned}$$
(6)

Where \(C_{a}\) represents the nanoscale behavior and the impact of gas desorption from the bulk matrix on the flow in the shale matrix and is defined by Civan et al. (2011) as

$$C_{a} { = }\frac{{\rho_{s} M_{g} }}{{\rho \beta_{\rho } V_{std} }}\frac{{q_{L} p_{L} }}{{(p_{L} + p)^{2} }}.$$
(7)

\(C_{tm}\) denotes the total compressibility of shale gas. For the detailed derivation process of the differential Eq. (6), readers can refer to the papers published by Sheng et al. (2012) and Civan et al. (2011).

The continuity equation for the flow in the micro-mecro scale fracture network is written as

$$\rho_{f} \varphi_{f} C_{tf} \frac{{\partial p_{f} }}{\partial t} - \nabla \left( {\rho_{f} \frac{{K_{f} }}{{\mu_{f} }}\nabla p_{f} } \right) - \alpha \frac{{\rho_{m} K_{m} }}{{\mu_{m} }}(p_{m} - p_{f} ) = 0$$
(8)

In the DPM, the flow in the micro-mecro scale fracture network is seen as continuous field in most of the SRV domain, which is, however, weak discontinuous across the large-scale fracture due to the pressure gradient jump. The shape factor \(\alpha\) is introduced to accurately describe the single-phase quasi-steady-state transfer flow between matrix and fracture (Warren and Root 1963; Lemonnier and Bourbiaux 2010).

The continuity equation for the flow in the macroscale fracture (main fracture) is written as

$$\rho_{F} \varphi_{F} C_{tF} \frac{{\partial p_{f} }}{\partial t} - \nabla^{\prime } \left( {\rho_{F} \frac{{K_{F} }}{{\mu_{F} }}\nabla^{\prime } p_{f} } \right) = 0,$$
(9)
$$\rho_{F} \varphi_{F} C_{tF} \frac{{\partial p_{f} }}{\partial t} - \nabla^{\prime \prime } \left( {r\frac{{\rho_{F} K_{F} }}{{\mu_{F} }}\nabla^{\prime \prime } p_{f} } \right) = 0.$$
(10)

Equation 9 is used to describe the linear flow in the away-from-wellbore region of the macro-fracture, while Eq. 10 describes the radial flow in the near-wellbore region. The symbol \(\nabla\) denotes the vector gradient operator in the total Cartesian coordinate system \((x,y)\), while \(\nabla^{\prime }\) denotes that in the local Cartesian coordinate system \((x^{\prime } ,y^{\prime } )\) (see Fig. 2). To account for the feature of radial flow in the near-wellbore egion of the main hydraulic fractures, we use another local Cartesian coordinate \((r,y^{\prime } )\) and \(\nabla^{\prime \prime }\), respectively, to replace \((x^{\prime } ,y^{\prime } )\) and \(\nabla^{\prime }\).

Fig. 2
figure 2

Local Cartesian coordinate systems in the fracture

Full size image

Weak form

According to the above strong-form equations, weak-form equations can be derived based on the Galerkin formulation. The two weak-form equations of flow in the micro-mecro scale fracture network and macroscale fracture can be coupled to get the governing equation of the fracture system by considering the fluid transfer.The weak form of the continuity equation of fluid flow in the shale matrix is given by

$$\begin{aligned} \int_{\varOmega } {\delta p_{m} \left[ {\rho_{m} \varphi_{m} C_{tm} + (1 - \varphi_{m} )C_{a} \rho_{m} \beta_{\rho } - q_{L} \varphi_{m} \beta_{\phi } } \right]\frac{{\partial p_{m} }}{\partial t}d\varOmega } \hfill \\ + \int_{\varOmega } {\nabla \delta p_{m} \cdot \rho_{m} \frac{{K_{m} }}{{\mu_{m} }} \cdot \nabla p_{m} d\varOmega } \hfill \\ + \int_{\varOmega } {\delta p_{m} \cdot \alpha \frac{{\rho_{m} K_{m} }}{{\mu_{m} }} \cdot (p_{m} - p_{f} )d\varOmega } = 0 \hfill \\ \end{aligned}$$
(11)

Equation (11) is derived by the application of Galerkin–FEM, the divergence theorem and the boundary condition (Eq. 1) based on the strong form (Eq. 6).

In the reservoir domain outside the SRV, the third term on the left-hand side of Eq. 11 should be ignored.

The weak form of the continuity equation of fluid flow in the micro-mecro scale fracture network is therefore given by

$$\begin{aligned} \int_{{\varOmega_{s} }} {\delta p_{f} \left( {\rho_{f} \varphi_{f} C_{tf} } \right)\frac{{\partial p_{f} }}{\partial t}d\varOmega } \hfill \\ + \int_{{\varOmega_{s} }} {\nabla \delta p_{f} \cdot \rho_{f} \frac{{K_{f} }}{{\mu_{f} }} \cdot \nabla p_{f} d\varOmega_{s} } \hfill \\ + \int_{{\varGamma_{d} }} {\delta p_{f} \cdot \left[\kern-0.15em\left[ {\dot{W}_{f} } \right]\kern-0.15em\right]\varvec{n}_{{\varGamma_{d} }} d\varGamma } \hfill \\ - \int_{{\varOmega_{s} }} {\delta p_{f} \cdot \alpha \frac{{\rho_{m} K_{m} }}{{\mu_{m} }} \cdot (p_{m} - p_{f} )d\varOmega_{s} } \hfill \\ = 0. \hfill \\ \end{aligned} .$$
(12)

Similarly, the strong-form Eq. (8) is used to construct the Galerkin formulation, and the Divergence theorem and the inner boundary condition (Eq. 3) are adopted. In addition, the impermeable boundary condition (Eq. 13) is imposed on the external boundary of the SRV.

$$\int_{{\varGamma_{s} }} {\delta p_{f} \cdot \rho_{f} \frac{{K_{f} }}{{\mu_{f} }} \cdot \nabla p_{f} \varvec{n}_{{\varGamma_{s} }} d\varGamma_{s} } = 0$$
(13)

The weak form of the continuity equation of fluid flow in the macroscale fractures (main hydraulic fractures) is given by

$$\begin{aligned} \int_{{\varGamma_{d} }} {\delta p_{f} (w_{d} \rho_{F} \varphi_{F} C_{tF} )\frac{{\partial p_{f} }}{\partial t}d\varGamma } \hfill \\ + \int_{{\varGamma_{d} }} {\frac{{w_{d} \rho_{F} k_{{x^{\prime } F}} }}{{\mu_{F} }} \cdot \frac{{\partial \delta p_{f} }}{{\partial x^{\prime } }} \cdot R(r) \cdot \frac{{\partial p_{f} }}{{\partial x^{\prime } }}d\varGamma } \hfill \\ + \int_{{\varGamma_{w} }} {\delta p_{f} \cdot R(r) \cdot \bar{q}_{w} d\varGamma } \hfill \\ + \int_{{\varGamma_{\phi } }} {\left( {\frac{{\rho_{F} k_{{x^{\prime } F}} }}{{\mu_{F} }}} \right) \cdot R(r) \cdot \left( {\delta p_{f} \frac{{\partial p_{f} }}{{\partial x^{\prime } }} + \frac{{\partial \delta p_{f} }}{{\partial x^{\prime } }}p_{f} } \right)d\varGamma } \hfill \\ - \int_{{\varGamma_{d} }} {\delta p_{f} \left[\kern-0.15em\left[ {\dot{W}_{F} } \right]\kern-0.15em\right]\varvec{n}_{{\varGamma_{d} }} d\varGamma } \hfill \\ = \int_{{\varGamma_{\phi } }} {\left( {\frac{{\rho_{F} k_{{x^{\prime } F}} }}{{\mu_{F} }}} \right) \cdot R(r) \cdot \frac{{\partial \delta p_{f} }}{{\partial x^{\prime } }}p_{wf} d\varGamma } , \hfill \\ \end{aligned}$$
(14)

where

$$R\left( r \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {r > H_{f} /2} \hfill \\ {r + r_{w} } \hfill & {0 \le r \le H_{f} /2} \hfill \\ \end{array} } \right..$$
(15)

\(r\) denotes the distance between any point on the hydraulic fracture line and its corresponding wellbore. The function \(R(r)\) is defined to distinguish the radial flow in the near-wellbore region of the hydraulic fracture from the linear flow in the away-from-wellbore region of the hydraulic fracture. Fracture radial flow exists within a circle in the vertical plane with center at the wellbore and diameter equal to reservoir thickness \(H_{f}\) (Furui et al. 2003; Guo et al. 2009).

The Galerkin formulation of the strong-form Eq. 10 is given by

$$\begin{aligned} \int_{{\varOmega^{\prime}}} {\delta p_{f} \left\{ {\rho_{F} \varphi_{F} C_{tF} \frac{{\partial p_{f} }}{\partial t} - \nabla^{\prime \prime } \left( {r\frac{{\rho_{F} K_{F} }}{{\mu_{F} }}\nabla^{\prime \prime } p_{f} } \right)} \right\}d\varOmega^{\prime } } \hfill \\ + \int_{{\varGamma_{\phi } }} {\delta \lambda }^{\text{T}} (p_{f} - p_{wf} )\text{d}\varGamma_{\phi } \text{ + }\int_{{\varGamma_{\phi } }} \lambda^{\text{T}} \delta (p_{f} - p_{wf} )\text{d}\varGamma_{\phi } = 0 \hfill \\ \end{aligned}$$
(16)

The second row of Eq. (16) is introduced to load the Dirichlet boundary condition on the internal boundary of the reservoir according to the method of the Lagrangian multiplier.

Equation 16 can be solved by the application of the Divergence theorem and the assumption (e) which can lead to simplification, as indicated by Eq. 17.

$$\int_{{\varOmega^{\prime } }} {\nabla^{\prime } \delta p_{f} \frac{{\rho_{F} K_{F} }}{{\mu_{F} }}\nabla^{\prime } p_{f} d\varOmega^{\prime } } = \int_{{\varGamma_{d} }} {\frac{{\partial \delta p_{f} }}{{\partial x^{\prime } }}\frac{{w_{d} \rho_{F} k_{{x^{\prime } F}} }}{{\mu_{F} }}\frac{{\partial p_{f} }}{{\partial x^{\prime } }}d\varGamma } .$$
(17)

Assuming that at any point on the macroscale fracture lines, the pressures of the two-scale fracture media are the same, couple the flow in the micro-mecro scale fracture network and the macro-fractures by canceling the fluid transfer terms in Eqs. 12 and 14, and finally the coupled governing equation of gas flow in the fracture system can be derived.

Calculation formula of productivity

The total productivity of multi-fractured horizontal well can be predicted by adding together the productivity of all the hydraulic fractures.

$$Q = \sum\limits_{i = 1}^{{2n_{F} }} {\frac{{\pi r_{w} k_{F} w_{F} }}{{\mu B_{g} }}\left. {\frac{{\partial p_{F} }}{\partial r}} \right|_{{\left( {r = r_{w} } \right)_{i} }} }$$
(18)

Skin factor S can be easily taken into account by substituting the effective wellbore radius for the actual wellbore radius \(r_{w}\) or adopting the equivalent permeability in the near-wellbore region of hydraulic fracture.

Discretization formulation

The extended finite element method

According to assumption (c), both the matrix pressure field and the fracture pressure field are assumed to be weak discontinuous across the main fracture line. The fluid flow jump across the main fracture line can be reflected by using the improved weak-discontinuity enrichment function given by Moës et al. (2003).

The fracture pressure is approximated as the linear combination of the standard and enriched shape function as

$$p^{h} (\varvec{x}) = \sum\limits_{i \in N} {N_{i} (\varvec{x})P_{i} } + \sum\limits_{{j \in N_{s}^{enr} }} {N_{j} (\varvec{x})\left[ {\varPhi \left( \varvec{x} \right) - \varPhi (\varvec{x}_{j} )} \right]a_{j} } ,$$
(19)

where \(N_{i} (\varvec{x})\) is the classical finite element shape function; \(P_{i}\) is the nodal value; and \(a_{j}\) is the additional degree of freedom at the enriched nodes. \(I\) is a set of all nodes, while \(J\) is a set of all enriched nodes. Nodes in \(J\) are such that their support are bisected by a single fracture. The first term on the right-hand side of Eq. 19 represents the classical finite element approximation, while the second term denotes the weak-discontinuous enrichment.

In the second term, the improved enrichment function is utilized to avoid a decrease in the convergence rate of the blending element. The shape enrichment function and its gradient are given by

$$\varPhi (\varvec{x}) = \sum\limits_{I} {\left| {\phi (\varvec{x}_{I} )} \right|N_{I} (\varvec{x})} - \left| {\sum\limits_{I} {\phi (\varvec{x}_{I} )N_{I} (\varvec{x})} } \right|,$$
(20)
$$\begin{aligned} \nabla \varPhi (\varvec{x}) \cdot \varvec{n}_{{\varGamma_{d} }} = \sum\limits_{I} {\left| {\phi (\varvec{x}_{I} )} \right|\nabla N_{I} (\varvec{x})} \varvec{n}_{{\varGamma_{d} }} \hfill \\ + H\left( {\phi (\varvec{x})} \right) \cdot \sum\limits_{I} {\phi (\varvec{x}_{I} )\nabla N_{I} (\varvec{x})} \varvec{n}_{{\varGamma_{d} }} , \hfill \\ \end{aligned}$$
(21)

The general Heaviside function \(H\left( {\phi (\varvec{x})} \right)\) (Eq. 22) makes the gradient of the enrichment function discontinuous across the fracture line, while the enrichment function itself is continuous.

$$H\left( \varvec{x} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if} \hfill & {(\varvec{x} - \varvec{x}^{*} ) \cdot \varvec{n}_{{\varGamma_{d} }} > 0} \hfill \\ { - 1} \hfill & {else} \hfill & {} \hfill \\ \end{array} } \right..$$
(22)

Discretized form of the governing equations

Based on the extended finite element method, the discretized form of the governing Eqs. (11), (12) and (14) is as follows:

$$\varvec{Q}_{mm} \dot{\varvec{P}}_{m} + \varvec{C}_{mm} \varvec{P}_{m} + \varvec{T}_{mm} \varvec{P}_{m} - \varvec{T}_{mf} \varvec{P}_{f} = 0,$$
(23)
$$\varvec{Q}_{ff} \dot{\varvec{P}}_{f} + \varvec{C}_{ff} \varvec{P}_{f} + \varvec{T}_{ff} \varvec{P}_{f} - \varvec{T}_{fm} \varvec{P}_{m} - \varvec{F}^{\text{int}} = \varvec{F}^{\text{ext}} .$$
(24)

The definition of the coefficient matrices and the flux vectors is given in “Appendix”.

The direct solution procedure is used to discretize Eqs. 23 and 24 in the time domain, and the iterative algorithm is implemented to linearize the nonlinear system of equations.

Numerical example

In this section, a case is utilized to determine the reliability of the improved XFEM–DPM model for multi-scale flow in fractured shale gas reservoir. The basic data (Table 1) of the case are from Civan et al. (2011) and Guo et al. (2012).

Table 1 Reported reservoir and well data
Full size table

A horizontal well with two vertical hydraulic fractures in shale is producing gas in a condition of constant wellbore flowing pressure.

Figures 3, 4 and 5 show the pressure contours of the matrix system corresponding to the production time 0.1, 10 and 1000 days, respectively. Figures 6, 7 and 8 show the pressure contours of the fracture system corresponding to the production time 0.1, 10 and 1000 days, respectively. Figures 9, 10 and 11 show the transient production rate and the accumulated production versus time.

Fig. 3
figure 3

Matrix pressure distribution (0.1 day)

Full size image
Fig. 4
figure 4

Matrix pressure distribution (10 days)

Full size image
Fig. 5
figure 5

Matrix pressure distribution (1000 days)

Full size image
Fig. 6
figure 6

Fracture pressure distribution (0.1 day)

Full size image
Fig. 7
figure 7

Fracture pressure distribution (10 days)

Full size image
Fig. 8
figure 8

Fracture pressure distribution (1000 days)

Full size image
Fig. 9
figure 9

Impact of the Langmuir gas volume \(q_{L}\) on the production rate (PR) and the accumulated production (AP)

Full size image
Fig. 10
figure 10

Impact of the matrix–fracture transfer shape factor on the production rate (PR) and the accumulated production (AP)

Full size image
Fig. 11
figure 11

Impact of the micro-mecro scale fracture permeability on the production rate (PR) and the accumulated production (AP)

Full size image

As the production time increases, both the matrix pressure and the fracture pressure decrease, but the fracture pressure falls faster.

Figures 3, 4 and 5 indicate that for a long period, the matrix pressure inside the SRV domain decreases faster than that outside the SRV where the matrix pressure hardly decreases. So in the early to middle production period, it can be inferred that the SRV domain determines the main contribution of gas production, and to some extent, the contribution of the matrix domain outside the SRV can even be negligible. After a long period, the matrix pressure drop somewhere outside the SRV domain becomes obvious.

Figures 6, 7 and 8 show a dramatic change in the fracture pressure distribution. Because the micro-mecro scale fracture networks are directly linked to the macroscale fractures and the permeability of the fracture system is higher than that of the matrix, it is reasonable that the pressure of the fracture system falls faster than the matrix pressure for a long time. However, as the porosity of the fracture system is lower, the fall of the fracture pressure slows down.

Figures 9, 10 and 11 separately show the impact of Langmuir gas volume, matrix–fracture transfer shape factor and micro-mecro scale fracture permeability on production rate and accumulated production.

Figure 9 shows that when Langmuir gas volume increase, both production rate and accumulated production increase. Moreover, the gap of the accumulated productions resulted from the different Langmuir gas volume increases rapidly with time.

Figures 10 and 11 indicate that matrix–fracture transfer shape factor and micro-mecro scale fracture permeability have a similar impact. As the influential factor decreases, the decline curve tends to be gentle. The bigger the influential factor, the higher the initial production. However, for a long time in the later stage, there is an opposite situation. In addition, the different accumulated production curves tend to merge in the final stage, which indicates that the two influential factors do not influence the ultimate shale gas recovery.

Concluding remarks

This paper presents an improved XFEM–DPM model for multi-scale flow in fractured shale gas reservoir and the corresponding solution scheme.

Due to their different effects on shale gas flow, fractures are subsumed under two scales (micro-mecro scale fractures and macroscale hydraulic fractures). The notion of SRV is highlighted to reflect the coverage area (namely inner reservoir) of micro-mecro scale fracture networks and its impact on the drainage of shale gas.

The Lagrangian multiplier method is integrated to introduce the internal well boundary condition so that the physical condition can be asymmetrical.

The case study illustrates the reliability of the improved model and its favorable prospect in engineering application. Sensitivity analyses are conducted to quantify the effects of Langmuir gas volume, matrix–fracture transfer shape factor and micro-mecro scale fracture permeability on production rate and accumulated production.