Introduction

Shale gas is an unconventional natural gas resource which is hard to develop, and its commercial development requires multi-stage fracture and high investment. It is of great theoretical and practical significance to develop productivity evaluation methods and investigate major factors affecting the productivity of multi-stage fractured horizontal well in shale gas reservoirs.

To handle the fracture networks after hydraulic fracturing, several semi-analytical models based on boundary element method and Green’s function are proposed (Jia et al. 2016; Chen et al. 2016; Cheng et al. 2017; He et al. 2017; Zhang et al. 2018). And to further consider pressure-dependent gas PVT properties and dynamic gas desorption, many numerical methods are applied (Mayerhofer et al. 2010; Wu et al. 2013; Zhang et al. 2015; Mi et al. 2017).

Bello and Wattenbarger (2010) established a dual-porosity slab model for multi-stage fractured horizontal shale gas wells, made type curves of production rate, and classified gas flow regimes into matrix linear flow, bilinear flow, linear flow in natural fractures, and boundary-influenced flow from matrix into well. Al-Ahmadi and Wattenbarger (2011) introduced natural fractures and hydraulic fractures into the dual-porosity slab model, assuming that hydraulic fractures are perpendicular to well while natural fractures are parallel with the well, and he presented the productivity evaluation model of linear flow in triple media. Tivayanonda et al. (2012) considered that conductivity in hydraulic fractures is much greater than that in natural fractures, making further simplification of Al-Ahmadi’s model by regarding conductivity in hydraulic fractures as infinite conductivity. Ozkan et al. (2011) presented the concept of trilinear flow and classified the whole reservoir into the SRV inner zones between hydraulic fractures and the SRV outer zones without being fractured. The SRV inner zones completely consist of dual porosity and the SRV outer zones only consist of single porosity. Brohi et al. (2011) made type curves of non-steady trilinear flow, on the condition of constant borehole pressure (BHP) coupled with constant pressure of outer boundary or closed outer boundary respectively. Xu et al. (2013) considered that horizontal shale gas wells treated with stimulated reservoir volume (SRV) could be represented by dual-porosity slab multiple linear flow model in outer and inner zone, and he derived non-steady productivity equations on the condition of constant BHP. Stalgorova and Mattar (2013) considered that SRV inner zones were not completely of dual porosity but fractures in SRV inner zones were of single porosity, and he presented the model indicating that along the length of horizontal well were not completely fractured dual-porosity zones, and non-fractured zones existed between different fractured zones along the well, which supplied fluid to SRV inner zones in the form of linear flow as SRV outer zones at the end of fractures.

However, aforementioned studies failed to include stress sensitivity of hydraulic fractures and nonlinear factors such as nonlinear desorption and PVT properties. In this paper, we proposed an analytical model for multi-stage fractured horizontal wells from shale gas reservoirs to obtain the performance. Fracture networks, gas desorption, stress-sensitive fracture permeability, and pressure-dependent gas PVT properties are considered in the analytical model. Then a material balance method and a successive iteration procedure are proposed to obtain gas production vs. time and production contribution of desorbed gas. Finally, the effects of different model parameters on shale gas production and production composition are investigated.

Physical model

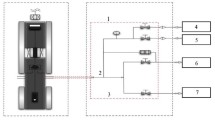
Multi-stage fractured horizontal well is important for efficient exploitation of shale reservoirs, especially the horizontal well with SRV, which tremendously increases the productivity of shale gas producers. As shown in Fig. 1, in the shale formation where stratification and lamellae are well developed (such as the lower part of Longmaxi formation in Southwest China), complicated small-scale fracture networks can be established after being fractured, and productivity is better than before. This paper presents the productivity evaluation model with fracture networks for the shale reservoirs where stratification and lamellae are undeveloped. Other assumptions are shown below:

  1. a.

    The formation is assumed to be horizontal, with the same thickness and fully penetrated by the hydraulic fractures.

  2. b.

    Each zone of the model shown in Fig. 2 is assumed to be heterogeneous and isotropic.

  3. c.

    Single-phase gas is considered for flow in the formation, and gravity effect is neglected.

  4. d.

    Langmuir adsorption is used to characterize shale gas adsorption in the matrix, and gas desorption is also assumed to obey the Langmuir isotherm.

Fig. 1
figure 1

A shale core from Longmaxi formation in South China

Full size image
Fig. 2
figure 2

Physical model for multi-stage fractured horizontal shale gas wells with fracture networks

Full size image

In this paper, the induced fractures are assumed to be perpendicular to the planner hydraulic fractures to derive the analytical solution of the model, as shown in Fig. 2. The flow in each region for the model is assumed to be linear. Gas in the outer zone is assumed to be linearly flow into the hydraulic fractures. There is a skin factor because of the convergence flow in to the fractures. Gas in shale matrix of inner zone linearly flows into induced fractures, and then gas in the induced fractures linearly flows into the hydraulic fractures. Eventually, gas in the hydraulic fractures flows into the horizontal well linearly along the fracture.

Mathematical model

Mathematical model with fracture networks

For gas flow in the formation, pseudo-pressure and pseudo-time (Gerami et al. 2008) are often used the handle the gas PVT properties and respectively defined as

$$ {\psi}_m=2\underset{0}{\overset{p_m}{\int }}\frac{p_m}{\mu Z}d{p}_m $$
(1)
$$ {t}_a={\int}_0^t\frac{\mu_{gi}{c}_{tm i}}{\mu_g\left({\overline{p}}_m\right){c}_{tm}\left({\overline{p}}_m\right)} dt $$
(2)

According to assumptions, as shown in Fig. 2, using the dimensionless variables shown in Table 1, the model of outer zone can be represented in dimensionless form as follows:

$$ \Big\{{\displaystyle \begin{array}{l}\frac{\partial^2{\psi}_{oD}}{\partial {y}_D^2}={\eta}_D\frac{\partial {\psi}_{oD}}{\partial {t}_D}\\ {}\\ {}{\left.{\psi}_{oD}\left({y}_D,{t}_D\right)\right|}_{t_D=0}=0\\ {}\\ {}{\psi}_{FD}\left({y}_D,{t}_D\right){\left|{}_{y_D={y}_{FD}}={\psi}_{oD}\Big({y}_D,{t}_D\Big)\right|}_{y_D={y}_{FD}}+{s}_c\\ {}\\ {}\frac{\partial {\psi}_{FD}\left({y}_D,{t}_D\right)}{\partial {y}_D}{\left|{}_{y_D={y}_{FD}}=\frac{1}{\xi}\frac{\partial {\psi}_{oD}\left({y}_D,{t}_D\right)}{\partial {y}_D}\right|}_{y_D={y}_{FD}}\\ {}\\ {}{\left.{\psi}_{oD}\left({y}_D,{t}_D\right)\right|}_{y_D\to \infty }=0\end{array}} $$
(3)
Table 1 Definition of dimensionless variables
Full size table

It should be noticed that the sc in the model is considering the convergence flow effect when gas flows from the outer zone to the fracture tips.

Given that gas flows in the form of matrix nonlinear flow and along the direction of Z axis, from matrix into induced fractures, coupled with desorption of absorbed gas in shale matrix and three migration mechanisms of gas in nano-scaled porosity, the model of inner matrix can be expressed as follows:

$$ \Big\{{\displaystyle \begin{array}{l}\frac{\partial^2{\psi}_{mD}}{\partial {z}_D^2}=\frac{3{\omega}_m}{\lambda_{fm}}\frac{\partial {\psi}_{mD}}{\partial {t}_D}\\ {}\\ {}{\left.{\psi}_{mD}\left({z}_D,{t}_D\right)\right|}_{t_D=0}=0\\ {}\\ {}{\left.\frac{\partial {\psi}_{mD}\left({z}_D,{t}_D\right)}{\partial {z}_D}\right|}_{z_D=0}=0\\ {}\\ {}{\left.{\psi}_{mD}\left({z}_D,{t}_D\right)\right|}_{z_D=1}={\psi}_{fD}\end{array}} $$
(4)

Similar to the flow model for gas flow from shale matrix into the induced fracture systems, and considering the flux contribution from shale matrix, the dimensionless form of equations of induced fracture can be expressed as follows:

$$ \Big\{{\displaystyle \begin{array}{l}\frac{\partial^2{\psi}_{fD}}{\partial {x}_D^2}=\frac{3{\omega}_f}{\lambda_{fm}}\frac{\partial {\psi}_{fD}}{\partial {t}_D}-\frac{\lambda_{fm}}{\lambda_{Ff}}{\left|\frac{\partial {\psi}_{mD}}{\partial {z}_D}\right|}_{z_D=1}\\ {}\\ {}{\left.{\psi}_{fD}\left({x}_D,{t}_D\right)\right|}_{t_D=0}=0\\ {}\\ {}{\left.\frac{\partial {\psi}_{fD}\left({x}_D,{t}_D\right)}{\partial {x}_D}\right|}_{x_D=0}=1\\ {}\\ {}{\left.{\psi}_{fD}\left({x}_D,{t}_D\right)\right|}_{x_D=1}={\psi}_{FD}\end{array}} $$
(5)

Considering the gas contribution from the induced fracture systems, and coupling the flow with the outer zone, the dimensionless form of hydraulic fracture model can be expressed as follows:

$$ \Big\{{\displaystyle \begin{array}{l}\frac{\partial^2{\psi}_{FD}}{\partial {y}_D^2}={\omega}_F\frac{\partial {\psi}_{FD}}{\partial {t}_D}-\frac{\lambda_{Ff}}{3}{\left|\frac{\partial {\psi}_{fD}}{\partial {x}_D}\right|}_{x_D=1}\\ {}\\ {}{\left.{\psi}_{FD}\left({y}_D,{t}_D\right)\right|}_{t_D=0}=0\\ {}\\ {}{\left.{\psi}_{FD}\left({y}_D,{t}_D\right)\right|}_{y_D=0}=1\\ {}\\ {}{\psi}_{FD}\left({y}_D,{t}_D\right){\left|{}_{y_D={y}_{FD}}={\psi}_{oD}\Big({y}_D,{t}_D\Big)\right|}_{y_D={y}_{FD}}+{s}_c\\ {}\\ {}\frac{\partial {\psi}_{FD}\left({y}_D,{t}_D\right)}{\partial {y}_D}{\left|{}_{y_D={y}_{FD}}=\frac{1}{\xi}\frac{\partial {\psi}_{oD}\left({y}_D,{t}_D\right)}{\partial {y}_D}\right|}_{y_D={y}_{FD}}\end{array}} $$
(6)

Handling gas desorption and stress sensitivity of fracture permeability

In the matrix of shale gas reservoirs, the continuity equation incorporating desorption is given below:

$$ \frac{\partial }{\partial x}\left(-\rho v\right)=\frac{\partial \left(\rho \phi \right)}{\partial t}+\rho {B}_g\frac{\partial V}{\partial t} $$
(7)

The second term on the right side of Eq. (7) represents the influx into fractures from matrix due to desorption. In this paper, the Langmuir isotherm model is used:

$$ V=\frac{V_Lp}{p_L+p} $$
(8)

Substituting gas and pore compressibility and Eq. (8) into Eq. (7), to arrive at

$$ \frac{\partial^2\psi }{\partial {x}^2}=\frac{\phi \mu}{k}\left[{c}_m+{c}_g+\frac{Z{p}_{sc}T}{\phi {Z}_{sc}{T}_{sc}}\frac{V_L{p}_L}{p{\left({p}_L+p\right)}^2}\right]\frac{\partial \psi }{\partial t} $$
(9)

Desorption compressibility (Bumb and McKee 1988; Wu et al. 2016) is a good method to handle gas desorption:

$$ {c}_d=\frac{p_{sc} ZT}{\phi {Z}_{sc}{T}_{sc}}\frac{V_L{p}_L}{p{\left({p}_L+p\right)}^2} $$
(10)

Substituting Eqs. (1), (2), and (10) into Eq. (9), the diffusivity equation becomes:

$$ \frac{\partial^2\psi }{\partial {x}^2}=\frac{\phi {\mu}_{gi}{c}_{ti}}{0.0864k}\frac{\partial \psi }{\partial {t}_a} $$
(11)

The format of Eq. (11) is the same as diffusivity equations of conventional gas flow model.

Many experimental tests show that stress sensitivity is strong in shale formation (Guo et al. 2012; Zhao et al. 2013). And permeability of hydraulic fracture shows a good exponential relationship with effective stress under the overburden pressure (Huang et al. 2018). Pseudo-permeabilityγFof hydraulic fracture can be introduced into the model and expressed as follows:

$$ {\gamma}_F=\frac{1}{k_F}\frac{d{k}_F}{d\psi} $$
(12)

Pseudo-pressure of hydraulic fracture can be shown as follows:

$$ {k}_F={k}_{Fi}{e}^{\gamma_F\left({\psi}_F-{\psi}_i\right)} $$
(13)

kFi represents permeability of hydraulic fractures without overburden pressure, mD. γF represents pseudo-permeability of hydraulic fractures, (mPa·s)/(MPa)2. ψi − ψF represents pseudo-effective stress of hydraulic fractures, (MPa)2/(mPa·s).

Given that the quadratic term of pressure gradient on the left hand of equation is nonlinear, an intermediate variable is introduced and expressed as follows (Huang et al. 2018):

$$ {\psi}_{FD}=-\frac{1}{\gamma_{FD}}\ln \left[1-{\gamma}_{FD}\cdot {\eta}_F\right] $$
(14)

After changing the equation with intermediate variable, the nonlinear right hand of equation can be changed with regular perturbation method. With the use of Taylor expansion, the right hand can be changed as follows:

$$ \frac{1}{1-{\gamma}_{FD}{\eta}_F\left({y}_D,{t}_D\right)}=1+{\gamma}_{FD}{\eta}_F\left({y}_D,{t}_D\right)+{\gamma}_{FD}^2{\eta}_F^2\left({y}_D,{t}_D\right)+\dots \dots $$
(15)

For γFD ⋅ ηF ≪ 1 and it is extremely small, the zero order perturbation solution is accurate. So the first term on right hand should be kept to simplify the whole equation, and the model of hydraulic fracture can be simplified as follows:

$$ \Big\{{\displaystyle \begin{array}{l}\frac{\partial^2{\eta}_F}{\partial {y}_D^2}=\omega \frac{\partial {\eta}_F}{\partial {t}_D}-\frac{\lambda_{cw}}{3}{\left|\frac{\partial {\psi}_{mD}}{\partial {x}_D}\right|}_{x_D=1}\\ {}\\ {}{\left.{\eta}_F\left({y}_D,{t}_D\right)\right|}_{t_D=0}=0\\ {}\\ {}{\left.{\eta}_F\left({y}_D,{t}_D\right)\right|}_{y_D=0}=\frac{1}{\gamma_{FD}}\left(1-{e}^{-{\gamma}_{FD}}\right)\\ {}\\ {}\frac{\partial {\eta}_F\left({y}_D,{t}_D\right)}{\partial {y}_D}{\left|{}_{y_D={y}_{FD}}=\frac{1}{\xi}\frac{\partial {\psi}_{oD}\left({y}_D,{t}_D\right)}{\partial {y}_D}\right|}_{y_D={y}_{FD}}\\ {}\\ {}{\eta}_F\left({y}_D,{t}_D\right){\left|{}_{y_D={y}_{FD}}={\psi}_{oD}\Big({y}_D,{t}_D\Big)\right|}_{y_D={y}_{FD}}+{s}_c\end{array}} $$
(16)

It should be noticed that the model considering stress sensitive fracture permeability shown in Eq. (16) is similar to Eq. (6); the only difference is that the dimensionless pseudo-pressure ψFD in Eq. (6) is replaced by the intermediate variable ηF.

Solution of the model

On the condition of constant BHP, gas flows into well in the form of linear flow in hydraulic fractures, and dimensionless productivity of fractured horizontal shale gas well with fracture networks can be expressed as follows:

$$ {\left.{q}_D=-\frac{1}{2\pi}\frac{\partial {\psi}_F\left({y}_D,{t}_D\right)}{\partial {y}_D}\right|}_{y_D=0} $$
(17)

Given stress sensitivity of hydraulic fractures, dimensionless productivity of fractured horizontal shale gas well with fracture networks can be expressed as follows:

$$ {\left.{q}_D=-\frac{1}{2\pi}\frac{\partial {\eta}_F\left({y}_D,{t}_D\right)}{\partial {y}_D}\right|}_{y_D=0} $$
(18)

With the use of Laplace transformation, the general solution of aforementioned model with finite outer boundary can be achieved in the Laplace space. Associated with initial conditions and boundary conditions, productivity of fractured horizontal shale gas well with fracture networks can be expressed as follows:

$$ {\overline{q}}_D=\frac{\sqrt{sf(s)}}{2\pi s}\frac{1-{e}^{-{\gamma}_{FD}}}{\gamma_{FD}}\frac{I+M}{N+O} $$
(19)

where

$$ I=\frac{\sqrt{s{\eta}_D}}{\xi}\left[{\mathrm{e}}^{2\sqrt{s{\eta}_D}{y}_{eD}}-{e}^{2\sqrt{s{\eta}_D}\cdot {y}_{FD}}\right]\left\{\cosh \left[\sqrt{sf(s)}\cdot {y}_{FD}\right]-{s}_c\frac{\gamma_{FD}}{1-{e}^{-{\gamma}_{FD}}}\right\} $$
(20)
$$ M=\left[{\mathrm{e}}^{2\sqrt{s{\eta}_D}{y}_{eD}}+{e}^{2\sqrt{s{\eta}_D}\cdot {y}_{FD}}\right]\sqrt{sf(s)}\sinh \left[\sqrt{sf(s)}\cdot {y}_{FD}\right] $$
(21)
$$ N=\frac{\sqrt{s{\eta}_D}}{\xi}\left[{\mathrm{e}}^{2\sqrt{s{\eta}_D}{y}_{eD}}-{e}^{2\sqrt{s{\eta}_D}\cdot {y}_{FD}}\right]\sinh \left[\sqrt{sf(s)}\cdot {y}_{FD}\right] $$
(22)
$$ O=\left[{\mathrm{e}}^{2\sqrt{s{\eta}_D}{y}_{eD}}+{e}^{2\sqrt{s{\eta}_D}\cdot {y}_{FD}}\right]\sqrt{sf(s)}\cosh \left[\sqrt{sf(s)}\cdot {y}_{FD}\right] $$
(23)

In which, f(s) is defined as

$$ \Big\{{\displaystyle \begin{array}{l}f(s)={\omega}_F+\frac{\lambda_{Ff}}{3s}\sqrt{s{f}_f(s)}\tanh \left[\sqrt{s{f}_f(s)}\right]\\ {}{f}_f(s)=\frac{3{\omega}_f}{\lambda_{Ff}}+\frac{\lambda_{fm}}{\lambda_{Ff}}\sqrt{\frac{3{\omega}_m}{\lambda_{fm}s}}\tanh \sqrt{\frac{3s{\omega}_m}{\lambda_{fm}}}\end{array}} $$
(24)

If skin (sc = 0) and production of outer matrix (ξ → ∞, yeD = yFD) are not taken into account, the productivity equations of fracture networks model could be written as

$$ {\overline{q}}_D=\frac{\sqrt{sf(s)}}{2\pi s}\tanh \left[\sqrt{sf(s)}\cdot {y}_{eD}\right] $$
(25)

Equation (25) is identical to that of Al-Ahmadi and Wattenbarger (2011); this validates the productivity model of horizontal well with fracture networks in this paper.

Production prediction considering pressure-dependent gas PVT properties

Owing to extremely low permeability of shale matrix, pressure systems of two adjacent wells can hardly connect with each other. Thus, each fractured horizontal well can be regarded as an independent gas reservoir with artificial treatment. Material balance principle of gas reservoir engineering can be utilized to determine the average reservoir pressure in different moments:

$$ \frac{{\overline{p}}_m}{Z\left({\overline{p}}_m\right)}=\frac{p_i}{Z\left({p}_i\right)}\left(1-\frac{G_P}{G}\right) $$
(26)

In which, \( {\overline{p}}_m \) means average matrix pressure in certain moment, MPa.pi means initial matrix pressure, MPa.Gp and G means cumulative production and geological reserves.

As the application of Eq. (2), with the introduction of dimensionless pseudo-time, the model for fractured horizontal wells with fracture networks can be transformed into linear form, and their general solution of productivity is in the same form of linear solution. However, the calculated solution is on the condition of dimensionless pseudo-time, which means it must be transformed into real form.

Because changing real time into pseudo-time requires average pressure in different moments, and average pressure is associated with production rate as well as cumulative production which require pseudo-time for calculation, the whole calculated process of all parameters is closed and different parameters have mutual influence, requiring iterative method for solution. The process of iterative method is shown as Fig. 3.

  1. 1.

    Initialization of parameters including fundamental parameters of gas and reservoir.

  2. 2.

    With the use of general productivity equations of slab fractures or network model, calculating dimensionless production rate with Stefest numerical inversion in every dimensionless time step.

  3. 3.

    Assume average reservoir pressure as \( {\overline{p}}_m \) in current time step.

  4. 4.

    Calculate gas physical parameters under current \( {\overline{p}}_m \), including compressibility, density, and viscosity.

  5. 5.

    Calculate real time and real production rate with Eq. (19) and gas physical parameters.

  6. 6.

    Calculating real cumulative production.

  7. 7.

    Calculating new average reservoir pressure \( {\overline{p}}_m^{\hbox{'}} \) with Eq. (25).

  8. 8.

    Repeat steps from (3) to (7) until the difference of \( {\overline{p}}^{\hbox{'}} \) and last \( {\overline{p}}_m \) meets requirement of accuracy.

  9. 9.

    Calculate composition of production rate in current time step with real average reservoir pressure.

  10. 10.

    Calculate the next time step until the whole calculating process ends.

Fig. 3
figure 3

Flow chart of iteration for production composition model for fractured horizontal wells in shale reservoir

Full size image

If real average reservoir pressure is worked out, the proportion of desorbed gas can be calculated. Owing to depletion development of shale gas reservoir, the proportion of desorption compressibility equals to the proportion of desorbed gas. The proportion of absorbed gas production to the whole gas production can be represented as follows:

$$ {R}_a=\frac{c_d\left({\overline{p}}_m\right)}{c_{tm}\left({\overline{p}}_m\right)}\times 100\% $$
(27)

Results and discussion

The effects of fracture parameters on production

With the use of model, we analyzed the effects of different parameters on gas production of the well. Parameters of the case are shown in Table 2.

Table 2 Parameters for calculation of productivity of horizontal wells with fracture networks
Full size table

The effect of inner zone fissure aperture on productivity of horizontal wells with fracture networks is shown as Fig. 4. It is apparent that higher fissure aperture leads to higher effective permeability of inner matrix, higher production rate in earlier stage as well as higher cumulative production.

Fig. 4
figure 4

The effect of inner zone fissure aperture on horizontal wells productivity with fracture networks

Full size image

The effect of inner zone fissure density on productivity of horizontal wells with fracture networks is shown as Fig. 5. It is clear that higher fissure density results in higher effective permeability of inner matrix, higher production rate in earlier stage, and higher cumulative production.

Fig. 5
figure 5

The effect of inner zone fissure density on horizontal wells productivity with fracture networks

Full size image

Figure 6 shows the effect of half-length of hydraulic fractures on productivity of horizontal wells with fracture network, on the condition of the same amount of induced fractures. If the number of induced fractures is the same, productivity of different fractured horizontal wells in earlier stage is of little difference. It is because that conductivity of primary fracture can be regarded to be infinite, and initial production rate is mainly influenced by induced fractures. If primary fracture is longer, there will be more matrix directly connected with primary fracture, and production rate in later stage as well as cumulative production will be higher.

Fig. 6
figure 6

The effect of hydraulic fractures half-length on horizontal wells productivity with fracture network

Full size image

Production composition of model with fracture networks

In order to further clarify the effect of different parameters on initial production rate and recovery of fractured horizontal wells with fracture networks in shale reservoir, orthogonal experiments are implemented. Experimental parameters include permeability of matrix in outer and inner zone, half-length of hydraulic fractures, induced fractures spacing, width of inner zone, and SRV spacing. Each parameter has three different levels. With the introduction of one additional auxiliary parameter with one level, the final orthogonal experimental scheme can be set as shown in Table 3.

Table 3 Experimental design and calculated results for fractures network model
Full size table

Cumulative production in 20 years and the average production rate in the first year can be calculated with parameters of orthogonal experimental scheme. What’s more, cumulative production in 20 years and the average production rate in the first year in different levels of all parameters can be worked out. The range represents the influence of different parameters on the average production rate in the first year and cumulative production in 20 years, which is shown in Tables 4 and 5. Figure 7 reveals the proportion of range of different parameters of the average production rate in the first year and the proportion of range of different parameters of cumulative production in 20 years.

Table 4 Mean and range of production rate in the first year for fractures network model
Full size table
Table 5 Mean and range of recovery within 20 years for fractures network model
Full size table
Fig. 7
figure 7

The rank of parameters of initial production rate and recovery for fractures network model

Full size image

It is apparent that the rank of parameters of the average production rate in the first year for fractures network model is the following: hydraulic fracture spacing > half-length of hydraulic fracture > conductivity of hydraulic fracture > induced fracture spacing > induced fracture length/hydraulic fracture spacing > conductivity of induced fractures. And the rank of parameters of cumulative production in 20 years is the following: half-length of hydraulic fracture > induced fracture length/hydraulic fracture spacing > hydraulic fracture spacing > conductivity of induced fractures > conductivity of hydraulic fracture > induced fracture spacing.

Analysis of production contribution from desorbed gas

The production composition of fracture networks model can be analyzed with parameters in Table 2. Figure 8 shows the effect of matrix permeability of inner zone on production composition of horizontal wells with fracture networks. Higher matrix permeability of inner zone can increase flowing capacity of both free gas and desorbed gas, and accelerate spread of pressure drop in inner matrix, which is helpful for the desorption of absorbed gas.

Fig. 8
figure 8

The effect of matrix permeability of inner zone on production composition

Full size image

Figure 9 shows the effect of fissure aperture of inner zone on production composition of horizontal wells with fracture networks. Greater fissure aperture increases effective matrix permeability of inner zone and accelerates spread of pressure drop in inner matrix, which is helpful for the desorption of absorbed gas.

Fig. 9
figure 9

The effect of fissure aperture of inner zone on production composition

Full size image

Figure 10 shows the effect of fissure density of inner zone on production composition of horizontal wells with fracture networks. Higher fissure density increases effective matrix permeability of inner zone and accelerates spread of pressure drop in inner matrix, which is helpful for the desorption of absorbed gas.

Fig. 10
figure 10

The effect of fissure density of inner zone on production composition

Full size image

Figure 11 shows the effect of outer matrix permeability on production composition of horizontal wells with fracture networks. Higher matrix permeability of outer zone increases accelerates spread of pressure drop in inner matrix, which is helpful for the desorption of absorbed gas. However, the influence of matrix permeability of outer zone is less than that of inner matrix.

Fig. 11
figure 11

The effect of matrix permeability of outer zone on production composition

Full size image

Figure 12 shows the effect of half-length of primary fracture on production composition of horizontal wells with fracture networks, on the condition of the same amount of secondary fractures. It is evident that half-length of primary fracture exerts great influence on production composition of fractured horizontal wells. Longer primary fracture decreases spacing of secondary fractures and helps mutual interference of secondary fractures, which has the same effect of closed boundary and results in fast drop of average pressure as well as the desorption of absorbed gas.

Fig. 12
figure 12

The effect of half-length of primary fracture on production composition

Full size image

Figure 13 shows the effect of induced fracture spacing on production composition of horizontal wells with fracture networks on the condition of the same half-length of primary fracture. Smaller induced fracture spacing helps mutual interference of secondary fractures and facilitates the desorption of absorbed gas.

Fig. 13
figure 13

The effect of induced fracture spacing on production composition

Full size image

Conclusions

In this paper, we proposed an analytical model for MFHW in shale reservoirs with the consideration of secondary fractures, gas desorption, stress-sensitive fracture permeability, and pressure-dependent gas PVT properties. Based on the above analysis, the following conclusions can be obtained:

  1. 1.

    Based on the theory of linear flow, the model for fracture horizontal well with fracture networks in shale reservoirs is established respectively. Compared with models established formerly, production from outer zone into hydraulic fractures and stress sensitivity of hydraulic fracture are considered in the new model. What’s more, dynamic productivity equations of the model are derived.

  2. 2.

    For fracture networks model, matrix permeability, half-length of hydraulic fractures, and spacing of hydraulic fractures will largely influence production of the well. In addition, spacing of secondary fractures is another influence factor of productivity.

  3. 3.

    With the introduction of nonlinear desorption into matrix control equations, production composition of fractured horizontal shale gas wells in different moments is deeply analyzed with material balance principle and iterative method. The rank of parameters that influence the ultimate recovery is the following: half-length of hydraulic fracture > induced fracture length/hydraulic fracture spacing > hydraulic fracture spacing > conductivity of induced fractures > conductivity of hydraulic fracture > induced fracture spacing.