Oblique Wave Trapping by a Surface-Piercing Flexible Porous Barrier in the Presence of Step-Type Bottoms

Abstract

The present study deals with the oblique wave trapping by a surface-piercing flexible porous barrier near a rigid wall in the presence of step-type bottoms under the assumptions of small amplitude water waves and the structural response theory in finite water depth. The modified mild-slope equation along with suitable jump conditions and the least squares approximation method are used to handle the mathematical boundary value problem. Four types of edge conditions, i.e., clamped-moored, clamped-free, moored-free, and moored-moored, are considered to keep the barrier at a desired position of interest. The role of the flexible porous barrier is studied by analyzing the reflection coefficient, surface elevation, and wave forces on the barrier and the rigid wall. The effects of step-type bottoms, incidence angle, barrier length, structural rigidity, porosity, and mooring angle are discussed. The study reveals that in the presence of a step bottom, full reflection can be found periodically with an increase in (i) wave number and (ii) distance between the barrier and the rigid wall. Moreover, nearly zero reflection can be found with a suitable combination of wave and structural parameters, which is desirable for creating a calm region near a rigid wall in the presence of a step bottom.

1 Introduction

Over the past few decades, the problem of wave interaction with vertical porous barriers is of considerable interest to the scientific community for the protection of offshore facilities from different wave attacks. Various analytical, numerical, and experimental approaches have been performed to investigate the importance of vertical porous barriers with different configurations. The study on wave interaction with a perforated wall breakwater started after Jarlan (1961). Since then, various modified Jarlan-type breakwaters have been proposed and investigated for reducing wave force depending on applications. Sahoo et al. (2000) studied the wave trapping by a partial porous barrier near a rigid wall using the least squares approximation method. They found that the curves of reflection coefficients are periodic and each curve repeats itself in every half-wavelength, which is similar to that of a fully submerged porous barrier studied by Chwang and Dong (1984). Li et al. (2003) conducted a research on the reflection of oblique incident waves by breakwaters with double-layered perforated walls. They observed that if a single-layered perforated caisson could reduce the wave reflection notably, it is not necessary to place a second perforated wall in such a single-perforated caisson. Nevertheless, if the single-layered perforated caisson produces little reduction on wave reflection, installing a second perforated wall can significantly reduce the wave reflection. Liu et al. (2007a) examined the wave interaction with a new modified perforated breakwater, consisting of a perforated front wall, a solid back wall, and a wave-absorbing chamber between them with a two-layer rock-filled core. The reflection of oblique waves from a structure consisting of an infinite array of partially perforated caissons was also investigated by Liu et al. (2007b). A thorough review of the developments on wave interaction with various perforated breakwaters can be found in Huang et al. (2011) and the literature cited therein.

On the other side, there is a wide interest on wave interaction with flexible porous structures as these structures are light in weight, economical, reusable, and environmentally friendly. These kinds of structures are often used for temporary protection of coastal infrastructures/facilities and in construction sites. For example, the use of flexible barriers for chord grass seedling, oil spilling, and pollution control is well studied in the literature. Williams (1996) investigated the hydrodynamic properties of a flexible floating breakwater consisting of a membrane structure attached to a small float restrained by moorings. Cho et al. (1998) developed an analytical solution to study oblique wave interaction with a dual vertical flexible membrane wave barrier hinged at the seafloor in the context of the two-dimensional linear wave-body interaction theory. Moreover, they have compared the analytical results with their developed boundary element method results. Using eigenfunction expansions for the velocity potential and linear membrane theory, Lo (1998) studied the performance of a wave barrier consisting of two vertical flexible membranes spaced at a fixed distance apart. Later, Lo (2000) investigated the interaction of water waves with a vertical flexible membrane of a finite extent which is less than the water depth. Yip et al. (2002) studied wave trapping by a partial flexible porous barrier near a rigid wall. Behera et al. (2013) investigated the performance of a partial flexible porous structure on wave trapping in a two-layer fluid. Karmakar et al. (2013) investigated gravity wave scattering by multiple surface-piercing floating porous membranes. Later, Karmakar and Soares (2014) considered oblique wave scattering by multiple bottom-standing flexible porous barriers by using the least squares method. Recently, using Green’s function technique, Koley et al. (2015) investigated the effects of a bottom-standing and surface-piercing flexible porous plate on wave scattering. Afterwards, Kaligatla et al. (2015) have extended their study on wave trapping by a vertical submerged flexible porous plate located near a vertical rigid wall. Most recently, Koley and Sahoo (2017) investigated oblique wave trapping by vertical permeable membrane barriers located near a wall.

In the aforementioned studies, the problems are considered in the case of uniform water depth or in the presence of a vertical step. However, there are few studies on wave interaction with vertical partial structures near a rigid wall in the presence of a step-type bottom bed. Using the Galerkin eigenfunction method, an analytical model has been developed by Suh and Park (1995) to predict the reflection coefficient of a perforated wall caisson mounted on a rubble mound foundation when waves are obliquely incident to the breakwater at an arbitrary angle. Using the extended modified mild-slope equation along with suitable jump conditions developed by Porter and Staziker (1995), Behera et al. (2015) investigated wave trapping by a fully extended porous barrier near a rigid wall in the presence of an undulated bottom. Later, Behera et al. (2016) studied wave scattering by a bottom-standing flexible porous barrier in the presence of various step bottoms. However, there is a negligible number of investigations on wave trapping by single/double flexible permeable/impermeable barriers near a rigid wall in the presence of an undulated bottom.

In the current study, wave interaction with a surface-piercing flexible porous barrier near a rigid wall is considered in the presence of sloping step-type bottoms. To determine the velocity potential in an undulated region, the modified mild-slope equation as in Porter and Staziker (1995) is used and solved by using the Runge-Kutta method, while the eigenfunction expansion method is used to find out the velocity potentials in the fluid domain having a uniform water depth. It is worth pointing out that although the modified mild-slope approximation method is a classic one, it still has to be used properly in various mathematical models in order to achieve the solution efficiently. Moreover, the least squares approximation method is used for finding the solutions in the presence of a partial surface-piercing flexible porous barrier. To keep the barrier at a desired position of interest, clamped-moored, clamped-free, moored-free, and moored-moored edge conditions are considered. The effects of the step bottom, porous-effect parameter and rigidity of the flexible barriers, oblique angle of incidence, and other wave and structural parameters are analyzed on wave reflection, free surface elevations, and wave forces on the barrier as well as the rigid wall.

2 Mathematical Formulation

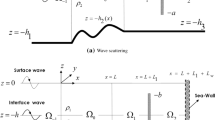
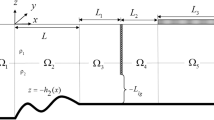
Oblique wave trapping by a surface-piercing flexible porous barrier near a rigid wall in the presence of an undulated bottom bed is investigated under the assumptions of the linearized water wave theory and small amplitude structural response. The problem is considered in the three-dimensional Cartesian coordinate system with x − y being the horizontal plane and the z-axis being the vertically downward negative direction as in Fig. 1. It is apprehended that the undulated bottom bed occupies the region 0  <  x  <  L with variable depth h(x) and the uniform open water regions − ∞   <  x  <  0 and L  <  x  <  ∞ with constant water depths h₁ and h₂, respectively. The flexible porous barrier of length a is located at a distance D and L₁ from the rigid wall and end edge of the step, respectively. The fluid is supposed to be extended horizontally along the y− axis over y  <  ∞. Assuming that the fluid is inviscid and incompressible, and the motion is irrotational and simple harmonic in time with angular frequency ω, the form of the velocity potential for four different regions with j  =  1,2,3,4 is given by ${\Phi}_j\left(x,y,z,t\right)\kern0.5em =\operatorname{Re}\kern0.1em \left\{{\phi}_j\left(x,z\right){\mathrm{e}}^{-\mathrm{i}\left({k}_yy+\omega t\right)}\right\}$, where θ is the incidence angle with the x-axis and k_y  =  k₁₀ sin θ with k₁₀ being the wave number of the incident wave in region 1. H_b  =  (−a, 0) and H_g  =  (−h₂, −a) denote the regions of the barrier and the gap along the vertical z− direction, respectively. The spatial velocity potential ϕ_j(x, z) for j  =  1,2,3,4 satisfies the governing partial differential equation given by

$$ \left({\nabla}_{xz}^2\kern0.5em -\kern0.5em {k}_y^2\right){\phi}_j\kern0.5em =\kern0.5em 0 $$

(1)

where ${\nabla}_{xz}^2\kern0.5em =\kern0.5em \left({\partial}^2/\partial {x}^2\kern0.5em +\kern0.5em {\partial}^2/\partial {z}^2\right)$. The linearized free surface boundary condition is given by

$$ \frac{\partial {\phi}_j}{\partial z}\kern0.5em -\kern0.5em K{\phi}_j\kern0.5em =\kern0.5em 0\kern1.10em \mathrm{on}\kern0.60em z\kern0.5em =\kern0.5em 0,\mathrm{for}\kern0.1em \ j\kern0.5em =\kern0.5em \mathrm{1,2,3,4}, $$

(2)

where K  =  ω²/g and g is the acceleration due to gravity. Further, the rigid uniform bottom boundary condition is given by

$$ \frac{\partial {\phi}_j}{\partial z}\kern0.5em =\kern0.5em 0\kern1.1em \mathrm{on}\kern1.1em z\kern0.5em =\kern0.5em -{h}_i $$

(3)

Fig. 1

Schematic diagrams of wave interaction with a flexible porous barrier near a rigid wall

where i  =  1 for j  =  1 and i  =  2 for j  =  3, 4. On the other hand, the bottom boundary condition for the undulated region 2 on z  =   − h(x) is given by

$$ \frac{\partial {\phi}_2}{\partial z}\kern0.5em +\kern0.5em \frac{\mathrm{dh}}{\mathrm{dx}}\frac{\partial {\phi}_2}{\partial x}\kern0.5em =\kern0.5em 0 $$

(4)

The horizontal velocity on the rigid wall vanishes, which is given as

$$ \frac{\partial {\phi}_4}{\partial x}\kern0.5em =\kern0.5em 0\kern1.1em \mathrm{on}\kern1.1em x\kern0.5em =\kern0.5em {M}_2 $$

(5)

where M₂  =  M₁  +  D with M₁  =  L  +  L₁. The flexible barrier is undertaken to be oscillating in the horizontal direction with a displacement of the form $\xi \left(y,z,t\right)\kern0.5em =\kern0.5em \operatorname{Re}\left\{\zeta (z){\mathrm{e}}^{-\mathrm{i}\left({k}_yy-\omega t\right)}\right\}$, where ζ(z) is the complex deflection amplitude of the flexible porous barrier. Thus, the boundary condition on the flexible porous barrier at x  =  M₁ is given by

$$ \frac{\partial {\phi}_j}{\partial x}\kern0.5em =\kern0.5em {\mathrm{i}k}_{10}G\left({\phi}_3\kern0.5em -\kern0.5em {\phi}_4\right)-\mathrm{i}\upomega \upzeta, \kern1.1em \mathrm{for}\kern1.1em j\kern0.5em =\kern0.5em 3,4,\kern1em z\in {H}_b $$

(6)

where G is the complex porous-effect parameter as in Kaligatla et al. (2015). The equation of motion of the barrier acted upon by fluid pressure yields

$$ EI{\left(\frac{{\mathrm{d}}^2}{{\mathrm{d}\mathrm{z}}^2}\kern0.5em -\kern0.5em {k}_y^2\right)}^2\zeta \kern0.5em +\kern0.5em Q\left(\frac{{\mathrm{d}}^2}{{\mathrm{d}\mathrm{z}}^2}\kern0.5em -\kern0.5em {k}_y^2\right)\zeta \kern0.5em -\kern0.5em {m}_s{\omega}^2\zeta \kern0.5em =\kern0.5em \mathrm{i}\uprho \upomega \left({\phi}_3\kern0.5em -\kern0.5em {\phi}_4\right),\kern1em z\in {H}_b $$

(7)

Further, $EI\kern0.5em =\kern0.5em {Ed}_s^3/12\left(1\kern0.5em -\kern0.5em {\nu}^2\right)$ is the rigidity of the barrier, E is the Young modulus, d_s is the thickness of the barrier, ν is the Poisson ratio, Q is the uniform compressive force acting on the barrier, m_s  =  ρ_sd_s is the uniform mass per unit length with ρ_s being the barrier density, and ρ is the density of water. The continuity of pressure and normal velocity along the gap is given by

$$ {\phi}_3={\phi}_4,\kern1.25em \frac{\partial {\phi}_3}{\partial x}=\frac{\partial {\phi}_4}{\partial x},\kern1.1em \mathrm{on}\kern1.1em x={M}_1,\kern1em z\in {H}_g. $$

(8)

To keep the barrier in position and for the unique solution of the boundary value problem, four different types of edge conditions can be used, which are as follows:

• (i) Clamped-free: In this case, the barrier is assumed to be clamped at the upper end at (M₁, 0) and free at the lower end at (M₁, −a).

• (ii) Clamped-moored: In this case, the barrier is assumed to be clamped at the upper end at (M₁, 0) and moored at the lower end at (M₁, −a).

• (iii) Moored-free: In this case, the barrier is assumed to be moored at the upper end at (M₁, 0) and free at the lower end at (M₁, −a).

• (iv) Moored-moored: In this case, the barrier is assumed to be moored at the upper and lower ends at (M₁, 0) and (M₁, −a), respectively.

• (v) In the case of the clamped edge, barrier deflection and the slope of the barrier deflection will be vanished which are given as

$$ \zeta (z)\kern0.5em =\kern0.5em 0,{\zeta}^{\prime }(z)\kern0.5em =\kern0.5em 0\kern1.1em \mathrm{at}\kern0.6em z\kern0.5em =\kern0.5em {l}_u, $$

(9)

while in the case of the moored edge, the bending moment will be vanished and the horizontal components of the dynamic mooring line tensions relate the restoring forces due to the axial load to the shearing forces, which are given as

$$ \left.\begin{array}{l}\left(\frac{{\mathrm{d}}^2}{{\mathrm{d}\mathrm{z}}^2}\kern0.5em -\kern0.5em \nu {k}_y^2\right)\zeta (z)\kern0.5em =\kern0.5em 0\\ {}\left[ EI\left\{\frac{{\mathrm{d}}^2}{{\mathrm{d}\mathrm{z}}^2}\kern0.5em -\kern0.5em \left(2\kern0.5em -\kern0.5em \nu \right){k}_y^2\right\}\frac{\mathrm{d}}{\mathrm{d}\mathrm{z}}\kern0.5em +\kern0.5em Q\frac{\mathrm{d}}{\mathrm{d}\mathrm{z}}\right]\zeta (z)\kern0.5em =\kern0.5em 2{K}_m{\sin}^2\left({\sigma}_m\right)\zeta (z)\end{array}\right\}\kern1.1em \mathrm{at}\kern1.1em z\kern0.5em =\kern0.5em {l}_u $$

(10)

where K_m is the mooring line stiffness and σ_m is the mooring line angle in the static position. It may be noted that for σ_m  =  0, Eq. (10) will be the free edge condition at which the bending moment and shear force are zero. In Eqs. (9)–(10), l_u is 0, − b as appropriate.

The far field boundary conditions are given by

$$ {\phi}_1\kern0.5em =\kern0.5em \left({I}_0{\mathrm{e}}^{{\mathrm{ip}}_{10}x}\kern0.5em +\kern0.5em {R}_0{\mathrm{e}}^{-{\mathrm{ip}}_{10}x}\right){f}_{10}\left({k}_{10},z\right),\kern1.1em \mathrm{as}\kern1.1em x\kern0.5em \to \kern0.5em -\infty $$

(11)

where R₀ is the complex amplitude of the reflected wave and I₀ is the incident wave amplitude. Further, k₁₀ is the real root of the dispersion relation in region 1 with ${p}_{10}\kern0.5em =\kern0.5em \sqrt{k_{10}^2\kern0.5em -\kern0.5em {k}_y^2}$ and f₁₀(k₁₀, z) is the associated vertical eigenfunction.

3 Method of Solution

This section briefly describes the method of solution for the wave interaction with the surface-piercing flexible porous barrier in the presence of bottom undulation. Using the expansion formulae, the form of the spatial velocity potentials ϕ_j(x, z) for j  =  1,2,3,4 in each region is expressed as

$$ {\phi}_j\left(x,z\right)=\left\{\begin{array}{l}{I}_0{\mathrm{e}}^{{\mathrm{i}p}_{10}x}{f}_{10}\left({k}_{10},z\right)\kern0.5em +\kern0.5em \sum \limits_{n=0}^{\infty }{R}_n{\mathrm{e}}^{-{\mathrm{i}p}_{1n}x}{f}_{1n}\left({k}_{1n},z\right),\kern0.5em x\kern0.5em <\kern0.5em 0,j\kern0.5em =\kern0.5em 1\\ {}\sum \limits_{n\kern0.5em =\kern0.5em 0}^{\infty }{\psi}_n(x)\ {W}_n\left(h(x),z\right),\kern8.25em 0\kern0.5em <\kern0.5em x\kern0.5em <L,j\kern0.5em =\kern0.5em 2\\ {}\sum \limits_{n\kern0.5em =\kern0.5em 0}^{\infty}\left({A}_n{\mathrm{e}}^{{\mathrm{i}p}_{2n}x}\kern0.5em +\kern0.5em {B}_n{\mathrm{e}}^{-{\mathrm{i}p}_{2n}x}\right){f}_{2n}\left({k}_{2n},z\right),\kern3em L\kern0.5em <\kern0.5em x\kern0.5em <\kern0.5em {M}_1,j\kern0.5em =\kern0.5em 3\\ {}\sum \limits_{n\kern0.5em =\kern0.5em 0}^{\infty }{T}_n\cos {p}_{2n}\left(x\kern0.5em -\kern0.5em {M}_2\right){f}_{2n}\left({k}_{2n},z\right),\kern3.75em {M}_1\kern0.5em <\kern0.5em x\kern0.5em <\kern0.5em {M}_2,j\kern0.5em =\kern0.5em 4\end{array}\right. $$

(12)

where f_in(k_in, z) for i  =  1, 2 and n  =  0,1,2,3, ⋯ are the eigenfunctions and given as

$$ {f}_{in}\left({k}_{in},z\right)\kern0.5em =\kern0.5em \frac{\cosh \kern0.2em {k}_{in}\kern0.15em \left(z\kern0.5em +\kern0.5em {h}_i\right)}{\cosh \kern0.2em {k}_{in}{h}_i} $$

(13)

and ${p}_{in}\kern0.5em =\kern0.5em \sqrt{k_{in}^2\kern0.5em -\kern0.5em {k}_y^2}$ with k₁₀ and k₂₀ are the positive real roots, k_in for n  =  1,2,3, ⋯ are the purely imaginary roots that satisfy the dispersion relation

$$ {\omega}^2\kern0.5em =\kern0.5em {gk}_{in}\tanh \kern0.2em {k}_{in}{h}_i. $$

(14)

Further, in Eq. (12), ψ_n(x)s are unknown functions and the eigenfunctions W_n are expressed as

$$ {W}_n\kern0.5em =\kern0.5em \frac{\cosh \kern0.5em {\overset{\sim }{k}}_n\left(z\kern0.5em +\kern0.5em h\right)}{\cosh \kern0.5em {\overset{\sim }{k}}_nh} $$

(15)

where ${\tilde{p}}_n\kern0.5em =\kern0.5em \sqrt{{\tilde{k}}_n^2\kern0.5em -\kern0.5em {k}_y^2}$. The wave number ${\tilde{k}}_0$ is a positive real root and ${\tilde{k}}_1,{\tilde{k}}_2,{\tilde{k}}_3,\cdots$ are purely imaginary roots of the dispersion relation

$$ {\omega}^2\kern0.5em =\kern0.5em g{\overset{\sim }{k}}_n\tanh \kern0.2em {\overset{\sim }{k}}_nh. $$

(16)

It may be mentioned that the roots ${\tilde{k}}_0,{\tilde{k}}_1,{\tilde{k}}_2,{\tilde{k}}_3\dots$ are functions of the bottom profile h(x) and the eigenfunctions W_ns which are borrowed from the flat bottom solution as in Porter and Staziker (1995). R_n, A_n, B_n, and T_n are unknown constants to be determined. Hereafter, the infinite series associated with the evanescent modes for the velocity potentials are truncated after N terms. Using the procedure of extended modified mild-slope equation (MMSE) as in Porter and Staziker (1995) to obtain ψ_n(x) for the undulated region, it is derived that

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{x}}\left({a}_n\frac{\mathrm{d}{\psi}_n}{\mathrm{d}\mathrm{x}}\right)\kern0.5em +\kern0.5em \sum \limits_{m=0}^N\left[\left({b}_{mn}\kern0.5em -\kern0.5em {b}_{nm}\right)\frac{\mathrm{d}\mathrm{h}}{\mathrm{d}\mathrm{x}}\frac{\mathrm{d}{\psi}_m}{\mathrm{d}\mathrm{x}}\kern0.5em +\kern0.5em \left\{{b}_{mn}\frac{{\mathrm{d}}^2h}{{\mathrm{d}\mathrm{x}}^2}\kern0.5em +\kern0.5em {c}_{mn}{\left(\frac{\mathrm{d}\mathrm{h}}{\mathrm{d}\mathrm{x}}\right)}^2\kern0.5em +\kern0.5em {\mathrm{d}}_{mn}\kern0.5em -\kern0.5em {k}_y^2{a}_n\right\}{\psi}_m\right]\kern0.5em =\kern0.5em 0 $$

(17)

where

$$ {a}_n(h)\kern0.5em =\kern0.5em {\int}_{-h}^0{W}_n^2\ \mathrm{dz},\kern0.5em {b}_{mn}(h)\kern0.5em =\kern0.5em {\int}_{-h}^0{W}_n\frac{\partial {W}_m}{\partial h}\ \mathrm{dz}, $$

$$ {c}_{mn}(h)\kern0.5em =\kern0.5em \frac{{\mathrm{d}\mathrm{b}}_{mn}}{\mathrm{d}\mathrm{h}}\kern0.5em -\kern0.5em {\int}_{-h}^0\frac{\partial {W}_m}{\partial h}\frac{\partial {W}_n}{\partial h}\mathrm{dz},\kern0.5em {\mathrm{d}}_{mn}(h)\kern0.5em =\kern0.5em {\int}_{-h}^0{W}_n\frac{\partial^2{W}_m}{\partial {z}^2}\mathrm{dz} $$

for n  =  0,1,2, ⋯, N. Taking the velocity potential as in Eq. (12) and continuity of pressure across the interfaces x  =  0 and x  =  L yields

$$ \left.\begin{array}{l}{\psi}_0(x)\kern0.5em =\kern0.5em {I}_0{\mathrm{e}}^{{\mathrm{i}p}_{10}x}\kern0.5em +\kern0.5em {R}_0{\mathrm{e}}^{-{\mathrm{i}p}_{10}x}0.2 cm\\ {}{\psi}_n(x)\kern0.5em =\kern0.5em {R}_n{\mathrm{e}}^{-{\mathrm{i}p}_{1n}x}\end{array}\right\}\kern0.6em \mathrm{at}\kern0.6em x\kern0.5em =\kern0.5em 0\kern0.5em \mathrm{for}\kern0.5em n\kern0.5em =\kern0.5em 1,2,\cdots, N $$

(18)

and

$$ {\psi}_n(x)\kern0.5em =\kern0.5em {A}_n{e}^{ip_{2n}x}\kern0.5em +\kern0.5em {B}_n{e}^{-{ip}_{2n}x}\kern0.6em \mathrm{at}\kern0.6em x\kern0.5em =\kern0.5em L\kern0.5em \mathrm{for}\kern1em n\kern0.5em =\kern0.5em \mathrm{0,1,2},\cdots, N. $$

(19)

Using Eqs. (18) and (19) and the conservation of mass across the interface boundaries similar to Porter and Staziker (1995) at x  =  0 and L brings out the jump conditions which are given by

$$ \left.\begin{array}{l}{a}_0\frac{d{\psi}_0}{dx}\kern0.5em +\kern0.5em {ip}_{10}{a}_0{\psi}_0\kern0.5em +\kern0.5em {h}^{\prime}\sum \limits_{m\kern0.5em =\kern0.5em 0}^N{b}_{m0}{\psi}_m\kern0.5em -\kern0.5em 2{ip}_{10}{a}_0{I}_0\kern0.5em =\kern0.5em 0,\\ {}{a}_n\frac{d{\psi}_n}{dx}\kern0.5em +\kern0.5em {ip}_{1n}{a}_n{\psi}_n\kern0.5em +\kern0.5em {h}^{\prime}\sum \limits_{m\kern0.5em =\kern0.5em 0}^N{b}_{mn}{\psi}_m\kern0.5em =\kern0.5em 0,\end{array}\right\}\kern0.60em \mathrm{at}\kern0.6em x\kern0.5em =\kern0.5em 0+,\kern0.5em n\kern0.5em =\kern0.5em 1,2,\cdots, N $$

(20)

and

$$ {a}_n\frac{d{\psi}_n}{dx}\kern0.5em -\kern0.5em {ip}_{2n}{a}_n{\psi}_n\kern0.5em +\kern0.5em {h}^{\prime}\sum \limits_{m\kern0.5em =\kern0.5em 0}^N{b}_{mn}{\psi}_m\kern0.5em -\kern0.5em 2{ia}_n{p}_{2n}{B}_n{\mathrm{e}}^{-{\mathrm{i}p}_{2n}x}\kern0.5em =\kern0.5em 0\kern0.60em \mathrm{at}\kern0.6em x\kern0.5em =\kern0.5em L-,\kern0.5em n\kern0.5em =\kern0.5em \mathrm{0,1,2},\cdots, N. $$

(21)

Considering the velocity potentials ϕ_j for j  =  3, 4 as in Eq. (12) and continuity of velocity conditions at x  =  M₁ as in Eq. (8) along with the orthogonal characteristics of the eigenfunctions f_2n(k_2n, z), the following is derived

$$ {A}_n\kern0.5em -\kern0.5em {B}_n{e}^{-2{ip}_{2n}{M}_1}\kern0.5em =\kern0.5em -{iT}_n\sin {p}_{2n}D\kern0.5em \mathrm{at}\kern0.5em x\kern0.5em =\kern0.5em {M}_1,n\kern0.5em =\kern0.5em \mathrm{0,1,2},\cdots . $$

(22)

The plate deflection ξ(z) is obtained by using Eq. (12) in Eq. (7),

$$ \zeta (z)\kern0.5em =\kern0.5em \sum \limits_{m\kern0.5em =\kern0.5em 1}^4{C}_m{g}_m(z)\kern0.5em +\kern0.5em \sum \limits_{n\kern0.5em =\kern0.5em 0}^{\infty}\left({e}_n{A}_n\kern0.5em +\kern0.5em {d}_n{T}_n\right){f}_{2n}\left({k}_{2n},z\right),\kern1em z\in {H}_b, $$

(23)

where e_n  =  β_1nt_n, d_n  =  β_2nt_n with ${\beta}_{1n}\kern0.5em =\kern0.5em 2{e}^{-{ip}_{2n}{M}_1}$, β_2n  =  i sin p_2nD  −   cos p_2nD, ${t}_n\kern0.5em =\kern0.5em \frac{i\rho \omega}{EIp_{2n}^4\kern0.5em +\kern0.5em {Qp}_{2n}^2\kern0.5em -\kern0.5em {m}_s{\omega}^2}$, ${g}_1(z)\kern0.5em =\kern0.5em \frac{\cosh \kern0.2em {\tau}_1z}{\cosh \kern0.2em {\tau}_1{h}_2}$, ${g}_2(z)\kern0.5em =\kern0.5em \frac{\sinh \kern0.2em {\tau}_2z}{\sinh \kern0.2em {\tau}_2{h}_2},{g}_3(z)=\frac{\sinh \kern0.2em {\tau}_2z}{\sinh \kern0.2em {\tau}_2{h}_2},\mathrm{and}{g}_4(z)=\frac{\sinh \kern0.2em {\tau}_2z}{\sinh \kern0.2em {\tau}_2{h}_2}$. Further, C_m (for m  =  1,2,3,4) are the unknowns and τ_ns are the roots of the characteristic equation $EI{\left({\tau}_n^2-{k}_y^2\right)}^2\kern0.5em +\kern0.5em Q\left({\tau}_n^2-{k}_y^2\right)\kern0.5em -\kern0.5em {m}_s{\omega}^2\kern0.5em =\kern0.5em 0$ with τ_n  =  iτ_n for n  =  3, 4. By making use of ζ(z) (from Eq. (23)) in Eq. (6), a series relation for the unknowns is derived as

$$ \sum \limits_{n\kern0.5em =\kern0.5em 0}^{\infty}\left({H}_n{A}_n\kern0.5em +\kern0.5em {G}_n{T}_n\right){f}_{2n}(z)\kern0.5em +\kern0.5em i\omega \sum \limits_{m\kern0.5em =\kern0.5em 1}^4{C}_m{g}_m(z)\kern0.5em =\kern0.5em 0,\kern1.1em \mathrm{for}\kern1.1em z\in {H}_b $$

(24)

where H_n  =  iωe_n  −  ik₁₀Gβ_1n and G_n  =  p_2n sin p_2nD  +  iωe_nt_n  −  ik₁₀Gt_n. Moreover, using the continuity of the velocity potential as in Eq. (8) and the relations in Eq. (22), another series relation is obtained,

$$ \sum \limits_{n\kern0.5em =\kern0.5em 0}^{\infty}\left({\beta}_{1n}{A}_n\kern0.5em +\kern0.5em {\beta}_{2n}{T}_n\right){f}_{2n}(z)\kern0.5em =\kern0.5em 0,\kern1.1em \mathrm{for}\kern1.1em z\in {H}_g. $$

(25)

The series relations in Eqs. (24) and (25) are satisfied in disjoint intervals and are referred to as dual series relations. These dual series relations are rewritten as

$$ \mathcal{S}(z)\kern0.5em =\kern0.5em \sum \limits_{n\kern0.5em =\kern0.5em 0}^{\infty}\left\{{\mathcal{U}}_n(z)\kern0.5em +\kern0.5em {\mathcal{V}}_n(z){T}_n\right\}\kern0.5em =\kern0.5em 0,\kern1em -{h}_2\kern0.5em <\kern0.5em z\kern0.5em <\kern0.5em 0 $$

(26)

where

$$ {\mathcal{U}}_n(z)\kern0.5em =\kern0.5em \left\{\begin{array}{ll}{\beta}_{1n}{A}_n{f}_{2n}(z),& \kern0.1em \mathrm{for}\kern1.1em z\in {H}_g\\ {}{H}_n{A}_n{f}_{2n}(z)\kern0.5em +\kern0.5em \sum \limits_{m\kern0.5em =\kern0.5em 1}^4{C}_m{g}_m(z),\kern1em & \kern0.1em \mathrm{for}\kern1.1em z\in {H}_b\end{array}\right. $$

$$ {\mathcal{V}}_n(z)\kern0.5em =\kern0.5em \left\{\begin{array}{ll}{\beta}_{2n}{f}_{2n}(z),& \kern0.1em \mathrm{for}\kern1.1em z\in {H}_g,\\ {}{G}_n{f}_{2n}(z),\kern1em & \kern0.1em \mathrm{for}\kern1.1em z\in {H}_b,\end{array}\right. $$

and let ${\mathcal{S}}_N(z)$ be the Nth partial sum of the series $\mathcal{S}(z)$. With help of the least squares approximation method, Eq. (26) can be written as

$$ {\int}_{-{h}_2}^0{\mathcal{S}}_M^{\ast }(z){\mathcal{S}}_{T_n}(z)\mathrm{dz}\kern0.5em =\kern0.5em 0,\kern1.1em \mathrm{for}\kern1.1em n\kern0.5em =\kern0.5em \mathrm{0,1,2,3},\cdots, M $$

(27)

where ^∗ denotes the complex conjugate and ${\mathcal{S}}_{T_n}(z)$ is the derivative of ${\mathcal{S}}_M(z)$ with respect to T_n. Thereafter, using Eq. (26) in Eq. (27), a system of linear equations is obtained as follows:

$$ \sum \limits_{m\kern0.5em =\kern0.5em 0}^N{T}_m^{\ast }{\mathcal{Y}}_{mn}\kern0.5em =\kern0.5em {\mathcal{J}}_n,\kern1.1em \mathrm{for}\kern1.1em n\kern0.5em =\kern0.5em \mathrm{0,1,2},\cdots, M, $$

(28)

where

$$ {\mathcal{J}}_n\kern0.5em =\kern0.5em {\int}_{-{h}_2}^0{\mathcal{U}}_n^{\ast }(z){\mathcal{U}}_n(z)\mathrm{dz},\kern1em {\mathcal{Y}}_{mn}\kern0.5em =\kern0.5em {\int}_{-{h}_2}^0{\mathcal{V}}_n^{\ast }(z){\mathcal{V}}_n(z)\mathrm{dz},\kern1.1em \mathrm{for}\kern0.6em m,n\kern0.5em =\kern0.5em \mathrm{0,1,2},\cdots, M. $$

(29)

Once and for all, Eq. (17) is solved using the fourth-order Runge-Kutta method to determine the unknown function ψ_n for specific bed profile h(x). A system of 6N equations is derived from Eqs. (18)–(22) and (28) by using the computed values of ψ_n. Another four linear equations are obtained from the edge conditions as in Eqs. (9) and (10). The set of 6N  +  4 linear equations are then solved for the various physical quantities of interest.

4 Numerical Results and Discussion

In this section, we discuss results for a wide range of parameters, generated by a MATLAB code which has been developed for investigating the effect of various wave and structural parameters on wave reflection, free surface elevations, and hydrodynamic forces on the barrier and rigid back wall. In the present study, time period T  =  8 s, acceleration due to gravity g  =  9.81 m/s², depth ratio h₂/h₁  =  0.5, L/h₁  =  0.5, L₁/λ₁  =  0.5, D/λ₁  =  0.25, λ₁  =  2π/k₁₀, $\gamma = EI/\left(\rho {gh}_2^4\right)\kern0.5em =\kern0.5em 0.01$, $\beta \kern0.5em =\kern0.5em Q/\left(\rho {gh}_2^2\right)\kern0.5em =\kern0.5em 0.1$, υ  =  m_s/(ρh₂)  =  0.1, ν  =  0.3, a/h₂  =  0.8, σ_m  =  45^∘, K_m  =  10³ Nm^‐1, and θ  =  30^∘ are kept fixed unless it is mentioned otherwise. The reflection coefficient is defined by

$$ {K}_r\kern0.5em =\kern0.5em \left|\frac{R_0}{I_0}\right| $$

(30)

The magnitude of the horizontal wave forces acting on the porous barrier K_f and on the rigid wall K_w is defined as

$$ {\left.{K}_f\kern0.5em =\kern0.5em \mathrm{i}\rho \omega {\int}_{-{h}_2}^0\left\{{\phi}_4\left(x,z\right)\kern0.5em -\kern0.5em {\phi}_3\right(x,z\left)\right\}\right|}_{x\kern0.5em =\kern0.5em {M}_1}\mathrm{dz}, $$

(31)

$$ {\left.{K}_w\kern0.5em =\kern0.5em \mathrm{i}\rho \omega {\int}_{-{h}_2}^0{\phi}_4\left(x,z\right)\right|}_{x\kern0.5em =\kern0.5em {M}_2}\mathrm{dz}. $$

(32)

Further, the non-dimensional form of the horizontal wave forces on the barrier C_f and rigid wall C_w is derived using the formulae

$$ {C}_f\kern0.5em =\kern0.5em \frac{\mid {K}_f\mid }{\rho {gh}_2^2}\kern1.1em \mathrm{and}\kern1.1em {C}_w\kern0.5em =\kern0.5em \frac{\mid {K}_w\mid }{\rho {gh}_2^2}. $$

(33)

The undulated bed profile is considered using the bed function h(x) as

$$ h(x)\kern0.5em =\kern0.5em {h}_1\kern0.5em -\kern0.5em c\left\{1\kern0.5em -\kern0.5em \alpha {\left(1\kern0.5em -\kern0.5em x/L\right)}^2\kern0.5em +\kern0.5em \left(\alpha \kern0.5em -\kern0.5em 1\right)\left(1\kern0.5em -\kern0.5em x/L\right)\right\},\kern1em 0\kern0.5em <\kern0.5em x\kern0.5em <\kern0.5em L $$

(34)

where c  =  h₁  −  h₂. From the bed function h(x) as in Eq. (34), various bed profiles can be obtained for different values of α such as the following: (i) α  =  0 refers to the sloping step-type bed, (ii) α  >  1 refers to the protrusion above the depth h₂, (iii) for −1  ≤  α  <  0 the bed is concave, and (iv) an increase in the depression of the bed profile will occur for α  <   − 1 (more details can be found in Behera et al. (2018)).

In Fig. 2a, b, the reflection coefficients K_r versus the non-dimensional wave number k₁₀h₁ are plotted for different values of depth ratio h₂/h₁ and porous-effect parameter G, respectively. In Fig. 2a, the results for h₂/h₁  =  0.5 and the larger rigidity of the fully extended barrier agrees well with the result of Li et al. (2003; Fig. 8) in the case of wave interaction with the porous barrier near a rigid wall in the presence of a vertical step. This figure shows that there is a right shift of full and minimum reflections with an increase in water depth for k₁₀h₁  <  5.8. However, for k₁₀h₁  >  5.8, there is a negligible effect of depth ratio h₂/h₁ in the wave reflection. From both figures, it is found that full reflection occurs periodically with an increase in k₁₀h₁. In the case of uniform water depth, full reflection occurs with a period 3.6, while in the presence of a step, the period decreases. With an increase in absolute value of the porous-effect parameter G, more wave energy passes through the porous barrier and is reflected by the rigid wall, and thus, the wave reflection increases with an increase in absolute value of the porous-effect parameter as shown in Fig. 2b.

Fig. 2

Variation of K_r versus k₁₀h₁ for different values of ah₂/h₁ with G  =  1 and bG with h₂/h₁  =  0.5. The other parameters are γ  =  5, β  =  0, a/h₂  =  1, D/h₁  =  1, L/h₁  =  0.1, and θ  =  30^∘

Reflection coefficients K_r against the dimensionless wave number k₁₀h₁ are plotted in Fig. 3a, b to check the effects of various edge conditions and the non-dimensional distance between the barrier and the rigid wall D/h₁, respectively. Figure 3a depicts that the wave reflection is more in the case of the moored-free edge condition, whereas the wave reflection is less for the clamped-moored edge condition. This is due to the fact that in the case of the moored-free edge, more waves get transmitted through the barrier and then reflected by the rigid wall which results in more wave reflection as compared to the other edge conditions. However, the clamped-moored edge condition results in less flexibility at the edges of the barrier; thus, less waves get transmitted through the barrier and as a result, the wave reflection is less in this case. It may be noted that in other figures throughout the manuscript, the clamped-moored edge condition is used. Figure 3b shows that the number of full reflections increases due to the increase in distance between the barrier and rigid wall (D/h₁) with a period 0.25 of D/h₁. It is also observed that for D/h₁  ≥  0.5 at k₁₀h₁  =  6.2, full reflection is obtained for each interval of D/h₁  =  0.5. Further, the wave reflection attains a minimum value between two consecutive wave numbers for which full reflection occurs.

Fig. 3

Variation of K_r as a function of k₁₀h₁ for different a edge conditions with D/h₁  =  1 and b values of D/h₁ with the clamped-moored edge condition. For both panels, γ  =  0.01, h₂/h₁  =  0.5, β  =  0, a/h₂  =  1, G  =  1, L/h₁  =  0.1, and θ  =  0^∘

The comparative study of the performance of (i) partial and fully extended and (ii) rigid and flexible porous barriers is presented in Fig. 4a, b. In Fig. 4a, the rigid porous barrier is considered, while the flexible porous barrier is considered in Fig. 4b with γ  =  0.01. From both figures, it is seen that the reflection coefficient diminishes with an increase in the length of the barrier. This is due to the dissipation of more wave energy by the porous barrier as an increase in the length of the barrier. In the case of the rigid partial porous barrier (Fig. 4a), wave reflection is greater compared to the flexible partial porous barrier (Fig. 4b). However, in the case of the fully extended barrier (a/h₂  =  1), an opposite trend is observed. In literature, it is examined that in the case of a uniform bottom, full reflection is observed periodically when the distance between the porous barrier and the rigid wall becomes an integer multiple of half of the wavelength of the incident waves (see Yip et al. (2002) and Kaligatla et al. (2015)). However, from Fig. 4a, b, it is seen that in the presence of a step, full reflection can be found when the distance between the porous barrier and the rigid wall becomes an integer multiple of less than half of the wavelength of the incident waves. Moreover, it is observed that one minimum in the wave reflection occurs in between two consecutive maxima and it increases when the step height decreases.

Fig. 4

Variation of K_r with respect to D/λ₁ for different values of a/h₂ with β  =  0, G  =  1, θ  =  30^∘, and h₂/h₁  =  0.5. aγ  =  5 (rigid porous barrier). bγ  =  0.01 (flexible porous barrier)

The influences of non-dimensional flexural rigidity γ and compressive force β on the variation of reflection coefficients K_r are elaborated in Fig. 5a, b. It is observed that the reflection increases with increase of flexural rigidity as shown in Fig. 5a. Such a conclusion was also made earlier by Yip et al. (2002) and Kaligatla et al. (2015) in the case of wave trapping by flexible porous plates in a uniform water bottom. However, with an increase in compressive force β, the wave reflection increases.

Fig. 5

Mutation of K_r as a function of D/λ₁ for a different γ with β  =  0 and b different β with γ  =  0.01, and in both, h₂/h₁  =  0.5, a/h₂  =  0.8, G  =  1, and θ  =  30^∘

Mooring angle ϑ and porous-effect parameter G are two monumental parameters. The dependence of the reflection coefficients K_r on ϑ and G (as a function of γ) is shown in Fig. 6a and b, respectively. From both figures, it is observed that the reflection coefficient decreases until it reaches a uniform pattern with an increase in the structural rigidity. Figure 6a shows that for less structural rigidity, wave reflection decreases with an increase of the mooring angle, while in the case of the highly flexible barrier, the mooring angle has a negligible effect on the wave reflection which may be due to the predominant role of higher modes of vibration of the highly flexible plate. On the other hand, with an increase in absolute value of the porous-effect parameter, the wave reflection increases as shown in Fig. 6b.

Fig. 6

Variation of K_r versus γ for different values of aσ_m with G  =  1 and bG with σ_m  =  45^∘, when h₂/h₁  =  0.5, a/h₂  =  0.8, and θ  =  30^∘

In Fig. 7a, b, the reflection coefficients K_r versus the non-dimensional slope length L/λ₁ are plotted for the different values’ protrusion and depression parameter α of the bed function h(x) and porous-effect parameter G, respectively. In the case of a larger sloping length, the water depth in all regions becomes the same; thus, with an increase in the sloping length, the oscillatory pattern of the wave reflection decreases as shown in both figures. Figure 7a depicts that wave reflection is greater in the case of protrusion in the step, while wave reflection is less for the step having depression. From Fig. 7b, it is manifested that the reflection coefficient decreases with an increase in length of the barrier which is because of the dissipation of more amount of wave energy by the porous barrier.

Fig. 7

Variation of K_r versus L/λ₁ for different values of aα with a/h₂  =  0.8 and ba/h₂ with α  =  0. The other parameters are G  =  1, σ_m  =  45^∘, h₂/h₁  =  0.5, and θ  =  30^∘

Figure 8 displays the parametric results in the K_r  −  θ plane system for two different values of water depth, h₂/h₁  =  1 (panel a) and h₂/h₁  =  0.5 (panel b). Figure 8a indicates that for θ  =  0^∘, full reflection occurs periodically with the period D/λ₁  =  0.5 which follows the same as in Fig. 4a and is analogous to earlier results of Sahoo et al. (2000). However, full reflection does not occur at the same period in the presence of a step as shown in Fig. 8b. Moreover, in both cases, with an increase in D/λ₁, the minimum of the wave reflection exponentially increases with respect to θ. It is also seen that the number of full reflections is less in the presence of a step. Figure 8b shows that at θ  =  72^∘, full reflection occurs at each interval D/λ  =  0.5, and this angle is said to be a critical angle.

Fig. 8

Change of K_r in terms of θ for different values of D/λ₁ in ah₂/h₁  =  1 and in bh₂/h₁  =  0.5 with a/h₂  =  0.8, α  =  0, G  =  1, and σ_m  =  45^∘

The changes of wave forces exerted on the barrier C_f and the rigid wall C_w versus the non-dimensional wave number k₁₀ for several values of the porous-effect parameter G are plotted in Fig. 9a and b, respectively. In general, with an increase in G, more wave energy passes through the pores of the barrier; thus, the wave force decreases on the barrier and it increases on the rigid wall as the absolute value of the porous-effect parameter G increases. A comparison between Figs. 3b and 9a, b suggests the values of k₁₀ for which full reflection occurs correspond to zero wave force on the barrier, and minimum reflection corresponds to maximum wave force on the rigid wall.

Fig. 9

Dependence of aC_f and bC_w on k₁₀h₁ for different values of G with h₂/h₁  =  0.5, a/h₂  =  0.8, α  =  0, D/h₁  =  1, θ  =  30^∘, and σ_m  =  45^∘

Panels a and b of Fig. 10 reveal the free surface elevations in open water (η₁/h₁) and confined (η₄/h₁) regions, respectively, for various values of the porous-effect parameter G. It is found that the amplitude of the free surface elevation in the confined region η₄/h₁ is less as compared to the open water region’s free surface amplitude, which is due to the dissipation of wave energy by the porous structure. It is also seen that with an increase in the absolute value of the porous-effect parameter G, the amplitude of the free surface elevations decreases in both regions. In Fig. 10b, the deflection of the flexible barrier is plotted for various values of the porous-effect parameter G. It is observed that with an increase in the barrier rigidity γ, the barrier deflection decreases. Since the barrier is fixed near the free surface and moored near the submerged end, the deflection is zero at the upper end and non-zero at the other end. Moreover, the barrier deflection decreases with an increase in the absolute value of the porous-effect parameter.

Fig. 10

Curves of a surface elevations η_j with γ  =  0.01 and b barrier deflection ζ for different values of G with h₂/h₁  =  0.5, a/h₂  =  0.8, α  =  0, θ  =  30^∘, and σ_m  =  45^∘

5 Conclusion

The influence of a surface-piercing flexible porous barrier near a rigid wall in the presence of step-type bottoms is examined based on the linearized theory of water waves. The barrier is analyzed under (i) clamped-free, (ii) clamped-moored, (iii) moored-free, and (iv) moored-moored edge conditions to determine its preference as a breakwater in the lee side of the coastal region. The associated boundary value problem is solved by using the modified mild-slope approximation method along with the least squares approximation method. Numerical results are computed for reflection coefficients, free surface elevations, and wave forces on the barrier and the rigid wall. The computed results are validated with available results in the literature in the case of wave interaction with the flexible porous barrier near a rigid wall in uniform water depth. The study reveals that the edge conditions play an important role not only for keeping the flexible barrier in position but also for the reduction of wave reflection. It is seen that the wave reflection is reduced for the clamped-moored barrier as compared to the barrier having the other edge conditions. Apart from uniform water depth, it is found that in the presence of a step, full reflection occurs periodically. However, the period for full reflection is less in the case of the step bottom as compared to the uniform bottom. It is observed that full reflection occurs in the period D/h₁  =  0.25 with an increase in the scaled wave number k₁₀h₁, and it is also seen that full reflection occurs in each interval at k₁₀h₁  =  6.2 for D/h₁  ≥  0.5. Further, at k₁₀h₁  =  1.2, nearly zero reflection occurs for certain values of wave and structural parameters, which is referred to as nearly full wave trapping in the confined zone. In the case of the uniform bottom, full reflection was obtained at θ  =  0^∘ and D/λ₁  =  0.5, while it does not occur at θ  =  0^∘ and D/λ₁  =  0.5 in the presence of a step. But full reflection was observed at each period of D/λ₁  =  0.5 when the angle θ  =  72^∘. It is found that full reflection is associated with zero force on the barrier and maximum force on the rigid wall, and the maximum wave force on the barrier is associated with less force on the rigid wall. Further, in the confined region, the amplitude of the free surface elevation reduced significantly due to the dissipation of wave energy by the porous barrier. Finally, the overall conclusion is that with a suitable combination of wave and structural parameters, the surface-piercing partial flexible porous barrier can be used as an effective breakwater, and the above important observations may help ocean engineers in the design of a perforated breakwater to create a calm region near sea walls, ports, and harbor walls.