1 Introduction

The study of water wave propagation through an array of porous walls or screens is of longstanding interest to applied mathematicians and coastal engineers since porous walls are found to be very useful in dissipating wave energy. Porous walls as wave reduction devices are extensively used in harbors, ports, and marinas to create tranquility zones. Also, these have been used in reducing coastal erosion. The typical perforated/slotted breakwaters and pile breakwaters in the form of multiple rows have been considered to attenuate waves in harbors. For instance, a perforated caisson breakwater with three wave-absorbing chambers in Porto Torres industrial harbour, Italy (Franco [7]), a breakwater with five chambers for the Dalian Chemical Production Terminal in China and a bottom-standing surface piercing pile breakwater in Singapore (see Huang et al. [8]) were constructed. Also, porous barriers are proposed to enhance the effectiveness of wetlands habitat restoration projects (see Williams and Wang [30]). The thin porous walls, considered in the present study, are very similar to perforated/slotted/pile breakwaters. The fluid flow through a porous structure having fine porosity is modeled by Darcy law. The research on the performance of multiple porous walls in reducing waves in different scenarios has been carried out for the past few decades. Several mathematical techniques have been proposed to deal with various physical settings of porous walls in the process. In this Section, we have discussed some useful models and methods of the solution developed by investigators. Employing the matrix method, wave reflection from several porous screens, modeled as wave dampers, spaced equally in a narrow wave tank, which was ended with a vertical wall, was studied by Evans [6]. Using the eigenfunction expansion method, Twu and Lin [27, 28] analyzed multiple porous plates to attenuate wave energy in a semi-infinite long channel of constant water-depth. Liu et al. [19] considered the problem of oblique interaction of waves with a multi-chambered caisson made up of multiple porous walls and solved analytically by making use of the matched eigenfunction expansion method. This study was further extended to perforated caisson breakwaters with perforated partition walls by Liu et al. [20]. Huang et al. [8] presented an extensive review related to hydraulic conductance in the presence of a perforated breakwater near the coast. This review concludes that destructive waves can be controlled by reducing waves’ transmission over a wide range of frequency through multi-perforated walls. Karmakar and Guedes Soares [13, 14] described the impact of multiple flexible porous barriers on the transmission of progressive waves. An application of a multi-domain boundary element method to the analysis of reflection and transmission of oblique waves from double porous thin walls can be found in [9]. Kaligatla et al. [12] investigated the effect of varying bottom topography on wave scattering by multiple porous barriers by applying a modified mild-slope equation and matched eigenfunction expansion. A further extension of the idea of Kaligatla et al. [12], which considers flexible porous barriers, was illustrated by Behera and CO Ng [2]. By employing the eigenfunction expansion method along with least square approximation, Das and Bora [5] studied wave damping phenomena by two vertical porous plates of different lengths in two different cases concerned with the submerged and surface piercing positions.

Due to global warming, frequent climate change is one of the severe natural threats, and it causes an increase in sea level, which eventually leads to an increase in waves. A solid sea wall is a protection measure against coastal erosion and flooding in coastal areas. When waves interact with a sea wall, the dissipation of incident wave energy occurs mostly by its run-up and reflection. In the case of a vertical wall, wave heights near it increase twice the incident wave amplitude at most. It accounts for scouring near its toe, and thus safety measures are needed for the wall’s stability. Using porous breakwaters at a distance from the solid wall offers a possible solution to reduce wave heights. Many investigators examined the performance of porous breakwaters near sea walls in the homogeneous ocean. Using matched eigenfunction expansion method, Das and Bora [4] investigated the reflection of water wave by a rectangular porous structure situated at an elevated bottom near a solid wall. Through the eigenfunction expansion method and the boundary-element method, Koley et al. [16] studied the trapping of waves by thick porous structures placed near a wall. Using the Green’s function technique, Kaligatla et al. [17] investigated the phenomenon of an oblique wave trapping by a flexible porous plate in finite and infinite water depths. They also obtained the distances between the plate and the rigid wall to get zero force on the wall. In these investigations, the bottom is assumed to be uniform. However, in the case of bottom undulations, Kaligatla et al. [11] studied a problem of wave trapping by dual porous walls kept in front of a rigid wall by applying the modified mild-slope equation and method of matched eigenfunction expansion. Later, Tabssum et al. [26] extended this study for thick porous structures.

In the literature mentioned above, the authors investigated wave motion characteristics through porous structures in a homogeneous fluid. However, temperature or salinity variations and gravitational settling are some of the reasons for ocean stratification. Thus, a multi-layered fluid is sometimes present. Such a phenomenon draws coastal researchers’ attention towards the hydrodynamic problems within the regime of distinct superposed homogeneous fluids. One such situation of superposed fluids has been modeled as a two-layer or three-layer fluid system. The other aspect that impetus to deal with a multi-layered fluid system is the oil slicking in oceans that occasionally happens in the fast-growing industrializing countries. To understand the phenomenon of wave scattering in two-layer fluid, many researchers have modeled and investigated water wave problems involving thin-type permeable (porous) and impermeable structures in a two-layer fluid system under the assumption of constant water-depth. Using the eigenfunction expansion method in conjunction with the least square method, Lee and Chwang [18] studied wave scattering of progressive incident waves by partial vertical impermeable barriers in a two-layer fluid. Through Havelock’s type of expansion, a study on the radiation and scattering of waves past a porous structure in a two-layer fluid of finite and infinite depths was carried out by Manam and Sahoo [21]. The scattering of surface and interfacial waves by a porous membrane barrier in a stratified ocean was analyzed by Kumar et al. [15] by orthogonality relation and least-square approximation method. Wave propagation problems in two-layer fluid over uneven bottom topography (with no porous structures) were treated long ago. For example, using the WKBJ (Wentzel–Kramers–Brillouin–Jeffreys) technique, Barthelemy et al. [1] explored the scattering of long progressive waves by a vertical step in the bottom in a two-layer fluid. Later, Chamberlain and Porter [3] generalized the study of [1] for arbitrary bottom topography (slowly varying) by deriving model equations through variational principle. The model equations are a generalized form of shallow-water approximations called mild-slope equations and can be applied to all wavelengths. The mild-slope approximation is one of the most effective methods of handling linear wave scattering by varying bottom topography. The mild-slope equation is a result of the depth-averaging technique, which eliminates vertical coordinate. Thus, the dimensional complexity of problems is reduced by one. However, the study, which includes arbitrary bottom topography in the above-stratified ocean models with porous structures, is minimal. Tabssum et al. [25] illustrated the application of Chamberlain and Porter’s mild-slope equation for the study of wave-interaction with a thick porous breakwater in a two-layer ocean of varying depth. However, a breakwater consisting of an array of porous walls is also in coastal engineering practice, as discussed above. With an array of porous walls, trapping of more wave energy in the chambers between walls may also be possible.

The present article deals with the scattering of linear gravity waves (surface and interfacial waves) in a two-layer fluid when they impinge obliquely on an array of porous walls of thin-type in the presence of undulated sea bottom. This study extends the research work of Kaligatla et al. [12] on wave scattering by multiple porous walls in a homogeneous ocean of varying depth. The porous walls are assumed to extend from the bottom to free- surface at lower sea-depth. A shelf type sea bottom is assumed in the present study. The bottom is composed of two different horizontal bottom levels and a varying bottom. The bottom is viewed as an approximation to continental margin. A typical example of such sloping topography is the Australian North West Shelf, which was considered by Holloway et al. [10]. Rattray et al. [23] investigated the generation of long internal waves at a continental slope. A study on the scattering of internal waves by different slope-shelf bottom topographies can be found from [22]. Furthermore, using the linear theory of two-layer flow, Talipova and Pelinovsky [29] derived an analytical solution to study the internal wave transformation over a oceanic slope-shelf. In the present study, we have used the eigenfunction expansion method for uniform bottom levels, and an approximate method for varying bottom, known as mild-slope equation derived by Chamberlain and Porter [3]. However, a modified form of Chamberlain and Porter’s equation for oblique incident waves is employed here. The solutions from two approaches are matched at shared boundaries under defined physical conditions. All the unknown constants of the problem are obtained by solving a set of linear algebraic equations. In this paper, we study two problems, namely wave scattering problem and wave trapping problem. The scattering problem is designed in an unbounded water domain in the horizontal direction, whereas the trapping problem is designed in the water domain, which ends with a vertical impermeable back wall at the lee side. These two problems are explored for different bottom geometries. The scattering coefficients, such as reflection and transmission coefficients of surface and interfacial waves, are investigated for different wave and structural parameters. In this article, porous walls’ effectiveness in reducing wave transmission is analyzed. Moreover, we examined the performance of porous walls in reducing wave force on the vertical backwall.

2 Formulation of boundary value problems

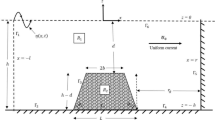
In this Section, we stated two model problems concerned with oblique wave scattering and trapping by porous walls in a two-layer ocean of varying depth. The mathematical formulation of these problems is done using linear water wave theory in the Cartesian coordinate system (x, y, z). The xy-plane is considered as mean free-surface while positive z-axis is directed vertically upward. The two-layer fluid is deemed incompressible and inviscid and its motion is irrotational. The two homogeneous fluids are separated by a mean interface at \(z=-h\). We assume that the upper layer fluid has density \(\rho _1\) whereas the lower layer fluid has density \(\rho _2\) with \(\rho _2>\rho _1\). The sea bottom is designed as a step-type bottom like continental shelf. It is constructed by linking a varying bottom of finite length \(z=- h_2(x)\) ( \(0\le x \le L\)) to two semi-infinite horizontal bottom levels \(z=- h_1\) and \(z=- h_3\) with \(h_1>h_3\). The entire sea bottom is impermeable. As shown in Fig. 1, an array of s number of thin porous walls extending from bottom to free-surface are located at \(z=- h_3\). In particular, Fig. 1a illustrates a scattering model whereas Fig. 1b illustrates a trapping model. The walls are of fine porosity and fluid flow past porous walls obeys Darcy law. To handle this problem in a simple way, the whole fluid region is divided into three regions: \(\Omega \) = \(\{-\infty<x<0, -\infty<y<\infty , -h_1\le z \le 0\}\) first region, \({\overline{\Omega }}\) = \(\{0\le x \le L, -\infty<y<\infty , -h_2(x)\le z \le 0\}\) second region, \(\overline{{\overline{\Omega }}}\) = \(\{L<x<\infty , -\infty<y<\infty , -h_3\le z \le 0\}\) third region. The third region \(\overline{{\overline{\Omega }}}\) is further divided into \(s+1\) subregions and are designated by \(\Omega _j\) for \(j = 1,2,3,\dots ,s+1\). In Fig. 1, \(L_1\) denotes the distance between the first porous wall and the end point of varying bottom. \(L_j\), \(j = 2,3,\dots ,s\) represents the spacing between two adjacent barriers, and \(L_{w}\) denotes the spacing between the backwall and the last porous wall as in Fig. 1b.

Fig. 1
figure 1

Schematic of multiple porous walls in a two-layer sea of undulating bottom

Full size image

The problems determine scattering of monochromatic surface and interfacial waves which impinge on porous walls obliquely from the region \(\Omega \). Henceforth, we abbreviate the surface and interfacial waves and write SW and IW respectively. The incident wave will be assumed to be either surface wave or interfacial wave. The phenomenon of wave scattering is described in terms of reflection and transmission coefficients of both SW and IW under wave-wave interaction. Based on the assumptions on waves and fluid, the fluid motion in each region can be described by velocity potential \(\Phi _j(x,y,z,t)\) = \(\text{ Re }\{\phi _j(x,z)\mathrm {e}^{-\mathrm {i}(\alpha _y y +\omega t)}\}\) for \(j = -1,0,1,2,\dots ,s,s+1\) with \(\alpha _y\)= \(k_I\text {sin}\theta \), where \(k_I\) is a wavenumber of incident SW making an angle \(\theta \) with \(x-\) axis and \(\text{ Re }\) is meant for real part. The spatial velocity potential \(\phi _j\) for \(j=-1,0\) corresponds to the regions \({\Omega }\) and \({\overline{\Omega }}\) respectively. Here \(\omega \) denotes an angular frequency and \(\mathrm {i}^2=-1\). The velocity potential \(\phi _j(x,z)\) for \(j=-1,0,1,2,\dots ,s,s+1\) satisfies the equation

$$\begin{aligned} \bigg (\frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial z^2} - \alpha _y^2\bigg ) \phi _j =0, \end{aligned}$$
(1)

in the respective fluid region \(\Omega _j\).

The free-surface boundary condition is written as

$$\begin{aligned} \frac{\partial \phi _j}{\partial z}- K\phi _j=0\; \,\,\hbox { on}\,\,\,\, z=0\;\hbox {for }\ j=-1,0,1,2,\dots ,s,s+1, \end{aligned}$$
(2)

where \(K=\omega ^2/g\) and \(g\) is the gravitational constant.

The no-flow boundary condition on flat sea bottom is expressed as

$$\begin{aligned} \frac{\partial \phi _j}{\partial z}=0 \;\,\,\text{ on }\;z=-h_1, -h_3\; \;\,\hbox { for}\ j=-1,1,2,\dots ,s,s+1. \end{aligned}$$
(3)

The boundary condition for varying bottom is given by

$$\begin{aligned} \frac{\partial \phi _{0}}{\partial z}+\frac{dh_2}{dx}\frac{\partial \phi _{0}}{\partial x}=0\,\,\text{ on } \,\,z=-h_2\,\,\text{ for }\,\,0\le x \le L. \end{aligned}$$
(4)

The kinematic and dynamic conditions at mean interface \((z=-h)\) are expressed as

$$\begin{aligned} \bigg (\frac{\partial \phi _j}{\partial z}\bigg )_{z=-h_{-}}= & {} \bigg (\frac{\partial \phi _j}{\partial z}\bigg )_{z=-h_{+}}\;\nonumber \\&\quad \text{ for }\,\,j=-1,0,1,2,\dots ,s,s+1, \end{aligned}$$
(5)
$$\begin{aligned} \bigg (\frac{\partial \phi _j}{\partial z}- K\phi _j\bigg )_{z=-h_{-}}= & {} \rho ~ \bigg (\frac{\partial \phi _j}{\partial z}- K\phi _j\bigg )_{z=-h_{+}}\;\;\nonumber \\&\quad \hbox {for}\,\,j=-1,0,1,2,\dots ,s,s+1, \end{aligned}$$
(6)

where \(\rho ={\rho _1}/ {\rho _2}\).

Since the fluid pressure and mass flux are continuous across the interface between the regions \(\Omega \) and \({\overline{\Omega }}\), and \({\overline{\Omega }}\) and \(\Omega _1\), the associated velocity potentials are matched and suitable mass flux conditions are applied at the inerface. This is illustrated in the following method of solution.

The horizontal velocity of fluid flow past porous walls must be continuous. Thus, the conditions on the porous walls at \(x=L+L_1+\dots +L_j\), \(j=1,2,\dots ,s\) are given by

$$\begin{aligned} \frac{\partial \phi _j}{\partial x} =\frac{\partial \phi _{j+1}}{\partial x}\,\,\,\text{ for }\,\,-h_3\le z \le 0, \end{aligned}$$
(7)

According to the Darcy law, the horizontal velocity of fluid flow through a porous wall is proportional to the pressure jump across the wall. Yu [31] derived a boundary condition for a thin porous wall by simplifying the porous medium theory of Sollitt and Cross [24]. The boundary condition for a jth porous wall is expressed as

$$\begin{aligned} \frac{\partial \phi _j}{\partial x}=\mathrm {i}k_IG_j(\phi _j-\phi _{j+1})\,\,\,\text{ for }\,\,-h_3\le z \le 0, \end{aligned}$$
(8)

where

$$\begin{aligned} \displaystyle G_j=\frac{\epsilon _j}{k_I d_j(f_j-\mathrm {i}r_j)}, \end{aligned}$$
(9)

where \(G_j\) is a complex porous effect parameter of jth wall, \(\epsilon _j\) is porosity, \(f_j\) is the resistance force coefficient, \(r_j\) is an inertial force coefficient and \(d_j \;(=d)\) is the thickness of porous wall. The real and imaginary parts of \(G_j\) have the physical meaning: real part refers to the resistance effect of the porous medium against the flow while imaginary part refers to the inertial effect of fluid inside the porous medium. The resistance effect causes wave energy dissipation whilst the inertial effect causes a phase shift in wave motion. Hence, wave energy dissipation is introduced by the conditions in (7) and (8). The value of \(r_j\) has been treated as unity whereas the value of \(f_j\) must be determined through an experiment. The value of \(|G_j|\) lies within the interval \((0,\infty )\). A porous wall becomes impermeable structure when \(|G_j|=0\) and transparent one when \(|G_j|\rightarrow \infty \).

Moreover, on the impermeable backwall as in Fig. 1b, the no-flow condition in the positive x-direction is given by

$$\begin{aligned} \frac{\partial \phi _{s+1}}{\partial x}=0 \;\hbox {at}\;x=L+L_1+ \dots +L_{w}. \end{aligned}$$
(10)

3 Method of solution

To determine the solutions of present problems, the eigenfunction expansion method in the region of constant water-depth, whereas the mild-slope equation (MSE) of Chamberlain and Porter [3] in the region of varying water-depth are employed. The variable bottom geometry is assumed to be smooth in a finite interval (0, L). Furthermore, the bottom is likely to have slope discontinuity at \(x=0\) and \(x=L\). The MSE associated with only propagating wave modes is used in this solution method, since for a two-layer ocean model of varying depth, a mild-slope equation that includes eigenmodes related to all evanescent waves is not available in the literature. The two solutions in the regions of constant depth and varying depth are matched at the interface boundaries using continuity in fluid pressure. Moreover, mass conserving jump conditions are also applied at the slope discontinuities of the bottom profile. Here, we illustrated the derivation of the solution for the scattering problem.

Following Chamberlain and Porter [3], the spatial velocity potentials in the fluid regions are expressed as

$$\begin{aligned} \phi _{-1}(x,z)= & {} \sum _{n=I}^{II}(I _ne^{\mathrm {i}k_{nx}{x}}+R_ne^{-\mathrm {i}k_{nx}{x}}) f_n(k_n,z)\;\;\text{ in }\;\Omega \end{aligned}$$
(11)
$$\begin{aligned} \phi _0(x,z)= & {} \sum _{n=I}^{II}\Psi _n(x) Z_n(h_2(x),z)\;\;\text{ in }\;{\overline{\Omega }} \end{aligned}$$
(12)

and

$$\begin{aligned} \phi _j(x,z) =\left\{ \begin{array}{l} \displaystyle \sum _{n=I}^{II}(B _n^je^{\mathrm {i}p_{nx}{x}}+ C_n^je^{-\mathrm {i}p_{nx}{x}}) g_n(p_n,z)\;\;\text {for}\;j=1,2,\dots ,s\\ \displaystyle \sum _{n=I}^{II}T_ne^{\mathrm {i}p_{nx}{x}} g_n(p_n,z)\;\;\text {for}\;j=s+1. \\ \end{array} \right. \end{aligned}$$
(13)

in \(\overline{{\overline{\Omega }}}\) where \(I_n\) for \(n=I,II\) are amplitudes of incident SW and IW which will be specified. The constants \(R_n\) and \(T_n\) for \(n=I,II\) are the amplitudes of reflected and transmitted waves respectively and that are to be determined. The constants \(B_n^j\), \(C_n^j\), for \(n=I,II\) and \(j=1,2,\dots ,s\) are also to be determined. The wavenumbers \(k_{nx}\) and \(p_{nx}\) can be calculated from the relations \(k_{nx}=\sqrt{k_n^2-\alpha _y^2}\) and \(p_{nx}=\sqrt{p_n^2-\alpha _y^2}\). In the Galerkin’s expansion (12), \(\Psi _n\) are unknown functions and the eigenfunctions \(f_n(k_n,z)\), \(Z_n(q_n,z)\) and \(g_n(p_n,z)\) for \(n=I,II\) are derived as

$$\begin{aligned} f_n(k_n,z) =\left\{ \begin{array}{l}\displaystyle \alpha _n (k_n\cosh k_nz + K\sinh k_nz),\;\;-h<z<0 \\ \displaystyle \beta _n(\cosh k_n(z+h_1)),\;\;-h_1<z<-h\\ \end{array} \right. \end{aligned}$$
(14)
$$\begin{aligned} Z_n(q_n,z) =\left\{ \begin{array}{l}\displaystyle \gamma _n (q_n\cosh q_nz + K\sinh q_nz),\;\;-h<z<0 \\ \displaystyle \delta _n(\cosh q_n(z+h_2(x))),\;\;-h_2<z<-h \\ \end{array} \right. \end{aligned}$$
(15)
$$\begin{aligned} g_n(p_n,z) =\left\{ \begin{array}{l}\displaystyle \tau _n (p_n\cosh p_nz + K\sinh p_nz),\;\;-h<z<0 \\ \displaystyle \zeta _n(\cosh p_n(z+h_3)),\;\;-h_3<z<-h, \\ \end{array} \right. \end{aligned}$$
(16)

where

$$\begin{aligned}&\alpha _n=\frac{\rho K \sinh k_n(h_1-h)}{k_n \sinh k_nh_1 (K \cosh k_nh - k_n \sinh k_nh) },\;\; \beta _n=\frac{\rho K}{k_n \sinh k_nh_1},\\&\gamma _n=\frac{\rho K \sinh q_n(h_2(x)-h)}{q_n \sinh q_nh_2 (K\cosh q_nh - q_n \sinh q_nh)},\;\; \delta _n=\frac{\rho K}{q_n \sinh q_nh_2},\\&\tau _n=\frac{\rho K \sinh p_n(h_3-h)}{p_n \sinh p_nh_3 (K \cosh p_nh - p_n \sinh p_nh) },\;\;\zeta _n=\frac{\rho K}{p_n \sinh p_nh_3}. \end{aligned}$$

The \(k_n\), \(q_n\) and \(p_n\) are the positive real roots of the dispersion equations

$$\begin{aligned}&K^2\{\rho + \coth kh \coth k(h_1-h)\}-k K \{\coth kh + \coth k(h_1-h)\}\nonumber \\&\quad +k^2(1-\rho )=0, \end{aligned}$$
(17)
$$\begin{aligned}&K^2\{\rho + \coth qh \coth q(h_2-h)\}-q K \{\coth qh + \coth q(h_2-h)\}\nonumber \\&\quad +q^2(1-\rho )=0, \end{aligned}$$
(18)
$$\begin{aligned}&K^2\{\rho + \coth ph \coth p(h_3-h)\}-p K \{\coth ph + \coth p(h_3-h)\}\nonumber \\&\quad +p^2(1-\rho )=0, \end{aligned}$$
(19)

respectively. It is analyzed that each dispersion relation has infinite purely imaginary roots that correspond to evanescent waves. In the present investigation, the effect of evanescent waves on wave scattering is not taken into account. In the case of constant water depths i.e. \(z = -h_1\) and \(z = -h_3\), the wavenumbers \(k_n\) and \(p_n\) for \(n = I, II\) are ordered as \(k_I < k_{II}\) and \(p_I < p_{II}\). Moreover, in the case of \(z = -h_2(x)\), the wavenumber \(q_n = q_n(h_2(x))\) needs to be obtained locally from the Eq. (18). It may be observed that the eigenfunctions are orthogonal by the relation

$$\begin{aligned} \langle U_n,U_m \rangle = \rho _2\int _{-h_l}^{-h} {U_n U_m\;\mathrm {d}z}+\rho _1 \int _{-h}^{0} {U_n U_m\;\mathrm {d}z}=0,\;\;m\ne n \end{aligned}$$

for \(m,n=1,2,3\), where \(h_l= h_1\) or \(h_2(x)\) or \(h_3\) and \(U_n\) is any of the eigenfunctions given above.

For water wave scattering by bottom undulations in a two-layer ocean, Chamberlain and Porter [3] derived a system of two partial differential equations by employing variational principle in the case of normal incidence. For oblique wave incidence, with a little modification to the differential equations of [3], a set of coupled differential equations for \(\Psi _n\) in Eq. (12) are derived as

$$\begin{aligned}&\sum _{n=I}^{II}\bigg \{\frac{d}{d x}\bigg (a_{nm}\frac{d\Psi _n }{d x}\bigg )+ \bigg ((b_{nm}-b_{mn})\frac{d h_2}{d x} \frac{d \Psi _n}{d x}\bigg )\nonumber \\&\quad +\bigg (c_{nm}+b_{nm}\frac{d^2h_2}{d x^2}+(\frac{db_{nm}}{d h_2}-d_{nm})\bigg (\frac{d h_2}{dx}\bigg )^2-\alpha _y^2a_{nm}\bigg )\Psi _n \bigg \}=0\, \end{aligned}$$
(20)

for \(m=I,II\), where

$$\begin{aligned} a_{nm}=\langle Z_n,Z_m \rangle ~=\rho _1 \int _{-h}^{0}{Z_n Z_m \mathrm {d}z}+\rho _2\int _{-h_2}^{-h}{Z_n Z_m \mathrm {d}z}, \\ b_{nm} = \rho _1 \int _{-h}^{0}{\frac{\partial Z_n}{\partial h_2} Z_m \mathrm {d}z}+\rho _2\int _{-h_2}^{-h}{\frac{\partial Z_n}{\partial h_2} Z_m \mathrm {d}z}, \\ c_{nm} = \rho _1 \int _{-h}^{0}{\frac{\partial ^2 Z_n}{\partial z^2} Z_m \mathrm {d}z}+\rho _2 \int _{-h_2}^{-h}{\frac{\partial ^2 Z_n}{\partial z^2} Z_m \mathrm {d}z}, \\ d_{nm} = \rho _1 \int _{-h}^{0}{\frac{\partial Z_n}{\partial h_2} \frac{\partial Z_m}{\partial h_2} \mathrm {d}z}+\rho _2 \int _{-h_2}^{-h}{\frac{\partial Z_n}{\partial h_2} \frac{\partial Z_m}{d h_2} \mathrm {d}z}. \end{aligned}$$

The differential equation in (20) can be solved numerically. It may be noted that the evanescent waves are neglected in the derivation of Eq. (20). Hence, it is valid in the case of slowly varying bottom, in the sense that \(|(dh_2/dx)/(q_Ih_2)| \ll 1\). When the sea bottom is very steep, one needs to consider a sufficient number of evanescent modes in the trial solution.

Next, a system of algebraic equations for the unknown constants, involved in the above expansions, shall be derived by applying continuity of pressure and mass conserving jump conditions at \(x=0\) and \(x=L\) together with the matching conditions (7) and (8) of porous walls. Continuity of fluid pressure at \(x=0\) and \(x=L\) yields

$$\begin{aligned}&\sum _{n=I}^{II}\bigg (\Psi _na_{nm}-R_ne^{\mathrm {-i}k_{nx}x}a_{nm}\bigg )\nonumber \\&\quad =\sum _{n=I}^{II}I_ne^{\mathrm {i}k_{nx}}a_{nm}\,\,\text {at}\,\, x=0 \,\,\text{ for }\,\, m=I,II \end{aligned}$$
(21)
$$\begin{aligned}&\quad \sum _{n=I}^{II}\bigg (\Psi _n-\big (B_n^1e^{\mathrm {i}p_{nx}x}+C_n^1e^{\mathrm {-i}p_{nx}x}\big )\bigg )a_{nm}=0\nonumber \\&\quad \text {at}\,\,x=L \,\,\text{ for }\,\, m=I,II \end{aligned}$$
(22)

Also, as mass flux must be continuous at those interfaces, we derive

$$\begin{aligned}&\sum _{n=I}^{II}\bigg (a_{nm}\frac{d \Psi _n}{d x}+(b_{nm}\frac{d h_2}{d x}+\mathrm {i}k_{nx}a_{nm})\Psi _n\bigg )\nonumber \\&\quad =\sum _{n=I}^{II}2\mathrm {i}k_{nx}a_{nm} I_ne^{\mathrm {i}{k_{nx}}x}\,\,\text {at}\,\,\, x=0 \,\,\text{ for }\,\, m=I,II \end{aligned}$$
(23)
$$\begin{aligned}&\sum _{n=I}^{II}\bigg (a_{nm}\frac{d \Psi _n}{d x}+(b_{nm}\frac{d h_2}{d x}+{\mathrm {i}p_{nx}a_{nm})\Psi _n-2\mathrm {i}}a_{nm}p_{nx}B_n^1 e^{\mathrm {i}{p_{nx}}x}\bigg )\nonumber \\&\quad =0\,\,\text {at}\,\,\, x=L\,\,\text{ for }\,\, m=I,II \end{aligned}$$
(24)

Upon utilizing the conditions (7) and (8) at \(\displaystyle x=L+\sum _{j=1}^{s-1} L_j\) for the first \(s-1\) porous walls, we get

$$\begin{aligned} \sum _{n=I}^{II} \left[ (B _n^j-B _n^{j+1})e^{ \mathrm {i}p_{nx}{x}}-(C_n^j-C_n^{j+1})e^{\mathrm {-i}p_{nx}{x}}\right] \nonumber \\ ~ p_{nx}\langle g_n,g_m \rangle =0 \end{aligned}$$
(25)
$$\begin{aligned} \sum _{n=I}^{II} \left[ B _n^j(p_{nx}-k_I G_j)e^{\mathrm {i}p_{nx}{x}}-C _n^j(p_{nx}+k_I G_j)e^{\mathrm {-i}p_{nx}{x}}\right. \nonumber \\ \left. +k_I G_j(B _n^{j+1}e^{\mathrm {i}p_{nx}{x}}+C _n^{j+1}e^{\mathrm {-i}p_{nx}{x}})\right] \langle g_n,g_m \rangle =0. \end{aligned}$$
(26)

Finally, the same conditions on the last porous wall gives

$$\begin{aligned}&\sum _{n=I}^{II} \left[ (B _n^j-T_n) e^{\mathrm {i}p_{nx}{x}}-C_n^j e^{\mathrm {-i}p_{nx}{x}}\right] \nonumber \\&\quad ~ p_{nx}\langle g_n,g_m \rangle =0\;\; \text{ at }\; x=L+\sum _{j=1}^s L_j, \end{aligned}$$
(27)
$$\begin{aligned}&\quad \sum _{n=I}^{II} \left[ B _n^j(p_{nx}-k_I G_j) e^{\mathrm {i}p_{nx}{x}}-C _n^j(p_{nx}+k_I G_j)e^{\mathrm {-i}p_{nx}{x}}\right. \nonumber \\&\quad \left. +T_n k_I G_j e^{\mathrm {i}p_{nx}{x}} \right] \nonumber \\&\quad \langle g_n,g_m \rangle =0\;\; \text{ at }\; x=L+\sum _{j=1}^s L_j. \end{aligned}$$
(28)

On solving Eqs. (21)–(28), one can find \(4(s+2)\) number of unknowns for s number of porous walls.

On the other hand, in the case of impermeable backwall, the velocity potential \(\phi _{s+1}(x,z)\) in the region \(\Omega _{s+1}\) is to be replaced by

$$\begin{aligned} \phi _{s+1}(x,z) = \sum _{n=I}^{II}T_n \cos p_{nx}(L^\prime -x)\;g_n(p_n,z), \end{aligned}$$
(29)

where \(L^\prime =L+L_1+\dots +L_{w}\) and \(T_n\) represents the amplitude of trapped wave. In this case as well, one can obtain the same number of unknowns for s number of porous walls.

4 Computational results

This section describes numerical results for the scattering and trapping of surface and interfacial waves by the multiple porous walls in two possible situations: (i) surface wave incidence when the lower fluid layer is in still position and (ii) interfacial wave incidence when the upper fluid layer is in still position. In each incident case, one needs to evaluate four scattering coefficients to describe the reflection and transmission of SW and IW. The mild-slope equation (20) is solved numerically for different bottom profiles by employing the in-built function NDSolve in Mathematica programming. By \(K^{lm}_r\) and \(K^{lm}_t\), we denote the normalized reflection and transmission coefficients respectively of the wave in lth layer due to an incident wave in mth layer (for \(l,m=1,2\)). According to Chamberlain and Porter [3], the normalized scattering coefficients are derived explicitly as

$$\begin{aligned} K^{11}_r= & {} \frac{\sqrt{q_1(0)a_{11}(0)}}{\sqrt{q_1(0)a_{11}(0)}} \frac{|R_1|}{|I_1|},\; K^{11}_t = \frac{\sqrt{q_1(L)a_{11}(L)}}{\sqrt{q_1(0)a_{11}(0)}}\frac{|T_1|}{|I_1|},\nonumber \\ K^{21}_r= & {} \frac{\sqrt{q_2(0)a_{22}(0)}}{\sqrt{q_1(0)a_{11}(0)}} \frac{|R_2|}{|I_1|}, \;K^{21}_t = \frac{\sqrt{q_2(L)a_{22}(L)}}{\sqrt{q_1(0)a_{11}(0)}}\frac{|T_2|}{|I_1|} \end{aligned}$$
(30)

for surface wave incidence whereas

$$\begin{aligned} K^{12}_r= & {} \frac{\sqrt{q_1(0)a_{11}(0)}}{\sqrt{q_2(0)a_{22}(0)}} \frac{|R_1|}{|I_2|},\;K^{21}_t = \frac{\sqrt{q_1(L)a_{11}(L)}}{\sqrt{q_2(0)a_{22}(0)}}\frac{|T_1|}{|I_2|},\nonumber \\ K^{22}_r= & {} \frac{\sqrt{q_2(0)a_{22}(0)}}{\sqrt{q_2(0)a_{22}(0)}} \frac{|R_2|}{|I_2|},\;K^{22}_t = \frac{\sqrt{q_2(L)a_{22}(L)}}{\sqrt{q_2(0)a_{22}(0)}}\frac{|T_2|}{|I_2|} \end{aligned}$$
(31)

for interfacial wave incidence. For the present problem, these coefficients constitute the energy balance relations involving an energy loss coefficient \(K_e\),

$$\begin{aligned} (K^{11}_r)^2+(K^{11}_t)^2+(K^{21}_r)^2+(K^{21}_t)^2+K_e=1 \end{aligned}$$
(32)

and

$$\begin{aligned} (K^{12}_r)^2+(K^{12}_t)^2+(K^{22}_r)^2+(K^{22}_t)^2+K_e=1. \end{aligned}$$
(33)

In the case of the absence of porous walls, these relations are analogous to those without \(K_e\), derived in [3]. The coefficient \(K_e\) refers to the amount of wave energy dissipation by the porous walls, and it is zero in the case of impermeable walls. We analyzed the dependency of \(K_e\) on seabed configurations and the number of porous walls. Incident wave amplitudes \(I_1\) and \(I_2\) of surface and interfacial waves are assumed to be one, and the gravitational constant \(g= 9.81\mathrm {m}/\mathrm {s}^2\) is fixed for all the results. For computational purpose, we consider relative parameters in dimensionless form such as length of varying bottom KL, gap between porous walls \(L_i/\lambda _1\) \((i=2,3,\dots ,s)\) where \(\lambda _1\) is wavelength in the first region, depth of interface Kh or \(h/h_1\) and depth ratio \(h_3/h_1\). The graphical representation of bottom profiles are shown in Fig. 2 with their mathematical functions in Eq. (34)

Fig. 2
figure 2

Bottom configurations

Full size image
$$\begin{aligned} Z = \left\{ \begin{array}{l} \displaystyle -h_1,\;\;-\infty<x\le 0 \\ \displaystyle -h_2(x),\;\;0\le x\le L \\ \displaystyle -h_3,\;\;L \le x<\infty \displaystyle \end{array} \right. \end{aligned}$$
(34)

where

$$\begin{aligned} h_2(x) =\left\{ \begin{array}{l}\displaystyle h_1 - ({h_1} - {h_3}){{\frac{x}{L}} } \mathrm{{ }},\;\;\text {Inclined plane bottom} \\ \displaystyle {h_3} - \frac{{{h_3} - {h_1}}}{{2\delta ^{'} - 1}}{\left( {\frac{{L - x}}{L}} \right) ^2}\left\{ {3{{\left( {\frac{{L - x}}{L}} \right) }^2} - 4(1 + \delta ^{'} )\left( {\frac{{L - x}}{L}} \right) + 6\delta ^{'}} \right\} \mathrm{{ }},\;\;\text {Inclined curved bottom} \\ \displaystyle h_3+(h_1-h_3)\bigg \{1+2\bigg (\frac{x}{L}\bigg )^3-3\bigg (\frac{x}{L}\bigg )^2 - d^{'}[1 - \cos \frac{2 \nu \pi x}{L}] \bigg \},\;\;\text {Diagonal sinusoidal bottom} \displaystyle \end{array} \right. \end{aligned}$$
(35)

The parameter \(\delta ^{\prime }\) is restricted to (0, 1/2) and \(\nu \) refers to number of ripples in sinusoidal bottom with amplitude \(d^{\prime }\) and \(L=\nu l\) where l is bottom wavelength. It may be noted that the inclined curved bottom will have a raised protrusion as \(\delta ^{\prime } \rightarrow 1/2\) at the level \(z=-h_3\). This is plotted for \(\delta ^{\prime } =0.2\) in Fig. 2b and this value is fixed for all the results of scattering and trapping. In addition, the parameter values \(L_i/\lambda _1=0.4\) \((i=1,2,\dots ,s)\), \(\nu =4\), \(KL=1\), \(d^{\prime }/h_1=0.08\) and \(\rho =0.1\) are fixed for all the results of scattering and trapping unless otherwise mentioned. As a particular case of mound bottom, the present results are compared with that in Fig. 1a of [3]. The mound bottom profile, as shown in Fig. 3, is represented by

$$\begin{aligned} h_2(x) = h_1\bigg \{\frac{3}{5}+\frac{2}{5} \cos \frac{2\pi x}{L}\bigg \},\;0\le x \le L \end{aligned}$$
(36)

with \(Kh_1 = 0.8\), \( Kh = 0.1\), \(\rho = 0.1\). Here \(h_1\; (=h_3)\) is the constant water-depth both sides of the mound.

Fig. 3
figure 3

Mound bottom

Full size image
Fig. 4
figure 4

Variations in scattering coefficients \(K_r^{11}\), \(K_t^{11}\), \(K_r^{21}\) and \(K_t^{21}\) against KL due to s number of porous walls when \(\theta =0^\circ \) and \(G_j=G=1+0.5\mathrm {i}\) for \(j=1,2,3\)

Full size image

4.1 Wave scattering

4.1.1 Effect of the number of porous walls

Figure 4a–d show the variations of scattering coefficients in Eq. (30) with bottom length KL in the case of incidence of SW on s number of porous walls in the presence of mound bottom. The present results are compared with that in Fig. 1a of Chamberlain and Porter [3] when no porous wall is present (\(s=0\)). The reflection coefficient \(K_r^{11}\) of SW decreases when \(s=0\) and becomes zero with the increase in KL. On the other hand, higher reflection in SW occurs due to porous walls. Moreover, \(K_r^{11}\) further increases with an increment in the number of porous walls. As a result, the transmission coefficient \(K_t^{11}\) of SW reduces with the increasing number of porous walls, as evident from Fig. 4b. The variation in \(K_r^{11}\) is little for two and three porous walls. However, there is a considerable variation in \(K_t^{11}\) for the same number of porous walls, indicating that much wave energy is dissipated by increasing porous walls. In Fig. 4c and d, a similar scattering phenomenon occurs in IW with the same number of porous walls, however it is opposite with KL. Thus, multiple porous walls reduce wave propagation into lee side regions by attenuating wave energy, and tranquillity can be maintained in coastal areas.

Fig. 5
figure 5

Variations in scattering coefficients \(K_r^{12}\), \(K_t^{12}\), \(K_r^{22}\) and \(K_t^{22}\) against KL for the parametric values used in Fig. 4

Full size image

Figure 5a–d illustrate the variations of scattering coefficients given in Eq. (31) with bottom length KL when IW impinges on s number of porous walls in the presence of mound bottom. The study of Chamberlain and Porter [3], as shown in Fig. 1a of their article, reveals that wider mound induces high transmission of IW. Here also, consideration of porous walls leads to higher reflection and lower transmission of SW and IW. Results reveal that \(K_r^{21}\) and \(K_r^{12}\) are similar due to the symmetry of the mound bottom, as noticed in [3] for no porous wall. However, \(K_t^{21}\) and \(K_t^{12}\) are not similar due to porous walls. The figure shows that IW is also highly dissipated by a large number of porous walls. However, from Figs. 4a and 5c, it reveals that for a fixed porous wall, reflection in SW increases as the mound widens, whereas reflection in IW decreases. Nevertheless, transmission in SW and IW decreases with mound width as in 4(b) and 5(d). Hence, internal wave energy is highly dissipated by porous walls as compared to surface wave energy.

Table 1 shows the energy loss coefficient \((K_e)\) for the number of porous walls \(s=1,2,3\) associated with Fig. 4. For the mound bottom of smaller length, wave energy dissipation increases with the increase in the number of porous walls in the case of incidence of SW. Table 2 shows the energy loss coefficient \((K_e)\) for the number of porous walls \(s=1,2,3\) associated with Fig. 5. Unlike in the Table 1, for the mound bottom of larger length, considerable loss of wave energy occurs with the increase of porous walls in the case of incidence of IW.

Table 1 Energy loss coefficient \((K_e)\) by porous walls in the case of incidence of SW
Full size table
Table 2 Energy loss coefficient \((K_e)\) by porous walls in the case of incidence of IW
Full size table

4.1.2 Effect of bottom profiles

Fig. 6
figure 6

Variations in scattering coefficients \(K_r^{11}\), \(K_t^{11}\), \(K_r^{21}\) and \(K_t^{21}\) against KL for different bottom profiles when \(h_3/h_1=0.5\), \(h/h_1=0.3\), \(Kh_1=1\), \(\theta =60^\circ \), \(\rho =0.3\) when \(G_1=G=1+0.5i\)

Full size image

In Fig. 6, the reflection and transmission coefficients against the bottom length KL are depicted for different bottom profiles and one porous wall in the case of incoming SW. From Fig. 6a, the reflection coefficient \(K_r^{11}\) of SW decreases up to certain bottom lengths. \(K_r^{11}\) increases for higher values of KL in the case of diagonal sinusoidal bottom. Not much variation occurs in the associated transmission coefficient \(K_t^{11}\) which may be due to the porous wall. Moreover, the reflection coefficient \(K_r^{21}\) of IW decreasing with an oscillatory nature as bottom length KL increases. Inclined curved bottom accounts for high oscillations in the reflection coefficient \(K_r^{21}\) of IW. Unlike the high transmission of SW, IW is little less transmitted over bottoms.

Fig. 7
figure 7

Variations of scattering coefficients \(K_r^{12}\), \(K_t^{12}\), \(K_r^{22}\) and \(K_t^{22}\) against KL for different bottom profiles with the parametric values used in Fig. 6

Full size image

Figure 7 shows the effects of different bottom profiles on wave scattering in the case of incoming IW. As in Fig. 6c and d, the reflection and transmission coefficients of SW in Fig. 7a and b are decreasing with the bottom length KL. The variations in \(K_r^{12}\) due to inclined plane bottom are moderate compared to the curved and sinusoidal bottoms. Bottom profiles are accounted for little effect on transmission coefficient \(K_t^{22}\) of IW. A comparison between Figs. 6b and 7d reveals that transmission in IW is less in IW incidence.

4.1.3 Effect of porous parameter (G)

In Fig. 8, the resistance and inertial effects of four porous walls on waves are illustrated by plotting scattering coefficients versus wave angle \(\theta \) in the case of incoming SW over the inclined curved bottom. The real value of the porous effect parameter G refers to the resistance effect of the porous medium whilst the imaginary value refers to the inertial effect of the porous medium. The plots reveal that increasing real values of G results in decreasing in the reflection of SW and IW. When imaginary values are assigned to G, higher reflection occurs for angles greater than \(35^\circ \). Furthermore, for a fixed real value of G, increment in its imaginary value leads to even higher reflection in SW and IW. Lower transmission occurs in SW and IW for smaller values of |G|. Hence, in order to achieve less transmission of waves, smaller real vales of G seem to be suitable. For higher reflection, G with larger imaginary value plays a vital role. Further, \(K_r^{11}\) attains a minimum value for \(\theta \in (60^\circ ,80^\circ )\) while the corresponding \(K_t^{11}\) does not attain its maximum value within this range due to dissipation of wave energy by the walls. On the other hand, \(K_r^{21}\) attains maximum for incident angles around \(30^\circ \) and then monotonically decreases for higher angles. The corresponding coefficient \(K_t^{21}\) of IW is significantly reduced by the walls. When the incident angle of SW is \(90^\circ \), \(\mid K_r^{11}\mid =1\) while \(\mid K_r^{21}\mid =0\) which means that transfer of energy from SW to IW does not occur at this angle.

Fig. 8
figure 8

Variations of scattering coefficients \(K_r^{11}\), \(K_t^{11}\), \(K_r^{21}\) and \(K_t^{21}\) against \(\theta \) due to different porosity \(G=G_j,j=1,2,3,4\), when \(Kh_1 = 1\), \(h_3/h_1=0.5\), \(h/h_1=0.3\) and \(\rho =0.3\)

Full size image
Fig. 9
figure 9

Variations of scattering coefficients \(K_r^{12}\), \(K_t^{12}\), \(K_r^{22}\) and \(K_t^{22}\) against \(\theta \) due to different porosity \(G=G_j,j=1,2,3,4\) for parametric values used in Fig. 8

Full size image

In Fig. 9, the resistance and inertial effects of four porous walls on wave scattering are illustrated in the event of incoming IW over the inclined curved bottom. In this incident case, the role of porous effect parameter G is analogous to the case studied in Fig. 8. The surface wave incidence in Fig. 8a reveals that SW is significantly less reflected for angles between \(60^\circ \) and \(80^\circ \). Similarly, in the present case, SW also gets a minimum for smaller angles and higher angles. Moreover, reflection and transmission of waves in each layer due to incoming IW are significantly less than the case of incoming SW.

4.1.4 Effect of density ratio \((\rho )\)

Fig. 10
figure 10

Variations of scattering coefficients \(K_r^{11}\), \(K_t^{11}\), \(K_r^{21}\) and \(K_t^{21}\) against interface depth \(h/h_1\) for different density ratio \((\rho )\), when \(Kh_1 = 0.1\), \(h_3/h_1=0.75\), \(\theta =60^\circ \) and \(G_j=G=1+0.5\mathrm {i}\) for \(j=1,2,3,4\)

Full size image

In Fig. 10, the influence of fluid density ratio \(\rho =\rho _2/\rho _1\) on scattering coefficients in the event of SW incidence on a single porous wall in the presence of the inclined curved bottom is shown. Here, the reflection and transmission coefficients are drawn as functions of dimensionless interface depth \(h/h_1\) for different values of \(\rho \). It may be recalled that \(\rho _2>\rho _1\). From Fig. 10a, an increase in \(\rho \) leads to a decrease in the reflection of SW when the interface is closer to the free-surface and an increase in the reflection of SW when the interface is closer to the bottom. Further, it is found that the variations in \(\rho \) do not significantly affect the transmission of SW, as shown in Fig. 10b. The reflection and transmission in IW are negligible, which may be due to no transfer of energy between waves.

Fig. 11
figure 11

Variations of scattering coefficients \(K_r^{12}\), \(K_t^{12}\), \(K_r^{22}\) and \(K_t^{22}\) against interface depth \(h/h_1\) for different density ratio \((\rho )\) for the same parametric values used in Fig. 10

Full size image

Figure 11 describes the scattering coefficients as in Fig. 10, but in the case of incoming IW. It may be noticed that the trends of \(K_r^{12}\) and \(K_t^{12}\) of SW in Fig. 11a and b are almost similar to \(K_r^{21}\) and \(K_t^{21}\) of IW in Fig. 10c and d, respectively, except for their magnitude. The increasing values of \(\rho \) lead to an increment to the reflection coefficient \(K_r^{22}\) whereas a reduction to the transmission coefficient \(K_t^{22}\). The variations are in an opposite trend in IW incidence, unlike the case of SW incidence. It may be due to the bottom effect on IW. Since negligible reflection and transmission in SW occurs, there is no energy transfer between waves in this incident case as well. From the Figs. 10 and 11 , it brings out that more transmission in SW occurs in the incidence of SW.

4.1.5 Wave-induced force on porous walls

Wave force on jth porous wall is obtained by integrating the pressure jump over water-depth and is expressed in the dimensionless form

$$\begin{aligned} {F_{j}}= & {} \frac{{\mathcal {I}}_1}{{{\rho _1 gh_1 h}}},\nonumber \\ \text {where}\; {\mathcal {I}}_1= & {} \mathrm {i}\rho \omega \int _{-h_3}^0 [\phi _{j+1}(x,z)- \phi _j(x,z)] \mathrm {d}z\; \text {at}\; x = L + \sum \limits _{i = 1}^j {{L_i}} \end{aligned}$$
(37)
Fig. 12
figure 12

Variations of force against the porous effect parameter G in the cases a \(G_1=G, G_2=2G, G_3=3G, G_4=4G\), b \(G_1=4G, G_2=3G, G_3=2G, G_4=G\) and c \(G_j=G\) for \(j=1,2,3,4\) when \(\rho =0.5\), \(Kh_1 = 1\), \(h_3/h_1=0.5\), \(h/h_1=0.2\) and \(\theta =30^\circ \)

Full size image

Figure 12 depicts the wave-induced force \(F_j\) on four consecutive porous walls against the porous effect parameter G in the case SW incidence over the inclined plane bottom. In this plot, three different arrangements of G) values in the positive x-direction are taken into account. The first one is concerned with increasing G values, the second with decreasing G values, and the third with equal values of G. In the first arrangement, the first porous wall receives higher force and the force then decreases monotonically with the increasing value of G. As the wave approaches the next consecutive porous walls, a decrease in the force is found, and hence least force is encountered by the fourth porous wall. A similar phenomenon has also been observed by Kaligatla et al. [12] in the case of homogeneous fluid. The wave load on the walls gets reversed when the order of G gets reversed, as shown in Fig. 12b. Further, the present results reveal that due to transmission of wave energy between waves, the porous walls experience a lesser force than the homogeneous fluid model (see Fig. 13 of [12]). Moreover, for any value of G except \(G=0\), the variations in force on walls are similar for the second and third arrangements. On the other hand, in the case of homogeneous fluid, the variations in force on walls are similar for the first and third arrangements, as shown in [12].

Fig. 13
figure 13

Variations of force against the porous effect parameter G in those three cases as considered for Fig. 12, but for incoming IW

Full size image

Figure 13 plots the wave-induced force \(F_j\) on the four consecutive porous walls as a function of the porous parameter G, in the case of incidence of IW over the inclined plane bottom. Again, the three different cases of G are discussed here. Results show that the magnitudes of wave load on walls in all the three cases are less than that in Fig. 12. In contrast to the results in Fig. 12a and c, variations in force in the first and third arrangements are similar. However, the second arrangement of porosity distinguishes with others within a certain higher range of G. Moreover, in each case, the fourth porous wall gets zero force for some values of G.

4.2 Wave trapping

This section analyzes the performance of three porous walls in trapping waves to mitigate wave-induced force on impermeable backwall. In computation, \(G_1\), \(G_2\) and \(G_3\) are given nonzero values whereas \(G_4=0\) is considered to set up the fourth wall as an impermeable backwall. The inclined curved profile for bottom is assumed for the results. Force on impermeable backwall \(F_{w}\) in dimensionless form is expressed as

$$\begin{aligned} {F_{w}}= & {} \frac{{\mathcal {I}}_2}{{\rho _1 g{h_1} h}},\; \text {where}\;\; {\mathcal {I}}_2= \mathrm {i}\rho \omega \int _{-h_3}^0 \phi _{s+1}(x,z)\;dz\nonumber \\ \text {at}\;\; x= & {} L + L_w+\sum \limits _{i = 1}^3 {{L_i}}. \end{aligned}$$
(38)

4.2.1 Effect of porous parameter G

In Fig. 14, the effects of porous parameter G of porous walls on wave scattering are illustrated. Three arrangements such as (i) \(G_1=G, G_2=2G, G_3=3G\), (ii) \(G_1=3G, G_2=2G, G_3=G\) and (iii) \(G_j=G\) for \(j=1,2,3\) in the direction of wave propagation are considered. Figure 14a and b are depicted for incoming SW while Fig. 14c and d are depicted for incoming IW. The results reveal that the incident wave’s reflection becomes a minimum in each arrangement for values of \(G \in [0,2]\). On the other hand, the induced wave reflection attains a minimum in each arrangement for values of \(G \in [0,4]\). Wave reflection is least for larger values of G in the third arrangement, whereas it is least for smaller values of G in the second arrangement. These arrangements can be made by the requirement of higher and lower reflection of waves.

Fig. 14
figure 14

Variations of reflection coefficients \(K_r^{11}\), \(K_r^{21}\), \(K_r^{12}\) and \(K_r^{22}\) against G for \(\rho =0.1\), \(Kh_1 = 0.8\), \(h_3/h_1=0.75\), \(Kh=0.2\), \(L_w/\lambda _1=0.4\) and \(\theta =30^\circ \)

Full size image
Fig. 15
figure 15

Variations of force on backwall \((F_w)\) against G for a incident surface wave and b incident interfacial wave with the same parametric values used in Fig. 14

Full size image

The wave-induced force on backwall \((F_w)\) for incoming SW and IW is depicted in Fig. 15a and b respectively for the arrangements made in Fig. 14. When \(G=0\), the first wall itself becomes a rigid wall, hence in either case of incoming waves, the backwall does not have wave load. The results show that in the third arrangement, the backwall gets the least force. This arrangement leads to the least reflection and least force on backwall, which implies the dissipation of more wave energy by the porous walls.

4.2.2 Effect of depth ratio \((h_3/h_1)\)

Fig. 16
figure 16

Variations of reflection coefficients \(K_r^{11}\), \(K_r^{21}\), \(K_r^{12}\) and \(K_r^{22}\) against \(L_w/\lambda _1\) for different depth ratios \(h_3/h_1\) when \(G_1=G_2=G_3=G=1+0.5\mathrm {i}\), \(\rho =0.1\), \(Kh_1 = 1\), \(Kh=0.2\), \(\theta =30^\circ \)

Full size image

For analyzing the effect of chamber width \(L_w/\lambda _1\) between the third porous wall and backwall, on wave scattering, the reflection coefficients are illustrated in Fig. 16. The coefficients are plotted for different values of depth ratio \(h_3/h_1\). The first two subfigures are regarded with incoming SW, while the last two subfigures are regarded with incoming IW. The porous walls are considered to have equal porosity \(G=1+0.5\mathrm {i}\). Reflection coefficients exhibit almost periodic nature with \(L_w/\lambda _1\). For the SW incidence, results indicate that the reflection of SW increases up to \(h_3/h_1=0.5\) and then decreases. On the other hand, the reflection of IW decreases with an increasing depth ratio for a fixed chamber width. However, in the IW incidence, results indicate that the reflection of both SW and IW decreases with increasing depth ratio for the most values of chamber width. In the case of flat bottom, the induced waves are negligibly reflected. From these results, optimum chamber widths for which maximum reflection in waves occurs can be obtained.

Fig. 17
figure 17

Variations of force on backwall \(F_w\) for a incident surface wave and b incident interfacial wave against \(L_w/\lambda _1\) with the parametric values used in Fig. 16

Full size image

Wave force on backwall related to the parameter values used in Fig. 16 are shown in Fig. 17. Particularly, Fig. 17a and b are regarded with SW and IW incidence, respectively. In the first incident case, for certain values of \(L_w/\lambda _1\), wall gets higher force at the depth ratios \(h_3/h_1=0.5,0.99\). The less reflection of IW at these depth ratios may account for the higher force. On the other hand, in the second incident case, the wall gets the higher force at smaller depth ratio values. Moreover, these figures show values of \(L_w/\lambda _1\) for which zero force is attained on backwall. The achievement of zero force on backwall indicates that porous walls trap more wave energy.

Fig. 18
figure 18

Variations of force on backwall \(F_w\) for a incident surface wave and b incident interfacial wave against wave angle \(\theta \) for different depth ratios \(h_3/h_1\) with the parametric values used in Fig. 14

Full size image

Figure 18 depicts wave force \(F_w\) on backwall as a function of wave angle \(\theta \) when depth ratio \(h_3/h_1\) changes. For these results, porous walls are assumed to have equal porosity \(G=1+\mathrm {i}\). Figure 18a displays force for incoming SW, whereas Fig. 18b shows force for incoming IW. The results show angles of wave incidence by which negligible force acts on the backwall. Further, at higher incident angles, the force increases with the increase in depth ratio in SW incidence, whereas force decreases with the increase in depth ratio in IW incidence. In the first incident case, negligible force occurs at many incident angles compared to the second incident case.

4.2.3 Effect of wave period (T)

Figure 19 plots the reflection coefficients versus incident angle \((\theta )\) of SW and IW for different wave periods (T). Figure 19a and b are related to incoming SW, whilst Fig. 19c and d are related to incoming IW. Figure 19a and b illustrate that surface waves of all periods are reflected uniformly at a particular range of lower angles, and then they are highly reflected at higher angles. At the same time, reflection in IW decreases with increasing angle of incidence. Further, the reflection phenomenon in the second incident case is quite similar to the first case. It is seen that reflection coefficients have little variations as the wave period increases in both incident wave cases.

Fig. 19
figure 19

Variations of reflection coefficients \(K_r^{11}\), \(K_r^{21}\), \(K_r^{12}\) and \(K_r^{22}\) against incident wave angle \(\theta \) for different wave periods T when \(G_1=G_2=G_3=G=0.5+0.5\mathrm {i}\), \(\rho =0.1\), \(h_3/h_1=0.5\), \(L_w/\lambda _1=0.4\) and \(h/h_1=0.2\)

Full size image
Fig. 20
figure 20

Variations of force on backwall \(F_w\) for a incident surface wave and b incident interfacial wave against wave angle \(\theta \) with the parametric values used in Fig. 19

Full size image

Figure 20 displays the variations of resulting force on backwall \((F_w)\) associated with Fig. 19. Figure 20a demonstrates force for incoming SW, and Fig. 20b is for incoming IW. These results illustrate that the variations of forces in both the incident cases are approximately analogous concerning the incident wave angle. However, the backwall gets a higher force in the first incident case. Moreover, the force decreases as the wave period increases. We remark that zero force is achieved at some wave angles due to porous walls.

5 Conclusions

In this paper, wave scattering and trapping by multiple porous walls in a two-layer ocean with different bottom configurations are studied. This is carried out by applying the eigenfunction expansion method for constant water-depth and a mild-slope equation for varying water-depth. The solution is derived by matching the solutions at interface regions. In the incidence of surface and interfacial waves, the four scattering coefficients and the energy loss coefficient are investigated for the effects of several prominent factors. We made the following conclusions from the results.

Wave scattering

  1. (a)

    Porous walls are found to be significant for particular bottoms over which more transmission of waves occurs.

  2. (b)

    An increment in the number of porous walls results in higher reflection and lower transmission in SW and IW.

  3. (c)

    By the porous walls, under different bottom profiles, the changes in wave reflection are observed to be of much damping nature as compared to the wave transmission.

  4. (d)

    Increasing resistance effect of porous wall leads to lower reflection and higher transmission in SW and IW. Moreover, small inertial effect of porous walls results in less transmission of both waves.

  5. (e)

    Transmission in SW does not change with density ratio higher than 0.5 for incoming SW. However, the transmission in IW reduces with increasing density ratio for incoming IW.

  6. (f)

    In comparison with a homogeneous fluid, the magnitude of wave forces on porous walls is observed to be less in two-layer fluid which may be due to transmission of wave energy between waves.

  7. (g)

    In SW incidence, porous walls get higher wave load than that in IW incidence.

Wave trapping

  1. (a)

    In the presence of an impermeable backwall, less reflection and transmission in SW and IW is noticed when the porous walls have equal and large values of the porous effect parameter G.

  2. (b)

    The wave force on the wall is less in case of porous walls of equal porosities in the incidence of either SW or IW, which may be due to more wave trapping.

  3. (c)

    The varying depth ratio has no significant effect on the reflection of IW comparatively.

  4. (d)

    Optimum distances between the backwall and porous wall are found to attain zero force on wall.

  5. (e)

    The force on wall increases with the increased depth ratio in SW incidence whereas the force decreases with the increased depth ratio in IW incidence. Relatively, wall gets higher force in SW incidence.

  6. (f)

    The force acting on wall in SW incidence is higher than that in IW incidence.

  7. (g)

    Waves of higher periods have a negligible effect on reflection.

  8. (h)

    Waves of smaller periods, either SW or IW, exert a large amount of force on wall. Moreover, considerable force occurs at moderate incident wave angles.

The results of the model have significance for the stratified water regions having small amplitude water waves. These results shall be useful for experimental model test results. Since the evanescent modes are neglected in this study, the results are valid for slowly varying bottoms but not for steep bottoms. Thus, the shortcoming may be taken up for further investigation. The model can be extended for partial porous breakwaters. Moreover, for wave trapping chambers, impermeable partition walls between the porous walls may be assumed for the extension of this model.