1 Introduction

Uncertainty is a significant factor in stochastic simulation, as ignoring uncertainty often affects the realization generated by using the stochastic simulation methods. Stochastic simulation methods can automatically characterize geological structures and multivariate properties, thereby facilitating our understanding of complex geological phenomena [1]. As a significant branch of stochastic simulation methods, multiple-point geostatistics (MPS) has been applied in many fields in geosciences, such as reservoir characterization [2–4], hydrological facies modeling [5], reconstruction of subsurface structures [6, 7], and quality improvement of remote sensing images [8]. MPS-based simulation methods aim to extract spatial patterns from training images (TIs) to characterize spatially heterogeneous structures. Subsurface observations are difficult to obtain, so the known data are very sparse. The observations are regarded as the conditioning data in stochastic simulation processes. Based on the limited conditioning data, stochastic simulation methods can generate multiple sets of possible realizations to approximate complex geological structures. In addition, most MPS-based simulation methods are performed along a random simulation path during stochastic simulations. The simulated values obtained by the Monte Carlo method are statistical values. This leads to inherent uncertainty in the simulated values. Since the simulated values are regarded as conditioning data in the subsequent simulation progress, the uncertainty will gradually increase as the sequential simulation proceeds.

Many different types of parameters are employed in MPS approaches. Different parameters can affect the performance of generated realizations in various ways. Among these input parameters, there are multiple parameters that interact with each other. This ultimately contributes to the diversity and uncertainty in these realizations. In the presence of non-linear interactions when performing a stochastic simulation, the input parameter analysis and the uncertainty quantification of output realizations are of great significance. Even using the same parameters and the same experimental data, we obtain different realizations with uncertainty, especially when the conditioning data are sparse. It remains difficult to evaluate and analyze MPS approaches because such MPS simulation parameters and uncertainty in the simulation process may lead to different realizations. Thus, an interactive uncertainty visualization and visual analysis method is required for good quality realization in stochastic simulations.

In addition, the optimal parameter configuration is essential for MPS-based methods. Selecting the optimal parameters can accurately characterize the subsurface structures and reduce uncertainty. To obtain the optimal parameter configuration, one of the most commonly used strategies is to simulate a large number of realizations and record the optimal input parameters. Under the condition that the common parameter setting range is known, it is still time-consuming to obtain these large numbers of realizations. Thus, there is an urgent need for an intuitive parameter analysis and visualization method to select the optimal parameters in MPS simulations.

In this study, uncertainty evaluation metrics were used to examine the realization’s uncertainty and parameter sensitivity in MPS stochastic simulations. This paper focuses on two main issues. First, uncertainty evaluation is more beneficial for realiztions of the conditional MPS simulations. Second, there is no intuitive visualization method to represent uncertainty and parameter sensitivity for MPS stochastic simulations. To address these issues, we first performed a series of simulations using different MPS algorithms with different parameters. The simulation realizations were then used to generate an ensemble dataset with different structural features according to different input parameters. For such a high-dimensional dataset, visualization and visual analysis can help us better understand the data. Therefore, we proposed a workflow for exploring integrated datasets with geospatial structures to facilitate the exploration of uncertainty in the realizations and parameter sensitivity in MPS simulations. In summary, the proposed visualization framework makes three main contributions to the literature.

(1) We proposed a visualization framework of uncertainty evaluation for MPS stochastic simulations.

(2) We integrated the uncertainty assessment metrics for the realizations and TIs and proposed a composite indicator to assist in model optimization.

(3) We presented the parallel coordinates-scatter matrix plot to efficiently analyze the parameter configurations of MPS methods and the uncertainty of the realizations.

2 Related work

2.1 Multiple-point geostatistical stochastic simulation

Multiple-point geostatistics (MPS)-based methods are a meaningful branch of stochastic simulation methods in geosciences. In recent years, the continuous development of its basic theory and various algorithms has made distinct contributions to the 3D reconstruction of subsurface structures. MPS-based approaches are derived from reservoir modeling and incorporate the advantages of two-point geostatistical and object-based simulation methods [9, 10]. MPS-based stochastic simulations aim to describe heterogeneous geometric features by extracting spatial patterns from training images (TIs). A TI is a conceptual model abstracted from real phenomena and plays a crucial role in stochastic simulation methods. To quickly extract the probability distribution function of TIs during an MPS simulation, Strebelle [11] proposed a dynamic data structure in the SNESIM algorithm: the search tree. The method uses the structure to save all patterns existent in the TIs once in advance. Mariethoz et al. [12] presented the direct sampling (DS) algorithm. To retrieve conditional probabilities for the DS algorithm, the data event samples directly TI instead of being stored in a database. The simulated values obtained by MPS stochastic simulations are statistical values, which inherit the uncertainty realizations. The simulated values are regarded as conditioning data, and the uncertainty in its realizations gradually increases during the MPS stochastic simulation process.

2.2 Uncertainty and ensemble visualization

Since stochastic simulations generate multiple realizations with equal probability, uncertainty is inevitable. In the field of uncertainty visualization, Liu et al. [13] represented uncertainty implicitly by directly displaying a carefully chosen subset of the prediction set. It not only preserves the spatial statistical information of the original set but also prevents the elements in the set from being obscured. Yang et al. [14] derived an independent realization through Monte Carlo sampling and visualized the uncertainty of geological surfaces in terms of smoothed movies by using the level sets and Markov chain Monte Carlo (MCMC) methods. In a broad sense, ensemble data are a subset of uncertainty data. To mitigate uncertainty and investigate parameter sensitivity, ensemble datasets are generated by MPS simulations. Since ensemble data are often multiple-variate, multiple-valued, time-varying and intricate, these properties bring challenges in the analysis and visualization of uncertainty. For spatial ensemble data visualization, the Gaussian mixture model was introduced by Jarema et al. [15]. The model quickly identifies the most similar members of the ensemble by clustering and lobular glyphs. Hazarika et al. [16] employed the parallel coordinates plots to express the sequel statistics of ensemble data. Wang et al. [17] used a heatmap and treemap to present an overview of the member similarity in multiple-resolution climate ensemble data. Despite these efforts, uncertainty evaluation and sensitivity analysis of ensemble data in stochastic simulations still lack an intuitive visualization method.

2.3 Uncertainty analysis and sensitivity analysis

To explore the uncertainty of MPS realizations, uncertainty analysis and sensitivity analysis are two commonly used tools. Uncertainty analysis is a quantitative assessment of the uncertainty in the model due to model parameters, model methods, and structure. Sensitivity analysis is a method to select the optimal parameters from a set of parameters. Uncertainty analysis addresses the question of how to measure the uncertainty of multiple MPS realizations, while sensitivity analysis answers the source of the uncertainty.

The main methods of uncertainty analysis include fuzzy theory [18], interval theory [19], and probabilistic analysis [20]. Probabilistic analysis is most commonly used to assess the uncertainty of geospatial objects. It is adopted to construct the probability distribution of a model based on conditioning data. Yang et al. [14] used Monte Carlo to obtain independent realizations to evaluate uncertainty. In addition, using the MCMC method sampled the uncertainty of a model and gradually evolved geological surfaces for visualization [21]. Sensitivity analysis increases the understanding between the model’s input and output. It is able to provide more credible, understandable, and convincing recommendations for scientists. Sensitivity analysis has two main types: global sensitivity and local sensitivity. Local sensitivity analysis is concerned with a point of interest in a model space. It typically computes important feature points of a model, such as the mean and the standard deviation. Local sensitivity analysis [22–24] was popular in the early period and was also applied to geological simulations. Compared with local sensitivity analysis, global sensitivity [25–28] takes into account all dimensions in a model. Neumann et al. [29] compared these two types of methods and noted that global sensitivity produces better performance in terms of accuracy in theory and practice. Although uncertainty analysis and sensitivity analysis have evolved considerably in stochastic simulations, both of them are relatively obscure, and there is a lack of visual representation for them. As a result, there is an urgent need for a visual framework to analyze uncertainty based on sensitivity analysis.

3 Methodology

3.1 Uncertainty evaluation framework in MPS simulations

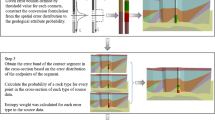
Figure 1 shows a schematic overview of our workflow. We propose a framework for evaluating the uncertainty of the realizations and exploring parameter sensitivity in stochastic simulations. Based on the integration datasets generated by MPS stochastic simulations, there are two types of visualization exploration: the exploration of uncertainty and the exploration of parameter sensitivity.

Figure 1
figure 1

A schematic overview of our workflow

Full size image

In uncertainty exploration, we use a multiple-point histogram (MPH), connectivity function, and semi-variogram to compute spatial features. To obtain a more accurate result, we propose a composite indicator, which is a weighted metric of MPH, connectivity, and semi-variogram. The weight of each uncertainty indicator can be freely selected and explored. Based on the composite indicator, a new circular treemap and a hierarchy dataset can be constructed. The circular treemap is a vital interaction component between the exploration of uncertainty in realizations and the parameter sensitivity in MPS simulations. Based on the dataset with different levels of hierarchy, we can choose to visualize the uncertainty at different layers: the bottom layer is an individual realization of an MPS simulation, and the top layer represents multiple realizations generated by an MPS simulation under the same parameters. For an individual realization, we visualize the uncertainty of the realization using line plots and MPH plots. The variogram map shows the variance in each direction, and the chart is a vital visual representation of spatial structures. The bar_3D chart and Etype plot visualize the uncertainty of multiple realizations.

To explore parameter sensitivity, MDS and parallel coordinates -scatter matrix plots show the diversity and uncertainty of the realizations and the parameter sensitivity in MPS simulations. We propose parallel coordinate-scatter matrix plots to visualize the ensemble data uncertainty and perform the global sensitivity analysis of the used parameters. Parallel coordinates can show each uncertainty indicator in the realizations, and a scatter matrix can express the potential characteristics among the uncertainty indicators. Parallel coordinates and a scatter matrix are combined into a new visualization approach. It is an intuitive and efficient diagram to visualize the parameter sensitivity and uncertainty in the ensemble dataset. MDS plots facilitate the understanding of the realization uncertainty under different parameter configurations.

Figure 2 shows the detailed process of the uncertainty evaluation framework in MPS simulations proposed in this work.

Figure 2
figure 2

Workflow of the uncertainty evaluation of multiple realizations and the analysis of parameter sensitivity in MPS simulations: (a) Data pre-processing; (b) Circular diagram; (c) and (e) Exploring uncertainty of multiple realizations; (d) Exploring parameter sensitivity

Full size image

3.2 Exploration of uncertainty evaluation in MPS simulations

3.2.1 Uncertainty evaluation indicator

To evaluate the uncertainty of MPS realizations, we select three representative uncertainty assessment metrics: connectivity function, semi-variogram and MPH.

Connectivity functions have been widely used in the field of subsurface characterization to depict spatial connectivity characteristics. Renard et al. [30] have demonstrated how lag distance connectivity function \(\tau (h)\) and global percolation volume \(\Gamma (p)\) are able to represent the connectivity of categorical and continuous properties. Let us define a variable X and a distance h. The lag distance connectivity function \(\tau ( h )\) is defined as the probability of connectivity of two h-distance points: s and \(s+h\). We can calculate the lag distance connectivity function \(\tau ( h )\) as follows:

$$\begin{aligned} \tau ( h ) =\operatorname{Prob} \bigl( s \leftrightarrow s+h \vert X ( s ) =X ( s+h ) \bigr). \end{aligned}$$
(1)

In the generated realizations, two regions are connected if there are paths with the same properties \(X ( s ) =X ( s+h )\). The global percolation volumes \(\Gamma (p)\) express the proportion of pairs connected in the realizations:

$$\begin{aligned} \Gamma ( p ) = \sum_{i=1}^{N ( x_{p} )} p_{i}^{2}, \end{aligned}$$
(2)

where \(p_{i}\) indicates the proportion of connected components, \(N( x_{p} )\) is the number of attributes in the realizations, and \(x_{p}\) means distinct connected components. To convert the uncertainty into a scalar value, Pirot et al. [31] calculated the difference between two realizations using lag distance and global percolation volumes.

$$\begin{aligned} &D_{\mathrm{conn}} ( \operatorname{real}1,\operatorname{real}2 ) \\ &\quad= \sum _{i=1}^{N_{C}} \frac{1}{N_{C}} \Biggl[ l_{\tau} \Biggl( \sum_{h=1}^{N_{\mathrm{lag}}} \frac{ \Vert \tau _{1} ( h ) - \tau _{2} ( h ) \Vert }{N_{\mathrm{lag}}} \Biggr) \\ &\qquad{} + ( 1- l_{\tau} ) \bigl\Vert \Gamma _{1} ( i ) - \Gamma _{2} ( i ) \bigr\Vert \Biggr], \end{aligned}$$
(3)

where \(l_{\tau} \) represents the indicator that can be selected between connectivity functions τ and Γ. \(N_{C}\) refers to the number of the considered classes’ values and \(N_{\mathrm{lag}}\) represents the number of configured lags. The semi-variance function measures the variability of the values taken by a random variable in different positions [32]. It represents the anisotropy of the realizations. Using the Monte Carlo method, the space V is divided into lag distances, and then a semi-variogram over h lags is calculated. The semi-variance function can be written as:

$$\begin{aligned} \hat{\gamma} ( V ) = \frac{1}{2n(h)} \sum_{s=1}^{n(V)} \bigl[ x ( s ) -x(s+V) \bigr]^{2}, \end{aligned}$$
(4)

where s is a sample point, \(x ( s )\) is the value of point s, and \(n ( V )\) is the number of pairs of points at a distance of V. \(\hat{\gamma} ( V )\) is the mean square error between the attributes of the sample point s and the points at distance h from it. To compare the semi-variance functions of two realizations, we select n regions and compare the semi-variance functions of two realizations, which can be defined as Eq. (5):

$$\begin{aligned} D_{\mathrm{vario}} ( \mathrm{real}1,\mathrm{real}2 ) = \sum _{i=1}^{n} \bigl\vert \hat{\gamma}_{1} ( i ) - \hat{\gamma}_{2} ( i ) \bigr\vert ^{2}. \end{aligned}$$
(5)

MPH is an essential metric of the spatial structure characteristics in simulated realizations [33]. Priot et al. [31] proposed classifying all patterns into \(N_{c}\) clusters with each cluster center defined as the cluster representative. The distance between two clusters can be computed as follows:

$$\begin{aligned} d \bigl( C_{1}^{i}, C_{2}^{j} \bigr) = \Biggl( \sum_{k=1}^{N_{k}} \bigl( C_{1}^{i} ( k ) - C_{2}^{j} ( k ) \bigr) \Biggr)^{\frac{1}{2}}, \end{aligned}$$
(6)

where \(C_{1}^{i} ( k )\) is defined as the i-th cluster of the first realization, and \(C_{2}^{j} ( k )\) is denoted as the j-th cluster of the second realization. \(N_{k}\) denotes the number of sliding windows in the pattern. We use MPH to compute the uncertainty of the two realizations with Eq. (7):

$$\begin{aligned} &D_{\mathrm{mph}} ( \mathrm{real}1,\mathrm{real}2 ) \\ &\quad= \sum _{i=1}^{N_{c}} \frac{1}{N_{c}} \biggl[ \bigl( 1+d \bigl( C_{1}^{i}, C_{2}^{i} \bigr) \bigr) \\ &\qquad{}\times \biggl( 1+ \frac{ \vert p_{1}^{i} - p_{2}^{i} \vert }{p_{1}^{i} + p_{2}^{i}} \biggr) -1 \biggr]. \end{aligned}$$
(7)

Here, the proportions of the numbers in clusters \(C_{1}^{i}\) and \(C_{2}^{i}\) divided by the total number of patterns in the first and second realizations are \(p_{1}^{i}\) and \(p_{2}^{i}\), respectively. In geological applications, connectivity describes the connection degree of the same attribute, which can help us understand the structure and characteristics of the models well. The semi-variogram represents the spatial variability of random variables. MPH is a method based on pattern recognition to measure the quality of the realizations of MPS stochastic simulations. These indicators evaluate different respects for the characteristics of the realizations of stochastic simulations. Therefore, we propose a composite indicator to unify the differences among the indicators so that the uncertainty in the parameter sequence can be evaluated straightforwardly. To explore the differences in the spatial structures more conveniently in MPS realizations and TI, we give each metric an indicator that ranges from 0 ∼100. Then, we can obtain a generalized evaluation index table to represent the uncertainty:

$$\begin{aligned} D_{\mathrm{total}} ={}& \bigl(D_{\mathrm{mph}} ( \mathrm{real},TI ) \times w_{1} + D_{\mathrm{vario}} ( \mathrm{real},TI ) \times w_{2} \\ &{} + D_{\mathrm{conn}} ( \mathrm{real}1, T I ) \times w_{3}\bigr) \\ &{}/(w1+w2+w3), \end{aligned}$$
(8)

where \(w_{1}\), \(w_{2}\) and \(w_{3}\) are the ranges of each metric to select freely for individual realization.

3.2.2 Visualization of uncertainty evaluation

To visualize the uncertainty of MPS realizations, we generated multiple realizations by configuring different parameters. As illustrated in Fig. 2(a), the multiple realizations constitute an ensemble dataset with a hierarchical structure. The uncertainty of the ensemble dataset cannot be visualized directly due to its multi-dimensional and multivariate characteristics. To facilitate uncertainty visualization in the ensemble dataset with a hierarchical structure, we use a circular treemap as a visual interaction framework to explore the uncertainty and parameter sensitivity in MPS simulations (Fig. 2(b)). There is a unified aspect ratio of the area and a clear hierarchy of data, which fits well with the hierarchal structure of the ensemble dataset. In addition, the circular treemap provides some interactive functions, such as a distortion-based contextual view and drill-down function.

The circular treemap divides the hierarchical ensemble dataset into three layers. The first layer is the root node, the second layer is different parameter members of the ensemble dataset during MPS simulations, and the third layer represents the individual realization. The composite indicator determines the size of circles in a circular treemap. The larger the indicator, the larger the size of the circles in the circular treemap. The composite indicator is defined by Eq. (8). On the second level of the circular treemap, we develop a bar_3D plot and Etype plot to characterize the uncertainty for multiple realizations (Fig. 2(c)). The bar_3D plot is easy to use to evaluate the uncertainty among multiple realizations and to observe the indicators in each realization. To show the uncertainty of multiple realizations with the same parameters, we also provide an Etype plot. It is a heatmap that clearly presents the degree of uncertainty in terms of the mean and variance of MPS realizations. The diagram is a detailed presentation of the realizations under the same parameter configuration on the second layer. The mean and standard deviation are calculated separately for each position in a realization by Eq. (9):

$$\begin{aligned} \begin{aligned}&\overline{x} = \frac{1}{N_{c}} \sum_{c =1}^{N_{c}} x_{c}, \\ &x_{\mathrm{std}} = \Biggl( \frac{1}{N_{c}} \sum _{c =1}^{N_{c}} ( x_{c} - \overline{x} )^{2} \Biggr)^{\frac{1}{2}}, \end{aligned} \end{aligned}$$
(9)

where \(x_{c}\) is the vector in a realization, and \(N_{c}\) is the number of realizations generated with the parameters. In the third layer, MPH, connectivity, and semi-variogram functions are all indicators for evaluating the spatial characteristics of the realizations. As demonstrated in Fig. 2(e), we provide various visualization techniques of these three indicators to facilitate a detailed evaluation of the uncertainty of an individual realization and TIs.

3.3 Exploration of parameter sensitivity in MPS simulations

Parameter sensitivity analysis answers the uncertainty sources in MPS simulations. Sensitivity analysis of the realizations of stochastic simulations poses a significant challenge. Due to the multi-dimensional and multivariate characteristics of the ensemble dataset, it is a terrific option to analyze parameter sensitivity by extracting representative features in the ensemble dataset.

A parallel coordinates plot is an efficient multi-dimensional visualization method that maps datasets onto a two-dimensional plane. In the diagram, each line represents a data tuple, and the line shape reflects the characteristics of the ensemble dataset. If the size of the ensemble dataset is too large, the lines tend to overlap. Parallel coordinates can present features where two axes are adjacent, but features that are not adjacent may be helpless for the use of a parallel coordinate plot.

Scatter matrix plots are a common method for multi-dimensional visualization. In the ensemble dataset with multiple dimensions, scatter matrix plots are beneficial for determining correlations between two selected variables and discovering different clusters of individuals. Scatter plots can only describe correlations between two dimensions. To visualize multi-dimensional data, a scatter matrix consisting of \(\frac{N\times N}{2}\) permutations has been developed in this work.

We propose a parallel coordinates-scatter matrix plot for better analysis of the ensemble dataset from stochastic simulation. The uncertainty indicators generated by MPS simulations are treated as axes of parallel coordinates and scatter matrix. Parallel coordinates plots are used as a global visualization for parameter sensitivity analysis. This method visualizes multiple spatial characteristics of ensemble datasets with different parameters and analyzes the uncertainty of ensemble datasets caused by different parameters. Scatter matrix plots show a local visualization of parameter sensitivity analysis. It is an effective tool for analyzing uncertainty under different parameters and identifying correlated features of uncertainty, outliers, and other characteristics. To avoid overlaps in the parallel coordinates-scatter matrix plot, we provide several fundamental functions, such as partial region selection, region clearing function, and category parameter selection. When employing these functions to explore the sensitivity analysis of the ensemble datasets generated by MPS simulations, the efficiency of the exploration increases significantly. MDS is also a popular technique for reducing high-dimensional datasets to two dimensions. Not only does it preserve the achieved high-dimensional distances in the lower dimensions, but it is also a non-linear dimensionality reduction technique. In MDS plots, we can see the projection of the difference in the distance between TIs and MPS realizations in two dimensions. As displayed in Fig. 2(d), the MDS plot and the parallel coordinates-scatter matrix plot facilitate us to explore parameter sensitivity in MPS simulation.

4 Results

SNESIM and DS are two representative MPS simulation algorithms. Tables 1 and 2 show the range and the description of the parameters for the two algorithms. We used the two algorithms to generate two ensemble datasets with different parameter configurations: the SNESIM dataset and DS dataset. Figure 3 illustrates the summary view of the dataset simulated by the SNESIM dataset. It has ensemble members consisting of m parameter sequences, n realizations in each ensemble member, and vector X (red dot) in each realization to record attribute values. The SNESIM dataset has six parameter sequence members, and each member has multiple realizations that are named according to the order of generation. The parameter sequence is a combination of the parameters of the SNESIM dataset. The parameter sequence is composed of algorithm parameter names and values according to specific rules. The rules can be sorted by the length of the parameter names or the first letter of the parameter names. For example, TS7_7L3 indicates that the search template sizes X and Y are 7, and the number of multiple grids is 3. It is not written when the search template size Z is 1. Sg3 shows the third realization under this parameter sequence.

Figure 3
figure 3

A summary of the SNESIM dataset

Full size image
Table 1 Description and range of the input parameters for the SNESIM dataset
Full size table
Table 2 Description and range of the input parameters for the DS dataset
Full size table

4.1 Uncertainty evaluation

We used the SNESIM dataset and selected four parameters of the SNESIM algorithm in this test. There are five ensemble members in the SNESIM dataset. Fifty realizations were simulated in an ensemble member. The training image is a section of the reservoirs provided by Strebelle [34] with a resolution of 250 × 250 pixels. The circular treemap for calculating different weights of the indicators in this dataset is illustrated in Fig. 4. In the three circular treemaps based on different indicators, the yellow circle represents individual realization, and the cyan circle represents multiple implementations under the same parameter sequence. The circle’s size indicates the degree of uncertainty in realization. Figure 4 shows that among these parameter sequences, the parameter sequence TS3_3L2 has the highest uncertainty, and the parameter sequence TS7_7L3 has the lowest uncertainty. It can generally display the uncertainty under different parameter sequences, which is convenient for uncertainty evaluation and visualization of specific realizations.

Figure 4
figure 4

Circular treemap in different weights for indicators. (a), (b) and (c) indicate semi-variogram, connectivity and MPH weighted at 100%, respectively

Full size image

As displayed in Fig. 5, we selected two different members of the parameter sequence for the uncertainty evaluation in the ensemble dataset. The first row in Fig. 5 shows a circular treemap of these two displays of combined uncertainty. The size of the bubble reflects the degree of uncertainty in the circular treemap. Therefore, we can use the size of the bubble to provide initial assistance in the decision-making process for experts. This enables experts to conveniently explore bubbles with lower uncertainty at the same time and delve deeper into those bubbles that they consider necessary for further investigation. The second and third rows show the Etype_mean and Etype_std of the two ensemble members. The parameter sequence TS7_7L3 converges more closely to the maximum and minimum values in most regions. In the fourth row of the bar_3D plot, the values in Fig. 5(a) are lower than in Fig. 5(b). The Bar_3D plot can assist domain experts in visualizing the different indicators of each realization. It helps address our need for specific analysis of each indicator within a single realization, ultimately aiding experts in understanding the uncertainty associated with the realization. Combining the above diagrams, the uncertainty in the parameter sequence TS7_7L3 is significantly lower than that in the parameter sequence TS5_5L3.

Figure 5
figure 5

Exploring the uncertainty of different parameters for the SNESIM algorithm. (a) and (b) visualize and evaluate the uncertainty in TS7_7L3 and TS5_5L3, respectively

Full size image

In the uncertainty evaluation of an individual realization, we compare the similarity of the spatial structure between the TI and the realization generated by MPS stochastic simulations. As illustrated in Fig. 6, MPH represents the histogram and size between the TI and a realization. The left column shows the TI and an individual realization. The other columns show ten cluster representatives and their counts. The count of cluster representatives is the number of pattern representatives in individual realization or TI. The patterns of an individual realization and the TI depend on the degree of uncertainty. We computed these ten pattern representatives and derived a distance to evaluate the uncertainty between the TI and the generated realization. Based on the size of ten cluster representatives between a realization and TI, we calculated the distance of both to be approximately 20.46.

Figure 6
figure 6

Uncertainty evaluation of training image (TI) and realization by MPH: the left column shows the TI and a realization. The others display ten patterns, the size and distance for the TI and a realization

Full size image

The uncertainty evaluation of the TI and the corresponding realizations is displayed in Fig. 7. A randomly selected realization and the TI in the parameter sequence TS7_7L3 are depicted in Fig. 7(a). As shown in Fig. 7(b), the semi-variogram and connectivity curves between the TI and a realization can be observed. It can visually compare the uncertainty of the TI and a realization at different lag distances. We converted the trends of the connectivity and variogram into scalar indicators by using Eq. (5) and Eq. (7). The variogram value for each direction is indicated in the variogram plots. The plots are based on a polar coordinate system, setting \(r\in [0,60]\) and \(\theta \in \{ 0, \frac{\Pi}{36},\dots,\pi \}\). We can see the difference between the TI and realizations in each direction (Fig. 7(c)).

Figure 7
figure 7

Uncertainty evaluation of the TI and the corresponding realizations. (a) The TI and a realization; (b) Semi-variogram and connectivity curves between the TI and a realization. (c) Variogram plots of the TI and a realization

Full size image

During exploring the uncertainty evaluation, the uncertainty in the realization was estimated in several aspects. As summarized in Table 3, the composite indicator was calculated with a connectivity weight of 100%. In addition, it can be seen that the uncertainty in the realization Sg35 is the lowest in connectivity and MPH. The worst realizations are Sg20, Sg17, and Sg47 in connectivity, MPH and variogram, respectively. In the composite indicator, we found that the best realization is Sg43, and the worst realization is Sg20. Figure 8 illustrates the comparative analysis of the four indicators in the parameter sequences TS5_5L3 and TS7_7L3. In Fig. 8(a), the blue curve of TS7_7L3 is much lower than the yellow curve of TS5_5L3. It reveals that the parameter sequence TS7_7L3 is better than TS5_5L3 in the connectivity indicator. Although the curve of TS5_5L3 and the curve of TS7_7L3 are interlaced, the overall blue curve is still lower than the yellow curve in Fig. 8(b). This demonstrates that the parameter sequence TS7_7L3 is more stable than TS5_5L3 for finding the similarity of multiple-point patterns in MPS simulations. Figure 8(c) shows that nearly half of the realizations of the parameter sequence TS5_5L3 (yellow curve) are lower than TS7_7L3 (blue curve), but the yellow curve fluctuates more violently than the blue curve. Thus, the parameter sequence TS7_7L3 is more stable than TS5_5L3 for reducing the uncertainty of MPS stochastic simulations. As demonstrated in Fig. 8(d), we also observed that the blue curve is much lower than the yellow curve. This illustrates that the parameter sequence TS7_7L3 is better than TS5_5L3 in a composite indicator. All the statistics demonstrate that the composite indicator can combine the characteristics of multiple indicators and assist the uncertainty evaluation in MPS simulations.

Figure 8
figure 8

Comparison of four indicators in the parameter sequences TS5_5L3 and TS7_7L3. (a), (b), (c), and (d) show the curves of the connectivity, MPH, semi-variogram, and total indicator from 50 generated realizations in the parameter sequences TS5_5L3 and TS7_7L3, respectively

Full size image
Table 3 Summary of the uncertainty evaluation in the parameter sequence TS7_7L3
Full size table

4.2 Parameter sensitivity

We visualized the indicators of MPS realizations to analyze the parameter sensitivity under different parameter sequences. MDS [35] and parallel coordinates-scatter matrix plots were adopted to explore parameter sensitivity during MPS simulations. To verify the validity of these approaches, we applied DS and SNESIM different parameter sequences to generate two datasets: DS_dataset and SNESIM_dataset. The specific information of the parameters for both algorithms is summarized in Tables 1 and 2.

4.2.1 SNESIM

As described in Figs. 9 and 10, the effect of configuring different parameters generated in the dataset for realizations can be observed. Assembling the two plots can facilitate parameter sensitivity analysis in MPS simulations. The randomly selected realizations in Fig. 10 verify the validity of the parallel coordinates-scatter matrix plot. Figure 9 indicates that purple lines are at the bottom of the axis in parallel coordinates, and gray lines are at the top of the axis in parallel coordinates. In the scatter matrix, purple points are at the bottom left of every scatter plot, and gray points are generally at the top right. This demonstrates that the realizations generated under the two parameter sequences TS7_7L3 and TS7_7L2 work far better than the others, and TS3_3L2 is the worst in the six parameter sequences. The uncertainties of parameter sequences TS7_7L3 and TS7_7L2 are lower than others, and the parameter sequence TS3_3L2 has the highest uncertainty.

Figure 9
figure 9

Exploring parametric sensitivity via parallel coordinate−scatter matrix plot in the SNESIM dataset

Full size image
Figure 10
figure 10

Stochastic realizations of SNESIM by using different parameter sequences

Full size image

Although the uncertainty and the parameter sensitivity of all parameters can be observed in Fig. 9, data overlap remains inevitable. To analyze parameter sensitivity better, we regarded the two parameter sequences TS7_7L3 and TS3_3L2 as an example, as illustrated in Fig. 11. The realizations of the parameter sequence TS7_7L3 are both positioned in the lower left corner of the scatter matrix plot, while the realizations of TS3_3L2 are in the upper right corner. In the parallel coordinates plot, the parameter sequence TS7_7L3 has lower indicator values than TS3_3L2. In the semi-variogram, the indicator ranges of the parameter sequences TS3_3L2 and TS7_7L3 are similar in Fig. 11. To further compare the parameter sensitivity, we constructed the MDS plot (Fig. 12) by projecting all realizations in TS7_7L3 and TS3_3L2 into two dimensions. We chose the TI as the reference, and all realizations revolved around the reference. The 50 realizations of TS7_7L3 follow the reference closer than the 50 realizations of TS3_3L2. This indicates that the uncertainty of the realizations under the parameter sequence TS7_7L3 is lower than that under TS3_3L2. The selection of TS7_7L3 can significantly reduce the uncertainty in the SNESIM algorithm. In short, the parallel coordinates-scatter matrix plot is relatively easy to use to identify the parameter sequences with the highest uncertainty since the values of the indicator are reflected in the respective subplots. The MDS plot can validate visualization for the realization uncertainty of the different parameter sequences in stochastic simulation.

Figure 11
figure 11

Parallel coordinates−scatter matrix plots when we are specifying special parameters in SNESIM

Full size image
Figure 12
figure 12

MDS plot of 50 realizations of two different parameter sequences in SNESIM

Full size image

4.2.2 DS

We used our method to visualize the DS dataset and compare uncertainty among different parameter sequences. In DS, there are four main parameters: fraction of TI (F), maximum number of points (N), search radius (R), and distance threshold (T). The DS_dataset was generated by setting different values for the four parameters to investigate the parameter sensitivity. The naming rule of the DS dataset is the same as that of the SNESIM_dataset. As illustrated in Figs. 13 and 14, we selected different parameter sequences separately to explore parameter sensitivity. Figure 13 describes the parallel coordinates-scatter matrix plots and Fig. 14 depicts the corresponding realizations under the different parameter sequences. We found that the red lines are below the parallel axis, and the blue lines are above the parallel axis. This indicates that the realizations of the parameter sequence D0.2_F0.5_N40_R30 (red) are closer to the spatial features of the TI. Meanwhile, the effect of the parameter sequence D0.1_F0.1_N10_R20 (blue) is the worst among the parameter sequences. To further analyze the parameter sensitivity of different parameter sequences in DS, various cases of parameter sensitivity were implemented via a parallel coordinates-scatter matrix plot (Fig. 15). As displayed in Fig. 15(a) and Fig. 15(b), realizations of the individual parameter sequence we selected can be visualized, and others are not directly visualized. This indicates that performing the analysis and visualization on an individual parameter sequence avoids data overlap. The parameter sequence D0.2_F0.5_N20_R20 is higher than the parameter sequence D0.2_F0.5_N40_R30 (Fig. 15(c)). This shows that the parameter sequence D0.2_F0.5_N40_R30 has lower uncertainty than the parameter sequence D0.2_F0.5_N20_R20. To compare the effect of individual parameters on the realization uncertainty, the parameter sequences D0.1_F0.1_N10_R20 and D0.1_F0.1_N20_R20 are selected for visualization analysis (Fig. 15(d)). The parameter sequence D0.1_F0.1_N20_R20 is basically under the parameter sequence D0.1_F0.1_N10_R20. The larger the indicator of the parameter N within a certain range, the smaller the realization uncertainty. As demonstrated in Fig. 16, the red points represent TI, the green points are D0.2_F0.5_N40_R30, and the purple points represent D0.1_F0.1_N10_R20 in the MDS plot. The green and purple points surround the red points, and the vast majority of the purple points are closer to the red points. When the parameter sequences were selected for comparison, the parallel coordinates-scatter matrix plot displays the three parameters: N, R, and T. The MDS plot compares the differences between multiple parameter sequences and TI.

Figure 13
figure 13

Exploring parametric sensitivity via the parallel coordinates-scatter matrix plots in the DS_dataset

Full size image
Figure 14
figure 14

TI and stochastic realizations of the DS dataset under different parameter sequences

Full size image
Figure 15
figure 15

Various cases of parameter sensitivity via parallel coordinates-scatter matrix plots when we are specifying special parameters in DS

Full size image
Figure 16
figure 16

MDS plot of 50 realizations for the different parameters in DS

Full size image

5 Discussion and conclusions

In this work, we propose a novel visualization framework to evaluate the uncertainty and parameter sensitivity of MPS stochastic simulations. A composite indicator for the ensemble dataset is presented to facilitate uncertainty evaluation and parameter sensitivity analysis. The composite indicator is based on three typical metrics: MPH, connectivity, and semi-variogram, which can conveniently evaluate the uncertainty of MPS realizations. Using this indicator, a circular treemap conforming to the hierarchical structures of ensemble datasets is constructed. Furthermore, the novel framework is built on the circular treemap for exploring uncertainty and parameter sensitivity in ensemble datasets.

For uncertainty exploration in MPS stochastic simulations, the Etype diagram presents the mean and standard deviation in MPS realizations. The bar_3D plot details the specific values of the indicators in multiple realizations. The spatial characteristics of an individual realization are extracted to portray their uncertainty by using a connectivity function and semi-variogram plots. The MPH plot is used to describe the degree of dissimilarity of the heterogeneous patterns in MPS realizations. The variogram and semi-variance plots show the anisotropy of the generated realizations.

The parallel coordinates-scatter matrix plot is presented to explore the parameter sensitivity in MPS stochastic simulations. The parallel coordinates plot is able to analyze the degree of uncertainty in different parameter sequences. Meanwhile, the scatter matrix plot can describe the relationship between the features extracted from different realizations. The appropriate parameter sequences of MPS simulations can be selected through the parallel coordinates-scatter matrix plot. According to the parallel coordinates-scatter matrix plot, we can use analogical analysis to compare the uncertainty of two parameter sequences, thereby assisting experts in parameter analysis and decision-making. The diagram provides an intuitive visual representation, enabling experts to quickly identify and comprehend the relationships between the parameters of MPS simulations. We can simultaneously display the values of multiple parameters and reveal the similarities and differences between parameter sequences by observing the distribution of the scatter points. This comparative approach helps domain experts gain deeper insights into the characteristics and trends of parameter sequences, facilitating more accurate decisions. In addition, the MDS plot is used to compare the difference between the realizations generated according to specific parameters.

The results based on two representative MPS algorithms demonstrate the effectiveness and applicability of the proposed visualization framework. The framework facilitates the visualization of uncertainty evaluation and parameter sensitivity analysis, and it is able to apply to other similar stochastic simulation methods in geosciences.