Introduction

Geostatistical algorithms reproduce input statistics within ergodic fluctuations, that is, the statistical fluctuations due to a limited model size relative to spatial correlation range (Deutsch and Journel, 1998). Yet, errors may occur due to the complexity of geostatistical algorithms, workflows, and the associated trade craft. These errors may result in significant bias in reserves estimates, fluid flow, or mineral recovery prediction. These errors may include blunders (e.g., inflated correlation due to the application of the same random number seed for primary and secondary variables in collocated co-simulation), poor implementation (e.g., loss of long range correlation due to overly constrained search limits), or algorithm limitations [e.g., unreasonable short range variability inherent to the sequential indicator simulation (SIS) method]. To avoid such errors, it is essential to compare statistics of simulation output against input statistics.

Leuangthong, McLennan, and Deutsch (2004) described the minimum acceptance criteria approach to variogram-based geostatistics. They demonstrated the need to check the expectation of first and second-order moments, the property distribution functions, and the spatial continuity as characterized by the semivariogram. They also propose the use of cross validation and accuracy plots as additional checks of local accuracy and uncertainty models. The goal of this article is to go beyond the first and second-order moments and present metrics that assess the higher-order statistics of geostatistical realizations; therefore, extend minimum acceptance to multiple point simulation (MPS) methods.

The increasing popularity of MPS is due to the recognition that statistics beyond the second-order variogram have a significant impact on resource models (Strebelle, 2002; Liu and others, 2004). All spatial statistics not explicitly controlled in geostatistical modeling tend to be maximum entropy. This results in disconnection of high and low values, the absence of ordering relationships, and the reproduction of only linear spatial features (Deutsch and Journel, 1998). This can lead to a bias in subsequent transfer functions such as flow simulation, mine design, or reserve calculations. For example, in flow simulation, maximum entropy spatial continuity results in the break up of barriers, baffles, and conduits, resulting in dispersive flow patterns and biased high estimates of sweep efficiency. MPS mitigates some of these limitations by imposing multiple point statistics beyond the semivariogram from a representative training image (TI); however, if MPS algorithms are to be used to generate geostatistical realizations with the desired multiple point statistics, the reproduction of these multiple point statistics should be assessed. Literature on assessing the multiple point characteristics of realizations is lacking because of the inherently complex nature of a multiple point statistic. Consider the multiple point density function (Fig. 1) often used as the input to MPS algorithms. This density function counts the frequency of a particular facies configuration. The multiple point density function can be used to generate MPS realizations, but due to its high dimensionality and lack of simple, intuitive bin ordering it is not easily visualized and it cannot be modeled analytically, rendering it a poor criteria for judging the acceptability of a model. This article describes alternative metrics and summary statistics that can be used to compare the multiple point statistics of input TIs and the associated simulated realizations. Given the greater degree of control of spatial heterogeneity available with multiple point geostatistics, checking these higher-order statistics will be even more important to ensure a reasonable reproduction of input statistics.

Figure 1
figure 1

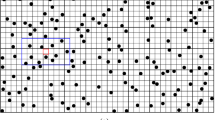
A multiple point density function of the example TI. This example demonstrates a four-point configuration with two indicators (Boisvert, Pyrcz, and Deutsch 2007)

Full size image

The proposed metrics are not limited to assessing MPS realizations, they could also be used to (1) compare MPS algorithms with other facies modeling techniques such as SIS or truncated Gaussian simulation, (2) rank realizations, (3) determine the fitness of realizations, (4) help select algorithmic input parameters, or (5) assess the MPS characteristics of traditional geostatistical realizations. Previously, a subset of these metrics was applied to test TI and conditioning data consistency (Boisvert, Pyrcz, and Deutsch, 2007).

Background

Recognition of the limitations of the multiGuassian distribution led to the initial work on multiple point geostatistics (Deutsch, 1992; Guardiano and Srivastava, 1993). The subsequent development of a practical MPS algorithm, SNESIM (Strebelle, 2002), led to the wide adoption of MPS for reservoir facies simulation. Numerous published case studies are available to demonstrate the practice and advantages of MPS (Caers, Strebelle, and Payrazyan, 2003; Strebelle, Payrazyan, and Caers, 2003; Harding and others, 2004; Liu and others, 2004, to name a few).

Multiple Point Statistics

Multiple point statistics consider the relationship between more than two locations. Simulation methods based on multiple point statistics are often compared to those based on two-point statistics. The semivariogram quantifies two-point spatial expected square differences. With such a stationary statistic, it is not possible to describe curvilinear features and data ordering relationships. The extension to MPS allows for the reproduction of curvilinear heterogeneity patterns and data ordering relationships.

The multiple point density function is commonly used in MPS algorithms. The traditional histogram counts the frequency of times a particular continuous variable falls in a bin, or counts the frequency of times that a particular categorical variable occurs. The multiple point density function counts the frequency of times a multiple point configuration occurs; in other words, the conditional probability of an outcome given the specific categories at surrounding locations. Consider a 4-point configuration that could take two different values, there are a total of 16 (24) unique configurations. The frequency of each configuration in the image constitutes the multiple point density function (Fig. 1). Note that the ordering of the bins (Fig. 1) is arbitrary, only order consistency is required. Considering a larger template or more categories significantly increases the number of bins in the multiple point density function (number of bins is equal to the number of categories to the power of the number of points), making visualizing the multiple point density function for large templates challenging to impossible.

Using Multiple Point Statistics

Multiple point density functions can be calculated along wells, but in general this would provide statistics on a very limited set of possible spatial configurations. A TI is required that provides a quantification of the patterns likely to be encountered.

Techniques available for MPS include using the single normal equations (Guardiano and Srivastava, 1993; Strebelle, 2002); using simulated annealing with the multiple point density function as the objective function (Deutsch, 1992); updating conditional distributions with multiple point statistics (Ortiz and Deutsch, 2004); training neural networks on TIs (Caers, 2001); using a GIBBS sampler (Lyster and Deutsch, 2008); and pattern-based approaches (Arpat and Caers, 2007; Eskandari 2008; Wu, Zhang, and Journel, 2008).

Methodology

The true distribution at any geologic site will remain unknown and it is impossible to completely validate or verify a numerical geological model (Oreskes, Shrader-Frechette, and Belitz, 1994). Nevertheless, geological models can be subjected to a series of checks that increase their credibility and identify significant bias, rather than verify their correctness; this is deemed model confirmation (Oreskes, Shrader-Frechette, and Belitz, 1994). A basic model confirmation would be a check on the first and second-order statistical properties of the models (Leuangthong, McLennan, and Deutsch, 2004). Models failing to reproduce the basic histogram and semivariogram should be rejected.

The primary confirmation of any geologic model is a visual assessment. In the case of MPS models the visual inspection should be an examination for artifacts specific to the algorithm used and the reproduction of large/small-scale features. Specific attention should be given to features that may significantly impact the transfer function. Multiple point statistic-based techniques are implemented because there is a belief that non-linear features, such as channels or complex folding patterns, and ordering relationships are important to the transfer function. Frequently, the assessment of the reproduction of non-linear features and ordering relationships is best performed with a qualitative visual inspection rather than some type of quantitative summary statistic or multiple point statistic metric. This is the first level of model confirmation for MPS models.

Model confirmation for multiple point statistic-based techniques can also include quantitative assessments because of access to the target multiple point statistics in the form of the TI. Higher-order statistics are explicitly contained in the TI and should be reproduced in the MPS realizations. Visualization and a direct comparison of input and output higher-order statistics are not possible, but the proposed metrics provide a relative measure of higher-order statistical reproduction from the TI.

On a realization-by-realization basis model confirmation provides a measure of statistical mismatch that may indicate the need to investigate modeling implementation decisions. Reasons for not reproducing the exact multiple point statistics of the TI include (1) realizations are conditioned to data which imposes a constraint on the possible multiple point statistics of the realizations, (2) MPS algorithms are often non-exact and even iterative and may become trapped in a sub-optimum solution, and (3) ergodic fluctuations. It is not possible to calculate the expected ergodic fluctuations in multiple point statistics for a specific TI and model size. Such a calculation is limited to simple cases such as the one-point statistic as characterized by dispersion variance of the model within an infinite domain. Neither is there a known error distribution that would allow for hypothesis testing. This precludes the use of purely objective criteria for departures from input statistics for model confirmation. Yet, these measures of departure may still be useful in a heuristic assessment of model performance, indication of data model contradiction and comparison between realizations.

The application of these metrics to a suite of realizations provides a more objective form of model confirmation. Comparisons of the input multiple point statistics to the expectations over multiple realizations are more straightforward as the expectation should remove ergodic fluctuations and match the input statistics.

Five metrics will be presented to assess the reproduction of input statistics in multiple point realizations: (1) first and second-order checks, (2) trends, (3) multiscale histograms, (4) the multiple point density function, and (5) missing bins in the multiple point density function.

The specifics of each metric will be discussed with the following case study.

The Case Study

The proposed metrics are demonstrated with a simple case study. For this study a TI was generated by a simple binary object-based TI generator with channel objects within background overbank. Channel objects with concave upward bases and flat tops where generated with stochastic geometries (width 40 m, width-to-depth ratio 10:1 and sinuosity 1.6) parameterized by constant amplitude and wavelength. These channels were positioned by a Poisson point process until the global proportion of 27% was matched in a model with extents 2000 m × 1000 m and 80 m vertically. The grid cells are 10 m in the horizontal and 1 m in the vertical. Unconditional geostatistical realizations were generated on the same grid used for the TI with the version of SNESIM presented in Strebelle (2007). Conditional realizations could have been generated, but for demonstration of the methods for checking the multiple point characteristics, unconditional realizations are sufficient.

To assess the proposed metrics, 10 realizations are generated using various multiple point template sizes (1, 2, 8, 16, 24, and 56) in the simulation. A simple trend model is constructed with polygons and a filter as described by Strebelle (2007). The trend is intended to represent a depositional fairway with greater concentration of channel elements. The global average of the trend model is set to the target channel proportion in the MPS realizations to ensure consistency. This resulted in MPS realizations with varying consistency with the TI (Fig. 2).

Figure 2
figure 2

Visualizations of the input TI, trend model, and realizations with 1, 4, 16, or 56-point templates, excluding the origin. All models are the same size. TI and realizations contain only two facies

Full size image

These realizations are checked against the input TI. The following metrics are applied: (1) first and second-order statistics, (2) trends, (3) multiscale histogram, (4) multiple point density function, and (5) missing bins in the multiple point density function.

First and Second-Order Statistics

While the goal of MPS is to reproduce higher-order statistics, the lower-order checks proposed by Leuangthong, McLennan, and Deutsch (2004) should still be preformed:

  1. 1.

    Ensure that the exact data values are reproduced at data locations.

  2. 2.

    Histogram and variogram reproduction. Within acceptable ergodic fluctuations these statistics should be well reproduced.

  3. 3.

    Cross validation and accuracy plots to check local accuracy and uncertainty.

The purpose of this article is to supplement (not replace) these basic tools with metrics that can better assess the multiple point characteristics of geostatistical models.

Trends

All geostatistical modeling techniques assume a form of stationarity. This allows the practitioner to “pool” their data and infer meaningful statistics for modeling. In the context of MPS, the multiple point density function is often assumed stationary that is, the multiple point density function of the TI is assumed to apply everywhere in the modeling domain. As in traditional geostatistical techniques, a trend can be used to enforce non-stationary proportions of specific facies that cannot be captured in the TI. If a trend is used in geostatistical modeling, its reproduction in subsequent realizations should be checked. The reproduction of a trend will be assessed in two ways: (1) globally for a single realization or (2) locally over a set of realizations.

Evaluating the reproduction of the trend for a single realization ensures that the trend is reproduced in expected terms over the realization. For example, all locations where the trend map indicates a proportion between 0.2 and 0.3 can be examined (Fig. 3). For a single realization the proportion in these locations should be about 0.25. The expected trend proportion from the trend model (0.25 in this case) can be compared to the actual proportion in the realization (Fig. 4). Using a different multiple point templates for this example generates a range of results. Using 2, 4, 8, 16, or 24 points seems to generate models where too much emphasis is placed on the trend; where the trend proportion is high the realization proportion is even higher, where the trend proportion is low the realization proportion is even lower. A sufficiently large template (in this case at least 32 points) must be selected for reasonable trend reproduction. Alternatively, the trend may not be given sufficient weight (Fig. 5).

Figure 3
figure 3

Proportion map. The shaded region indicates areas where the realization proportions should total between 0.2 and 0.3

Full size image
Figure 4
figure 4

Global trend check. Each plot represents a different set of 75 realizations (red lines) using 1, 2, 4, 8, 16, 24, 32, and 56-point statistics in SNESIM. All axes are identically sized. The black line indicates the average of all 75 realizations

Full size image
Figure 5
figure 5

Global trend check interpretation guide

Full size image

Assessing the local trend ensures that on average the realizations honor a local trend at a specific location. The average proportion over all realizations at each location is compared to the actual trend proportion by calculating the local difference (Fig. 6). A randomized plot with values close to zero is desirable, as shown by the realizations with multiple point templates larger than 16 points. Areas that are consistently high or low do not reproduce the trend well (upper plots in Fig. 6).

Figure 6
figure 6

Local trend check. Plotted is the difference (trend map—average realization proportion)

Full size image

Multiscale Histograms

Geostatistical realizations are commonly used to generate an average value at a scale larger than the modeled block size (e.g., selective mining unit in mineral resources and upscaled flow simulation grid in reservoirs). The behavior of the multiscale histogram is dependent on the underlying spatial structure of the TIs and realizations. In this application the behavior of the realizations as they are scaled to the desired volumetric support is critical. One possibility is to visually assess and compare the behavior of the scaled histogram of the TI to that of the realizations. Ideally, the histograms of the TI and the MPS realization at different scales would be identical.

In this case study the upscaled realizations average to the global proportions quicker than the TI (Fig. 7). This indicates more structure (i.e., connected channels) in the TI than in the MPS realizations. Less structured models quickly scale to the global average/proportion (Fig. 7). More structured models will remain bimodal at larger scales.

Figure 7
figure 7

Effect of block averaging on the histogram. The histogram represents the TI. The average of 75 16 MPSs are shown as horizontal dashes. Overlain are slices for each volumetric support for the TI (below in each histogram) and a slice of an MPS realization (above in each histogram)

Full size image

The behavior of the tails of the multiscale distribution is critical to resource calculation. How these tails change as the support of the histogram increases is a function of the multiple point distribution of the realization. If the tails in the MPS realizations disappear or average out at a smaller volume than the TI there is too little structure in the realizations (Fig. 8). Specifically, this indicates that the highs and/or lows in the MPS realizations are too disconnected and the practitioner should assess if this will affect the desired upscaled properties. Conversely, the realizations may contain additional structure, in which case the tails of the TI will disappear more quickly. In this case the practitioner should examine the cause of the increased connectivity of extremes in the MPS realizations and again assess the importance. This could be due to a trend model that does not appear in the TI or unwarranted structure added by the simulation algorithm. MPS parameters (e.g., template size) can be adjusted to better match the scaling properties of the TI.

Figure 8
figure 8

Checking the fraction in the tails when block averaging. The TI and realizations are binary; therefore, the tails represent the only indicators present

Full size image

Multiple Point Density Function

Akin to checking the variogram reproduction for semivariogram-based geostatistical approaches, the reproduction of the multiple point density function should be assessed. Checking the multiple point density function is complicated by its high dimensionality; even small templates are difficult to visualize because of the large number of bins. Moreover, the lack of an intuitive ordering to the multiple point density function bins negates any reduction in dimensionality (Fig. 1). A solution to this problem was proposed by Boisvert, Pyrcz, and Deutsch (2007) where a difference measure is calculated between two multiple point density functions. This can be applied to compare MPS realizations to the input TI (Fig. 9). The difference measure is the sum of the absolute difference between each bin in the multiple point density function. Ideally this would be near zero, indicating similar multiple point density functions. This metric can be used to tune input parameters; for example, in the case study using more than 24 points in MPS does not provide significant gains based on this metric (Fig. 9).

Figure 9
figure 9

Left: Sum of the absolute difference between the multiple point density function of the TI and realizations. Right: Proportion of implausible configurations. The minimum, maximum, and average are presented using 4, 8, or 24-point templates. The number of bins in the multiple point density function is plotted in brackets to emphasize the nonlinearity of the scale

Full size image

While this comparison is useful for assessing multiple point characteristics, it is important to realize this difference measure reduces a very high order statistic to a single value. Much information contained in the multiple point density function is lost.

Missing or Zero Bins

The absence of specific multiple point configurations may also indicate important information concerning the spatial heterogeneity. Although, zero bins in the multiple point density function may also be the result of a limited TI size. An assumption is made that the TI is representative of the modeling domain; therefore, if a configuration does not exist in the TI it should not appear in the realizations. In practice, these unanticipated configurations do exist in MPS realizations. Consider the significant proportion of implausible configurations found the case study for large template sizes (Fig. 9). This check should be preformed for each MPS realization, with preference given to realizations that have a lower proportion.

Discussion

This article presents seven metrics to assess the multiple point statistical characteristics of geostatistical realizations (Table 1). Each metric summarizes a high-level statistical relationship in a way that can be compared to a reference statistic provided by the TI. Not all metrics will be useful in all applications. Poor performance of a model on one metric is not a reason to reject the model if the metric is not relevant to the intended purpose of the model; however, good performance on any metric increases the credibility of the model and a failure should raise suspicions as to the models appropriateness.

Table 1 Summary of assessment metrics
Full size table

MPS model confirmation cannot be addressed without discussing the inference of input statistics. All metrics discussed in this article compare the models to the input statistics (e.g., global proportions, trends, and the TI), assuming appropriate input statistics. Selection of an inappropriate TI will produce inappropriate geological models and such errors will not be discovered by the proposed metrics. Pyrcz and others (2006) discuss methods for inference of representative input statistics (one- and two-point and trends) and Boisvert, Pyrcz, and Deutsch (2007) attempted to provide objective measures to select a TI for use in MPS; however, literature on this topic is sparse. The use of MPS in geological modeling is in its infancy and it is likely that as the field matures more emphasis will be placed on practical issues such as TI selection, rather than the current focus on MPS algorithmic development. Currently, for validation of MPS modeling choices a more intensive assessment of the models credibility should be undertaken using accepted methods such as hold out analysis (Davis, 1987), performance measuring or history matching.

Conclusions

A set of metrics are demonstrated within the context of model confirmation. In addition, visual inspection of the model and histogram and semivariogram reproduction checks should be prerequisites. The appropriate metrics (Table 1) should be applied to assess the reproduction of higher-order multiple point statistics. In the face of significant deviation from the input statistics, adjustments to the implementation workflow and parameters should be made and contradiction between input statistics and conditioning should be addressed. The proposed metrics are one step in model confirmation as they are intended to assess algorithmic performance rather than model performance. Model performance should be tested with application-specific transfer functions such as recoverable reserves, flow simulation, effective permeability readings, connectivity of extremes, volume above a cutoff value.

In the context of testing algorithm performance the proposed metrics provide minimum confirmation tools. One important aspect of geological modeling is the diverse range of applications for each model created. Every application demands a set of checks to assess the higher-order statistical properties relevant to the models intended use. The tools described here test common uses of geological categorical models.