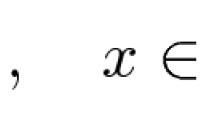1 Introduction and main result

Consider the following fractional Choquard equation

$$\begin{aligned} (-\Delta )^su+V(x)u=f(x,u)+\lambda \left[ |x|^{-\mu }*|u|^p\right] p|u|^{p-2}u, \quad x \in {\mathbb {R}}^N, \end{aligned}$$
(1.1)

where \(0<s<1\), \((-\Delta )^s\) denotes the fractional Laplacian of order s, \(N>2s\), \(0<\mu <2s\) and \(p\ge 2_{\mu ,s}^*:=\frac{2N-\mu }{N-2s}\).

Problem (1.1) has nonlocal characteristics in the nonlinearity as well as in the (fractional) diffusion. When \(s=1, \ \mu =1, \ \lambda =1, \ p=2\) and \(f(x,u)=0\), then (1.1) boils down to the so-called Choquard equation

$$\begin{aligned} -\Delta u+V(x)u = \left[ |x|^{-1}*|u|^2\right] u, \quad x \in {\mathbb {R}}^3, \end{aligned}$$
(1.2)

which goes back to the description of the quantum theory of a polaron at rest by Pekar in 1954 [15] and the modeling of an electron trapped in its own hole in 1976 in the work of Choquard, as a certain approximation to Hartree-Fock theory of one-component plasma [6]. In some particular cases, this equation is also known as the Schrödinger-Newton equation, which was introduced by Penrose in his discussion on the selfgravitational collapse of a quantum mechanical wave function [16]. The first investigations for existence and symmetry of the solutions to (1.2) go back to the works of Lieb [6] and Lions [7]. Since then many efforts have been made to study the existence of nontrivial solutions for nonlinear Choquard equations, see for instance [3, 12, 13].

For fractional Laplacian with nonlocal Hartree-type nonlinearities, the problem has also attracted a lot of interest, we refer to Refs. [2, 4, 5, 8, 10, 11] and their references therein.

Most of the works afore mentioned are set in \({\mathbb {R}}^N\), \(N>2s\), with subcritical and critical growth nonlinearities and to the authors’ best knowledge no results are available on the existence for problem (1.1) with supercritical exponent. We aim at studying the existence of nontrivial solutions for critical or supercritical problem (1.1).

In order to reduce the statements for main result, we list the assumption as follows: (V) \(V\in C\left( {\mathbb {R}}^N,{\mathbb {R}}\right)\), \(0<V_0:=\inf \limits _{x\in {\mathbb {R}}^{N}}V(x)\) and \(\lim \limits _{|x|\rightarrow +\infty }V(x)=+\infty\).

\((f_1)\) \(f \in C\left( {\mathbb {R}}^N \times {\mathbb {R}},{\mathbb {R}}\right)\) and there exists \(q \in \left( 2,\frac{2(N-\mu )}{N-2s}\right)\) such that \(|f(x,t)|\le C\left( 1+|t|^{q-1}\right)\) for all \((x,t) \in {\mathbb {R}}^N \times {\mathbb {R}}\).

\((f_2)\) \(f(x,t)=o(|t|)\) uniformly in \(x \in {\mathbb {R}}^N\) as \(|t|\rightarrow 0\).

\((f_3)\) \(f(x,t)t\ge qF(x,t):=q\int _0^tf(x,\tau )d\tau\) for all \((x,t) \in {\mathbb {R}}^N \times {\mathbb {R}}\).

\((f_4)\) \(c_0:=\inf \limits _{x \in {\mathbb {R}}^N, |t|=1}F(x,t)>0\).

For any \(0<s<1\), the fractional Sobolev space \(H^s\left( {\mathbb {R}}^N\right)\) is defined by

$$\begin{aligned} H^s\left( {\mathbb {R}}^N\right) =\left\{ u \in L^2\left( {\mathbb {R}}^N\right) : \frac{|u(x)-u(y)|}{|x-y|^{\frac{N+2s}{2}}} \in L^2\left( {\mathbb {R}}^N \times {\mathbb {R}}^N\right) \right\} , \end{aligned}$$

endowed with the natural norm

$$\begin{aligned} \Vert u\Vert _{H^s\left( {\mathbb {R}}^N\right) }=\left( \int _{{\mathbb {R}}^N}u^2dx+\int _{{\mathbb {R}}^{2N}} \frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}dxdy\right) ^{\frac{1}{2}}, \end{aligned}$$

where the term

$$\begin{aligned}{}[u]_{H^s\left( {\mathbb {R}}^N\right) }=\left( \int _{{\mathbb {R}}^{2N}}\frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}dxdy\right) ^{\frac{1}{2}} \end{aligned}$$

is the so-called Gagliardo semi-norm of u. Moreover, we can see that an alternative definition of the fractional Sobolev space \(H^s\left( {\mathbb {R}}^N\right)\) via the Fourier transform as follows:

$$\begin{aligned} H^s\left( {\mathbb {R}}^N\right) =\left\{ u \in L^2\left( {\mathbb {R}}^N\right) : \int _{{\mathbb {R}}^N}\left( 1+|\xi |^{2s}\right) \left| {\hat{u}}(\xi )\right| ^2d\xi < +\infty \right\} . \end{aligned}$$

Here we denote the Fourier transform of u by \({\hat{u}}:= {\mathscr {F}}(u)\). Propositions 3.4 and 3.6 in [14] imply that

$$\begin{aligned} 2C_{N,s}^{-1}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi = 2C_{N,s}^{-1}\left\| (-\Delta )^{\frac{s}{2}}u\right\| _{L^2({\mathbb {R}}^N)}^2 =[u]_{H^s({\mathbb {R}}^N)}^2. \end{aligned}$$

As a consequence, the norms on \(H^s\left( {\mathbb {R}}^N\right)\),

$$\begin{aligned} \begin{array}{ll} \begin{array}{ll} u\mapsto \Vert u\Vert _{H^s\left( {\mathbb {R}}^N\right) },\\ u\mapsto \left( \Vert u\Vert _{L^2\left( {\mathbb {R}}^N\right) }^2+\Vert (-\Delta )^{\frac{s}{2}}u\Vert _{L^2\left( {\mathbb {R}}^N\right) }^2\right) ^{\frac{1}{2}},\\ u\mapsto \left( \Vert u\Vert _{L^2\left( {\mathbb {R}}^N\right) }^2+\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi \right) ^{\frac{1}{2}} \end{array} \end{array} \end{aligned}$$

are all equivalent.

Set \(E=\left\{ u \in H^s\left( {\mathbb {R}}^N\right) : \int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\int _{{\mathbb {R}}^N}V(x)u^2dx<+\infty \right\}\) with the norm

$$\begin{aligned} \Vert u\Vert _E^2=\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\int _{{\mathbb {R}}^N}V(x)u^2dx \end{aligned}$$

and \({\mathcal {D}}^{s,2}({\mathbb {R}}^N)=\left\{ u \in L^{2_s^*}\left( {\mathbb {R}}^N\right) :\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi <+\infty \right\}\) with the norm

$$\begin{aligned} \Vert u\Vert _{{\mathcal {D}}^{s,2}}^2=\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi . \end{aligned}$$

Then \(\Vert u\Vert _E^2=\Vert u\Vert _{\mathcal {D}^{s,2}}^2+\int _{{\mathbb {R}}^N}V(x)u^2dx.\)

Our main result is the following:

Theorem 1.1

Suppose that (V) and \((f_1)\)–\((f_4)\) are satisfied. Then there exists some \(\lambda _0>0\) such that for \(\lambda \in (0,\lambda _0]\), Eq. (1.1) admits a nontrivial solution \(u_\lambda\).

Remark 1.2

Bhattarai in [1] studied the following fractional Schrödinger equation

$$\begin{aligned} (-\Delta )^su+\omega u = a|u|^{q-2}u+\lambda \left[ |x|^{-\mu }*|u|^p\right] |u|^{p-2}u, \end{aligned}$$

where \(0<\mu <N\), \(2<q<2+\frac{4s}{N}<2_s^*\), \(2\le p<1+\frac{2s+N-\mu }{N}<2_{\mu ,s}^*\). Consequently, our result extends his result to some extent.

2 Proof of Theorem 1.1

Proposition 2.1

[9] (Hardy-Littlewood-Sobolev inequality) Let \(r, \ t>1\) and \(0<\mu <N\) with \(\frac{1}{r}+\frac{\mu }{N}+\frac{1}{t}=2\). Let \(g \in L^r\left( {\mathbb {R}}^N\right)\) and \(h \in L^t\left( {\mathbb {R}}^N\right)\). Then there exists a sharp constant \(C_{r,N,\mu ,t}\) independent of g and h such that

$$\begin{aligned} \int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{g(x)h(y)}{|x-y|^\mu }dxdy\le C_{r,N,\mu ,t}\Vert g\Vert _r\Vert h\Vert _t. \end{aligned}$$

Remark 2.2

In general, set \(F(u)=|u|^q\) for some \(q>0\). By Hardy-Littlewood-Sobolev inequality, \(\int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{F(u(x))F(u(y))}{|x-y|^\mu }dxdy\) is well defined if \(F(u) \in L^t\left( {\mathbb {R}}^N\right)\) for \(t>1\) defined by \(\frac{2}{t}+\frac{\mu }{N}=2\). Thus, for \(u \in H^s({\mathbb {R}}^N)\), there must hold

$$\begin{aligned} \frac{2N-\mu }{N}\le q\le \frac{2N-\mu }{N-2s}=2_{\mu ,s}^*. \end{aligned}$$

It is well known to us that a weak solution of problem (1.1) is a critical point of the following functional

$$\begin{aligned} \begin{aligned} I_\lambda (u)=&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}V(x)u^2dx -\int _{{\mathbb {R}}^N}F(x,u)dx-\frac{\lambda }{2}\int _{{\mathbb {R}}^N}\left[ |x|^{-\mu }*|u|^p\right] |u|^pdx. \end{aligned} \end{aligned}$$

Clearly, we cannot apply variational methods directly because the functional \(I_\lambda\) is not well defined on E unless \(p=2_{\mu ,s}^*\). To overcome this difficulty, we define a function

$$\begin{aligned} \begin{array}{ll} \phi (t)= \left\{ \begin{array}{ll} p|t|^{p-2}t, &{} |t|\le M,\\ pM^{p-q}|t|^{q-2}t, &{} |t|> M, \end{array} \right. \end{array} \end{aligned}$$

where \(M>0\). Then \(\phi \in C({\mathbb {R}},{\mathbb {R}})\), \(\phi (t)t\ge q\Phi (t):=q\int _0^t\phi (s)ds\ge 0\) and \(|\phi (t)|\le pM^{p-q}|t|^{q-1}\) for all \(t \in {\mathbb {R}}\). Moreover, there exists a constant \(C>0\) such that

$$\begin{aligned} \left| \left[ |x|^{-\mu }*\Phi (u)\right] \right| \le CM^{p-q} \end{aligned}$$
(2.1)

for all \(u \in H^s\left( {\mathbb {R}}^N\right)\). Indeed, for any \(u \in H^s\left( {\mathbb {R}}^N\right)\), taking \(t \in \left( \frac{N}{N-\mu },\frac{2N}{q(N-2s)}\right]\), by the Hölder inequality we can calculate that

$$\begin{aligned} \begin{aligned}&\left| |x|^{-\mu }*\Phi (u)\right| =\left| \int _{{\mathbb {R}}^N}\frac{\Phi (u(y))}{|x-y|^\mu }dy\right| \\&\quad \le CM^{p-q} \int _{{\mathbb {R}}^N}\frac{|u(y)|^q}{|x-y|^\mu }dy\\&\quad = CM^{p-q}\int _{|x-y|\le 1}\frac{|u(y)|^q}{|x-y|^\mu }dy+CM^{p-q}\int _{|x-y|>1}\frac{|u(y)|^q}{|x-y|^\mu }dy\\&\quad \le CM^{p-q}\left( \int _{|x-y|\le 1}|u(y)|^{tq}dy\right) ^{\frac{1}{t}}\left( \int _{|x-y|\le 1}\frac{1}{|x-y|^{\frac{\mu t}{t-1}}}dy\right) ^{\frac{t-1}{t}}+CM^{p-q}\\&\quad \le CM^{p-q}\left( \int _0^1\rho ^{N-1-\frac{\mu t}{t-1}}d\rho \right) ^{\frac{t-1}{t}}+CM^{p-q}\le CM^{p-q}. \end{aligned} \end{aligned}$$

Set \(h_\lambda (x,t)=\lambda \left[ |x|^{-\mu }*\Phi (t)\right] \phi (t)+f(x,t)\) for all \((x,t) \in {\mathbb {R}}^N \times {\mathbb {R}}\). Then

\((h_1)\) \(h_\lambda \in C\left( {\mathbb {R}}^N \times {\mathbb {R}},{\mathbb {R}}\right)\) and \(|h_\lambda (x,t)|\le C\lambda M^{2(p-q)}|t|^{q-1}+C\left(1+|t|^{q-1}\right)\) for all \((x,t) \in {\mathbb {R}}^N \times {\mathbb {R}}\).

\((h_2)\) \(h_\lambda (x,t)=o(|t|)\) uniformly in \(x \in {\mathbb {R}}^N\) as \(|t|\rightarrow 0\).

\((h_3)\) \(h_\lambda (x,t)t\ge qH_\lambda (x,t):=q\int _0^th_\lambda (x,\tau )d\tau \ge 0\) for all \((x,t) \in {\mathbb {R}}^N \times {\mathbb {R}}\).

\((h_4)\) \(\inf \limits _{x\in {\mathbb {R}}^N,|t|=1}H_\lambda (x,t)\ge c_0>0\).

Let

$$\begin{aligned} \begin{aligned} J_\lambda (u)=&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}V(x)u^2dx -\int _{{\mathbb {R}}^N}H_\lambda (x,u)dx\\ =&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}V(x)u^2dx -\int _{{\mathbb {R}}^N}F(x,u)dx\\&-\frac{\lambda }{2}\int _{{\mathbb {R}}^N}\left[ |x|^{-\mu }*\Phi (u)\right] \Phi (u)dx\\ =&\frac{1}{4}C_{N,s}[u]_{H^s}^2+\frac{1}{2}\int _{{\mathbb {R}}^N}V(x)u^2dx -\int _{{\mathbb {R}}^N}F(x,u)dx\\&-\frac{\lambda }{2}\int _{{\mathbb {R}}^N}\left[ |x|^{-\mu }*\Phi (u)\right] \Phi (u)dx. \end{aligned} \end{aligned}$$

By mountain pass theorem, using a standing argument we can prove that the equation

$$\begin{aligned} (-\Delta )^su+V(x)u=h_\lambda (x,u) \end{aligned}$$

has a nontrivial \(u_\lambda \in E\) with \(J_\lambda ^\prime (u_\lambda )=0\) and \(J_\lambda (u_\lambda )=c_\lambda :=\inf \limits _{\gamma \in \Gamma _\lambda }\sup \limits _{t \in [0,1]}J_\lambda (\gamma (t))\), where

$$\begin{aligned} \Gamma _\lambda :=\left\{ \gamma \in C([0,1], E):\gamma (0)=0, \ J_\lambda (\gamma (1))<0\right\} . \end{aligned}$$

In the sequel, set

$$\begin{aligned} J(u)=\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}V(x)u^2dx -\int _{{\mathbb {R}}^N}F(x,u)dx \end{aligned}$$

and

$$\begin{aligned} \Gamma :=\left\{ \gamma \in C([0,1], E):\gamma (0)=0, \ J(\gamma (1))<0\right\} \end{aligned}$$

and \(c:=\inf \limits _{\gamma \in \Gamma }\sup \limits _{t \in [0,1]}J(\gamma (t))\). Then \(\Gamma \subset \Gamma _\lambda\) and \(c_\lambda \le c\).

Lemma 2.3

The solution \(u_\lambda\) satisfies \(\Vert u_\lambda \Vert _{{\mathcal {D}}^{s,2}}^2\le \frac{2q}{q-2}c_\lambda\) and there exists a constant \(A>0\) independent on \(\lambda\) such that \(\Vert u_\lambda \Vert _{{\mathcal {D}}^{s,2}}^2\le A\).

Proof

Taking into account \((f_3)\) we can see that

$$\begin{aligned} \begin{aligned} qc_\lambda& =qJ_\lambda (u_\lambda )=qJ_\lambda (u_\lambda )-\left\langle J_\lambda ^\prime (u_\lambda ),u_\lambda \right\rangle \\ &= \left( \frac{q}{2}-1\right) \int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}_\lambda (\xi )|^2d\xi +\left( \frac{q}{2}-1\right) \int _{{\mathbb {R}}^N}V(x)|u_\lambda |^2dx+\int _{{\mathbb {R}}^N}\left[ f(x,u_\lambda )u_\lambda -qF(x,u_\lambda )\right] dx\\&\quad +\lambda \int _{{\mathbb {R}}^N}\left[ |x|^{-\mu }*\Phi (u_\lambda )\right] \left[ \phi (u_\lambda )u_\lambda -\frac{q}{2}\Phi (u_\lambda )\right] dx\\ & \ge\left( \frac{q}{2}-1\right) \int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}_\lambda (\xi )|^2d\xi =\left( \frac{q}{2}-1\right) \Vert u_\lambda \Vert _{\mathcal {D}^{s,2}}^2, \end{aligned} \end{aligned}$$

which implies that \(\Vert u_\lambda \Vert _{{\mathcal {D}}^{s,2}}^2\le \frac{2q}{q-2}c_\lambda \le \frac{2q}{q-2}c:=A>0\). This completes the proof. \(\square\)

Lemma 2.4

There exist two constants \(B, \ D>0\) independent on \(\lambda\) such that \(\Vert u_\lambda \Vert _{L^{\infty }}\le B(1+\lambda )^D\), where \(\Vert u\Vert _{L^{\infty }}:=\displaystyle \sup _{x\in {{\mathbb {R}}^N}}|u(x)|\).

Proof

For any \(L>0\) and \(\beta >1\), set

$$\begin{aligned} \gamma (u_\lambda ):=\gamma _{L,\beta }(u_\lambda )=u_\lambda u_{\lambda , L}^{2(\beta -1)} \in H^s\left( {\mathbb {R}}^N\right) , \end{aligned}$$

where \(u_{\lambda , L}:=\min \{u_\lambda , L\}\). Since \(\gamma\) is an increasing function, one has

$$\begin{aligned} (a-b)[\gamma (a)-\gamma (b)]\ge 0 \end{aligned}$$

for all \(a, \ b \in {\mathbb {R}}\). Furthermore, set \(\Gamma (t):=\int _0^t\left( \gamma ^\prime (\tau )\right) ^{\frac{1}{2}}d\tau\) for \(t\ge 0\). Then for any \(a, \ b \in {\mathbb {R}}\), if \(a>b\) we obtain

$$\begin{aligned} \begin{aligned} (a-b)[\gamma (a)-\gamma (b)]&=(a-b)\int _b^a\gamma ^\prime (t)dt=(a-b)\int _b^a(\Gamma ^\prime (t))^2dt\ge \left( \int _b^a\Gamma ^\prime (t)dt\right) ^2\\&=|\Gamma (a)-\Gamma (b)|^2. \end{aligned} \end{aligned}$$

We can use a similar argument to obtain the above conclusion if \(a\le b\). Therefore,

$$\begin{aligned} (a-b)[\gamma (a)-\gamma (b)]\ge \left| \Gamma (a)-\Gamma (b)\right| ^2 \end{aligned}$$

for all \(a, \ b \in {\mathbb {R}}\). Consequently,

$$\begin{aligned} |\Gamma (u_\lambda )(x)-\Gamma (u_\lambda )(y)|^2\le [u_\lambda (x)-u_\lambda (y)]\left[ \left( u_\lambda u_{\lambda , L}^{2(\beta -1)}\right) (x)-\left( u_\lambda u_{\lambda , L}^{2(\beta -1)}\right) (y)\right] , \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned}\frac{C_{N,s}}{2}& [\Gamma (u_\lambda )]^2+\int _{{\mathbb {R}}^N}V(x)u_\lambda ^2 u_{\lambda , L}^{2(\beta -1)}dx\\ \le&\frac{C_{N,s}}{2}\int _{{\mathbb {R}}^{2N}}\frac{u_\lambda (x)-u_\lambda (y)}{|x-y|^{N+2s}}\left[ \left( u_\lambda u_{\lambda , L}^{2(\beta -1)}\right) (x)-\left( u_\lambda u_{\lambda , L}^{2(\beta -1)}\right) (y)\right] dxdy+\int _{{\mathbb {R}}^N}V(x)u_\lambda ^2 u_{\lambda , L}^{2(\beta -1)}dx\\ =&\int _{{\mathbb {R}}^N}f(x,u_\lambda )u_\lambda u_{\lambda , L}^{2(\beta -1)}dx+\lambda \int _{{\mathbb {R}}^N}\left[ |x|^{-\mu }*\Phi (u_\lambda )\right] \phi (u_\lambda )u_\lambda u_{\lambda , L}^{2(\beta -1)}dx. \end{aligned} \end{aligned}$$
(2.2)

By the fact that \(\Gamma (u_\lambda )\ge \frac{1}{\beta }u_\lambda u_{\lambda , L}^{\beta -1}\) we see that

$$\begin{aligned}{}[\Gamma (u_\lambda )]^2\ge S_*\Vert \Gamma (u_\lambda )\Vert _{2_s^*}^2\ge \left( \frac{1}{\beta }\right) ^2S_*\Vert u_\lambda u_{\lambda , L}^{\beta -1}\Vert _{2_s^*}^2, \end{aligned}$$
(2.3)

where \(S_*=S(N,s)>0\) is a sharp constant that satisfies \(S_*\Vert u\Vert _{2_s^*}^2\le [u]^2\) for any \(u \in H^s({\mathbb {R}}^N)\)( [14]). By the proof of (2.1) we know that there exists a constant \(C_0>0\) such that

$$\begin{aligned} \left| |x|^{-\mu }*\Phi (u_\lambda )\right| \le C_0 M^{p-q} \end{aligned}$$
(2.4)

Moreover, by virtue of \((f_1)\)–\((f_2)\) we know that for any \(\varepsilon >0\), there exists \(C_\varepsilon >0\) such that

$$\begin{aligned} |f(x,t)|\le \varepsilon |t|+C_\varepsilon |t|^{q-1} \end{aligned}$$
(2.5)

for all \((x,t) \in {\mathbb {R}}^N \times {\mathbb {R}}\). For fixed \(\lambda >0\) and small \(\varepsilon >0\), by (2.5) and properties of \(\phi\) we have

$$\begin{aligned} |f(x,t)+\lambda \phi (t)|\le \frac{V_0}{\max \{1,C_0M^{p-q}\}}|t|+C(1+\lambda )|t|^{q-1} \end{aligned}$$
(2.6)

for all \((x,t) \in {\mathbb {R}}^N \times {\mathbb {R}}\). Therefore, in view of (2.2)–(2.4) and (2.6) one has

$$\begin{aligned} \begin{aligned}&\frac{C_{N,s}}{2}\left( \frac{1}{\beta }\right) ^2S_*\left\Vert u_\lambda u_{\lambda , L}^{\beta -1}\right\Vert _{2_s^*}^2 \le \frac{C_{N,s}}{2}[\Gamma (u_\lambda )]^2\\ \le&\,\max \left\{ 1,C_0M^{p-q}\right\} \int _{{\mathbb {R}}^N}\left[ \frac{V_0}{\max \{1,C_0M^{p-q}\}}|u_\lambda |+C(1+\lambda )|u_\lambda |^{q-1}\right] \left| u_\lambda u_{\lambda ,L}^{2(\beta -1)}\right| dx\\&-\int _{{\mathbb {R}}^N}V(x)u_\lambda ^2 u_{\lambda , L}^{2(\beta -1)}dx\\ \le&C(1+\lambda )\int _{{\mathbb {R}}^N}|u_\lambda |^q \left| u_{\lambda ,L}^{2(\beta -1)}\right| dx. \end{aligned} \end{aligned}$$
(2.7)

Set \(w_{\lambda ,L}:=u_\lambda u_{\lambda ,L}^{\beta -1}\). By applying the Hölder inequality and (2.7), we get

$$\begin{aligned} \begin{aligned}&\Vert w_{\lambda ,L}\Vert _{2_s^*}^2=\left\| u_\lambda u_{\lambda ,L}^{\beta -1}\right\| _{2_s^*}^2\\ & \le\beta ^2C(1+\lambda )\int _{{\mathbb {R}}^N}|u_\lambda |^q \left| u_{\lambda ,L}^{2(\beta -1)}\right| dx\\& =\beta ^2C(1+\lambda )\int _{{\mathbb {R}}^N}|u_\lambda |^{q-2} w_{\lambda ,L}^2dx\\ & \le \beta ^2C(1+\lambda )\left( \int _{{\mathbb {R}}^N}|u_\lambda |^{2_s^*}dx\right) ^{\frac{q-2}{2_s^*}} \left( \int _{{\mathbb {R}}^N}w_{L,\lambda }^{\alpha _s^*}dx\right) ^{\frac{2}{\alpha _s^*}}\\ & \le\beta ^2C(1+\lambda ) \Vert w_{L,\lambda }\Vert _{\alpha _s^*}^2, \end{aligned} \end{aligned}$$
(2.8)

where \(\alpha _s^*:=\frac{22_s^*}{2_s^*-(q-2)} \in (2,2_s^*)\). Now, we observe that if \(u_\lambda ^\beta \in L^{\alpha _s^*}({\mathbb {R}}^N)\), from the definition of \(w_{\lambda ,L}\), and by using the fact that \(u_{\lambda ,L}\le u_\lambda\) and (2.8) we obtain

$$\begin{aligned} \Vert w_{\lambda ,L}\Vert _{2_s^*}^2 \le C\beta ^2(1+\lambda )\left( \int _{{\mathbb {R}}^N}|u_\lambda |^{\beta \alpha _s^*}\right) ^{\frac{2}{\alpha _s^*}}<+\infty . \end{aligned}$$

Using the Fatou Lemma in \(L\rightarrow +\infty\) one has

$$\begin{aligned} \Vert u_\lambda \Vert _{\beta 2_s^*} \le C^{\frac{1}{\beta }}\beta ^{\frac{1}{\beta }}(1+\lambda )^{\frac{1}{2\beta }}\Vert u_\lambda \Vert _{\beta \alpha _s^*}, \end{aligned}$$
(2.9)

where \(u_\lambda ^{\beta \alpha _s^*} \in L^1({\mathbb {R}}^N)\).

Now, we take \(\beta =\frac{2_s^*}{\alpha _s^*}>1\). By \(u_\lambda \in L^{2_s^*}\left( {\mathbb {R}}^N\right)\), we know that (2.9) still holds for this choice of \(\beta\). Then, observing that \(\beta ^2\alpha _s^*=\beta 2_s^*\), it follows that (2.9) holds with \(\beta\) replaced by \(\beta ^2\). Therefore,

$$\begin{aligned} \begin{aligned} \Vert u_\lambda \Vert _{\beta ^22_s^*}&\le\,\, C^{\frac{1}{\beta ^2}}\beta ^{\frac{2}{\beta ^2}}(1+\lambda )^{\frac{1}{2\beta ^2}}\Vert u_\lambda \Vert _{\beta ^2\alpha _s^*}\\&\,=\,\,C^{\frac{1}{\beta ^2}}\beta ^{\frac{2}{\beta ^2}}(1+\lambda )^{\frac{1}{2\beta ^2}}\Vert u_\lambda \Vert _{\beta 2_s^*}\\&\le C^{\frac{1}{\beta }+\frac{1}{\beta ^2}}\beta ^{\frac{1}{\beta }+\frac{2}{\beta ^2}}(1+\lambda )^{\frac{1}{2\beta }+\frac{1}{2\beta ^2}}\Vert u_\lambda \Vert _{\beta \alpha _s^*}. \end{aligned} \end{aligned}$$

Iterating this process and recalling that \(\beta \alpha _s^*=2_s^*\), we can infer that for every \(m \in {\mathbb {N}}\),

$$\begin{aligned} \begin{aligned} \Vert u_\lambda \Vert _{\beta ^m2_s^*}\le&C^{\frac{1}{\beta }+\frac{1}{\beta ^2}+\cdots +\frac{1}{\beta ^m}} \beta ^{\frac{1}{\beta }+\frac{2}{\beta ^2}+\cdots +\frac{m}{\beta ^m}}(1+\lambda )^{\frac{1}{2\beta }+\frac{1}{2\beta ^2}+\cdots +\frac{1}{2\beta ^m}}\Vert u_\lambda \Vert _{2_s^*}\\ =&C^{\sum _{j=1}^m\frac{1}{\beta ^j}} \beta ^{\sum _{j=1}^m\frac{j}{\beta ^j}}(1+\lambda )^{\frac{1}{2}\sum _{j=1}^m\frac{1}{\beta ^j}}\Vert u_\lambda \Vert _{2_s^*}. \end{aligned} \end{aligned}$$

Let \(m\rightarrow +\infty\) and recalling that \(\Vert u_\lambda \Vert _{2_s^*}\le K\) we obtain

$$\begin{aligned} \Vert u_\lambda \Vert _{L^{\infty }}\le C^{\sigma _1} \beta ^{\sigma _2}(1+\lambda )^{\frac{1}{2}\sigma _1}K=C^{\sigma _1} \left( \frac{2_s^*}{\alpha _s^*}\right) ^{\sigma _2}K(1+\lambda )^{\frac{1}{2}\sigma _1}:=B(1+\lambda )^D. \end{aligned}$$

This completes the proof. \(\square\)

Proof of Theorem 1.1

For large \(M>0\), we can choose small \(\lambda _0>0\) such that \(\Vert u_\lambda \Vert _{L^{\infty }}\le B(1+\lambda )^D\le M\) for all \(\lambda \in (0,\lambda _0]\). Consequently, \(u_\lambda\) is a nontrivial solution of (1.1) with \(\lambda \in (0,\lambda _0]\). This completes the proof. \(\square\)