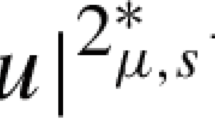Concentration phenomenon of solutions for fractional Choquard equations with upper critical growth

Abstract

In this article, we focus on the following fractional Choquard equation involving upper critical exponent

$$\begin{aligned} \varepsilon ^{2s}(-\varDelta )^su+V(x)u=P(x)f(u)+\varepsilon ^{\mu -N}Q(x)[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*-2}u, \ x \in {\mathbb {R}}^N, \end{aligned}$$

where $\varepsilon >0$, $0<s<1$, $(-\varDelta )^s$ denotes the fractional Laplacian of order s, $N>2s$, $0<\mu <N$ and $2_{\mu ,s}^*=\frac{2N-\mu }{N-2s}$. Under suitable assumptions on the potentials V(x), P(x) and Q(x), we obtain the existence and concentration of positive solutions and prove that the semiclassical solutions $w_\varepsilon$ with maximum points $x_\varepsilon$ concentrating at a special set ${\mathcal {S}}_p$ characterized by V(x), P(x) and Q(x). Furthermore, for any sequence $x_\varepsilon \rightarrow x_0 \in {\mathcal {S}}_p$, $v_\varepsilon (x):=w_\varepsilon (\varepsilon x+x_\varepsilon )$ converges in $H^s({\mathbb {R}}^N)$ to a ground state solution v of

$$\begin{aligned} (-\varDelta )^sv+V(x_0)v=P(x_0)f(v)+Q(x_0)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*-2}v, \ x \in {\mathbb {R}}^N. \end{aligned}$$

1 Introduction and main results

Consider the following fractional Choquard equation involving upper critical exponent

$$\begin{aligned} \varepsilon ^{2s}(-\varDelta )^su+V(x)u=P(x)f(u)+\varepsilon ^{\mu -N}Q(x)[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*-2}u, \ x \in {\mathbb {R}}^N,\nonumber \\ \end{aligned}$$

(1.1)

where $\varepsilon >0$, $0<s<1$, $(-\varDelta )^s$ denotes the fractional Laplacian of order s, $N>2s$, $0<\mu <N$ and $2_{\mu ,s}^*=\frac{2N-\mu }{N-2s}$. As $\varepsilon$ goes to zero in (1.1), the existence and asymptotic behavior of the solutions of the singularly perturbed equation (1.1) is known as the semi-classical problem. It was used to describe the transition between of quantum mechanics and classical mechanics.

The nonlinear evolution equation usually refers to a kind of mathematical model that describes the physical phenomena evolving with time. It is one of the most advanced topics in the study of the soliton theory for nonlinear science. Erection of soliton solutions to the nonlinear evolution equations (NLEEs) arising in nonlinear science plays an important role to understand nonlinear phenomena. We recall that the problem (1.1) is motivated by the search of standing wave solutions for the following evolution equation

$$\begin{aligned} \begin{aligned} i\hbar \partial _t\psi =&\left( \frac{\hbar ^2}{2m}\right) ^s(-\varDelta )^s \psi +W(x)\psi -\left( \frac{\hbar ^2}{2m}\right) ^{\frac{\mu -N}{2}}Q(x)[K(x)*|\psi |^{2_{\mu , s}^*}]|\psi |^{2_{\mu , s}^*-2}\psi \\&-P(x)\eta (|\psi |^2)\psi , \end{aligned} \end{aligned}$$

where m is the mass of the bosons, $\hbar$ is the Planck constant, W is the external potential, $\eta : {\mathbb {R}}^+\rightarrow {\mathbb {R}}$ is a suitable function and K is the response function that admits information on the mutual interaction between the bosons. An important issue concerning the above nonlinear evolution equation is to study its standing wave solutions, and a solution of the form $\psi (x,t)=u(x)e^{-iEt}$ is called a standing wave solution. It is easy to see that u(x) solves (1.1) if and only if $\psi (x,t)=u(x)e^{\frac{-iE}{\hbar }t}$ solves the above equation, where $V(x)=W(x)-E$, $\varepsilon ^2=\frac{\hbar ^2}{2m}$ and $f(u)=\eta (|u|^2)u$.

If the response function is the Dirac function, i.e., $K(x)=\delta (x)$, then the nonlinear response is local indeed and the above equation becomes the following fractional Schrödinger equation:

$$\begin{aligned} \varepsilon ^{2s}(-\varDelta )^su+V(x)u=h(u), \ x \in {\mathbb {R}}^N, \end{aligned}$$

where $h: {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a suitable function. In recent years, such kind of equation has attracted much attention, since it appears in diverse physical phenomena, such as anomalous diffusion and quasi-geostrophic flows, turbulence and water waves, molecular dynamics, relativistic quantum mechanics of stars and probability and finance. There is a considerable amount of work on investigating the properties of this type equation. We refer the readers to [2, 3, 24, 27, 29, 30] for subcritical case, [7, 11, 13, 26] for critical case, and [15] for supercritical case. Furthermore, the space derivative of order $s=1$ (the standing Schrödinger equation) and its variants have been extensively studied in the mathematical literature, and a fairly complete theory has been developed to study them.

If the response function K(x) is a function of Coulomb type, for example $|x|^{-\mu }$, then the above equation turns into doubly nonlocal fractional elliptic equation (1.1). This type of nonlocal nonlinearities has attracted considerable interest as a means of eliminating collapse and stabilizing multidimensional solitary waves.

When $s=1$, Eq. (1.1) is usually called the nonlinear Choquard or Choquard-Pekar equation. There are a lot of works on the existence, multiplicity and concentration of solutions for such type of equations. It seems almost impossible for us to give a complete list of references. We refer the readers to [9, 20, 21] and the references therein. When $s \in (0,1)$, Eq. (1.1) is called fractional Choquard equation, which has also attracted a lot of interest. In the light of penalization method and Ljusternik-Schnirelmann category theory, Ambrosio [1] investigated the multiplicity and concentration of positive solutions for the following fractional Choquard equation

$$\begin{aligned} \varepsilon ^{2s}(-\varDelta )^su+V(x)u=\varepsilon ^{\mu -N}[|x|^{-\mu }*F(u)]f(u), \ x \in {\mathbb {R}}^N, \end{aligned}$$

but f is a superlinear continuous function with subcritical growth and satisfied monotonic condition. Belchior et al. [5] dealt with existence, regularity and polynomial decay for a fractional Choquard equation involving the fractional p-Laplacian. Especially, the authors in [18] investigated the Brézis-Nirenberg type problem

$$\begin{aligned} \begin{array}{ll} \left\{ \begin{array}{ll} (-\varDelta )^su-\beta u=[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*-2}u, &{} x \in \varOmega ,\\ u=0, &{} x \not \in \varOmega , \end{array} \right. \end{array} \end{aligned}$$

in a bounded domain $\varOmega$ and obtained some existence, multiplicity, regularity and nonexistence results by using of variational methods. Using the same method, Ma and Zhang [22] considered the following fractional Choquard equation

$$\begin{aligned} (-\varDelta )^su+[\lambda V(x)-\beta ]u = [|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*-2}u, \ x \in {\mathbb {R}}^N, \end{aligned}$$

and established the existence and multiplicity of weak solutions. Guo and Hu [8] gave existence and asymptotic behavior of the least energy solutions for fractional Choquard equations with potential well. Specifically, they considered the equation

$$\begin{aligned} (-\varDelta )^su+\lambda V(x)u=[|x|^{-\mu }*F(u)]f(u), \ x \in {\mathbb {R}}^N, \end{aligned}$$

and proved the existence of least energy solution that localizes near the bottom of potential well $int(V^{-1}(0))$ for large $\lambda$. Recently, when V and f are asymptotically periodic in x, we [16] studied the following fractional Choquard equation involving upper critical exponent

$$\begin{aligned} (-\varDelta )^su+V(x)u=[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*-2}u+\lambda f(x,u), \end{aligned}$$

and obtained the existence of a ground state solution for large $\lambda$ by Nehari method. With respect to super upper critical case $p>2_{\mu ,s}^*$, please see [17].

A solution $\psi$ is referred to as a bound state of (1.1) if $\psi \rightarrow 0$ as $|x|\rightarrow +\infty$. When $\varepsilon >0$ is sufficiently small, bound states of (1.1) are called semiclassical states and an important feature of semiclassical states is their concentration as $\varepsilon \rightarrow 0$. To our best knowledge, most of the existing papers consider the existence and property of the solutions for the fractional Choquard equation with subcritical growth. In the present paper, motivated by the works above, especially [7], we consider more general equation and obtain the existence and concentration phenomenon of solutions for the fractional Choquard equation (1.1) with upper critical growth.

To resume the statements for main results, we list the assumptions as follows:

$(f_1)$$f\in C({\mathbb {R}},{\mathbb {R}})$ and there exists $2< p<2_s^*$ such that

$$\begin{aligned} |f(t)|\le C(1+|t|^{p-1}) \end{aligned}$$

for all $t \in {\mathbb {R}}$, where C is a positive constant.

$(f_2)$$f(t)=o(|t|)$ as $|t|\rightarrow 0$.

$(f_3)$$f(t)t-2F(t)\ge f(\tau t)\tau t-2F(\tau t)$ for all $t \in {\mathbb {R}}$ and $\tau \in [0,1]$.

$(f_4)$$f(t)t>0$ for all $t>0$ and $f(t)\equiv 0$ for all $t<0$.

In addition, we set

(V):

$V \in C({\mathbb {R}}^N, {\mathbb {R}})$, $\alpha _{\infty }=\liminf \limits _{|x|\rightarrow \infty }V(x)<+\infty$, $\alpha _{\min }=\min \limits _{x \in {\mathbb {R}}^N}V(x)>0$, $\alpha _{\max } =\sup \limits _{x \in {\mathbb {R}}^N}V(x)<+\infty$ and ${\mathcal {V}}=\{x \in {\mathbb {R}}^N:V(x)=\alpha _{\min }\}$.

(P):

$P \in C({\mathbb {R}}^N, {\mathbb {R}})$, $\beta _{\infty }=\limsup \limits _{|x|\rightarrow \infty }P(x)<+\infty$, $\beta _{\max }=\max \limits _{x \in {\mathbb {R}}^N}P(x)$, $\beta _{\min } =\inf \limits _{x \in {\mathbb {R}}^N}P(x)>0$ and $\mathcal {P}=\{x \in {\mathbb {R}}^N:P(x)=\beta _{\max }\}$.

(Q):

$Q \in C({\mathbb {R}}^N, {\mathbb {R}})$, $\gamma _{\infty }=\limsup \limits _{|x|\rightarrow \infty }Q(x)<+\infty$, $\gamma _{\max }=\max \limits _{x \in {\mathbb {R}}^N}Q(x)$, $\gamma _{\min } =\inf \limits _{x \in {\mathbb {R}}^N}Q(x)>0$ and ${\mathcal {Q}}=\{x \in {\mathbb {R}}^N:Q(x)=\gamma _{\max }\}$.

(VP):

$\alpha _{{\mathcal {Q}}}=\min \limits _{x \in \mathcal {Q}}V(x)$ and $\beta _{{\mathcal {Q}}}=\max \limits _{x \in \mathcal {Q}}P(x)$.

In what follows, we propose two kinds of assumptions that will give the concentration sets. First, we assume

$$\begin{aligned} \beta _{\mathcal {Q}}>\beta _{\infty }~\hbox {and there exists}~x_p \in {\mathcal {C}}_p ~\hbox {such that}~ V(x_p)\le V(x)~\text{ for } \text{ all }~|x|\ge R,\nonumber \\ \end{aligned}$$

(1.2)

where ${\mathcal {C}}_p:=\{x \in {\mathcal {Q}}:P(x)=\beta _\mathcal {Q}\}$. Set

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_p:=&\{x \in {\mathcal {C}}_p:V(x)\le V(x_p)\}\cup \{x \in {\mathcal {Q}}\setminus {\mathcal {C}}_p:V(x)<V(x_p)\}\\&\cup \{x \not \in {\mathcal {Q}}:P(x)>\beta _{\mathcal {Q}} \ \text{ or } \ V(x)<V(x_p)\}. \end{aligned} \end{aligned}$$

Secondly, we assume

$$\begin{aligned} \alpha _{\mathcal {Q}}<\alpha _{\infty }~\hbox {and there exists}~ x_V \in {\mathcal {C}}_V~\hbox {such that}~ P(x_V)\ge P(x)~\hbox {for all}~ |x|\ge R,\nonumber \\ \end{aligned}$$

(1.3)

where ${\mathcal {C}}_V:=\{x \in {\mathcal {Q}}:V(x)=\alpha _\mathcal {Q}\}$. Set

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_V:=&\{x \in {\mathcal {C}}_V:P(x)\ge P(x_V)\}\cup \{x \in {\mathcal {Q}}\setminus {\mathcal {C}}_V:P(x)>P(x_V)\}\\&\cup \{x \not \in {\mathcal {Q}}:V(x)<\alpha _{\mathcal {Q}} \ \text{ or } \ P(x)>P(x_V)\}. \end{aligned} \end{aligned}$$

Before stating our main results, we introduce some useful notations and definitions. For any $0<s<1$, the fractional Sobolev space $H^s({\mathbb {R}}^N)$ is defined as follows

$$\begin{aligned} H^s({\mathbb {R}}^N)=\{u \in L^2({\mathbb {R}}^N): \frac{|u(x)-u(y)|}{|x-y|^{\frac{N+2s}{2}}} \in L^2({\mathbb {R}}^N \times {\mathbb {R}}^N)\}, \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert u\Vert :=\Vert u\Vert _{H^s({\mathbb {R}}^N)}=\Big (\int _{{\mathbb {R}}^N}u^2dx +\int _{{\mathbb {R}}^{2N}} \frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}dxdy\Big )^{\frac{1}{2}}, \end{aligned}$$

where the term

$$\begin{aligned}{}[u]_{H^s({\mathbb {R}}^N)}:=\Big (\int _{{\mathbb {R}}^{2N}}\frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}dxdy\Big )^{\frac{1}{2}} \end{aligned}$$

is the so-called Gagliardo semi-norm of u.

Set ${\mathcal {D}}^{s,2}({\mathbb {R}}^N)=\{u \in L^{2_s^*}({\mathbb {R}}^N):\int _{{\mathbb {R}}^N}|\xi |^{2s}| {\hat{u}}(\xi )|^2d\xi <+\infty \}$ with the norm

$$\begin{aligned} \Vert u\Vert _{{\mathcal {D}}^{s,2}}^2=\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi . \end{aligned}$$

It follows from Propositions 3.4 and 3.6 in [23] that

$$\begin{aligned} 2C_{N,s}^{-1}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi =2C_{N,s}^{-1}\Vert (-\varDelta )^{\frac{s}{2}}u\Vert _{L^2({\mathbb {R}}^N)}^2 =[u]_{H^s({\mathbb {R}}^N)}^2. \end{aligned}$$

As a result, the norms on $H^s({\mathbb {R}}^N)$,

$$\begin{aligned} \begin{array}{ll} \begin{array}{ll} u\mapsto \Vert u\Vert _{H^s({\mathbb {R}}^N)},\\ u\mapsto (\Vert u\Vert _{L^2({\mathbb {R}}^N)}^2+\Vert (-\varDelta )^{\frac{s}{2}}u \Vert _{L^2({\mathbb {R}}^N)}^2)^{\frac{1}{2}},\\ u\mapsto (\Vert u\Vert _{L^2({\mathbb {R}}^N)}^2+\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}} (\xi )|^2d\xi )^{\frac{1}{2}} \end{array} \end{array} \end{aligned}$$

are equivalent. Hence,

$$\begin{aligned} \Vert u\Vert ^2=\Vert u\Vert _{H^s({\mathbb {R}}^N)}^2=\Vert u\Vert _{{\mathcal {D}}^{s,2}}^2 +\int _{{\mathbb {R}}^N}u^2dx=\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\int _{{\mathbb {R}}^N}u^2dx. \end{aligned}$$

By [23] we know that the embedding $H^s({\mathbb {R}}^N)\hookrightarrow L^t({\mathbb {R}}^N)$ is continuous for any $t \in [2,2_s^*]$, and is locally compact whenever $t \in [2,2_s^*)$.

Our main results are the following:

Theorem 1

Suppose that (V), (P), (Q), (VP) and $(f_1)-(f_4)$ and (1.2) hold. Then for any $\varepsilon >0$ small enough, problem (1.1) admits a positive solution $w_\varepsilon$ satisfying $\lim \limits _{\varepsilon \rightarrow 0}dist(x_\varepsilon , {\mathcal {S}}_P)=0$, where $x_\varepsilon \in {\mathbb {R}}^N$ is a maximum point of $w_\varepsilon$. Moreover, setting $v_\varepsilon (x)=w_\varepsilon (\varepsilon x+x_\varepsilon )$, for any $x_\varepsilon \rightarrow x_0$ as $\varepsilon \rightarrow 0$, $v_\varepsilon$ converges in $H^s({\mathbb {R}}^N)$ to a positive ground state solution v of

$$\begin{aligned} (-\varDelta )^sv+V(x_0)v=P(x_0)f(v) + Q(x_0)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*-2}v, \ x \in {\mathbb {R}}^N. \end{aligned}$$

Theorem 2

Suppose that (V), (P), (Q), (VP) and $(f_1)-(f_4)$ and (1.3) hold. Then for any $\varepsilon >0$ small enough, problem (1.1) admits a positive solution $w_\varepsilon$ satisfying $\lim \limits _{\varepsilon \rightarrow 0}dist(x_\varepsilon , {\mathcal {S}}_V)=0$, where $x_\varepsilon \in {\mathbb {R}}^N$ is a maximum point of $w_\varepsilon$. Moreover, setting $v_\varepsilon (x)=w_\varepsilon (\varepsilon x+x_\varepsilon )$, for any $x_\varepsilon \rightarrow x_0$ as $\varepsilon \rightarrow 0$, $v_\varepsilon$ converges in $H^s({\mathbb {R}}^N)$ to a positive ground state solution v of

$$\begin{aligned} (-\varDelta )^sv+V(x_0)v=P(x_0)f(v) +Q(x_0)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*-2}v, \ x \in {\mathbb {R}}^N. \end{aligned}$$

Making the change of variable $x\mapsto \varepsilon x$, we can rewrite (1.1) as the following equivalent equation

$$\begin{aligned} (-\varDelta )^su+V(\varepsilon x)u=P(\varepsilon x)f(u)+Q(\varepsilon x)[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*-2}u, \ x \in {\mathbb {R}}^N,\nonumber \\ \end{aligned}$$

(1.4)

whose Euler-Lagrange energy functional is

$$\begin{aligned} \begin{aligned} I_\varepsilon (u)=&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}V(\varepsilon x)u^2dx -\int _{{\mathbb {R}}^N}P(\varepsilon x)F(u)dx\\&-\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*}dx. \end{aligned} \end{aligned}$$

Set

$$\begin{aligned} \Vert u\Vert _\varepsilon =\Big (\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\int _{{\mathbb {R}}^N}V(\varepsilon x)u^2]dx\Big )^{\frac{1}{2}}. \end{aligned}$$

In view of (V), the norms $\Vert u\Vert _\varepsilon$ and $\Vert u\Vert$ are equivalent and by [23] the embedding $H^s({\mathbb {R}}^N)\hookrightarrow L^t({\mathbb {R}}^N)$ is continuous for each $2\le t \le 2_s^*$ and locally compact for each $2\le t < 2_s^*$. It is easy to see that $I_\varepsilon$ is well defined on $H^s({\mathbb {R}}^N)$ and $I_\varepsilon \in C^1(H^s({\mathbb {R}}^N), {\mathbb {R}})$. Let

$$\begin{aligned} {\mathcal {N}}_\varepsilon =\{u \in H^s({\mathbb {R}}^N)\backslash \{0\}: \langle I_\varepsilon ^\prime (u), u\rangle =0\}. \end{aligned}$$

Remark 1

Since we are going to discuss the existence of positive solution of problem (1.4), we rewrite the corresponding variational functional $I_\varepsilon (u)$ in the following form:

$$\begin{aligned} \begin{aligned} I_\varepsilon (u)=&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}V(\varepsilon x)u^2dx -\int _{{\mathbb {R}}^N}P(\varepsilon x)F(u)dx\\&-\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx, \end{aligned} \end{aligned}$$

where $u^+:=\max \{u,0\}$. Then, for $\varphi \in H^s({\mathbb {R}}^N)$ we have

$$\begin{aligned} \begin{aligned} \langle I_\varepsilon ^\prime (u), \varphi \rangle =&\int _{{\mathbb {R}}^N}(-\varDelta )^su \varphi dx+\int _{{\mathbb {R}}^N}V(\varepsilon x)u\varphi dx-\int _{{\mathbb {R}}^N}P(\varepsilon x)f(u)\varphi dx\\&-\int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*-1}\varphi dx\\ =&\int _{{\mathbb {R}}^N}|\xi |^{2s}{\hat{u}}(\xi )\bar{{\hat{\varphi }}}(\xi )d\xi +\int _{{\mathbb {R}}^N}V(\varepsilon x)u\varphi dx-\int _{{\mathbb {R}}^N}P(\varepsilon x)f(u)\varphi dx\\&-\int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}] (u^+)^{2_{\mu ,s}^*-1}\varphi dx\\ =&\frac{1}{2}C_{N,s} \int _{{\mathbb {R}}^{2N}}\frac{[u(x)-u(y)][\varphi (x)-\varphi (y)]}{|x-y|^{N+2s}}dxdy +\int _{{\mathbb {R}}^N}V(\varepsilon x)u\varphi dx\\&-\int _{{\mathbb {R}}^N}P(\varepsilon x)f(u)\varphi dx-\int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*-1}\varphi dx. \end{aligned} \end{aligned}$$

We assert that all nontrivial critical points of $I_\varepsilon$ are the positive solutions of (1.4).

Remark 2

We would like to remark that there are some difficulties in studying the existence and concentration of positive solutions for (1.1). The first difficulty origins from the competition of potentials. The linear potential V has global minimum, the nonlinear potentials P and Q have global maximum, there is a competition between V, P and Q, which makes finding the concentration points become more complex. The second one comes from that the appearance of critical exponent leads to the lack of compactness. It is very difficult for us to verify that the $(PS)_c$ condition holds. We shall borrow the idea in [7] to overcome this difficulty and furthermore study the concentration of solutions. But we require some fine estimates that are complicated because of the appearance of fractional Laplacian operator and the convolution-type nonlinearity. The third one is that there is no Ambrosetti-Rabinowitz-type assumption that plays a quite important role in studying variational problems, whose role consists in ensuring the boundedness of the Palais-Smale sequences of the energy functional associated with the problem under consideration. The fourth one is that Eq. (1.1) possesses double nonlocal terms.

Remark 3

Condition $(f_3)$ is weaker than the following condition:

$$\begin{aligned} ({\tilde{f}}_3) \ \text{ the } \ \text{ map } \ t\mapsto \frac{f(t)}{|t|} \ \text{ is } \ \text{ nondecreasing } \ \text{ for } \ \text{ all } \ t \ \in {\mathbb {R}}\backslash \{0\}. \end{aligned}$$

Such a function satisfying $(f_3)$ and not satisfying $({\tilde{f}}_3)$ can be found in [14].

Remark 4

The authors of [7] considered the following fractional Schrödinger equations with critical growth

$$\begin{aligned} \varepsilon ^{2s}(-\varDelta )^su+V(x)u =P(x)f(u)+Q(x)|u|^{2_s^*-2}u, \ x \in {\mathbb {R}}^N \end{aligned}$$

and proved the existence and concentration of positive solutions, where f satisfies monotone condition $({\tilde{f}}_3)$. Differently from this, in our setting a more accurate investigation is needed due to the presence of two nonlocal terms. Moreover, the nonlinearity f appearing in Eq. (1.1) satisfies $(f_3)$, while f satisfies monotone condition $({\tilde{f}}_3)$ in [7]. In this article, we have considered a class of fractional Choquard equation more general than the considered in the above references. Simultaneously, the equation we considered is more complicated than the fractional Schrödinger equation that is considered in [7], since the nonlinearity is also nonlocal. Hence our results are different from their results, and improve and extend their results to some extent.

2 Coefficient problem

To begin with, we give some auxiliary results.

Proposition 1

( [12]) (Hardy-Littlewood-Sobolev inequality) Let $r, \ t>1$ and $0<\mu <N$ with $\frac{1}{r}+\frac{\mu }{N}+\frac{1}{t}=2$. Let $g \in L^r({\mathbb {R}}^N)$ and $h \in L^t({\mathbb {R}}^N)$. Then there exists a sharp constant $C_{r,N,\mu ,t}$ independent of g and h such that

$$\begin{aligned} \big |\int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{g(x)h(y)}{|x-y|^\mu }dxdy\big |\le C_{r,N,\mu ,t}\Vert g\Vert _r\Vert h\Vert _t. \end{aligned}$$

Remark 5

In general, set $H(u)=|u|^q$ for some $q>0$. By the Hardy-Littlewood-Sobolev inequality, $\int _{{\mathbb {R}}^N}\int _{{\mathbb {R}}^N}\frac{H(u(x))H(u(y))}{|x-y|^\mu }dxdy$ is well defined if $H(u) \in L^t({\mathbb {R}}^N)$ for $t>1$ such that $\frac{2}{t}+\frac{\mu }{N}=2$. Thus, recalling that $H^s({\mathbb {R}}^N)$ is continuously embedded into $L^r({\mathbb {R}}^N)$ for any $r \in [2,2_s^*]$, for $u \in H^s({\mathbb {R}}^N)$, there must hold $tq \in [2,2_s^*]$, which leads to assume that

$$\begin{aligned} \frac{2N-\mu }{N}\le q\le \frac{2N-\mu }{N-2s}=2_{\mu ,s}^*. \end{aligned}$$

Thus $\frac{2N-\mu }{N}$ is called the lower critical exponent and $\frac{2N-\mu }{N-2s}$ is the upper critical exponent due to the Hardy-Littlewood-Sobolev inequality. Let $S_H$ be the best constant

$$\begin{aligned} S_H=\inf \limits _{u \in {\mathcal {D}}^{s,2}({\mathbb {R}}^N)\backslash \{0\}} \frac{\Vert u\Vert _{\mathcal {D}^{s,2}}^2}{\big (\int _{{\mathbb {R}}^N}[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}] |u|^{2_{\mu ,s}^*}dx\big )^{\frac{N-2s}{2N-\mu }}}. \end{aligned}$$

In the following, we consider the constant coefficient equations. For any $\alpha \in [\alpha _{\min }, \alpha _{\max }]$, $\beta \in [\beta _{\min }, \beta _{\max }]$ and $\gamma \in [\gamma _{\min }, \gamma _{\max }]$, we study the following constant coefficient equation

$$\begin{aligned} (-\varDelta )^su+\alpha u=\beta f(u)+\gamma [|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*-1}, \ x \in {\mathbb {R}}^N, \end{aligned}$$

(2.1)

whose energy functional is

$$\begin{aligned} \begin{aligned} J_{\alpha ,\beta ,\gamma }(u)=&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}| {\hat{u}}(\xi )|^2d\xi +\frac{1}{2}\alpha \int _{{\mathbb {R}}^N}u^2dx -\beta \int _{{\mathbb {R}}^N}F(u)dx\\&-\frac{\gamma }{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}] (u^+)^{2_{\mu ,s}^*}dx. \end{aligned} \end{aligned}$$

Set

$$\begin{aligned} \Vert u\Vert _\alpha =\Big (\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\alpha \int _{{\mathbb {R}}^N}u^2dx\Big )^{\frac{1}{2}}, \end{aligned}$$

which is equivalent to the norm $\Vert u\Vert$. By $(f_1)$ and $(f_2)$, for any $\tau >0$, there exists $C_\tau >0$ such that

$$\begin{aligned} |f(t)|\le \tau |t|+C_\tau |t|^{p-1} \end{aligned}$$

(2.2)

and

$$\begin{aligned} |F(t)|\le \tau |t|^2+C_\tau |t|^p \end{aligned}$$

(2.3)

for all $t \in {\mathbb {R}}$. It follows by the Hardy-Littlewood-Sobolev inequality and the embedding theorem that the functional $J_{\alpha ,\beta ,\gamma }(u)$ is well defined on $H^s({\mathbb {R}}^N)$ and belongs to $C^1(H^s({\mathbb {R}}^N), {\mathbb {R}})$. Set

$$\begin{aligned} {\mathcal {N}}_{\alpha ,\beta ,\gamma }:=\{u \in H^s({\mathbb {R}}^N)\setminus \{0\}:\langle J_{\alpha ,\beta ,\gamma }^\prime (u),u\rangle =0\}. \end{aligned}$$

Lemma 1

For $t>0$, let $h(t):=J_{\alpha ,\beta ,\gamma }(tu)$. For each $u \in H^s({\mathbb {R}}^N) \setminus \{0\}$, there exists a unique $t_u>0$ such that $h(t_u)=\max \limits _{t\ge 0}h(t)$, $h^{\prime }(t)>0$ for $0<t<t_u$ and $h^{\prime }(t)<0$ for $t>t_u$. Moreover, $tu \in {\mathcal {N}}_{\alpha ,\beta ,\gamma }$ if and only if $t=t_u$.

Proof

By (2.3), we have

$$\begin{aligned} \left| \int _{{\mathbb {R}}^N}F(u)dx\right| \le \tau \Vert u\Vert ^2+CC_\tau \Vert u\Vert ^p \end{aligned}$$

(2.4)

for all $u \in {\mathbb {R}}$. By virtue of the Hardy-Littlewood-Sobolev inequality one has

$$\begin{aligned} \big |\int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx\big |\le C\Vert |u|^{2_{\mu ,s}^*}\Vert _{\frac{2N}{2N-\mu }}^2=C\Vert u\Vert _{2_s^*}^{22_{\mu , s}^*}\le C\Vert u\Vert ^{22_{\mu , s}^*}.\nonumber \\ \end{aligned}$$

(2.5)

Consequently, it follows from (2.4)-(2.5) that

$$\begin{aligned} \begin{aligned} h(t)=&J_{\alpha ,\beta ,\gamma }(tu)\ge \frac{1}{2}\min \{1,\alpha _{\min }\}t^2\Vert u\Vert ^2-\beta (\tau t^2\Vert u\Vert ^2+CC_\tau t^p \Vert u\Vert ^p)\\&-C \gamma t^{22_{\mu , s}^*}\Vert u\Vert ^{22_{\mu , s}^*}>0 \end{aligned} \end{aligned}$$

for small $\tau >0$ and $t>0$. Moreover,

$$\begin{aligned} \begin{aligned} h^\prime (t)=&\langle J_{\alpha ,\beta ,\gamma }^\prime (tu),u\rangle \ge \min \{1,\alpha _{\min }\}t\Vert u\Vert ^2-\beta (\tau t\Vert u\Vert ^2+CC_\tau t^{p-1} \Vert u\Vert ^p)\\&-C \gamma t^{22_{\mu , s}^*-1}\Vert u\Vert ^{22_{\mu , s}^*}>0 \end{aligned} \end{aligned}$$

for small $\tau >0$ and $t>0$. In view of $(f_4)$ we get that

$$\begin{aligned} \begin{aligned} h(t)=&J_{\alpha ,\beta ,\gamma }(tu)\le \frac{1}{2}\max \{1,\alpha _{\max }\}t^2\Vert u\Vert ^2\\&-\frac{\gamma }{22_{\mu ,s}^*}t^{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx\rightarrow -\infty \end{aligned} \end{aligned}$$

as $t\rightarrow +\infty$. Hence h has a positive maximum and there exists $t_u>0$ such that $h^\prime (t_u)=0$ and $h^\prime (t)>0$ for $0<t<t_u$.

We assert that $h^\prime (t)\ne 0$ for all $t>t_u$. Otherwise, we can suppose that there exists $t_u< t_2< +\infty$ such that $h^\prime (t_2)=0$ and $h(t_u)\ge h(t_2)$. By means of $(f_3)$ we obtain that

$$\begin{aligned} \begin{aligned} h(t_2)=&h(t_2)-\frac{t_2}{2}h^\prime (t_2)\\ =&\beta \int _{{\mathbb {R}}^N}[\frac{1}{2}f(t_2u)t_2u-F(t_2u)]dx\\&+\gamma \left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) t_2^{22_{\mu ,s}^*} \int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx\\ >&\beta \int _{{\mathbb {R}}^N}[\frac{1}{2}f(t_uu)t_uu-F(t_uu)]dx\\&+\gamma \left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) t_u^{22_{\mu ,s}^*} \int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx\\ =&h(t_u)-\frac{t_u}{2}h^\prime (t_u)\\ =&h(t_u), \end{aligned} \end{aligned}$$

a contradiction.

Combining the claim with prior arguments, we obtain the first conclusion of (i). The second conclusion is an immediate consequence of the fact that $h^{\prime }(t)=t^{-1}\langle J_{\alpha ,\beta ,\gamma }^{\prime }(tu), tu\rangle$. This completes the proof. $\square$

For any $\rho >0$, set $S_\rho :=\{u \in H^s({\mathbb {R}}^N): \Vert u\Vert =\rho \}$. Then the following lemma holds.

Lemma 2

• (i) There exists $t_0>0$ such that $t_u\ge t_0$ for each $u \in S_1$ and for each compact subset $W\subset S_1$, there exists $C_W>0$ such that $t_u\le C_W$ for all $u \in W$.

• (ii) There exists $\rho >0$ such that

  $$\begin{aligned} m_{\alpha ,\beta ,\gamma }:=\inf \limits _{u \in \mathcal {N}_{\alpha ,\beta ,\gamma }} J_{\alpha ,\beta ,\gamma }(u)\ge \inf \limits _{u \in S_\rho }J_{\alpha ,\beta ,\gamma }(u)>0. \end{aligned}$$

• (iii) There exists $r^*>0$ such that $\Vert u\Vert \ge r^*$ for all $u \in {\mathcal {N}}_{\alpha ,\beta ,\gamma }$.

Proof

(i) Set

$$\begin{aligned} \varSigma (u):=\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}[|x|^{-\mu } *|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*}dx \end{aligned}$$

for $u \in H^s({\mathbb {R}}^N)$ and set

$$\begin{aligned} \begin{aligned} h(t):=&\varSigma \left( \frac{tu}{\Vert u\Vert }\right) =\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N} [|x|^{-\mu }*|\frac{tu}{\Vert u\Vert }|^{2_{\mu ,s}^*}]|\frac{tu}{\Vert u\Vert }|^{2_{\mu ,s}^*}dx\\ =&\frac{1}{22_{\mu ,s}^*}t^{22_{\mu ,s}^*}\frac{1}{\Vert u\Vert ^{22_{\mu ,s}^*}} \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*}dx \end{aligned} \end{aligned}$$

for $t>0$. Clearly,

$$\begin{aligned} \begin{aligned} h^\prime (t)&=t^{22_{\mu ,s}^*-1}\frac{1}{\Vert u\Vert ^{22_{\mu ,s}^*}}\int _{{\mathbb {R}}^N} [|x|^{-\mu }*|u|^{2_{\mu ,s}^*}]|u|^{2_{\mu ,s}^*}dx\\&=\frac{1}{t}\int _{{\mathbb {R}}^N}[|x|^{-\mu }*|\frac{tu}{\Vert u\Vert }|^{2_{\mu ,s}^*}] |\frac{tu}{\Vert u\Vert }|^{2_{\mu ,s}^*}dx\\&=\frac{22_{\mu ,s}^*}{t}h(t). \end{aligned} \end{aligned}$$

Integrating on $[1,t\Vert u\Vert ]$ with $t>\frac{1}{\Vert u\Vert }$, we have $h(t\Vert u\Vert )\ge h(1)t^{22_{\mu ,s}^*}\Vert u\Vert ^{22_{\mu ,s}^*}$, i.e.,

$$\begin{aligned} \varSigma (tu)\ge \varSigma \left( \frac{u}{\Vert u\Vert }\right) t^{22_{\mu ,s}^*}\Vert u\Vert ^{22_{\mu ,s}^*}:=Ct^{22_{\mu ,s}^*}\Vert u \Vert ^{22_{\mu ,s}^*}. \end{aligned}$$

(2.6)

For $u \in S_1$, by Lemma 1 there exists $t_u>0$ such that $t_uu \in {\mathcal {N}}_{\alpha ,\beta ,\gamma }$. It follows from (2.2) and (2.5) that

$$\begin{aligned} \begin{aligned} 0=&\langle J_{\alpha ,\beta ,\gamma }^\prime (t_uu),t_uu\rangle \\ \ge&\min \{1,\alpha _{\min }\}t_u^2\Vert u\Vert ^2-\beta (\tau t_u^2\Vert u\Vert ^2+CC_\tau t_u^p\Vert u\Vert ^p)-Ct_u^{22_{\mu , s}^*}\Vert u\Vert ^{22_{\mu , s}^*}\\ \ge&\frac{1}{2}\min \{1,\alpha _{\min }\}t_u^2-\beta CC_\tau t_u^p-Ct_u^{22_{\mu , s}^*} \end{aligned} \end{aligned}$$

for $\tau >0$ small, which means that there exists $t_0>0$ such that $t_u\ge t_0$ for all $u \in S_1$. Suppose there exists $\{u_n\}\subset W\subset S_1$ such that $t_n:=t_{u_n}\rightarrow +\infty$ as $n\rightarrow \infty$. Since W is compact, there exists $u \in W$ such that $u_n\rightarrow u$ in $H^s({\mathbb {R}}^N)$. By (2.6) and $(f_4)$,

$$\begin{aligned} \begin{aligned} J_{\alpha ,\beta ,\gamma }(t_nu_n)\le&\frac{1}{2}\max \{1,\alpha _{\max }\}t_n^2\Vert u_n\Vert ^2-\varSigma (t_nu_n)\le \frac{1}{2} \max \{1,\alpha _{\max }\}t_n^2\Vert u_n\Vert ^2\\&-Ct_n^{22_{\mu ,s}^*}\Vert u_n\Vert ^{22_{\mu ,s}^*}\\ \rightarrow&-\infty \end{aligned} \end{aligned}$$

as $n\rightarrow \infty$. Nevertheless, by $(f_3)$ we can see that

$$\begin{aligned} \begin{aligned} J_{\alpha ,\beta ,\gamma }(t_nu_n)=&J_{\alpha ,\beta ,\gamma }(t_nu_n)-\frac{1}{2}\langle J_{\alpha ,\beta ,\gamma }^\prime (t_nu_n),t_nu_n\rangle \\ =&\beta \int _{{\mathbb {R}}^N}[\frac{1}{2}f(t_nu_n)t_nu_n-F(t_nu_n)]dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \gamma t_n^{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u_n^+)^{2_{\mu ,s}^*}](u_n^+)^{2_{\mu ,s}^*}dx\\ \ge&0, \end{aligned} \end{aligned}$$

a contradiction.

(ii) For $u \in S_\rho$ and small $\tau >0$, combining (2.4) with (2.5) we obtain that

$$\begin{aligned} \begin{aligned} J_{\alpha ,\beta ,\gamma }(u)\ge&\frac{1}{2}\min \{1,\alpha _{\min }\}\Vert u\Vert ^2-\beta (\tau \Vert u\Vert ^2+CC_\tau \Vert u\Vert ^p)-C\Vert u\Vert ^{22_{\mu , s}^*}\\ \ge&\frac{1}{8}\Vert u\Vert ^2=\frac{1}{8}\rho ^2>0 \end{aligned} \end{aligned}$$

for small $\rho >0$. Moreover, for every $u \in \mathcal {N}_{\alpha ,\beta ,\gamma }$, there exists $t_0>0$ such that $t_0u \in S_\rho$. Hence

$$\begin{aligned} 0<\frac{1}{8}\rho ^2\le \inf \limits _{u \in S_\rho }J_{\alpha ,\beta ,\gamma }(u) \le J_{\alpha ,\beta ,\gamma }(t_0u)\le \max \limits _{t>0}J_{\alpha ,\beta ,\gamma }(tu)=J_{\alpha ,\beta ,\gamma }(u) \end{aligned}$$

and so $m_{\alpha ,\beta ,\gamma }=\inf \limits _{u \in \mathcal {N}_{\alpha ,\beta ,\gamma }}J_{\alpha ,\beta ,\gamma }(u)\ge \inf \limits _{u \in S_\rho }J_{\alpha ,\beta ,\gamma }(u)>0$.

(iii) Assuming by contradiction that there exists a sequence $\{u_n\}\subset {\mathcal {N}}_{\alpha ,\beta ,\gamma }$ $\subset H^s({\mathbb {R}}^N)\setminus \{0\}$ such that $\Vert u_n\Vert \rightarrow 0$ as $n \rightarrow \infty$. By virtue of (2.2) and (2.5), we can see that

$$\begin{aligned} \begin{aligned} 0=\langle J_{\alpha ,\beta ,\gamma }^\prime (u_n),u_n\rangle \ge&\min \{1,\alpha _{\min }\}\Vert u_n\Vert ^2-\beta (\tau \Vert u_n\Vert ^2+CC_\tau \Vert u_n\Vert ^p)\\&-C \gamma \Vert u_n\Vert ^{22_{\mu , s}^*}\\ \ge&\frac{1}{4}\min \{1,\alpha _{\min }\}\Vert u_n\Vert ^2 \end{aligned} \end{aligned}$$

for small $\tau >0$ and large n, which contradicts with $u_n \in H^s({\mathbb {R}}^N)\setminus \{0\}$. This completes the proof. $\square$

Lemma 3

$J_{\alpha ,\beta ,\gamma }$ is coercive on $\mathcal {N}_{\alpha ,\beta ,\gamma }$, i.e., $J_{\alpha ,\beta ,\gamma }(u)\rightarrow +\infty$ as $u \in \mathcal {N}_{\alpha ,\beta ,\gamma }$ and $\Vert u\Vert \rightarrow \infty$.

Proof

For any $u \in {\mathcal {N}}_{\alpha ,\beta ,\gamma }$, by $(f_3)$ and (2.6) we can conclude that

$$\begin{aligned} \begin{aligned} J_{\alpha ,\beta ,\gamma }(u)=&J_{\alpha ,\beta ,\gamma }(u)-\frac{1}{2}\langle J_{\alpha ,\beta ,\gamma }^\prime (u,u\rangle \\ =&\beta \int _{{\mathbb {R}}^N}\left[ \frac{1}{2}f(u)u-F(u)\right] dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \gamma \int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx\\ \ge&C\Vert u\Vert ^{22_{\mu , s}^*}\rightarrow +\infty \end{aligned} \end{aligned}$$

as $\Vert u\Vert \rightarrow \infty$. This completes the proof. $\square$

Lemma 4

Let ${\mathcal {W}} \subset H^s({\mathbb {R}}^N)\setminus \{0\}$ be a compact subset. Then there exists $r>0$ such that $J_{\alpha ,\beta ,\gamma }(u)<0$ on $({\mathbb {R}}^+\mathcal {W})\setminus B_r$ for each $u \in {\mathcal {W}}$, where ${\mathbb {R}}^+{\mathcal {W}}:=\{tw: t>0, w\in {\mathcal {W}}\}$.

Proof

Without loss of generality, we may assume that $\Vert u\Vert =1$ for every $u \in {\mathcal {W}}$. Arguing by contradiction, suppose there exist $u_n \in {\mathcal {W}}$ and $w_n=t_nu_n$ such that $J_{\alpha ,\beta ,\gamma }(w_n)\ge 0$ and $t_n\rightarrow \infty$ as $n\rightarrow \infty$. Up to a subsequence, we may assume that $u_n\rightarrow u \in S_1=\{u \in H^s({\mathbb {R}}^N): \Vert u\Vert =1\}$ in ${\mathcal {W}}\subset H^s({\mathbb {R}}^N)\setminus \{0\}$. Consequently, it follows from $(f_4)$ and (2.6) that

$$\begin{aligned} \begin{aligned} 0\le&J_{\alpha ,\beta ,\gamma }(w_n)&=J_{\alpha ,\beta ,\gamma }(t_nu_n)\le \frac{1}{2}\max \{1,\alpha _{\max }\}t_n^2\Vert u_n\Vert ^2-Ct_n^{22_{\mu , s}^*}\Vert u_n\Vert ^{22_{\mu , s}^*}\\ \rightarrow&-\infty \end{aligned} \end{aligned}$$

as $n \rightarrow \infty$, a contradiction. This completes the proof. $\square$

Obviously, $J_{\alpha ,\beta ,\gamma }$ exhibits the mountain pass geometry.

Lemma 5

The functional $J_{\alpha ,\beta ,\gamma }$ satisfies the following conditions:

• (i) there exist $\delta , \rho >0$ such that $J_{\alpha ,\beta ,\gamma }(u)\ge \delta$ for $\Vert u\Vert =\rho$;

• (ii) there exists an $e \in H^s({\mathbb {R}}^N)$ with $\Vert e\Vert > \rho$ such that $J_{\alpha ,\beta ,\gamma }(e)<0$.

Combining with the Mountain Pass Theorem without (PS) condition ( [28]) and the characterization of minimax value, there exists a $(PS)_{m_{\alpha ,\beta ,\gamma }}$ sequence $\{u_n\}\subset H^s({\mathbb {R}}^N)$ such that $J_{\alpha ,\beta ,\gamma }(u_n)\rightarrow m_{\alpha ,\beta ,\gamma }$ and $J_{\alpha ,\beta ,\gamma }^\prime (u_n)\rightarrow 0$ in $H^{-s}({\mathbb {R}}^N)$ at the minimax level

$$\begin{aligned} m_{\alpha ,\beta ,\gamma }=\inf \limits _{g \in \varGamma }\sup \limits _{t \in [0,1]}J_{\alpha ,\beta ,\gamma }(g(t)), \end{aligned}$$

where

$$\begin{aligned} \varGamma :=\{g \in C([0,1],H^s({\mathbb {R}}^N)):g(0)=0, J_{\alpha ,\beta ,\gamma }(g(1))<0\}. \end{aligned}$$

Moreover,

$$\begin{aligned} m_{\alpha ,\beta ,\gamma }=\inf \limits _{u \in H^s({\mathbb {R}}^N)\backslash \{0\}}\max \limits _{t\ge 0}J_{\alpha ,\beta ,\gamma }(tu)>0. \end{aligned}$$

Lemma 6

Let $\alpha \in [\alpha _{\min }, \alpha _{\infty }]$, $\beta \in (\beta _{\infty }, \beta _{\max }]$ and $\gamma \in [\gamma _{\min }, \gamma _{\max }]$, then

$$\begin{aligned} m_{\alpha ,\beta ,\gamma }<\frac{1}{\gamma ^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )} \cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}, \end{aligned}$$

and Eq. (2.1) admits a positive ground state solution u satisfying $J_{\alpha ,\beta ,\gamma }(u)=m_{\alpha ,\beta ,\gamma }$ and $u \in {\mathcal {N}}_{\alpha ,\beta ,\gamma }$.

Proof

By [4, 10] we easily know

$$\begin{aligned} m_{\alpha ,\beta ,\gamma }<\frac{1}{\gamma ^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )}\cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}. \end{aligned}$$

By Lemma 5, let $\{u_n\}\subset H^s({\mathbb {R}}^N)$ be a $(PS)_{m_{\alpha ,\beta ,\gamma }}$ sequence for $J_{\alpha ,\beta ,\gamma }$, then by Lemma 3 we know that $\{u_n\}$ is bounded in $H^s({\mathbb {R}}^N)$. By using of the fact that

$$\begin{aligned} (u-v)(u^--v^-)\ge |u^--v^-|^2 \end{aligned}$$

for any $u, v \in {\mathbb {R}}$, we can prove that

$$\begin{aligned} \begin{aligned} o(1)=&\langle J_{\alpha ,\beta ,\gamma }^\prime (u_n),u_n^-\rangle \ge \frac{1}{2}C_{N,s}\int _{{\mathbb {R}}^{2N}}\frac{|u_n^-(x)-u_n^-(y)|^2}{|x-y|^{N+2s}}dxdy \\ +&\alpha _{\min }\int _{{\mathbb {R}}^N}|u_n^-|^2dx \ge \min \{1,\alpha _{\min }\}\Vert u_n^-\Vert ^2, \end{aligned} \end{aligned}$$

i.e., $\Vert u_n^-\Vert \rightarrow 0$, so we can assume that $u_n\ge 0, \ \forall n \in {\mathbb {N}}$. We assert that there exist a sequence $\{y_n\}\subset {\mathbb {R}}^N$ and constants $R, \ \sigma >0$ such that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\int _{B_R(y_n)}u_n^2dx\ge \sigma . \end{aligned}$$

(2.7)

Otherwise, by virtue of Lemma 1.21 in [28], we have $u_n\rightarrow 0$ in $L^t({\mathbb {R}}^N)$ for $2<t<2_s^*$. Consequently, by (2.2)-(2.3) we know that

$$\begin{aligned} \int _{{\mathbb {R}}^N}F(u_n)dx\rightarrow 0 \ \hbox {and} \int _{{\mathbb {R}}^N}f(u_n)u_ndx\rightarrow 0 \end{aligned}$$

as $n\rightarrow \infty$. As a consequence,

$$\begin{aligned} o(1)=\Vert u_n\Vert _\alpha ^2-\gamma \int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u_n^+)^{2_{\mu ,s}^*}] (u_n^+)^{2_{\mu ,s}^*}dx. \end{aligned}$$

Assume that $\Vert u_n\Vert _\alpha ^2\rightarrow l$ as $n\rightarrow \infty$. Then $\gamma \int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u_n^+)^{2_{\mu ,s}^*}](u_n^+)^{2_{\mu ,s}^*}dx\rightarrow l$ as $n\rightarrow \infty$. Consequently, by the fact that

$$\begin{aligned} \begin{aligned} m_{\alpha ,\beta ,\gamma }+o(1)=&J_{\alpha ,\beta ,\gamma }(u_n)\\ =&\frac{1}{2}\Vert u_n\Vert _\alpha ^2 -\frac{\gamma }{22_{\mu ,s}}\int _{{\mathbb {R}}^N}[|x|^{-\mu }*(u_n^+)^{2_{\mu ,s}^*}] (u_n^+)^{2_{\mu ,s}^*}dx\\&-\beta \int _{{\mathbb {R}}^N}F(u_n)dx, \end{aligned} \end{aligned}$$

we deduce that

$$\begin{aligned} 0<m_{\alpha ,\beta ,\gamma }=\frac{1}{2}l-\frac{1}{22_{\mu ,s}}l, \end{aligned}$$

(2.8)

which implies that $l>0$. Hence, by the definition of $S_H$ we have

$$\begin{aligned} S_H\le \frac{\Vert u_n\Vert _\alpha ^2}{\big (\int _{{\mathbb {R}}^N}[|x|^{-\mu }*|u_n|^{2_{\mu ,s}^*}] |u_n|^{2_{\mu ,s}^*}dx\big )^{\frac{N-2s}{2N-\mu }}} \rightarrow \frac{l}{\left( \frac{l}{\gamma }\right) ^{\frac{N-2s}{2N-\mu }}} =\gamma ^{\frac{N-2s}{2N-\mu }}\cdot l^{\frac{N+2s-\mu }{2N-\mu }},\nonumber \\ \end{aligned}$$

(2.9)

as $n \rightarrow \infty$. It follows from (2.8) and (2.9) that

$$\begin{aligned} m_{\alpha ,\beta ,\gamma }=\frac{1}{2}l-\frac{1}{22_{\mu ,s}}l \ge \frac{1}{\gamma ^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )} \cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}, \end{aligned}$$

a contradiction. Therefore, (2.7) holds. Set ${\bar{u}}_n(\cdot )=u_n(\cdot +y_n)$. Up to a subsequence, there exists ${\bar{u}} \in H^s({\mathbb {R}}^N)$ such that ${\bar{u}}_n\rightharpoonup {\bar{u}}$ in $H^s({\mathbb {R}}^N)$, ${\bar{u}}_n\rightarrow {\bar{u}}$ in $L_{loc}^t({\mathbb {R}}^N)$ for $2\le t< 2_s^*$ and ${\bar{u}}_n(x)\rightarrow {\bar{u}}(x)$ a.e. on ${\mathbb {R}}^N$. By (2.7) we have ${\bar{u}}\ne 0$. Using a standard argument we can conclude that $J_{\alpha ,\beta ,\gamma }^\prime ({\bar{u}})=0$, and so ${\bar{u}} \in {\mathcal {N}}_{\alpha ,\beta ,\gamma }$. Indeed, since $J_{\alpha ,\beta ,\gamma }$ is invariant under translations of the form $u\mapsto u(\cdot + k)$ with $k \in {\mathbb {R}}^N$, we may assume that $\{{\bar{u}}_n\} \subset H^s({\mathbb {R}}^N)$ is a $(PS)_{m_{\alpha ,\beta ,\gamma }}$ sequence for $J_{\alpha ,\beta ,\gamma }$. Consequently, for all $\varphi \in C_0^{\infty }({\mathbb {R}}^N)$,

$$\begin{aligned} \begin{aligned} o(1)=&\langle J_{\alpha ,\beta ,\gamma }^\prime ({\bar{u}}_n), \varphi \rangle \\ =&\int _{{\mathbb {R}}^N}\varphi (-\varDelta )^s{\bar{u}}_n dx+\alpha \int _{{\mathbb {R}}^N}{\bar{u}}_n \varphi dx-\beta \int _{{\mathbb {R}}^N}f({\bar{u}}_n)\varphi dx\\&-\gamma \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|{\bar{u}}_n|^{2_{\mu ,s}^*}] |{\bar{u}}_n|^{2_{\mu ,s}^*-2}{\bar{u}}_n \varphi dx. \end{aligned} \end{aligned}$$

Since ${\bar{u}}_n\rightharpoonup {\bar{u}}$ in $H^s({\mathbb {R}}^N)$,

$$\begin{aligned} \int _{{\mathbb {R}}^N}\varphi (-\varDelta )^s{\bar{u}}_n dx\rightarrow \int _{{\mathbb {R}}^N}\varphi (-\varDelta )^s{\bar{u}}dx \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}{\bar{u}}_n \varphi dx\rightarrow \int _{{\mathbb {R}}^N}{\bar{u}} \varphi dx \end{aligned}$$

as $n \rightarrow \infty$. By ${\bar{u}}_n\rightarrow {\bar{u}}$ in $L_{loc}^t({\mathbb {R}}^N)$ for $2\le t< 2_s^*$, together with (2.2) we get

$$\begin{aligned} \int _{{\mathbb {R}}^N}f({\bar{u}}_n)\varphi dx \rightarrow \int _{{\mathbb {R}}^N}f({\bar{u}})\varphi dx \end{aligned}$$

as $n \rightarrow \infty$. Moreover,

$$\begin{aligned} \int _{{\mathbb {R}}^N}\big ||{\bar{u}}_n|^{2_{\mu ,s}^*}\big |^{\frac{2N}{2N-\mu }}dx =\int _{{\mathbb {R}}^N}|{\bar{u}}_n|^{\frac{2N}{N-2s}}dx\le C\Vert {\bar{u}}_n\Vert ^{2_s^*}\le C. \end{aligned}$$

Thereby, by the Hölder inequality and [19], we conclude that

$$\begin{aligned}&\begin{aligned}&\int _{{\mathbb {R}}^N}\big |[|x|^{-\mu }*|{\bar{u}}_n|^{2_{\mu ,s}^*}]| {\bar{u}}_n|^{2_{\mu ,s}^*-2}{\bar{u}}_n \big |^{\frac{2N}{N+2s}}dx\\ =&\int _{{\mathbb {R}}^N}\big |[|x|^{-\mu }*|{\bar{u}}_n|^{2_{\mu ,s}^*}]|^{\frac{2N}{N+2s}} \big |{\bar{u}}_n\big |^{(2_{\mu ,s}^*-1)\frac{2N}{N+2s}}dx \\ \le&\left( \int _{{\mathbb {R}}^N}\big ||x|^{-\mu }*|{\bar{u}}_n|^{2_{\mu ,s}^*} \big |^{\frac{2N}{N+2s}\cdot \frac{N+2s}{\mu }}dx\right) ^{\frac{\mu }{N+2s}}\\&\times \, \left( \int _{{\mathbb {R}}^N}\big |{\bar{u}}_n\big |^{(2_{\mu ,s}^*-1)\cdot \frac{2N}{N+2s}\cdot \frac{N+2s}{N+2s-\mu }}dx\right) ^{\frac{N+2s-\mu }{N+2s}} \end{aligned} \\&\begin{aligned} =&\left( \int _{{\mathbb {R}}^N}\big ||x|^{-\mu }*|{\bar{u}}_n|^{2_{\mu ,s}^*} \big |^{\frac{2N}{\mu }}dx\right) ^{\frac{\mu }{N+2s}}\cdot \left( \int _{{\mathbb {R}}^N}\big |{\bar{u}}_n\big |^{\frac{2N}{N-2s}}dx\right) ^{\frac{N+2s -\mu }{N+2s}}\\ \le&C \left( \int _{{\mathbb {R}}^N}\big |{\bar{u}}_n\big |^{2_{\mu ,s}^*\cdot \frac{2N}{2N-\mu }}dx\right) ^{\frac{2N-\mu }{N+2s}}\cdot \left( \int _{{\mathbb {R}}^N}\big |{\bar{u}}_n\big |^{\frac{2N}{N-2s}}dx\right) ^{\frac{N+2s -\mu }{N+2s}}\\ =&C\left( \int _{{\mathbb {R}}^N}\big |{\bar{u}}_n\big |^{2_s^*}dx \right) ^{\frac{3N+2s-2\mu }{N+2s}}\le C\Vert {\bar{u}}_n\Vert ^{2_s^*\cdot \frac{3N+2s-2\mu }{N+2s}}\le C. \end{aligned} \end{aligned}$$

Then we may assume that

$$\begin{aligned}{}[|x|^{-\mu }*|{\bar{u}}_n|^{2_{\mu ,s}^*}]|{\bar{u}}_n|^{2_{\mu ,s}^*-2}{\bar{u}}_n \rightharpoonup [|x|^{-\mu }*|{\bar{u}}|^{2_{\mu ,s}^*}]|{\bar{u}}|^{2_{\mu ,s}^*-2}{\bar{u}} \end{aligned}$$

in $L^{\frac{2N}{N+2s}}({\mathbb {R}}^N)$. Hence,

$$\begin{aligned} \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|{\bar{u}}_n|^{2_{\mu ,s}^*}] |{\bar{u}}_n|^{2_{\mu ,s}^*-2}{\bar{u}}_n\varphi dx \rightarrow \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|{\bar{u}}|^{2_{\mu ,s}^*}] |{\bar{u}}|^{2_{\mu ,s}^*-2}{\bar{u}}\varphi dx \end{aligned}$$

as $n\rightarrow \infty$. It follows that

$$\begin{aligned} \begin{aligned} 0=&\int _{{\mathbb {R}}^N}\varphi (-\varDelta )^s{\bar{u}}dx+\alpha \int _{{\mathbb {R}}^N}{\bar{u}}\varphi dx-\beta \int _{{\mathbb {R}}^N}f({\bar{u}})\varphi dx\\&-\gamma \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|{\bar{u}}|^{2_{\mu ,s}^*}]| {\bar{u}}|^{2_{\mu ,s}^*-2}{\bar{u}}\varphi dx. \end{aligned} \end{aligned}$$

For any $\varphi \in H^s({\mathbb {R}}^N)$, there exists a sequence $\{\varphi _n\} \subset C_0^{\infty }({\mathbb {R}}^N)$ such that $\varphi _n \rightarrow \varphi$ in $H^s({\mathbb {R}}^N)$. As a consequence,

$$\begin{aligned} \begin{aligned} 0=&\int _{{\mathbb {R}}^N}\varphi _n(-\varDelta )^s{\bar{u}}dx+\alpha \int _{{\mathbb {R}}^N}{\bar{u}}\varphi _n dx-\beta \int _{{\mathbb {R}}^N}f({\bar{u}})\varphi _n dx\\&-\gamma \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|{\bar{u}}|^{2_{\mu ,s}^*}]| {\bar{u}}|^{2_{\mu ,s}^*-2}{\bar{u}}\varphi _n dx. \end{aligned} \end{aligned}$$

Let $n\rightarrow \infty$, then

$$\begin{aligned} \begin{aligned} 0=&\int _{{\mathbb {R}}^N}\varphi (-\varDelta )^s{\bar{u}}dx+\alpha \int _{{\mathbb {R}}^N}{\bar{u}}\varphi dx-\beta \int _{{\mathbb {R}}^N}f({\bar{u}})\varphi dx\\&-\gamma \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|{\bar{u}}|^{2_{\mu ,s}^*}] |{\bar{u}}|^{2_{\mu ,s}^*-2}{\bar{u}}\varphi dx, \end{aligned} \end{aligned}$$

i.e., $\langle J_{\alpha ,\beta ,\gamma }^\prime ({\bar{u}}), \varphi \rangle =0$ for all $\varphi \in H^s({\mathbb {R}}^N)$. And so $J_{\alpha ,\beta ,\gamma }^\prime ({\bar{u}})=0$. Hence by Fatou Lemma and $(f_3)$ we deduce that

$$\begin{aligned} \begin{aligned}&m_{\alpha ,\beta ,\gamma }\le \max \limits _{t\ge 0}J_{\alpha ,\beta ,\gamma }(t{\bar{u}})=J_{\alpha ,\beta ,\gamma }({\bar{u}}) =J_{\alpha ,\beta ,\gamma }({\bar{u}})-\frac{1}{2}\langle J_{\alpha ,\beta ,\gamma }^\prime ({\bar{u}}),{\bar{u}}\rangle \\ =&\beta \int _{{\mathbb {R}}^N}[\frac{1}{2}f({\bar{u}}){\bar{u}}-F({\bar{u}})]dx +\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \gamma \int _{{\mathbb {R}}^N} [|x|^{-\mu }*({\bar{u}}^+)^{2_{\mu ,s}^*}]({\bar{u}}^+)^{2_{\mu ,s}^*}dx\\ \le&\beta \liminf \limits _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}[\frac{1}{2}f({\bar{u}}_n){\bar{u}}_n-F({\bar{u}}_n)]dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \gamma \liminf \limits _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}[|x|^{-\mu }*({\bar{u}}_n^+)^{2_{\mu ,s}^*}] ({\bar{u}}_n^+)^{2_{\mu ,s}^*}dx\\ \le&\liminf \limits _{n\rightarrow \infty }[J_{\alpha ,\beta ,\gamma }({\bar{u}}_n)-\frac{1}{2}\langle J_{\alpha ,\beta ,\gamma }^\prime ({\bar{u}}_n),{\bar{u}}_n\rangle ]=m_{\alpha ,\beta , \gamma }, \end{aligned} \end{aligned}$$

and so $J_{\alpha ,\beta ,\gamma }({\bar{u}})=m_{\alpha ,\beta ,\gamma }$. Again by virtue of the fact that

$$\begin{aligned} (u-v)(u^--v^-)\ge |u^--v^-|^2 \end{aligned}$$

for any $u, v \in {\mathbb {R}}$, we can derive that ${\bar{u}}$ is positive. This completes the proof. $\square$

Lemma 7

For $i=1,2$, let $\alpha _i \in [\alpha _{\min },\alpha _{\infty }]$, $\beta _i \in (\beta _{\infty },\beta _{\max }]$, $\gamma _i \in [\gamma _{\min },\gamma _{\max }]$. If $\min \{\alpha _2-\alpha _1,\beta _1-\beta _2,\gamma _1-\gamma _2\}\ge 0$, then $m_{\alpha _1,\beta _1,\gamma _1}\le m_{\alpha _2,\beta _2,\gamma _2}$. Moreover, if additionally $\max \{\alpha _2-\alpha _1,\beta _1-\beta _2,\gamma _1-\gamma _2\}> 0$, then $m_{\alpha _1,\beta _1,\gamma _1}< m_{\alpha _2,\beta _2,\gamma _2}$.

Proof

By Lemma 6, let u be a positive solution of (2.1) with coefficients $\alpha _2,\beta _2,\gamma _2$ such that $J_{\alpha _2,\beta _2,\gamma _2}(u)=m_{\alpha _2,\beta _2,\gamma _2}$ and $u \in {\mathcal {N}}_{\alpha _2,\beta _2,\gamma _2}$. Then arguing as in Lemma 1 by $(f_1)-(f_4)$ we can deduce that $J_{\alpha _2,\beta _2,\gamma _2}(u)=\max \limits _{t\ge 0}J_{\alpha _2,\beta _2,\gamma _2}(tu)$ and there exists $t_0>0$ such that $t_0u \in {N}_{\alpha _1,\beta _1,\gamma _1}$ and

$$\begin{aligned} J_{\alpha _1,\beta _1,\gamma _1}(t_0u) = \max \limits _{t\ge 0}J_{\alpha _1,\beta _1,\gamma _1}(tu). \end{aligned}$$

Consequently, if $\min \{\alpha _2-\alpha _1,\beta _1-\beta _2,\gamma _1-\gamma _2\}\ge 0$,

$$\begin{aligned} \begin{aligned}&m_{\alpha _1,\beta _1,\gamma _1}\le \max \limits _{t\ge 0}J_{\alpha _1,\beta _1,\gamma _1}(tu)=J_{\alpha _1,\beta _1,\gamma _1}(t_0u)\\ =&J_{\alpha _2,\beta _2,\gamma _2}(t_0u)+\frac{\alpha _1-\alpha _2}{2}t_0^2 \int _{{\mathbb {R}}^N}u^2dx-(\beta _1-\beta _2)\int _{{\mathbb {R}}^N}F(t_0u)dx\\&-\frac{\gamma _1-\gamma _2}{22_{\mu ,s}^*}t_0^{22_{\mu ,s}^*} \int _{{\mathbb {R}}^N}[|x|^{-\mu }*({\bar{u}}^+)^{2_{\mu ,s}^*}] ({\bar{u}}^+)^{2_{\mu ,s}^*}dx\\ \le&J_{\alpha _2,\beta _2,\gamma _2}(t_0u) \le \max \limits _{t\ge 0}J_{\alpha _2,\beta _2,\gamma _2}(tu)=J_{\alpha _2,\beta _2,\gamma _2}(u) =m_{\alpha _2,\beta _2,\gamma _2}. \end{aligned} \end{aligned}$$

If additionally $\max \{\alpha _2-\alpha _1,\beta _1-\beta _2,\gamma _1-\gamma _2\}> 0$, the above proof implies that $m_{\alpha _1,\beta _1,\gamma _1}< m_{\alpha _2,\beta _2,\gamma _2}$. This completes the proof. $\square$

3 Auxiliary problem

In what follows, we introduce some auxiliary problems for Eq. (1.4). Without loss of generality, we may assume that $x_P=0 \in {\mathcal {C}}_P$ in (1.2) or $x_P=0 \in {\mathcal {V}}\cap {\mathcal {P}}\cap {\mathcal {Q}}$ if ${\mathcal {V}}\cap {\mathcal {P}}\cap {\mathcal {Q}}\not =\emptyset$. Consequently, by (1.2) we set

$$\begin{aligned} e:=V(0)\le V(x) \ \ \hbox {for} \ \ \hbox {all} \ |x|\ge R. \end{aligned}$$

(3.1)

For any $a \in [\alpha _{\min },\alpha _{\infty }]$, $b \in (\beta _{\infty }, \beta _{\max }]$ and $d \in [\gamma _{\min }, \gamma _{\max }]$, by Lemma 6 one has

$$\begin{aligned} m_{a,b,d}<\frac{1}{\gamma ^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )}\cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}. \end{aligned}$$

Define the truncated potentials by

$$\begin{aligned} V_\varepsilon ^a(x):=\max \{a,V(\varepsilon x)\}, \ P_\varepsilon ^b(x):=\min \{b,P(\varepsilon x)\}, \ Q_\varepsilon ^d(x):=\min \{d,Q(\varepsilon x)\} \end{aligned}$$

and consider the auxiliary problem

$$\begin{aligned} (-\varDelta )^su+V_\varepsilon ^a(x)u=P_\varepsilon ^b(x)f(u)+Q_\varepsilon ^d(x) [|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*-2}u^+, \ x \in {\mathbb {R}}^N,\nonumber \\ \end{aligned}$$

(3.2)

whose energy functional is

$$\begin{aligned} \begin{aligned} I_\varepsilon ^{a,b,d}(u)=&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}} (\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}V_\varepsilon ^a(x)u^2dx-\int _{{\mathbb {R}}^N} P_\varepsilon ^b(x)F(u)dx\\&-\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}Q_\varepsilon ^d(x)[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx. \end{aligned} \end{aligned}$$

Set

$$\begin{aligned} {\mathcal {N}}_\varepsilon ^{a,b,d}=\{u \in H^s({\mathbb {R}}^N)\backslash \{0\}:\langle (I_\varepsilon ^{a,b,d})^\prime (u),u\rangle =0\} \end{aligned}$$

and

$$\begin{aligned} c_\varepsilon ^{a,b,d}:=\inf \limits _{u \in {\mathcal {N}}_\varepsilon ^{a,b,d}}I_\varepsilon ^{a,b,d}(u). \end{aligned}$$

Lemma 8

• (i) $m_{a,b,d}\le c_\varepsilon ^{a,b,d}$.

• (ii) Let u be a solution of (2.1) with coefficients $\alpha :=V^a(0)=\max \{a,V(0)\}$, $\beta :=P^b(0)=\min \{b,P(0)\}$ and $\gamma :=Q^d(0)=\min \{d,Q(0)\}$ such that

  $$\begin{aligned} J_{V^a(0),P^b(0),Q^d(0)}(u)=m_{V^a(0),P^b(0),Q^d(0)}. \end{aligned}$$

  Then

  $$\begin{aligned} \limsup \limits _{\varepsilon \rightarrow 0}c_\varepsilon ^{a,b,d}\le m_{V^a(0),P^b(0),Q^d(0)}. \end{aligned}$$

Proof

• (i) It is easy to see that

  $$\begin{aligned} \begin{aligned} I_\varepsilon ^{a,b,d}(u)=&J_{a,b,d}(u)+\frac{1}{2}\int _{{\mathbb {R}}^N} [V_\varepsilon ^a(x)-a]u^2dx +\int _{{\mathbb {R}}^N}[b-P_\varepsilon ^b(x)]F(u)dx\\&+\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}[d-Q_\varepsilon ^d(x)][|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx\ge J_{a,b,d}(u). \end{aligned} \end{aligned}$$

  Therefore, for any $u \in H^s({\mathbb {R}}^N)\backslash \{0\}$,

  $$\begin{aligned} m_{a,b,d}\le \max \limits _{t\ge 0}J_{a,b,d}(tu)\le \max \limits _{t\ge 0}I_\varepsilon ^{a,b,d}(tu), \end{aligned}$$

  which implies that

  $$\begin{aligned} m_{a,b,d}\le \inf \limits _{u \in H^s({\mathbb {R}}^N)\backslash \{0\}}\max \limits _{t\ge 0} I_\varepsilon ^{a,b,d}(tu) =c_\varepsilon ^{a,b,d}. \end{aligned}$$

• (ii) By Lemma 6, let u be a positive solution of problem (2.1) with coefficients $\alpha :=V^a(0)$, $\beta :=P^b(0)$ and $\gamma :=Q^d(0)$ such that $J_{V^a(0),P^b(0),Q^d(0)}(u)=m_{V^a(0),P^b(0),Q^d(0)}$ and $u \in {\mathcal {N}}_{V^a(0),P^b(0),Q^d(0)}$. Then again arguing as in Lemma 1 by $(f_1)-(f_4)$, there exists a unique $t_\varepsilon :=t_\varepsilon (u)>0$ such that $t_\varepsilon u \in {\mathcal {N}}_\varepsilon ^{a,b,d}$. Hence

  $$\begin{aligned} 0<c_\varepsilon ^{a,b,d}\le I_\varepsilon ^{a,b,d}(t_\varepsilon u) =\max \limits _{t\ge 0}I_\varepsilon ^{a,b,d}(tu). \end{aligned}$$

  Taking into account the boundedness of V, P, Q and $(f_4)$ we can deduce that

  $$\begin{aligned} \begin{aligned} I_\varepsilon ^{a,b,d}(tu)=&\frac{1}{2}t^2\int _{{\mathbb {R}}^N}|\xi |^{2s} |{\hat{u}}(\xi )|^2d\xi +\frac{1}{2}t^2\int _{{\mathbb {R}}^N}V_\varepsilon ^a(x)u^2dx\\&-\int _{{\mathbb {R}}^N} P_\varepsilon ^b(x)F(tu)dx\\&-\frac{1}{22_{\mu ,s}^*}t^{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}Q_\varepsilon ^d(x) [|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx\\ \le&C_1t^2-C_2t^{22_{\mu ,s}^*}, \end{aligned} \end{aligned}$$

which yields that there exists $T>0$ independent of $\varepsilon$ such that $I_\varepsilon ^{a,b,d}(tu)<0$ for $t\ge T$. Consequently, $t_\varepsilon <T$ and we may assume that $t_\varepsilon \rightarrow t_0$ as $\varepsilon \rightarrow 0$. Combining with the continuity and boundedness of V, P, Q, by virtue of Lebesgue dominated convergence theorem we obtain

$$\begin{aligned} \int _{{\mathbb {R}}^N}[V_\varepsilon ^a(x)-V^a(0)]|t_\varepsilon u|^2dx\rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}[P^b(0)-P_\varepsilon ^b(x)]F(t_\varepsilon u)dx\rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}[Q^d(0)-Q_\varepsilon ^d(x)][|x|^{-\mu }*(t_\varepsilon u^+)^{2_{\mu ,s}^*}](t_\varepsilon u^+)^{2_{\mu ,s}^*}dx\rightarrow 0 \end{aligned}$$

as $\varepsilon \rightarrow 0$. Consequently,

$$\begin{aligned} \begin{aligned} I_\varepsilon ^{a,b,d}(t_\varepsilon u) =&J_{V^a(0),P^b(0),Q^d(0)}(t_\varepsilon u)+\frac{1}{2}\int _{{\mathbb {R}}^N}[V_\varepsilon ^a(x)-V^a(0)]|t_\varepsilon u|^2dx\\&+\int _{{\mathbb {R}}^N}[P^b(0)-P_\varepsilon ^b(x)]F(t_\varepsilon u)dx\\&+\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}[Q^d(0)-Q_\varepsilon ^d(x)] [|x|^{-\mu }*(t_\varepsilon u^+)^{2_{\mu ,s}^*}](t_\varepsilon u^+)^{2_{\mu ,s}^*}dx\\ =&J_{V^a(0),P^b(0),Q^d(0)}(t_\varepsilon u)+o_\varepsilon (1). \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} \limsup \limits _{\varepsilon \rightarrow 0}c_\varepsilon ^{a,b,d}\le&\limsup \limits _{\varepsilon \rightarrow 0}I_\varepsilon ^{a,b,d}(t_\varepsilon u)=\limsup \limits _{\varepsilon \rightarrow 0}[J_{V^a(0),P^b(0),Q^d(0)}(t_\varepsilon u)+o_\varepsilon (1)]\\ =&J_{V^a(0),P^b(0),Q^d(0)}(t_0u)\le J_{V^a(0),P^b(0),Q^d(0)}(u)\\ =&m_{V^a(0),P^b(0),Q^d(0)}. \end{aligned} \end{aligned}$$

This completes the proof. $\square$

It is not difficult to see that the functional $I_\varepsilon$ possesses a Mountain Pass level defined by

$$\begin{aligned} c_\varepsilon :=\inf \limits _{u \in H^s({\mathbb {R}}^N)\backslash \{0\}} \max \limits _{t\ge 0}I_\varepsilon (tu). \end{aligned}$$

Moreover, there exists some $c>0$ independent of $\varepsilon$ such that $c_\varepsilon \ge c$.

Lemma 9

$\limsup \limits _{\varepsilon \rightarrow 0}c_\varepsilon \le m_{e,\beta _{{\mathcal {Q}}},\gamma _{\max }}$, where e comes from (3.1).

Proof

Take $a=\alpha _{\min }$, $b=\beta _{\max }$ and $d=\gamma _{\max }$. Then

$$\begin{aligned} V_\varepsilon ^a(x)=V(\varepsilon x), \ P_\varepsilon ^b(x):=P(\varepsilon x), \ Q_\varepsilon ^d(x)=Q(\varepsilon x). \end{aligned}$$

Hence the fact that $I_\varepsilon ^{a,b,d}=I_\varepsilon$ implies that $c_\varepsilon ^{a,b,d}=c_\varepsilon$. Noting that $0 \in {\mathcal {C}}_P$, by Lemma 8 (ii) we conclude that

$$\begin{aligned} \limsup \limits _{\varepsilon \rightarrow 0}c_\varepsilon =\limsup \limits _{\varepsilon \rightarrow 0}c_\varepsilon ^{a,b,d} \le m_{V^a(0),P^b(0),Q^d(0)}=m_{e,\beta _{\mathcal {Q}},\gamma _{\max }}. \end{aligned}$$

This completes the proof. $\square$

Finally, we may only truncate the potentials V(x) and P(x) with $a=e$ and $b \in (\beta _{\infty },\beta _{\mathcal {Q}})$. Simultaneously, we define the truncated energy functional by

$$\begin{aligned} \begin{aligned} I_\varepsilon ^{e,b}(u)=&\frac{1}{2} \int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi +\frac{1}{2} \int _{{\mathbb {R}}^N}V_\varepsilon ^e(x)u^2dx -\int _{{\mathbb {R}}^N}P_\varepsilon ^b(x)F(u)dx\\&-\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx. \end{aligned} \end{aligned}$$

Set ${\mathcal {N}}_\varepsilon ^{e,b}:=\{\langle (I_\varepsilon ^{e,b})^\prime (u),u\rangle =0\}$ and $c_\varepsilon ^{e,b}:=\inf \limits _{u \in \mathcal {N}_\varepsilon ^{e,b}}I_\varepsilon ^{e,b}(u)$.

Lemma 10

$c_\varepsilon ^{e,b}\ge m_{e,b,\gamma _{\max }}$.

Proof

Similarly,

$$\begin{aligned} \begin{aligned} I_\varepsilon ^{e,b}(u)=&J_{e,b,\gamma _{\max }}(u) +\frac{1}{2}\int _{{\mathbb {R}}^N}[V_\varepsilon ^e(x)-e]u^2dx +\int _{{\mathbb {R}}^N}[b-P_\varepsilon ^b(x)]F(u)dx\\&+\frac{1}{22_{\mu ,s}^*} \int _{{\mathbb {R}}^N}[\gamma _{\max }\! - Q(\varepsilon x)] [|x|^{-\mu }*(u^+)^{2_{\mu ,s}^*}](u^+)^{2_{\mu ,s}^*}dx \ge J_{e,b,\gamma _{\max }}(u). \end{aligned} \end{aligned}$$

Consequently,

$$\begin{aligned} \inf \limits _{u \in H^s({\mathbb {R}}^N)\backslash \{0\}}\max \limits _{t\ge 0}I_\varepsilon ^{e,b}(tu)\ge \inf \limits _{u \in H^s({\mathbb {R}}^N)\backslash \{0\}}\max \limits _{t\ge 0}J_{e,b,\gamma _{\max }}(tu), \end{aligned}$$

which indicates that the conclusion holds. This completes the proof. $\square$

Arguing as in Lemmas 1, 2 and 4, we can conclude that the following Lemmas 11-13 hold.

Lemma 11

For each $u \in H^s({\mathbb {R}}^N)\setminus \{0\}$, there exists a unique $t_u>0$ such that $h(t_u)=\max \limits _{t\ge 0}h(t)$, $h^{\prime }(t)>0$ for $0<t<t_u$ and $h^{\prime }(t)<0$ for $t>t_u$. Moreover, $tu \in {\mathcal {N}}_\varepsilon$ if and only if $t=t_u$. Here $h(t):=I_\varepsilon (tu)$.

Lemma 12

For any $\varepsilon >0$ fixed,

• (i) there is a constant $\rho >0$ such that $c_\varepsilon =\inf \limits _{{\mathcal {N}}_\varepsilon } I_\varepsilon \ge \inf \limits _{S_\rho }I_\varepsilon >0$, where

  $$\begin{aligned} S_\rho =\{u \in H^s({\mathbb {R}}^N): \Vert u\Vert =\rho \}, \end{aligned}$$

• (ii) there exists $r_0>0$ such that $\Vert u\Vert \ge r_0$ for all $u \in {\mathcal {N}}_\varepsilon$.

Lemma 13

Let ${\mathcal {W}} \subset H^s({\mathbb {R}}^N)\setminus \{0\}$ be a compact subset. Then there exists $r>0$ such that $I_\varepsilon (u)<0$ on $({\mathbb {R}}^+{\mathcal {W}})\setminus B_r$ for each $u \in {\mathcal {W}}$, where ${\mathbb {R}}^+\mathcal {W}:=\{tw: t>0, w\in {\mathcal {W}}\}$.

Define the mapping ${\tilde{m}}_\varepsilon : H^s({\mathbb {R}}^N)\setminus \{0\}\rightarrow \mathcal {N}_\varepsilon$ and $m_\varepsilon : S\rightarrow {\mathcal {N}}_\varepsilon$ by setting

$$\begin{aligned} {\tilde{m}}_\varepsilon (u)=t_uu \ \ \hbox {and} \ \ m_\varepsilon ={\tilde{m}}_\varepsilon |_S, \end{aligned}$$

where S is the unit sphere in $H^s({\mathbb {R}}^N)$. We also consider the functionals ${\tilde{\psi }}_\varepsilon : H^s({\mathbb {R}}^N)\setminus \{0\}\rightarrow {\mathbb {R}}$ and $\psi _\varepsilon : S\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} {\tilde{\psi }}_\varepsilon (u)=I_\varepsilon ({\tilde{m}}_\varepsilon (u)) \ \ \hbox {and} \ \ \psi _\varepsilon ={\tilde{\psi }}_\varepsilon |_S. \end{aligned}$$

Since $H^s({\mathbb {R}}^N)$ is a Hilbert space and Lemmas 11-13 imply that the hypotheses $A_2$ and $A_3$ hold in [25], Hence, the following Lemmas 14-15 are valid.

Lemma 14

( [25]) The mapping ${\tilde{m}}_\varepsilon : H^s({\mathbb {R}}^N)\setminus \{0\}\rightarrow \mathcal {N}_\varepsilon$ is continuous and $m_\varepsilon$ is a homeomorphism between S and $\mathcal {N_\varepsilon }$, and the inverse of $m_\varepsilon$ is given by $m_\varepsilon ^{-1}(u)=\frac{u}{\Vert u\Vert }$.

Lemma 15

( [25]) For each $\varepsilon >0$,

• (i) $\psi _\varepsilon \in C^1(S, {\mathbb {R}})$ and

  $$\begin{aligned} \psi _\varepsilon ^{\prime }(w)z=\Vert m_\varepsilon (w)\Vert I_\varepsilon ^{\prime }(m_\varepsilon (w))z \end{aligned}$$

  for all $z \in T_w(S):=\{u \in H^s({\mathbb {R}}^N): \langle w,u\rangle =0\}$.

• (ii) If $\{w_n\}$ is a Palais-Smale sequence for $\psi _\varepsilon$, then $\{m_\varepsilon (w_n)\}$ is a Palais-Smale sequence for $I_\varepsilon$. If $\{u_n\} \subset {\mathcal {N}}_\varepsilon$ is a bounded Palais-Smale sequence for $I_\varepsilon$, then $\{m_\varepsilon ^{-1}(u_n)\}$ is a Palais-Smale sequence for $\psi _\varepsilon$.

• (iii) $w \in S$ is a critical point of $\psi _\varepsilon$ if and only if $m_\varepsilon (w)$ is a nontrivial critical point of $I_\varepsilon$. Moreover, the corresponding values of $\psi _\varepsilon$ and $I_\varepsilon$ coincide and $\inf \limits _{S}\psi _\varepsilon =\inf \limits _{\mathcal {N}_\varepsilon }I_\varepsilon$.

• (iv) If $I_\varepsilon$ is even, then so is $\psi _\varepsilon$.

Lemma 16

The level $c_\varepsilon$ is achieved if $\varepsilon >0$ is small enough, i.e., problem (1.4) admits a positive solution if $\varepsilon >0$ is small enough.

Proof

Set

$$\begin{aligned} \zeta (u)=\int _{{\mathbb {R}}^N}|\xi |^{2s}|{\hat{u}}(\xi )|^2d\xi + \int _{{\mathbb {R}}^N}u^2dx-1, \ \forall u \in H^s({\mathbb {R}}^N). \end{aligned}$$

Notice that $S=\{u\in H^s({\mathbb {R}}^N): \zeta (u)=0\}$ and for each $u \in S$, one has

$$\begin{aligned} \langle \zeta ^{\prime }(u), u\rangle =2\Vert u\Vert ^2=2>0. \end{aligned}$$

By Proposition 9 in [25] we know that ${\tilde{\psi }}_\varepsilon : H^s({\mathbb {R}}^N)\setminus \{0\}\rightarrow {\mathbb {R}}$ is class of $C^1$, and

$$\begin{aligned} \langle {\tilde{\psi }}_\varepsilon ^{\prime }(u), v\rangle =\frac{\Vert {\tilde{m}}_\varepsilon (u)\Vert }{\Vert u\Vert }\langle I_\varepsilon ^{\prime }({\tilde{m}}_\varepsilon (u)),v\rangle , \ \ \forall 0\ne u, v\in H^s({\mathbb {R}}^N). \end{aligned}$$

Hence, Corollary 3.4 in [6] implies that there exists a sequence $\{w_n\} \subset S$ such that $\psi _\varepsilon (w_n)\rightarrow c_\varepsilon$ and there exists $\alpha _n\in {\mathbb {R}}$ such that

$$\begin{aligned} \Vert {\tilde{\psi }}_\varepsilon ^{\prime }(w_n)-\alpha _n\zeta ^{\prime }(w_n) \Vert _{H^{-s}({\mathbb {R}}^N)} \rightarrow 0. \end{aligned}$$

It implies

$$\begin{aligned} \alpha _n=\frac{\langle {\tilde{\psi }}_\varepsilon ^{\prime }(w_n), \zeta ^{\prime }(w_n)\rangle }{\Vert \zeta ^{\prime }(w_n)\Vert _{H^{-s}({\mathbb {R}}^N)}^2}+o(1). \end{aligned}$$

Hence

$$\begin{aligned} {\tilde{\psi }}_\varepsilon ^{\prime }(w_n) -\frac{\langle {\tilde{\psi }}_\varepsilon ^{\prime }(w_n),\zeta ^{\prime }(w_n)\rangle }{\Vert \zeta ^{\prime }(w_n)\Vert _{H^{-s}({\mathbb {R}}^N)}^2}\zeta ^{\prime }(w_n) =o(1), \ \ \text{ i.e. }, \ \ \psi _\varepsilon ^{\prime }(w_n)=o(1). \end{aligned}$$

Set $u_n=m_\varepsilon (w_n) \in {\mathcal {N}}_\varepsilon$. Then Lemma 15 (ii) implies that $I_\varepsilon (u_n)=\psi _\varepsilon (w_n)\rightarrow c_\varepsilon$ and $I_\varepsilon ^\prime (u_n)\rightarrow 0$ in $H^{-s}({\mathbb {R}}^N)$. As before, we can assume that $u_n\ge 0, \ \forall n \in {\mathbb {N}}$. It follows from $(f_3)$ and (2.6) that

$$\begin{aligned} \begin{aligned}&c_\varepsilon +o(1)+o(1)\Vert u_n\Vert \\ =&I_\varepsilon (u_n)-\langle I_\varepsilon ^\prime (u_n), u_n\rangle \\ =&\int _{{\mathbb {R}}^N}P(\varepsilon x)[\frac{1}{2}f(u_n)u_n-F(u_n)]dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*|u_n|^{2_{\mu ,s}^*}]|u_n|^{2_{\mu ,s}^*}dx\\ \ge&\gamma _{\min }\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|u_n|^{2_{\mu ,s}^*}]|u_n|^{2_{\mu ,s}^*}dx\ge C\Vert u_n\Vert ^{22_{\mu ,s}^*}, \end{aligned} \end{aligned}$$

which indicates that $\{u_n\}$ is bounded in $H^s({\mathbb {R}}^N)$. Consequently, up to a subsequence, there exists $u_\varepsilon \in H^s({\mathbb {R}}^N)$ such that $u_n\rightharpoonup u_\varepsilon$ in $H^s({\mathbb {R}}^N)$, $u_n\rightarrow u_\varepsilon$ in $L_{loc}^t({\mathbb {R}}^N)$ for $2\le t<2_s^*$ and $u_n(x)\rightarrow u_\varepsilon (x)$ a.e. on ${\mathbb {R}}^N$. Arguing as in Lemma 6, we can prove that $I_\varepsilon ^\prime (u_\varepsilon )=0$. In the following, we prove that $u_\varepsilon \not =0$ if $\varepsilon >0$ is small enough.

Indeed, if the conclusion is false, there exists a sequence $\varepsilon _j\rightarrow 0$ as $j\rightarrow +\infty$ with $u_{\varepsilon _j}=0$. Clearly, by Lemma 12 (ii) there exists a constant $C>0$ such that $\Vert u_n\Vert ^2\ge C>0$. Choose $b \in (\beta _{\infty },\beta _{{\mathcal {Q}}})$ and consider the truncated functional $I_{\varepsilon _j}^{e,b}$. For each $u_n$, there exists a unique $t_n:=t_{u_n}>0$ such that $t_nu_n \in \mathcal {N}_{\varepsilon _j}^{e,b}$. Consequently, it follows by (2.6) and Lemma 12 (ii) that

$$\begin{aligned} \begin{aligned} Ct_n^2\ge&t_n^2\Vert u_n\Vert _{\mathcal {D}^{s,2}}^2+t_n^2\int _{{\mathbb {R}}^N}V_{\varepsilon _j}^e(x)u_n^2dx\\ =&\int _{{\mathbb {R}}^N}P_{\varepsilon _j}^b(x)f(t_nu_n)t_nu_ndx + t_n^{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}Q(\varepsilon _j x) [|x|^{-\mu }*|u_n|^{2_{\mu ,s}^*}]|u_n|^{2_{\mu ,s}^*}dx\\ \ge&\, t_n^{22_{\mu ,s}^*}\gamma _{\min } \int _{{\mathbb {R}}^N}[|x|^{-\mu }*|u_n|^{2_{\mu ,s}^*}]|u_n|^{2_{\mu ,s}^*}dx\ge Ct_n^{22_{\mu ,s}^*}\Vert u_n\Vert ^{22_{\mu ,s}^*}\ge Ct_n^{22_{\mu ,s}^*}, \end{aligned} \end{aligned}$$

which yields that $\{t_n\}$ is bounded in ${\mathbb {R}}$. Hence, up to a subsequence we may assume that $t_n\rightarrow t_0$ as $n\rightarrow \infty$. Noticing that (3.1) implies that $\{x \in {\mathbb {R}}^N: V(\varepsilon _jx)\le e\}$ is bounded in ${\mathbb {R}}^N$ for each $j \in {\mathbb {N}}$, we have

$$\begin{aligned} \int _{{\mathbb {R}}^N}[V_{\varepsilon _j}^e(x)-V(\varepsilon _jx)]|t_nu_n|^2dx =\int _{\{x \in {\mathbb {R}}^N:V(\varepsilon _jx)\le e\}}[e-V(\varepsilon _jx)]|t_nu_n|^2dx\rightarrow 0 \end{aligned}$$

as $n\rightarrow \infty$. Simultaneously, by $b>\beta _{\infty }$ we know that $\{x \in {\mathbb {R}}^N:P(\varepsilon _jx)\ge b\}$ is bounded in ${\mathbb {R}}^N$ for each $j \in {\mathbb {N}}$. And so

$$\begin{aligned} \int _{{\mathbb {R}}^N}[P(\varepsilon _jx)-P_{\varepsilon _j}^b(x)]F(t_nu_n)dx =\int _{\{x \in {\mathbb {R}}^N:P(\varepsilon _jx)\ge b\}}[P(\varepsilon _jx)-b]F(t_nu_n)dx\rightarrow 0 \end{aligned}$$

as $n\rightarrow \infty$. As a consequence, altogether with the above estimates we have

$$\begin{aligned} \begin{aligned} c_{\varepsilon _j}^{e,b}\le&I_{\varepsilon _j}^{e,b}(t_nu_n)=I_{\varepsilon _j}(t_nu_n)+\frac{1}{2} \int _{{\mathbb {R}}^N}[V_{\varepsilon _j}^e(x)-V(\varepsilon _jx)]|t_nu_n|^2dx\\&+\int _{{\mathbb {R}}^N}[P(\varepsilon _jx)-P_{\varepsilon _j}^b(x)]F(t_nu_n)dx\\ =&I_{\varepsilon _j}(t_nu_n)+o(1)\le I_{\varepsilon _j}(u_n)+o(1)=c_{\varepsilon _j}+o(1). \end{aligned} \end{aligned}$$

It yields that $c_{\varepsilon _j}^{e,b}\le c_{\varepsilon _j}$. It follows from Lemma 10 that $m_{e,b,\gamma _{\max }}\le c_{\varepsilon _j}$. Let $j\rightarrow +\infty$, by Lemma 9 one has $m_{e,b,\gamma _{\max }}\le m_{e,\beta _{{\mathcal {Q}}},\gamma _{\max }}$. But $b<\beta _{{\mathcal {Q}}}$ and Lemma 7 imply that $m_{e,\beta _{\mathcal {Q}},\gamma _{\max }}<m_{e,b,\gamma _{\max }}$, a contradiction. Therefore, $u_\varepsilon \not =0$ as long as $\varepsilon >0$ is small enough. Furthermore, as before, one has $u_\varepsilon >0$ if $\varepsilon >0$ is small enough. Combining with Fatou Lemma and $(f_3)$ we deduce that

$$\begin{aligned} \begin{aligned} c_{\varepsilon }\le&I_{\varepsilon }(u_\varepsilon )=I_{\varepsilon }(u_\varepsilon )-\frac{1}{2}\langle I_{\varepsilon }^\prime (u_\varepsilon ),u_\varepsilon \rangle \\ =&\int _{{\mathbb {R}}^N}P(\varepsilon x)[\frac{1}{2}f(u_\varepsilon )u_\varepsilon -F(u_\varepsilon )]dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*|u_\varepsilon |^{2_{\mu ,s}^*}]|u_\varepsilon |^{2_{\mu ,s}^*}dx\\ \le&\liminf \limits _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}P(\varepsilon x)[\frac{1}{2}f(u_n)u_n-F(u_n)]dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \liminf \limits _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}Q(\varepsilon x)[|x|^{-\mu }*|u_n|^{2_{\mu ,s}^*}]|u_n|^{2_{\mu ,s}^*}dx\\ \le&\liminf \limits _{n\rightarrow \infty }[I_\varepsilon (u_n)-\frac{1}{2}\langle I_\varepsilon ^\prime (u_n)u_n\rangle ]=c_\varepsilon , \end{aligned} \end{aligned}$$

that is, $I_\varepsilon (u_\varepsilon )=c_\varepsilon$. This completes the proof. $\square$

Lemma 17

Let $\{u_n\}$ be the positive solution obtained in Lemma 16 with $\varepsilon _n\rightarrow 0$. Then there exists $y_n \in {\mathbb {R}}^N$ with $\varepsilon _ny_n\rightarrow y_0 \in {\mathcal {S}}_P$, i.e.,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }dist(\varepsilon _ny_n,{\mathcal {S}}_P)=0, \end{aligned}$$

such that the sequence $v_n(x):=u_n(x+y_n)$ converges in $H^s({\mathbb {R}}^N)$ to a positive ground state solution v of

$$\begin{aligned} (-\varDelta )^sv+V(y_0)v=P(y_0)f(v)+Q(y_0)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*-2}v, \ x \in {\mathbb {R}}^N.\nonumber \\ \end{aligned}$$

(3.3)

Proof

Let $\{u_n\}$ be the positive solution obtained in Lemma 16 with $\varepsilon _n\rightarrow 0$. Then $I_{\varepsilon _n}(u_n)=c_{\varepsilon _n}$ and $I_{\varepsilon _n}^\prime (u_n)=0$ and $u_n>0, \ \forall n \in {\mathbb {N}}$. Following the arguments in Lemma 16, using $(f_3)$ and (2.6) we obtain that $\{u_n\}$ is bounded in $H^s({\mathbb {R}}^N)$, and there exist a sequence $\{y_n\}\subset {\mathbb {R}}^N$ and constants $r, \ \delta >0$ such that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\int _{B_r(y_n)}|u_n|^2dx\ge \delta >0. \end{aligned}$$

(3.4)

If not, arguing as in the proof of Lemma 6 we can infer that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }c_{\varepsilon _n}\ge \frac{1}{\gamma _{\max }^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )}\cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}. \end{aligned}$$

But by Lemmas 6 and 3.2 we get

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }c_{\varepsilon _n}\le m_{e,\beta _{\mathcal {Q}},\gamma _{\max }} <\frac{1}{\gamma _{\max }^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )}\cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}, \end{aligned}$$

a contradiction. Set $v_n(x)=u_n(x+y_n)$, ${\widetilde{V}}_{\varepsilon _n}(x)=V(\varepsilon _n(x+y_n))$, ${\widetilde{P}}_{\varepsilon _n}(x)$ $=P(\varepsilon _n(x+y_n))$ and ${\widetilde{Q}}_{\varepsilon _n}(x)=Q(\varepsilon _n(x+y_n))$. Then $v_n$ satisfies

$$\begin{aligned} (-\varDelta )^sv+{\widetilde{V}}_{\varepsilon _n}(x)v ={\widetilde{P}}_{\varepsilon _n}(x)f(v)+{\widetilde{Q}}_{\varepsilon _n}(x) {[}|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*-2}v, \ x \in {\mathbb {R}}^N, \end{aligned}$$

whose energy functional is

$$\begin{aligned} \begin{aligned} {\tilde{I}}_{\varepsilon _n}(v)=&\frac{1}{2}\int _{{\mathbb {R}}^N}|\xi |^{2s}| {\hat{v}}(\xi )|^2d\xi +\frac{1}{2}\int _{{\mathbb {R}}^N}{\widetilde{V}}_{\varepsilon _n}(x)v^2dx -\int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)F(v)dx\\&-\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x) [|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}dx. \end{aligned} \end{aligned}$$

By (3.4) we may assume that $v_n\rightharpoonup v$ in $H^s({\mathbb {R}}^N)$, $v_n\rightarrow v$ in $L_{loc}^t({\mathbb {R}}^N)$ for $2 \le t<2_s^*$ and $v_n(x)\rightarrow v(x)$ a.e. on ${\mathbb {R}}^N$, where $v\ge 0$ and $v\not =0$. We next continue our arguments by dividing the proof into three steps.

Step 1. We prove that $\{\varepsilon _ny_n\}$ is bounded in ${\mathbb {R}}^N$. Or else, up to a subsequence, we may assume that $\varepsilon _ny_n\rightarrow +\infty$. By the boundedness of V, P, Q and (3.1), there exist $V_0$, $P_0$ and $Q_0$ such that $V(\varepsilon _ny_n)\rightarrow V_0\ge e$, $P(\varepsilon _ny_n)\rightarrow P_0<\beta _{\mathcal {Q}}$ and $Q(\varepsilon _ny_n)\rightarrow Q_0\le \gamma _{\max }$. For all $\varphi \in C_0^{\infty }({\mathbb {R}}^N)$, it is easy to see that

$$\begin{aligned} \begin{aligned} 0=&\int _{{\mathbb {R}}^N}\varphi (-\varDelta )^sv_n dx+\int _{{\mathbb {R}}^N}{\widetilde{V}}_{\varepsilon _n}(x)v_n\varphi dx-\int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)f(v_n)\varphi dx\\&-\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v_n|^{2_{\mu ,s}^*}]|v_n|^{2_{\mu ,s}^*-2}v_n \varphi dx. \end{aligned} \end{aligned}$$

By the continuity and boundedness of V, P and Q one has

$$\begin{aligned} \int _{{\mathbb {R}}^N}\! {\widetilde{V}}_{\varepsilon _n}(x)v_n\varphi dx \rightarrow V_0\! \int _{{\mathbb {R}}^N}v\varphi dx \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)f(v_n)\varphi dx\rightarrow P_0\int _{{\mathbb {R}}^N}f(v)\varphi dx \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v_n|^{2_{\mu ,s}^*}]|v_n|^{2_{\mu ,s}^*-2}v_n \varphi dx\rightarrow Q_0\int _{{\mathbb {R}}^N}[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*-2}v \varphi dx \end{aligned}$$

as $n\rightarrow \infty$. The proof of last formula follows from Lemma 6. It follows that

$$\begin{aligned} (-\varDelta )^s v+V_0v=P_0f(v)+Q_0[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*-2}v , \ x \in {\mathbb {R}}^N. \end{aligned}$$

By the fact that $I_{\varepsilon _n}(u_n)={\tilde{I}}_{\varepsilon _n}(v_n)$, Fatou Lemma, $(f_3)$ and Lemmas 7, 3.2 we deduce that

$$\begin{aligned} \begin{aligned}&m_{e,\beta _{{\mathcal {Q}}},\gamma _{\max }}< m_{V_0,P_0,Q_0}\le J_{V_0,P_0,Q_0}(v)=J_{V_0,P_0,Q_0}(v)-\frac{1}{2}\langle J_{V_0,P_0,Q_0}^\prime (v),v\rangle \\ =&P_0\int _{{\mathbb {R}}^N}[\frac{1}{2}f(v)v-F(v)]dx +\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) Q_0\int _{{\mathbb {R}}^N}[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}dx\\ \le&\liminf \limits _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)[\frac{1}{2}f(v_n)v_n-F(v_n)]dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \liminf \limits _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v_n|^{2_{\mu ,s}^*}]|v_n|^{2_{\mu ,s}^*}dx\\ \le&\liminf \limits _{n\rightarrow \infty }[{\tilde{I}}_{\varepsilon _n}(v_n)-\frac{1}{2} \langle {\tilde{I}}_{\varepsilon _n}^\prime (v_n),v_n\rangle ]\\ =&\liminf \limits _{n\rightarrow \infty }[I_{\varepsilon _n}(u_n)-\frac{1}{2}\langle I_{\varepsilon _n}^\prime (u_n),u_n\rangle ]=\liminf \limits _{n\rightarrow \infty }c_{\varepsilon _n}\le \limsup \limits _{n\rightarrow \infty }c_{\varepsilon _n}\le m_{e,\beta _{\mathcal {Q}},\gamma _{\max }}, \end{aligned} \end{aligned}$$

a contradiction. Therefore, $\{\varepsilon _ny_n\}$ is bounded in ${\mathbb {R}}^N$ and we may assume that $\varepsilon _ny_n\rightarrow y_0 \in {\mathbb {R}}^N$ as $n\rightarrow \infty$.

Step 2. We prove that $y_0 \in {\mathcal {S}}_P$ and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }{\tilde{I}}_{\varepsilon _n}(v_n) = m_{V(y_0),P(y_0),Q(y_0)}=J_{V(y_0),P(y_0),Q(y_0)}(v). \end{aligned}$$

Otherwise,

$$\begin{aligned} \begin{aligned} y_0 \not \in {\mathcal {S}}_p=&\{x \in {\mathcal {C}}_p:V(x)\le V(x_p)\} \cup \{x \in {\mathcal {Q}}\setminus {\mathcal {C}}_p:V(x)<V(x_p)\}\\&\cup \{x \not \in {\mathcal {Q}}:P(x)>\beta _{\mathcal {Q}} \ \, \text{ or } \ \, V(x)<V(x_p)\}. \end{aligned} \end{aligned}$$

If $y_0 \in {\mathcal {C}}_p$, then $V(y_0)>V(x_p)=V(0)=e$ and $P(y_0)=\beta _{\mathcal {Q}}$. Therefore,

$$\begin{aligned} \max \{V(y_0)-e,\beta _{\mathcal {Q}}-P(y_0),\gamma _{\max }-Q(y_0)\}>0. \end{aligned}$$

If $y_0 \in {\mathcal {Q}}\setminus {\mathcal {C}}_p$, then $V(y_0)\ge V(x_p)=V(0)=e$ and $P(y_0)<\beta _{\mathcal {Q}}$ and $Q(y_0)=\gamma _{\max }$. Consequently,

$$\begin{aligned} \max \{V(y_0)-e,\beta _{\mathcal {Q}}-P(y_0),\gamma _{\max }-Q(y_0)\}>0. \end{aligned}$$

If $y_0 \not \in {\mathcal {Q}}$, then $V(y_0)\ge V(x_p)=V(0)=e$ and $P(y_0)\le \beta _{\mathcal {Q}}$ and $Q(y_0)<\gamma _{\max }$. Hence

$$\begin{aligned} \max \{V(y_0)-e,\beta _{\mathcal {Q}}-P(y_0),\gamma _{\max }-Q(y_0)\}>0. \end{aligned}$$

In summary,

$$\begin{aligned} \max \{V(y_0)-e,\beta _{\mathcal {Q}}-P(y_0),\gamma _{\max }-Q(y_0)\}>0, \end{aligned}$$

which implies that

$$\begin{aligned} m_{e,\beta _{{\mathcal {Q}}},\gamma _{\max }}< m_{V(y_0),P(y_0),Q(y_0)} \end{aligned}$$

by Lemma 7. Similar to the arguments as in Step 1, we conclude that v solves Eq. (3.3) and

$$\begin{aligned} m_{e,\beta _{\mathcal {Q}},\gamma _{\max }}<\liminf \limits _{n\rightarrow \infty }c_{\varepsilon _n}\le \limsup \limits _{n\rightarrow \infty }c_{\varepsilon _n}\le m_{e,\beta _{\mathcal {Q}},\gamma _{\max }}, \end{aligned}$$

a contradiction. Consequently, $y_0 \in {\mathcal {S}}_P$ and $\lim \limits _{n\rightarrow \infty }dist(\varepsilon _ny_n,\mathcal {S}_P)=0$. Moreover, by the above argument we have

$$\begin{aligned} \begin{aligned} m_{V(y_0),P(y_0),Q(y_0)}\le&J_{V(y_0),P(y_0),Q(y_0)}(v)\\ =&J_{V(y_0),P(y_0),Q(y_0)}(v)-\frac{1}{2}\langle J_{V(y_0),P(y_0),Q(y_0)}^\prime (v),v\rangle \\ \le&\liminf \limits _{n\rightarrow \infty }[{\tilde{I}}_{\varepsilon _n}(v_n)-\frac{1}{2}\langle {\tilde{I}}_{\varepsilon _n}^\prime (v_n),v_n\rangle ]\\ =&\liminf \limits _{n\rightarrow \infty }[{\tilde{I}}_{\varepsilon _n}(v_n)-\frac{1}{2}\langle I_{\varepsilon _n}^\prime (u_n),u_n\rangle ]\\ =&\liminf \limits _{n\rightarrow \infty }{\tilde{I}}_{\varepsilon _n}(v_n)=\liminf \limits _{n\rightarrow \infty }I_{\varepsilon _n}(u_n)=\liminf \limits _{n\rightarrow \infty }c_{\varepsilon _n}. \end{aligned} \end{aligned}$$

On the other hand,

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }{\tilde{I}}_{\varepsilon _n}(v_n)\le m_{V(y_0),P(y_0),Q(y_0)}. \end{aligned}$$

Taking into account the above two inequalities we can see that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }{\tilde{I}}_{\varepsilon _n}(v_n)= m_{V(y_0),P(y_0),Q(y_0)}=J_{V(y_0),P(y_0),Q(y_0)}(v). \end{aligned}$$

(3.5)

Hence v is a ground state solution of (3.3).

Step 3. We show that $v_n\rightarrow v$ in $H^s({\mathbb {R}}^N)$. Indeed, by the continuity of V, P and Q we obtain

$$\begin{aligned} \int _{{\mathbb {R}}^N}{\widetilde{V}}_{\varepsilon _n}(x)|v|^2dx \rightarrow V(y_0)\int _{{\mathbb {R}}^N}|v|^2dx \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)F(v)dx\rightarrow P(y_0)\int _{{\mathbb {R}}^N}F(v)dx \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}dx\rightarrow Q(y_0)\int _{{\mathbb {R}}^N}[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}dx \end{aligned}$$

as $n\rightarrow \infty$, which implies that ${\tilde{I}}_{\varepsilon _n}(v)\rightarrow J_{V(y_0),P(y_0),Q(y_0)}(v)$ as $n\rightarrow \infty$. Noting that

$$\begin{aligned} \begin{aligned}&{\tilde{I}}_{\varepsilon _n}(v_n-v)-{\tilde{I}}_{\varepsilon _n}(v_n) +{\tilde{I}}_{\varepsilon _n}(v)\\ =&\frac{1}{2}[\langle v_n-v,v_n-v\rangle _{{\mathcal {D}}^{s,2}}-\langle v_n,v_n \rangle _{{\mathcal {D}}^{s,2}}+\langle v,v\rangle _{{\mathcal {D}}^{s,2}}]\\&+\frac{1}{2}\int _{{\mathbb {R}}^N}{\widetilde{V}}_{\varepsilon _n}(x)[|v_n-v|^2 -|v_n|^2+|v|^2]dx\\&-\int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)[F(v_n-v)-F(v_n)+F(v)]dx\\ -&\frac{1}{22_{\mu ,s}^*}\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x) \big \{[|x|^{-\mu }*|v_n-v|^{2_{\mu ,s}^*}]|v_n-v|^{2_{\mu ,s}^*}-[|x|^{-\mu }*|v_n|^{2_{\mu ,s}^*}]|v_n|^{2_{\mu ,s}^*}\\&+[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}\big \}dx. \end{aligned} \end{aligned}$$

(3.6)

It is easy to prove that

$$\begin{aligned} \langle v_n-v,v_n-v\rangle _{{\mathcal {D}}^{s,2}} -\langle v_n,v_n\rangle _{{\mathcal {D}}^{s,2}}+\langle v,v\rangle _{{\mathcal {D}}^{s,2}} \rightarrow 0 \end{aligned}$$

(3.7)

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}{\widetilde{V}}_{\varepsilon _n}(x)[|v_n-v|^2-|v_n|^2+|v|^2]dx = 2\int _{{\mathbb {R}}^N}{\widetilde{V}}_{\varepsilon _n}(x)v(v-v_n)dx\rightarrow 0\nonumber \\ \end{aligned}$$

(3.8)

as $n\rightarrow \infty$. By (2.2)-(2.3), differential mean value theorem, Young inequality and the boundedness of P, there exists $\theta \in (0,1)$ such that

$$\begin{aligned} \begin{aligned}&\big |{\widetilde{P}}_{\varepsilon _n}(x)[F(v_n-v)-F(v_n)+F(v)]\big |\\ \le&\beta _{\max }\big ||v_n-\theta v||v|+C|v_n-\theta v|^{p-1}|v|+|v|^2+C|v|^p\big |\\ \le&C[|v_n||v|+|v|^2+C|v_n|^{p-1}|v|+C|v|^p]\\ \le&C[|v_n-v||v|+C|v_n-v|^{p-1}|v|+C|v|^2+C|v|^p]\\ \le&\delta |v_n-v|^2+\delta |v_n-v|^p+CC_\delta |v|^2+CC_\delta |v|^p. \end{aligned} \end{aligned}$$

Set

$$\begin{aligned} G_{\delta ,n}(x):=\max \{\big |{\widetilde{P}}_{\varepsilon _n}(x) [F(v_n-v)-F(v_n)+F(v)]\big |-\delta |v_n-v|^2-\delta |v_n-v|^p,0\}. \end{aligned}$$

Then $0\le G_{\delta ,n}(x)\le CC_\delta |v|^2+CC_\delta |v|^p \in L^1({\mathbb {R}}^N)$ and $G_{\delta ,n}(x)\rightarrow 0$ a.e. on ${\mathbb {R}}^N$. By Lebesgue dominated convergence theorem we have $\int _{{\mathbb {R}}^N}G_{\delta ,n}(x)dx\rightarrow 0$ as $n\rightarrow \infty$. Hence

$$\begin{aligned} \begin{aligned}&\limsup \limits _{n\rightarrow \infty }\big |\int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x) [F(v_n-v)-F(v_n)+F(v)]dx\big |\\ \le&\limsup \limits _{n\rightarrow \infty } \int _{{\mathbb {R}}^N}G_{\delta ,n}(x)dx+\delta \limsup \limits _{n\rightarrow \infty }\int _{{\mathbb {R}}^N} |v_n\!-\!v|^2dx + \delta \limsup \limits _{n\rightarrow \infty } \int _{{\mathbb {R}}^N} |v_n\!-\!v|^pdx\\ \le&C\delta . \end{aligned} \end{aligned}$$

By the arbitrariness of $\delta$,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)[F(v_n-v)-F(v_n)+F(v)]dx=0. \end{aligned}$$

(3.9)

In the following, we prove that

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)\big \{[|x|^{-\mu }*|v_n-v|^{2_{\mu ,s}^*}]|v_n-v|^{2_{\mu ,s}^*}-[|x|^{-\mu }*|v_n|^{2_{\mu ,s}^*}]|v_n|^{2_{\mu ,s}^*}\\ +&[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}\big \}dx\rightarrow 0 \end{aligned} \end{aligned}$$

(3.10)

as $n \rightarrow \infty$. In fact, by differential mean value theorem and Young inequality, we have

$$\begin{aligned} \begin{aligned}&\big | |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*}\big |^{\frac{2N}{2N-\mu }}\\ \le&C\big (|v_n-v|^{2_{\mu ,s}^*-1}\cdot |v|+|v|^{2_{\mu ,s}^*}\big )^{\frac{2N}{2N-\mu }}\\ \le&C|v_n-v|^{(2_{\mu ,s}^*-1)\cdot \frac{2N}{2N-\mu }}\cdot |v|^{\frac{2N}{2N-\mu }}+C|v|^{2_{\mu ,s}^*\cdot \frac{2N}{2N-\mu }}\\ =&C|v_n-v|^{\frac{N+2s-\mu }{N-2s}\cdot \frac{2N}{2N-\mu }}\cdot |v|^{\frac{2N}{2N-\mu }}+C|v|^{2_s^*}\\ \le&\delta |v_n-v|^{2_s^*}+C_\delta |v|^{2_s^*}. \end{aligned} \end{aligned}$$

Set

$$\begin{aligned} H_{\delta ,n}(x):=\max \{\big | |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*} \big |^{\frac{2N}{2N-\mu }}-\delta |v_n-v|^{2_s^*}, 0\}. \end{aligned}$$

Then $0\le H_{\delta ,n}(x)\le C_\delta |v|^{2_s^*} \in L^1({\mathbb {R}}^N)$ and $H_{\delta ,n}(x)\rightarrow 0$ a.e. on ${\mathbb {R}}^N$. Again by the Lebesgue dominated convergence theorem we have $\int _{{\mathbb {R}}^N}H_{\delta ,n}(x)dx\rightarrow 0$ as $n\rightarrow \infty$. Hence, with a similar argument as the proof of (3.9) we can prove that $|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*}\rightarrow 0$ in $L^{\frac{2N}{2N-\mu }}({\mathbb {R}}^N)$. Noting that -10pt

$$\begin{aligned} \begin{aligned} I:=&\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)\big \{[|x|^{-\mu }*|v_n|^{2_{\mu ,s}^*}]|v_n|^{2_{\mu ,s}^*}-[|x|^{-\mu }*|v_n-v|^{2_{\mu ,s}^*}]|v_n-v|^{2_{\mu ,s}^*}\big \}dx\\ =&\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*(|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*})](|v_n|^{2_{\mu ,s}^*} -|v_n-v|^{2_{\mu ,s}^*})dx\\&+2\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*(|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*})]|v_n-v|^{2_{\mu ,s}^*}dx\\ :=&I_1+I_2. \end{aligned} \end{aligned}$$

For $I_1$, by (Q) and the boundedness of $\{\Vert v_n\Vert \}$, which together with Hardy-Littlewood-Sobolev inequality we deduce that

$$\begin{aligned} \begin{aligned}&\big |\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*(|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*})](|v_n|^{2_{\mu ,s}^*} -|v_n-v|^{2_{\mu ,s}^*})dx\\&-\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}dx\big |\\ =&\left| \int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*(|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*})]\right. \\&\times \, (|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*})dx\\&\left. +\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}](|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*})dx \right| \\ \le&C\big \Vert |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\cdot \big \Vert |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\\&+C\big \Vert |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\cdot \big \Vert |v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\\ \le&C\big \Vert |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\\ \rightarrow&\ 0 \end{aligned} \end{aligned}$$

as $n\rightarrow \infty$. Moreover,

$$\begin{aligned} I_2= & {} 2\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*(|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*})]|v_n-v|^{2_{\mu ,s}^*}dx \nonumber \\= & {} 2\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*(|v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*})]|v_n-v|^{2_{\mu ,s}^*}dx\nonumber \\&+2\int _{{\mathbb {R}}^N}{\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v_n-v|^{2_{\mu ,s}^*}dx\nonumber \\= & {} I_2^1+I_2^2. \end{aligned}$$

By [19], we have $|x|^{-\mu }*|v|^{2_{\mu ,s}^*} \in L^{\frac{2N}{\mu }}({\mathbb {R}}^N)$. Combining the fact that $|v_n-v|^{2_{\mu ,s}^*}\rightharpoonup 0$ in $L^{\frac{2N}{2N-\mu }}({\mathbb {R}}^N)$, by the definition of weak convergence one has $I_2^2\rightarrow 0$ as $n\rightarrow \infty$. Again by (Q), the boundedness of $\{\Vert v_n\Vert \}$ and Hardy-Littlewood-Sobolev inequality, we deduce that

$$\begin{aligned} \begin{aligned} |I_2^1|&\le C\big \Vert |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\cdot \big \Vert |v_n-v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\\&\le C\big \Vert |v_n|^{2_{\mu ,s}^*}-|v_n-v|^{2_{\mu ,s}^*}-|v|^{2_{\mu ,s}^*} \big \Vert _{\frac{2N}{2N-\mu }}\\&\rightarrow 0 \end{aligned} \end{aligned}$$

as $n \rightarrow \infty$. So (3.10) is completely proved. It follows from (3.5)-(3.10) and Step 2 that

$$\begin{aligned} {\tilde{I}}_{\varepsilon _n}(v_n-v)= & {} {\tilde{I}}_{\varepsilon _n}(v_n)-{\tilde{I}}_{\varepsilon _n}(v)+o(1) ={\tilde{I}}_{\varepsilon _n}(v_n)\\&-J_{V(y_0),P(y_0),Q(y_0)}(v)+o(1)=o(1). \end{aligned}$$

Similarly,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\langle {\tilde{I}}_{\varepsilon _n}^\prime (v_n-v),v_n-v\rangle =0. \end{aligned}$$

Consequently, by $(f_3)$, (Q) and (2.6) we deduce that

$$\begin{aligned} \begin{aligned} o(1)=&{\tilde{I}}_{\varepsilon _n}(v_n-v)-\frac{1}{2} \langle {\tilde{I}}_{\varepsilon _n}^\prime (v_n-v),v_n-v\rangle \\ =&\int _{{\mathbb {R}}^N}{\widetilde{P}}_{\varepsilon _n}(x)[\frac{1}{2}f(v_n-v)(v_n-v) -F(v_n-v)]dx\\&+\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \int _{{\mathbb {R}}^N} {\widetilde{Q}}_{\varepsilon _n}(x)[|x|^{-\mu }*|v_n-v|^{2_{\mu ,s}^*}]|v_n-v|^{2_{\mu ,s}^*}dx\\ \ge&\left( \frac{1}{2}-\frac{1}{22_{\mu ,s}^*}\right) \gamma _{\min }\int _{{\mathbb {R}}^N}[|x|^{-\mu }*|v_n-v|^{2_{\mu ,s}^*}]|v_n-v|^{2_{\mu ,s}^*}dx\\ \ge&C\Vert v_n-v\Vert ^{22_{\mu ,s}^*}, \end{aligned} \end{aligned}$$

which indicates that $v_n\rightarrow v$ in $H^s({\mathbb {R}}^N)$. This completes the proof. $\square$

In the following, we give the proofs of Theorem 1 and Theorem 2.

Proof of Theorem 1

By Lemma 16, problem (1.4) admits a positive solution $u_\varepsilon$ for $\varepsilon >0$ small enough. Hence $w_\varepsilon (x)=u_\varepsilon \left( \frac{x}{\varepsilon }\right)$ is a positive solution of (1.1). Let $x_\varepsilon$ and $z_\varepsilon$ be the maximum points of $w_\varepsilon$ and $u_\varepsilon$, respectively. Then $x_\varepsilon =\varepsilon z_\varepsilon$. Set $v_\varepsilon (x):=w_\varepsilon (\varepsilon x+x_\varepsilon )$. Then $w_\varepsilon (x)=v_\varepsilon \left( \frac{x-x_\varepsilon }{\varepsilon }\right)$. By Lemma 17, for any $x_\varepsilon \rightarrow x_0$, $\lim \limits _{\varepsilon \rightarrow 0}dist(x_\varepsilon ,\mathcal {S}_P)=0$ and $v_\varepsilon$ converges in $H^s({\mathbb {R}}^N)$ to a positive ground state solution of

$$\begin{aligned} (-\varDelta )^sv+V(x_0)v=P(x_0)f(v)+Q(x_0)[|x|^{-\mu }*|v|^{2_{\mu ,s}^*}]|v|^{2_{\mu ,s}^*}, \ x \ \in {\mathbb {R}}^N. \end{aligned}$$

This completes the proof. $\square$

Proof of Theorem 2

Without loss of generality, we may assume that $x_V=0 \in \mathcal {C}_V$ in (1.3). Consequently, by (1.3) we set $e:=P(0)\ge P(x)$ for all $|x|\ge R$. By the proof of Lemma 6, for any $\alpha \in [\alpha _{\min }, \alpha _{\infty })$, $\beta \in [\beta _{\infty }, \beta _{\max }]$ and $\gamma \in [\gamma _{\min }, \gamma _{\max }]$ we have

$$\begin{aligned} m_{\alpha ,\beta ,\gamma }<\frac{1}{\gamma ^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )}\cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}. \end{aligned}$$

(3.11)

Arguing as before, the same conclusion in Lemma 8 holds for the present case. Instead of Lemma 9, one has

$$\begin{aligned} \limsup \limits _{\varepsilon \rightarrow 0}c_\varepsilon \le m_{\alpha _{\mathcal {Q}},e,\gamma _{\max }}. \end{aligned}$$

Moreover, by only truncating the potential V and P with $a \in (\alpha _{\mathcal {Q}},\alpha _{\infty })$ we deduce that $c_\varepsilon ^{a,e}\ge m_{a,e,\gamma _{\max }}$. Consequently, by (3.11) we have

$$\begin{aligned} \limsup \limits _{\varepsilon \rightarrow 0}c_\varepsilon <\frac{1}{\gamma ^{\frac{N-2s}{N+2s-\mu }}}\cdot \frac{N+2s-\mu }{2(2N-\mu )}\cdot S_H^{\frac{2N-\mu }{N+2s-\mu }}. \end{aligned}$$

By the characterization of $c_\varepsilon$ we can choose a minimizing sequence $\{u_n\} \subset {\mathcal {N}}_\varepsilon$ of $I_\varepsilon$ at $c_\varepsilon$, which is positive and bounded $(PS)_{c_\varepsilon }$ for $I_\varepsilon$ and $u_n\rightharpoonup u_\varepsilon$ in $H^s({\mathbb {R}}^N)$. Using a standard argument (see Lemma 6), we can prove that $I_\varepsilon ^\prime (u_\varepsilon )=0$. We claim that $u_\varepsilon \not =0$ for $\varepsilon >0$ small enough. Otherwise, there exists a sequence $\varepsilon _j\rightarrow 0$ as $j\rightarrow +\infty$ with $u_{\varepsilon _j}=0$. Take $a \in (\alpha _{\mathcal {Q}},\alpha _{\infty })$. Considering the functional $I_{\varepsilon _j}^{a,e}$, we repeat the arguments in Lemma 16 to obtain a contradiction. Hence the assertion is valid. The rest proof is similar to the analysis in that of Theorem 1. This completes the proof. $\square$