1 Introduction

In recent decades, the coupled vibration caused by high-speed trains passing through bridges has been extensively studied [1]. Over the years, both the train and bridge models have been well refined [2]. The research on numerical algorithms and other aspects of train–bridge system research are also constantly evolving [3]; however, the uncertainty of train and bridge parameters is not considered much, and the values of train and bridge are usually regarded as exact values [4]. In reality, the uncertainty of structural parameters will inevitably occur during the construction and service of bridges, and the mass of train also presents uncertainty during running [5]. Obviously, the traditional dynamic analysis of the train–bridge-coupled system, which considers structural parameters as exact values, is not applicable to the real complex situation [6].

Various stochastic finite element methods have been proposed and applied to train–bridge-coupled systems [7], such as Monte Carlo method [8], stochastic perturbation method [9], orthogonal expansion theory [10], point estimation method [11], and probability density evolution theory [12]. These methods are used for dynamic analysis of train–bridge-coupled systems with uncertain parameters. In reality, certain structural parameters, like the extent of damage to piers, exhibit uncertainty that cannot be adequately explained by randomness. Analyzing these parameters through probability is inconvenient and inaccurate due to their varying magnitudes. The uncertainty of damage belongs to another kind of uncertainty different from randomness-fuzziness. Fuzziness refers to the objective attribute of things in the intermediate transition process, which is the result of the actual intermediate transition process between things [13]. Fuzziness is very suitable for explaining the uncertainty of parameters such as damage.

Despite Professor Zadeh [14] introducing the concept of fuzzy sets in the 1960s, many fuzzy finite element methods have been proposed [15]. However, it still cannot effectively address the challenges posed by fuzzy parameters in solving fuzzy dynamics problems [16]. The scanning method is generally used to calculate fuzzy response [17], and due to its large computational complexity, scholars have begun to study for fuzzy methods to reduce computational complexity. Rao et al. [18] proposed a fuzzy finite element method that considers the geometric shape, material properties, external loads, and boundary conditions of the structure as fuzzy parameters for static analysis. Massa et al. [19] proposed a new and effective method to improve the predictive ability of numerical models in static analysis situations. Yang et al. [20] proposed the fuzzy variational principle, which is also used for static analysis of structural systems with fuzzy parameters. Wasfy et al. [21] proposed a computational method for predicting the dynamic response of flexible multibody systems and evaluating their sensitivity coefficients containing fuzzy parameters. Möller B et al. [22] developed and formulated an α-generalized method for fuzzy structural analysis using an improved evolutionary strategy. It should be noted that when the fuzzy output is non-monotonic and the evaluation cost is high, the cost of solving these optimization problems may be high [23]. Pham et al. [24] proposed an improved optimization method based on Jaya, which can save a lot of computation while ensuring sufficient accuracy. Some scholars try to reduce the calculation cost of fuzzy analysis by response surface method [25], the reliability of fuzzy analysis depends entirely on the accuracy of approximate model [26].

Some scholars reduce the computational complexity of fuzzy analysis from the perspective of entropy. Cherki A et al. [27] adopted λ-level cutting method to transform the fuzzy equilibrium equation into interval equilibrium equation, which was used to analyze the fuzzy structure. However, this method requires a large amount of computation and is complicated. Lei et al. [28] proposed a new finite element analysis method of fuzzy structure using the concept of information entropy. The fuzzy variables are transformed into random variables, and the mean and variance of structural response are obtained. However, the upper and lower limits of the response are not obtained, and this method is not complete enough. The majority of the aforementioned methods focus on straightforward static problems. When applied to dynamic problems, they either involve complex and extensive calculations or are embedded, limiting their applicability to broader dynamic analyses. In this paper, the mean and variance of the obtained structural response are further calculated based on the previous work by Lei et al. [28] and combined with the new point estimation method to obtain the upper and lower limits of the response of the train and the bridge, that is, the fuzzy response of the train and the bridge. The proposed fuzzy finite element method is non-embedded and can be applied to other dynamics problems.

This paper is organized as follows: Sect. 2 introduces the model of train–bridge-coupled system, Sect. 3 briefly introduces information entropy method and fuzzy calculation processing, Sect. 4 verifies the reliability of the proposed method, considers whether the degree of pier damage is fuzzy, and uses stiffness reduction to simulate pier damage. The fuzzy dynamic response of train and bridge is studied when the pier structure and train mass are fuzzy parameters, and the conclusion is presented in the last section.

2 The motion equation of train–track–bridge systems

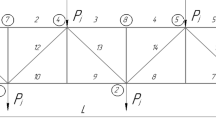
The train model is constructed with multiple rigid bodies, and each car is composed of a car body, two bogies, four wheelsets, and linear spring dampers connected between them [29]. The car body contains six degrees of freedom (vertical, longitudinal, lateral, yaw, roll, pitch), each wheelset contains five degrees of freedom (vertical, longitudinal, lateral, yaw, roll), and each bogie contains six degrees of freedom (vertical, longitudinal, lateral, yaw, roll, pitch), so this paper establishes a fine train model with 38 degrees of freedom [30]. The track structure is mainly composed of base, CA mortar layer, track plate, elastic fasteners, rails, and other components [31]. The rail is modeled as a beam element, and the track plate and the base are modeled as plate elements, which are connected by linear spring dampers [32]. Taking a three-span simply supported concrete bridge as an example, the bridge model is established based on the finite element method, and the pier and beam are simulated as Euler–Bernoulli beam elements. The train–track–bridge-coupled system model is shown in.

Figure 1, the corresponding parameters are detailed in Ref. [33].

Fig. 1
figure 1

Train–track–bridge-coupled system

Full size image

According to the mass matrix, stiffness matrix and damping matrix obtained by the finite element method, multi rigid body dynamics, and other processing methods, based on the energy principle, the train–track–bridge-coupled vibration equation can be derived, as shown below

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{cc} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{rr} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{bb} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{X}}}_{cc} } \\ {{\mathbf{\ddot{X}}}_{rr} } \\ {{\mathbf{\ddot{X}}}_{bb} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{cc} } & {{\mathbf{C}}_{cr} } & {\mathbf{0}} \\ {{\mathbf{C}}_{rc} } & {{\mathbf{C}}_{rr} } & {{\mathbf{C}}_{rb} } \\ {\mathbf{0}} & {{\mathbf{C}}_{br} } & {{\mathbf{C}}_{bb} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{X}}}_{cc} } \\ {{\dot{\mathbf{X}}}_{rr} } \\ {{\dot{\mathbf{X}}}_{bb} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{cc} } & {{\mathbf{K}}_{cr} } & {\mathbf{0}} \\ {{\mathbf{K}}_{rc} } & {{\mathbf{K}}_{rr} } & {{\mathbf{K}}_{rb} } \\ {\mathbf{0}} & {{\mathbf{K}}_{br} } & {{\mathbf{K}}_{bb} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{X}}_{cc} } \\ {{\mathbf{X}}_{rr} } \\ {{\mathbf{X}}_{bb} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{\mathbf{Q}}_{cc} } \\ {{\mathbf{Q}}_{rr} } \\ {\mathbf{0}} \\ \end{array} } \right\}, $$
(1)

where \({\mathbf{X}}_{cc}\),\({\mathbf{X}}_{rr}\), and \({\mathbf{X}}_{bb}\) represent the displacement vectors of the train, rail, and bridge, respectively. \({\mathbf{Q}}_{cc}\) and \({\mathbf{Q}}_{rr}\) denote the load train vectors of the train and rail, respectively.

In this paper, Eq. (1) is solved based on the Wilson-θ method in the prepared MATLAB program, when θ > 1.37, this algorithm is unconditionally stable. The value for θ is taken as 1.4 in our calculations [34].

3 Information entropy

3.1 Equivalent transformation of entropy

Shannon [35], the father of information theory, believed that information is random in nature. He borrowed the term "entropy" from statistical mechanics, and proposed information entropy to measure probabilistic information, called probabilistic entropy. The greater the uncertainty, the greater the entropy.

For a continuous random variable X, its probability entropy is defined as follows:

$$ H = - \int_{x} {p(x)\ln } p(x)dx, $$
(2)

where \(p(x)\) is the probability density function of the random variable X.

When random variable is obeyed Gaussian distribution, probability entropy can be expressed as [36]

$$ H = \ln (\sqrt {2\pi e} \sigma ) $$
(3)

As understanding deepens, researchers have come to recognize that information carries non-probabilistic uncertainty, specifically in the form of fuzziness. Fuzzy information can also be measured using information entropy, called fuzzy entropy. Aldo De Luca and Settimo Termini [37] first defined fuzzy entropy as follows, where \(f(y)\) is the membership function of fuzzy variable Y:

$$ G = - \int_{y} {f(y)\ln f(y)} + \left[ {1 - f(y)} \right]\ln \left[ {1 - f(y)} \right]{\text{d}}y $$
(4)

Achintya Haldar and Rajasekhar K. Reddy [38] also proposed a simple computational form of fuzzy entropy, as shown below

$$ G^{\prime} = - \int_{y} {f^{\prime}(y)\ln f^{\prime}(y)} {\text{d}}y $$
(5)
$$ f^{\prime}(y) = f(y)/\int_{y} {f(y))} {\text{d}}y $$
(6)

The definition equation of fuzzy entropy makes the membership function \(f(y)\) normalized as well as the probability density function \(p(x)\)

$$ \int_{y} {f^{\prime}(y)} {\text{d}}y = 1 $$
(7)

Entropy is a measure of information uncertainty, and there is essentially no difference between probabilistic entropy and fuzzy entropy. Fuzzy variables can be transformed into random variables by retaining the invariability of the measure of uncertainty. The principle of this transformation is that the equivalent probabilistic entropy equals to the fuzzy entropy [28]. In this paper, the total entropy is converted into the equivalent stochastic entropy \(H_{eq}\), and the structural parameters are converted into stochastic parameters for calculation, as shown in Eq. (8)

$$ G = H_{eq} $$
(8)

To convert the uncertain variables into equivalent normal random variables, and obtain the mean \(\mu\) and standard deviation \(\sigma\) of random variables, we assume that the mean \(\mu\) of the equivalent normal random variable is the value of the fuzzy variable at the membership degree of 1.

The standard deviation \(\sigma\) of the equivalent normal random variable can be obtained from Eq. (3)and (8), as follows:

$$ \sigma = \frac{1}{{\sqrt {2\pi } }}e^{G - 0.5} $$
(9)

3.2 New point estimation method (NPEM)

Zhao et al. [39] proposed a new point estimation of probability moments, which greatly improves the practicability and accuracy of point estimation. Jiang et al. [7] used NPEM based on adaptive dimensionality reduction to study the stochastic dynamic response of the axle system, and the results are verified to be accurate and efficient. The specific solution steps for the vibration response of the stochastic axle system are as follows:

  • (1) Determine the distribution state of the random parameters, and transform the original relevant random parameters into mutually independent standard normal random parameters. The random parameters in this paper all obey normal distribution, therefore, they can be standardized as

    $$ X(i) = \mu + \sigma u(i) $$
    (10)

where \(X(i)\) denotes the value of the random parameter corresponding to the ith estimation point, \(\mu\) and \(\sigma\) denote the mean and standard deviation of the random parameter, respectively, and \(u(i)\) denotes the ith estimation point.

  • (2) Choose a suitable reference point \(u_{c}\), and determine the number of Gaussian integration points r (r is usually an odd number, usually taken as 5 or 7). In this paper, we take \(u_{c} = 0\), and use 7 Gaussian integration points, corresponding to the integration points \(x_{GH,i}\) and weights \(w_{GH,i}\) of the Gauss–Hermite product formula as shown:

  • (3) Based on the data in Table 1 , substitute \(\sqrt 2 x_{GH,i}\) as \(u(i)\) in Eq. (10), and the weight coefficients \(P_{i}\) are calculated, and the estimated points and corresponding weight coefficients in the standard normal space are shown in Table 2:

    $$ P_{i} = \frac{{w_{GH,i} }}{\sqrt \pi } $$
    (11)

Calculate the time-range dynamic responses \({\mathbf{h}}(X_{l} (i),t)\) and \({\mathbf{h}}(X_{l} (i),X_{m} (j),t)\) of the axle coupled system with different random variables and different estimation points respectively, where l and m denote the lth and mth random parameters, and i and j denote the ith and jth estimation points, respectively.

  • (4) Substitute the values of the dynamic responses, h, into Eq. (12) and Eq. (13), and calculate the mean value of the time-range response and the central moments of each order

    $$ \begin{gathered} \mu (t) \approx \sum\limits_{l < m} E \left[ {{\mathbf{h}}\left( {X_{l} ,X_{m} ,u_{c} ,t} \right)} \right] - (n - 2) \\ \, \sum\limits_{k = 1}^{n} E \left[ {{\mathbf{h}}\left( {X_{k} ,u_{c} ,t} \right)} \right] + \frac{(n - 1)(n - 2)}{2}{\mathbf{h}}\left( {u_{c} ,t} \right) \\ \end{gathered} $$
    (12)
    $$ \begin{gathered} {\mathbf{M}}_{q} (t) \approx \sum\limits_{l < m} E \left[ {\left( {{\mathbf{h}}\left( {X_{l} ,X_{m} ,u_{c} ,t} \right) - \mu (t)} \right)^{q} } \right] - (n - 2) \\ \, \sum\limits_{k = 1}^{n} E \left[ {\left( {{\mathbf{h}}\left( {X_{k} ,u_{c} ,t} \right) - \mu (t)} \right)^{q} } \right] + \frac{(n - 1)(n - 2)}{2}\left( {{\mathbf{h}}\left( {u_{c} ,t} \right) - \mu (t)} \right)^{q} , \\ \end{gathered} $$
    (13)

where \(\mu (t)\) denotes the time-response mean, \({\mathbf{M}}_{q} (t)\) denotes the time-response qth (q = 2,3,4) order center distance, n denotes the number of random parameters, and \({\mathbf{h}}\left( {u_{c} ,t} \right)\) denotes the time-response at \(u(i) = u_{c}\). The expressions for E in Eq. (11) and (12) above can be rewritten as

$$ E\left[ {\left( {{\mathbf{h}}\left( {X_{l} ,u_{c} ,t} \right) - \mu (t)} \right)^{q} } \right] = \sum\limits_{i = 1}^{r} {P_{i} } \left( {{\mathbf{h}}\left( {X_{l,i} ,u_{c} ,t} \right) - \mu (t)} \right)^{q} $$
(14)
$$ E\left[ {\left( {{\mathbf{h}}\left( {X_{l} ,X_{m} ,u_{c} ,t} \right) - \mu (t)} \right)^{q} } \right] = \sum\limits_{i = 1}^{r} {\sum\limits_{j = 1}^{r} {P_{i} P_{j} } } \left( {{\mathbf{h}}\left( {X_{l,i} ,X_{m,j} ,u_{c} ,t} \right) - \mu (t)} \right)^{q} $$
(15)
Table 1 The integral points and weights for Gauss–Hermite quadrature with r = 7
Full size table
Table 2 The estimating points and corresponding weights
Full size table

When there is only one random parameter, Eq. (12) and Eq. (13) here can be simply expressed as

$$ {{\varvec{\upmu}}}(t) \approx E\left[ {{\mathbf{h}}\left( {X_{l} ,u_{c} ,t} \right)} \right] $$
(16)
$$ {\mathbf{M}}_{q} (t) \approx E\left[ {\left( {{\mathbf{h}}\left( {X_{l} ,u_{c} ,t} \right) - \mu (t)} \right)^{q} } \right]. $$
(17)

  • (5) Transform the first four central moments of the time-range response into the corresponding mean \(\mu_{z}\), standard deviation \(\alpha_{2}\), skewness coefficient \(\alpha_{3}\), and kurtosis coefficient \(\alpha_{4}\) according to Eq. (18)

    $$ \left\{ {\begin{array}{*{20}l} {\mu_{z} = \mu } \hfill \\ {\alpha_{2} = \sqrt {{\rm M}_{2} } } \hfill \\ {\alpha_{3} = {\rm M}_{3} /\mu_{z}^{3} } \hfill \\ {\alpha_{4} = {\rm M}_{4} /\mu_{z}^{4} } \hfill \\ \end{array} } \right. $$
    (18)

3.3 Fuzzy response

After obtaining the mean and standard deviation of the response volume Y, we use \(\mu_{y} \pm k(\lambda )\sigma_{y}\) to approximate the range of variation of the response volume Y. \(k(\lambda )\) is a function of \(\lambda\)-cut level that varies with \(\lambda\)-cut level. In this paper, we consider the membership function of fuzzy variable as normal membership function and transformed the fuzzy variables into equivalent normal random variable. The normal membership function [40] is as follows, such fuzzy variables can be denoted as \(\tilde{A} = (a,\alpha^{2} )\):

$$ f(x) = e^{{ - \frac{{(x - a)^{2} }}{{\alpha^{2} }}}} $$
(19)

Referring to a random normal distribution, the fuzzy coefficient of variation (COV) is defined in Eq. (19). Obviously, the larger the COV, the greater the ambiguity of the fuzzy parameters

$$ {\text{COV}} = \frac{\alpha }{a} $$
(20)

From Eq. (5) and Eq. (9), we can obtain the mean \(\mu\) and the standard deviation \(\sigma\) of the equivalent random variable, as follows:

$$ \mu = a,\;\sigma = \frac{\alpha }{\sqrt 2 } $$
(21)

For each \(\lambda\)-cut level, the upper and lower bounds of the fuzzy variable X will be obtained, denoted by the interval \(\left[ {xl,xr} \right]\), as shown in Fig. 2a. From Eq. (19) and Eq. (21), we can obtain the following equation:

$$ \begin{gathered} \left[ {xl,xr} \right] = a + \alpha [ - \sqrt { - \ln \lambda } ,\sqrt { - \ln \lambda } ] \\ = \mu + \sigma [ - \sqrt { - 2\ln \lambda } ,\sqrt { - 2\ln \lambda } ] \\ \end{gathered} $$
(22)
Fig. 2
figure 2

Normal fuzzy membership degree: a upper and lower bounds of the fuzzy variable X; b relationship between fuzzy membership degree and uncertainty level

Full size image

After the interval \(\left[ {xl,xr} \right]\) is obtained by \(\lambda\)-cut set, according to the interval analysis method [41], the interval midpoint \(X^{C}\) and the interval radius \(X^{R}\) are defined as

$$ \begin{gathered} X^{C} = \left( {xl + xr} \right)/2 \hfill \\ X^{R} = \left( {xr - xl} \right)/2 \hfill \\ \end{gathered} $$
(23)

The uncertainty level of the interval is defined as

$$ \gamma = \frac{{X^{R} }}{{\left| {X^{C} } \right|}} \times 100\% $$
(24)

In this paper, the normal fuzzy membership degree is adopted, so the interval midpoint here is a. The uncertainty level of the interval can be obtained as shown in Eq. (25)

$$ \gamma = \frac{xr - xl}{{2a}} = \frac{{2\alpha \sqrt { - \ln \lambda } }}{2a} = COV\sqrt { - \ln \lambda } $$
(25)

As can be seen from Eq. (25) and Fig. 2b, the uncertainty level of the interval increases significantly with the increase of COV. When the COV is determined, the uncertainty level of the interval increases significantly with the increase of \(\lambda\).This means that the smaller the membership degree, the fuzzier the interval obtained after the \(\lambda\)-cut and the higher the uncertainty level of the interval.

Whether triangular fuzzy membership, normal fuzzy membership or other fuzzy membership functions are used to describe the fuzziness of fuzzy parameters, \(\lambda\)- cut are finally carried out to get the corresponding interval, and the uncertainty level of the corresponding interval is calculated. The smaller \(\lambda\) is, the greater the uncertainty level of the interval is. To fully consider the large uncertainty of parameters, this paper takes \(\lambda\) as 0.01.

The upper and lower intervals of the fuzzy variable X can also be represented by the mean and standard deviation of the equivalent random variable and \(k(\lambda )\). We make an approximate assumption that the \(k(\lambda )\) part of the response quantity Y is equivalent to the \(k(\lambda )\) of the upper and lower bound intervals of the fuzzy variable X. We demonstrate in Sect. 4.1 that the assumption is reliable

$$ \begin{gathered} f:x \to y \hfill \\ \left[ {yl,yr} \right] = \mu_{y} + \sigma_{y} [ - \sqrt { - 2\ln \lambda } ,\sqrt { - 2\ln \lambda } ], \hfill \\ \end{gathered} $$
(26)

where \(\mu_{y}\) and \(\sigma_{y}\) denote the mean and standard deviation of the response volume Y, respectively. In the actual problem-solving process, there may be more than one fuzzy variable. Therefore, for the applicable range of n fuzzy variables, Eq. (22) can be rewritten as

$$ \begin{gathered} f_{i} :x_{i} \to y_{i} \hfill \\ f:x_{1} ,x_{2} , \cdots x_{n} \to y \hfill \\ \left[ {yl,yr} \right] = \mu_{y} + \sigma_{y} \cdot \frac{{\sum\limits_{i = 1}^{n} {\sigma_{yi} } }}{{\sqrt {\sum\limits_{i = 1}^{n} {\sigma_{yi}^{2} } } }}[ - \sqrt { - 2\ln \lambda } ,\sqrt { - 2\ln \lambda } ], \hfill \\ \end{gathered} $$
(27)

where \(\sigma_{yi}\) denotes the standard deviation of the ith response volume \(Y_{i}\) obtained by the ith fuzzy variable \(X_{i}\) acting alone, and \(\sigma_{y}\) denotes the standard deviation of the response volume \(Y\) obtained by the interaction of all fuzzy variables.

Certainly, fuzzy membership functions can also be other types of functions, such as triangular membership function, with a similar processing process and unchanged core ideas. Calculate the upper and lower limit intervals through the membership function, expressed in the form of \(\mu_{x} \pm k(\lambda )\sigma_{x}\). We use \(\mu_{y} \pm k(\lambda )\sigma_{y}\) to approximate the range of variation of the response volume Y, and make an approximate assumption that the \(k(\lambda )\) part of the response quantity Y is equivalent to the \(k(\lambda )\) of the upper and lower bound intervals of the fuzzy variable X. The specific verification is shown in Fig. 3 and Table 5.

Fig. 3
figure 3

Fuzzy response with different COVs (0.15 0.20 0.25 0.30): a–d vertical displacement of bridge midspan with fuzzy parameter Eb; e–f vertical acceleration of the 1st train with fuzzy parameter Mc

Full size image

Obviously, when \(\lambda = 1\), the fuzzy variables are transformed into deterministic values, and the response volume is exactly the result obtained by conventional calculations ignoring parameter uncertainty (fuzziness).

4 Fuzzy response of train–bridge-coupled vibration with pier damage

Bridges that have been in operation for an extended period inevitably undergo damage due to various factors, and the extent of this damage is uncertain, varying from significant to minor. Simulating the uncertainty of bridge damage solely through randomness is not accurate enough. The uncertainty of damage is consistent with the definition of fuzziness, which refers to the objective attributes that things exhibit during the intermediate transition process. Fuzziness is very suitable for explaining the uncertainty of parameters such as damage.

Given that the pier constitutes a crucial component of a bridge structure, this article addresses the uncertainty associated with pier damage to investigate the fuzzy response in the coupled vibration of trains and bridges. Pier stiffness reduction is used to simulate bridge pier damage. In the construction and manufacturing of concrete bridges, discrepancies between structural parameters and calibration data are inevitable, introducing uncertainty. Similarly, during train operation, encountering uncertainty in the mass of the train is also unavoidable. The uncertainty arising from both situations can be effectively simulated using the concept of fuzziness. Therefore, the fuzzy variables considered in this paper are the elastic modulus of pier, the concrete density of pier, and the mass of locomotive.

As shown in Table 3, the fuzzy distribution of each parameter obeys the normal fuzzy distribution. The speed of the train passing through the bridge is 250 km/h, and the train grouping is: locomotive + trailer × 2 + locomotive. The detailed parameters of the train can be found in Ref. [42].

Table 3 Fuzzy parameters’ distribution
Full size table

To verify the influence of different fuzzy parameters and different fuzzy distributions on the fuzzy response of train–bridge. The fuzzy coefficient of variation (COV) of the studied fuzzy parameters are 0.10, 0.15, 0.20, 0.25, and 0.30. Five working conditions are studied, as shown in Table 4. The symbol '√' denotes the consideration of a fuzzy parameter, while a blank indicates the exclusion of a parameter from being treated as fuzzy.

Table 4 Fuzzy parameters under different working conditions
Full size table

4.1 Comparison of the fuzzy method with the other researcher’s work

Most dynamic problems are extremely complex and lack analytical solutions. Currently, many researchers use scanning methods to solve fuzzy dynamics problems [17]. After λ is taken, the fuzzy parameter will become an interval number, and the scanning method uniformly takes a large number of values within the interval and substitutes them into the dynamic equation, taking their maximum and minimum values as the fuzzy result. However, the scanning method is evidently characterized by extremely low efficiency.

To verify the feasibility of applying the method proposed in this paper to train–bridge problems, the fuzzy vertical displacement of the bridge midspan with fuzzy parameter (elastic modulus of bridge concrete Eb) and the fuzzy vertical acceleration of the first train with fuzzy parameters (mass of locomotive Mc) were solved, and the results were compared with those calculated by the scanning method. The corresponding parameters are shown in Table 3 and the value of \(\lambda\) is taken as 0.01. From.

Figure 3, IE represents the fuzzy method based on information entropy (proposed method), and SM represents the fuzzy method based on scanning method. It can be seen that the results obtained by the fuzzy method in this paper are very close to those obtained by the scanning method.

As shown in Table 5, the calculation efficiency of this method is much higher than that of the scanning method. It should be noted that when \(\lambda\) is taken as 0.01, the corresponding uncertainty level for the interval with COV of 0.10, 0.15, 0.20, 0.25, and 0.30 are 21.46%, 32.19%, 42.92%, 53.65%, and 64.38%. Many articles believe that when the uncertain level is greater than 20% [43], the problem studied is a large-range uncertainty problem [44]. Therefore, the results in the table are acceptable. For a fuzzy parameter, it only needs to calculate the train–bridge model 7 times, which takes much less time and has good results. Therefore, it is reliable to apply this method to the train–bridge problems.

Table 5 Comparison of the fuzzy method with scanning method
Full size table

4.2 Total damage

Considering the elastic modulus and density of four piers and the mass of locomotive as fuzzy parameters.

4.2.1 Fuzzy response and standard deviation at the top of pier

Taking the fuzzy coefficient of variation \({\text{COV}} = 0.3\), Fig. 4 shows the vertical displacement and standard deviation at the top of pier with different fuzzy parameters. From our computed results, we observed that the maximum amplitude of the fuzzy vertical displacement at the top of the four piers exceeds the conventional vertical response by 37.13%, 36.57%, 35.68%, and 35.96%, respectively.

Fig. 4
figure 4

Vertical displacement and standard deviation at the top of pierwith different fuzzy parameters

Full size image

Figure 5 demonstrates the standard deviation of the response corresponding to the maximum mean vertical displacement at the top of pier. It can be observed that the fuzziness of the elastic modulus of the pier has the greatest influence on the response at the top of pier, and the pier density has a similar influence as the mass of the locomotive. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 5
figure 5

The standard deviation of the response corresponding to the maximum mean vertical displacement at the top of pier with different COVs

Full size image

4.2.2 Fuzzy response and standard deviation of bridge and locomotive

Figure 6 shows the vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters. From our calculation results, we observed that the maximum amplitudes of the fuzzy vertical displacement at the midspan of three spans bridge and the fuzzy vertical acceleration of locomotive exceed the conventional vertical response by 1.77%, 1.74%, 1.43%, and 78.62%, respectively. This also reflects that the elastic modulus of the pier, the density of the pier, and the mass of locomotive have less influence on the vertical displacement of the bridge midspan, and the mass of locomotive has a significant influence on the vertical acceleration of locomotive.

Fig. 6
figure 6

Vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters

Full size image

Figure 7 demonstrates the standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive. It can be observed that the fuzziness of the elastic modulus of pier has the greatest influence on the vertical response of the bridge midspan, and the pier density has a similar influence as the mass of locomotive. The fuzziness of the mass of locomotive has the greatest influence on the vertical acceleration of locomotive, and the elastic modulus of pier has a similar influence as the pier density. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 7
figure 7

The standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive with different COVs

Full size image

4.3 1st Pier damage

Consider the elastic modulus and density of 1st pier and the mass of the locomotive as fuzzy parameters.

4.3.1 Fuzzy response and standard deviation at the top of pier

Taking the fuzzy coefficient of variation \({\text{COV}} = 0.3\). Figure 8 demonstrates the vertical displacement and standard deviation at the top of pier with different fuzzy parameters. From our calculation results, we observed that the maximum amplitude of the fuzzy vertical displacement at the top of the four piers exceeds the conventional vertical response by 35.94%, 0.17%, 0.08%, and 0.05%, respectively.

Fig. 8
figure 8

Vertical displacement and standard deviation of piers with different fuzzy parameters

Full size image

Figure 9 demonstrates the standard deviation of the response corresponding to the maximum mean vertical displacement at the top of the pier. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response at the top of the 1st and 2nd piers, and the fuzziness of the three parameters has a similar influence on the response at the top of 3rd and 4th piers. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 9
figure 9

The standard deviation of the response corresponding to the maximum mean vertical displacement at the pier top with different COVs

Full size image

4.3.2 Fuzzy response and standard deviation of bridge and locomotive

Figure 10 demonstrates the vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters. From the calculation results, it can be observed that the maximum amplitudes of the fuzzy vertical displacement at the midspan of the three span bridge and the fuzzy vertical acceleration of locomotive exceed the conventional vertical response by 0.7%, 0.1%, 0.07%, and 76.96%, respectively.

Fig. 10
figure 10

Vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters

Full size image

Figure 11 demonstrates the standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response of the 1st midspan, and the pier density has a similar influence as the mass of locomotive. The influence of locomotive, the elastic modulus of pier, and the density of pier on the response of the 2nd and 3rd midspan decreases in turn, but they belong to the same order of magnitude. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 11
figure 11

The standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive with different COVs

Full size image

4.4 2nd Pier damage

Consider the elastic modulus and density of 2nd pier and the mass of the locomotive as fuzzy parameters.

4.4.1 Fuzzy response and standard deviation at the top of pier

Taking the fuzzy coefficient of variation \({\text{COV}} = 0.3\). Figure 12 demonstrates the vertical displacement and standard deviation at the top of pier with different fuzzy parameters. From the calculation results, it can be observed that the maximum amplitude of the fuzzy vertical displacement at the top of the four piers exceeds the conventional vertical response by 0.58%, 36.24%, 0.08%, and 0.07%, respectively.

Fig. 12
figure 12

Vertical displacement and standard deviation of piers with different fuzzy parameters

Full size image

Figure 13 shows the standard deviation of the response corresponding to the maximum mean vertical displacement at the top of the pier. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response at the top of the 1st, 2nd, and 3rd piers, and the fuzziness of the three parameters has a similar influence on the response at the top of 4th pier. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 13
figure 13

The standard deviation of the response corresponding to the maximum mean vertical displacement at the pier top with different COVs

Full size image

4.4.2 Fuzzy response and standard deviation of bridge and locomotive

Figure 14 demonstrates the vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters. From the calculation results, it can be observed that the maximum amplitudes of the fuzzy vertical displacement at the midspan of the three spans bridge and the fuzzy vertical acceleration of locomotive exceed the conventional vertical response by 0.77%, 0.88%, 0.08%, and 77.78%, respectively.

Fig. 14
figure 14

Vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters

Full size image

Figure 15 demonstrates the standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response of the 1st and 2nd midspan, the pier density has a similar influence as the mass of locomotive. The influence of locomotive, the elastic modulus of pier, and the density of pier on the response of the 3rd midspan decreases in turn, but they belong to the same order of magnitude. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 15
figure 15

The standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive with different COVs

Full size image

4.5 3rd Pier damage

Consider the elastic modulus and density of 3rd pier and the mass of the locomotive as fuzzy parameters.

4.5.1 Fuzzy response and standard deviation at the top of pier

Taking the fuzzy coefficient of variation \({\text{COV}} = 0.3\). Figure 16 demonstrates the vertical displacement and standard deviation at the top of pier with different fuzzy parameters. From the calculation results, it can be observed that the maximum amplitude of the fuzzy vertical displacement at the top of the four piers exceeds the conventional vertical response by 0.23%, 0.23%, 35.66%, and 0.13%, respectively.

Fig. 16
figure 16

Vertical displacement and standard deviation of piers with different fuzzy parameters

Full size image

Figure 17 demonstrates the standard deviation of the response corresponding to the maximum mean vertical displacement at the top of the pier. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response at the top of the 2nd, 3rd, and 4th piers, and the fuzziness of the three parameters has a similar influence on the response at the top of 1st pier. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 17
figure 17

The standard deviation of the response corresponding to the maximum mean vertical displacement at the pier top with different COVs

Full size image

4.5.2 Fuzzy response and standard deviation of bridge and locomotive

Figure 18 demonstrates the vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters. From the calculation results, it can be observed that the maximum amplitudes of the fuzzy vertical displacement at the midspan of the three spans bridge and the fuzzy vertical acceleration of locomotive exceed the conventional vertical response by 0.19%, 0.92%, 0.88%, and 76.61%, respectively.

Fig. 18
figure 18

Vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters

Full size image

Figure 19 demonstrates the standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response of the 2nd and 3rd midspan, and the pier density has a similar influence as the mass of locomotive. The influence of the elastic modulus of pier, the density of pier, and locomotive on the response of the 1st midspan decreases in turn, but they belong to the same order of magnitude. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 19
figure 19

The standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive with different COVs

Full size image

4.6 4th Pier damage

Consider the elastic modulus and density of 4th pier and the mass of the locomotive as fuzzy parameters.

4.6.1 Fuzzy response and standard deviation at the top of pier

Taking the fuzzy coefficient of variation \({\text{COV}} = 0.3\). Figure 20 demonstrates the vertical displacement and standard deviation at the top of pier with different fuzzy parameters. From the calculation results, it can be observed that the maximum amplitude of the fuzzy vertical displacement at the top of the four piers exceeds the conventional vertical response by 0.22%, 0.21%, 0.06%, and 36.09%, respectively.

Fig. 20
figure 20

Vertical displacement and standard deviation of piers with different fuzzy parameters

Full size image

Figure 21 demonstrates the standard deviation of the response corresponding to the maximum mean vertical displacement at the top of the pier. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response at the top of the 3rd and 4th piers, and the fuzziness of the three parameters has a similar influence on the response at the top of 1st and 2nd piers. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 21
figure 21

The standard deviation of the response corresponding to the maximum mean vertical displacement at the pier top with different COVs

Full size image

4.6.2 Fuzzy response and standard deviation of bridge and locomotive

Figure 22 demonstrates the vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters. From the calculation results, it can be observed that the maximum amplitudes of the fuzzy vertical displacement at the midspan of the three spans bridge and the fuzzy vertical acceleration of locomotive exceed the conventional vertical response by 0.18%, 0.11%, 0.48%, and 76.57%, respectively.

Fig. 22
figure 22

Vertical response and standard deviation of bridge midspan and locomotive with different fuzzy parameters

Full size image

Figure 23 demonstrates the standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive. It can be observed that the fuzziness of the elastic modulus of piers has the greatest influence on the response of the 3rd midspan, the pier density has a similar influence as the mass of locomotive. The fuzziness of the three parameters has a similar influence on the response of the 1st and 2nd midspan. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

Fig. 23
figure 23

The standard deviation of the response corresponding to the maximum mean vertical response at the bridge midspan and locomotive with different COVs

Full size image

5 Conclusion

In this paper, we present a fuzzy computational framework utilizing the information entropy method and the new point estimation method to analyze dynamic train–bridge interactions, accounting for pier damage. The framework is applied to study the train–bridge-coupled vibration system with fuzzy structural parameters. The effectiveness and accuracy of the proposed framework are validated. The following concluding remarks are drawn from our numerical studies and results:

  1. (1)

    The combination of information entropy method and new point estimation method effectively reduces computational complexity, improves computational efficiency, and increases efficiency by 2–3 orders of magnitude compared to scanning method.

  2. (2)

    The fuzziness of the mass of locomotive has the greatest influence on the vertical acceleration of locomotive, and the elastic modulus of pier has a similar influence as the pier density. The standard deviation of the response is approximately linear with the fuzzy coefficient of variation.

  3. (3)

    The fuzziness of the elastic modulus of piers has the greatest influence on the vertical response of the adjacent top of piers and the midspan of the bridge, and the three parameters have a similar influence on the response of non-adjacent places.

  4. (4)

    The response of the train–bridge, when considering damage, significantly surpasses that obtained from conventional deterministic parameter calculations. Investigating the response of the train–bridge-coupled vibration system with fuzzy parameters is crucial for ensuring running safety.