1 Introduction

With the continuous increase of train speed, various problems of train-bridge coupling effects gradually attracted the attention of the engineering community, and many researchers have carried out a lot of research on related issues [1,2,3,4]. The deformation of bridge is closely related to the deformation of track [5,6,7]. The deformation of the bridge is mainly caused by the creep of the bridge, the earthquake action, the settlement of the pier and other reasons, and then the bridge deformation directly affects the safety and comfort of driving by changing the track deformation under the influence of the above reasons [8, 9].

As we all know, seismic design is one of the most important design contents in bridge design. Most of the literatures [10,11,12,13] studied the response of the vehicle-bridge coupling system in earthquake. Wang et al. [14] showed that the influence of the lateral seismic component on the wheel derailment coefficient is greater than the vertical seismic component, and Xia et al. [15] and Zhang et al. [16] studied train-bridge system subjected to non-uniform seismic excitations. However, after the bridge structure is subjected to a relatively large earthquake, there will be a certain degree of residual deformation [17,18,19,20], which directly leads to the deformation of the track, affecting the roughness of the track and then affecting the driving safety after the earthquake. A nonlinear numerical analytical model with multiple degrees of freedom was established to study the cumulative residual deformation of high-speed railway bridge piers under multiple earthquakes [21], but the residual deformation of the structure corresponding to the deformation of the track was not considered. Lai et al. [22] presented an analytical method of track geometry state of high-speed railway bridge under different lateral deformations, which can be conveniently obtained by the lateral displacement of bridge structure caused by external forces.

In the above literature, although the bridge deformation model and the mapping relationship between bridge deformation and track deformation have been established, the vehicle–bridge coupling problem on the deformed track under the influence of earthquake has not been studied. However, the discussion of this problem has important guiding significance for railway transportation after earthquake. At the same time, considering that most high-speed railway bridges are prestressed concrete structures, this type of structure will shrink and creep over time [23], which will cause the rise and fall of the arch of the bridge [24, 25]. Yang et al. [26] showed that the inhomogeneity of periodic creep had a significant excitation effect on both the natural and forced vibration of the vehicle, which would lead to a severe impact on the beam end of the vehicle body, thus significantly increasing the acceleration and contact force of the vehicle body.

Wen et al. [27] showed that the train parameters including load reduction rate, vertical acceleration and vertical Sperling index with temperature and creep effects were significantly different from the train parameters without these effects, indicating that creep has a greater impact on running safety. Although the influence of bridge creep on track deformation and traffic response has been studied in the literature, the comprehensive influence of vehicle–bridge coupling combined with multiple factors of track irregularity corresponding to random initial track irregularity, structural creep and post-earthquake structural residual deformation has not been considered. At the present stage, the problems of vehicle–bridge coupling need to consider the randomness of vehicle-bridge coupling vibration. The traditional deterministic model cannot satisfy the representativeness of the results due to too few excitation samples. The application of randomness can improve the representativeness of the conclusion [28]. Commonly used methods for studying randomness mainly include MCS [29], PEM [30, 31] and PDEM [32]. Compared with the former two methods, multi-coupling excitation, such as track irregularity excitation, random vehicle load and random structural parameters, can be input into the vehicle-to-bridge coupling model established through PDEM, which greatly improves the computational efficiency [33]. Xu et al. [34] applied a probability density evolution method to solve the relationship between random track irregularity and system response, which has been turned out to be fairly effective [35, 36]. Liu [37] proposed a point estimation method (NPEM) based on adaptive dimension decomposition, which is simple to implement and highly efficient. Literatures [38,39,40] all used this method to solve special problems. Liu [41] analysed the influence of multiple random parameters, including random track irregularity and structural parameters, on the vehicle-axle system by combining Karhunen–Loeve expansion (KLE) and this method, and compared with MCS. It is found that the accuracy and efficiency are very high. This paper also uses this method to analyse the stochastic process.

In order to study the comprehensive effect of residual deformation and structural creep caused by earthquake on the response of vehicle and bridge system, a three-dimensional vehicle–bridge coupling model is established based on the randomness of initial track irregularity and the influence of comprehensive working conditions on track irregularity. KLE is used to reduce the dimension of initial track irregularity. The random process of the vehicle–bridge coupling system is analysed by using NPEM, and the effects of different ground motion amplitudes and different train speeds on the system response are studied.

2 Model and Method

2.1 Bridge and Track Models

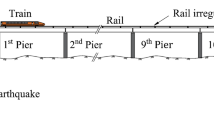
As shown in Fig. 1, the main body of the bridge is composed of prestressed box girder and prestressed pier, and the track is composed of rail, track plate and base plate. In the model, the rail, beam and pier are all modelled using Bernoulli–Euler beams, and the mass and mass moment of inertia of the foundation on the bridge are included in the beam. The track plate and the base plate are thin plates. In addition, based on the finite element method, the rail, beam and pier are transformed into a series of spatial beam elements, and the track plate and base plate are transformed into plane plate elements. It is easy to know that the longitudinal, transverse and vertical elastic and damping characteristics between each of structure divisions can be simulated with discrete or continuous springs and dampers, the coefficient of which can be obtained from Fig. 1. In addition, each beam element has two nodes, and each node has six degrees of freedom. Each plate element has four nodes, and each node has three degrees of freedom.

Fig. 1
figure 1

Train-Track -Bridge Mode

Full size image

2.2 Train Model

As shown in Fig. 2, it is assumed that the car body, bogie and wheelset are rigid bodies. The connections between the car body and the bogie, and between the bogie and the wheelset (spring, buffer) are linear. Meanwhile, it is assumed that the wheelset is always closely attached to the rail throughout the whole process, that is, derailment will not occur. In this paper, the degrees of freedom of each car are shown in Table 1.

Fig. 2
figure 2

Three-dimensional model for train–slab track–bridge interaction system: a frontal view, b jth trailer car moving on jth span girder, c left side view, and d top view (without bridge)

Full size image
Table 1 Degrees of freedom of train
Full size table

According to Ref. [42], the total mass matrix \({M}_{v}\) the total stiffness \({K}_{v}\) and the total damping matrix \({C}_{v}\) of the whole train can be deduced according to the energy principle.

Considering that a complete train should contain power cars at the front and rear ends and non-power cars in the middle, the total mass matrix \({M}_{v}\) is expressed as follows:

$$ M_{vv} = {\text{diag}}\left[ {M_{Jv1} \, M_{v1} \, \ldots \, M_{vNv} \, M_{Jv2} } \right], $$
(1)

where the ones with subscripts containing 'J ' denote the power carriages, the others denote the non-power carriages, \({N}_{v}\) denotes the total number of non-power carriages, and the submatrix \({M}_{vi}\) denotes the mass matrix of each carriage, which takes the following form:

$$ M_{vi} = {\text{diag}}\left[ {M_{ci} \, M_{t2i} \, M_{w1i} \, M_{w2i} \, M_{w3i} \, M_{w4i} } \right], $$
(2)

where, \({M}_{ci}\), \({M}_{tji}\) and \({M}_{wji}\) denote the mass matrix of the car-body, the jth bogie and the jth wheelset of the ith train, which takes the following form:

$$ M_{ci} = {\text{diag}}\left[ {\begin{array}{*{20}c} {m_{ci} } & {m_{ci} } & {m_{ci} } & {J_{cxi} } & {J_{cyi} } & {J_{czi} } \\ \end{array} } \right] $$
(3)
$$ M_{tji} = {\text{diag}}\left[ {\begin{array}{*{20}c} {m_{ti} } & {m_{ti} } & {m_{ti} } & {J_{txi} } & {J_{tyi} } & {J_{tzi} } \\ \end{array} } \right] $$
(4)
$$ M_{wji} = {\text{diag}}\left[ {\begin{array}{*{20}c} {m_{wi} } & {m_{wi} } & {J_{wxi} } & {J_{wzi} } \\ \end{array} } \right], $$
(5)

where \({m}_{ci}\), \({m}_{ti}\) and \({m}_{wi}\) denote the mass of car body, bogie and wheelset. \({J}_{cji}\), \({J}_{tji}\) and \({J}_{wji}\), respectively, denote the moment of inertia of the car body, bogie and wheelset, which, respectively, represent the moment of inertia about the longitudinal, transverse and vertical axes when the subscript \(j\) is \(x\), \(y\) or \(z\). The form of the mass matrix of the power car is the same as that of the non-power car, obtained by adding "\(J\)" before the subscript of these letters.

Respectively, considering that the train carriages are divided into power carriages and non-power carriages, the total stiffness matrix \(K_{v}\) of the train takes the following form:

$$ K_{vv} = {\text{diag}}\left[ {K_{Jv1} \, K_{v1} \, \ldots \, K_{vNv} \, K_{Jv2} } \right], $$
(6)

where the one with subscript '\(J\)' denotes power cars, and the others denote non-power cars; \({K}_{vi}\) denotes the stiffness matrix of the ith carriage, which can be expressed as

$$ K_{vi} { = }\left[ {\begin{array}{*{20}c} {K_{ci} } & {K_{ct1i} } & {K_{ct2i} } & 0 & 0 & 0 & 0 \\ {} & {K_{t1i} } & 0 & {K_{t1wi} } & {K_{t1w2i} } & 0 & 0 \\ {} & {} & {K_{t2i} } & 0 & 0 & {K_{t2w3i} } & {K_{t2w4i} } \\ {} & {} & {} & {K_{w1i} } & 0 & 0 & 0 \\ {} & {} & {} & {} & {K_{w2i} } & 0 & 0 \\ {} & {} & {} & {} & {} & {K_{w3i} } & 0 \\ {syms} & {} & {} & {} & {} & {} & {K_{w4i} } \\ \end{array} } \right]. $$
(7)

The submatrix \(K_{ci}\) is expressed as

$$ K_{ci} = 4\left[ {\begin{array}{*{20}c} {k_{2x} } & 0 & 0 & 0 & { - h_{1} k_{2x} } & 0 \\ {} & {k_{2y} } & 0 & {h_{1} k_{2y} } & 0 & 0 \\ {} & {} & {k_{2z} } & 0 & 0 & 0 \\ {} & {} & {} & {b_{1}^{2} k_{2z} + h_{1}^{2} k_{2y} } & 0 & 0 \\ {} & {} & {} & {} & {h_{1}^{2} k_{2x} + L_{c}^{2} k_{2z} } & 0 \\ {syms} & {} & {} & {} & 0 & {b_{3}^{2} k_{2x} + L_{c}^{2} k_{2y} } \\ \end{array} } \right]. $$
(8)

The submatrix \(K_{tji}\) is expressed as

$$ K_{tji} = 2\left[ {\begin{array}{*{20}c} {2k_{1x} + k_{2x} } & 0 & 0 & 0 & { - 2h_{3} k_{1x} - h_{2} k_{2x} } & 0 \\ {} & {2k_{1y} + k_{2y} } & 0 & {2h_{3} k_{1y} } & 0 & 0 \\ {} & {} & {2k_{1z} + k_{2z} } & 0 & 0 & 0 \\ {} & {} & {} & {\left( \begin{gathered} b_{1}^{2} k_{2z} + 2b_{2}^{2} k_{1z} \hfill \\ + h_{2}^{2} k_{2y} + 2h_{3}^{2} k_{1y} \hfill \\ \end{gathered} \right)} & 0 & 0 \\ {} & {} & {} & 0 & \begin{gathered} \left( \begin{gathered} h_{2}^{2} k_{2x} + 2h_{3}^{2} k_{1x} \hfill \\ + 2L_{t}^{2} k_{1z} \hfill \\ \end{gathered} \right) \hfill \\ \hfill \\ \end{gathered} & 0 \\ {syms} & {} & {} & {} & {} & {\left( \begin{gathered} b_{3}^{2} k_{2x} + 2b_{4}^{2} k_{1x} \hfill \\ + 2L_{t}^{2} k_{1y} \hfill \\ \end{gathered} \right)} \\ \end{array} } \right]. $$
(9)

The submatrix \(K_{wji}\) is expressed as

$$ K_{wji} = 2\left[ {\begin{array}{*{20}c} {k_{1x} } & {} & {} & {} \\ {} & {k_{1y} } & {} & {} \\ {} & {} & {b_{0}^{2} k_{1z} } & {} \\ {syms} & {} & {} & {b_{4}^{2} k_{1x} } \\ \end{array} } \right]. $$
(10)

The submatrix \(K_{ctji}\) is expressed as

$$ K_{ctji} = - 2\left[ {\begin{array}{*{20}l} {k_{2x} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {h_{1} k_{2x} } \hfill & 0 \hfill \\ 0 \hfill & {k_{2y} } \hfill & 0 \hfill & { - h_{2} k_{2y} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {k_{2z} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {h{}_{1}k_{2y} } \hfill & 0 \hfill & {b_{1}^{2} k_{2z} - h_{1} h_{2} k_{2y} } \hfill & 0 \hfill & 0 \hfill \\ { - h_{1} k_{2x} } \hfill & 0 \hfill & {\left( { - 1} \right)^{j} L_{c} k_{2z} } \hfill & 0 \hfill & { - h_{1} h_{2} k_{2x} } \hfill & 0 \hfill \\ 0 \hfill & {\left( { - 1} \right)^{j + 1} L_{c} k_{2y} } \hfill & 0 \hfill & {\left( { - 1} \right)^{j} h_{2} L_{c} k_{2y} } \hfill & 0 \hfill & {b_{3}^{2} k_{2x} } \hfill \\ \end{array} } \right]. $$
(11)

The submatrix \(K_{tjwki}\) is expressed as

$$ K_{tjwki} = - 2\left[ {\begin{array}{*{20}l} {k_{1x} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {k_{1y} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & h \hfill & {\left( { - 1} \right)^{k + 1} b_{0} b_{2} k_{1z} } \hfill & 0 \hfill \\ { - h_{3} k_{1x} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\left( { - 1} \right)^{k} L_{1} k_{1y} } \hfill & 0 \hfill & {b_{4}^{2} k_{1x} } \hfill \\ \end{array} } \right]. $$
(12)

The damping matrix \({C}_{vv}\) of the train model is in the same form as the stiffness matrix \({K}_{vv}\), which can be obtained by replacing k of the latter with c directly.

2.3 Wheel–Rail Interaction

In this paper, trace method is used to calculate the wheel-rail spatial contact relationship. As shown in Fig. 3, its wheel–rail contact point \({O}_{R}\) coordinates in the absolute coordinate system and takes form as [43], as shown in Fig. 3.

$$ \left\{ {\begin{array}{*{20}l} {x_{{O^{R} }} = x_{B}^{R} + l_{x} R_{w}^{R} \tan \delta^{R} } \hfill \\ {y_{{O^{R} }} = y_{B}^{R} - \frac{{R_{w}^{R} }}{{1 - l_{x}^{2} }}\left( {l_{x}^{2} l_{y}^{2} \tan \delta^{R} + l_{z} \sqrt {1 - l_{x} \left( {1 + \tan^{2} \delta^{R} } \right)} } \right)} \hfill \\ {z_{{O^{R} }} = z_{B}^{R} - \frac{{R_{w}^{R} }}{{1 - l_{x}^{2} }}\left( {l_{x}^{2} l_{z}^{2} \tan \delta^{R} - l_{y} \sqrt {1 - l_{x} \left( {1 + \tan^{2} \delta^{R} } \right)} } \right)} \hfill \\ \end{array} } \right. $$
(13)
$$ \left\{ {\begin{array}{*{20}l} {l_{x} = - \cos \phi_{w} \sin \psi_{w} } \hfill \\ {l_{y} = \cos \phi_{w} \cos \psi_{w} } \hfill \\ {l_{z} = \sin \phi_{w} } \hfill \\ \end{array} } \right. $$
(14)
$$ \left\{ {\begin{array}{*{20}l} {x_{B}^{R} = d_{w}^{R} l_{x} } \hfill \\ {y_{B}^{R} = d_{w}^{R} l_{y} + Y_{w} } \hfill \\ {z_{B}^{R} = d_{w}^{R} l_{z} } \hfill \\ \end{array} } \right., $$
(15)

where the specific meaning of the letters in the picture can be referred to Ref. [43].

Fig. 3
figure 3

Wheel-rail geometric contact

Full size image

At present, the solution of wheel-rail normal force is generally based on the Hertz nonlinear elastic contact theory [44]. Although the residual deformation caused by the seismic plastic deformation was taken into account in the irregularity of the track, the model was built after the earthquake. It was assumed that the rail remained elastic throughout the whole process, and the stiffness degradation was not considered, so Hertz elastic contact theory could still be used. By the way, although the model is set after the earthquake and the structure has undergone plastic deformation, the Hertz elastic contact theory can still be used if the rail remains elastic throughout the whole process and the stiffness degradation is not taken into account. The normal compression can be found in Ref. [41].

2.4 Seismic-Induced Track Irregularity

Lai et al. [45] established the finite element model with ANSYS program and verified the reliability of the model with the results of shaking table test. The track deformations at the seismic conditions of the ground motion acceleration amplitude of 0.1 g, 0.2 g, 0.3 g and 0.4 g are obtained, as shown in Fig. 4. In this work, the data will be directly applied into the track irregularity.

Fig. 4
figure 4

Rail irregularity caused by residual structural deformation

Full size image

2.5 Bridge-Creep-Induced Track Irregularity

In prestressed concrete girder bridges, concrete creep often leads to excessive deflection of the bridge and indirectly leads to vertical deformation of the rail of the track [24]. Thus, the creep is not smooth and has a great impact on running safety and comfort, so the creep of the girder bridge cannot be ignored [27].

Xiang et al. [46] established the mapping relationship between track deformation and bridge creep amplitude. Based on this method and results, the track deformation under different creep amplitude of bridge is directly obtained in this paper, as shown in Fig. 5.

Fig. 5
figure 5

Irregularity of the rail for different attitudes of creep

Full size image

2.6 Simulation of Initial Track Irregularity

Before the track is affected by earthquake, there is an original track irregularity, which is a random process. In this paper, KLE will be applied on multiple samples to investigate the randomness effect of initial track irregularity.

2.6.1 Simulate Method of Track Irregularity

The initial sample can be generated by multiple methods, including white noise filtering method, secondary filtering method, trigonometric series method and inverse Fourier inverse transformation method. In this work, trigonometric series method [47] is applied to generate the initial track irregularity by the German low-disturbance power spectral density (PSD).

German low interference orbit irregularity spectrum can be expressed as

$$ \left\{ {\begin{array}{*{20}c} {S_{v} \left( \Omega \right) = \frac{{A_{v} \Omega_{c}^{2} }}{{\left( {\Omega^{2} + \Omega_{r}^{2} } \right)\left( {\Omega^{2} + \Omega_{c}^{2} } \right)}}} \\ {S_{a} \left( \Omega \right) = \frac{{A_{a} \Omega_{c}^{2} }}{{\left( {\Omega^{2} + \Omega_{r}^{2} } \right)\left( {\Omega^{2} + \Omega_{c}^{2} } \right)}}} \\ \end{array} } \right., $$
(16)

where \({S}_{v}\left(\Omega \right)\) and \({S}_{a}\left(\Omega \right)\) (\({\mathrm{m}}^{2}/\left(\mathrm{rad}/\mathrm{m}\right)\)) denote the power spectral density of high and low orbit irregularity; \(\Omega\) denotes the spatial frequency of orbital irregularity (\(\mathrm{rad}/\mathrm{m}\)); \({\Omega }_{c}\) and \({\Omega }_{r}\) denote the truncation frequency (\(\mathrm{rad}/\mathrm{m}\)); \({A}_{a}\) and \({A}_{v}\) denote the roughness constant (\({\mathrm{m}}^{2}\cdot \mathrm{rad}/\mathrm{m}\)). The value of parameters can be found in Table 2.

Table 2 Parameters of orbital irregularity spectrum
Full size table

Sample Generation Formula of vertical track irregularity can be expressed as

$$ \tilde{z}_{R} (x) = \sqrt 2 \sum\limits_{i = 1}^{n} {\sqrt {S_{v} \left( {\Omega_{i} } \right)\Delta \Omega } } \cos \left( {\Omega_{i} x + \phi_{i} } \right) $$
(17)
$$ \left\{ {\begin{array}{*{20}l} {\Delta \Omega = \left( {\Omega_{n} - \Omega_{1} } \right)/n} \hfill \\ {\Omega_{i} = \Omega_{1} + \Delta \Omega \left( {i - 1} \right) \, \left( {i = 1,2, \ldots ,n} \right)} \hfill \\ \end{array} } \right., $$
(18)

where \({\Omega }_{1}\)= 0 rad/m and \({\Omega }_{n}\)= 3 rad/m.

The sample generation formula of track alignment irregularity is similar to the one of vertical irregularity. The samples are shown in Fig. 6a. The PSD of samples of track irregularity is very close to the target spectrum, which denotes that the samples can be used for simulating the track irregularity. The simulated spectrum is similar to the target spectrum as shown in Fig. 6b, providing that the examples can be used to numerical analysis. The generation process and inspection result of horizon track irregularity are the same as those of the vertical ones.

Fig. 6
figure 6

a Primary track irregularity along rail on vertical rail profile. b The PSD of primary track irregularity along rail on vertical rail profile

Full size image

2.6.2 Karhunen–Loeve Expansion (KLE)

KLE expansion is a method for representing random processes and is useful for random signal processing. The realization process is to compress the original data and obtain the expression with sufficient probability information of the original data by using fewer random variable dimensions.

It is assumed that \(u\left(x,\theta \right)\) is the Gaussian random distribution process, \(x\) and \(\theta \) are the position variable and parameter variable of the random process. Correspondingly, \(\overline{u}\left( x \right)\) is the mean value of \(u\left(x,\theta \right)\). It is the covariance function of a random process. According to Mercer theory, the covariance function can be expressed as

$$ C\left( {x_{1} ,x_{2} } \right) = \sum\limits_{n = 1}^{\infty } {\lambda_{n} \varphi_{n} \left( {x_{1} } \right)} \varphi_{n} \left( {x_{2} } \right), $$
(19)

where \({\lambda }_{n}\) and \({\varphi }_{n}\) are the eigenvalues and eigenvectors of \(C\left({x}_{1},{x}_{2}\right)\), and the above equation can be solved using the following equation:

$$ \int_{D} {C\left( {x_{1} ,x_{2} } \right)} \varphi_{n} \left( {x_{1} } \right){\text{d}}x = \lambda_{n} \varphi_{n} \left( {x_{2} } \right). $$
(20)

The eigenvector meets orthogonality, which is described as

$$ \int\limits_{D} {\varphi_{n} \left( {x_{1} } \right)} \varphi_{m} \left( {x_{2} } \right){\text{d}}x = \delta_{nm} , $$
(21)

where \({\delta }_{nm}\) is the Kronecker function, which is described as

$$ \delta_{nm} = \left\{ {\begin{array}{*{20}c} 1 & {n = m} \\ 0 & {n \ne m} \\ \end{array} } \right.. $$
(22)

Therefore, stochastic process \(u\left(x,\theta \right)\) can be obtained by

$$ u\left( {x,\theta } \right) = \overline{u}\left( {x,\theta } \right) + \tilde{u}\left( {x,\theta } \right) = \overline{u}\left( {x,\theta } \right) + \sum\limits_{n = 1}^{\infty } {\xi_{n} } \left( \theta \right)\sqrt {\lambda_{n} } \varphi_{n} , $$
(23)

where \(\xi \left(\theta \right)\) is a set of unrelated random variables, which can be obtained by

$$ \xi \left( \theta \right) = \frac{1}{{\sqrt {\lambda_{n} } }}\int_{D} {\tilde{u}\left( {x,\theta } \right)} \varphi_{n} \left( x \right){\text{d}}x. $$
(24)

In practical application, it is only necessary to extract the first M eigenvectors and the corresponding eigenvalue to achieve data compression and reduce the amount of calculation. The modified stochastic process takes the form of

$$ u\left( {x,\theta } \right) = \overline{u}\left( {x,\theta } \right) + \sum\limits_{n = 1}^{M} {\xi_{n} } \left( \theta \right)\sqrt {\lambda_{n} } \varphi_{n} , $$
(25)

where M determines the accuracy of data compression.

In this paper, it is assumed that the initial track irregularity is a one-dimensional stationary random process, and the vertical rail irregularity and the lateral one are unrelated. For each total length of artificial rail irregularity, the work has been done that a set of variable point have been taken at intervals of \(\Delta x\) along the longitudinal direction, while each sample has \(\left(L/dx+1\right)\) points.

Sufficient samples are obtained through the previous method of artificially generating rail irregularities. Assuming M samples are obtained, the total sample is \(R\left(x,\theta \right)=\left\{\begin{array}{cccc}{r}_{1}\left(x,\theta \right)& {r}_{2}\left(x,\theta \right)& \cdots & {r}_{n}\left(x,\theta \right)\end{array}\right\}\), and any sample vector \({r}_{i}\left(x,\theta \right)\) is the vector sample of \(n\times 1\), while \(n=L/\mathrm{d}x+1\).

The corresponding covariance formula \({\Gamma }_{R,R}\) is as follows

$$ \Gamma_{R,R} = \left[ {\begin{array}{*{20}c} {C\left( {r\left( {x_{1} ,\theta } \right),r\left( {x_{1} ,\theta } \right)} \right)} & \cdots & {C\left( {r\left( {x_{1} ,\theta } \right),r\left( {x_{j} ,\theta } \right)} \right)} & \cdots & {C\left( {r\left( {x_{1} ,\theta } \right),r\left( {x_{n} ,\theta } \right)} \right)} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {C\left( {r\left( {x_{i} ,\theta } \right),r\left( {x_{1} ,\theta } \right)} \right)} & \cdots & {C\left( {r\left( {x_{i} ,\theta } \right),r\left( {x_{j} ,\theta } \right)} \right)} & \cdots & {C\left( {r\left( {x_{i} ,\theta } \right),r\left( {x_{n} ,\theta } \right)} \right)} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {C\left( {r\left( {x_{n} ,\theta } \right),r\left( {x_{1} ,\theta } \right)} \right)} & \cdots & {C\left( {r\left( {x_{n} ,\theta } \right),r\left( {x_{j} ,\theta } \right)} \right)} & \cdots & {C\left( {r\left( {x_{n} ,\theta } \right),r\left( {x_{n} ,\theta } \right)} \right)} \\ \end{array} } \right]_{n \times n} . $$
(26)

The eigenvalues and eigenvectors can be obtained by

$$ \left( {\Gamma_{R,R} \Delta x} \right)\varphi_{i} - \lambda_{i} \varphi_{i} = 0. $$
(27)

Then the random process function is obtained through KLE \(r\left( {x,\theta } \right)\) as

$$ r\left( {x,\theta } \right) = \overline{r}\left( {x,\theta } \right) + \sum\limits_{i = 1}^{M} {\sqrt {\lambda_{i} } \xi_{i} \left( \theta \right)\varphi_{i} \left( x \right)} . $$
(28)

where \(\overline{r}\left( {x,\theta } \right)\) is the mean of \(R\left(x,\theta \right)\).

In this paper, 5000 samples are generated by manually generating track irregularities, and 5000 sampling points are taken along the longitudinal direction, which are separated by 0.2 m. \({\lambda }_{i}\) and \({\varphi }_{i}\) are obtained by Equations [20, 21], 130 terms of which are used to generate new samples of stochastic track irregularities. To test the accuracy of new samples, 5000 samples are generated by these 130 items to be compared with 5000 samples without KLE. As the difference of the mean and variance of these two sets of samples is almost zero according to Fig. 7, it can be verified that the 130 items obtained from KLE can represent the majority of rail irregularity.

Fig. 7
figure 7

Comparison of rail irregularity between KLE and TSM on vertical rail profile

Full size image

2.7 Comprehensive Simulation Model of Track Irregularity

After obtaining the KLE expression for the stochastic process of track irregularities, the track irregularities caused by bridge creep and the track irregularities caused by earthquake need to be added to the track irregularities part of the expression. Considering that the artificially generated track irregularity is a Gaussian random process with an average value of 0 [47], i.e. \(\overline{r}\left( {x,\theta } \right) = 0\), the corresponding track irregularity and track irregularity can be expressed as follows:

$$ \left\{ {\begin{array}{*{20}c} {r_{z} \left( {x,\theta } \right) = r_{z}^{{{\text{creep}}}} \left( x \right) + \left( {\sum\limits_{i = 1}^{M} {\sqrt {\lambda_{i} } \xi_{i} \left( \theta \right)\varphi_{i} \left( x \right)} } \right)_{z} } \\ {r_{y} \left( {x,\theta } \right) = r_{y}^{{{\text{earth}}}} \left( x \right) + \left( {\sum\limits_{i = 1}^{M} {\sqrt {\lambda_{i} } \xi_{i} \left( \theta \right)\varphi_{i} \left( x \right)} } \right)_{y} } \\ \end{array} } \right.. $$
(29)

2.8 Dynamic Equation of TTBS

According to the energy principle, it is easy to establish the dynamic equation of TTBS as

$$ \begin{gathered} \left[ {\begin{array}{*{20}l} {M_{vv} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {M_{rr} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {M_{ss} } \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {M_{bb} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {M_{gg} } \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {M_{pp} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\ddot{X}_{vv} } \hfill \\ {\ddot{X}_{rr} } \hfill \\ {\ddot{X}_{ss} } \hfill \\ {\ddot{X}_{bb} } \hfill \\ {\ddot{X}_{gg} } \hfill \\ {\ddot{X}_{pp} } \hfill \\ \end{array} } \right]{ + }\left[ {\begin{array}{*{20}l} {C_{vv} } \hfill & {C_{vr} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {C_{rv} } \hfill & {C_{rr} } \hfill & {C_{rs} } \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {C_{sr} } \hfill & {C_{ss} } \hfill & {C_{sb} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {C_{bs} } \hfill & {C_{bb} } \hfill & {C_{bg} } \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {C_{gb} } \hfill & {C_{gg} } \hfill & {C_{gp} } \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {C_{pg} } \hfill & {C_{pp} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\dot{X}_{vv} } \hfill \\ {\dot{X}_{rr} } \hfill \\ {\dot{X}_{ss} } \hfill \\ {\dot{X}_{bb} } \hfill \\ {\dot{X}_{gg} } \hfill \\ {\dot{X}_{pp} } \hfill \\ \end{array} } \right] \hfill \\ { + }\left[ {\begin{array}{*{20}l} {K_{vv} } \hfill & {K_{vr} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {K_{rv} } \hfill & {K_{rr} } \hfill & {K_{rs} } \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {K_{sr} } \hfill & {K_{ss} } \hfill & {K_{sb} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {K_{bs} } \hfill & {K_{bb} } \hfill & {K_{bg} } \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {K_{gb} } \hfill & {K_{gg} } \hfill & {K_{gp} } \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {K_{pg} } \hfill & {K_{pp} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {X_{vv} } \hfill \\ {X_{rr} } \hfill \\ {X_{ss} } \hfill \\ {X_{bb} } \hfill \\ {X_{gg} } \hfill \\ {X_{pp} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {F_{v} } \hfill \\ {F_{r} } \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right], \hfill \\ \end{gathered} $$
(30)

where \({X}_{vv}\), \( {X}_{rr}\), \({X}_{ss}\), \({X}_{{b}^{\mathrm{^{\prime}}}{b}^{\mathrm{^{\prime}}}}\), \({X}_{bb}\) and \({X}_{pp}\) denote the displacement of train, rail, track plate, base plate, main girder and bridge pier, respectively.

After obtaining the relevant global matrix and load column vector, the time-history analysis operation is carried out by the \(\mathrm{Newmark}-\beta \) method of step-by-step integration, and the system response data can be obtained.

2.9 New Point Estimation Method

Jiang et al. [41] proposed that when there are multiple random variables in the system and considering that the variables may be interrelated, the application of the new point estimation method (NPEM) can obtain the system response data more efficiently than MCS, so this work adopts NPEM in the simulation of the system response.

At the time t, the mean value \(\mu \left(t\right)\) and variance \({\sigma }^{2}\left(t\right)\) of the system time history response are expressed as

$$ \begin{gathered} \mu \left( t \right) \approx \sum\limits_{l < m} {E\left[ {h\left( {X_{l} ,X_{m} ,u_{c} ,t} \right)} \right]} - \left( {n - 2} \right)\sum\limits_{k = 1}^{n} {E\left[ {h\left( {X_{k} ,u_{c} ,t} \right)} \right]} \\ + \frac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2}h\left( {u_{c} ,t} \right), \\ \end{gathered} $$
(31)
$$ \begin{gathered} \sigma^{2} \left( t \right) \approx \sum\limits_{l < m} {E\left[ {h\left( {X_{l} ,X_{m} ,u_{c} ,t} \right) - \mu \left( t \right)^{2} } \right]} - \left( {n - 2} \right) \\ \sum\limits_{k = 1}^{n} {E\left[ {h\left( {X_{k} ,u_{c} ,t} \right) - \mu \left( t \right)^{2} } \right]} + \frac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2} \\ \left[ {h\left( {u_{c} ,t} \right) - \mu \left( t \right)} \right]^{q} , \\ \end{gathered} $$
(32)

where \(h\left({X}_{l},t\right)\) denotes the response of the system when only considering that the first variable is random and the other variables are deterministic.

$$ E\left[ {\left( {h\left( {X_{l} ,u_{c} ,t} \right) - \mu \left( t \right)} \right)^{2} } \right] = \sum\limits_{i = 1}^{r} {\frac{{w_{GH,i} }}{\sqrt \pi }} \left( {h\left( {X_{l,i} ,u_{c} ,t} \right) - \mu \left( t \right)} \right)^{2} , $$
(33)
$$ E\left[ {\left( {h\left( {X_{l} ,X_{m} ,u_{c} ,t} \right) - \mu \left( t \right)} \right)^{2} } \right] = \sum\limits_{i = 1}^{r} {\frac{{w_{GH,i} w_{GH,j} }}{\sqrt \pi }} \left( {h\left( {X_{l,i} ,X_{m,j} ,u_{c} ,t} \right) - \mu \left( t \right)} \right)^{2} , $$
(34)

where ith and jth, respectively, denote ith and jth Gauss point; lth and mth, respectively, denote \({l}^{th}\) and \({m}^{th}\) random variable

$$ X_{l,i} = \left[ {\begin{array}{*{20}c} {x_{c} } & {x_{c} } & \cdots & {\sqrt 2 x_{GH,li} } & \cdots & {x_{c} } & {x_{c} } \\ \end{array} } \right], $$
(35)

where \({x}_{GH,li}\) and \({w}_{GH,i},\) respectively, denote the abscissa and weight of distribution of \({l}^{th}\) variable, when \({x}_{c}\) is the determined value of the other variables.

As shown in Table 3, the random variable is zero when the \({x}_{GH,l2}\) is zero. The total random variable can be described as \({X}_{l,2}=\left[\begin{array}{ccccccc}{x}_{c}& {x}_{c}& \cdots & 0& \cdots & {x}_{c}& {x}_{c}\end{array}\right]\), with the corresponding random process result of \(h\left({X}_{l2},t\right)\). When all random variables are considered as constants, the corresponding total constants are \({u}_{c}=\left[\begin{array}{ccccccc}{x}_{c}& {x}_{c}& \cdots & {x}_{c}& \cdots & {x}_{c}& {x}_{c}\end{array}\right]\) and the corresponding random process result is \(h\left({u}_{c}\right)\). When the random variable is constant, it is exactly equal to the case when the variable takes the Gaussian point as the middle point. Therefore, \(h\left({X}_{l2},t\right)\) and \(h\left({u}_{c},t\right)\) belong to the same situation, calculation times can be greatly reduced. The total rail irregularity can be described as

$$ \left\{ {\begin{array}{*{20}c} {r_{z} \left( {x,\theta } \right) = r_{z}^{{{\text{creep}}}} } \\ {r_{y} \left( {x,\theta } \right) = r_{y}^{{{\text{residue}}}} } \\ \end{array} } \right.. $$
(36)
Table 3 Value of Gauss point
Full size table

With this rail irregularity sample as the excitation, it is substituted into the vehicle and axle system, and the response \(h\left({X}_{l2},t\right)\) and \(h\left({u}_{c},t\right)\) can be obtained.

Taking vertical irregularity establishing as an example, the orbit irregularities of any Gaussian point corresponding to any random variable are as follows:

$$ r_{li}^{z} \left( {x,\theta } \right) = r_{z}^{{{\text{creep}}}} \left( x \right) + \sqrt 2 x_{GH,li} \sqrt {\lambda_{n} } \varphi_{n} \left( x \right) $$
(37)
$$ r_{c}^{z} = r_{z}^{{{\text{creep}}}} . $$
(38)

The establishment of track alignment irregularity is consistent with the establishment of vertical irregularity.

3 Result and Analysis of Dynamic Response

A 5-span prestressed concrete simply supported beam model is established. Each span is 32.5 m long, and the pier is 14 m high. The German ICE-3 train carriage model is adopted as the train model, and the LM model is adopted for the wheel. The structural parameters of train and bridge are shown in Tables 4 and 5. The initial track irregularity is generated by the German low interference track power spectrum. KLE-NPEM is used to analyse the dynamic responses of random vibration of the vehicle-bridge coupling system, and the combined effects of residual deformation, bridge creep and initial track irregularities are also considered. For the upper and lower limits of the system response, the range of \(\left[\mu -3\sigma ,\mu +3\sigma \right]\) is adopted, and the maximum absolute value is taken as the maximum value of system response.

Table 4 Parameters of train
Full size table
Table 5 Parameters of PSC bridge
Full size table

3.1 Comparison Between MCS and NPEM

In order to verify the accuracy and efficiency of NPEM, MCS is mainly used. For the purpose of comparing MCS and KLE-NPEM, a specific case was selected with a train speed of 200 km/h, a creep amplitude of 8 mm and a seismic acceleration of 0.2 g, and the randomness of the original track irregularity is considered.

According to the calculation, MCS conducts statistics through a large number of random initial irregularity samples of the track. In this case, the total number of calculation times of the model is 5000. KLE-NPEM conducts statistics by obtaining representative specific random samples from random samples through KLE, and intercepts the first 130 items in total. A total of 3 Gaussian points are considered for each specific random sample, so the total number of calculations is \(\left(130\times 2+1\right)\).

Figure 8 represents the mean and variance of the time-history responses of the vertical displacement and acceleration in the mid-span of the third span main girder. It also represents the process of the train passing through the bridge. When the train has not entered the bridge, the bridge is not affected, and the mean and variance of the main girder are 0. When the train is on the bridge, the displacement starts to change, but it is relatively small. When it increases to a certain value, the change tends to be stable. The peak MEAN values calculated by NPEM and MCS were 1.2572 mm and 1.2619 mm, respectively, and the error rate was only 0.44%. The Std.D values at the same position calculated by NPEM and MCS were 0.01387 mm and 0.01415 mm, respectively, and the error rate was only 0.19%. It is clear that the mean and variance of NPEM and MCS are almost identical.

Fig. 8
figure 8

Comparison of vertical displacement of the third bridge midspan: a the mean value curve. b The standard deviation value curve

Full size image

The other comparison results of dynamics response show the same conclusion, but for the limit of space of this paper, these results cannot be given here.

Based on all analysis results, the mean and variance of dynamic responses obtained by NPEM and MCS methods are highly consistent, so the NPEM method has high accuracy and reliability in analysing the random process. At the same time, the calculation times of NPEM are much lower than that of MCS, so the former has higher computational efficiency and high feasibility. Therefore, in this work, NPEM method can be used to analyse the random process.

3.2 Effect of Different Peaks of Ground Motion Acceleration on Dynamic Response

Figure 9a, b shows the maximum lateral response and vertical response of the train body under different DBGA, respectively. For car body lateral response, the increase of the intensity of earthquake will directly lead to the increase of lateral response, illustrating that the residual deformation of the track after the earthquake has a great impact on the running safety of train after the main earthquake. However, it has little influence on the vertical response, which may be related to the vertical structure of train-bridge system and weak coupling between the transverse structure. In specific cases with large creep, seismic-induced rail irregularity and train speed, the acceleration of train exceeds the specified limit of 1.3 m/s2. Based on the body acceleration limit, the DBGA limit for the lateral response is 0.3 g at all speed tested.

Fig. 9
figure 9

Maximum value of the lateral and the vertical acceleration of the first car-body and mid-span of the third bridge at different peaks of ground motion acceleration. a Lateral acceleration of car-body, b vertical acceleration of car-body, c lateral acceleration of bridge, d vertical acceleration of bridge

Full size image

Figure 9c, d shows the maximum lateral response and the maximum vertical response of the third span under different DBGA. In the case of different velocities, the influence of increased seismic intensity on bridge transverse response increases when DBGA increases from 0.1 to 0.3 g, but decreases after 0.3 g, indicating that the response of bridge does not change monotonously with the change of strength. However, it should depend on the actual situation that the residual deformation under different strength leads to the track irregularity. At the speed of 250–300 km/h, there is a large fluctuation at 0.3 g, even exceeding the speed of 350 km/h and above, because in this case, the external load fluctuation is close to the frequency of the mid-span of the bridge. The law of vertical response is consistent with that of car, and it is not affected by the DBGA change.

3.3 Effect of Different Attitude of Creep on Dynamic Response

Figure 10a, b, respectively, show the maximum lateral response and maximum vertical response of the train body under different creep amplitudes. The variation of creep amplitude has a great effect on the vertical response of the vehicle body, and the effect increases with the increase of the vehicle speed. On the contrary, it has little effect on the lateral response.

Fig. 10
figure 10

Maximum value of the lateral and vertical acceleration of the first car-body and mid-span of the third bridge at different creep amplitudes. a Lateral acceleration of car-body, b vertical acceleration of car-body, c lateral acceleration of bridge, d vertical acceleration of bridge

Full size image

Figure 10c, d, respectively, shows the maximum lateral response and maximum vertical response of the third span under different creep amplitudes. The change of creep has a certain influence on the lateral response of the mid-span, and the change of influence is not consistent at different speeds. For example, when the speed is 250 km/h and below, it almost does not change with the creep, while there is an increasing trend at 300 km/h and above. It is interesting to find that bridge creep, a kind of vertical deformation, has less effect on the vertical response than the lateral response of mid-span acceleration. For the results, the reason is that the load caused by track irregularity and bridge creep gets closer to the natural frequencies of lateral degrees of freedom of bridges with the increase of the creep amplitude.

In summary, the development law of vertical response is consistent with the existing research results [46], but the influence of bridge creep on vertical response is very small.

3.4 Effect of Different Speed of Train on Dynamic Response

Figure 11a, b, respectively, show the maximum lateral response and maximum vertical response of the train body at different train speeds. The influence of change of velocity on the vertical response is much greater than that on the horizontal response. It can be clearly seen from Fig. 11a that when DBGA is 0.4 g, the change with the speed is not monotonous, and the response in the other cases is little affected by the change of the speed. It can be clearly seen in Fig. 11b that the vertical acceleration response increases monotonically with the increase of the vehicle speed.

Fig. 11
figure 11

Maximum value of the lateral and vertical acceleration of the first car-body and mid-span of the third bridge at different train speeds. a Lateral acceleration of car-body, b vertical acceleration of car-body, c lateral acceleration of bridge, d vertical acceleration of bridge

Full size image

Figure 11c, d shows the maximum lateral response of the third span of the third span at different train speeds. As it can be seen from Fig. 11c, except for the case when DBGA is 0.3 g, the acceleration will increase slowly with the increase of vehicle speed in other cases. In the case when DBGA is 0.3 g, the change of acceleration with vehicle speed is not monotonic. It will increase sharply before 250 km/h and decrease sharply after 300 km/h. There is an extreme value between 250 and 300 km/h. Resonance may occur when DBGA is 0.3 g and the speed is between 250 km/h and 300 km/h. The relationship between the vertical response and the velocity is relatively simple and monotonically increasing.

4 Conclusion

In this paper, the train system is simulated as a mass-damp-stiffness system, the bridge model is established by finite element method, and the dynamic equation is obtained by energy method. On this basis, a three-dimensional vehicle-bridge coupling model is constructed. The bridge creep model and seismic bridge model are established by related software, and the additional irregularity of track is obtained. Several initial track irregularity samples obtained by trigonometric series method were used to obtain the random data through KLE. Then, the additional track irregularity was added into the random data, the accuracy of the random data was verified by probability distribution, and the random vibration response was calculated by NPEM. The results obtained by MCS simulation verify the reliability and high efficiency of NPEM. The sensitivity of the response of the vehicle body and the bridge under different ground motion acceleration amplitudes, mid-span bridge creep amplitudes and different speeds are analysed. Conclusions are obtained as follows:

  1. (1)

    First, NPEM can quickly and accurately calculate random TTBS with nonzero mean random irregularity. At the same time, the comparison between MCS and NPEM proves that NPEM is an effective method to analyse TTBCS. The average peak displacement error rate calculated by the two methods is only 0.44%.

  2. (2)

    Second, considering track irregularity of bridge creep and earthquake simultaneously, the test results of train-bridge system are more comprehensive. Although the two kinds of deformation are not in the same direction dimension, their results affect each other. For example, for bridge, the lateral seismic-induced deformation has almost no effect on the vertical response, but the vertical creep deformation has an obvious effect on the lateral response.

  3. (3)

    Third, the responses of trains and bridges have different sensitivities to the three parameters. The parameters affecting the train response from large to small are seismic peak acceleration, train speed and mid-span creep amplitude, while the parameters affecting the bridge response from large to small are vehicle speed, seismic peak acceleration and mid-span creep amplitude, which can be used as a reference for the train and the design parameters of bridges.

  4. (4)

    Finally, by considering the comprehensive situation of three kinds of track irregularities, a relatively comprehensive simulation of train running conditions after the earthquake is realized, which has a certain indicative effect on running safety after the earthquake (such as the train transportation of a large number of rescue materials after the earthquake).