Seismic running safety assessment for stochastic vibration of train–bridge coupled system

Abstract

With the rapid development of high-speed railway, the seismic running safety problem of high-speed train passing on bridge is becoming increasingly prominent. Since different wheel–rail contact states including uplifting, climbing up, detachment, recontact and derailment have been introduced into the simulation of train–bridge coupled (TBC) system, there are many problems arising for the mainstream derailment index in evaluating seismic running safety and stochastic analysis of train. To this end, a seismic running safety assessment for stochastic response of TBC system was first proposed in this paper. In this system, a detailed wheel–rail contact model was built to calculate the time-varying contact point and the contact force, which can be applied to simulate the detachment and recontact between the wheel flange and rail. Meanwhile, a stochastic analysis framework for derailment of the TBC system is developed. The stochastic vibration of a high-speed train traversing a multi-span prestressed simply supported box-girder bridge under earthquake with random magnitude was studied. In addition, an improved train running safety index, lateral wheel–rail relative displacement, was proposed and compared with the derailment factor and the offload factor to verify its feasibility. It shows an intuitive result as a derailment index in a stochastic train running safety analysis under earthquake. Furthermore, the lateral wheel–rail relative displacement and pertinent derailment probability were significantly affected by the intensity of the earthquake. The methodology herein can be helpful in seismic running safety assessment of high-speed train.

1 Introduction

In 2021s, total mileage of China’s high-speed railway (HSR) network is expected to exceed 37,900 km [1]. In the network, bridges account for a high proportion of HSR line, hence the possibility of train passing a bridge is unprecedentedly high when an earthquake occurs. The earthquake will seriously affect the safe operation of train and could cause train derailment or overturning even if the bridge is not seriously damaged. The derailment accidents caused by Niigata Chuetsu earthquake (magnitude 6.8, 2004 Oct. 23, Japan) [2], Jiashian earthquake (magnitude 6.4, 2010 Mar. 04, Taiwan) [3] and Kumamoto earthquake (magnitude 6.2, 2016 Apr. 14, Japan) [4] are typical cases, as shown in Fig. 1.

Fig. 1

Derailment of HSR trains on bridges due to earthquakes: Niigata Chuetsu earthquake in Japan (a) [2], Jiashian earthquake in Taiwan (b) [3] and Kumamoto earthquake in Japan (c) [4]

Although the reasons affecting train running safety under earthquake may be varied and complex, many studies have already considered this issue. Xia et al. [5] analysed the train operation safety over multi-span continuous girder bridge with different train speed under non-uniform seismic excitation. Besides, they proposed the speed thresholds of train operation safety under earthquakes of various intensities. Jin et al. [6] found the effect of vertical ground motion will likely increase the earthquake-induced derailment chance on simply supported bridges, and they showed that the vertical ground motion component is necessary to include in an earthquake-induced derailment analysis. Furthermore, they proposed a probabilistic approach based on fragility analysis and developed derailment fragility curves as the probabilistic assessment of vehicle derailment in a performance-based manner [7]. Not only the seismic ground motion, but also the wheel–rail contact model is an important factor to determine train running safety. Ju [8, 9] developed a simple-model moving wheel–rail contact element to simulate the sticking, sliding and separation modes of the wheel–rail contact. Moreover, based on the developed wheel–rail contact model, the influences of rail irregularity, bridge parameters, train speed and soil liquefaction on train running safety over a bridge under earthquake were studied [10]. Likewise, Zeng and Dimitrakopoulos [4, 11] proposed a wheel–rail contact simulation model to calculate the contact point and direction of the contact force on a practical nonlinear profiles of wheel and rail and determine the wheel–rail contact state according to a linear complementarity approach and an offline contact searching approach. Nevertheless, the accuracy of the existing TBC system simulating train running safety during earthquake is far from enough.

Stochastic analysis of train running safety is necessary due to the randomness of external excitations and system parameters [12, 13]. Previously, the stochastic analysis related to train running safety is relatively few and most of them focus on the dynamic response of train and bridge, such as displacement and acceleration, rather than a specific train running safety index. Zhang et al. [14] and Zeng et al. [15] conducted stochastic analysis of a train traversing different bridge subjected to travelling seismic wave and track irregularity by the pseudo-excitation method. Mao et al. [16] established a dynamic reliability evaluation method for three-dimensional TBC system subjected to random system parameters and Xu [17] obtained the response results of a system under earthquake and track random irregularities by probability density evolution method. Subsequently, Liu et al. applied Karhunen–Loéve expansion combine with the point estimate method (PEM) [18] or the new point estimate method (NPEM) [19] to simulate random rail irregularities and calculated the system dynamic response subjected to multiple random parameters [20]. In summary, the difficulty of train running safety stochastic analysis is no longer the random analysis method but the lack of an intuitive train running safety index.

If the earthquake-induced derailment of train can be accurately described, the reliability of train running safety analysis will be dramatically improved. Therefore, a simple and precise derailment index is the foundation for the TBC system simulation. As observed in Table 1, various derailment indexes are proposed for different applications. However, the inherent limitations of these train running safety indexes are gradually revealed since the different wheel–rail contact states are introduced into the simulation model. For instance, detachment and recontact between wheel and rail occurs frequently due to the seismic loads, when a train is running over a bridge during an earthquake. Specially, when the wheel–rail detachment occurs, the wheel–rail force disappears and the corresponding derailment factor and offload factor are therefore incalculable, but the possibility of derailment is relatively high. Consequently, a continuous and limited derailment index is necessary for the stochastic analysis of the system.

Table 1 The existing derailment indexes and the corresponding criterions

In this paper, a detailed wheel–rail contact model considering the dynamic interaction between wheel flange and rail was adopted. Besides, the lateral wheel–rail relative displacement (LWRRD) was first proposed to evaluate the seismic train running safety. On this basis, the comparison among the derailment factor, offload factor and LWRRD was carried out. Furthermore, a stochastic analysis model with the random seismic magnitude was developed to evaluate the train operation safety based on the PEM, and the extreme results of LWRRD were predicted at the end. The stochastic analysis of TBC system proposed herein is enlightening for seismic running safety assessment with various wheel–rail contact states.

The rest of this paper is organised as follows. First, the model and methodology of seismic running safety assessment for train–bridge coupled (TBC) system was presented in Sect. 2. Second, the proposed derailment indexes are described in detail in Sect. 3. Subsequently, some comparisons about different derailment indexes and wheel–rail contact models, and the results of LWRRD of a stochastic analysis model were obtained in Sect. 4. Finally, the conclusions are drawn in Sect. 5.

2 Simulation model

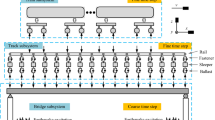
In this paper, the TBC system subjected to uniform seismic excitations was established based on the bridge seismic theory [27] and the TBC theory [28] (Fig. 2). A system consisting of a series of train vehicles, ballastless track slab models with three layers of elastic point-support and a bridge finite element model was established. Besides, a detailed model was built for solving the spatial wheel–rail contact under earthquake. The program of seismic running safety assessment was compiled and verified based on the commercial mathematical software MATLAB, and the equation of motion (EOM) of TBC system under seismic excitations were solved by implicit integral method [29]. In addition, the PEM was used to calculate the stochastic seismic running safety reliability assessment.

Fig. 2

Schematic diagram of TBC model

2.1 Solution of system matrices

According to D'Alembert’s principle, the dynamic equation of the system can be transformed into an equivalent static equilibrium equation, expressed as

$$ {\varvec{f}}_{{\text{e}}} = {\varvec{f}}_{\rho } + {\varvec{f}}_{{\text{c}}} - {\varvec{F}}{\text{sign}} ({\varvec{u}}) + {\varvec{p}}(t) + {\varvec{G}} $$

(1)

where ${\varvec{f}}_{\rho } = \int \left( { - \rho u^{\prime\prime}} \right){\text{d}}v{, }\;{\varvec{f}}_{{\text{c}}} = \int \left( { - cu^{\prime}} \right){\text{d}}v$; $u$, $f_{{\text{e}}}$, $f_{\rho }$, $f_{{\text{c}}}$, $F$, $p\left( t \right)$ and $G$ are the displacement vector, the elastic force, the inertia force, the damping force, the friction force, the loading, and the gravity, respectively.

By multiplying variation of displacement $\delta u$ on both sides of Eq. (1), the energy equation of the system at specific time t can be derived as

$$ \delta U_{{\text{e}}} = - \int \delta \mathbf{u}^{{\text{T}}} \rho \mathbf{u^{\prime\prime}}~{\text{d}}v - \int \delta \mathbf{u}^{{\text{T}}} c\mathbf{u^{\prime}}{\text{d}}v - \delta \mathbf{u}^{{\text{T}}} {\mathbf{F}}\text{sign} (\mathbf{u}) + \delta \mathbf{u}^{{\text{T}}} \mathbf{p}(t) + \delta \mathbf{u}^{{\text{T}}} \mathbf{G} $$

(2)

with

$$\left\{ \begin{gathered} U_{\rho } = \int {\mathbf{u}^{{\text{T}}} } \rho \mathbf{u^{\prime\prime}}~{\text{d}}v\quad \hfill \\ U_{{\text{c}}} = \int {\mathbf{u}^{{\text{T}}} } c\mathbf{u^{\prime}}{\text{d}}v \hfill \\ V_{{\text{F}}} = \mathbf{u}^{{\text{T}}} \mathbf{F}\text{sign} (\mathbf{u}) \hfill \\ V_{{\text{p}}} = - \mathbf{u}^{{\text{T}}} \mathbf{p}(t) \hfill \\ V_{{\text{g}}} = - \mathbf{u}^{{\text{T}}} \mathbf{G} \hfill \\ \end{gathered} \right.,$$

(3)

where ${U}_{\mathrm{e}}$ means the elastic strain energy of the system; ${U}_{\rho }$ means the work of inertia force; ${U}_{\mathrm{c}}$ represents the work of damping force; ${V}_{\mathrm{F}}$ represents the work of friction; ${V}_{\mathrm{p}}$ means the work of loading; ${V}_{\mathrm{g}}$ means the gravitational potential energy.

The total potential energy of the system, ${\Pi }_{\mathrm{d}}$, satisfies ${\Pi }_{\mathrm{d}}={U}_{\mathrm{e}}+{U}_{\rho }+{U}_{\mathrm{c}}+{V}_{\mathrm{F}}+{V}_{\mathrm{p}}+{V}_{\mathrm{g}}$. Based on energy variational method, it can be concluded that [30]

$$ \delta_{\epsilon } \Pi_{{\text{d}}} = \mathop \sum \limits_{i = 1}^{N} \frac{{\partial \Pi_{{\text{d}}} }}{{\partial p_{i} }}\delta p_{i} = 0 \, \left( {i = 1,2, \ldots ,n} \right), $$

(4)

where $\delta_{\epsilon }$ is a variational operator for the displacement or strain of the system and ${p}_{i}$ represents the generalised displacement of the system.

The stiffness matrix, mass matrix, damping matrix and load matrix of motion equations of entire system can be generated by Eq. (4) [31, 32].

2.2 Model of train

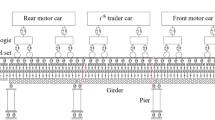
First and foremost, it can be assumed that the car-body, bogies and wheelsets of the HSR train are rigid bodies assembly with elastic suspension device in operation safety analysis during earthquake [19]. Second, the train is composed of four-axle motor cars and trailers in a certain formation, which connected in series by couplers. Each vehicle has one car-body with six DOFs, two bogies with six DOFs each and four wheelsets with five DOFs each, whose schematic diagram is shown in Fig. 3. In addition, the specific symbols of basic motions are shown in Table 2. Accordingly, the DOF symbols of train vibration can be expressed as

$$ {\mathbf{X}}_{v} = \left\{ {\left( {{\mathbf{X}}_{c,v} ,{\mathbf{X}}_{t1,v} ,{\mathbf{X}}_{t2,v} ,{\mathbf{X}}_{w1,v} ,{\mathbf{X}}_{w2,v} ,{\mathbf{X}}_{w3,v} ,{\mathbf{X}}_{w4,v} } \right)_{v} |1 \le v \le n_{v} \, v,n_{v} \in Z} \right\}, $$

(5)

with

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{X}}_{i,v} = \left( {x_{i,v} ,y_{i,v} ,z_{i,v} ,\phi_{i,v} ,\psi_{i,v} ,\varphi_{i,v} } \right), \, i \subseteq \left( {c,\;t1,\;t2} \right)} \hfill \\ {{\mathbf{X}}_{j,v} = \left( {x_{j,v} ,y_{j,v} ,z_{j,v} ,\phi_{j,v} ,\psi_{j,v} } \right), \, j \subseteq \left( {w1,w2,w3,w4} \right)} \hfill \\ \end{array} } \right. $$

(6)

where the subscript c, t1 and t2 denote car-body, front bogie and rear bogie, respectively. The subscript v means the vth vehicle and the subscript wi means the ith wheelset of the vehicle, which is n_v in total.

Fig. 3

Schematic diagram of train model: side view (a), top view (b) and rear view (c)

Table 2 DOFs of the train

Appendix 1 gives the details of mass matrices and stiffness matrices of the train vehicle model and the main parameters of the train are listed in Appendix 2. Further, the damping matrix ${\mathbf{C}}_{vv}$ of the train system has a stiffness matrix form similar to like Eq. (53), which can be obtained only by displacing damping coefficient c with stiffness coefficient k.

2.3 Model of track slab and bridge

In 2018s, almost 90% of HSR bridges are simply support box-girder bridges in China [4]. Consequently, a prestressed HSR two-way simply supported box-girder with concrete piers (bridge) and the China railway track system type II ballastless track slab were adopted in this paper, as reference in Fig. 4. The track-bridge system was modelled according to finite element method. Specifically, each bridge unit was simulated with beam element, plate element and shell element, and the rail was consisted of a series of beam elements [33,34,35]. Besides, the seismic excitations were directly be forced at supporting nodes in the bottom of the bridge piers and their effect on bridge was reflected by influence matrix [36].

Fig. 4

Schematic diagrams of track slab and bridge model: side view (a) and rear view (b)

Liu et al. [20] compared the influence of Rayleigh damping model and Caughey damping model on the stochastic analysis, and indicated that Rayleigh damping model has enough accuracy to show the dissipation of the system. Accordingly, damping matrix ${\mathbf{C}}_{bb}$ herein satisfies Rayleigh type to avoid the excessive calculation, which can be expressed as follows:

$$ {\mathbf{C}}_{bb} = \frac{{2\omega_{i} \omega_{j} \zeta_{b} }}{{\omega_{i} + \omega_{j} }}{\mathbf{M}}_{bb} + \frac{{2\zeta_{b} }}{{\omega_{i} + \omega_{j} }}{\mathbf{K}}_{bb} , $$

(7)

where ${\omega }_{i}$ means first-order natural frequency of the bridge, ${\omega }_{j}$ means the maximum excitation frequency induced by track irregularities, and ${\zeta }_{b}$ represents the damping ratio of the bridge.

The first four vibration modes of the bridge have been drawn in Fig. 5. Besides, the main parameters of the bridge and the track slab are listed in Appendix 2. In addition, the interactive stiffness matrices and damping matrices of rail and bridge satisfy

$$ {\mathbf{K}}_{br} = {\mathbf{K}}_{br}^{{\mathbf{T}}} {, }{\mathbf{C}}_{br} = {\mathbf{C}}_{br}^{{\mathbf{T}}} . $$

(8)

Fig. 5

Vibration modes of bridge: first mode of the bridge (a); second mode of the bridge (b); third mode of the bridge (c); fourth mode of the bridge (d)

2.4 Model of wheel–rail contact

See Table 3.

Table 3 Notations for the parameters in the wheel–rail contact model (variable means it changes in each time step)

2.4.1 Wheel–rail contact geometry

The wheel–rail contact model in this paper was established based on two assumptions. First, the wheel–rail contact satisfies knife-edge contact constraints (Fig. 6b), which means only single point contact is considered [11, 37, 38]. Second, the spatial geometric contour of wheel flange is simulated by two circular arcs and there is a specific angle between them (Fig. 6d). Consequently, the spatial geometric relationship of wheel–rail contact can be identified according to the assumptions, and the schematic diagram is shown in Fig. 6a.

Fig. 6

Schematic diagram of wheel–rail contact model: spatial wheel–rail relationship (a); wheel–rail knife-edge contact constrains (b); LM_a wheel profile (unit: mm, c); the simulation mode of LM_a wheel (d); and three different wheel–rail states (e–g)

The coordinate of wheel–rail contact point in the absolute coordinate system can be depicted as follows [28, 30]:

$$ \left\{ \begin{gathered} x_{{C^{{\text{R}}} }} = x_{{\text{B}}} + l_{x} R_{{\text{w}}} \tan \delta_{R} \hfill \\ y_{{C^{{\text{R}}} }} = y_{{\text{B}}} - \frac{{R_{{\text{w}}} }}{{1 - l_{x}^{2} }}\left( {l_{x}^{2} l_{y} \tan \delta_{{\text{R}}} + l_{z} \sqrt {1 - l_{x}^{2} \left( {1 + \tan^{2} \delta_{{\text{R}}} } \right)} } \right) \hfill \\ z_{{C^{{\text{R}}} }} = z_{{\text{B}}} - \frac{{R_{{\text{w}}} }}{{1 - l_{x}^{2} }}\left( {l_{x}^{2} l_{y} \tan \delta_{{\text{R}}} - l_{y} \sqrt {1 - l_{x}^{2} \left( {1 + \tan^{2} \delta_{{\text{R}}} } \right)} } \right), \hfill \\ \end{gathered} \right. $$

(9)

with

$$ \left\{ \begin{gathered} x_{{\text{B}}} = d_{{\text{w}}} l_{x} \hfill \\ y_{{\text{B}}} = d_{{\text{w}}} l_{y} + Y_{{\text{w}}} \hfill \\ z_{{\text{B}}} = d_{{\text{w}}} l_{z} \hfill \\ \end{gathered} \right. $$

(10)

$$ \left\{ \begin{gathered} l_{x} = - \cos \phi_{{\text{w}}} \sin \psi_{{\text{w}}} \hfill \\ l_{y} = \cos \phi_{{\text{w}}} \cos \psi_{{\text{w}}} \hfill \\ l_{z} = \sin \phi_{{\text{w}}} \hfill \\ \end{gathered} \right.. $$

(11)

where ${\delta }_{\mathrm{R}}$ means the contact angle of right wheel tread. ${l}_{x}$, ${l}_{y}$ and ${l}_{z}$ are the direction cosines of the x-axis, y-axis and z-axis, respectively. ${x}_{\mathrm{B}}$, ${y}_{\mathrm{B}}$ and ${z}_{\mathrm{B}}$ represent the coordinates of the wheel rolling circle centre, respectively.

2.4.2 Wheel–rail normal force

Due to the knife-edge contact constraints assumption, the wheel–rail normal force can be directly solved by the Hertz nonlinear elastic contact theory [28], where the time-varying function of wheel–rail normal force can be expressed as

$$ N(t) = \left[ {\frac{1}{G}\delta Z(t)} \right]^{3/2} . $$

(12)

A simplified simulation model (Fig. 6d) was adopted to deduce the wheel–rail normal compression displacement $\delta {Z}_{Lj}(t)$ and $\delta {Z}_{Rj}(t)$. The wheel–rail normal compression can be deduced from the wheel–rail vertical relative displacement based on spatial geometric relationship. Therefore, the normal compression displacement of left and right wheel–rail contact points satisfies

$$ \left\{ \begin{gathered} \delta Z_{Lj} (t) = (R_{1} - Z_{cL} )\cos \phi_{wi} - Z_{wj} (t) - b_{0} \cos \phi_{wi} + Z_{{{\text{rou}}}} + Z_{{{\text{rail}}}} , \, \;0 < D_{rwiL} < R_{1} \sin \theta_{{R_{1} R_{2} }} \hfill \\ \delta Z_{Rj} (t) = (R_{1} - Z_{cR} )\cos \phi_{wi} - Z_{wj} (t) + b_{0} \cos \phi_{wi} + Z_{{{\text{rou}}}} + Z_{{{\text{rail}}}} , \, \;0 < D_{rwiR} < R_{1} \sin \theta_{{R_{1} R_{2} }} \hfill \\ \delta Z_{Lj} (t) = (R_{1} - Z_{cL} )\cos \phi_{wi} - Z_{wj} (t) - b_{0} \cos \phi_{wi} + Z_{{{\text{rou}}}} + Z_{{{\text{rail}}}} , \, \;R_{1} < D_{rwiL} < (R_{1} + R_{2} )\sin \theta_{{R_{1} R_{2} }} \hfill \\ \delta Z_{Rj} (t) = (R_{1} - Z_{cR} )\cos \phi_{wi} - Z_{wj} (t) + b_{0} \cos \phi_{wi} + Z_{{{\text{rou}}}} + Z_{{{\text{rail}}}} , \, \;R_{1} < D_{rwiR} < (R_{1} + R_{2} )\sin \theta_{{R_{1} R_{2} }} \hfill \\ \end{gathered} \right.. $$

(13)

with

$$ \left\{ \begin{gathered} Z_{cL} = \sqrt {R_{1}^{2} - D_{rwiL} /(\cos \phi_{wi} \cos \psi_{wi} )} { , 0 < }D_{rwiL} < R^{\prime} \hfill \\ Z_{cR} = \sqrt {R_{1}^{2} - D_{rwiR} /(\cos \phi_{wi} \cos \psi_{wi} )} {, 0 < }D_{rwiR} < R^{\prime}_{1} \hfill \\ Z_{cL} = \sqrt {R_{2}^{2} - \left( {R^{\prime}_{2} + R^{\prime}_{1} - D_{rwiL} /(\cos \phi_{wi} \cos \psi_{wi} )} \right)^{2} } {, }R^{\prime}_{1} { < }D_{rwiL} < R^{\prime}_{1} + R^{\prime} \hfill \\ Z_{cR} = \sqrt {R_{2}^{2} - \left( {R^{\prime}_{2} + R^{\prime}_{1} - D_{rwiR} /(\cos \phi_{wi} \cos \psi_{wi} )} \right)^{2} } {, }R^{\prime}_{1} { < }D_{rwiR} < R^{\prime}_{1} + R^{\prime} \hfill \\ \end{gathered} \right.. $$

(14)

where ${R}_{1}^{^{\prime}}$ and ${R}_{2}^{^{\prime}}$ satisfies

$$ \left\{ \begin{gathered} R^{\prime}_{1} = R_{1} \cos \phi_{wi} \cos \psi_{wi} \hfill \\ R^{\prime}_{2} = R_{2} \cos \phi_{wi} \cos \psi_{wi} \hfill \\ \end{gathered} \right.. $$

(15)

In particular, the wheel–rail normal force $N(t)$ equals to zero and the wheel–rail detachment occurs, when the normal compression deformation between wheel and rail $\delta Z(t)<0$.

2.4.3 Wheel–rail creep force

The wheel–rail creep force was formulated according to Kalker linear rolling contact theory [28]. The longitudinal wheel–rail creep force ${F}_{x}$, lateral creep force ${F}_{y}$, and rotating creep moment ${M}_{z}$ within the linear range can be expressed as

$$ \left\{ \begin{gathered} F_{x} = - f_{11} \xi_{x} \hfill \\ F_{y} = - f_{22} \xi_{y} - f_{23} \xi_{\varphi } \hfill \\ M_{z} = f_{23} \xi_{y} - f_{33} \xi_{\varphi } \hfill \\ \end{gathered} \right.. $$

(16)

where ${\xi }_{x}$, ${\xi }_{y}$, and ${\xi }_{\varphi }$ are the longitudinal creep rate, lateral creep rate and rotating creep rate, respectively. In wheel–rail contact spot coordinate, the longitudinal creep rate ${\xi }_{x}$, lateral creep rate ${\xi }_{y}$ and rotating creep rate ${\xi }_{\varphi }$ are defined as [28]

$$ \left\{ {\begin{array}{*{20}l} {\xi_{x} = \frac{{v_{wx} - v_{rx} }}{{v_{w} }}} \hfill \\ {\xi_{y} = \frac{{v_{wy} - v_{ry} }}{{v_{w} }}} \hfill \\ {\xi_{\varphi } = \frac{{\Omega _{wz} -\Omega _{rz} }}{{v_{w} }}} \hfill \\ \end{array} } \right.. $$

(17)

where ${v}_{w}$ is the wheelset speed in the absolute coordinate system. ${v}_{wx}$, ${v}_{wy}$, and ${\Omega }_{wz}$ are the speed of contact ellipse on the wheel along x-axis, y-axis and around z-axis, respectively. ${v}_{rx}$, ${v}_{ry}$, and ${\Omega }_{rz}$ are the speed of contact ellipse on the rail along x-axis, y-axis and around z-axis, respectively. In addition, ${f}_{ij}$ represents the creep coefficient, which can be accurately calculated according to Ref. [39]:

$$ \left\{ \begin{gathered} f_{11} = 0.5E_{r} (1 + \nu_{r} )^{ - 1} (ab)C_{11} \hfill \\ f_{22} = 0.5E_{r} (1 + \nu_{r} )^{ - 1} (ab)C_{22} \hfill \\ f_{23} = 0.5E_{r} (1 + \nu_{r} )^{ - 1} (ab)^{3/2} C_{23} \hfill \\ f_{33} = 0.5E_{r} (1 + \nu_{r} )^{ - 1} (ab)^{2} C_{33} \hfill \\ \end{gathered} \right., $$

(18)

where ${C}_{ij}$ are the Kalker’s creep and spin coefficients, which depends on the ratios of the semi-axil lengths of the wheel–rail contact ellipse a and b. Furthermore, a and b can be obtained by inducting parameters ${a}_{\mathrm{e}}$ and ${b}_{\mathrm{e}}$ as

$$ \left\{ \begin{gathered} a = a_{{\text{e}}} \left( {{\text{NR}}_{w} } \right)^{1/3} \hfill \\ b = b_{{\text{e}}} \left( {{\text{NR}}_{w} } \right)^{1/3} \hfill \\ ab = a_{{\text{e}}} b_{{\text{e}}} \left( {{\text{NR}}_{w} } \right)^{2/3} \hfill \\ \end{gathered} \right., $$

(19)

where ${a}_{\mathrm{e}}$ and ${b}_{\mathrm{e}}$ can be expressed as

$$ \left\{ \begin{gathered} \begin{array}{*{20}c} {a_{{\text{e}}} = 0.1506m\left( {\frac{\rho }{{R_{{\text{w}}} }}} \right)^{1/3} \times 10^{ - 3} } \\ {b_{{\text{e}}} = 0.1506n\left( {\frac{\rho }{{R_{{\text{w}}} }}} \right)^{1/3} \times 10^{ - 3} } \\ \end{array} {, }\rho /R_{{\text{w}}} \le 2 \hfill \\ \begin{array}{*{20}c} {a_{{\text{e}}} = 0.1506n\left( {\frac{\rho }{{R_{{\text{w}}} }}} \right)^{1/3} \times 10^{ - 3} } \\ {b_{{\text{e}}} = 0.1506m\left( {\frac{\rho }{{R_{{\text{w}}} }}} \right)^{1/3} \times 10^{ - 3} } \\ \end{array} {, }\rho /R_{{\text{w}}} > 2. \hfill \\ \end{gathered} \right. $$

(20)

where $\rho$ satisfies

$$ \frac{1}{\rho } = \frac{1}{4}\left[ {\frac{1}{{R_{{\text{w}}} }} + \left( {\frac{1}{{r_{{\text{w}}} }} + \frac{1}{{r_{{\text{r}}} }}} \right)} \right]. $$

(21)

where m and n are coefficients which can be obtained by looking up table in Ref. [28].

The seismic wheel–rail contact is complicate and far from the small creep rate and small rotating creep conditions, hence the nonlinear Shen–Hedrick–Euristic creep model [40] is necessary to be adopted. Accordingly, a creep correction factor $\varepsilon$ and expressed as

$$ \varepsilon = \frac{{F^{\prime}}}{F}, $$

(22)

where $F^{\prime}$ and $F$ can be written as

$$ F = \sqrt {F_{x}^{2} + F_{y}^{2} } $$

(23)

$$ F^{\prime} = \left\{ {\begin{array}{*{20}l} {fN\left[ {\frac{F}{fN} - \frac{1}{3}\left( \frac{F}{fN} \right)^{2} + \frac{1}{27}\left( \frac{F}{fN} \right)^{3} } \right],{ (}F \le 3fN{)}} \hfill \\ {fN{ , (}F > 3fN{)}} \hfill \\ \end{array} } \right.. $$

(24)

Henceforth, the longitudinal creep force $F^{\prime}_{x}$, lateral creep force $F^{\prime}_{y}$ and rotating creep moment $M^{\prime}_{z}$ are corrected as

$$ \left\{ {\begin{array}{*{20}l} {F^{\prime}_{x} = \varepsilon F_{x} } \hfill \\ {F^{\prime}_{y} = \varepsilon F_{y} } \hfill \\ {M^{\prime}_{z} = \varepsilon M_{z} } \hfill \\ \end{array} } \right.. $$

(25)

2.5 EOM under uniform earthquake excitations

In the system, the seismic loads were treated as the external excitations and the acceleration of earthquake was input in each bridge pier uniformly. Thus, the EOM of the system was partitioned as supporting nodes block matrix (supporting nodes) and other structures block matrix (structure nodes) in the absolute coordinate system, which can be expressed as follows:

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{ss} } & {{\mathbf{M}}_{sb} } \\ {{\mathbf{M}}_{bs} } & {{\mathbf{M}}_{bb} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X^{\prime\prime}_{s} } \\ {X^{\prime\prime}_{b} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{ss} } & {{\mathbf{C}}_{sb} } \\ {{\mathbf{C}}_{bs} } & {{\mathbf{C}}_{bb} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X^{\prime}_{s} } \\ {X^{\prime}_{b} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{ss} } & {{\mathbf{K}}_{sb} } \\ {{\mathbf{K}}_{bs} } & {{\mathbf{K}}_{bb} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X_{s} } \\ {X_{b} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ {f_{b}^{ } } \\ \end{array} } \right\}. $$

(26)

where $\{{X}_{b}\}$ means the enforced displacements of the supporting nodes; $\{{X}_{s}\}$ represents the displacements of structure nodes; $\{{\mathbf{M}}_{\mathrm{ss}}\}$, $\{{\mathbf{C}}_{\mathrm{ss}}\}$ and $\{{\mathbf{K}}_{\mathrm{ss}}\}$ are mass matrix, damping matrix and stiffness matrix of the structure nodes, respectively; $\{{\mathbf{M}}_{\mathrm{bb}}\}$, $\{{\mathbf{C}}_{\mathrm{bb}}\}$ and $\{{\mathbf{K}}_{\mathrm{bb}}\}$ are mass matrix, damping matrix and stiffness matrix of the supporting nodes, respectively; $\{{\mathbf{M}}_{\mathrm{sb}}\}$, $\{{\mathbf{M}}_{\mathrm{bs}}\}$, $\{{\mathbf{C}}_{\mathrm{sb}}\}$, $\{{\mathbf{C}}_{\mathrm{bs}}\}$, $\{{\mathbf{K}}_{\mathrm{sb}}\}$ and $\{{\mathbf{K}}_{\mathrm{bs}}\}$ denote the coupling mass matrices, the coupling damping matrices and the coupling stiffness matrices of the supporting nodes and the structure nodes; $\{{f}_{b}\}$ is the force of the supporting nodes subject to the ground.

Considering $\left\{{X}_{b}^{^{\prime\prime} }\right\}=\{{x}_{g}^{^{\prime\prime} }(t)\}$ and the influence matrix $\left[\mathbf{R}\right]=-{\left[{\mathbf{K}}_{\mathrm{ss}}\right]}^{-1}\left[{\mathbf{K}}_{\mathrm{sb}}\right]$, Eq. (26) can be rewritten as

$$ \left[ {{\mathbf{M}}_{ss} } \right]\left\{ {Y^{\prime\prime}_{r} } \right\} + \left[ {{\mathbf{C}}_{ss} } \right]\left\{ {Y^{\prime}_{r} } \right\} + \left[ {{\mathbf{K}}_{ss} } \right]\left\{ {Y_{r} } \right\} = - \left[ {{\mathbf{M}}_{ss} } \right]\left[ {\mathbf{R}} \right]\{ x^{\prime\prime}_{g} {(}t{)}\} . $$

(27)

where t denote time; ${x}_{g}^{^{\prime\prime} }(t)$ means the earthquake acceleration of ith support node in a direction, which is a time-varying function.

2.6 Model of rail irregularity

The track irregularities appreciably affect the lateral vibration and the short-wavelength irregularities will activate a high-frequency vibration in the vertical direction [41]. Thus, the influence of primary rail irregularity on train dynamic response should be considered. The rail irregularity in the TBC system is generated by the harmonic synthesis method [42] combined with German low-orbit interference power spectral density (PSD) [43], which can be expressed as

$$ \left\{ \begin{gathered} S_{v} (\Omega ) = \frac{{A_{v} \Omega_{c}^{2} }}{{\left( {\Omega^{2} + \Omega_{r}^{2} } \right)\left( {\Omega^{2} + \Omega_{c}^{2} } \right)}} \hfill \\ S_{a} (\Omega ) = \frac{{A_{a} \Omega_{c}^{2} }}{{\left( {\Omega^{2} + \Omega_{r}^{2} } \right)\left( {\Omega^{2} + \Omega_{c}^{2} } \right)}} \hfill \\ S_{c} (\Omega ) = \frac{{A_{v} b^{ - 2} \Omega_{c}^{2} \Omega }}{{\left( {\Omega^{2} + \Omega_{r}^{2} } \right)\left( {\Omega^{2} + \Omega_{c}^{2} } \right)\left( {\Omega^{2} + \Omega_{s}^{2} } \right)}} \hfill \\ S_{g} (\Omega ) = \frac{{A_{g} \Omega_{c}^{2} \Omega^{2} }}{{\left( {\Omega^{2} + \Omega_{r}^{2} } \right)\left( {\Omega^{2} + \Omega_{c}^{2} } \right)\left( {\Omega^{2} + \Omega_{s}^{2} } \right)}}, \hfill \\ \end{gathered} \right. $$

(28)

where $S_{v}$, $S_{a}$, and $S_{g}$ are the irregularity PSD function of vertical rail profile, rail alignment and gauge distance $\left[ {{\text{m}}^{2} /\left( {{\text{rad}}/{\text{m}}} \right)} \right]$, respectively; $S_{c}$ is the PSD function of rail cross-level irregularity $\left[ {1/\left( {{\text{rad}}/{\text{m}}} \right)} \right]$; $A_{v}$, $A_{a}$, and $A_{g}$ represent the roughness coefficients; ${\Omega }_{c}$, ${\Omega }_{r}$ and ${\Omega }_{s}$ mean the truncation frequency; b denotes the half distance between two sides of rail. The detailed parameters of the irregularity PSD function are shown in Fig. 7. The vertical rail profile irregularity of left rail $r^{{{\text{ZL}}}}$ and right rail $r^{{{\text{ZR}}}}$, and alignment irregularity of left rail $r^{{{\text{YL}}}}$ and right rail $r^{{{\text{YR}}}}$ can be expressed as [19]

$$ \left\{ \begin{gathered} r^{{{\text{ZL}}}} (x) = r_{v} (x) + r_{g} (x)b + r_{cr} (x) \hfill \\ r^{{{\text{ZR}}}} (x) = r_{v} (x) - r_{g} (x)b + r_{cr} (x) \hfill \\ r^{{{\text{YL}}}} (x) = r_{a} (x) + r_{v} (x)/2 \hfill \\ r^{{{\text{YR}}}} (x) = r_{a} (x) - r_{v} (x)/2, \hfill \\ \end{gathered} \right. $$

(29)

where ${r}_{v}$ represents the vertical rail profile irregularity, ${r}_{a}$ represents the rail cross-level irregularity, ${r}_{cr}$ represents the rail alignment irregularity and ${r}_{g}$ represents the rail-distance irregularity, respectively (see Table 4).

Fig. 7

Graph of rail irregularity PSD function

Table 4 Parameters of German low-orbit interference PSD of rail irregularity (all data refer to [28])

2.7 Model of earthquake

Clough–Penzien PSD functions were adopted to simulate the seismic wave sample, in the form of [15, 44]

$$ S_{{a_{y} a_{y} }} (\omega ) = \frac{{\omega_{gy}^{4} + 4\zeta_{gy}^{2} \omega_{gy}^{2} \omega^{2} }}{{\left( {\omega_{{{\text{gy}}}}^{2} - \omega^{2} } \right)^{2} + 4\zeta_{gy}^{2} \omega_{{{\text{gy}}}}^{2} \omega^{2} }}\frac{{\omega^{4} }}{{\left( {\omega^{2} - \omega_{fy}^{2} } \right)^{2} + 4\zeta_{fy}^{2} \omega_{fy}^{2} \omega^{2} }}S_{0y} $$

(30)

$$ S_{{a_{z} a_{z} }} (\omega ) = \frac{{\omega_{gz}^{4} + 4\zeta_{gz}^{2} \omega_{gz}^{2} \omega^{2} }}{{\left( {\omega_{gz}^{2} - \omega^{2} } \right)^{2} + 4\zeta_{gz}^{2} \omega_{gz}^{2} \omega^{2} }}\frac{{\omega^{4} }}{{\left( {\omega^{2} - \omega_{fz}^{2} } \right)^{2} + 4\zeta_{fz}^{2} \omega_{fz}^{2} \omega^{2} }}S_{0z} , $$

(31)

where $\omega_{gy}$ and $\omega_{gz}$ denote the predominant frequency of the bridge site; $\zeta_{fy}$ and $\zeta_{fz}$ mean the damping ratios of the bridge site; $\zeta_{fy}$, $\zeta_{fz}$, $\omega_{fy}$ and $\omega_{fz}$ denote the parameters of the filter; $S_{0y}$ and $S_{0z}$ represent the spectral intensity factor. In addition, $\zeta_{gy} = \zeta_{gz}$, $\zeta_{fy} = \zeta_{gy}$, $\zeta_{fz} = \zeta_{gz}$, $\omega_{fy} = 0.1\omega_{gy} \sim 0.2\omega_{gy}$, $\omega_{fz} = 0.1\omega_{gz} \sim 0.2\omega_{gz}$ and $S_{0z} = 0.218S_{0y}$. The other parameters of the PSD functions are listed in Table 10 (see Fig. 8).

Fig. 8

Graph of earthquake PSD function

Seismic wave has obvious non-stationarity of intensity; hence, seismic acceleration wave is described as a product of a stationary zero mean filtered wave and a deterministic envelope function in engineering application [43], i.e.

$$ x^{\prime\prime}_{g} (t) = D(t)X^{\prime\prime}_{g} (t) $$

(32)

with

$$ D(t) = 12.21 \times (e^{ - 0.4t} - e^{ - 0.5t} ) $$

(33)

2.8 Stochastic method and random variable

The PEM proposed by Rosenblueth provides a practical solution to reduce computation cost in stochastic analysis [45, 46]. Afterwards, the PEM is greatly improved and becomes one of the mainstream estimation methods [18,19,20]. Therefore, the PEM can be adopted in the TBC system, which is organised as follows.

First, the seismic magnitude-frequency statistics is assumed to satisfy the truncated Gutenberg–Richter (G–R) distribution [47, 48], as shown in Eq. (34). Subsequently, the distribution of random variable was transformed to a standard normal distribution based on Nataf transformation [49]. The density function of truncated G–R model and the relation between the seismic peak ground acceleration (PGA) and the magnitude of the seismic ground motion attenuation model employed herein can be formulated as Eqs. (34) and (36), respectively:

$$ f\left( {m_{j} } \right) = I_{{[m_{0} ,M_{u} ]}} (y) \cdot t\exp \left[ { - t\left( {m_{j} - m_{0} } \right)} \right]/\left\{ {1 - \exp \left[ { - t\left( {M_{u} - m_{0} } \right)} \right]} \right\} $$

(34)

$$ I_{{[m_{0} ,M_{u} ]}} (y) = \left\{ \begin{gathered} 0{\text{ if }}y \le m_{0} \hfill \\ 1{\text{ if }}m_{0} \le y \le M_{u} \, \hfill \\ 0{\text{ if }}M_{u} \le y \hfill \\ \end{gathered} \right. \, $$

(35)

$$ \lg a_{E} = A + Bm_{j} + C\lg \left( {R + De^{{Em_{j} }} } \right), $$

(36)

where t = bln10; ${a}_{E}$ represents the seismic PGA of pertinent magnitude; ${m}_{j}$ means the random seismic magnitude, respectively; ${m}_{0}$ and ${M}_{u}$ are the lower and upper limits of seismic magnitude; R denotes the epicentral distance and maintains a constant value of 27 (km); A, B, C, D and E are all regression coefficients of the elliptical attenuation relationship, which are listed in Table 5. The coefficients of Eastern Active Region are used in this paper.

Table 5 Coefficients of elliptical attenuation relationship relation of ${a}_{E}$ for Chinese mainland (all data refer to [50])

In this paper, the random variable can be expressed as follows:

$$ X_{i} = F^{ - 1} \left( {\Phi \left( {Y_{i} } \right)} \right), $$

(37)

where X_i means the random variable after Nataf transformation; $\Phi (\cdot )$ means the standard normal cumulative distribution function (CDF) and ${F}^{-1}(\cdot )$ means the inverse function of CDF of random variable; Y_i represents the gauss point of standard Gaussian distribution.

Second, the number of Gauss point r needs to be confirmed. Afterwards, each estimate point $\sqrt{2}{x}_{{\rm GH},i}$ should be substituted into the Eq. (37) as Y_i, and then the calculated X_i ought to be incorporated into the TBC system as parameters. Afterwards, the time-history response $\mathrm{h}\left({X}_{i}, t\right)$ can be obtained.

Third, the actual time-history response moments (mean value $\mu (t)$ and qth (q = 2,3,4) order centre moment ${M}_{q}(t)$) of each time point can be calculated by substituting the $\mathrm{h}\left({X}_{i},t\right)$ into Eqs. (38) and (39), as

$$ \mu (t) \approx \sum\limits_{i = 1}^{r} {\frac{{w_{{\rm GH},i} }}{\sqrt \pi }} h\left( {X_{i} ,t} \right) $$

(38)

$$ M_{q} (t) \approx \sum\limits_{i = 1}^{r} {\frac{{w_{{\rm GH},i} }}{\sqrt \pi }} \left( {h\left( {X_{i} ,t} \right) - \mu (t)} \right)^{q} , $$

(39)

where r is the number of estimate point (r = 9 here), which means only 9 times of calculations are needed for one random variable; ${w}_{{\rm GH},i}$ and ${w}_{{\rm GH},j}$ are the weights of Gaussian–Hermite estimate point, which are listed in Table 6.

Table 6 Abscissas and weights for Gaussian–Hermite integration with r = 9 (all data refer to [19])

Fourth, statistics required for reliability analysis can be obtained according to the probability density functions (PDFs) of results. Furthermore, the PDF can be obtained based on all the origin moments (origin moments and centre moment can be transformed to each other) calculated by the PEM [51], which can be organised as follows:

$$ \left[ {\begin{array}{*{20}c} {\int_{a}^{b} { {\text{d}}x} } & {\int_{a}^{b} x {\text{d}}x} & \cdots & {\int_{a}^{b} {x^{n} } {\text{d}}x} \\ {\int_{a}^{b} x {\text{d}}x} & {\int_{a}^{b} {x^{2} {\text{d}}x} } & \cdots & {\int_{a}^{b} {x^{n + 1} } {\text{d}}x} \\ \vdots & \vdots & {} & \vdots \\ {\int_{a}^{b} {x^{n} } {\text{d}}x} & {\int_{a}^{b} {x^{n + 1} } {\text{d}}x} & \cdots & {\int_{a}^{b} {x^{n + n} } {\text{d}}x} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {a_{0} } \\ {a_{1} } \\ \vdots \\ {a_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mu_{0} } \\ {\mu_{1} } \\ \vdots \\ {\mu_{n} } \\ \end{array} } \right], $$

(40)

where a and b are the upper and lower bounds of the random variable, respectively, and ${\mu }_{n}$ means the n-order of origin moment.

After the coefficients ${a}_{n}$ are calculated, the best square approximation of the PDF can be described as

$$ S_{n} (x) = a_{0} \varphi_{0} (x) + a_{1} \varphi_{1} (x) + \cdots + a_{n} \varphi_{n} (x) $$

(41)

where the polynomial basis $\varphi (x)=span\{1,{x}^{1},{x}^{2},\cdots ,{x}^{n}\}$. Specially, the order n is recommended to be 4 or 5.

3 Derailment index

It is impractical to simulate a realistic derailment of train passing the bridge in a numerical simulation at present due to the complex wheel–rail interaction calculation. As a compromise, some derailment indexes (Table 1) are used to evaluate the operation safety performance of the train in form of a threshold. In this paper, the LWRRD was compared with the derailment factor and the offload factor to verify its feasibility and show advantages in the stochastic analysis.

3.1 Derailment factor

The derailment factor was first proposed by Nadal to describe the danger of derailment in 1896 [4], which is still the most commonly use parameter at present (2021). In detail, the derailment factor is defined as the quotient of the lateral component divided by the vertical component of the wheel–rail force according to force condition of a wheel (Fig. 9a), which can be described as follows:

$$ \frac{Q}{P} = \frac{N\sin \theta - T\cos \theta }{{N\cos \theta + T\sin \theta }}, $$

(42)

where T and N are tangential force and normal force of wheel–rail contact point respectively; Q and P are the lateral and vertical components of wheel–rail force F respectively; θ is the angle between tangential force T and the horizontal plane.

Fig. 9

Schematic diagram of wheel–rail interaction: force condition of wheel–rail contact (a) and three different wheel–rail contact states (b–d)

It is considered that the wheel–rail climbing up (Fig. 9d) occurs when the derailment factor exceeds the threshold and the wheel–rail climbing up state is the derailment state. In the simulation, lateral and vertical components of wheel–rail force are calculated in each time step, so the time-history curve of derailment factor can be obtained. In practice, impact and vibration between wheel and rail occur frequently under earthquake, which causes the derailment factor to oscillate dramatically. Consequently, the derailment factor curve is discontinuous and the results are invalid due to the wheel–rail detachment. In addition, the specification standards for derailment prevention in various regions/nations are listed in Table 7. Although these standards are all ill-considered for a seismic derailment analysis, the Chinese standard was adopted in this paper.

Table 7 Specification standards for derailment prevention in various regions/nations (all data refer to [3])

3.2 Offload factor

When the vertical wheel–rail force is small, the lateral wheel–rail force is always small accordingly during train running. Therefore, it is difficult to obtain an accurate derailment factor due to the calculation error, especially when the vertical wheel–rail force is close to zero. Instead, offload factor is another derailment index to make up for the deficiency of derailment factor according to wheel unloading. Therefore, the offload factor and the derailment factor are frequently used together to evaluate the train operation safety [11, 21]. The offload factor is defined as the ratio of wheel unloading to average loading of single wheel, namely $\Delta F/\overline{F }$. The wheel unloading $\Delta F$ and the average loading $\overline{F }$ can be expressed as follows:

$$ \Delta F = \overline{F} - F_{s}^{i} $$

(43)

$$ \overline{F} = \left( {F_{s}^{L} + F_{s}^{R} } \right)/2, $$

(44)

where ${F}_{s}^{L}$ and ${F}_{s}^{R}$ represent the wheel–rail vertical force of left and right wheels, respectively; ${F}_{s}^{i}$ means either ${F}_{s}^{L}$ or ${F}_{s}^{R}$, which depends on the wheel discussed.

However, if the offload factor exceeds the recommended limit instantaneously, it will not endanger the normal operation of the train. Specifically, the over-limit offload factor is primarily due to the instantaneous wheel load mutation caused by short wave track irregularity, concavity of rail joint, and turnout, which rarely lead to train derailment. More importantly, the offload factor remains unchanged when the wheel detaches, which does not help to distinguish the recontact and the detach-induced derailment. Hence, the offload factor is unsuitable as a seismic derailment index.

3.3 LWRRD

Previously, wheel uplift and lateral displacement of wheel are commonly used together as the evaluation criterion of wheel–rail contact geometry because the geometric boundary of wheel flange is ignored in simulation. These indexes directly show the geometric state of wheel and rail, and have an intuitive performance in evaluating the derailment of wheel. However, the earthquake-induced detachment and recontact of wheel and rail can lead to the wheel uplift fluctuation, so wheel uplift cannot be limited by a threshold. Besides, the lateral displacement of wheel is geometrically independent of the wheel uplift, which is impractical for wheel derailment. On balance, an improved lateral displacement index, LWRRD, was used in this paper.

The lateral wheel–rail relative displacement ${D}_{Lrwi}$ and ${D}_{Rrwi}$ can be expressed as

$$ \left\{ \begin{gathered} D_{rwiL} = D_{wi} - D_{rL} - D_{rouL} - C_{wr} \times \cos \phi_{wi} \times \cos \psi_{wi} \hfill \\ D_{rwiR} = D_{wi} - D_{rR} - D_{rouR} - C_{wr} /\cos \phi_{wi} \times \cos \psi_{wi} \hfill \\ \end{gathered} \right., \, \phi_{wi} \ge 0 $$

(45)

$$ \left\{ \begin{gathered} D_{rwiL} = D_{wi} - D_{rL} - D_{rouL} - C_{wr} /\cos \phi_{wi} \times \cos \psi_{wi} \hfill \\ D_{rwiR} = D_{wi} - D_{rR} - D_{rouR} - C_{wr} \times \cos \phi_{wi} \times \cos \psi_{wi} \hfill \\ \end{gathered} \right., \, \phi_{wi} < 0 $$

(46)

$$ \left\{ \begin{gathered} D_{rwiL} \left( {D_{rwiL} < 0} \right) = 0 \hfill \\ D_{rwiR} \left( {D_{rwiR} < 0} \right) = 0 \hfill \\ \end{gathered} \right.. $$

(47)

where ${D}_{wi}$ means the displacement of the ith wheelset; ${D}_{rL}$ and ${D}_{rR}$ represent the displacement of the rail under the corresponding wheel; ${D}_{rouL}$ and ${D}_{rouR}$ denote the primary rail irregularity under the corresponding wheel; ${C}_{wr}$ is the clearance between the wheel flange and the initial contact point in the wheelset coordinate system.

In addition, the Chinese LM_A wheel is adopted herein, and the profile of LM_A wheel is shown as Fig. 6c. According to geometric of the wheel profile, it is considered that the train derails when the wheel–rail climbing up occurs (Fig. 9d), namely LWRRD equals to 20 mm [22].

4 Illustrative examples

First, an ICE-3 train was applied herein and the main parameters of train are listed in Table 8 (Sect. 2.2). Second, a multi-span 32-m prestressed HSR two-way, simply supported box-girder bridge (type II bridge site, Fig. 4) was established based on Sect. 2.3. Besides, the main parameters of track slab and bridge are listed in Table 9. Third, the primary rail irregularity was considered and German low-orbit interference PSD functions were adopted (Sect. 2.4). Moreover, the same rail irregularity was used in the simulations. Fourth, Clough–Penzien PSD functions of earthquake were adopted to generate a set of three-dimensional seismic wave samples (Fig. 10) with a series of PGAs (Sect. 2.8) inputted to the supporting nodes. In addition, the train maintains a constant speed throughout its operation on the bridge.

Fig. 10

The three-dimensional seismic acceleration time-histories and pertinent Fourier spectra of the three components

4.1 Validation of the TBC system under earthquake

In this section, a comparison between the simulated model and the experiment using a full-scale half-vehicle with a real bogie in Ref. [22, 52] was made to verify the feasibility of the TBC system.

The schematic diagram of the simulated model and the experiment equipment is shown in Fig. 11a, b, respectively. In the experiment, a full-scale half-vehicle set on a real track is subjected to sinusoidal wave excitations [22, 52]. The results of wheel–rail vertical force under two different sinusoidal wave excitations are presented in Fig. 11c, d. It can be observed that the wheel–rail vertical force time-history curves of the simulated model and the experiment results are very close in trend and in amplitude. In addition, the wheel–rail detachment interval (normal force equal to zero) in the simulation is also consistent with that in the experiment. Therefore, it can be considered that the established simulation model can simulate dynamic response of train and wheel–rail relationship under earthquake correctly.

Fig. 11

The simulated model of the vibration test (a), front view of vibration test rig (b) [22, 52], and the comparison results of vertical wheel force under two sinusoidal wave excitations (0.8 Hz 105 mm and 0.5 Hz 320 mm, c, d)

4.2 Comparison with the wheel–rail tight contact model

The proposed wheel–rail contact model (Sect. 2.4) was compared with a more conventional wheel–rail tight contact model [53] in this section. In the wheel–rail tight contact model, it was assumed that the wheel is always contact with the rail throughout whole process. Meanwhile, the simplified flange contact model and knife-edge-shaped rail (Fig. 12b) were adopted. Besides, the rail irregularity was treated as the constraints of wheel–rail model and wheel–rail forces are not involved in load matrix. Hence, the wheel–rail forces can be calculated according to the result of each time step, and the formulas are as follows.

$$ F_{wi} = M_{{\text{c}}} Z^{\prime\prime}_{{\text{c}}} /4 + ( - 1)^{j + 1} J_{{{\text{c}}y}} \varphi^{\prime\prime}_{{\text{c}}} /4L_{{\text{c}}} + M_{tj} Z^{\prime\prime}_{tj} /2 + ( - 1)^{j + 1} J_{tjy} \theta^{\prime\prime}_{tj} /2L_{bw} + M_{wi} Z^{\prime\prime}_{wi} - W_{i} $$

(48)

$$ F_{wiL} = F_{wi} - J_{cx} \theta^{\prime\prime}_{c} /b_{0} /8 - J_{tjx} \theta^{\prime\prime}_{tj} /b_{0} /4 $$

(49)

$$ F_{wiR} = F_{wi} + J_{cx} \theta^{\prime\prime}_{c} /b_{0} /8 + J_{tjx} \theta^{\prime\prime}_{tj} /b_{0} /4 $$

(50)

where $i$ and $j$ mean the ${i}{\mathrm{th}}$ wheelset and the ${j}{\mathrm{th}}$ bogie of the train vehicle, respectively; herein $i = 1 - 4$ and $j = i/2$, where $\cdot$ means the round up operator. ${J}_{cx}$ and ${\theta }_{c}$ are the moment of inertia of the car-body in the x direction. Similarly, ${J}_{tjx}$ and ${\theta }_{tj}$ are the moment of inertia of the ${j}{\mathrm{th}}$ bogie in the x direction.

Fig. 12

The comparison of time-history response results of the TBC system between the proposed wheel–rail contact model and the wheel–rail tight contact model under earthquake: the schematic diagram of TBC model and the simplified flange contact model (a, b); the lateral and vertical displacement of 1st span midpoint (c, d); the lateral and vertical displacement (e, f) and acceleration (g, h) of 1st car-body; lateral displacement of wheelset 1 (i) and normal contact force of wheel 1 (left wheel of wheelset 1, j)

A train with two motor vehicles and six trailer vehicles running over a three-span bridge at a constant speed of 250 km/h (69.44 m/s) is considered in this section (Fig. 12a). Besides, three-dimensional seismic wave was loaded exactly at the instant when the train arrived the bridge. The longitudinal, lateral and vertical components of the seismic wave act along the longitudinal, lateral and vertical directions of the bridge in the system, respectively. In addition, the PGAs of the longitudinal, lateral and vertical seismic wave components are 0.41 g, 0.41 g and 0.17 g, respectively.

Some observation results have been summarised according to Fig. 12. First, the bridge response histories of two wheel–rail contact models are identical in both lateral and vertical directions (Fig. 12c, d). Obviously, the two contact models nearly have no difference in the bridge response under earthquake. Second, in the tight contact model, an unreal oscillation takes place in the interval (1, 2), which does not exist in the proposed contact model (Fig. 12e, g, h and j). Third, in the proposed contact model, there is significant fluctuation in the interval (3, 4) due to the increasing seismic load (Fig. 12g, i). In contrast, this phenomenon is inconspicuous in tight contact model. Lastly, the vertical acceleration of 1st car-body and normal contact force of wheel 1 are close overall except for the oscillation in the tight contact model but the response of the tight contact model shows a lower change frequency. In summary, the proposed wheel–rail contact model could have a better performance in car-body and wheel time-history response under earthquake compared with the tight contact model.

4.3 Comparison among the three running safety criterions

A preliminary study on the derailment indexes of train passing the bridge under earthquake was conducted in this section. In this study, the train consists of only one motor vehicle running at a constant speed of 250 km/h (69.44 m/s) and bridge is a five-span prestressed HSR bridge (Fig. 13a). Similarly, seismic wave was loaded exactly at the instant when the train arrived the bridge. In addition, the PGAs of the longitudinal, lateral and vertical seismic wave components are, respectively, 0.41 g, 0.41 g and 0.41 g in this section for generating a more significant result [6]. Figure 13 illustrates the lateral and vertical responses of the train and the time-history curves of the derailment factor, the offload factor and the LWRRD in the simulation. In addition, the part of the offload factor curve (Fig. 13e) above zero is more important; hence, the offload factor curves are not displayed wholly.

Fig. 13

Schematic diagram of TBC model (a), the lateral and vertical acceleration of 1st car-body (b, c) and the comparison among the derailment factor (d), offload faction (e) and LWRRD (f) of the simulation results

As depicted in Fig. 13, the lateral and vertical accelerations of 1st car-body show that the vibration of the train enhances sharply at about t = 2.5 s under seismic effect. Accordingly, the significant rise interval of the curves of the derailment factor is identical for the detachment interval, the offload factor and the LWRRD. Besides, it can be concluded that the derailment factor curve loses many intervals due to the wheel–rail detachment, which is actually important for evaluating derailment. For the offload factor curve, the offload factor is the most conservative, which is equal to one during wheel detaching. It fails after wheel–rail detaching and can hardly be used in seismic stochastic analysis. In contrast, the LWRRD curve is continuous and fluctuates obviously in Fig. 13. As a result of the simulation, a reduced safety threshold can be proposed in this section, which is ${R}_{1}+{R}_{2}=10\, \mathrm{mm}$. In fact, the derailment factor and offload factor are also pointed out to be over-conservative in the seismic running safety assessment in other Refs. [4, 11].

4.4 LWRRD under random seismic magnitude

It is assumed that the seismic magnitude follows the truncated G–R distribution [47, 48, 54] and only strong earthquake (magnitude equal or greater than six) is considered. Besides, the upper magnitude limit (${M}_{u}$) is defined as nine degree, thus the magnitude interval could cover the whole range of strong earthquake. Furthermore, the seismic ground motion attenuation model in Ref. [50] is adopted to calculate the relationship between the PGA and earthquake magnitude. In addition, the parameters and formulas of the truncated G–R relation and the seismic ground motion attenuation model are shown in Sect. 2.8.

In this model, the train consists of four vehicles with motor cars in front and rear, with two trailer cars in the middle, and the bridge is a three-span prestressed HSR bridge (Fig. 14a). Similarly, the seismic waves were input to the system exactly at the moment when the train entered the bridge at a constant speed of 250 km/h (69.44 m/s). The seismic wave sample is the same as Fig. 10, and the input seismic waves are generated by changing the PGA proportionally. Thus, the LWRRD of the system can be obtained according to the PEM and the results are shown as follows.

Fig. 14

Schematic diagram of TBC model (a), the acceleration mean value and Std.D of 1st car-body in the lateral and vertical direction (b, c), the lateral and vertical acceleration reliability curves of 1st car-body (d, e), the LWRRD reliability curves of wheel 1 and wheel 2 (left and right wheel of wheelset 1, f, g) and partially enlarged drawing from f and g (h, i)

According to the probability theory, the reliability prediction of the train response and the LWRRD could be determined, and the results are provided in Fig. 14, which can evaluate the derailment of the TBC system from the perspective of probability. On this basis, it can be seen that the LWRRD reliability curves share the same general trend with the lateral and vertical acceleration of the 1st car-body. Moreover, the results indicate that the train is at risk of derailment from 2.5 to 3 s, and the probability of derailment increases significantly with the seismic magnitude and the duration of earthquake. In summary, the LWRRD can accurately evaluate the train derailment, and this reliability analysis is intuitive and feasible for the train running safety.

5 Conclusion

This study presented a three-dimensional TBC system with a detailed wheel–rail contact model which can simulate the detachment and recontact between the wheel flange and rail. In order to make up for the deficiencies of existing derailment indexes in a stochastic analysis under earthquake, the LWRRD was used to evaluate train running safety and compared with the derailment factor and the offload factor to verify its feasibility and show advantages in stochastic analysis. Besides, the operation safety of a high-speed train traversing a multi-span prestressed simply supported box-girder bridge excited by earthquake with random magnitude is studied. In summary, the main conclusions are as follows:

• (1) The simulated TBC model captures the wheel–rail contact phenomena (flange contact, single detachment, double detachment, climbing up, recontact and derailment) correctly and is verified feasible by comparing with existing experiments.

• (2) Compared with the wheel–rail tight contact model, the proposed wheel–rail contact model is more sensitive and realistic for the TBC system under seismic effect, and the simulated response becomes stable in a shorter time.

• (3) The LWRRD presents the same regulation with the derailment factor and offload factor, but the derailment factor and offload factor cannot evaluate the wheel derailment when the wheel detaches and are more conservative than the LWRRD. In addition, the LWRRD is intuitive and continuous as a derailment index. It shows a significant risk interval (about 2.7–2.9 s herein), which is blank for the derailment factor and flat for the offload factor.

• (4) The reliability assessment for train running safety proposed in this paper is feasible with the random seismic magnitude, and the risk of wheel derailment is evaluated correctly by combining LWRRD with the PEM. Besides, the upper limit of the LWRRD and the derailment probability are significantly affected by the intensity of the earthquake.

In the future, the developed simulation model in this paper will be employed for the further studies to investigate the train running safety assessment under near-fault earthquake in contrast to a TBC scale model experiment.

Appendices

Appendix 1

The train mass matrix can be described as

$$ {\mathbf{M}}_{vv} = {\text{diag}} \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{v1} } \hfill & {{\mathbf{M}}_{v2} } \hfill & \cdots \hfill & {{\mathbf{M}}_{{v\left( {n_{v} - 1} \right)}} } \hfill & {{\mathbf{M}}_{{vn_{v} }} } \hfill \\ \end{array} } \right], $$

(51)

with

$$ \left\{ {\begin{array}{*{20}l} {{\mathbf{M}}_{vi} = {\text{diag}} \left( {\left[ {{\mathbf{M}}_{c,i} \quad {\mathbf{M}}_{t1,i} \quad {\mathbf{M}}_{t2,i} \quad {\mathbf{M}}_{w1,i} \quad {\mathbf{M}}_{w2,i} \quad {\mathbf{M}}_{w3,i} \quad {\mathbf{M}}_{w4,i} } \right]} \right),\;1 \le i \le n_{v} |i,n_{v} {\mathbf{ \in }}Z)} \hfill \\ {{\mathbf{M}}_{j,i} = \left( {m_{x,j} ,m_{y,j} ,m_{z,j} ,J_{\phi ,j} ,J_{\varphi ,j} ,J_{\psi ,j} } \right), \, j \subseteq (c,t1,t2)} \hfill \\ {{\mathbf{M}}_{k,i} = \left( {m_{x,k} ,m_{y,k} ,m_{z,k} ,J_{\phi ,k} ,J_{\psi ,k} } \right), \, k \subseteq (w1,w2,w3,w4)} \hfill \\ \end{array} } \right., $$

(52)

where ‘diag’ represents the matrix is diagonal with other elements being equal to zero, the submatrix ${\mathbf{M}}_{vi}$ means the mass of the ith vehicle, ${\mathbf{M}}_{j,i}$ represents the mass of car-body, front bogie or rear bogie of the ith vehicle, and ${\mathbf{M}}_{k,i}$ denotes the mass of kth wheelset of the ith vehicle.

The train stiffness matrix is

$$ {\mathbf{K}}_{vv} = {\text{diag}} \left[ {\begin{array}{*{20}l} {{\mathbf{K}}_{v1} } \hfill & {{\mathbf{K}}_{v2} } \hfill & \cdots \hfill & {{\mathbf{K}}_{{v\left( {n_{v} - 1} \right)}} } \hfill & {{\mathbf{K}}_{{vn_{v} }} } \hfill \\ \end{array} } \right]. $$

(53)

where the submatrix ${\mathbf{K}}_{vi}$ means the stiffness of each carriage, which has form of

$$ {\mathbf{K}}_{vi} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{ci} } & {{\mathbf{K}}_{ct1i} } & {{\mathbf{K}}_{ct2i} } & 0 & 0 & 0 & 0 \\ {} & {{\mathbf{K}}_{t1i} } & 0 & {{\mathbf{K}}_{t1w1i} } & {{\mathbf{K}}_{t1w2i} } & 0 & 0 \\ {} & {} & {{\mathbf{K}}_{t2i} } & 0 & 0 & {{\mathbf{K}}_{t2w3i} } & {{\mathbf{K}}_{t2w4i} } \\ {} & {} & {} & {{\mathbf{K}}_{w1i} } & 0 & 0 & 0 \\ {} & {} & {} & {} & {{\mathbf{K}}_{w2i} } & 0 & 0 \\ {} & {} & {} & {} & {} & {{\mathbf{K}}_{w3i} } & 0 \\ {\text{ syms }} & {} & {} & {} & {} & {} & {{\mathbf{K}}_{w4i} } \\ \end{array} } \right], $$

(54)

where the submatrix ${\mathbf{K}}_{ci}$ is

$$ {\mathbf{K}}_{ci} = 4\left[ {\begin{array}{*{20}c} {k_{2x} } & 0 & 0 & 0 & { - h_{1} k_{2x} } & 0 \\ {} & {k_{2y} } & 0 & {h_{1} k_{2y} } & 0 & 0 \\ {} & {} & {k_{2z} } & 0 & 0 & 0 \\ {} & {} & {} & {b_{1}^{2} k_{2z} + h_{1}^{2} k_{2y} } & 0 & 0 \\ {} & {} & {} & {} & {h_{1}^{2} k_{2x} + L_{c}^{2} k_{2z} } & 0 \\ {\text{ syms }} & {} & {} & {} & {} & {b_{3}^{2} k_{2x} + L_{c}^{2} k_{2y} } \\ \end{array} } \right]. $$

(55)

The submatrix ${\mathbf{K}}_{tji}$, $(\mathrm{l}\le j\le 2, j\in Z)$ is

$$ {\mathbf{K}}_{tji} = 2\left[ {\begin{array}{*{20}c} {2k_{1x} + k_{2x} } & 0 & 0 & 0 & { - 2h_{3} k_{1x} - h_{2} k_{2x} } & 0 \\ {} & {2k_{1y} + k_{2y} } & 0 & {2h_{3} k_{1y} - h_{2} k_{2y} } & 0 & 0 \\ {} & {} & {2k_{1z} + k_{2x} } & 0 & 0 & 0 \\ {} & {} & {} & {\left( {\begin{array}{*{20}l} {b_{1}^{2} k_{2z} + 2b_{2}^{2} k_{1z} } \hfill \\ { + h_{2}^{2} k_{2y} + 2h_{3}^{2} k_{1y} } \hfill \\ \end{array} } \right)} & 0 & 0 \\ {} & {} & {} & {} & {\left( \begin{gathered} h_{2}^{2} k_{2y} + 2h_{3}^{2} k_{1y} \hfill \\ + 2L_{bw}^{2} k_{1z} \hfill \\ \end{gathered} \right)} & 0 \\ {{\text{syms}}} & {} & {} & {} & {} & {\left( {\begin{array}{*{20}l} {b_{3}^{2} k_{2x} + 2b_{4}^{2} k_{1x} } \hfill \\ { + 2L_{bw}^{2} k_{1z} } \hfill \\ \end{array} } \right)} \\ \end{array} } \right]. $$

(56)

The submatrix ${\mathbf{K}}_{wji} (\mathrm{l}\le j\le 4, j\in Z)$ is

$$ {\mathbf{K}}_{wji} = 2\left[ {\begin{array}{*{20}c} {k_{1x} } & {} & {} & {} & {} \\ {} & {k_{1y} } & {} & {} & {} \\ {} & {} & {k_{1z} + k_{{\text{rail }}} } & {} & {} \\ {} & {} & {} & {b_{0}^{2} \left( {k_{1z} + k_{{\text{rail }}} } \right)} & {} \\ {\text{ syms }} & {} & {} & {} & {b_{4}^{2} k_{1x} } \\ \end{array} } \right]. $$

(57)

The submatrix ${\mathbf{K}}_{ctji}$, $(\mathrm{l}\le j\le 2, j\in Z)$ is

$$ {\mathbf{K}}_{ctji} = - 2\left[ {\begin{array}{*{20}c} {k_{2x} } & 0 & 0 & 0 & {h_{1} k_{2x} } & 0 \\ 0 & {k_{2y} } & 0 & { - h_{2} k_{2y} } & 0 & 0 \\ 0 & 0 & {k_{2z} } & 0 & 0 & 0 \\ 0 & {h_{1} k_{2y} } & 0 & {b_{1}^{2} k_{2z} - h_{1} h_{2} k_{2y} } & 0 & 0 \\ { - h_{1} k_{2x} } & 0 & {( - 1)^{j} L_{c} k_{2z} } & 0 & { - h_{1} h_{2} k_{2x} } & 0 \\ 0 & {( - 1)^{j + 1} L_{c} k_{2y} } & 0 & {( - 1)^{j} h_{2} L_{c} k_{2y} } & 0 & {b_{3}^{2} k_{2x} } \\ \end{array} } \right] $$

(58)

The submatrix ${\mathbf{K}}_{tjwki}({\text{l}}\le i\le 8,\mathrm{ l}\le j\le 2, l\le k\le 4, i,j,k\in Z)$ is

$$ {\mathbf{K}}_{tjwki} = - 2\left[ {\begin{array}{*{20}c} {k_{1x} } & 0 & 0 & 0 & 0 \\ 0 & {k_{1y} } & 0 & 0 & 0 \\ 0 & 0 & {k_{1z} } & 0 & 0 \\ 0 & {h_{3} k_{1y} } & 0 & {( - 1)^{k + 1} b_{0} b_{2} k_{1z} } & 0 \\ { - h_{3} k_{1x} } & 0 & {( - 1)^{k} L_{bw} k_{1z} } & 0 & 0 \\ 0 & {( - 1)^{k} L_{bw} k_{1y} } & 0 & 0 & {b_{4}^{2} k_{1x} } \\ \end{array} } \right]. $$

(59)

Appendix 2

See Tables 8, 9 and 10.

Table 8 Parameters of tractor and trailer (partial data refer to [19])

Table 9 Parameters of track slab and bridge (partial data refer to [15, 18])

Table 10 Parameters of seismic PSD for different site conditions (partial data refer to [15, 44])