1 Introduction

Safety and comfort are the most important requirements for rapid transit trains, so accurate simulation of the three-dimensional (3D) wheel/rail dynamic behavior of a moving train is necessary. One can use a large finite element mesh with solid and contact elements to model rails and wheels, but it is difficult to simulate a whole moving train problem due to computational complexity, and thus the CPU time needed to the calculations. Therefore, a number of alternative methods have been proposed in the literature to simplify modeling of the wheel and rail contact behavior. One approach is to set a constant stiffness between the wheel and rail and to perform the analysis without considering the separation mode [1–9]. The Lagrange multiplier method or the interface compatibility scheme can also be used to simplify the modeling [10–19]. However, while these two methods are suitable to simulate the vibrations induced by moving trains, they may not be appropriate for examining train derailment problems. Several researchers have recently performed nonlinear analyses of train derailments [20–29], and the literature review will focus on these references. Seo et al. [20] modeled the nonlinear behavior of the pantograph/catenary systems, while a 3D multibody railroad vehicle model was developed to demonstrate the use of their formulation. Tanabe et al. [21] developed a numerical method to solve the dynamic interaction of a high-speed train and railway structure during an earthquake using the theory of multibody dynamics, and a mechanical model for contact dynamics between the wheel and rail was presented. Dinh et al. [22] developed a formulation of 3D dynamic interactions between a bridge and a high-speed train, while contact loss is allowed. The vertical contact is represented by finite tensionless stiffness, and the lateral contact is idealized by finite contact stiffness and creepage damping. Nishimura et al. [23] studied the vehicle safety in terms of the dynamic stability during earthquakes, and the rail vehicles involved severe vehicle body motions, wheel lifts, and derailing behaviors. Li et al. [24] developed a numerical method for analyzing coupled railway vehicle–bridge systems of nonlinear features, and established a bridge model with the flexible vehicle effect with the wheel–rail contact including wheel jumps. Ju [25] developed a nonlinear moving wheel element based on a point contact scheme to simulate moving train problems, where the element stiffness is set to a power function directly fitted from the finite element result of the wheel and rail contact analysis. Pombo and Ambrosio [26] studied the dynamic behavior of the railway vehicles, and a multibody formulation was used to build the vehicle model with a wheel–rail contact formulation including normal and tangential forces. Antolin et al. [27] modeled nonlinear wheel–rail contact forces for analyzing the dynamic interaction between high-speed trains and bridges, while nonlinear contact models including Hertz’s and Kalker’s nonlinear theories were considered. Kouroussis and Verlinden [28] performed the numerical analysis of train/track/foundation dynamics, and the proposed model was emphasized by presenting free-field ground vibration responses generated by a high-speed train obtained by a revisited two-step prediction model. Montenegro et al. [29] proposed a wheel–rail contact formulation to analyze the train–structure interaction using a finite element contact method, and the contact location is calculated with an online contact search algorithm. Hertzian contact theory or nonlinear creep theory is often used in these nonlinear wheel/rail dynamic models, but few of them included the frictional sliding mode of the wheel and rail contact. Moreover, due to the difficulty of simulating multiple contact behaviors between the wheel and rail, these are rarely considered in the simple finite element models proposed in the literature.

This study develops a moving wheel/rail contact element, including sliding, sticking, and separation modes, where normal and tangent stiffness are connected to the element and directly fitted from the finite element results of the wheel and rail contact analysis. Moreover, multiple contact regions can be considered in this element.

2 Stiffness matrix of the moving wheel/rail contact element

2.1 Stiffness matrix of three-node contact element

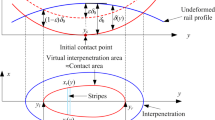
In this study, a frictional contact system is developed to simulate the wheel/rail behavior with sliding, sticking, and separation modes. Figure 1 shows the system, where three springs (\(k_{1}\), \(k_{2}\), and \(k_{3)}\) at the wheel center are used to simulate the nonlinear behavior of the wheel and rail, and cubic spline contact elements are used to calculate the contact locations of the wheel and rail. This section will illustrate the cubic-spline contact element of the wheel and rail.

Fig. 1
figure 1

Moving wheel contact element (C and B are master nodes, and nodes along the contact surfaces of the rail and wheel are slave nodes)

Full size image

The cubic-spline contact element is based on the contact scheme on the local 1–2 coordinates, where the 1–2 axes are obtained from the initial input and are then calculated according to the direction-3 rotation at point-C, as shown in Fig. 1. The rail is modeled using a number of slave nodes controlled by master node C, which means that the displacements of the slave nodes are calculated from the direction-3 rotation and direction-1–2 displacements of master node C, according to the rigid-body theory. Similarly, the wheel is modeled using a number of slave nodes controlled by the master B. The slave nodes of the rail and wheel are mainly input along the possible contact region, and thus the regions along the rail bottom and wheel center are not required. According to an earlier work [30], the sticking, sliding, and separation stiffness matrices at one point are as follows:

$$\begin{aligned} \mathbf{K}_\mathbf{C}= & {} \left[ {{\begin{array}{cc} k&{} 0 \\ 0&{} k \\ \end{array} }} \right] \hbox { for sticking mode},\end{aligned}$$
(1)
$$\begin{aligned} \mathbf{K}_\mathbf{C}= & {} \left[ {{\begin{array}{cc} 0&{} 0 \\ 0&{} 0 \\ \end{array} }} \right] \hbox {for separation mode},\end{aligned}$$
(2)
$$\begin{aligned} \mathbf{K}_\mathbf{C}= & {} \left[ {{\begin{array}{cc} 0&{} {\mu k} \\ 0&{} k \\ \end{array} }} \right] \hbox { for sliding mode}. \end{aligned}$$
(3)

where k is the penalty constant. \(\mu \) is the frictional coefficient with the positive or negative sign, while \(\mu \) is positive for \(\Delta U<0\) and negative for \(\Delta U>0\), and \(\Delta U\) is the difference in the relative tangential displacement between the current and previous time steps. The frictional force at the wheel and rail contact region is three-dimensional, while the longitudinal direction one is dependent on the engine force, braking force, wind force, train speed and so on, so it is extremely difficult to accurately calculate. The alternative is to set an appropriate frictional coefficient in the lateral direction, and this frictional coefficient eliminates the fraction in the longitudinal direction. The frictional force due to the rotating wheel can be further complicated, when contact occurs between the wheel flange and rail side. At this condition, the frictional force is mostly in the longitudinal direction, and a zero frictional coefficient can be set along this region, such as region from points a to b shown in Fig. 1. The stiffness matrix of the sliding mode is unsymmetrical. An alternative approach is to use the following symmetric matrix:

$$\begin{aligned} \mathbf{K}_\mathbf{C} =k \left[ {{\begin{array}{cc} {\mu ^{2}}&{} \mu \\ \mu &{} 1 \\ \end{array} }} \right] \end{aligned}$$
(4)

Equation (4), an approximate sliding stiffness matrix, obeys the Mohr–Coulomb friction theory. In the nonlinear finite element analysis, the balance between internal and external nodal forces will be achieved at the convergent state, while the incremental displacement between two iterations are near zero, so that both Eqs. (3) and (4) obtain similar results. Next, the local stiffness matrices shown in Eqs. (1)–(3) in the contact coordinates are transformed into the 1–2 coordinates with the transformation matrix T.

$$\begin{aligned} \mathbf{K}_{1{-}2} =\mathbf{T}^{\mathrm{T}}{} \mathbf{K}_\mathbf{C}~\mathbf{T} \end{aligned}$$
(5)

where

$$\begin{aligned} \mathbf{T=}\left[ {{\begin{array}{c@{\quad }c} \hbox {cos}\,\theta &{} \hbox {sin}\,\theta \\ -\hbox {sin}\,\theta &{} \hbox {cos}\,\theta \\ \end{array} }} \right] {=}\left[ {{\begin{array}{c@{\quad }c} \hbox {c}&{} \hbox {s} \\ -\hbox {s}&{}\hbox {c} \\ \end{array} }} \right] \end{aligned}$$
(6)

\(\hbox {cos}\,\theta \) and \(\hbox {sin}\,\theta \) are the components of the tangent direction at the current contact node in the 1–2 coordinates, and this tangent direction is always continuous along these cubic splines generated from the wheel nodes.

The two-node stiffness matrix is similar to the four-degree-of-freedom truss element, as follows:

$$\begin{aligned} \mathbf{K}_4 =\left[ {{\begin{array}{c@{\quad }c} \mathbf{K}_{1{-}2}&{} -\mathbf{K}_{1{-}2} \\ -\mathbf{K}_{1{-}2}&{} \mathbf{K}_{1{-}2} \\ \end{array}}} \right] \end{aligned}$$
(7)

The above four-by-four matrix is then transformed to the stiffness matrix of the two master nodes, B and C, in Fig. 1, with two translations (directions 1 and 2) and a rotation (direction 3) degree of freedom at each master node. The six degrees of freedom are point-B 1-direction translation, point-B 2-direction translation, point-C 1-direction translation, point-C 2-direction translation, point-C 3-direction rotation, and point-B 3-direction rotation, respectively. The stiffness matrix is as follows:

$$\begin{aligned} \mathbf{K}_{\mathbf{BC}} =\mathbf{T}_{\mathbf{4}\times \mathbf{6}} ^{\mathrm{T}}\mathbf{K}_\mathbf{4} \mathbf{T}_{\mathbf{4} \times \mathbf{6}} \end{aligned}$$

where

$$\begin{aligned} \mathbf{T}_{\mathbf{4}\times \mathbf{6}} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{}0&{}0&{}0&{}0&{}-\Delta Y_\mathrm{BD}\\ 0&{}1&{}0&{}0&{}0&{}\Delta X_\mathrm{BD}\\ 0&{}0&{}1&{}0&{}-\Delta Y_\mathrm{CD}&{}0\\ 0&{}0&{}0&{}1&{}\Delta X_\mathrm{CD}&{}0\\ \end{array}}} \right] \end{aligned}$$
(8)

The current wheel position equals the initial wheel position plus the duration multiplied by the train speed. The two target nodes between which the wheel node is located can then be found. If the two target nodes and the wheel node are nodes I, J and B, respectively, the above six-degree-of-freedom stiffness matrix is transformed to an 18-by-18 global stiffness matrix of points B, I, and J with three global translation and three global rotation degrees of freedom at each node. The stiffness matrix is as follows:

$$\begin{aligned} \mathbf{K}_{\mathbf{BIJ}} =\mathbf{T}_{\mathbf{6}\times \mathbf{18}} ^{\mathrm{T}}~\mathbf{K}_{\mathbf{BC}}~\mathbf{T}_{\mathbf{6}\times \mathbf{18}} \end{aligned}$$
(9)

where

$$\begin{aligned} \mathbf{T}_{\mathbf{6}\times \mathbf{18}}^{\mathrm{T}} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \mathbf{u}_{1}&{}\mathbf{u}_{2}&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}\mathbf{u}_{3}\\ 0&{}0&{}N_{1}{} \mathbf{u}_{1}&{}N_{1}{} \mathbf{u}_{2}&{}0&{}0\\ 0&{}0&{}-N_{2}{} \mathbf{u}_{2}&{}N_{2}{} \mathbf{u}_{1}&{}S_{n}{} \mathbf{u}_{3}&{}0\\ 0&{}0&{}N_{3}{} \mathbf{u}_{1}&{}N_{3}{} \mathbf{u}_{2}&{}0&{}0\\ 0&{}0&{}-N_{4}{} \mathbf{u}_{2}&{}N_{4}{} \mathbf{u}_{1}&{}(1-S_{n})\mathbf{u}_{3}&{}0\\ \end{array}}} \right] \end{aligned}$$

in which \(\mathbf{u}_{1}\), \(\mathbf{u}_{2}\), and \(\mathbf{u}_{3}\) are the unit vectors of directions 1, 2, and 3, \(S_{n}\) is the ratio of length J–C over length I–J, as shown in Fig. 1, and \(N_{1}\) to \(N_{4}\) are the cubic Hermitian interpolation functions of a beam element with the two end nodes I and J.

2.2 Simulation of wheel/rail contact behavior using a two-node stiffness matrix

The vertical stiffness between the wheel and rail can be determined using the Hertz contact theory, such as a smooth sphere with the radius of R in contact with a smooth flat surface under a normal contact load \(f_{2}\), with the stiffness as follows [16]:

$$\begin{aligned} k_\mathrm{r} =\frac{3}{2}\left( {\frac{16RE_*^{2}}{9}} \right) ^{1/3}f_2 ^{1/3} \end{aligned}$$
(10)

where \(E_*\) is a material constant dependent on Young’s modulus and Poisson’s ratio for the sphere and plate. Hertz contact theory is generally used for regular disks or plates and may produce errors for actual rails and wheels. For this reason, Ju [25] used the following equation to model the stiffness between the wheel and rail.

$$\begin{aligned} k_\mathrm{r} =a+bf_2^c \end{aligned}$$
(11)

where a, b, and c are constant, and \(a=3\times 10^{4}~\hbox {KN}/\hbox {m}\), \( b=2.94\times 10^{5}~\hbox {KN}/\hbox {m}\), \(c=0.241104\) for UIC-60-kg rail and the wheel of the SKS-700 train [25].

It is clear that Eq. (11) can be used to model the Hertz contact stiffness. Ju [25] then evaluated a, b, and c, by fitting the results of a contact finite element analysis between the rail and wheel, in which 3D solid elements and contact elements are used to find the stiffness between the rail and wheel with good accuracy. The advantage is that this calculation only needs to be performed once, and one can then use the realistic stiffness to undertake the dynamic analyses of moving train problems. For the horizontal stiffness, the horizontal stiffness can be set to a constant, because the major displacement comes from the linear deformation of the wheel and rail in the horizontal direction, and the nonlinear contact deformation is relatively small. To model the above stiffness, three springs (\(k_{1}\), \(k_{2}\), and \(k_{3)}\) in the local 1, 2, and 3 directions at the wheel center are used to simulate the nonlinear behavior of the wheel and rail, as shown in Fig. 1. The two end nodes of the springs can be set to the same coordinates at the wheel center. One can set another three rotation springs to model the rotation stiffness of the wheel and rail. If the rotations are assumed to be rigid, the two nodes are simply set to the same rotation degrees of freedom. One can easily connect this proposed element to other types of elements, in which the target rail nodes, such as I, C, and J, as shown in Fig. 1, can be modeled using 3D beam elements, and node-A having six degrees of freedom can be connected to any structural element, including rigid links to a master node.

Fig. 2
figure 2

Contact conditions between two force steps and two iterations. 1 and 3 = The two edge nodes of the active segment of the cubic spline, \(2_{0}=\) node 2 at last time step at the convergent state, \(2_{n}= \) node 2 at this time step and last iteration (iteration n), \(2_{n+1}=\) node 2 at this time step and this iteration (iteration n, \(+1\)), \(C_{n+1}=\) contact node on the cubic spline at this time step and this iteration, \(D_{0}=\) contact node on line 1–3 at last time step at the convergent state, \(D_{n+1}=\) contact node on line 1–3 at this time step and this iteration, u \(=\) tangent direction at contact node \(C_{n+1}\), v \(=\) normal direction at contact node \(C_{n+1}\)

Full size image

3 Evaluation of normal and frictional forces on the contact surface

Figure 2 shows an active segment of the node-to-cubic-spline contact element during two time steps and two iterations, where node 2 is the contact node at the rail, nodes 1 and 3 on the wheel are the two edge nodes of the active segment of the cubic spline, and the active segment means that the contact node (node 2) touches the cubic spline within this segment. Node C is the contact node on the cubic spline, in which line 2-C is normal to the cubic spline. Node D is the intersection point of line 1–3 and line 2-C. All of the nodes in the figure have been updated by adding the displacement of the last iteration. The coordinates of nodes \(C_{n+1}\) and \(D_{n+1}\) are unknown and thus need be calculated in the current iteration, and one may solve the cubic and line equations using the Newton–Raphson method to obtain them. From Fig. 2, the tangent displacement (\(\Delta U\)) between the present force step and last force step is approximated to:

$$\begin{aligned} {\varDelta } U=(S_0 -S_n )L_{1{-}3} \end{aligned}$$
(12)

where \(L_{i-j}\) means the length between points i and j, \(S_{0} =\frac{L_{D_0 -3} }{L_{1{-}3} }\), \(S_{n} =\frac{L_{D_{n+1} -3} }{L_{1{-}3} }\), \(\mu \) is positive for \(\Delta U<0\) and negative for \(\Delta U>0\) . The total normal displacement (V) approximates to:

$$\begin{aligned} V=\overline{C_{n+1} 2_{n+1} } \cdot (-\mathbf{v}) \end{aligned}$$
(13)

where \(\overline{C_{n+1} 2_{n+1}}\) means vector \(C_{n+1}2_{n+1}\), and \(\cdot \) means vector dot. The normal and frictional forces at the contact node are computed as follows:

  1. (1)

    for sticking

    $$\begin{aligned} F_{n} =k|V|\hbox { and } F_s =k|U|+(\mathbf{u}_\mathrm{1} \cdot \mathbf{u})F_{s1} \end{aligned}$$
    (14)

    where k is the penalty constant, \(F_{s1}\) is the frictional force of the previous time step, and \(\mathbf{u}_{1}\) is the tangent direction at the current node in the previous time step.

  2. (2)

    for sliding

    $$\begin{aligned} F_n =k|V|\hbox { and } F_s =\mu F_n \end{aligned}$$
    (15)

    It is then necessary to check whether the results are the sticking, sliding, or separating mode. Equation (13) is first used to check the separating mode. If V of Eq. (13) is smaller than zero, then node 2 has separated from the target surface (Fig. 2), and thus the penalty constant and internal forces of the contact element are set to zero. To check for the sticking and sliding modes, the sticking mode is first assumed, and thus if \(F_s <\mu F_n \) it is sticking mode, while if \(F_s \ge \mu F_n \) it is sliding mode.

4 Accuracy study

4.1 A wheel and rail contact problem with a constant horizontal force

The accuracy of the proposed wheel/rail contact element is studied using dynamic analyses, as shown in Fig. 3, which includes a SKS-700 train wheel with s 0.858-m diameter and a 0.555-m UIC-60-kg rail fixed at the two rail ends. A horizontal Kelvin spring-damper with the stiffness of \(K_\mathrm{H}\) (\(1200~\hbox {kN}/\hbox {m})\) and damping of \(C_\mathrm{H}\) (40 kN s/m) is connected between the wheel center master node and a horizontal constant force of 20 kN. A vertical Kelvin spring-damper with the stiffness of \(K_\mathrm{V}\) (\(1200~\hbox {kN}/\hbox {m})\) and damping of \(C_\mathrm{V}\) (\(40~\hbox {kN-s}/\hbox {m})\) is then connected between the wheel center master node and a lumped mass M (6.25 t), where the wheel mass is \(m=0.283~\hbox {t}\). The above spring and damper constants are obtained from those of the vertical primary suspension for SKS-700 train. The vertical force F(t) applied to the location of the lumped mass is a sine function with the mean value of \(-10~\hbox {kN}\), the amplitude of 61.25 kN, and the frequency of 10 Hz. In this study, the derailment coefficient (Q/P) defined in Eq. (16) is calculated to study the accuracy of the proposed method.

$$\begin{aligned} (Q/P)=Q_{\mathrm{2\,m}} /P_{\mathrm{2\,m}} \end{aligned}$$
(16)

where \(Q_{\mathrm{2\,m}}\) and \( P_{\mathrm{2\,m}}\) are the average horizontal and vertical forces of the contact forces on the wheel and rail during the wheel movement distance of 2 m.

Fig. 3
figure 3

The wheel/rail contact example in Sect. 4 and the finite element mesh of the complex model

Full size image

Both complex and simple models were generated, where the complex model uses eight-node solid and contact elements to simulate the wheel and rail, and the simple model uses the proposed contact element to simulate the wheel and 20 two-node beam elements to simulate the rail. For the complex model, the finite element mesh is shown in Fig. 3, where eight-node brick isoparametric elements and Hermit contact elements with the penalty constant of \(10^{6}~\hbox {kN}/\hbox {m}\) and the coefficient of the friction of 0.5 are used, and a fine mesh is generated near the contact region in order to obtain a precise finite element contact analysis. It is noted that a large penalty constant was used to avoid the inaccuracy of the finite element analysis, while the error deformation from the penalty method is smaller than 1/1000 of the deformation at the wheel center. A master node is set at the center of the wheel to control the slave nodes along the inner circle of the wheel. Both models use the Newton–Raphson method and the Newmark direct integration to solve this problem. The time step length is 0.0005 s, and 520 time steps are simulated. Figure 4a shows the contact forces between the wheel and rail changing with time, while Fig. 4b shows the derailment coefficient using Eq. (16) assuming a train speed of \(300~\hbox {km}/\hbox {h}\) [Q and P are averaged during a 2-m (or 0.024 s) movement], and Fig. 5 shows the contact regions of the wheel and rail from the simple model at 0, 0.01, and 0.2 s of the finite element analyses. The three figures indicate:

  1. (1)

    Both the normal and horizontal contact forces of the complex and simple methods have similar finite element results. The derailment coefficients calculated from the complex and simple methods are thus also similar. This example shows that the proposed method can be used to simulate the multiple contact situation, as shown in Fig. 5, where the contacts between wheel flange and rail side can be accurately analyzed. Moreover, the sliding and sticking modes of the contact were well-simulated using the simple model.

  2. (2)

    It is almost impossible to use the 3D solid and contact model to analyze practical moving train problems, because the finite element model requires a very fine mesh between wheels and rails, as shown in Fig. 3. In contrast, the proposed simple method does not have these drawbacks. The numbers of degrees of freedom for the complex and simple models are 1,046,708 and 116, respectively, for the highly nonlinear frictional contact analyses, and the computer time needed for the two models is 38 h and 32 s, respectively, for 550 time steps using an 3.5-GHz-intel-i7 computer. This indicates that the simple model is significantly more efficient, since it requires much less computer time and memory, while the accuracy is not significantly lower.

Fig. 4
figure 4

Vertical (P) and horizontal (Q) contact forces and derailment coefficient (Q/P averaged between 0.024 s) from the finite element analyses in Sect. 4.1. a Contact forces (Q and P) between wheel and rail. b Derailment coefficient (Q/P)

Full size image
Fig. 5
figure 5

Positions of the wheel and rail contact region from the simple model analysis in Sect. 4.1

Full size image

4.2 A wheel and rail contact problem with a sine wave horizontal force

Fig. 6
figure 6

Vertical (P) and horizontal (Q) contact forces and derailment coefficient (Q/P) averaged between 0.024 s from the finite element analyses in Sect. 4.2 (regions A and B are during the separation mode of the wheel and rail). a Contact forces (Q and P) between wheel and rail. b Derailment coefficient (Q/P)

Full size image
Fig. 7
figure 7

Positions of the wheel and rail contact region from the simple model analysis in Sect. 4.2

Full size image
Fig. 8
figure 8

Derailment coefficients averaged between 0.024 s changing with time from the finite element analyses in Sect. 4.2 with torsion at the beam center

Full size image
Fig. 9
figure 9

Positions of the wheel and rail contact region from the simple model analysis in Sect. 4.2 with torsion at the beam center

Full size image

The previous example with a constant horizontal force on the wheel causes a steady state sticking mode of the contact behavior between the wheel flange and rail side. This section uses the same model as shown in Fig. 3, but only changes the constant horizontal force to a sine wave horizontal force, so that the contact between the wheel and rail shows complicated cyclic behavior, including sliding, sticking, and separation modes. The horizontal sine wave force has the amplitude of 10.4125 kN and the frequency of 10 Hz. Figure 6a shows the contact forces between the wheel and rail changing with time, while Fig. 6b shows the derailment coefficient using equation (16) assuming a train speed of \(300~\hbox {km}/\hbox {h}\) (Q and P are averaged during a 2-m (or 0.024 s) movement), and Fig. 7 shows the contact regions of the wheel and rail from the simple model at 0, 0.027, and 0.267 s of the finite element analyses. The three figures indicate a similar conclusion to that reported for the previous example, in that both the normal and horizontal contact forces of the complex and simple methods have similar finite element results. Additionally, the separation time and interval of the wheel and rail, as shown in the A and B regions of the figures, are also similar using both methods. The proposed simple method can thus be used to simulate the sliding, sticking, and separation modes of the wheel and rail contact problems and achieve results with good accuracy.

A more complicated simulation was performed using the same model as above. An additional torsion (\(183.25\hbox {sin}(10\pi t)~\hbox {kN}\)) in the X direction is applied to the beam center, and the wheel system moves from \(X=0\) with an X-direction speed of 0.5 m/s. The complex finite element analysis was omitted due to the fine mesh required for all the beam and wheel. Figure 8 shows the derailment coefficient averaged from \(0.024~\hbox {s}\), and Fig. 9 shows the contact regions of the wheel and rail from the simple analysis. The two figures indicate that the proposed method can be used to simulate significantly complicated wheel and rail contact problems using a simple finite element model.

5 Conclusions

This study developed a nonlinear moving wheel/rail contact element with the sticking, sliding, and separation modes, where the wheel and rail are simulated using the cubic-spline contact element connected with a power function normal stiffness and a constant horizontal stiffness, which were computed from the 3D contact finite element analysis for the realistic wheel and rail using a fine mesh. The validated examples in this paper show that the proposed nonlinear moving wheel element can simulate the complicated sliding, sticking, and separation contact problems with good accuracy compared with the 3D contact finite element analysis. Moreover, the derailment coefficients calculated from the proposed method are also accurate, not only for the complicated contact modes, but also for multiple contact situations, such as the contacts between wheel flange and rail side. This proposed element can be easily connected to other types of elements, such as spring-damper elements, lumped mass, plate elements, and rigid links, and a whole flexible or rigid-body train finite element model then can be generated without too many degrees of freedom. The major advantage of the proposed method is that the much less computer memory and CPU time required than with the 3D finite element contact model, but the accuracy of the resulting analysis accuracy is similar.