1 Introduction

The class of KdV equations is one of the most attractive classes of the nonlinear evolution equations. This popularity is due to the exceedingly applications in science and engineering. One of the most interesting members of this class is the coupled KdV system which is arisen from several branches of applications such as fluid dynamics [21], supersymmetric integrable systems [23], and ion-acoustic waves [34]. The general form of the coupled KdV system of equations reads as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\mathfrak {u}}_{t}+(\mathfrak {f}(\mathfrak {u}, \mathfrak {v}))_x+ \gamma \mathfrak {u}_{xxx}=&{} 0,\\ \displaystyle {\mathfrak {v}}_{t}+(\mathfrak {g}(\mathfrak {u}, \mathfrak {v}))_x + \delta \mathfrak {v}_{xxx}=&{}0, \end{array}\right. } \end{aligned}$$
(1)

where \(\gamma \) and \(\delta \) are known arbitrary real values and the sufficiently smooth functions \(\mathfrak {f}\) and \(\mathfrak {g}\) are considered as given nonlinear functions with respect to variables \(\mathfrak {u}\) and/or \(\mathfrak {v}\). By considering various \(\mathfrak {f},\mathfrak {g},\gamma \), and \(\delta \) (based on the studied models and physical systems), many types of the coupled KdV system of equations arise from the general form (1). Some of them are the Hirota-Satsuma equation [3, 17], coupled KdV dark equations [6], coupled Schrödinger-KdV equations [34], generalized complex Hirota-Satsuma coupled KdV equation [40], and also some other previous ones [14,15,16].

Although the Ito-type coupled KdV system [10, 18, 36] is nominated and investigated in this research, the proposed HDG method can be reformulated and analyzed for the other types of the coupled KdV system. With arbitrary constants \(\alpha \) and \(\beta \) and setting \(\delta = 0\), and

$$\begin{aligned} \mathfrak {f}(\mathfrak {u}, \mathfrak {v}) = \frac{\alpha }{2} \mathfrak {u}^2+ \frac{\beta }{2} \mathfrak {v}^2,\qquad \mathfrak {g}(\mathfrak {u}, \mathfrak {v}) = \beta \mathfrak {u}\mathfrak {v} \end{aligned}$$
(2)

in (1), the Ito-type coupled KdV system is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \mathfrak {u}_t + \Big (\frac{\alpha }{2}\mathfrak {u}^2 + \frac{\beta }{2}\mathfrak {v}^2\Big )_x + \gamma \mathfrak {u}_{xxx} = 0,\\ \mathfrak {v}_t + \beta (\mathfrak {u}\mathfrak {v})_x = 0, \end{array}\right. } \end{aligned}$$
(3)

where \((x,t)\in \varOmega \times I\) in which \(\varOmega = [a, b]\) and \(I=(0,T]\) such that \(0<T<\infty \) is specified as the final time. And besides, \(\mathfrak {u}(x,0)\) and \(\mathfrak {v}(x,0)\) for all \(x\in \varOmega \) are given as initial conditions and we need some admissible boundary conditions for the well-posedness of the Ito-type coupled KdV system (3). These boundary conditions may be either the periodic boundary conditions or a collection of \( \mathfrak {v}= b_{\mathfrak {v}}\) at \(x=a\) or \(x=b\), \(\mathfrak {u}_x= b_{\mathfrak {u}_x}\) at \(x=a\) or \(x=b\), and one of the following conditions:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathfrak {u} = b_{\mathfrak {u}} ~ \mathrm{{at}} ~ x=a~ \mathrm{{and}} ~ \mathfrak {u}_{xx} {\mathbf {n}} = b_{\mathfrak {u}_{xx}}~\mathrm{{at}} ~ x=b,\\ \mathfrak {u} = b_{\mathfrak {u}} ~ \mathrm{{at}} ~ x=b~ \mathrm{{and}} ~ \mathfrak {u}_{xx} {\mathbf {n}} = b_{\mathfrak {u}_{xx}}~\mathrm{{at}} ~ x=a,\\ \mathfrak {u} = b_{\mathfrak {u}}~ \mathrm{{at}}~ x=a~ \mathrm{{and}} ~x=b, \end{array} \right. \end{aligned}$$

where \(b_{\mathfrak {u}}\), \(b_{\mathfrak {v}}\), \(b_{\mathfrak {u}_x}\), and \(b_{\mathfrak {u}_{xx}}\) are boundary data of \(\mathfrak {u}\), \(\mathfrak {v}\), \(\mathfrak {u}_x\), and \(\mathfrak {u}_{xx}\), respectively.

It is known that there are several versions of what called Ito equations. Some of them are integrable and have soliton solutions. Although (3) is integrable, it is unclear that whether it has soliton solutions or not. Therefore, studying (3) is a hard problem from the viewpoint of integrable systems. On the other hand, it is well known that the third-order Ito-type coupled KdV system possesses infinitely many symmetries and conservation laws [24]. It is worth pointing out that these symmetries define a hierarchy of the Ito-type coupled KdV system. Each equation of the system (3) is a Hamiltonian with infinitely many constants of the motion, and also, the Ito-type coupled KdV system does not have a Lagrangian. Most of shallow water wave problems can be modelled in nonlinear KdV systems [33, 36] and proceeding of the interaction of two long internal waves can be shown by the Ito-type system (3) [16, 18].

To solve some complicated problems involving PDEs or systems of them, several numerical methods have been exploited. Among a variety of existing works, the finite difference [1, 3, 34], finite element [4], wavelet [9], discontinuous Galerkin (DG) [7, 13, 30, 35,36,37], and meshless [25,26,27] methods are more outstanding and applicable. Due to some limitations of the traditional DG method, e.g., existing inconsistency in numerical solutions, Cockburn and Shu [12] invented the local DG (LDG) method which can be applied for solving problems with higher order space derivatives [22, 28, 35, 37,38,39]. The framework of LDG methods is based on reformulating a higher order linear/nonlinear PDE to a first-order system of PDEs, see, e.g., [8, 28, 35,36,37,38,39]. Classical DG methods preserve high-order accuracy for both the solution and its derivatives but some continuous Galerkin (CG) methods such as the well-known finite-element method are more economical in particular in solving some steady-state problems. Some hybridized DG (HDG) methods have developed for keeping high-order accuracy of DG methods and improving their efficiencies. In fact, an HDG method exploits DG and CG solvers simultaneously for increasing performance of the method. According to what mentioned in [19], an HDG method in solving steady-state problems at high orders is actually quite computationally competitive with CG methods. Therefore, the HDG method is more accurate and efficient than some traditional methods. The first HDG method was introduced by Cockburn et al. in [11], and since then, this interesting method has been applied to the various classes of linear/nonlinear of fractional/nonfractional PDEs, see, e.g., [7, 13, 20, 30,31,32]. It is worth noting that HDG methods need less number of globally coupled degrees of freedom rather than DG methods. Numerical traces in the HDG method, as global unknowns, depend only on the number of elements for an arbitrary polynomial.

This paper is concerned with the numerical solution of the Ito-type coupled KdV system of equations equipped with specific initial/boundary conditions. In this work, we are interested in establishing and developing an HDG method for approximating the solutions of the Ito-type coupled KdV system of equations. The main step of all types of DG methods including the hybridized type, which is reformulating the higher order system into a corresponding first-order system, has to be performed. Based on this fact, we must define appropriate numerical fluxes that fit to the stability analysis of the HDG method. Since the coupled KdV equation (1) is first order with respect to time variable, the discretization in time can be performed using an unconditionally stable method. The structure of the variational formulation of the selected types of coupled KdV equations is complicated. Based on this fact and to avoid more complexity, we select a very simple unconditionally stable time-discretization method, called the backward Euler implicit method. We note that the analysis of any type of the DG method, in particular the HDG method, depends on special theoretical concepts that are not available in classical Sobolev spaces. Based on the definition of broken Sobolev spaces introduced in [5], we set up the relevant Sobolev spaces of the variational formulation of the HDG method for the Ito-type coupled KdV problem. By proving the stability of the method under certain conditions on the stabilization parameters and demonstrating numerical examples, the efficiency of the method is confirmed. By setting \(\alpha =\beta =0\), the coupled KdV system is reduced to the linear KdV equation which has been solved in [14] using an HDG method and an error estimate has been presented. The convergence analysis of the HDG method for this kind of coupled system is too complicated, and to the best of our knowledge, it has not yet been presented neither for the LDG nor for the HDG methods and we leave it to the next future. To compare the LDG and the proposed HDG methods, orders of convergence and computational costs of the methods, for solving some Ito-type coupled KdV systems, are reported.

The remainder of the paper is organized as follows. In Sect. 2, we recall and briefly summarize the needed preliminaries for the proposed HDG method. In Sect. 3, the variational formulation of the Ito-type coupled KdV system of equations is obtained in the framework of the HDG method. Section 4 is devoted to the stability analysis of the HDG method for the Ito-type coupled KdV system of equations. In Sect. 5, some numerical examples have been tested for demonstrating the efficiency and accuracy of the HDG method for the Ito-type coupled KdV system and dealing with some physical properties of the system. Last section is devoted to conclusions.

2 Necessary Preliminaries: Notations and Spaces

To design the HDG method for the Ito-type coupled KdV system, the appropriate broken Sobolev spaces and corresponding broken inner products, with respect to the spatial variable x, are proposed. Meanwhile, the elementary ingredients for performing the HDG method are given based on the spatial decomposition. In the coupled KdV system, the spatial domain is considered the interval \(\varOmega = [a, b]\). Let \(\varOmega \) be partitioned to

$$\begin{aligned} a= x_{-\frac{1}{2}}< x_{\frac{1}{2}}< x_{\frac{3}{2}}< \cdots < x_{N-\frac{1}{2}} = b. \end{aligned}$$

Without loss of generality, we suppose that \(\varOmega \) is regularly partitioned with the mesh size \(h=\frac{b-a}{N}\). The jth element of the partitioning of \(\varOmega \) is represented by

$$\begin{aligned} {\mathscr {I}}:={\mathscr {I}}_j=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}],\quad j = 0,\cdots , N-1. \end{aligned}$$

The collection of disjoint elements and the collection of boundaries of elements, respectively, are denoted by

$$\begin{aligned} {\mathscr {T}}_h:=\{{\mathscr {I}}_0,{\mathscr {I}}_1,\cdots , {\mathscr {I}}_{N-1}\},\quad \partial {\mathscr {T}}_h:=\{\partial {\mathscr {I}}_0,\partial {\mathscr {I}}_1,\cdots ,\partial {\mathscr {I}}_{N-1}\}, \end{aligned}$$

where \(\partial {\mathscr {I}}:=\partial {\mathscr {I}}_{j}=\{x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}\}\). The set of all nodes is denoted by \({\mathcal {E}}_h={\mathcal {E}}_h^0\cup {\mathcal {E}}_h^\partial \), where \({\mathcal {E}}_h^0\) and \({\mathcal {E}}_h^\partial \) are the sets of interior and boundary nodes of the partition, respectively. The average and jump of the function v are defined as follows:

$$\begin{aligned} \{\{v\}\}=\left\{ \begin{array}{ll} (v^++v^-)/2,&{}e\in {\mathcal {E}}_h^0,\\ v,&{}e\in {\mathcal {E}}_h^\partial , \end{array} \right. \quad [[v{\varvec{n}}]]=\left\{ \begin{array}{ll} v^+{\varvec{n}}^++v^-{\varvec{n}}^-,&{}e\in {\mathcal {E}}_h^0,\\ v{\varvec{n}},&{}e\in {\mathcal {E}}_h^\partial , \end{array} \right. \end{aligned}$$

where \(v^+\) and \(v^-\) on the node e represent, respectively, \(v(e^+)\) and \(v(e^-)\). The function v has a single value at the boundary nodes, then different definitions at those nodes are specified separately. The outward unit normal vectors for boundaries of the element \({\mathscr {I}}_j\) are given as \({\varvec{n}}^-_{j+1/2}=+1\) and \({\varvec{n}}^+_{j-1/2}=-1\). The sets of boundary nodes which boundary data are specified on \(\mathfrak {v}\) and \({\mathfrak {u}}\), and their first and second derivatives are denoted, respectively, by \(\Gamma _{\mathfrak {v}}, ~\Gamma _{\mathfrak {u}},~\Gamma _{\mathfrak {u}_x}, {\text{and}}~\Gamma _{\mathfrak {u}_{xx}}\).

The corresponding broken Sobolev spaces associated with the partition \({\mathscr {T}}_h\) and the node set \({\mathcal {E}}_h\), are defined as

$$\begin{aligned} L_2({\mathscr {T}}_h)= & {} \{v:\varOmega \rightarrow {\mathbb {R}}: v\mid _{\mathscr {I}}\,\in L_2({\mathscr {I}}),\forall {\mathscr {I}}\in {\mathscr {T}}_h \},\\ H^1({\mathscr {T}}_h)= & {} \{v:\varOmega \rightarrow {\mathbb {R}}: v\mid _{\mathscr {I}}\,\in H^1({\mathscr {I}}),\forall {\mathscr {I}}\in {\mathscr {T}}_h \},\\ {\mathcal {M}}^1({\mathcal {E}}_h)= & {} \{\mu :{\mathcal {E}}_h\rightarrow {\mathbb {R}}: \mu \mid _e\, \in H^1(e), \forall e \in {\mathcal {E}}_h\}. \end{aligned}$$

Similar to the standard Sobolev spaces, several broken embedding theorems, such as the broken Sobolev-Poincaré theorem, are proven for the broken Sobolev spaces [5]. The standard broken inner products with respect to \({\mathscr {T}}_h, \partial {\mathscr {T}}_h\), and \({\mathcal {E}}_h\), respectively, are defined as

$$\left\{ \begin{array}{ll} \langle \vartheta _1,\vartheta _2\rangle _{{\mathscr {T}}_h}= & {} \displaystyle \sum _{{\mathscr {I}} \in {\mathscr {T}}_h}\langle \vartheta _1,\vartheta _2\rangle _{\mathscr {I}}, \quad \langle \mu _1,\mu _2\rangle _{\partial {\mathscr {T}}_h}=\sum _{{\mathscr {I}}\in {\mathscr {T}}_h}\langle \mu _1,\mu _2\rangle _{\partial {\mathscr {I}}}, \nonumber \\ \displaystyle \langle \vartheta _1,\vartheta _2\rangle _{{\mathscr {I}}_j}= & {} \int _{x_{j-1/2}}^{x_{j+1/2}}\vartheta _1(x)\vartheta _2(x){\text{d}}x,\quad \displaystyle \langle \mu _1,\mu _2\rangle _{\partial {\mathscr {I}}_j}=\mu _{1,j+\frac{1}{2}}^- \mu _{2,j+\frac{1}{2}}^-+\mu _{1,j-\frac{1}{2}}^+\mu _{2,j-\frac{1}{2}}^+. \end{array} \right. $$
(4)

The superscripts − and \(+\) indicate the left- and right-hand limits of the function, respectively. In the broken inner products (4), \(\vartheta _1\, {\text{and}}\, \vartheta _2\) are defined on \({\mathscr {T}}_h,\) and \(\ \mu _1\, {\text{and}}\,\mu _2\) are defined on \(\partial {\mathscr {T}}_h\).

Let \({\mathcal {P}}^k({\mathscr {I}})\) be the set of polynomials of degree at most k over the element \({\mathscr {I}} \in {\mathscr {T}}_h\). The subspaces of discontinuous finite-element space and skeleton space (or trace space), respectively, are defined as

$$\left\{ \begin{array}{ll} S^k_h= & {} \bigl \{w\in H^1({\mathscr {T}}_h) : w\mid _{\mathscr {I}} \,\in {\mathcal {P}}^k({\mathscr {I}}), \forall {\mathscr {I}} \in {\mathscr {T}}_h\bigr \},\nonumber \\ M^k_h= & {} \{\mu \in {\mathcal {M}}^1({\mathcal {E}}_h): \mu \mid _e \,\in {\mathcal {P}}^k(e), \forall e \in {\mathcal {E}}_h\}. \end{array} \right. $$
(5)

Regarding the boundary conditions, it is needed to define some subspaces of \(M^k_h\) such as

$$\begin{aligned} M_h^{k,\mathfrak {u}}(l):=\{\mu \in M_h^k:\mu (x)=\Pi l(x),\ x \in \Gamma _{\mathfrak {u}}\}, \end{aligned}$$
(6)

where the \(L_2\)-projection \(\Pi \) maps the space of boundary functions into the skeleton space \(M^k_h.\)

3 Variational Formulation and Numerical Scheme

This section is concerned with establishing a numerical scheme derived from the HDG method to the Ito-type coupled KdV system. The numerical scheme is formed by the aid of the weak formulation of the Ito-type coupled KdV with the HDG method element by element over the partition \({\mathscr {T}}_h\). The significant subject in this formulation is to define appropriate numerical fluxes that leads to the stability of the numerical method based on the HDG method for the Ito-type coupled KdV system. We note that the numerical fluxes are defined globally over the domain \(\varOmega \). The usage of numerical fluxes leads to the main advantage of the HDG method and its superiority over other DG methods. In fact, imposing the continuity of the numerical fluxes and then applying the CG method establish a global system with less degree of freedom over the node set \(\partial {\mathscr {T}}_h\). The first-order system corresponding to the Ito-type coupled KdV system (3) is formulated as

$$\begin{aligned} \mathfrak {u}_t + \big (\mathfrak {s}(\mathfrak {u},\mathfrak {v},\mathfrak {p})\big )_x = 0,\qquad \mathfrak {v}_t + \big (\mathfrak {g}(\mathfrak {u},\mathfrak {v})\big )_x = 0,\qquad \mathfrak {q} - \mathfrak {u}_x = 0,\qquad \mathfrak {p} - \mathfrak {q}_x = 0, \end{aligned}$$
(7)

where \(\mathfrak {s}(\mathfrak {u},\mathfrak {v},\mathfrak {p}) = \mathfrak {f}(\mathfrak {u}, \mathfrak {v}) + \gamma \mathfrak {p}\). By multiplying all equations in (7) by test functions \(\mu , \nu , \varrho , \vartheta \in H^1({\mathscr {T}}_h)\), from top to bottom, respectively, and integrating both sides over the element \({\mathscr {I}}\in {\mathscr {T}}_h\), we end up with the variational problem of finding solution

$$\begin{aligned} (\mathfrak {u},\mathfrak {v},\mathfrak { q},\mathfrak {p})\in H^1({I};\,H^1({\mathscr {T}}_h))\times H^1({I};\,L_2({\mathscr {T}}_h))\times L_2({I};\,H^1({\mathscr {T}}_h))\times L_2({I};\,H^1({\mathscr {T}}_h)), \end{aligned}$$

such that for all \({\mathscr {I}} \in {\mathscr {T}}_h\) and for all test functions \(\mu , \nu , \varrho , \vartheta \in H^1({\mathscr {T}}_h),\)

$$\begin{aligned} \left\{ \begin{array}{ll} \langle \mathfrak {u}_t, \mu \rangle _{\mathscr {I}} + \langle \big (\mathfrak {s}(\mathfrak {u},\mathfrak {v},\mathfrak {p})\big )_x, \mu \rangle _{\mathscr {I}} = {} 0, \\ \langle \mathfrak {q}, \nu \rangle _{\mathscr {I}} - \langle \mathfrak {u}_x, \nu \rangle _{\mathscr {I}} = {} 0,\\ \langle \mathfrak {p}, \varrho \rangle _{\mathscr {I}} - \langle \mathfrak {q}_x, \varrho \rangle _{\mathscr {I}} = {} 0,\\ \langle \mathfrak {v}_t, \vartheta \rangle _{\mathscr {I}} + \langle \big (\mathfrak {g}(\mathfrak {u},\mathfrak {v})\big )_x, \vartheta \rangle _{\mathscr {I}} = {} 0.\end{array} \right. \end{aligned} $$
(8)

To obtain the discretized version of the variational problem (8), we substitute an approximate solution (u, v, q, p) into the weak formulation (8) and apply the integration by parts. Now, we seek \((u,v,q,p)\in (H^1({I};\,S_h^k))^2\times (L_2({I};\,S_h^k))^2\), such that

$$\begin{aligned} \left\{ \begin{array}{ll} \langle u_t, \mu \rangle _{\mathscr {I}} - \langle \mathfrak {s}(u,v,p), \mu _x\rangle _{\mathscr {I}} + \langle {\widehat{s}}{\varvec{n}}, \mu \rangle _{\partial {\mathscr {I}}} = {} 0, \\ \langle q, \nu \rangle _{\mathscr {I}} + \langle u, \nu _x\rangle _{\mathscr {I}} - \langle {\hat{u}}{\varvec{n}}, \nu \rangle _{\partial {\mathscr {I}}} = {} 0,\\ \langle p, \varrho \rangle _{\mathscr {I}} + \langle q, \varrho _x\rangle _{\mathscr {I}} - \langle {\widehat{q}}{\varvec{n}}, \varrho \rangle _{\partial {\mathscr {I}}} = {} 0,\\ \displaystyle \langle v_t, \vartheta \rangle _{\mathscr {I}} - \langle \mathfrak {g}(u, v), \vartheta _x\rangle _{\mathscr {I}} + \langle {\widehat{g}}{\varvec{n}}, \vartheta \rangle _{\partial {\mathscr {I}}} = {} 0,\end{array} \right. \end{aligned} $$
(9)

hold for all \((\mu ,\nu ,\varrho ,\vartheta )\in (S_h^k)^4\) and for all \({\mathscr {I}} \in {\mathscr {T}}_h\). Here, the following numerical fluxes are considered:

$$\begin{aligned} \left\{ \begin{array}{ll} {\widehat{s}}= \mathfrak {s}({\hat{u}},v,p) + \tau _ 1(u - {\hat{u}}){\varvec{n}}, \\ {\widehat{g}}= \frac{1}{2}(\mathfrak {g}({\hat{u}},{\hat{v}}) + \mathfrak {g}({\hat{u}},v)) + \tau _2(v-{\hat{v}}){\varvec{n}},\\ {\widehat{q}} = {\hat{q}} + \tau _ 3(q - {\hat{q}}){\varvec{n}}. \end{array} \right. \end{aligned} $$
(10)

The stabilization parameters \(\tau _1\), \(\tau _2\), and \(\tau _3\) are determined, such that the stability of the method is attained. Numerical traces \({\hat{u}}\in M^{k,\mathfrak {u}}_h (b_{\mathfrak {u}})\), \({\hat{v}}\in M^{k,\mathfrak {v}}_h (b_{{\mathfrak {v}}})\), and \({\hat{q}}\in M^{k,\mathfrak {q}}_h (b_{{\mathfrak {q}}})\) are defined as follows:

$$\begin{aligned} {\hat{u}}= \left\{ \begin{array}{ll} b_{\mathfrak {u}},&{}{\mathcal {E}} ^\partial _h \cap \Gamma _{\mathfrak {u}} ,\\ \lambda _u, &{} {\mathcal {E}}_h \setminus \Gamma _{\mathfrak {u}}, \end{array} \right. \qquad {\hat{v}}= \left\{ \begin{array}{ll} b_{\mathfrak {v}},&{} {\mathcal {E}} ^\partial _h \cap \Gamma _{\mathfrak {v}},\\ \lambda _v, &{} {\mathcal {E}}_h \setminus \Gamma _{\mathfrak {v}}, \end{array} \right. \qquad {\hat{q}}= \left\{ \begin{array}{ll} b_{\mathfrak {q}},&{} {\mathcal {E}} ^\partial _h\cap \Gamma _{\mathfrak {q}},\\ \lambda _q, &{} {\mathcal {E}}_h \setminus \Gamma _{\mathfrak {q}}, \end{array} \right. \end{aligned}$$
(11)

where \((\lambda _u,\lambda _v,\lambda _q)\in M^{k,\mathfrak {u}}_h(0)\times M^{k,\mathfrak {v}}_h(0)\times M^{k,\mathfrak {q}}_h(0)\). We simply figure out that in contrast to local unknowns u, v, p, and q over each element \({\mathscr {I}}\in {\mathscr {T}}_h\), the traces \({\hat{u}}, {\hat{v}}, {\hat{q}}\in {\mathcal {M}}^1({\mathcal {E}}_h)\) are global unknowns. Taking into account that three new unknowns \(\lambda _u,\lambda _v,\) and \(\lambda _q\) are added to the variational formulation (9), it is essentially needed to impose three appropriate equations. These equations can be obtained by enforcing conservation of the fluxes. Thanks to this fact, we have

$$\begin{aligned} \left\{ \begin{array}{ll} p {\varvec{n}} =b_{\mathfrak {p}},&{} e \in \Gamma _{\mathfrak {p}},\\ {[}[{\widehat{s}}{\varvec{n}} ]]=0, &{} e \in {\mathcal {E}}_h^0, \end{array} \right. \qquad \left\{ \begin{array}{ll} [[{\widehat{g}}{\varvec{n}} ]]=\beta uv {\varvec{n}} ,&{} e \in {\mathcal {E}}_h^\partial \setminus \Gamma _{\mathfrak {v}},\\ {[}[{\widehat{g}}{\varvec{n}} ]]=0, &{} e \in {\mathcal {E}}_h^0, \end{array} \right. \qquad \left\{ \begin{array}{ll} [[{\widehat{q}}{\varvec{n}} ]]=q {\varvec{n}} ,&{} e \in {\mathcal {E}}_h^\partial \setminus \Gamma _{\mathfrak {q}},\\ {[}[{\widehat{q}}{\varvec{n}} ]]=0, &{} e \in {\mathcal {E}}_h^0. \end{array} \right. \end{aligned}$$
(12)

Remark 1

By considering periodic boundary conditions, some small changes must be made to (11) and (12). The periodic boundary conditions state more simply that \(\mathfrak {u}|_a = \mathfrak {u}|_b\), \(\mathfrak {u}_x|_a = \mathfrak {u}_x|_b\), \(\mathfrak {u}_{xx}|_a = \mathfrak {u}_{xx}|_b\), and \(\mathfrak {v}|_a = \mathfrak {v}|_b\). Indeed, it must be guaranteed that the numerical traces \({\hat{u}}\), \({\hat{v}}\), and \({\hat{q}}\) get the same value at \(x=a\) and \(x=b\), that is

$$\begin{aligned} {\hat{u}}= \left\{ \begin{array}{ll} \lambda _u|_a = \lambda _u|_b,&{} {\mathcal {E}} _h^\partial ,\\ \lambda _u, &{} {\mathcal {E}} _h^0, \end{array} \right. ~ {\hat{v}}= \left\{ \begin{array}{ll} \lambda _v|_a = \lambda _v|_b,&{} {\mathcal {E}} _h^\partial ,\\ \lambda _v, &{}{\mathcal {E}} _h^0, \end{array} \right. ~ {\hat{q}}= \left\{ \begin{array}{ll} \lambda _q|_a = \lambda _q|_b,&{} {\mathcal {E}} _h^\partial ,\\ \lambda _q, &{}{\mathcal {E}} _h^0, \end{array} \right. \end{aligned}$$

where \((\lambda _u,\lambda _v,\lambda _q)\in { M^{k}_h\times M^{k}_h\times M^{k}_h}\). In this case, there exist N faces where \((\lambda _u,\lambda _v,\lambda _q)\) are unknown. On the other hand, we need N global equations which are defined as

$$\begin{aligned} \left\{ \begin{array}{ll} {\widehat{s}} |_a = {\widehat{s}}|_b,&{} e \in {\mathcal {E}}_h^\partial ,\\ {[}[{\widehat{s}}{\varvec{n}} ]]=0, &{} e \in {\mathcal {E}}_h^0, \end{array} \right. ~ \left\{ \begin{array}{ll} {\widehat{g}} |_a = {\widehat{g}}|_b ,&{} e \in {\mathcal {E}}_h^\partial ,\\ {[}[{\widehat{g}}{\varvec{n}} ]]=0, &{} e \in {\mathcal {E}}_h^0, \end{array} \right. ~ \left\{ \begin{array}{ll} {\widehat{q}} |_a = {\widehat{q}}|_b ,&{} e \in {\mathcal {E}}_h^\partial ,\\ {[}[{\widehat{q}}{\varvec{n}} ]]=0, &{} e \in {\mathcal {E}}_h^0. \end{array} \right. \end{aligned}$$

It is noteworthy that the extra equations (12) must be solved and then by substituting the solutions of the equations (12) into (9), all of the local unknowns in this weak form can be found in each element of \({\mathscr {T}}_h\). Finally, summing (9) up over all elements and substituting numerical traces (11) and the numerical fluxes (10) into (9) and (12), we achieve a semi-discrete HDG method that is the problem of finding \((u,v,q,p,\lambda _\mathfrak {u},\lambda _\mathfrak {q},\lambda _\mathfrak {v})\), such that for all

$$\begin{aligned}(\mu ,\nu ,\varrho ,\vartheta ,\eta _u,\eta _v,\eta _q)\in (S_h^k)^4\times M^{k,\mathfrak {u}}_h(0)\times M^{k,\mathfrak {v}}_h(0)\times M^{k,\mathfrak {q}}_h(0),\end{aligned}$$

the following system of equations holds:

$$\begin{aligned}\left\{ \begin{array}{ll}&\displaystyle \langle u_t,\mu \rangle _{{\mathscr {T}}_h}+ \gamma \langle p_x,\mu \rangle _{{\mathscr {T}}_h} - \frac{\alpha }{2}( u^2,\mu _x )_{{\mathscr {T}}_h} + \frac{\beta }{2} ( (v^2)_x,\mu )_{{\mathscr {T}}_h} + \frac{\alpha }{2}\langle \lambda _u^2{\varvec{n}},\mu \rangle _{\partial {{\mathscr {T}}_h}\setminus \Gamma _\mathfrak {u}} \nonumber \\& \displaystyle +\langle \tau _1 u, \mu \rangle _{\partial {{\mathscr {T}}_h}} - \langle \tau _1 \lambda _u,\mu \rangle _{\partial {{\mathscr {T}}_h}\setminus \Gamma _\mathfrak {u}}= l_1(\mu ),\nonumber \\&\displaystyle \langle q,\nu \rangle _{{\mathscr {T}}_h}+( u,\nu _x)_{{\mathscr {T}}_h}-\langle \lambda _u{\varvec{n}} ,\nu \rangle _{\partial {{\mathscr {T}}_h}\setminus \Gamma _\mathfrak {u}}=l_2(\nu ),\nonumber \\&\displaystyle \langle p,\varrho \rangle _{{\mathscr {T}}_h}+( q,\varrho _x)_{{\mathscr {T}}_h}-\langle ({\varvec{n}}-\tau _3)\lambda _q{\varvec{n}} ,\varrho \rangle _{\partial {{\mathscr {T}}_h}\setminus \Gamma _\mathfrak {q}} - \langle \tau _3 q, \varrho \rangle _{\partial {{\mathscr {T}}_h}}=l_3(\varrho ),\nonumber \\&\displaystyle \langle v_t,\vartheta \rangle _{{\mathscr {T}}_h}- \beta ( uv,\vartheta _x)_{{\mathscr {T}}_h}+ \frac{\beta }{2}\langle \lambda _u\lambda _v{\varvec{n}}, \vartheta \rangle _{\partial {{\mathscr {T}}_h}\setminus \Gamma _\mathfrak {v}} + \frac{\beta }{2}\langle \lambda _uv{\varvec{n}}, \vartheta \rangle _{\partial {{\mathscr {T}}_h}} +\frac{\beta }{2}\langle b_{\mathfrak {u}} v {\mathbf {n}},\vartheta \rangle _{\Gamma _u} \nonumber \\& +\displaystyle \langle \tau _2 v, \vartheta \rangle _{\partial {{\mathscr {T}}_h}} - \langle \tau _2 \lambda _v,\vartheta \rangle _{\partial {{\mathscr {T}}_h}\setminus \Gamma _\mathfrak {v}}= l_4(\vartheta ),\nonumber \\&\displaystyle \frac{\alpha }{2}\langle \lambda _u^2{\varvec{n}},\eta _u\rangle _{\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial }+\frac{\beta }{2}\langle v^2{\varvec{n}},\eta _u\rangle _{\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial } + \gamma \langle p{\varvec{n}}, \eta _u\rangle _{(\partial {\mathscr {T}}_h\setminus {\mathcal {E}}_h^\partial )\cup \Gamma _{\mathfrak {p}}}\nonumber \\& +\langle \tau _1 u,\eta _u\rangle _{\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial } -\langle \tau _1\lambda _u,\eta _u\rangle _{\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial } =l_5(\eta _u),\nonumber \\&\displaystyle \langle ({\varvec{n}} - \tau _3)\lambda _q, \eta _q\rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {q}} + \langle \tau _3 q, \eta _q\rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {q}} - \langle q {\varvec{n}}, \eta _q\rangle _{{\mathcal {E}}_h^\partial \setminus \Gamma _\mathfrak {q}} = 0,\nonumber \\&\displaystyle \frac{\beta }{2} \langle \lambda _u\lambda _v{\varvec{n}}, \eta _v \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}} + \frac{\beta }{2} \langle \lambda _uv{\varvec{n}}, \eta _v \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}} \nonumber \\& +\displaystyle \langle \tau _2 v,\eta _v\rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}} - \langle \tau _2\lambda _v,\eta _v\rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}} -\beta \langle uv{\varvec{n}}, \eta _v\rangle _{{\mathcal {E}}_h^\partial \setminus \Gamma _\mathfrak {v}}=0, \end{array} \right. \end{aligned}$$
(13)

where

$$\begin{aligned} \begin{array}{lc} \displaystyle l_1(\mu )= -\frac{\alpha }{2}\langle b _\mathfrak {u}^2{\varvec{n}},\mu \rangle _{\Gamma _{\mathfrak {u}}} + \langle \tau _1 b _\mathfrak {u},\mu \rangle _{ \Gamma _{\mathfrak {u}}},\quad \displaystyle l_2(\nu )=\langle b_{\mathfrak {u}}{\varvec{n}},\nu \rangle _{\Gamma _{\mathfrak {u}}},\quad \displaystyle l_3(\varrho )=\langle ({\varvec{n}}-\tau _3) b_{\mathfrak {q}},\varrho \rangle _{\Gamma _{\mathfrak {q}}},\\ \displaystyle l_4(\vartheta )= - \frac{\beta }{2}\langle b_\mathfrak {u}b_\mathfrak {v}{\mathbf {n}}, \vartheta \rangle {_{\Gamma _{\mathfrak {v}}} } + \langle \tau _2 b _v,\vartheta \rangle _{\Gamma _{\mathfrak {v}}}, \quad l_5(\eta _u) = {\gamma } \langle b_{\mathfrak {p}},\eta _u \rangle _{\Gamma _{\mathfrak {p}}}. \end{array} \end{aligned}$$

To have simultaneous space-time discretization for the Ito-type coupled KdV system, a suitable time discretization must be applied to (13). To do this, for time discretization, we choose the backward scheme which is actually the BDF(1), i.e., the backward differentiation formula [2], that is unconditionally stable and easy to implement. To have a corresponding matrix representation of (13), it is needed to apply a suitable linearization method like the Newton-Raphson or time-lagging method to the nonlinear weak formulation (13). We linearize the nonlinear weak form (13) using the time-lagging method that is formed by applying the following Taylor expansions:

$$\begin{aligned} u^2(\cdot ,t^n) = u(\cdot ,t^{n-1})u(\cdot ,t^n) + {{O}}(\Delta t), \end{aligned}$$

where \(\Delta t\) is a time-step size, and \(t^n=n\Delta t\) for \(n=0,1,\cdots \). The nonlinear terms \(v^2\), uv, \(\lambda _u^2\), \(\lambda _v^2\), and \(\lambda _u \lambda _v\) are linearized similarly. By defining some necessary linear functionals, bilinear, trilinear, and quadrilinear forms based on (13), the space-time-discretization scheme corresponding to the Ito-type coupled KdV system for \(n=1,2,\cdots \) reads as

$$\begin{aligned} \left\{ \begin{array}{ll} {\textsf {a}_1}(u^n, u^{n-1},\mu ) + {\textsf {a}_2}(v^n, v^{n-1},\mu ) +\gamma \textsf {b}_1(\mu , p^n)+{\textsf {a}_3}(\lambda _u^n, \lambda _u^{n-1},\mu )={}{\textsf {l}^{n,n-1}_1}(\mu ),\\ {\textsf {b}_1}(u^n,\nu )+{\textsf {b}_2}(q^n,\nu )+{\textsf {b}_3}(\lambda _u^n ,\nu )={}{\textsf {l}_2^n}(\nu ),\\ {\textsf {c}_1}(q^n,\varrho ) + {\textsf {b}_2}(p^n,\varrho ) + {\textsf {c}_2}(\lambda _q^n, \varrho )={}{\textsf {l}_3^n}(\varrho ),\\ {\textsf {d}_1}(v^n, u^{n-1}, \lambda _u^{n-1},\vartheta ) + {\textsf {d}_2}(\lambda _v^n, \lambda _u^{n-1},\vartheta ) ={}{\textsf {l}_4^{n,n-1}}(\vartheta ),\\ {\textsf {e}_1}(u^n,\lambda _u^{n-1},\eta _u) + {\textsf {e}_2}(v^n, v^{n-1},\eta _u) + \textsf {e}_3(p^n,\eta _u)+{\textsf {e}_4}(\lambda _u^n, \lambda _u^{n-1} ,\eta _u)={}{\textsf {l}_5^n}(\eta _u),\\ {\textsf {f}_1}(q^n,\eta _q)+{\textsf {f}_2}(\lambda _q^n ,\eta _q)={}0,\\ {\textsf {g}_1}(v^n, u^{n-1}, \lambda _u ^{n-1},\eta _v)+{\textsf {g}_2}(\lambda _v^n, \lambda _u^{n-1} ,\eta _v)={}0,\\ \end{array} \right. \end{aligned}$$
(14)

where the linear functionals and multilinear forms in (14) are given as

$$\begin{aligned}&{\textsf {a}_1}(u^n, u^{n-1},\mu ) = \big\langle \frac{u^n}{\Delta t}, \mu \big\rangle _{{\mathscr {T}}_h} -\frac{\alpha }{2}\langle u^{n - 1}u^n,\mu _x\rangle _{{\mathscr {T}}_h} + \langle \tau _1^{n-1}u^n, \mu \rangle _{\partial {\mathscr {T}}_h},\\&{\textsf {a}_2}(v^n, v^{n-1},\mu ) =\beta \langle v^{n - 1}v^n_x, \mu \rangle _{{\mathscr {T}}_h},\\&{\textsf {a}_3}(\lambda _u^n, \lambda _u^{n-1} ,\mu ) = \frac{\alpha }{2}\langle \lambda _u^{n - 1}\lambda _u^n{\varvec{n}}, \mu \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _{\mathfrak {u}}} - \langle \tau _1^{n-1} \lambda _u^n, \mu \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _{\mathfrak {u}}},\\&{\textsf {b}_1}(u^n,\nu )=\langle u^n,\nu _x\rangle _{{\mathscr {T}}_h},\qquad {\textsf {b}_2}(q^n,\nu )=\langle q^n,\nu \rangle _{{\mathscr {T}}_h},\qquad {\textsf {b}_3}(\lambda _u^n,\nu )=-\langle \lambda _ u^n{\varvec{n}}, \nu \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _{\mathfrak {u}}},\\&{\textsf {c}_1}(q^n,\varrho ) = \langle q^n, w_x\rangle _{{\mathscr {T}}_h} - \langle \tau _3 q^n, \varrho \rangle _{\partial {\mathscr {T}}_h},\qquad {\textsf {c}_2}(\lambda _q^n,\varrho ) = \langle (\tau _3 - {\varvec{n}})\lambda _q^n, \varrho \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _{\mathfrak {q}}},\\&{\textsf {d}_1}(v^n, u^{n-1}, \lambda _u^{n-1},\vartheta ) = \big\langle \frac{v^n}{\Delta t}, \vartheta \big\rangle _{{\mathscr {T}}_h} -\beta \langle u^{n - 1}v^n, \vartheta _x\rangle _{{\mathscr {T}}_h} + \langle \tau _2^{n-1}v^n, \vartheta \rangle _{\partial {\mathscr {T}}_h} + \frac{\beta }{2}\langle \lambda _u^{n-1}v^n {\varvec{n}}, \vartheta \rangle _{\partial {\mathscr {T}}_h}\\& \qquad\qquad\qquad\qquad\,\,\,+ \frac{\beta }{2}\langle b_\mathfrak {u} v^n {\mathbf {n}},\vartheta \rangle _{\Gamma _\mathfrak {u}},\\&{\textsf {d}_2}(\lambda _v^n, \lambda _u^{n-1},\vartheta ) =\frac{\beta }{2} \langle \lambda _u^{n - 1}\lambda _v^n{\varvec{n}}, \vartheta \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _{\mathfrak {v}}} - \langle \tau _2^{n-1} \lambda _v^n, \vartheta \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _{\mathfrak {v}}} ,\\ \end{aligned}$$
$$\begin{aligned}&{\textsf {e}_1}(u^n,\lambda _u^{n-1},\eta _u)=\langle \tau _1 ^{n-1} u^n,\eta _u \rangle _{\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial },\qquad {\textsf {e}_2}(v^n, v^{n-1},\eta _u) = \frac{\beta }{2}\langle v^{n-1}v^n{\varvec{n}} , \eta _u \rangle _{\partial {\mathscr {T}}_h\setminus {\mathcal {E}}_h^\partial },\\&{\textsf {e}_3}(p^n,\eta _u)=\gamma \langle p^n{\varvec{n}}, \eta _u\rangle _{(\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial )\cup \Gamma _\mathfrak {p}},\\&{\textsf {e}_4}(\lambda _u^n, \lambda _u^{n-1},\eta _u) = \frac{\alpha }{2}\langle \lambda _\mathfrak {u}^{n - 1}\lambda _\mathfrak {u}^n {\varvec{n}}, \eta _u\rangle _{\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial } - \langle \tau _1 ^{n-1} \lambda _\mathfrak {u}^n, \eta _u \rangle _{\partial {\mathscr {T}}_h \setminus {\mathcal {E}}_h^\partial },\\&{\textsf {f}_1}(q^n,\eta _q)=\langle \tau _3 q^n, \eta _q \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {q}} - \langle q^n {\varvec{n}}, \eta _q \rangle _{{\mathcal {E}}_h^\partial \setminus \Gamma _\mathfrak {q}},\\&{\textsf {f}_2}(\lambda _q^n,\eta _q) =\langle ({\varvec{n}} - \tau _3 ) \lambda _q^n, \eta _q \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {q}},\\&{\textsf {g}_1}(v^n, u^{n-1}, \lambda _u ^{n-1},\eta _v)=\langle \tau _2^{n-1} v^n, \eta _v\rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}} + \frac{\beta }{2}\langle \lambda _u^{n-1} v^n {\varvec{n}}, \eta _v\rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}} - \beta \langle u^{n-1}v^n {\varvec{n}}, \eta _v \rangle _{{\mathcal {E}}_h^\partial \setminus \Gamma _\mathfrak {v}},\\&{\textsf {g}_2}(\lambda _v^n, \lambda _u^{n-1},\eta _v) = \frac{\beta }{2} \langle \lambda _u^{n - 1}\lambda _v^n {\varvec{n}}, \eta _v \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}} - \langle \tau _2 ^{n-1} \lambda _v^n, \eta _v \rangle _{\partial {\mathscr {T}}_h \setminus \Gamma _\mathfrak {v}},\\&{\textsf {l}}_1^{n,n-1}(\mu )= \langle \frac{u^{n-1}}{\Delta t}, \mu \rangle _{{\mathscr {T}}_h} - \frac{\alpha }{2}\langle (b_\mathfrak {u}^2)^n{\varvec{n}}, \mu \rangle _{\Gamma _{\mathfrak {u}}} + \langle \tau _1 ^n b_\mathfrak {u}^n, \mu \rangle _{\Gamma _{\mathfrak {u}}},\\&{\textsf {l}}_4^{n,n-1}(\vartheta )= \big\langle \frac{v^{n-1}}{\Delta t}, \vartheta \big\rangle _{{\mathscr {T}}_h} - \frac{\beta }{2} \langle (b_\mathfrak {u}b _\mathfrak {v})^n{\varvec{n}}, \vartheta \rangle _{\Gamma _{\mathfrak {v}}} + \langle \tau _2 ^n b_\mathfrak {v}^n, \vartheta \rangle _{\Gamma _{\mathfrak {v}}},\\&{\textsf {l}}_2^{n}(\nu )= \big\langle b_\mathfrak {u}^n{\varvec{n}}, \nu \big\rangle _{\Gamma _{\mathfrak {u}}},\qquad {\textsf {l}}_3^{n}(\varrho )= \langle ({\varvec{n}}-\tau _3)b_\mathfrak {q}^n, \varrho \rangle _{\Gamma _{\mathfrak {q}}},\qquad {\textsf {l}}_5^{n}(\eta _u)= \langle b_\mathfrak {p}^n, \eta _u\rangle _{\Gamma _{\mathfrak {p}}}. \end{aligned}$$

Hence, (u, v, q, p) at \(t=t^n\) is obtained in terms of the values at \(t=t^{n-1}\) for \(n=1,2,\cdots \), by solving the system of linear equations (14). The corresponding matrix-vector equation of (14) is formulated as

$$\begin{aligned} MX^{n} = R^{n,n-1},\qquad n=1,2,\cdots , \end{aligned}$$
(15)

where

$$\begin{aligned} M= \left[ \begin{array}{ccccccc} A_1&{}A_2&{} 0&{}\gamma B_1^{\text{T}}&{}A_3&{}0&{}0\\ B_1&{}0&{}B_2&{}0&{}B_3&{}0&{}0\\ 0&{}0&{}C_1&{}B_2&{}0&{}0&{}C_2\\ 0&{}D_1&{}0&{}0&{}0&{}D_2&{}0\\ E_1&{}E_2&{}0&{}E_3&{}E_4&{}E_5&{}0\\ 0&{}0&{}F_1&{}0&{}0&{}0&{}F_2\\ 0&{}G_1&{}0&{}0&{}0&{}G_2&{}0 \end{array} \right] ,\qquad X^{n}=\left[ \begin{array}{c} U^{n}\\ V^{n}\\ Q^{n}\\ P^{n}\\ \Lambda _u^{n}\\ \Lambda _v^{n}\\ \Lambda _q^{n} \end{array} \right] ,\qquad R^{n,n-1}=\left[ \begin{array}{c} L_1^{n,n-1}\\ L_2^{n}\\ L_3^{n}\\ L_4^{n,n-1}\\ L_5^{n}\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

It is worth pointing out that the matrices \(A_1,A_2,\cdots ,G_1,G_2\) are the matrix representations of the \(\textsf {a}_1,\textsf {a}_2,\cdots ,\textsf {g}_1,\textsf {g}_2\), respectively, and also, the vectors \(L_1^{n,n-1},L_2^{n},\cdots ,L_5^{n}\) are the vector representations of the functionals \(\textsf {l}_1^{n,n-1},\textsf {l}_2^{n},\cdots ,\textsf {l}_5^{n}\), respectively, with respect to the standard basis functions for subspaces \(S^k _h, M^{k,\mathfrak {u}}_h(0),M^{k,\mathfrak {q}}_h(0), \text { and } M^{k,\mathfrak {v}}_h(0)\). To reduce the matrix computations for solving (15), it is very useful to consider the following notations:

$$\begin{aligned} M=\left[ \begin{array}{cc} M_{11}&{}M_{12}\\ M_{21}&{}M_{22} \end{array}\right] ,\quad X^{n}=\left[ \begin{array}{c} X_1^{n}\\ X_2^{n}\end{array}\right] ,\quad R^{n,n-1}=\left[ \begin{array}{c} R_1^{n,n-1}\\ R_2^{n,n-1}\end{array}\right] , \end{aligned}$$
(16)

where

$$\begin{aligned} X_1^n=[U^n\ V^n\ Q^n\ P^n]^{\text{T}}, ~ X_2^n=[\Lambda _u^n\ \Lambda _v^n\ \Lambda _q^n]^{\text{T}},~ R_1^{n,n-1}=[L_1^{n,n-1}\ L_2^{n} \ L_3^{n}\ L_4^{n,n-1}]^{\text{T}},~ R_2=[L_5^{n}~0~0]^{\text{T}}, \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{ll} M_{11}= & {} \left[ \begin{array}{ccccc} A_1&{}A_2&{}0&{} \gamma B_1^{\text{T}}\\ B_1&{}0&{}B_2&{}0\\ 0&{}0&{}C_1&{}B2\\ 0&{}D_1&{}0&{}0\\ \end{array} \right] ,\quad M_{12}= \left[ \begin{array}{cccc} A_3&{}0&{}0\\ B_3&{}0&{}0\\ 0&{}0&{}C_2\\ 0&{}D_2&{}0\\ \end{array} \right] , \nonumber \\ M_{21}= & {} \left[ \begin{array}{cccc} E_1&{}E_2&{}0&{}E_3\\ 0&{}0&{}F_1&{}0\\ 0&{}G_1&{}0&{}0\\ \end{array} \right] ,\quad M_{22}= \left[ \begin{array}{ccccc} E_4&{}E_5&{}0\\ 0&{}0&{}F_2\\ 0&{}G_2&{}0\\ \end{array} \right] \end{array} \right. \end{aligned}$$
(17)

Based on the Schur complement idea [29] and the introduced matrix and vector partitioning in (16), we propose a method that it can be exploited for solving (15). This method contains two steps at each time level \(n=1,2,\cdots \). At time level n, the first step is to find \(X_2^n\) by solving the following matrix-vector equation:

$$\begin{aligned} (M_{22}-M_{21}M_{11}^{-1}M_{12})X_2^n=R_2^{n,n-1}-M_{21}M_{11}^{-1}R_1^{n,n-1}. \end{aligned}$$
(18)

The second step of the proposed method at time level n is to compute \(X_1^n\) via solving the following matrix-vector equation:

$$\begin{aligned} M_{11} X_1^n=R_1^{n,n-1}-M_{12}X_2^n. \end{aligned}$$
(19)

The advantage of this method is that the large system of linear equations (15) is splitted to the systems of linear equations (18) and (19) with smaller sizes where three matrix-vector equations depend on the mesh size h. Since, in this method, the degree of freedom decreases simply, therefore, the computational complexity of the arithmetic operations for solving (14) or (15) is reduced remarkably. We finish this section with the following remark.

Remark 2

We note that the HDG method is almost local, and regarding the structure of the matrices and vectors given in (16) and (17), it is possible to solve matrix-vector equations (18) and (19) in parallel.

4 Stability Analysis of the Method

In this section, we aim to investigate the numerical stability of the proposed scheme which is based on the HDG method with the time-lagging linearization and backward Euler method. In our verifications, we consider two types of boundary conditions which mentioned along the Ito-type coupled KdV system, i.e., periodic boundary conditions and homogeneous Dirichlet boundary conditions.

To simplify the analysis, by setting \(\tau _1 = \tau _{11}+ \tau _{12}\), we decompose \({\widehat{s}}\) in (10) into linear and nonlinear parts as \({\widehat{s}}={\widehat{f}} + \widehat{\gamma p},\) where

$$\begin{aligned} {\widehat{f}}= \mathfrak {f}({\hat{u}},v) + \tau _ {12}(u - {\hat{u}}){\varvec{n}}, \qquad \widehat{\gamma p} = \gamma p + \tau _ {11} (u - {\hat{u}}){\varvec{n}}. \end{aligned}$$
(20)

Lemma 1

Setting

$$\begin{aligned} {S}_{1,j}= & {} \big ((\widehat{\gamma p})_{j+\frac{1}{2}}^- - \gamma ( p)_{j+\frac{1}{2}}^-\big ) u_{j+\frac{1}{2}}^- +\big (\gamma ( p)_{j-\frac{1}{2}}^+ -(\widehat{\gamma p})_{j-\frac{1}{2}}^+ \big ) u_{j-\frac{1}{2}}^+ \\&+\gamma {\hat{u}}_{j+\frac{1}{2}}( p)_{j+\frac{1}{2}}^- - \gamma {\hat{u}}_{j-\frac{1}{2}}( p)_{j-\frac{1}{2}}^+ +{\widehat{f}}_{j+\frac{1}{2}}^-{\hat{u}}_{j+\frac{1}{2}} - {\widehat{f}}_{j-\frac{1}{2}}^+{\hat{u}}_{j-\frac{1}{2}}, \\ {S}_{2,j}= & {} -\gamma \big (({\widehat{q}}^-_{j + \frac{1}{2}} - \frac{1}{2}q^-_{j + \frac{1}{2}})q^-_{j + \frac{1}{2}} - ({\widehat{q}}^+_{j - \frac{1}{2}} - \frac{1}{2}q^+_{j - \frac{1}{2}}) q^+_{j - \frac{1}{2}} \big ),\\ {S}_{3,j}= & {} \langle {\widehat{g}}{\varvec{n}},v\rangle _{\partial {{\mathscr {I}}}} + \langle {\widehat{f}}{\varvec{n}}, u-{\hat{u}}\rangle _{\partial {{\mathscr {I}}}}-\langle \mathfrak {f}(u,v), u_x\rangle _{{\mathscr {I}}}-\langle \mathfrak {g}(u,v), v_x\rangle _{{\mathscr {I}}}, \end{aligned}$$

we get

$$\begin{aligned} \displaystyle \frac{1}{2}\frac{\partial }{\partial t} \int _{\Omega }(u^2 + v^2){\text{d}}x+{S}_1+{S}_2+{S}_3 = 0, \end{aligned}$$
(21)

where \({S}_1= \sum _{j = 0}^{N-1} {S}_{1,j}\), \({S}_2=\sum _{j = 0}^{N-1} {S}_{2,j} \), and \({S}_3=\sum _{j = 0}^{N-1} {S}_{3,j} .\)

Proof

Getting \(\mu =u, \nu =- \gamma p, \varrho =\gamma q\), and \(\vartheta =v\) in (9), we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \langle u_t,u\rangle _{\mathscr {I}} - \langle \mathfrak {s}(u,v,p),u_x\rangle _{\mathscr {I}}+ \langle \widehat{\gamma p}{\varvec{n}},u\rangle _{\partial {\mathscr {I}}} + \langle {\widehat{f}}{\varvec{n}},u\rangle _{\partial {\mathscr {I}}}={}0,\\ -\gamma \langle q,p\rangle _{\mathscr {I}}-\gamma \langle u,p_x\rangle _{\mathscr {I}} + \gamma \langle {\hat{u}}{\varvec{n}},p\rangle _{\partial {\mathscr {I}}}={}0,\\ \gamma \langle p,q\rangle _{\mathscr {I}}+\gamma \langle q,q_x\rangle _{\mathscr {I}} - \gamma \langle {\widehat{q}}{\varvec{n}},q\rangle _{\partial {\mathscr {I}}}={}0,\\ \displaystyle \langle v_t,v\rangle _{\mathscr {I}} - \langle \mathfrak {g}(u,v),v_x\rangle _{\mathscr {I}} +\langle {\widehat{g}}{\varvec{n}},v\rangle _{\partial {\mathscr {I}}}={}0. \end{array} \right. \end{aligned}$$
(22)

Summing all equations of (22), using integration by parts formula, and adding and subtracting \(\langle {\widehat{f}}{\varvec{n}}, {\hat{u}}\rangle _{\partial {{\mathscr {I}}}}\), we get

$$\begin{aligned} \displaystyle \frac{1}{2}\frac{\partial }{\partial t} \int _{{\mathscr {I}}}(u^2 + v^2){\text{d}}x+{S}_{1,j}+{S}_{2,j} +{S}_{3,j} = 0, \end{aligned}$$
(23)

where

$$\begin{aligned} \begin{array}{l} {S}_{1,j} =-\langle \gamma pu,{\varvec{n}}\rangle _{\partial {{\mathscr {I}}}} +\langle \widehat{\gamma p} {\varvec{n}}, u\rangle _{\partial {{\mathscr {I}}}} + \gamma \langle {\hat{u}}, p{\varvec{n}}\rangle _{\partial {{\mathscr {I}}}} +\langle {\widehat{f}}{\varvec{n}}, {\hat{u}}\rangle _{\partial {{\mathscr {I}}}},\\ {S}_{2,j} = \frac{\gamma }{2} \int _{\mathscr {I}}(q^2)_x {\text{d}}x - \gamma \langle {\widehat{q}}{\varvec{n}}, q\rangle _{\partial {{\mathscr {I}}}} = \frac{\gamma }{2} \langle q^2,{\varvec{n}}\rangle _{\partial {{\mathscr {I}}}} - \gamma \langle {\widehat{q}}{\varvec{n}}, q\rangle _{\partial {{\mathscr {I}}}},\\ {S}_{3,j}= \langle {\widehat{g}}{\varvec{n}},v\rangle _{\partial {{\mathscr {I}}}} + \langle {\widehat{f}}{\varvec{n}}, u-{\hat{u}}\rangle _{\partial {{\mathscr {I}}}}-\langle \mathfrak {f}(u,v), u_x\rangle _{{\mathscr {I}}}-\langle \mathfrak {g}(u,v), v_x\rangle _{{\mathscr {I}}}, \end{array} \end{aligned}$$

which need to simplify by expanding boundary terms. The proof is completed by summing (23) up over all elements.

Theorem 1

The proposed HDG method is stable if the Ito-type coupled KdV system (3) is equipped with the periodic boundary condition and the stabilization parameters satisfy \(\tau _{11}> 0\), \(\tau _{12}>{\tilde{\tau }}\), \(\tau _2>0\), and \(2\gamma \tau _3<\gamma {\varvec{n}}\), where

$$\begin{aligned} \begin{array}{l} {\tilde{\tau }}(u, v,{\hat{u}}):=\displaystyle \frac{1}{(u-{\hat{u}})^2}\int _{{\hat{u}}}^u (f(w, v)-f({\hat{u}},v)){\varvec{n}}{\text{d}}w. \end{array} \end{aligned}$$
(24)

Proof

Using the definition of the numerical flux \(\widehat{\gamma p}\) from (20), we have

$$\begin{aligned} \begin{array}{ll} (\widehat{\gamma p})_{ j+\frac{1}{2}}^- = \gamma p_{ j+\frac{1}{2}}^- +\tau _{11, j+\frac{1}{2}}^{-} \big (u_{ j+\frac{1}{2}}^- - {\hat{u}}_{ j+\frac{1}{2}}\big ),\quad (\widehat{\gamma p})_{j-\frac{1}{2}}^+ =\gamma p_{j-\frac{1}{2}}^+ - \tau _{11, j-\frac{1}{2}}^{+}\big (u_{ j-\frac{1}{2}}^+ - {\hat{u}}_{j-\frac{1}{2}}\big ).\\ \end{array} \end{aligned}$$
(25)

By substituting \((\widehat{\gamma p})_{ j+\frac{1}{2}}^-\) and \((\widehat{\gamma p})_{j-\frac{1}{2}}^+\) from (25) into \({S}_{1,j}\), we get

$$\begin{aligned} {S}_{1,j}= {} & \tau _{11, j+\frac{1}{2}}^{-}((u^-_{j+\frac{1}{2}})^2 - {\hat{u}}_{j+\frac{1}{2}} u^-_{j+\frac{1}{2}}) + \tau _{11, j-\frac{1}{2}}^{+}((u^+_{j-\frac{1}{2}})^2 - {\hat{u}}_{j-\frac{1}{2}} u^+_{j-\frac{1}{2}}) \\& +\tau _{11, j+\frac{1}{2}}^{-}(({\hat{u}}_{j+\frac{1}{2}})^2 - {\hat{u}}_{j+\frac{1}{2}} u^-_{j+\frac{1}{2}}) + \tau _{11, j-\frac{1}{2}}^{+}(({\hat{u}}_{j-\frac{1}{2}})^2 - {\hat{u}}_{j-\frac{1}{2}} u^+_{j-\frac{1}{2}})\\& +\widehat{(\gamma p)}_{j+\frac{1}{2}}^- {\hat{u}}_{j+\frac{1}{2}} - \widehat{(\gamma p)}_{ j-\frac{1}{2}}^+ {\hat{u}}_{j-\frac{1}{2}} + {\widehat{f}}^-_{j+\frac{1}{2}}{\hat{u}}_{j+\frac{1}{2}} - {\widehat{f}}^+_{j-\frac{1}{2}}{\hat{u}}_{j-\frac{1}{2}}. \end{aligned}$$

Summing up over all elements \({\mathscr {I}}\), using conservation of the fluxes, and applying periodic boundary conditions, we obtain

$$\begin{aligned} {S}_1 = \sum \limits _{j = 0}^{N-1} {S}_{1,j} = \sum \limits _{j = 0}^{N-1} \tau _{11,j+\frac{1}{2}}^{-}\big (u^-_{j+\frac{1}{2}} - {\hat{u}}_{j + \frac{1}{2}}\big )^2 +\tau _{11,j-\frac{1}{2}}^{+}\big (u^+_{j-\frac{1}{2}} - {\hat{u}}_{j - \frac{1}{2}}\big )^2. \end{aligned}$$

If \(\tau _{11}>0\), then it is concluded that \({S}_1\) is nonnegative. On the other hand, from the last term of (10) with the assumption \(\tau _3 \ne 0\), we have

$$\begin{aligned} \begin{array}{ll} q^+_{ j-\frac{1}{2}}=\bigl ((1+\tau ^+_{3, j-\frac{1}{2}})\,{\hat{q}}_{j-\frac{1}{2}}-{\widehat{q}}^+_{ j-\frac{1}{2}}\bigr ) / (\tau ^+_{3, j-\frac{1}{2}}),\quad q^-_{ j+\frac{1}{2}}=\bigl ({\widehat{q}}^-_{ j+\frac{1}{2}}-(1-\tau ^-_{3, j+\frac{1}{2}}){\hat{q}}_{ j+\frac{1}{2}}\bigr ) / (\tau ^-_{3, j+\frac{1}{2}}). \end{array} \end{aligned}$$
(26)

Substituting (26) into \({S}_{2,j}\) leads to

$$\begin{aligned} {S}_{2,j}= & {} -\gamma \bigg (\dfrac{2\tau ^-_{3, j+\frac{1}{2}}-1}{2\bigl (\tau ^-_{3, j+\frac{1}{2}}\bigr )^2}\bigl (\bigl ({\widehat{q}}^-_{ j+\frac{1}{2}}\bigr )^2+\bigl ({\hat{q}}_{ j+\frac{1}{2}}\bigr )^2-2{\widehat{q}}^-_{ j+\frac{1}{2}}{\hat{q}}_{j+\frac{1}{2}}\bigr )-\dfrac{1}{2}\bigl ({\hat{q}}_{j+\frac{1}{2}}\bigr )^2+{\widehat{q}}^-_{ j+\frac{1}{2}}{\hat{q}}_{j+\frac{1}{2}}\\&+\dfrac{2\tau ^+_{3, j-\frac{1}{2}}+1}{2\bigl (\tau ^+_{3, j-\frac{1}{2}}\bigr )^2}\bigl ({\widehat{q}}^+_{ j-\frac{1}{2}}-{\hat{q}}_{j-\frac{1}{2}}\bigr )^2+\dfrac{1}{2}\bigl ({\hat{q}}_{ j-\frac{1}{2}}\bigr )^2-{\widehat{q}}^+_{ j-\frac{1}{2}}{\hat{q}}_{ j-\frac{1}{2}} \bigg ). \end{aligned}$$

Again summing up over all elements \({\mathscr {I}}\), using conservation of the fluxes, and imposing boundary conditions, we get

$$\begin{aligned} {S}_2=\sum \limits _{j = 0}^{N-1}{S}_{2,j} =\sum \limits _{j = 0}^{N-1}\bigg (\frac{-\gamma \bigl (2\tau ^-_{3, j+\frac{1}{2}}-1\bigr )}{2\bigl (\tau ^-_{3, j+\frac{1}{2}}\bigr )^2}\bigl ({\widehat{q}}^-_{ j+\frac{1}{2}}-{\hat{q}}_{ j+\frac{1}{2}}\bigr )^2 +\frac{-\gamma \bigl (2\tau ^+_{3, j-\frac{1}{2}}+1\bigr )}{2\bigl (\tau ^+_{3, j-\frac{1}{2}}\bigr )^2}\bigl ({\widehat{q}}^+_{ j-\frac{1}{2}}-{\hat{q}}_{ j-\frac{1}{2}}\bigr )^2\bigg ). \end{aligned}$$

If \(2\gamma \tau _3<\gamma {\varvec{n}}\), then \({S}_2 \geqslant 0\). According to the definition of \(\mathfrak {f}(u,v)\) and \(\mathfrak {g}(u,v)\) and letting \(F(u, v) = \frac{\alpha }{6} u^3 + \frac{\beta }{2} v^2u\), we obtain

$$\begin{aligned} -\langle \mathfrak {f}(u,v), u_x \rangle _{\mathscr {I}} - \langle \mathfrak {g}(u,v), v_x \rangle _{\mathscr {I}}=&{} -\left\langle {\frac{\text{d}}{\text{d}x}}F(u, v),1\right\rangle _{\mathscr {I}}\\ =&{}-\langle F(u, v),{\varvec{n}}\rangle _{\partial {\mathscr {I}}}\\ =&{} -\left\langle \int _{{\hat{u}}}^u \mathfrak {f}(w, v) {\text{d}}w, {\varvec{n}} \right\rangle _{\partial {\mathscr {I}}} - \langle \frac{\beta }{2} v^2 {\hat{u}}, {\varvec{n}} \rangle _{\partial {\mathscr {I}}} - \langle \frac{\alpha }{6} {\hat{u}}^3, {\varvec{n}} \rangle _{\partial {\mathscr {I}}}. \end{aligned}$$
(27)

Summing \({S}_{3,j}\) up over all elements, using (27), adding \(-\langle {\widehat{g}}{\varvec{n}}, {\hat{v}}\rangle _{\partial {{{\mathscr {T}}}_h}}= 0\), and finally using the definition of the numerical flux \({\widehat{g}}\), we have

$$\begin{aligned} {S}_{3}= & {} -\left\langle \int _{{\hat{u}}}^{u}(\mathfrak {f}(w,v) -\mathfrak {f}({\hat{u}}, v)){\text{d}}w,{\varvec{n}}\right\rangle _{\partial {{{\mathscr {T}}}_h}}+\langle {\widehat{f}} -\mathfrak {f}({\hat{u}}, v),(u-{\hat{u}}){\varvec{n}}\rangle _{\partial {{{\mathscr {T}}}_h}}\\&- \left\langle \frac{\beta }{2} v^2 {\hat{u}}, {\varvec{n}} \right\rangle _{\partial {{{\mathscr {T}}}_h}} - \left\langle \frac{\alpha }{6} {\hat{u}}^3, {\varvec{n}} \right\rangle _{\partial {{{\mathscr {T}}}_h}}\\&+\left\langle \frac{\beta }{2}{\hat{u}}v{\varvec{n}}, v\right\rangle _{\partial {{{\mathscr {T}}}_h}} - \left\langle \frac{\beta }{2}{\hat{u}}{\hat{v}}{\varvec{n}}, {\hat{v}}\right\rangle _{\partial {{{\mathscr {T}}}_h}} + \langle \tau _2, (v-{\hat{v}})^2\rangle _{\partial {{{\mathscr {T}}}_h}}. \end{aligned}$$

Noticing the definition of \({\widehat{f}}\), using (24), and applying boundary conditions, we get

$$\begin{aligned} {S}_3= \langle \tau _{12}-{\tilde{\tau }},(u-{\hat{u}})^2\rangle _{\partial {{{\mathscr {T}}}_h}} + \langle \tau _2, (v-{\hat{v}})^2\rangle _{\partial {{{\mathscr {T}}}_h}}. \end{aligned}$$

Therefore, it can be concluded that \(S_3\) will be positive when \(\tau _{12}>{\tilde{\tau }}\) and \( \tau _2>0\). Eventually, according to (21), we conclude that \(\frac{\partial }{\partial t}\int _{\varOmega }(u^2+v^2) {\text{d}}x \leqslant 0\) and, therefore, the numerical scheme is stable due to the cell entropy inequality [35].

Corollary 1

Assume that the Ito-type coupled KdV system (3) is equipped with the boundary conditions \(\mathfrak {u}(a,\cdot ) =\mathfrak {u}(b,\cdot )=\mathfrak {u}_x(a,\cdot ) = \mathfrak {v}(a,\cdot )=0\). The proposed HDG method is stable when

$$\begin{aligned} \tau _{11}>0, \qquad \tau _{12}>{{\tilde{\tau }}}, \qquad \tau _2>0, \qquad 2\gamma \tau _3<\gamma {\varvec{n}}. \end{aligned}$$

Proof

Steps of the proof are similar to the proof of Theorem 1. Let us consider \(\mathfrak {u}(a,\cdot ) =\mathfrak {u}(b,\cdot )=0\). Hence, all of the following summands:

$$\begin{aligned} (\widehat{\gamma p})_{j+\frac{1}{2}}^- {\hat{u}}_{j+\frac{1}{2}} - (\widehat{\gamma p})_{ j-\frac{1}{2}}^+ {\hat{u}}_{j-\frac{1}{2}} + {\widehat{f}}^-_{j+\frac{1}{2}}{\hat{u}}_{j+\frac{1}{2}} - {\widehat{f}}^+_{j-\frac{1}{2}}{\hat{u}}_{j-\frac{1}{2}}, \end{aligned}$$

and also \(- \langle \frac{\alpha }{6} {\hat{u}}^3, {\varvec{n}} \rangle _{\partial {{{\mathscr {T}}}_h}}\) and \( - \langle \frac{\beta }{2}{\hat{u}}{\hat{v}}{\varvec{n}}, {\hat{v}}\rangle _{\partial {{{\mathscr {T}}}_h}}\) are zero due to the conditions \(b_\mathfrak {u} = b_\mathfrak {v} = 0\). On the other hand, because of the boundary condition \(\mathfrak {u}_x(a,\cdot )=0\) we have \({\widehat{q}}^+_{ -\frac{1}{2}} {\hat{q}}_{ -\frac{1}{2}}= ({\widehat{q}}^+{\hat{q}}) |_a = 0\). Also, using (26) and the third global equation of (12) on the face b, i.e., \({\widehat{q}}^- |_b = q^-|_b\), we get \({\widehat{q}}^- |_b = {\hat{q}}|_b\). Therefore, \({\widehat{q}}^-_{N+\frac{1}{2}} {\hat{q}}_{N+\frac{1}{2}} = ({\widehat{q}}^-{\hat{q}})|_b = {\hat{q}}^2|_b\) which is a positive term. The rest of the proof is similar to Theorem 1.

Corollary 2

We have \({{\tilde{\tau }}} \leqslant \frac{1}{2}\sup _{w\in \mathfrak {I}}|\alpha w|\) where \(\mathfrak {I}\) is the interval \([\min \{u,{\hat{u}}\},\max \{u,{\hat{u}}\}]\).

Proof

The mean value theorem leads to

$$\begin{aligned} f(w, v)-f({\hat{u}},v)=\frac{\partial \mathfrak {f}}{\partial \mathfrak {u}}(\xi _w, v)(w- {\hat{u}})=\alpha \,\xi _w(w- {\hat{u}}), \end{aligned}$$

where \(\xi _w\) is a value between u and \({\hat{u}}\). Therefore

$$\begin{aligned} \begin{array}{l} \displaystyle {{\tilde{\tau }}}(u, v, {\hat{u}}) = \frac{1}{(u-{\hat{u}})^2}\int _{{\hat{u}}}^u \alpha \,\xi _w(w- {\hat{u}}){\varvec{n}}{\text{d}}w \leqslant \frac{1}{2} \sup _{w\in \mathfrak {I}}|\alpha w|. \end{array} \end{aligned}$$
(28)

Remark 3

Using Corollary 2, it is obvious that \(\tau _{12}>{{\tilde{\tau }}}\) holds when \(\tau _{12}>\frac{1}{2} \sup _{w\in \mathfrak {I}}|\alpha w|\).

5 Numerical Results

It is verified that the proposed numerical scheme is stable. Actually the desired numerical scheme is stemmed from three approximation techniques that are the HDG method for the spatial discretization, the backward Euler method for the temporal discretization, and the time-lagging method for linearizing the nonlinear terms of the Ito-type coupled KdV equations. Therefore, the full space-time discretization is formed by a matrix-vector equation that it has been studied in details in Sect.  3. In this section, we effort to show that the proposed method is efficient, valid, and reliable for solving the Ito-type coupled KdV system. To do this, the order of convergence of the obtained approximate solutions is compared with the expected rates. Also, the corresponding conservation laws of the Ito-type coupled KdV are investigated for the approximate solutions. As dealt with in [35], the dispersive or shock behavior of numerical solutions is also investigated in this section.

Fig. 1
figure 1

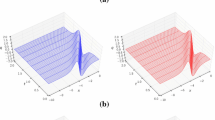
The HDG numerical solutions for the Ito-type coupled KdV system (30) in Example 1 with the initial condition \(\mathfrak {u}(x, 0) = \mathfrak {v}(x, 0) = \cos (x)\) at different times 0, 0.5, and 1 with the space of polynomials of degree two, 500 numbers of elements, and \(\Delta t = 0.000\,1\). The left are numerical solutions u and the rights are numerical solutions v

Full size image
Table 1 The order of convergence versus the refinements \(j=1,\cdots ,7\) in formula (29) with \(K=10\) for Example 1. When the number of refinements increases from 1 to 7, the order of convergence tends to 2, 3, and 4 corresponding to \(k=1,2\), and 3, respectively
Full size table

Example 1

([36]) We consider (3) with periodic boundary conditions and with setting \(\alpha = -6\), \(\beta = -2\), and \(\gamma = -1\), and proceed to the numerical solution of the HDG method. In Fig. 1, the results are shown for \(\mathfrak {u}(x, 0) = \mathfrak {v}(x, 0) = \cos (x)\) at different times \(t = 0, 0.5, 1\) with 500 quadratic elements and \(\Delta t = 0.000\,1\). The values \(\tau _{11}=40\), \(\tau _{12}=|\alpha {\hat{u}}|\), \(\tau _2=|\beta {\hat{u}}| + 40\), and \(\tau _3=40\) are chosen, so that the conditions mentioned in Theorem 1 are valid. Due to the lack of the dispersive term for \(\mathfrak {v}\) in (30), it is seen that \(\mathfrak {v}\) behaves like a shock wave. In contrast, u behaves like the dispersive wave solution. Briefly, results are as good as which were obtained by the LDG method in [36]. In the next, by exploiting the following formula:

$$\begin{aligned} {{O}}_j = \log _2 \bigg (\frac{\Vert u_{2jK} - u_{jK}\Vert _2}{\Vert u_{4jK} - u_{2jK}\Vert _2}\bigg ), \end{aligned}$$
(29)

we investigate the order of convergence. In above formula, \(u_{jK}\), \(u_{2jK}\), and \(u_{4jK}\) are the approximate solutions with number of elements jK, 2jK, and 4jK, respectively. As reported in Table 1, we obtain optimal convergence order for degree of polynomials \(k = 1, 2, 3\), with \(j=1,\cdots ,7\), and \(K=10\). To show the validation of the approximate solutions obtained by the HDG method, we test the following conservation quantities [10, 24]:

$$\begin{aligned} {\mathcal {C}}_1 = \int _\Omega (\mathfrak {u} + \mathfrak {v}){\text{d}}x,\qquad {\mathcal {C}}_2 = \frac{1}{2} \int _\Omega (\mathfrak {u}^2 + \mathfrak {v}^2){\text{d}}x,\qquad {\mathcal {C}}_3 = \int _\Omega \Big (-\frac{\alpha }{6}\mathfrak {u}^3 - \frac{\beta }{2}\mathfrak {u}\mathfrak {v}^2 + \frac{\gamma }{2}\mathfrak {u}_x^2\Big ){\text{d}}x. \end{aligned}$$

The values of conservation quantities are shown in the left side of Fig. 2 for \(t \in [0, 10]\), approximate polynomial of degree two, 600 number of elements, and \(\Delta t = 0.000\,1\). As expected, these values are constant in different times which implies the good performance of the HDG method in solving the Ito-type coupled KdV system.

Fig. 2
figure 2

The values of conservation quantities versus time for Example 1 (left) and for Example 2 (right). Solid, dashed, and dashed-dotted are, respectively, for \({\mathcal {C}}_1\), \({\mathcal {C}}_2\), and \({\mathcal {C}}_3\)

Full size image
Fig. 3
figure 3

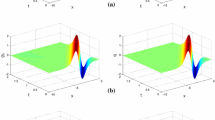
The HDG numerical solutions for the Ito-type coupled KdV system (30) in Example 2 with the initial condition \(\mathfrak {u}(x, 0) = \mathfrak {v}(x, 0) = \exp (-x^2)\) at different times 0, 1, and 2 with the space of polynomials of degree two, 500 numbers of elements, and \(\Delta t = 0.000\,1\). The left are numerical solutions u and the right are numerical solutions v

Full size image

Example 2

([36]) The next example is similar to Example 1 but with initial conditions \(\mathfrak {u}(x, 0) = \mathfrak {v}(x, 0) = \exp (-x^2)\). The choice of stabilization parameters is the same as the previous example. Similarly, in the right side of Fig. 2, conservation quantities are shown in different times. The order of convergence for different values of k and number of elements are reported in Table 2. As expected, the optimal convergence orders of the approximate solutions have been obtained using the proposed HDG method. In Fig. 3, u and v are demonstrated at different times \(t = 0, 1, 2\) with 500 quadratic elements, and \(\Delta t = 0.000\,1\).

Example 3

In this example, we intend to compare the proposed HDG method and the LDG method presented in [36]. For this purpose, we consider the following Ito-type coupled KdV system:

$$\begin{aligned} \left\{ \begin{array}{ll} &\mathfrak {u}_t + (-3 \mathfrak {u}^2 - \mathfrak {v}^2)_x- \mathfrak {u}_{xxx} ={} \mathfrak {r}_1(x, t), \\& \mathfrak {v}_t - 2(\mathfrak {u}\mathfrak {v})_x={} \mathfrak {r}_2(x, t), \end{array} \right. \end{aligned}$$
(30)

that is a special case of the general form (3) with considering nonzero right-hand sides. This special kind of problem lets us consider \({\mathfrak {u}}(x,t) = {\mathfrak {v}}(x,t)=\exp (-t)\sin (x)\) as the exact solution of the problem. We let \(\varOmega =[-\uppi , \uppi ],\) and \(\mathfrak {u}(x, 0) = \mathfrak {v}(x, 0) =\sin (x)\) obviously are the initial conditions. For this case, boundary conditions are homogenous Dirichlet boundary conditions. We use number of elements 10, 20, 40, 80, and 160 with appropriate time-step sizes. The values \(\tau _{11}=15\), \(\tau _{12}=|\alpha {\hat{u}}|\), \(\tau _2=|\beta {\hat{u}}| + 2\), and \(\tau _3=40\) are chosen, so that the conditions mentioned in Theorem 1 are valid. \(L_2\) error norms and corresponding numerical orders of accuracy of u, v, and their derivatives at the final time level \(T=0.1\) for the HDG and LDG methods are shown in Fig. 4 for different values of the polynomial degree k. To make a better comparison, we use the time-lagging method for linearization of both LDG and HDG methods. From the results reported in Fig. 4, we find out that the expected convergence order, namely \({{O}}(h^{k+1})\), is obtained for the approximate solutions and their derivatives are generated by using the proposed HDG and LDG methods. Also, the ratio of the computational time of the proposed HDG method to the LDG method can be seen in Fig. 5. Due to the small bandwidth of the matrices in the HDG method, the computational time of the HDG method is less than that of the LDG method.

Fig. 4
figure 4

\(L^2\) normalized absolute error norms \(\Vert u-{\mathfrak {u}}\Vert _{\Omega }\) (dashed), \(\Vert q-{\mathfrak {q}}\Vert _{\Omega }\) (dotted), \(\Vert p-{\mathfrak {p}}\Vert _{\Omega }\) (dashed-dotted), \(\Vert v-{\mathfrak {v}}\Vert _{\Omega }\) (solid), and expected rate (pink line) versus the number of nodes for the Ito-type coupled KdV system (30) in Example 3 solved by the DG methods with the space of polynomials of maximum degree \(k=0,1,2,3\), respectively, from up to down. LDG method (left) and HDG method (right)

Full size image
Fig. 5
figure 5

The ratio of the computational time of the proposed HDG method to the LDG method in [36], for degree of polynomials \(k=0\) (dashed), \(k=1\) (dotted), \(k=2\) (dashed-dotted), and \(k=3\) (solid) versus the number of nodes for the Ito-type coupled KdV system (30) in Example 3

Full size image

To show the advantage and strength of the proposed HDG method over the LDG method presented in [36], let us consider (30) with the exact solutions \({\mathfrak {u}}(x,t) = (x-0.5)^2|x-0.5|\) and \({\mathfrak {v}}(x,t)=0.1\sin (2\uppi x)\exp (-20t)\) with the periodic boundary conditions over \(\varOmega = [0, 1]\). With the stabilization parameters \(\tau _{11}=2\), \(\tau _{12}=|\alpha {\hat{u}}|\), \(\tau _2=|\beta {\hat{u}}| + 20\), and \(\tau _3=2\), the obtained results at the final time \(T = 0.1\) are listed in Table 3 for various numbers of elements and different time-step sizes. As seen, for the HDG method, errors are satisfactory and the convergence order is optimal whereas the disappointing results are obtained by the LDG method. This is due to the exact solution \(\mathfrak {u}\) which has discontinuous third derivative. If we apply the exponential time differencing method mentioned in [36] it might be predictable to get better results for the LDG method in this case.

Table 2 The order of convergence versus the refinements \(j=1,\cdots ,7\) in formula (29) with \(K=10\) for Example 2. When the number of refinements increases from 1 to 7, the order of convergence tends to 2, 3, and 4 corresponding to \(k=1,2\), and 3, respectively
Full size table
Table 3 \(L_2\) error norms and the order of accuracy of u, v, and their derivatives at the final time level \(T=0.1\) for both the proposed HDG and the LDG methods for Example 3
Full size table

6 Conclusion

In this paper, the Ito-type coupled KdV system of equations has been considered with some initial conditions together with periodic or homogeneous Dirichlet boundary conditions. The system considered is in fact a system of first order in time and third order in space PDEs. By introducing appropriate broken Sobolev spaces and corresponding finite-element spaces, the HDG method has been applied to the Ito-type KdV system. The method is based on the framework of the LDG method for nonlinear PDEs. In addition to the local approximate variables, we considered three other global unknowns called numerical traces, and also, we have added three equations into the local equations, such that it is guaranteed conservation of the numerical fluxes. After applying spatial discretization, the temporal discretization has been done using the backward Euler implicit method. To get rid of the nonlinearity, the time-lagging linearization method has been exploited to the nonlinear terms of the discrete weak form. Using the Schur complement method, the final matrix-vector equation, “arisen from the HDG method, time discretization, and time-lagging linearization method”, is splitted into two smaller matrix-vector operations. Using the energy method, the numerical stability of the method has been proved in the \(L_2\) norm under certain conditions on the stabilization parameters and specified boundary conditions. In comparison with the LDG methods, numerical experiments imply the capability of the proposed HDG method. In particular, the numerical results show that optimal convergence order is obtained at order \(k+1\) for a mesh with approximate solutions and their derivatives of degree k. Presented numerical conservations quantities of the approximate solution of the Ito-type coupled KdV system can be interpreted as a criteria for verification of validity of the proposed HDG method. We note that the HDG method is extremely local and so suitable for parallel implementations and easy for hp adaptivity in linear PDEs. To the best of our knowledge, any convergence analysis of both LDG and HDG methods for this kind of coupled nonlinear equations has not yet been presented. Just, for the linear case \(\alpha = \beta = 0\), a convergence analysis of the HDG method can be found in [13]. We leave the convergence analysis of the HDG method for the coupled KdV system to the future works.