A Note on Numerical Algorithm for the Time-Caputo and Space-Riesz Fractional Diffusion Equation

Abstract

Recently, Zhang and Ding developed a novel finite difference scheme for the time-Caputo and space-Riesz fractional diffusion equation with the convergence order ${\mathcal {O}}(\tau ^{2-\alpha } + h^2)$ in Zhang and Ding (Commun. Appl. Math. Comput. 2(1): 57–72, 2020). Unfortunately, they only gave the stability and convergence results for $\alpha \in (0,1) \;\;\mathrm {and} \;\; \beta \in \left[ {\frac{7}{8}+\frac{\root 3 \of {621+48\sqrt{87}}}{24}+\frac{19}{8\root 3 \of {621+48\sqrt{87}}}},2\right]$. In this paper, using a new analysis method, we find that the original difference scheme is unconditionally stable and convergent with order ${\mathcal {O}}(\tau ^{2-\alpha } + h^2)$ for all $\alpha \in (0,1) \;\;\mathrm {and} \;\; \beta \in \left( 1,2\right]$. Finally, some numerical examples are given to verify the correctness of the results.

1 Introduction

In this paper, we consider the following time-Caputo and space-Riesz fractional diffusion equation:

$$\begin{aligned} \left\{ \begin{aligned}&\,_{\text{C}}\mathrm {D}_{0,t}^{\alpha }u(x,t)=K\frac{\partial ^\beta u(x,t)}{\partial {|x|^\beta }}+f(x,t),~0< x<L, ~0< t\leqslant T,\\&u(x,0)=\varphi (x), ~0\leqslant x\leqslant L,\\&u(0,t)=u(L,t)=0, ~0< t\leqslant T, \end{aligned} \right. \end{aligned}$$

(1)

where $K>0$ is the diffusion coefficient. $\,_{\text{C}}\mathrm {D}_{0,t}^\alpha u(x,t)$ is the Caputo fractional derivative with respect to t, of order $0<\alpha <1$, defined by [4, 6, 7]

$$\begin{array}{lll} \displaystyle \,_{\text{C}}\mathrm {D}_{0,t}^\alpha u(x,t)=\frac{1}{{\Gamma }(1-\alpha )} \int _{0}^{t}\frac{\partial u(x,s)}{\partial s} \frac{1}{(t-s)^{\alpha }} {\text{ds}},\;0<\alpha <1. \end{array}$$

$\displaystyle \frac{\partial ^\beta u(x,t)}{\partial |x|^\beta }$ is the Riesz fractional derivative with respect to x of order $\beta \in (1,2]$, which is defined as [6,7,8]

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{\partial ^\beta u(x,t)}{\partial {|x|^\beta }}=\displaystyle -\frac{1}{2\cos \left( \frac{{{\uppi}} \beta }{2}\right) }\left( \,_{\text{RL}}\mathrm {D}_{a,x}^\beta +\,_{\text{RL}}\mathrm {D}_{x,b}^\beta \right) u(x,t),\;1<\beta \leqslant 2, \end{array} \end{aligned}$$

where $\,_{\text{RL}}\mathrm {D}_{a,x}^\beta$ denotes the left Riemann-Liouville fractional derivative

$$\begin{aligned} \begin{array}{lll}\displaystyle \,_{\text{RL}}{\mathrm {D}}_{a,x}^{\beta }u(x,t)= \frac{1}{{\Gamma }(2-\beta )}\frac{\partial ^2}{\partial x^2}\int _{a}^{x}\frac{u(\xi ,t)}{(x-\xi )^{\beta -1}}{\text{d}} \xi ,\;\;\;\; 1<\beta <2, \end{array} \end{aligned}$$

and $\,_{\text{RL}}\mathrm {D}_{x,b}^\beta$ is the right Riemann-Liouville fractional derivative

$$\begin{aligned} \begin{array}{lll}\displaystyle \,_{\text{RL}}{\mathrm {D}}_{x,b}^{\beta }u(x,t)= \frac{1}{{\Gamma }(2-\beta )}\frac{\partial ^2}{\partial x^2}\int _{x}^{b}\frac{u(\xi ,t)}{(\xi -x)^{\beta -1}}{\text{d}} \xi ,\;\;\;\; 1<\beta \leqslant 2. \end{array} \end{aligned}$$

Recently, Zhang and Ding [9] developed a novel finite difference scheme with convergence order ${\mathcal {O}}(\tau ^{2-\alpha } + h^2)$ for (1). However, it is a pity that they only proved that the stability and convergence in the case

$$\begin{aligned} \beta \in \left[ {\frac{7}{8}+\frac{\root 3 \of {621+48\sqrt{87}}}{24}+\frac{19}{8\root 3 \of {621+48\sqrt{87}}}},2\right] \;\;\mathrm {and} \;\;\alpha \in (0,1) \end{aligned}$$

based on the mathematical induction, while for case

$$\begin{aligned} \beta \in \left( 1,{\frac{7}{8}+\frac{\root 3 \of {621+48\sqrt{87}}}{24}+\frac{19}{8\root 3 \of {621+48\sqrt{87}}}}\right) \;\;\mathrm {and} \;\;\alpha \in (0,1), \end{aligned}$$

it seems difficult to prove the result using their method.

In this article, we will use another analysis method to reanalyze the difference scheme established in [9] and find that it is unconditionally stable and convergent with order ${\mathcal {O}}(\tau ^{2-\alpha } + h^2)$ for all $\beta \in (1,2]$ and $\alpha \in (0,1)$.

The paper is organized as follows. In Sect. 2, we review the difference scheme established in [2] and its theoretical analysis. New stability and convergence analysis are introduced in Sect. 3. Numerical experiments are provided in Sect. 4 to prove the rationality of the theoretical analysis and the effectiveness of the algorithm.

2 Review the Algorithm in [9]

2.1 Establishment of the Algorithm

Define $t_n=n\tau , n=0,1,\cdots ,N,$ and $x_j=jh, \; j=0,1,\cdots ,M,$ where $\tau =T/N$ and $h=L/M$ are time and space mesh sizes, respectively.

For the numerical approximation of the Caputo fractional derivative $\,_{\text{C}}\mathrm {D}_{0,t}^\alpha u(t)$ at $t=t_n\;(n=0,1,\cdots ,N)$, the authors used the following common L1 formula [2, 5]:

$$\begin{aligned} \begin{aligned} {}_{\text{C}}{\mathrm {D}}_{0,t}^{\alpha }u(t)|_{t=t_n}&=\frac{1}{{\Gamma }(1-\alpha )}\sum _{k=0}^{n-1} \int _{t_k}^{t_{k+1}}(t_n-s)^{-\alpha }\frac{\partial u(x,s)}{\partial s}\mathrm {d}s\\&=\frac{1}{{\Gamma }(1-\alpha )}\sum _{k=0}^{n-1} \int _{t_k}^{t_{k+1}}(t_n-s)^{-\alpha }\left[ \frac{u(x,t_{k+1})-u(x,t_k)}{\tau }+{{\mathcal {O}}}(\tau )\right] \mathrm {d}s\\&=\frac{\tau ^{-\alpha }}{{\Gamma }(2-\alpha )}\sum _{k=0}^{n-1}b_{n-k-1}\left( u(x,t_{k+1})-u(x,t_k)\right) +{\mathcal {O}}\left( \tau ^{2-\alpha }\right) , \end{aligned} \end{aligned}$$

(2)

where

$$\begin{aligned} b_k=(k+1)^{1-\alpha }-k^{1-\alpha },\;k=0,1,\cdots ,n-1. \end{aligned}$$

At the same time, an effective second-order formula is used to numerically treat the spatial Riesz fractional derivative in [1], that is

$$\begin{aligned} \displaystyle \frac{\partial ^\beta u(x_j,t_n)}{\partial {|x|^\beta }}= -\frac{1}{2\cos \left( \frac{{\uppi} }{2}\beta \right) }\left( \,^{\text{L}}{\mathcal {A}}_{2}^{\beta }+\,^{\text{R}}{\mathcal {A}}_{2}^{\beta }\right) u(x_j,t_n)+{\mathcal {O}}\left( h^2\right) , \end{aligned}$$

(3)

where

$$\begin{aligned} \begin{array}{lll} \displaystyle \,^{\text{L}}{\mathcal {A}}_{2}^{\beta }u(x_j,t_n) =\frac{1}{h^{\beta }}\sum \limits _{\ell =0}^{j+1} \kappa _{2,\ell }^{(\beta )}u\left( x_j-(\ell -1)h,t_n\right) \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{lll} \displaystyle \,^{\text{R}}{\mathcal {A}}_{2}^{\beta }u(x_j,t_n) =\frac{1}{h^{\beta }}\sum \limits _{\ell =0}^{M-j+1} \kappa _{2,\ell }^{(\beta )}u\left( x_j+(\ell -1)h,t_n\right) . \end{array} \end{aligned}$$

Here, the coefficients

$$\begin{aligned} \begin{array}{lll} \displaystyle \kappa _{2,\ell }^{(\beta )}=(-1)^{\ell } \left( \frac{3\beta -2}{2\beta }\right) ^{\beta }\sum \limits _{m=0}^{\ell } \left( \frac{\beta -2}{3\beta -2}\right) ^m\left( {\begin{array}{c}\beta \\ m\end{array}}\right) \left( {\begin{array}{c}\beta \\ \ell -m\end{array}}\right) ,\;\;\ell =0,1,\cdots , \end{array} \end{aligned}$$

which can also be calculated by the following recursive relations [1]:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \kappa _{2,0}^{(\beta )}&{}=&{}\displaystyle \left( \frac{3\beta -2}{2\beta }\right) ^{\beta },\\ \displaystyle \kappa _{2,1}^{(\beta )}&{}=&{}\displaystyle \frac{4\beta (1-\beta )}{3\beta -2}\kappa _{2,0}^{(\beta )},\\ \displaystyle \kappa _{2,\ell }^{(\beta )}&{}=&{}\displaystyle \frac{1}{\ell (3\beta -2)}\left[ 4(1-\beta )(\beta -\ell +1)\kappa _{2,\ell -1}^{(\beta )}\right. \\ &{}&{}\displaystyle \left. +(\beta -2)(2\beta -\ell +2)\kappa _{2,\ell -2}^{(\beta )} \right] ,\;\;\ell \geqslant 2. \end{array}\right. \end{aligned}$$

Next, substituting (2) and (3) into (1), we obtain

$$\begin{aligned} \begin{aligned}&\frac{\tau ^{-\alpha }}{{\Gamma }(2-\alpha )}\sum _{k=0}^{n-1}b_{n-k-1}\left( u(x,t_{k+1})-u(x,t_k)\right) \\ {}&=-\frac{K}{2\cos \left( \frac{{\uppi} }{2}\beta \right) }\left( \,^{\text{L}}{\mathcal {A}}_{2}^{\beta }+\,^{\text{R}}{\mathcal {A}}_{2}^{\beta }\right) u(x_j,t_n)+f(x_j,t_n)+R_j^n, \end{aligned} \end{aligned}$$

(4)

where there exists a constant C such that

$$\begin{aligned} \begin{aligned} |R_j^n|\leqslant C\left( \tau ^{2-\alpha }+h^2\right) ,\;\;1\leqslant j\leqslant M-1,\;1\leqslant n\leqslant N. \end{aligned} \end{aligned}$$

Finally, omitting the high order terms $R_j^n$ of (4). Replacing the function $u(x_j,t_n)$ with its numerical approximation value $u_j^n$, then we can obtain the following finite difference scheme [9]:

$$\begin{aligned} \left\{ \begin{aligned}&u_j^n+q\left[ \sum _{\ell =0}^{j+1}\kappa _{2,\ell }^{(\beta )}u_{j-\ell +1}^n+\sum _{\ell =0}^{M-j+1}\kappa _{2,\ell }^{(\beta )}u_{j+\ell -1}^n\right] \\& =u_j^{n-1}-\sum _{k=1}^{n-1}b_k\left( u_j^{n-k}-u_j^{n-k-1}\right) +\tau ^\alpha \Gamma (2-\alpha ) f_j^n,\\&u_j^0=\varphi \left( x_j\right) ,~0\leqslant j\leqslant M,\\&u_0^n=u_M^n=0,~1\leqslant n\leqslant N, \end{aligned}\right. \end{aligned}$$

(5)

where $q=\displaystyle \frac{\tau ^\alpha {\Gamma }(2-\alpha )K}{2h^\beta \cos \left( \frac{{\uppi} }{2}\beta \right) }$.

2.2 Theoretical Analysis of the Algorithm

Lemma 1

[1] Under the condition

$$\begin{aligned} {\frac{7}{8}+\frac{\root 3 \of {621+48\sqrt{87}}}{24}+\frac{19}{8\root 3 \of {621+48\sqrt{87}}}}\leqslant \beta <2, \end{aligned}$$

(6)

the coefficient $\displaystyle \kappa _{2,2}^{(\beta )}$ satisfies

$$\begin{aligned} \kappa _{2,2}^{(\beta )}\geqslant 0. \end{aligned}$$

In [9], by using mathematical induction, the stability and convergence results of the proposed scheme are stated as follows:

Theorem 1

Under the condition (6) and $0<\alpha <1$, the finite difference scheme (5) for time-Caputo and space-Riesz fractional diffusion (1) is unconditionally stable.

Theorem 2

Denote by $u(x_j,t_n)~(j=1,2,\cdots ,M-1;\; n=1,2,\cdots ,N)$ the exact solution of (1) at mesh point $(x_i,t_n)$, and let $\{U_j^n\,|\,0\leqslant j\leqslant M, 0 \leqslant n\leqslant N\}$ be the solution of the finite difference scheme (5). Define

$$\begin{aligned} \varepsilon _j^n=u(x_j, t_n)-U_j^n,\;\;j=1,2,\cdots ,M;~n=1,2,\cdots ,N, \end{aligned}$$

then there exists a positive constant C, such that

$$\begin{aligned} \begin{array}{lll} \displaystyle ||\varepsilon ^n||_\infty \leqslant C\,\left( \tau ^{2-\alpha }+h^2\right) ,\,\,0\leqslant n\leqslant N, \end{array} \end{aligned}$$

under the condition (6) and $0<\alpha <1.$

Remark 1

From the conclusion of the above two theorems, we find that the method in [9] can only prove that the difference scheme (5) is stable and convergent under the condition (6). Below, we will use another method to prove that the difference scheme (5) is unconditionally stable and convergent for all $\alpha \in (0,1)$ and $\beta \in (1,2]$.

3 A New Theoretical Analysis Method for the Algorithm in [9]

Let

$$\begin{aligned} \begin{array}{lll} \displaystyle {\mathcal {U}}_h=\left\{ u\vert u=(u_0,u_1,\cdots ,u_M),\;u_0=u_M=0\right\} \end{array} \end{aligned}$$

be the space grid functions. For any $u, v\in {\mathcal {U}}_h$, define the following inner product

$$\begin{aligned} \begin{array}{lll} \displaystyle (u,v)=h\sum _{j=1}^{M-1}u_jv_j \end{array} \end{aligned}$$

and the corresponding norm

$$\begin{aligned} \begin{array}{lll} \displaystyle \Vert u\Vert =\sqrt{(u,u)}\;. \end{array} \end{aligned}$$

For convenience, denote the operator

$$\begin{aligned} \displaystyle \delta _x^\beta =-\frac{1}{2\cos \left( \frac{{\uppi} }{2}\beta \right) }\left( \,^{\text{L}}{\mathcal {A}}_{2}^{\beta }+\,^{\text{R}}{\mathcal {A}}_{2}^{\beta }\right) , \end{aligned}$$

(7)

then the numerical algorithm (5) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&u_j^n-\sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) u_j^k-b_{n-1}u_j^0 =\mu K\delta _x^\alpha u_j^k+\mu f_j^k,\;\\ {}&1\leqslant j\leqslant M-1,\;1\leqslant n\leqslant N, \\&u_j^0=\varphi \left( x_j\right) ,~0\leqslant j\leqslant M,\\&u_0^n=u_M^n=0,~1\leqslant n\leqslant N, \end{aligned}\right. \end{aligned}$$

(8)

where $\mu =\tau ^\alpha {\Gamma }(2-\alpha )$.

Next, we list several lemmas for the stability and convergence analysis.

Lemma 2

[3] Let $b_k=(k+1)^{1-\alpha }-k^{1-\alpha },~k=0,1,2,\cdots$ and $0<\alpha <1$. Then there holds that

$$\begin{aligned} \displaystyle \begin{array}{lll} {\text{(i)}}\;\;1=b_0>b_1>b_2>\cdots>b_k\rightarrow 0, ~\mathrm {as} ~k\rightarrow +\infty ;\\ \displaystyle {\text{(ii)}}\;\;\sum _{k=0}^n(b_k-b_{k+1})+b_{n+1}=(1-b_1)+\sum _{k=1}^{n-1}(b_k-b_{k+1})+b_n=1. \end{array} \end{aligned}$$

Lemma 3

[1] Let the operator $\delta _x^{\beta }$ be defined by (7). Then the following inequality:

$$\begin{aligned} \begin{array}{lll} \displaystyle (\delta _x^{\beta }u,u)\leqslant 0 \end{array} \end{aligned}$$

holds for all $\beta \in (1,2].$

Now, we give the stability result of the finite difference scheme (5).

Theorem 3

The finite difference scheme (5) is unconditionally stable to the initial value $\varphi$ and right term f for all $\alpha \in (0,1)$ and $\beta \in (1,2]$.

Proof

Taking the inner product of the first equation of (8) with $u^n$ leads to

$$\begin{aligned} \begin{aligned} \left( u^n,u^n\right) -\sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) \left( u^k,u^n\right) -b_{n-1}\left( u^0,u^n\right) \\=\mu K\left( \delta _x^\alpha u^n,u^n\right) +\mu \left( f^n,u^n\right) . \end{aligned} \end{aligned}$$

(9)

For the second term of the left hand of (9), we obtain

$$\begin{aligned} \begin{aligned} -\sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) \left( u^k,u^n\right) \geqslant -\sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) \Vert u^k \Vert \cdot \Vert u^n\Vert \end{aligned} \end{aligned}$$

(10)

based on the Cauchy-Schwarz inequality and Lemma 2.

Similarly, for the third term of the left hand of (9), we also have

$$\begin{aligned} \begin{aligned} -b_{n-1}\left( u^0,u^n\right) \geqslant -b_{n-1}\Vert u^0 \Vert \cdot \Vert u^n\Vert. \end{aligned} \end{aligned}$$

(11)

For the first term of the right hand of (9), it follows from Lemma 3 that

$$\begin{aligned} \begin{aligned} \mu K\left( \delta _x^\alpha u^n,u^n\right) \leqslant 0. \end{aligned} \end{aligned}$$

(12)

As to the second term of the right hand of (9), we easily know that

$$\begin{aligned} \begin{aligned} \mu \left( f^n,u^n\right) \leqslant \mu \Vert f^n\Vert \cdot \Vert u^n\Vert. \end{aligned} \end{aligned}$$

(13)

Substituting (10), (11), (12) and (13) into (9) yields

$$\begin{aligned} \begin{aligned} \Vert u^n\Vert \leqslant \sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) \Vert u^k\Vert +b_{n-1}\Vert u^0\Vert +\mu \Vert f^n\Vert . \end{aligned} \end{aligned}$$

(14)

Note that

$$\begin{aligned} \begin{aligned} \mu =\tau ^\alpha {\Gamma }(2-\alpha )= (1-\alpha ){\Gamma }(1-\alpha )T^\alpha N^{-\alpha }, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} b_{n-1}=n^{1-\alpha }-(n-1)^{1-\alpha }=(1-\alpha )\zeta ^{-\alpha },\;n=1,2,\cdots ,N,\;\zeta \in (n-1,n), \end{aligned} \end{aligned}$$

then we obtain

$$\begin{aligned} \mu <T^\alpha {\Gamma }(1-\alpha )b_{n-1},\;\;n=1,2,\cdots ,N. \end{aligned}$$

Denote

$$\begin{aligned} \begin{aligned} U=\Vert u^0\Vert +T^\alpha {\Gamma }(1-\alpha )\max _{1\leqslant \ell \leqslant N} \Vert f^\ell \Vert , \end{aligned} \end{aligned}$$

then (14) can be rewritten as

$$\begin{aligned} \begin{aligned} \Vert u^n\Vert \leqslant \sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) \Vert u^k\Vert +b_{n-1}U,\;\;1\leqslant n\leqslant N. \end{aligned} \end{aligned}$$

Now, we will prove that

$$\begin{aligned} \begin{aligned} \Vert u^n\Vert \leqslant U,\;\;1\leqslant n\leqslant N \end{aligned} \end{aligned}$$

by the mathematical induction.

First of all, it is obviously true for $n = 1$. Secondly, we assume that

$$\begin{aligned} \begin{aligned} \Vert u^k\Vert \leqslant U \end{aligned} \end{aligned}$$

is true for $k=1,2,\cdots ,n-1.$ Then we can get further

$$\begin{aligned} \begin{aligned} \Vert u^n\Vert \leqslant \sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) \Vert u^k\Vert +b_{n-1}U\leqslant U,\;\;1\leqslant n\leqslant N, \end{aligned} \end{aligned}$$

that is

$$\begin{aligned} \begin{aligned} \Vert u^n\Vert \leqslant \Vert \varphi \Vert +T^\alpha {\Gamma }(1-\alpha )\max _{1\leqslant \ell \leqslant N} \Vert f^\ell \Vert ,\;\;1\leqslant n\leqslant N. \end{aligned} \end{aligned}$$

(15)

This ends the proof.

Finally, we consider the convergence of the difference scheme (5).

Theorem 4

Suppose that $u(x_j,t_n)~(j=1,2,\cdots ,M-1; \; n=1,2,\cdots ,N)$ and $\{u_j^n\,|\,0\leqslant j\leqslant M, 0 \leqslant n\leqslant N\}$ are the exact solution of (1) and finite difference scheme (5), respectively. Let

$$\begin{aligned} \varepsilon _j^n=u(x_j, t_n)-u_j^n,\;\;j=1,2,\cdots ,M;~n=1,2,\cdots ,N. \end{aligned}$$

Then it holds that

$$\begin{aligned} \begin{aligned} \Vert \varepsilon ^n\Vert \leqslant C T^\alpha {\Gamma }(1-\alpha )\sqrt{L}\left( \tau ^{2-\alpha }+h^2\right) ,\;\;1\leqslant n\leqslant N \end{aligned} \end{aligned}$$

for all $\alpha \in (0,1)$ and $\beta \in (1,2]$.

Proof

From (1) and (4), we obtain the following error equation:

$$\begin{aligned} \left\{ \begin{aligned}&\varepsilon _j^n-\sum _{k=1}^{n-1}\left( b_{n-k-1}-b_{n-k}\right) \varepsilon _j^k-b_{n-1}\varepsilon _j^0 =\mu K\delta _x^\alpha \varepsilon _j^k+\mu R_j^k,\;\\ {}&1\leqslant j\leqslant M-1,\;1\leqslant n\leqslant N, \\&\varepsilon _j^0=0,~0\leqslant j\leqslant M,\\&\varepsilon _0^n=\varepsilon _M^n=0,~1\leqslant n\leqslant N. \end{aligned}\right. \end{aligned}$$

(16)

For the first equation of (16), it follows from the inequality (15) that

$$\begin{aligned} \begin{aligned} \Vert \varepsilon ^n\Vert \leqslant T^\alpha {\Gamma }(1-\alpha )\max _{1\leqslant \ell \leqslant N} \Vert R^\ell \Vert ,\;\;1\leqslant n\leqslant N. \end{aligned} \end{aligned}$$

Due to

$$\begin{aligned} \begin{aligned} \Vert R^\ell \Vert ^2=\left( R^\ell ,R^\ell \right) \leqslant C^2L\left( \tau ^{2-\alpha }+h^2\right) ^2, \end{aligned} \end{aligned}$$

then we get

$$\begin{aligned} \begin{aligned} \Vert \varepsilon ^n\Vert \leqslant C T^\alpha {\Gamma }(1-\alpha )\sqrt{L}\left( \tau ^{2-\alpha }+h^2\right) ,\;\;1\leqslant n\leqslant N. \end{aligned} \end{aligned}$$

This completes the proof.

4 Numerical Example

In this section, we give some numerical results to prove the rationality of our theoretical analysis.

Example 1

Consider the following equation:

$$\begin{aligned} \,_{\text{C}}\mathrm {D}_{0,t}^{\alpha }u(x,t)=\beta ^4\frac{\partial ^\beta u(x,t)}{\partial {|x|^\beta }}+f(x,t), \;0 \leqslant x \leqslant 1,\; 0\leqslant t \leqslant 1 \end{aligned}$$

with a given force term

$$\begin{aligned} \begin{aligned} f(x,t) =&\frac{{\Gamma }(\alpha +\beta +2)}{{\Gamma }(\beta +2)}t^{\beta +1}x^4(1-x)^4\\ {}&+\frac{t^{\alpha +\beta +1}\beta ^4}{\cos \left( {{\uppi}} \beta /2\right) }\sum \limits _{\ell =0}^{{4}}(-1)^{\ell }\frac{({4}+\ell )!}{\ell !\;({4}-\ell )!\;{\Gamma }({5}+\ell -\beta )} \left[ x^{4+\ell -\beta }+(1-x)^{4+\ell -\beta }\right] . \end{aligned} \end{aligned}$$

Its exact solution is

$$\begin{aligned} u(x,t) = t^{\alpha +\beta +1}x^4(1-x)^4. \end{aligned}$$

By using the numerical algorithm (5), the maximum error, temporal convergence order and spatial convergence order were listed in Tables 1 and 2 for different values of $\alpha ,\beta , \tau$ and h, respectively. From these tables, we can conclude that the developed numerical algorithm is unconditionally stable and convergent with order ${\mathcal {O}}(\tau ^{2-\alpha } + h^2)$.

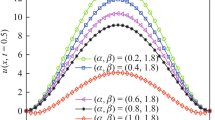
In addition, Figs. 1, 2, 3 and 4 compare the graphs of the exact and approximate solutions with different values of $\alpha$, $\beta$, $\tau$ and h. From these figures, we can conclude that the developed numerical solutions are in excellent agreement with the exact solution.

Table 1 The maximum error and temporal convergence order with $\beta =1.5$ and $h=\frac{1}{800}$

Table 2 The maximum error and spatial convergence order with $\alpha =0.7$ and $\tau =\frac{1}{1\,000}$

Fig. 1

The comparison of exact and numerical solutions for $\tau =\frac{1}{30}, h=\frac{1}{30}$ at $t=0.8$ with different $\alpha$

Fig. 2

The comparison of exact and numerical solutions for $\tau =\frac{1}{40}, h=\frac{1}{50}$ at $t=0.8$ with different $\beta$

Fig. 3

The comparison of exact and numerical solutions for $\tau =\frac{1}{40}, h=\frac{1}{40}$ at $x=0.4$ with different $\alpha$

Fig. 4

The comparison of exact and numerical solutions for $\tau =\frac{1}{40}, h=\frac{1}{20}$ at $x=0.4$ with different $\beta$