Numerical Algorithm for the Time-Caputo and Space-Riesz Fractional Diffusion Equation

Abstract

In this paper, we develop a novel finite-difference scheme for the time-Caputo and space-Riesz fractional diffusion equation with convergence order $\mathcal {O}(\tau ^{2-\alpha } + h^2)$. The stability and convergence of the scheme are analyzed by mathematical induction. Moreover, some numerical results are provided to verify the effectiveness of the developed difference scheme.

1 Introduction

With the development of science, it has been found that the fractional derivatives and fractional differential equations provide an excellent instrument for the description of memory and hereditary properties of various materials and processes. Therefore, they are widely used in the field of science and technology, such as the fields of control theory, biology, electrochemical processes, porous media, viscoelastic materials [7, 14, 15].

However, unfortunately, for most fractional differential equations, it is not an easy task to seek for their analytical solutions. For some simple linear equations, even if the analytic solutions are obtained, it is not convenient to calculate, because the analytic solutions contain some special functions. Therefore, it is essential to develop the effective numerical solutions of the fractional differential equations.

Since the numerical approximation of fractional derivatives is the most important step in numerical solutions of fractional differential equations, we first review the progress made in numerical approximation of fractional derivatives. As for the Caputo derivative, Gao et al. proposed a so-called $L1-2$ formula with order $(3-\alpha )$ [8]. Using the different methods, Li et al. also got a numerical differential formula with convergence order $(3-\alpha )$ [11]. Later, Alikhanov proposed another $(3-\alpha )$th order numerical differential formula at the superconvergence point $t = t_{j+\sigma }$, and named it as the ${L2-1}$ formula [1]. Furthermore, Li et al. developed a series of high-order formulas using the rth ($r\ge 4$ is a positive integer) degree interpolation function [9]. For approximating the Riesz fractional derivative, the first-order accurate normal/shifted Grünwald formula [13], second-order accurate weighted and shifted Grünwald by choosing the appropriate weight coefficients [16], second-order accurate fractional centered difference formula [3], and some other higher-order formulas [5, 6, 20] have been constructed. Based on the above mentioned and other approximation formulas, a tremendous amount of finite-difference methods for solving the fractional differential equations have been developed. For example, Cui constructed a compact finite-difference scheme with the temporal accuracy of first order and spatial accuracy of fourth order for the one-dimensional fractional diffusion equation in [2]. Wang and Vong [17] developed two high-order finite-difference schemes for the fractional modified anomalous subdiffusion equation and the diffusion-wave equation, respectively. Based on the fractional multistep methods in time and central difference formula in space, Zeng [19] proposed several finite-difference schemes for solving the time-fractional diffusion-wave equation.

In this paper, we propose a novel finite-difference scheme for the following time-Caputo and space-Riesz fractional diffusion equation:

$$\begin{aligned} \left\{ \begin{aligned}&\,_{C}\mathrm {D}_{0,t}^{\alpha }u(x,t)=\frac{\partial ^\beta u(x,t)}{\partial {|x|^\beta }}+f(x,t),~0< x<L, ~0< t\le T,\\&u(x,0)=\varphi (x), ~0\le x\le L,\\&u(0,t)=u(L,t)=0, ~0< t\le T. \end{aligned} \right. \end{aligned}$$

(1)

Here, $\,_{C}\mathrm {D}_{0,t}^\alpha u(x,t)$ denotes the Caputo derivative of order $\alpha \in (0,1)$ and defined by [15]

$$\begin{aligned} \begin{array}{lll} \displaystyle \,_{C}\mathrm {D}_{0,t}^\alpha u(x,t)=\frac{1}{\varGamma (1-\alpha )} \int _{0}^{t}\frac{\partial u(x,s)}{\partial s} \frac{1}{(t-s)^{\alpha }}{\mathrm d} s,\;0<\alpha <1, \end{array} \end{aligned}$$

and $\displaystyle \frac{\partial ^\beta u(x,t)}{\partial |x|^\beta }$ is the Riesz derivative of order $\beta \in (1,2)$ which is defined below [15],

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{\partial ^\beta u(x,t)}{\partial {|x|^\beta }}=\displaystyle -\frac{1}{2\cos \left( \frac{\pi \beta }{2}\right) }\left( \,_{RL}\mathrm {D}_{a,x}^\beta +\,_{RL}\mathrm {D}_{x,b}^\beta \right) u(x,t),\;1<\beta \le 2, \end{array} \end{aligned}$$

where $\,_{RL}\mathrm {D}_{a,x}^\beta$ denotes the left Riemann–Liouville derivative

$$\begin{aligned} \begin{array}{lll}\displaystyle \,_{RL}{\mathrm {D}}_{a,x}^{\beta }u(x,t)= \frac{1}{\varGamma (2-\beta )}\frac{\partial ^2}{\partial x^2}\int _{a}^{x}\frac{u(r,t)}{(x-r)^{\beta -1}}{\mathrm d} r,\;\;\;\; 1<\beta <2, \end{array} \end{aligned}$$

and $\,_{RL}\mathrm {D}_{x,b}^\beta$ is the right Riemann–Liouville derivative

$$\begin{aligned} \begin{array}{lll}\displaystyle \,_{RL}{\mathrm {D}}_{x,b}^{\beta }u(x,t)= \frac{1}{\varGamma (2-\beta )}\frac{\partial ^2}{\partial x^2}\int _{x}^{b}\frac{u(r,t)}{(r-x)^{\beta -1}}{\mathrm d} r,\;\;\;\; 1<\beta <2. \end{array} \end{aligned}$$

This paper is organized as follows. In Sect. 2, based on a second-order accuracy approximation operator for the Riesz fractional derivative, we develop a finite-difference scheme for the time-Caputo and space-Riesz fractional diffusion equation. The stability and convergence analysis of the constructed scheme is studied in Sect. 3. Numerical results are provided in Sect. 4 to demonstrate the effectiveness of the numerical algorithm.

2 The Development of the Numerical Algorithm

Let $h=\frac{L}{M}$ and $\tau =\frac{T}{N}$ be the spatial and temporal stepsizes, respectively. Set $x_j=jh~(0\le j\le M)$, $t_k=n\tau ~(0\le k\le N)$. Denote

$$\begin{aligned} u_j^j=u(x_j,t_k),~f_j^k=f(x_j,t_k). \end{aligned}$$

First, we introduce the following L1 formula [10, 14] to numerical treatment of the Caputo fractional derivative $\,_{C}\mathrm {D}_{0,t}^\alpha u(t)$ at $t=t_n\;(n=0,1,\ldots ,N)$:

$$\begin{aligned} \begin{aligned} {}_C{\mathrm D}_{0,t}^{\alpha }u(t)|_{t=t_n}&=\frac{1}{\varGamma (1-\alpha )}\sum _{k=0}^{n-1} \int _{t_k}^{t_{k+1}}(t_n-s)^{-\alpha }u'(s){\mathrm{d}} s\\&=\frac{1}{\varGamma (1-\alpha )}\sum _{k=0}^{n-1} \int _{t_k}^{t_{k+1}}(t_n-s)^{-\alpha }\left[ \frac{u(t_{k+1})-u(t_k)}{\tau }+{\mathcal {O}}(\tau )\right] {\mathrm{d}} s\\&=\frac{\tau ^{-\alpha }}{\varGamma (2-\alpha )}\sum _{k=0}^{n-1}b_{n-k-1}\left( u(t_{k+1})-u(t_k)\right) +\mathcal {O}\left( \tau ^{2-\alpha }\right) , \end{aligned} \end{aligned}$$

(2)

where the weights are defined by

$$\begin{aligned} b_k=(k+1)^{1-\alpha }-k^{1-\alpha },\;k=0,1,\ldots ,n-1, \end{aligned}$$

and which have the following properties.

Lemma 1

[12] Let$b_k=(k+1)^{1-\alpha }-k^{1-\alpha },~k=0,1,2,\ldots$and$0<\alpha <1$. Then, one has

$$\begin{aligned} \left\{ \begin{aligned}&1=b_0>b_1>b_2>\cdots >b_k\rightarrow 0, {as} ~k\rightarrow +\infty ,\\&c_1k^\alpha \le (b_{k})^{-1}\le c_2 k^{\alpha }, {where} ~~c_1 ~~{and} ~~c_2~~ {are} ~~{constants},\\&\sum _{k=0}^n(b_k-b_{k+1})+b_{n+1}=(1-b_1)+\sum _{k=1}^{n-1}(b_k-b_{k+1})+b_n=1. \end{aligned} \right. \end{aligned}$$

In [4], the authors constructed the following second-order numerical differential formula:

$$\begin{aligned} \displaystyle \frac{\partial ^\beta u(x)}{\partial {|x|^\beta }}= -\frac{1}{2\cos \left( \frac{\pi }{2}\beta \right) }\left( \,^{L}\mathcal {B}_{2}^{\beta }u(x)+\,^{R}\mathcal {B}_{2}^{\beta }u(x)\right) + \mathcal {O}(h^2) \end{aligned}$$

(3)

for the Riesz space fractional derivative, where the operators

$$\begin{aligned} \begin{array}{lll} \displaystyle \,^{L}\mathcal {B}_{2}^{\beta }u(x) =\frac{1}{h^{\beta }}\sum \limits _{\ell =0}^{\infty } \kappa _{2,\ell }^{(\beta )}u\left( x-(\ell -1)h\right) , \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{lll} \displaystyle \,^{R}\mathcal {B}_{2}^{\beta }u(x) =\frac{1}{h^{\beta }}\sum \limits _{\ell =0}^{\infty } \kappa _{2,\ell }^{(\beta )}u\left( x+(\ell -1)h\right) . \end{array} \end{aligned}$$

Here, the coefficients

$$\begin{aligned} \begin{array}{lll} \displaystyle \kappa _{2,\ell }^{(\beta )}=(-1)^{\ell } \left( \frac{3\beta -2}{2\beta }\right) ^{\beta }\sum \limits _{m=0}^{\ell } \left( \frac{\beta -2}{3\beta -2}\right) ^m\left( {\begin{array}{c}\beta \\ m\end{array}}\right) \left( {\begin{array}{c}\beta \\ \ell -m\end{array}}\right) ,\;\;\ell =0,1,\ldots \end{array} \end{aligned}$$

can be obtain by the novel generating function

$$\begin{aligned} \widetilde{W}_{2}(z)=\left( \frac{3\beta -2}{2\beta }-\frac{2(\beta -1)}{\beta }z+\frac{\beta -2}{2\beta }z^2\right) ^{\beta }. \end{aligned}$$

Besides, we can also calculate the coefficients $\kappa _{2,\ell }^{(\beta )}$ by the following recursive relations:

$$\begin{aligned}\left\{ \begin{array}{lll} \displaystyle \kappa _{2,0}^{(\beta )}&= \displaystyle \left( \frac{3\beta -2}{2\beta }\right) ^{\beta },\\ \displaystyle \kappa _{2,1}^{(\beta )}& = \displaystyle \frac{4\beta (1-\beta )}{3\beta -2}\kappa _{2,0}^{(\beta )},\\ \displaystyle \kappa _{2,\ell }^{(\beta )}& = \displaystyle \frac{1}{\ell (3\beta -2)}\left[ 4(1-\beta )(\beta -\ell +1)\kappa _{2,\ell -1}^{(\beta )}\right. \\ &\quad \displaystyle \left. +(\beta -2)(2\beta -\ell +2)\kappa _{2,\ell -2}^{(\beta )} \right] ,\;\;\ell \ge 2. \end{array}\right. \end{aligned}$$

Next, we list the properties of the coefficients $\kappa _{2,\ell }^{(\beta )}$$(\ell =0,1,\ldots )$.

Lemma 2

[4] The coefficients$\kappa _{2,\ell }^{(\beta )}\;(\ell =0,1,\ldots )$have the following properties for$1<\beta <2$:

• i) $\displaystyle \kappa _{2,0}^{(\beta )}=\left( \frac{3\beta -2}{2\beta }\right) ^{\beta }>0$, $\displaystyle \kappa _{2,1}^{(\beta )}=\frac{4\beta (1-\beta )}{3\beta -2}\kappa _{2,0}^{(\beta )}<0$;

• ii) $\displaystyle \kappa _{2,2}^{(\beta )}=\frac{\beta (8\beta ^3-21\beta ^2+16\beta -4)}{(3\beta -2)^2} \kappa _{2,0}^{(\beta )}$. $\kappa _{2,2}^{(\beta )}<0$if$\beta \in (1,\beta ^{*})$, while$\kappa _{2,2}^{(\beta )}\ge 0$if$\beta \in [\beta ^{*},2)$, where$\displaystyle \beta ^{*}=\frac{7}{8}+\frac{\root 3 \of {621+48\sqrt{87}}}{24}+\frac{19}{\root 3 \of {621+48\sqrt{87}}}\approx 1.533\,3$;

• iii) $\displaystyle \kappa _{2,\ell }^{(\beta )}\ge 0$if$\ell \ge 3$;

• iv) $\displaystyle \kappa _{2,\ell }^{(\beta )}\sim -\frac{\sin \left( \pi \beta \right) \varGamma (\beta +1)}{\pi }\ell ^{-\beta -1}$as$\ell \rightarrow \infty$;

• v) $\displaystyle \kappa _{2,\ell }^{(\beta )}\rightarrow 0$as$\ell \rightarrow \infty$;

• vi) $\displaystyle \sum \limits _{\ell =0}^{\infty }\kappa _{2,\ell }^{(\beta )}=0,\;\;\sum \limits _{\ell =0}^{m}\kappa _{2,\ell }^{(\beta )}<0,\;m\ge 2.$

Now, we consider Eq. (1) at point $(x_j,t_k)$. For the space fractional derivative, we apply the second-order formula (3) to approximate the Riesz derivative for $x\in (0,L)$, that is,

$$\begin{aligned} \displaystyle \frac{\partial ^\beta u(x_j,t_n)}{\partial {|x|^\beta }}= -\frac{1}{2\cos \left( \frac{\pi }{2}\beta \right) }\left( \,^{L}\mathcal {A}_{2}^{\beta }+\,^{R}\mathcal {A}_{2}^{\beta }\right) u(x_j,t_n)+\mathcal {O}\left( h^2\right) , \end{aligned}$$

(4)

where

$$\begin{aligned} \begin{array}{lll} \displaystyle \,^{L}\mathcal {A}_{2}^{\beta }u(x_j,t_n) =\frac{1}{h^{\beta }}\sum \limits _{\ell =0}^{j+1} \kappa _{2,\ell }^{(\beta )}u\left( x_j-(\ell -1)h,t_n\right) , \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{lll} \displaystyle \,^{R}\mathcal {A}_{2}^{\beta }u(x_j,t_n) =\frac{1}{h^{\beta }}\sum \limits _{\ell =0}^{M-j+1} \kappa _{2,\ell }^{(\beta )}u\left( x_j+(\ell -1)h,t_n\right) . \end{array} \end{aligned}$$

Finally, substituting (2) and (4) into (1), and omitting the high-order terms $\mathcal {O}\left( \tau ^{2-\alpha }+h^2\right)$. Replacing the function $u(x_j,t_n)$ with its numerical approximation value $U_j^n$, we can obtain the following finite-difference scheme:

$$\begin{aligned} \left\{ \begin{aligned}&U_j^n+q\left[ \sum _{\ell =0}^{j+1}\kappa _{2,\ell }^{(\beta )}U_{j-\ell +1}^n+\sum _{\ell =0}^{M-j+1}\kappa _{2,\ell }^{(\beta )}U_{j+\ell -1}^n\right] =U_j^{n-1}\\&-\sum _{k=1}^{n-1}b_k\left( U_j^{n-k}-U_j^{n-k-1}\right) +\tau ^\alpha \varGamma (2-\alpha ) f_j^n,\\&U_j^0=\varphi \left( x_j\right) ,~0\le j\le M,\\&U_0^n=U_M^n=0,~1\le n\le N, \end{aligned}\right. \end{aligned}$$

(5)

where $q=\displaystyle \frac{\tau ^\alpha \varGamma (2-\alpha )}{2h^\beta \cos \left( \frac{\pi }{2}\beta \right) }$.

3 Stability and Convergence Analysis

In this section, the stability and convergence analysis of the above difference scheme are studied in detail.

3.1 Stability Analysis

From Lemma 2, we easily know that

Lemma 3

Under the condition

$$\begin{aligned} \frac{7}{8}+\frac{\root 3 \of {621+48\sqrt{87}}}{24}+\frac{19}{\root 3 \of {621+48\sqrt{87}}}\le \beta <2, \end{aligned}$$

(6)

the coefficient $\displaystyle \kappa _{2,2}^{(\beta )}$ satisfy

$$\begin{aligned} \kappa _{2,2}^{(\beta )}\ge 0. \end{aligned}$$

Theorem 1

Under the condition (6) and$0<\alpha <1$, the finite-difference scheme for the time-Caputo and space-Riesz fractional diffusion equation (1) is unconditionally stable.

Proof

Let $V_j^n$ be the exact solution of the finite-difference scheme (5). Denote $\xi _j^n=V_j^n-U_j^n$, then we can obtain the following perturbation equation:

$$\begin{aligned} \left\{ \begin{aligned}&\left( 1+2q\kappa _{2,1}^{(\beta )}\right) \xi _j^1+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\xi _{j-\ell +1}^1+\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\xi _{j+\ell -1}^1\right] =\xi _j^0,\\&\left( 1+2q\kappa _{2,1}^{(\beta )}\right) \xi _j^n+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\xi _{j-\ell +1}^n+\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\xi _{j+\ell -1}^n\right] \\&=\left( 1-b_1\right) \xi _j^{n-1}+\sum _{k=2}^{n-1}\left( b_{k-1}-b_k\right) \xi _j^{n-k}+b_{n-1}\xi _j^0. \end{aligned}\right. \end{aligned}$$

Below, we will discuss the stability of the numerical algorithm by mathematical induction. Denote

$$\begin{aligned} \left\| E^1\right\| _\infty =\left| \xi _{\ell }^{1}\right| =\displaystyle \max _{1\le j\le M-1}\left| \xi _j^1\right| . \end{aligned}$$

Note that Lemma 2, that is, $\displaystyle \sum \limits _{\ell =0}^{m}\kappa _{2,\ell }^{(\beta )}<0\;(m\ge 2)$, then we have

$$\begin{aligned} \begin{aligned} \left\| E^1\right\| _\infty&=\left| \xi _{\ell }^{1}\right| \le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \xi _{\ell }^{1}\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \xi _{\ell }^{1}\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \xi _{\ell }^{1}\right| \right] \\&\le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \xi _j^1\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \xi _{j-\ell +1}^1\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \xi _{j+\ell -1}^1\right| \right] \\&\le \left| \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \xi _j^1+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\xi _{j-\ell +1}^1+\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\xi _{j+\ell -1}^1\right] \right| \\&=\left| \xi _l^0\right| \le \left\| E^0\right\| _\infty . \end{aligned} \end{aligned}$$

Furthermore, let

$$\begin{aligned} \left\| E^{n}\right\| _\infty =\left| \xi _{\ell }^{n}\right| =\displaystyle \max _{1\le j\le M-1}\left| \xi _j^{n}\right| , \end{aligned}$$

and assuming that we have proved that $\left\| E^k\right\| _\infty \le \left\| E^0\right\| _\infty$ for $1\le k\le n-1.$ Then, we also know that

$$\begin{aligned} \begin{aligned} \left\| E^{n}\right\| _\infty&=\left| \xi _{\ell }^{n}\right| \le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \xi _{\ell }^{n}\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \xi _{\ell }^{n}\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \xi _{\ell }^{n}\right| \right] \\&\le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \xi _j^n\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \xi _{j-\ell +1}^n\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \xi _{j+\ell -1}^n\right| \right] \\&\le \left| \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \xi _j^n+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\xi _{j-\ell +1}^n+\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\xi _{j+\ell -1}^n\right] \right| \\&=\left| \left( 1-b_1\right) \xi _j^n+\sum _{k=2}^{n-1}\left( b_{k-1}-b_k\right) \xi _j^{n-k}+b_{n-1}\xi _j^0\right| \\&\le \left( 1-b_1\right) \left\| E^n\right\| _\infty +b_{n-1}\left\| E^0\right\| _\infty +\sum _{k=2}^{n-1}\left( b_{k-1}-b_{k}\right) \left\| E^{n-k}\right\| _\infty \\&\le \left( 1-b_1\right) \left\| E^0\right\| _\infty +b_{n-1}\left\| E^0\right\| _\infty +\sum _{k=2}^{n-1}\left( b_{k-1}-b_{k}\right) \left\| E^{0}\right\| _\infty \\&=\Vert E^0\Vert _\infty . \end{aligned} \end{aligned}$$

This ends the proof.

3.2 Convergence Analysis

Theorem 2

Denote by$u(x_j,t_n)~(j=1,2,\ldots ,M-1;n=1,2,\ldots ,N)$the exact solution of (1) at mesh point$(x_i,t_n)$, and let$\{U_j^n\,|\,0\le j\le M, 0 \le n\le N\}$be the solution of the finite-difference scheme (5). Define

$$\begin{aligned} \varepsilon _j^n=u(x_j, t_n)-U_j^n,\;\;j=1,2,\ldots ,M;~n=1,2,\ldots ,N, \end{aligned}$$

then there exists a positive constantC, such that

$$\begin{aligned} \begin{array}{lll} \displaystyle ||\varepsilon ^n||_\infty \le C\,\left( \tau ^{2-\alpha }+h^2\right) ,\,\,0\le n\le N, \end{array} \end{aligned}$$

under the condition (6) and$0<\alpha <1.$

Proof

Denote ${\varepsilon }^n=\left( \varepsilon _1^n,\varepsilon _2^n,\ldots ,\varepsilon _{M-1}^n\right) ^\mathrm{T}$. then it follows from (1) and (5) that

$$\begin{aligned} \left\{ \begin{aligned}&\left( 1+2q\kappa _{2,1}^{(\beta )}\right) \varepsilon _j^1+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\varepsilon _{j-\ell +1}^1+\sum _{\ell =0,\ell \ne 1}^{M-j+1} \kappa _{2,\ell }^{(\beta )}\varepsilon _{j+\ell -1}^1\right] =\varepsilon _j^0+R_j^1,\\&\left( 1+2q\kappa _{2,1}^{(\beta )}\right) \varepsilon _j^n+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\varepsilon _{j-\ell +1}^n+\sum _{\ell =0,\ell \ne 1}^{M-j+1} \kappa _{2,\ell }^{(\beta )}\varepsilon _{j+\ell -1}^n\right] \\&=\left( 1-b_1\right) \varepsilon _j^n+\sum _{k=2}^{n-1} \left( b_{k-1}-b_k\right) \varepsilon _j^{n-k}+b_{n-1}\varepsilon _j^0+R_j^n. \end{aligned}\right. \end{aligned}$$

Here, the truncation error $R_j^n$ satisfies

$$\begin{aligned} \left| R_j^n\right| \le \widetilde{C}\left( \tau ^2+\tau ^\alpha h^2\right) ,~j=1,2,\ldots ,M-1; n=1,2,\ldots ,N, \end{aligned}$$

where $\widetilde{C}$ is a non-negative constant.

Below, we give the convergence result using mathematical induction. First, for the case of $n=1$, let

$$\begin{aligned} \left\| \varepsilon ^1\right\| _\infty =\left| \varepsilon _{\ell }^1\right| /\tau ^{\alpha }=\displaystyle \max _{1\le j\le M-1}\left| \varepsilon _j^1\right| /\tau ^{\alpha }. \end{aligned}$$

Then, one has

$$\begin{aligned} \begin{aligned} \tau ^{\alpha }\left\| \varepsilon ^1\right\| _\infty&=\left| \varepsilon _{\ell }^{1}\right| \le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \varepsilon _{\ell }^{1}\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{\ell }^{1}\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{\ell }^{1}\right| \right] \\&\le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \varepsilon _j^1\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{j-\ell +1}^1\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{j+\ell -1}^1\right| \right] \\&\le \left| \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \varepsilon _j^1+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\varepsilon _{j-\ell +1}^1+\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\varepsilon _{j+\ell -1}^1\right] \right| \\&=\left| \varepsilon _l^0+R_{\ell }^1\right| . \end{aligned} \end{aligned}$$

Using $\varepsilon ^0=0$ and $\left| R_{\ell }^1\right| \le \widetilde{C}(\tau ^{2}+\tau ^\alpha h^2)$, then there holds that

$$\begin{aligned} \left\| \varepsilon ^1\right\| _\infty \le \widetilde{C}\left( \tau ^{2-\alpha }+h^2\right) . \end{aligned}$$

As the before, set

$$\begin{aligned} \left\| \varepsilon ^n\right\| _\infty =\left| \varepsilon _{\ell }^n\right| /\tau ^{\alpha }=\displaystyle \max _{1\le j\le M-1}\left| \varepsilon _j^n\right| /\tau ^{\alpha }, \end{aligned}$$

and

$$\begin{aligned} \left\| \varepsilon ^k\right\| _\infty \le \widehat{C}(\tau ^2+\tau ^\alpha h^2),\;\;k=1,2,\ldots ,n-1, \end{aligned}$$

then we further have

$$\begin{aligned} \begin{aligned}\tau ^{\alpha } \left\| \varepsilon ^{n}\right\| _\infty&=\left| \varepsilon _{\ell }^{n}\right| \le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \varepsilon _{\ell }^{n}\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{\ell }^{n}\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{\ell }^{n}\right| \right] \\&\le \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \left| \varepsilon _j^n\right| +q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{j-\ell +1}^n\right| +\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\left| \varepsilon _{j+\ell -1}^n\right| \right] \\&\le \left| \left( 1+2q\kappa _{2,1}^{(\beta )}\right) \varepsilon _j^n+q\left[ \sum _{\ell =0,\ell \ne 1}^{j+1} \kappa _{2,\ell }^{(\beta )}\varepsilon _{j-\ell +1}^n+\sum _{\ell =0,\ell \ne 1}^{M-j+1}\kappa _{2,\ell }^{(\beta )}\varepsilon _{j+\ell -1}^n\right] \right| \\&=\left| \left( 1-b_1\right) \varepsilon _j^n+\sum _{k=2}^{n-1}\left( b_{k-1}-b_k\right) \varepsilon _j^{n-k}+b_{n-1}\varepsilon _j^0+R_j^n\right| \\&\le \left( 1-b_1\right) \left\| \varepsilon ^n\right\| _\infty +b_{n-1}\left\| \varepsilon ^0\right\| _\infty +\sum _{k=2}^{n-1}\left( b_{k-1}-b_{k}\right) \left\| \varepsilon ^{n-k}\right\| _\infty +\left| R_j^n\right| \\&\le \left\{ \left( 1-b_1\right) +\sum _{k=2}^{n-1}\left( b_{k-1}-b_{k}\right) \right\} \widehat{C}(\tau ^2+\tau ^\alpha h^2)+\widetilde{C}\left( \tau ^2+\tau ^\alpha h^2\right) . \end{aligned} \end{aligned}$$

Therefore, there exists a positive constant C, such that

$$\begin{aligned} \left\| \varepsilon ^n\right\| _\infty \le C(\tau ^{2-\alpha }+ h^2). \end{aligned}$$

This finishes the proof.

4 Numerical Examples

In this section, we apply the method proposed in this paper to solve the fractional partial differential equation. We obtain the numerical results and plot graphs for these problems with the help of MATLAB routines.

Example 1

Let us consider the following equation:

$$\begin{aligned} \,_{C}\mathrm {D}_{0,t}^{\alpha }u(x,t)=\frac{\partial ^\beta u(x,t)}{\partial {|x|^\beta }}+f(x,t), ~\alpha \in (0,1),~\beta \in (1,2) \end{aligned}$$

on a finite domain $0 \le x \le 1, 0 \le t \le 1$ with a given force term

$$\begin{aligned} f(x,t) =&\frac{\varGamma (3+\alpha )}{2}t^{2}x^2(1-x)^2\\ {}&+\frac{t^{2+\alpha }}{\cos \left( \pi \beta /2\right) }\sum \limits _{\ell =0}^{{2}}(-1)^{\ell }\frac{({2}+\ell )!}{\ell !({2}-\ell )! {\varGamma }({3}+\ell -\beta )} \left[ x^{2+\ell -\beta }+(1-x)^{2+\ell -\beta }\right] . \end{aligned}$$

Its analytical solution is

$$\begin{aligned} u(x,t) = t^{2+\alpha }x^2(1-x)^2. \end{aligned}$$

Tables 1 and 2 list the maximum errors and convergence orders using the finite-difference scheme (5) at time $t=1$ with different stepsizes. It is observed that the numerical convergence orders are consistent with our theoretical analysis. In addition, Figs. 1, 2, 3 and 4 compare the graphs of the exact and approximate solutions with different values of $\alpha$, $\beta$, $\tau$, and h. The graphs show excellent agrement between the solutions.

Table 1 Temporal convergence orders of Example 1 with $\beta =1.6$ and $h=\frac{1}{1 000}$

Table 2 Spatial convergence orders of Example 1 with $\alpha =0.4$ and $\tau =\frac{1}{1 000}$

Fig. 1

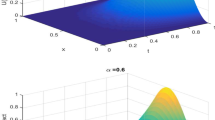
Comparison of exact and numerical solutions for Example 1 with $\tau =\frac{1}{20}, h=\frac{1}{40}$ at time $t=0.5$

Fig. 2

Comparison of exact and numerical solutions for Example 1 with $\tau =\frac{1}{50}, h=\frac{1}{30}$ at time $t=0.5$

Fig. 3

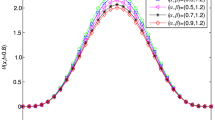
Comparison of exact and numerical solutions for Example 1 with $\tau =\frac{1}{30}, h=\frac{1}{20}$ at space $x=0.8$

Fig. 4

Comparison of exact and numerical solutions for Example 1 with $\tau =\frac{1}{25}, h=\frac{1}{50}$ at space $x=0.8$

Example 2

Consider the following equation:

$$\begin{aligned} \,_{C}\mathrm {D}_{0,t}^{\alpha }u(x,t)=\frac{\partial ^\beta u(x,t)}{\partial {|x|^\beta }}+f(x,t), \;\;0< x<1,\; 0< t < 1, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} f(x,t) =&\frac{\varGamma (5)}{\varGamma (5-\alpha )}t^{4-\alpha }x^4(1-x)^4\\ {}&+ \frac{t^{4}}{2\cos \left( \frac{\pi }{2}\beta \right) } \sum _{\ell =0}^{4}\frac{(-1)^{\ell }4!\,(4+\ell )!}{\ell !\,(4-\ell )!\,\varGamma (5+\ell -\beta )} \left[ x^{4+\ell -\beta }+(1-x)^{4+\ell -\beta }\right] . \end{aligned} \end{aligned}$$

The exact solution is

$$\begin{aligned} u(x,t) = t^{4}x^4(1-x)^4. \end{aligned}$$

In Table 3, we list the maximum error for $\beta =1.2,\;h=1/500$ and different values of $\alpha$. In Table 4, we list the maximum error for $\alpha =0.7,\;\tau =1/400$ and different values of $\beta$. From these tables, we can conclude that the developed numerical solutions are in excellent agreement with the exact solution.

Table 3 Temporal convergence orders of Example 2 with $\beta =1.2$ and $h=\frac{1}{500}$

Table 4 Spatial convergence orders of Example 2 with $\alpha =0.7$ and $\tau =\frac{1}{400}$