Adaptive Moving Mesh Central-Upwind Schemes for Hyperbolic System of PDEs: Applications to Compressible Euler Equations and Granular Hydrodynamics

Abstract

We introduce adaptive moving mesh central-upwind schemes for one- and two-dimensional hyperbolic systems of conservation and balance laws. The proposed methods consist of three steps. First, the solution is evolved by solving the studied system by the second-order semi-discrete central-upwind scheme on either the one-dimensional nonuniform grid or the two-dimensional structured quadrilateral mesh. When the evolution step is complete, the grid points are redistributed according to the moving mesh differential equation. Finally, the evolved solution is projected onto the new mesh in a conservative manner. The resulting adaptive moving mesh methods are applied to the one- and two-dimensional Euler equations of gas dynamics and granular hydrodynamics systems. Our numerical results demonstrate that in both cases, the adaptive moving mesh central-upwind schemes outperform their uniform mesh counterparts.

1 Introduction

We consider the hyperbolic system of conservation/balance laws:

$$\begin{aligned} {\varvec{U}}_t+\nabla \cdot {\mathcal {F}}({\varvec{U}})={\varvec{S}}({\varvec{U}}), \end{aligned}$$

(1.1)

where ${\varvec{U}}$ is a vector of the conserved quantities, ${\mathcal {F}}({\varvec{U}})$ are the flux functions, and ${\varvec{S}}({\varvec{U}})$ are the source terms.

The development of accurate, efficient and robust numerical methods for the system (1.1) is an important and challenging problem. A major difficulty is related to the fact that the system (1.1) admits nonsmooth solutions. Moreover, it is well-known that even smooth solutions may develop nonsmooth waves including shocks, rarefaction waves, and contact discontinuities.

There is a wide variety of shock capturing methods designed to accurately capture this type of solutions; see, e.g., the monographs [3, 7, 15, 25, 31, 43] and references therein.

Numerical methods for (1.1) are typically designed using fixed grids. This limits the efficiency of the methods since finer grids and special nonlinear techniques (such as nonlinear limiters) are required in “rough” parts of the computed solution (vicinities of nonsmooth waves), while the smooth parts can be captured using significantly smaller computation effort. In order to achieve high resolution as well as to improve the efficiency of the numerical methods, various adaptive strategies can be applied. The simplest one is a scheme adaption technique, according to which different schemes are used in “rough” and smooth parts of the computed solution. For example, one can use nonlinear limiters near shocks and possibly contact waves, while using a higher-order “nonlimited” scheme in the rest of the computational domain; see, for example, [11, 12, 24, 33]. Alternatively, instead of manipulating numerical schemes on uniform Cartesian meshes, one can use more flexible meshes. For instance, one can apply adaptive mesh refinement (AMR) or adaptive moving mesh (AMM) methods. In the AMR methods, the initial uniform Cartesian mesh is adaptively refined into layers of finer grids within the “rough” regions of the computed solution to increase the local resolution and then inter-grid projections are made to combine different layers using the intricate data structure; see, e.g., [4,5,6, 32, 36, 37] and references therein. In contrast, in the AMM methods, the mesh points are adaptively shifted towards the “rough” parts to capture the details in the regions where large variations in the computed solutions are found. A variety of AMM algorithms, including the variational approach [46], the moving mesh PDEs (MMPDE) approach [10], and moving mesh methods based on the harmonic mapping [13] have been developed. For AMM methods for compressible Euler and Navier–Stokes equations we refer the reader to, for example, [19, 22, 23, 42, 47].

In this paper, we present new AMM central-upwind schemes for the system (1.1) on both adaptive one-dimensional (1-D) nonuniform grids and two-dimensional (2-D) structured quadrilateral meshes. Our AMM method consists of two steps: the PDE time evolution and the mesh redistribution. The time evolution step is performed using the second-order semi-discrete central-upwind schemes on irregular meshes. Such schemes were derived on Cartesian meshes in [26, 28,29,30], and later extended to triangular [9, 27], quadrilateral [40] and cell-vertex polygonal [2] grids. These schemes are attractive alternatives to upwind methods because they are simple (Riemann-problem-solver-free), efficient, and can be used as a “black-box” solver for general (multidimensional) hyperbolic systems of conservation/balance laws. After evolving the solutions to the new time level, the mesh points are redistributed accordingly to the MMPDE which takes into account the size of the gradient of the computed solution or another smoothness indicator. However, when the computed solution contains very large gradients or discontinuities, the mesh movement has to be adjusted in order to avoid rapid changes in the local mesh size as such changes can affect the accuracy of the approximated solution. To this end, we develop a new simple and robust technique, which helps to guarantee that the mesh remains structured, no very small cells appear, and the ratio between the areas of nearby cells remains bounded. Additionally, in order to bridge the solutions and newly shifted mesh, a conservative solution projection is implemented to obtain the solution over the new mesh.

The paper is organized as follows. In Sect. 2, we present the second-order central-upwind schemes on 1-D nonuniform grids as well as on 2-D irregular quadrilateral meshes. In Sect. 3, we briefly review the moving mesh equations in both 1-D and 2-D cases and propose the associated conservative solution projection strategy. In Sect. 4, we demonstrate the high resolution and robustness of the proposed AMM method on Euler equations of gas dynamics in both 1-D and 2-D cases, where the advantages of the AMM methods over the corresponding uniform mesh methods can be clearly observed. In Sect. 5, we apply the developed AMM central-upwind schemes to the 1-D and 2-D granular hydrodynamics systems, which admit spiky solutions, which are efficiently and accurately captured by the developed AMM central-upwind schemes.

2 Central-Upwind Schemes on Structured Meshes

In this section, we present the central-upwind schemes on fixed 1-D nonuniform grids as well as on fixed 2-D structured quadrilateral meshes. The adaptive moving mesh techniques will be discussed in Sect. 3.

2.1 1-D Semi-Discrete Scheme

Consider the 1-D hyperbolic system of conservation/balance laws:

$$\begin{aligned} {\varvec{U}}_t+{\varvec{F}_x}({\varvec{U}})={\varvec{S}}({\varvec{U}}). \end{aligned}$$

Assume that the computational domain is covered with nonuniform cells $C_j=\left[{x_{j-\frac{1}{2}}},{x_{j+\frac{1}{2}}}\right]$ of the size $\Delta x_j:={x_{j+\frac{1}{2}}}-{x_{j-\frac{1}{2}}}$ centered at $x_j:=\left({x_{j-\frac{1}{2}}}+{x_{j+\frac{1}{2}}}\right)/2$, and that at a certain time t, the cell averages of the computed solution

$$\begin{aligned} {\overline{{\varvec{U}}}}_j(t)\approx \frac{1}{\Delta x_j}\int_{C_j}{\varvec{U}}(x,t)\,\mathrm{d}x \end{aligned}$$

are available. Using these data, we first reconstruct a conservative non-oscillatory piecewise polynomial interpolant

$$\begin{aligned} \widetilde{{\varvec{{\varvec{{{\mathcal {P}}}}}}}}(x,t):=\sum _j{\varvec{{\varvec{{{\mathcal {P}}}}}}}_j(x,t){{\chi }}_j(x), \end{aligned}$$

(2.1)

where ${{\chi }}_j(x)$ is the characteristic function of the interval $\left[{x_{j-\frac{1}{2}}},{x_{j+\frac{1}{2}}}\right]$ and ${\varvec{{\varvec{{{\mathcal {P}}}}}}}_j(x,\cdot )$ is the corresponding polynomial piece. A (formal) order of accuracy of the reconstruction (2.1) is determined by the accuracy of the polynomial interpolants at each cell. In this paper, our goal is to design second-order central-upwind schemes, which require second-order piecewise linear reconstructions

$$\begin{aligned} {\varvec{{\varvec{{{\mathcal {P}}}}}}}_j(x,t)={\overline{{\varvec{U}}}}_j(t)+({\varvec{U}}_x)_j(x-x_j), \end{aligned}$$

(2.2)

whose slopes $({\varvec{U}}_x)_j$ are (at least) first-order approximations of the derivatives at $x=x_j$, which are to be computed using a nonlinear limiter to ensure a non-oscillatory nature of the reconstruction. In this paper, we carry out the following two-step strategy for each component of the solution. We first use the generalized minmod limiter [35, 41, 45]

$$\begin{aligned} {(U_x^{(i)})}_j^{\mathrm{mm}}={\mathrm{minmod}}\left( \psi \,\frac{{\overline{U}}_{j+1}^{\,(i)}(t)-{\overline{U}}_j^{\,(i)}(t)}{{x_{j+1}}-{x_j}},\, \frac{{\overline{U}}_{j+1}^{\,(i)}(t)-{\overline{U}}_{j-1}^{\,(i)}(t)}{{x_{j+1}}-{x_{j-1}}},\, \psi \,\frac{{\overline{U}}_j^{\,(i)}(t)-{\overline{U}}_{j-1}^{\,(i)}(t)}{{x_j}-{x_{j-1}}}\right) , \end{aligned}$$

(2.3)

where $\,{\overline{U}}_j^{\,(i)}$ denotes the ith component of $\,{\overline{{\varvec{U}}}}_j$ and the minmod function is defined by

$$\begin{aligned} \text{ minmod }(z_1,z_2,\cdots ):=\left\{ \begin{array}{ll} \min (z_1,z_2,\cdots ),&{}\quad \text{ if }\,\,z_i>0,\,\,\forall i,\\ \max (z_1,z_2,\cdots ),&{}\quad \text{ if }\,\,z_i<0,\,\,\forall i,\\ 0,&{}\text{ otherwise,}\end{array}\right. \end{aligned}$$

and $\psi \in [1,2]$ is the parameter, which controls the amount of numerical viscosity: larger values of $\psi$ lead to sharper reconstructions, but (slightly) more oscillatory numerical solutions. Next, we notice that some components of the solution may represent positive physical quantities such as the density and the energy. Therefore, to maintain their positivity, we follow the strategy in [48] and correct the slopes ${(U_x^{(i)})}_j^{\mathrm{mm}}$ obtained in (2.3) by setting

$$\begin{aligned} {(U_x^{(i)})}_j:=\left\{ \begin{array}{ll} \tau ^{(i)}_j{(U_x^{(i)})}_j^{\mathrm{mm}}, &{}\quad \text{ if }\,\,U^{(i)}\,\,\text{ is } \text{ a } \text{ positive } \text{ physical } \text{ quantity,}\\ {(U_x^{(i)})}_j^{\mathrm{mm}}, &{}\quad \text{ otherwise,} \end{array}\right. \end{aligned}$$

where $\tau ^{(i)}_j$ is a positivity enforcing parameter computed by

$$\begin{aligned} \tau ^{(i)}_j= \min \left\{ 1,\left| \frac{{\overline{U}}_j^{\,(i)}}{\min \left\{ {{{\mathcal {P}}}}_j^{(i)}(x_{j+\frac{1}{2}}),{{{\mathcal {P}}}}_j^{(i)} (x_{j-\frac{1}{2}})\right\} -{\overline{U}}_j^{\,(i)}} \right| \right\} . \end{aligned}$$

We then follow the derivation of the second-order semi-discrete central-upwind scheme in [26] and obtain the following system of time-dependent ODEs:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\,{\overline{{\varvec{U}}}}_j(t)=-\frac{{\varvec{H}}_{j+\frac{1}{2}}(t)-{\varvec{H}}_{j-\frac{1}{2}}(t)}{\Delta x_j}+{\overline{{\varvec{S}}}}_j(t), \end{aligned}$$

(2.4)

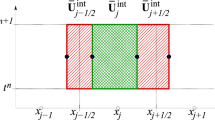
where the numerical fluxes are

$$\begin{aligned} {\varvec{H}}_{j+\frac{1}{2}}:=\frac{a_{j+\frac{1}{2}}^+{\varvec{F}}\left({\varvec{U}}_{j+\frac{1}{2}}^-\right)-a_{j+\frac{1}{2}}^-{\varvec{F}}\left({\varvec{U}}_{j+\frac{1}{2}}^+\right)}{a_{j+\frac{1}{2}}^+-a_{j+\frac{1}{2}}^-}+\frac{a_{j+\frac{1}{2}}^+a_{j+\frac{1}{2}}^-}{a_{j+\frac{1}{2}}^+-a_{j+\frac{1}{2}}^-} \left( {\varvec{U}}_{j+\frac{1}{2}}^+-{\varvec{U}}_{j+\frac{1}{2}}^--{\varvec{d}}_{j+\frac{1}{2}}\right) , \end{aligned}$$

(2.5)

where the built-in anti-diffusion term ${\varvec{d}}_{j+\frac{1}{2}}$ is

$$\begin{aligned} {\varvec{d}}_{j+\frac{1}{2}}={\mathrm{minmod}}\left( {\varvec{U}}_{j+\frac{1}{2}}^+-{\varvec{U}}_{j+\frac{1}{2}}^{\mathrm{int}},\,{\varvec{U}}_{j+\frac{1}{2}}^{\mathrm{int}}-{\varvec{U}}_{j+\frac{1}{2}}^-\right) , \end{aligned}$$

and the intermediate value ${\varvec{U}}_{j+\frac{1}{2}}^{\mathrm{int}}$ is computed by

$$\begin{aligned} {\varvec{U}}_{j+\frac{1}{2}}^{\mathrm{int}}=\frac{a_{j+\frac{1}{2}}^+{\varvec{U}}_{j+\frac{1}{2}}^+-a_{j+\frac{1}{2}}^-{\varvec{U}}_{j+\frac{1}{2}}^- -\left( {\varvec{F}}\left({\varvec{U}}_{j+\frac{1}{2}}^+\right)-{\varvec{F}}\left({\varvec{U}}_{j+\frac{1}{2}}^-\right)\right) }{a_{j+\frac{1}{2}}^+-a_{j+\frac{1}{2}}^-}. \end{aligned}$$

${\overline{{\varvec{S}}}}_j(t)$ are appropriate discretizations of the cell averages of the source terms

$$\begin{aligned} {\overline{{\varvec{S}}}}_j\approx \frac{1}{\Delta x_j}\int_{C_j}{\varvec{S}}({\varvec{U}}(x,t))\,\mathrm{d}x. \end{aligned}$$

(2.6)

In (2.5), ${\varvec{U}}_{j+\frac{1}{2}}^+$ and ${\varvec{U}}_{j+\frac{1}{2}}^-$ are the corresponding right- and left-sided values of the interpolant (2.2) at the cell interface $x={x_{j+\frac{1}{2}}}$, namely,

$$\begin{aligned} {\varvec{U}}_{j+\frac{1}{2}}^+:={\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j+1}\Big ({x_{j+\frac{1}{2}}}\Big )\quad \text{ and }\quad {\varvec{U}}_{j+\frac{1}{2}}^-:={\varvec{{\varvec{{{\mathcal {P}}}}}}}_j\Big ({x_{j+\frac{1}{2}}}\Big ), \end{aligned}$$

and $a_{j+\frac{1}{2}}^\pm$ are the one-sided local speeds of propagation, which, in the case of the convex flux function, can be estimated by

$$\left\{ \begin{aligned} a_{j+\frac{1}{2}}^+&=\max \left\{ \lambda _N\left( \frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}\Big ({\varvec{U}}_{j+\frac{1}{2}}^-\Big )\right) ,\, \lambda _N\left( \frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}\Big ({\varvec{U}}_{j+\frac{1}{2}}^+\Big )\right) ,\,0\right\} ,\\ a_{j+\frac{1}{2}}^-&=\min \left\{ \lambda _1\left( \frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}\Big ({\varvec{U}}_{j+\frac{1}{2}}^-\Big )\right) ,\, \lambda _1\left( \frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}\Big ({\varvec{U}}_{j+\frac{1}{2}}^+\Big )\right) ,\,0\right\} , \end{aligned} \right.$$

(2.7)

with $\lambda _1\leqslant \cdots \leqslant \lambda _N$ being N eigenvalues of the Jacobian $\frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}$. We note that the estimate (2.7) may be inaccurate. In the case of the 1-D Euler equation of gas dynamics, a more accurate estimate has been derived in [18].

Remark 2.1

Note that in (2.5)–(2.7), all of the indexed quantities depend on t, but from now on, we will omit this dependence for the sake of brevity.

Remark 2.2

Notice that if both $a_{j+\frac{1}{2}}^\pm$ are very close to zero, that is, if $a_{j+\frac{1}{2}}^+-a_{j+\frac{1}{2}}^-<\varepsilon$, where $\varepsilon >0$ is a prescribed small parameter, we replace the numerical flux (2.5) with

$$\begin{aligned} {\varvec{H}}_{j+\frac{1}{2}}:=\frac{1}{2}\left[ {\varvec{F}}\Big ({\varvec{U}}_{j+\frac{1}{2}}^+\Big )+{\varvec{F}}\Big ({\varvec{U}}_{j+\frac{1}{2}}^-\Big )\right] . \end{aligned}$$

In all of our numerical examples, we have used $\varepsilon =10^{-8}$.

2.2 2-D Semi-Discrete Scheme

We now consider the 2-D hyperbolic system of conservation/balance laws:

$$\begin{aligned} {\varvec{U}}_t+{\varvec{F}_x}({\varvec{U}})+{\varvec{G}_y}({\varvec{U}})={\varvec{S}}({\varvec{U}}). \end{aligned}$$

Assume that the computational domain is covered with a structured irregular quadrilateral mesh consisting of cells $C_{j,k}$ of size $|C_{j,k}|$, and use the following notations (see Fig. 1).

$$\begin{aligned} \begin{aligned} &{\varvec{z}}_{j+\frac{1}{2},k+\frac{1}{2}}:=({x_{j+\frac{1}{2},k+\frac{1}{2}}},{y_{j+\frac{1}{2},k+\frac{1}{2}}}):\,\text{ cell } \text{ vertices,}\\ &{\varvec{z}}_{j,k}:=(x_{j,k},y_{j,k}):\,\text{ center } \text{ of } \text{ mass } \text{ of }\,C_{j,k},\\ &\ell _{{j+\frac{1}{2}},k}:=|{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}-{\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}|:\,\text{ length } \text{ of } \text{ the } \text{ edge }\,{\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}\,{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}},\\ &{\varvec{z}}_{{j+\frac{1}{2}},k}:=\frac{1}{2}({\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}+{\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}):\,\text{ midpoint } \text{ of } \text{ the } \text{ edge }\,{\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}\,{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}},\\& {\varvec{n}}_{{j+\frac{1}{2}},k}:=(\cos (\theta _{{j+\frac{1}{2}},k}),\sin (\theta _{{j+\frac{1}{2}},k})): \,\text{ the } \text{ unit } \text{ outer } \text{ normal } \text{ vector } \text{ to } \text{ the } \text{ edge }\,{\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}\,{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}},\\& \ell _{j,{k+\frac{1}{2}}}:=|{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}-{\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}|:\,\text{ length } \text{ of } \text{ the } \text{ edge }\,{\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}\,{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}},\\& {\varvec{z}}_{j,{k+\frac{1}{2}}}:=\frac{1}{2}({\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}+{\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}):\,\text{ midpoint } \text{ of } \text{ the } \text{ edge }\,{\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}\,{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}},\\& {\varvec{n}}_{j,{k+\frac{1}{2}}}:=(\cos (\theta _{j,{k+\frac{1}{2}}}),\sin (\theta _{j,{k+\frac{1}{2}}})): \,\text{ the } \text{ unit } \text{ outer } \text{ normal } \text{ vector } \text{ to } \text{ the } \text{ edge }\,{\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}\,{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}. \end{aligned} \end{aligned}$$

Fig. 1

A typical quadrilateral cell $C_{j,k}$ with its four neighbors

Assume that at a certain time t, we have computed an approximate solution, realized in terms of its cell averages:

$$\begin{aligned} {\overline{{\varvec{U}}}}_{j,k}\approx \frac{1}{|C_{j,k}|}\iint_{C_{j,k}}{\varvec{U}}(x,y,t)\,\mathrm{d}x\,\mathrm{d}y. \end{aligned}$$

Using these data, we first construct a second-order conservative non-oscillatory piecewise polynomial interpolant

$$\begin{aligned} \widetilde{{\varvec{{\varvec{{{\mathcal {P}}}}}}}}(x,y)=\sum \limits _{j,k}{\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j,k}(x,y){{\chi }}_{C_{j,k}}, \end{aligned}$$

where ${{\chi }}_{C_{j,k}}$ is the characteristic function of the cell $C_{j,k}$ and ${\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j,k}(x,y)$ is the corresponding polynomial piece. To achieve the second-order accuracy, we employ the piecewise linear reconstruction

$$\begin{aligned} {\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j,k}(x,y)={\overline{{\varvec{U}}}}_{j,k}+({\varvec{U}}_x)_{j,k}(x-x_{j,k})+({\varvec{U}}_y)_{j,k}(y-y_{j,k}), \end{aligned}$$

(2.8)

where the slopes $({\varvec{U}}_x)_{j,k}$ and $({\varvec{U}}_y)_{j,k}$ are (at least) first-order approximations of the x- and y-derivatives of ${\varvec{U}}$ at ${\varvec{z}}_{j,k}$.

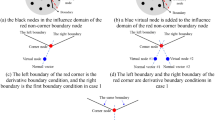
In order to calculate the ith component of the numerical derivatives of ${\varvec{U}}$, $(U_x^{(i)})_{j,k}$ and $(U_y^{(i)})_{j,k}$, we construct four linear interpolations: $L_{j,k}^{+,+}(x,y)$, $L_{j,k}^{-,+}(x,y)$, $L_{j,k}^{+,-}(x,y)$, and $L_{j,k}^{-,-}(x,y)$ outlined in Fig. 2. Each of these linear interpolations is obtained by passing a plane through the point $({\varvec{z}}_{j,k},{\overline{U}}_{j,k}^{\,(i)})$ and the corresponding points in the two neighboring cells. For example, $L_{j,k}^{+,+}(x,y)$ is obtained using the following three points: $({\varvec{z}}_{j,k},{\overline{U}}_{j,k}^{\,(i)})$, $({\varvec{z}}_{j+1,k},{\overline{U}}_{j+1,k}^{\,(i)})$, and $({\varvec{z}}_{j,k+1},{\overline{U}}_{j,k+1}^{\,(i)})$. Notice that since ${\varvec{z}}_{j,k}$ is the geometric center of $C_{j,k}$, the obtained linear interpolants are conservative in $C_{j,k}$, that is,

$$\begin{aligned} \frac{1}{|C_{j,k}|}\iint_{C_{j,k}}L_{j,k}^{\pm ,\pm }(x,y)\,\mathrm{d}x\,\mathrm{d}y={\overline{U}}_{j,k}^{\,(i)}. \end{aligned}$$

Fig. 2

Four linear interpolants over the cell $C_{j,k}$

In order to obtain a non-oscillatory reconstruction, we need to compute $({\varvec{U}}_x)_{j,k}$ and $({\varvec{U}}_y)_{j,k}$ using a nonlinear limiter. As in the 1-D case, we use a two-step strategy for each component of the solution. We first use the following generalization of the 1-D minmod limiter:

$$\left\{\begin{aligned} \begin{aligned} {(U_x^{(i)})}_{j,k}^{\mathrm{mm}}&= {{\mathrm{minmod}}}\bigg (\frac{1}{4}\Big [(L^{+,+}_{j,k})_x+(L^{-,+}_{j,k})_x +(L^{-,-}_{j,k})_x+(L^{+,-}_{j,k})_x\Big ],\\&\quad \psi (L^{+,+}_{j,k})_x,\psi (L^{-,+}_{j,k})_x, \psi (L^{-,-}_{j,k})_x,\psi (L^{+,-}_{j,k})_x\bigg ),\\ (U_y^{(i)})_{j,k}^{\mathrm{mm}}&= {\mathrm{minmod}}\bigg (\frac{1}{4}\Big [(L^{+,+}_{j,k})_y+(L^{-,+}_{j,k})_y +(L^{-,-}_{j,k})_y+(L^{+,-}_{j,k})_y,\Big ],\\&\quad \psi (L^{+,+}_{j,k})_y,\psi (L^{-,+}_{j,k})_y,\psi (L^{-,-}_{j,k})_y, \psi (L^{+,-}_{j,k})_y\bigg ), \end{aligned} \end{aligned}\right.$$

(2.9)

where, as in the 1-D case, $\psi \in [1,2]$ is the parameter that controls the amount of numerical dissipation. Next, in order to maintain the positivity of some components of the solution, we follow [48] and correct ${(U_x^{(i)})}_{j,k}^{\mathrm{mm}}$ and $(U_y^{(i)})_{j,k}^{\mathrm{mm}}$ obtained in (2.9) by setting

$$\begin{aligned} \left( {(U_x^{(i)})}_{j,k},\,{(U_y^{(i)})}_{j,k}\right) :=\left\{ \begin{array}{ll} \tau ^{(i)}_{j,k}\left( {(U_x^{(i)})}_{j,k}^{\mathrm{mm}}, \,{(U_y^{(i)})}_{j,k}^{\mathrm{mm}}\right) ,&{}\quad \text{ if }\,\,U^{(i)}\,\,\text{ is } \text{ a } \text{ positive } \text{ physical } \text{ quantity,}\\ \left( {(U_x^{(i)})}_{j,k}^{\mathrm{mm}},\,{(U_y^{(i)})}_{j,k}^{\mathrm{mm}}\right) , &{}\quad \text{ otherwise,} \end{array} \right. \end{aligned}$$

where $\tau ^{(i)}_{j,k}$ is a positivity enforcing parameter computed by

$$\begin{aligned} \tau ^{(i)}_{j,k}=\min \left\{ 1,\,\left| \frac{{\overline{U}}_{j,k}^{\,(i)}}{\min \Big \{{{{\mathcal {P}}}}_{j,k}^{(i)}({\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}), {{{\mathcal {P}}}}_{j,k}^{(i)}({\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}), {{{\mathcal {P}}}}_{j,k}^{(i)}({\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}), {{{\mathcal {P}}}}_{j,k}^{(i)}({\varvec{z}}_{{j-\frac{1}{2}},{k-\frac{1}{2}}})\Big \} -{\overline{U}}_{j,k}^{\,(i)}}\right| \right\} . \end{aligned}$$

The cell averages ${\overline{{\varvec{U}}}}_{j,k}$ are then evolved in time according to the second-order semi-discrete central-upwind scheme on quadrilateral grids developed in [40], which we modify here by reducing the numerical dissipation using the approach presented in [26]:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\,{\overline{{\varvec{U}}}}_{j,k}=-\frac{1}{|C_{j,k}|} \left( {\varvec{H}}_{{j+\frac{1}{2}},k}-{\varvec{H}}_{{j-\frac{1}{2}},k}+{\varvec{H}}_{j,{k+\frac{1}{2}}}-{\varvec{H}}_{j,{k-\frac{1}{2}}}\right) + \,{\overline{{\varvec{S}}}}_{j,k}, \end{aligned}$$

(2.10)

where ${\varvec{H}}_{j\pm \frac{1}{2},k}$ and ${\varvec{H}}_{j,k\pm \frac{1}{2}}$ are the numerical fluxes along the cell interfaces between $C_{j,k}$ and its four neighboring cells. For instance, the numerical flux between $C_{j,k}$ and $C_{j+1,k}$ is

$$\begin{aligned} \begin{aligned} {\varvec{H}}_{{j+\frac{1}{2}},k}&=\ell _{{j+\frac{1}{2}},k}\Bigg [\left( \cos \big (\theta _{{j+\frac{1}{2}},k}\big ){\varvec{H}}^x_{{j+\frac{1}{2}},k}+\sin \big (\theta _{{j+\frac{1}{2}},k}\big ){\varvec{H}}^y_{{j+\frac{1}{2}},k}\right) \\&\quad +\frac{a_{{j+\frac{1}{2}},k}^+a_{{j+\frac{1}{2}},k}^-}{a_{{j+\frac{1}{2}},k}^+-a_{{j+\frac{1}{2}},k}^-}\left( {\varvec{U}}_{{j+\frac{1}{2}},k}^+-{\varvec{U}}_{{j+\frac{1}{2}},k}^--{\varvec{d}}_{{j+\frac{1}{2}},k}\right) \Bigg ], \end{aligned} \end{aligned}$$

(2.11)

where the x- and y-directional fluxes are

$$\left\{\begin{aligned} \begin{aligned} {\varvec{H}}^x_{{j+\frac{1}{2}},k}&=\frac{a_{{j+\frac{1}{2}},k}^+{\varvec{F}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^-\big )-a_{{j+\frac{1}{2}},k}^-{\varvec{F}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^+\big )}{a_{{j+\frac{1}{2}},k}^+-a_{{j+\frac{1}{2}},k}^-},\\ {\varvec{H}}^y_{{j+\frac{1}{2}},k}&=\frac{a_{{j+\frac{1}{2}},k}^+{\varvec{G}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^-\big )-a_{{j+\frac{1}{2}},k}^-{\varvec{G}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^+\big )}{a_{{j+\frac{1}{2}},k}^+-a_{{j+\frac{1}{2}},k}^-}, \end{aligned} \end{aligned}\right.$$

(2.12)

the built-in anti-diffusion term is

$$\begin{aligned} \begin{aligned} {\varvec{d}}_{{j+\frac{1}{2}},k}&= {\mathrm{minmod}}\left( {\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j+1,k}\left({\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}\right)-{\varvec{U}}^{\mathrm{int}}_{{j+\frac{1}{2}},k}, \,{\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j+1,k}\left({\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}\right)-{\varvec{U}}^{\mathrm{int}}_{{j+\frac{1}{2}},k},\right. \\&\quad \left. {\varvec{U}}^{\mathrm{int}}_{{j+\frac{1}{2}},k}-{\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j,k}\left({\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}\right),\, {\varvec{U}}^{\mathrm{int}}_{{j+\frac{1}{2}},k}-{\varvec{{\varvec{{{\mathcal {P}}}}}}}_{j,k}\left({\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}\right) \right) , \end{aligned} \end{aligned}$$

and the intermediate value ${\varvec{U}}^{\mathrm{int}}_{{j+\frac{1}{2}},k}$ is computed by

$$\begin{aligned} \begin{aligned} {\varvec{U}}^{\mathrm{int}}_{{j+\frac{1}{2}},k}&=\frac{a^+_{{j+\frac{1}{2}},k}{\varvec{U}}^+_{{j+\frac{1}{2}},k}-a^-_{{j+\frac{1}{2}},k} {\varvec{U}}^-_{{j+\frac{1}{2}},k}}{a_{{j+\frac{1}{2}},k}^+-a_{{j+\frac{1}{2}},k}^-}\\&\quad -\cos \big (\theta _{{j+\frac{1}{2}},k}\big )\frac{{\varvec{F}}\big ({\varvec{U}}^+_{{j+\frac{1}{2}},k}\big ) -{\varvec{F}}\big ({\varvec{U}}^-_{{j+\frac{1}{2}},k}\big )}{a_{{j+\frac{1}{2}},k}^+-a_{{j+\frac{1}{2}},k}^-}- \sin \big (\theta _{{j+\frac{1}{2}},k}\big )\frac{{\varvec{G}}\big ({\varvec{U}}^+_{{j+\frac{1}{2}},k}\big ) -{\varvec{G}}\big ({\varvec{U}}^-_{{j+\frac{1}{2}},k}\big )}{a_{{j+\frac{1}{2}},k}^+-a_{{j+\frac{1}{2}},k}^-}. \end{aligned} \end{aligned}$$

(2.13)

The numerical fluxes ${\varvec{H}}_{j,{k+\frac{1}{2}}}$ can be computed in a similar way. In (2.11), (2.12) and (2.13) and similar formulae for ${\varvec{H}}_{j,{k+\frac{1}{2}}}$, ${\varvec{U}}^\pm _{{j+\frac{1}{2}},k}$ and ${\varvec{U}}^\pm _{j,{k+\frac{1}{2}}}$ are the point values of the corresponding linear pieces (2.8) at cell interfaces, namely,

$$\begin{aligned} \begin{aligned} {\varvec{U}}_{{j+\frac{1}{2}},k}^-&:={\varvec{{{\mathcal {P}}}}}_{j,k}\left({\varvec{z}}_{{j+\frac{1}{2}},k}\right),\quad {\varvec{U}}_{{j+\frac{1}{2}},k}^+:={\varvec{{{\mathcal {P}}}}}_{j+1,k}\left({\varvec{z}}_{{j+\frac{1}{2}},k}\right),\\ {\varvec{U}}_{j,{k+\frac{1}{2}}}^-&:={\varvec{{{\mathcal {P}}}}}_{j,k}\left({\varvec{z}}_{j,{k+\frac{1}{2}}}\right),\quad {\varvec{U}}_{j,{k+\frac{1}{2}}}^+:={\varvec{{{\mathcal {P}}}}}_{j,k+1}\left({\varvec{z}}_{j,{k+\frac{1}{2}}}\right), \end{aligned} \end{aligned}$$

and $a_{{j+\frac{1}{2}},k}^\pm$ and $a_{j,{k+\frac{1}{2}}}^\pm$ are the directional local speeds of propagation, which, in the case of convex flux function, can be estimated by

$$\left\{\begin{aligned} \begin{aligned} a_{{j+\frac{1}{2}},k}^+&=\max \Big \{\lambda _N\big (V_{{j+\frac{1}{2}},k}^+\big ),\lambda _N\big (V_{{j+\frac{1}{2}},k}^-\big ),0\Big \},\quad a_{{j+\frac{1}{2}},k}^-=\min \Big \{\lambda _1\big (V_{{j+\frac{1}{2}},k}^+\big ),\lambda _1\big (V_{{j+\frac{1}{2}},k}^-\big ),0\Big \},\\ a_{j,{k+\frac{1}{2}}}^+&=\max \Big \{\lambda _N\big (V_{j,{k+\frac{1}{2}}}^+\big ),\lambda _N\big (V_{j,{k+\frac{1}{2}}}^-\big ),0\Big \},\quad a_{j,{k+\frac{1}{2}}}^-=\min \Big \{\lambda _1\big (V_{j,{k+\frac{1}{2}}}^+\big ),\lambda _1\big (V_{j,{k+\frac{1}{2}}}^-\big ),0\Big \}, \end{aligned} \end{aligned}\right.$$

(2.14)

with $\lambda _1(V)\leqslant \lambda _2(V)\leqslant \cdots \leqslant \lambda _N(V)$ being the N eigenvalues of the matrix V and

$$\left\{\begin{aligned} \begin{aligned} V_{{j+\frac{1}{2}},k}^\pm&:=\cos \big (\theta _{{j+\frac{1}{2}},k}\big )\frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^\pm \big )+ \sin \big (\theta _{{j+\frac{1}{2}},k}\big )\frac{\partial {\varvec{G}}}{\partial {\varvec{U}}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^\pm \big ),\\ V_{j,{k+\frac{1}{2}}}^\pm&:=\cos \big (\theta _{j,{k+\frac{1}{2}}}\big )\frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}\big ({\varvec{U}}_{j,{k+\frac{1}{2}}}^\pm \big )+ \sin \big (\theta _{j,{k+\frac{1}{2}}}\big )\frac{\partial {\varvec{G}}}{\partial {\varvec{U}}}\big ({\varvec{U}}_{j,{k+\frac{1}{2}}}^\pm \big ). \end{aligned} \end{aligned}\right.$$

(2.15)

We note that as in the 1-D case, the estimate (2.14), (2.15) may be inaccurate; see [18].

Finally, the term $\,{\overline{{\varvec{S}}}}_{j,k}$ in (2.10) represents appropriate discretizations of the cell averages of the source terms:

$$\begin{aligned} {\overline{{\varvec{S}}}}_{j,k}\approx \frac{1}{|C_{j,k}|}\iint_{C_{j,k}}{\varvec{S}}({\varvec{U}}(x,y,t))\,\mathrm{d}x\,\mathrm{d}y. \end{aligned}$$

(2.16)

Remark 2.3

Notice that if both $a_{{j+\frac{1}{2}},k}^\pm$ are very close to zero, that is, if $a_{{j+\frac{1}{2}},k}^+-a_{{j+\frac{1}{2}},k}^-<\varepsilon$, where $\varepsilon >0$ is a small parameter, we replace the numerical fluxes ${\varvec{H}}_{{j+\frac{1}{2}},k}$ in (2.11) with

$$\begin{aligned} {\varvec{H}}_{{j+\frac{1}{2}},k}= & {} \frac{\ell _{{j+\frac{1}{2}},k}}{2}\left( \cos \big (\theta _{{j+\frac{1}{2}},k}\big ) \big ({\varvec{F}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^-\big )+{\varvec{F}}\big ({\varvec{U}}_{{j+\frac{F1}{2}},k}^+\big )\big )\right. \\&\left. + \sin \big (\theta _{{j+\frac{1}{2}},k}\big )\big ({\varvec{G}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^-\big ) +{\varvec{G}}\big ({\varvec{U}}_{{j+\frac{1}{2}},k}^+\big )\big )\right) . \end{aligned}$$

Similarly, if both $a_{j,{k+\frac{1}{2}}}^\pm$ are very close to zero, we replace the numerical fluxes ${\varvec{H}}_{j,{k+\frac{1}{2}}}$ in (2.11) with

$$\begin{aligned} {\varvec{H}}_{j,{k+\frac{1}{2}}}= & {} \frac{\ell _{j,{k+\frac{1}{2}}}}{2}\left( \cos \big (\theta _{j,{k+\frac{1}{2}}}\big ) \big ({\varvec{F}}\big ({\varvec{U}}_{j,{k+\frac{1}{2}}}^-\big )+{\varvec{F}}\big ({\varvec{U}}_{j,{k+\frac{1}{2}}}^+\big )\big )\right. \\&\left. + \sin \big (\theta _{j,{k+\frac{1}{2}}}\big )\big ({\varvec{G}}\big ({\varvec{U}}_{j,{k+\frac{1}{2}}}^-\big ) +{\varvec{G}}\big ({\varvec{U}}_{j,{k+\frac{1}{2}}}^+\big )\big )\right) . \end{aligned}$$

In all of our numerical experiments, we have used $\varepsilon =10^{-8}$.

Remark 2.4

The ODE systems (2.4)–(2.6) and (2.10)–(2.16) should be numerically solved by a stable ODE solver of a proper order. In all of the numerical examples in this paper, we have used the three-stage third-order strong stability-preserving (SSP) Runge–Kutta method; see, e.g., [16, 17]. The time step is restricted by the CFL condition, which, in the 1-D case, is

$$\begin{aligned} \Delta t\,\max _j\left\{ \frac{\max \left\{\left|a_{j-\frac{1}{2}}^+\right|,\left|a_{j+\frac{1}{2}}^-\right|\right\}}{\Delta x_j}\right\} \leqslant \frac{1}{2}, \end{aligned}$$

(2.17)

and in the 2-D case, is

$$\begin{aligned} \Delta t\,\max _{j,k}\left\{ \frac{\max \left\{\left|a_{{j+\frac{1}{2}},k}^-\right|,\left|a_{{j-\frac{1}{2}},k}^+\right|,\left|a_{j,{k+\frac{1}{2}}}^-\right|,\left|a_{j,{k-\frac{1}{2}}}^+\right|\right\}}{\mathrm{dist}({\varvec{z}}_{j,k},\partial C_{j,k})}\right\} \leqslant 1. \end{aligned}$$

(2.18)

3 AMM Methods

The main idea of AMM methods is to have more grid points in the “rough” parts of the solution to increase the resolution there. Assuming the mesh was adapted to the solution structure at a certain time level t, we evolve the solution to the new time level $t+\Delta t$ on this mesh. Upon completion of the evolution step, the mesh should be adapted to the structure of the evolved solution. In this section, we overview the moving mesh techniques that allow one to obtain a new mesh in both the 1-D and 2-D cases. After this, the solution should be projected to the new mesh in a conservative way as described below.

3.1 1-D Algorithm

We first describe the AMM method for 1-D nonuniform grids. In addition to the computational domain [a, b] covered by the nonuniform mesh $\{x_{j+\frac{1}{2}}\}$, we introduce the uniform logical mesh $\xi _{j+\frac{1}{2}}=j\Delta \xi ,\,j=0,\cdots ,N$ with $\Delta \xi =1/N$. Let us denote the one-to-one coordinate transformation from the logical domain to the computational one by

$$\begin{aligned} x=x(\xi ),\,\,\xi \in [0,1],\quad x(0)=a,\,\,x(1)=b, \end{aligned}$$

so that $x_{j+\frac{1}{2}}=x\left(\xi _{j+\frac{1}{2}}\right)$.

3.1.1 Mesh Redistribution

Following a variational approach (see, e.g., [20] for a detailed derivation), one can obtain the following moving mesh equation:

$$\begin{aligned} (\omega x_\xi )_\xi =0, \end{aligned}$$

(3.1)

where $\omega ({\varvec{U}})$ is a monitor function, which is designed to detect regions of large variations in the solution. A typical choice of the monitor function (see, e.g., [1, 20, 44]) is

$$\begin{aligned} \omega ({\varvec{U}})=1+\alpha \varphi (|D{\varvec{U}}|), \end{aligned}$$

(3.2)

where D is a differential operator (for example, one may use $D{\varvec{U}}=U_\xi ^{(i)}$ or $D{\varvec{U}}=U_{\xi \xi }^{(i)}$ for some component of ${\varvec{U}}$). In this paper, we compute the required numerical derivatives using the second-order centered differences applied to the ith component if ${\varvec{U}}$ satisfies

$$\begin{aligned} D{\varvec{U}}_j=\big (U^{(i)}_{\xi \xi }\big )_j=\frac{\,{\overline{U}}^{\,(i)}_{j+1}-2\,{\overline{U}}^{\,(i)}_j+\,{\overline{U}}^{\,(i)}_{j-1}}{(\Delta \xi )^2}. \end{aligned}$$

The function $\varphi$ in (3.2) is a smoothing filter needed since rapid changes in the solution may lead to the appearance of sharp gradients in the function $\xi =\xi (x)$. We design this filter by averaging over the neighboring cells for each j for a prescribed number of iterations, that is, we introduce

$$\begin{aligned} \varphi _j^{\ell +1}:=\frac{1}{4}\left( \varphi _{j+1}^\ell +2\varphi _j^\ell +\varphi _{j-1}^\ell \right) ,\quad \ell =0,1,\cdots ,m-1, \end{aligned}$$

where $\varphi _j^0:=|D{\varvec{U}}|$, and then set

$$\begin{aligned} (\varphi (|D{\varvec{U}}|))_j:=\varphi _j^m, \end{aligned}$$

(3.3)

which is used in (3.2). In our numerical experiments, we have taken $m=4$.

Finally, $\alpha$ in (3.2) is the intensity parameter employed to control the mesh concentration: the use of larger values of $\alpha$ leads to the higher concentration of grid points in the “rough” areas. In our computations, we follow [21] and choose $\alpha$ to be

$$\begin{aligned} \alpha =\bigg (\frac{1-\beta }{\beta (b-a)}\int_a^b\varphi (|D{\varvec{U}}|)\,{\mathrm{d}}x\bigg )^{-1}, \end{aligned}$$

where $\beta \in (0,1)$ is a prescribed fraction of mesh points to be concentrated in the “rough” areas of the computed solution.

Equipped with the monitor function $\omega$, we move the mesh according to the following iterative algorithm, in which we denote by $x_{j+\frac{1}{2}}^\nu$ the grid nodes in the beginning of the $(\nu +1)$th iteration step (with the initial guess $x_{j+\frac{1}{2}}^0$ being the grid nodes from the previous evolution step) and $x_j^\nu :=\left(x_{j-\frac{1}{2}}^\nu +x_{j+\frac{1}{2}}^\nu \right)\Big/2$.

We discretize the moving mesh equation (3.1) using the centered difference approximation, which results in the following linear algebraic system for the mesh points locations:

$$\begin{aligned} \left\{ \begin{aligned}&x_\frac{1}{2}=a,\\&\omega _{j+1}(x_{j+\frac{3}{2}}-x_{j+\frac{1}{2}})-\omega _j(x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}})=0,\,\,j=1,\cdots, N-1,\\&x_{N+\frac{1}{2}}=b. \end{aligned}\right. \end{aligned}$$

(3.4)

The obtained system is numerically solved using the Jacobi iterations combined with an adjusted mesh movement designed to avoid rapid changes of the mesh. We start the iteration process with the grid nodes from the previous evolution step, denoted by $\left\{x_{j+\frac{1}{2}}^0\right\}$, and move the mesh from $\left\{x_{j+\frac{1}{2}}^\nu \right\}$ to $\left\{x_{j+\frac{1}{2}}^{\nu +1}\right\}$ according to the following iterative algorithm.

Algorithm 3.1

(Adjusted 1-D Mesh Movement)

• Step 1 Take one Jacobi iteration sweep for (3.4):

  $$\begin{aligned} \omega _{j+1}\left(x_{j+\frac{3}{2}}^\nu -x_{j+\frac{1}{2}}^*\right)-\omega _j\left(x_{j+\frac{1}{2}}^*-x_{j-\frac{1}{2}}^\nu \right)=0,\,\,\,j=1,\cdots, N-1, \end{aligned}$$

  (3.5)

  which results in $\left\{x_{j+\frac{1}{2}}^*\right\}$.

• Step 2 Ensure that the mesh remains logically structured by setting

  $$\begin{aligned} x_{j+\frac{1}{2}}^{**}=\min \left\{ \max \big (x_{j+\frac{1}{2}}^*,x_j^\nu \big ),x_{j+1}^\nu \right\} ,\,\,\,j=1,\cdots, N-1, \end{aligned}$$

  (3.6)

  where $x_j^\nu :=\big (x_{j-\frac{1}{2}}^\nu +x_{j+\frac{1}{2}}^\nu \big )/2$ and denote by $\Delta x_j^{**}:=x_{j+\frac{1}{2}}^{**}-x_{j-\frac{1}{2}}^{**}$.

• Step 3 Set $\sigma =0$. Prevent rapid change in the mesh size as well as the appearance of very small cells as follows. For each $j=1,\cdots, N-1$, if either

  $$\begin{aligned} \frac{\Delta x_{j+1}^{**}}{\Delta x_j^{**}}>3\quad \text{ or } \quad \frac{\Delta x_{j+1}^{**}}{\Delta x_j^{**}}<\frac{1}{3}\quad \text{ or }\quad \min \left( \Delta x_j^{**},\Delta x_{j+1}^{**}\right) <\Delta x_{\min }, \end{aligned}$$

  where $\Delta x_{\min }$ is a prescribed minimal allowed cell size, set

  $$\begin{aligned} x_{j+\frac{1}{2}}^{***}=\min \bigg \{\max \bigg (\frac{x_{j-\frac{1}{2}}^{**}+x_{j +\frac{3}{2}}^{**}}{2},x_j^\nu \bigg ),x_{j+1}^\nu \bigg \}\quad \text{ and }\quad \sigma =1. \end{aligned}$$

  (3.7)

• Step 4 If $\sigma =1$, then set

  $$\begin{aligned} x_{j+\frac{1}{2}}^{**}=x_{j+\frac{1}{2}}^{***},\,\,\,j=1,\cdots, N-1, \end{aligned}$$

  and go to Step 3; otherwise set

  $$\begin{aligned} x_{j+\frac{1}{2}}^{\nu +1}=x_{j+\frac{1}{2}}^{**},\,\, \,j=1,\cdots, N-1. \end{aligned}$$

Remark 3.1

We note that according to Algorithm 3.1 the mesh does not evolve purely according to the moving mesh equation (3.1) as its movement is adjusted in order to ensure better properties of the resulting mesh.

Remark 3.2

It immediately follows from (3.6) and (3.7) that

$$\begin{aligned} x_j^\nu \leqslant x_{j+\frac{1}{2}}^{\nu +1}\leqslant x_{j+1}^\nu , \end{aligned}$$

which, in turn, implies that

$$\begin{aligned} x_{j+\frac{1}{2}}^{\nu +1}\in \left(x_{j-\frac{1}{2}}^{\nu +1},x_{j+\frac{3}{2}}^{\nu +1}\right), \end{aligned}$$

so that the logical structure of the mesh indeed does not change.

3.1.2 Conservative Solution Projection

After obtaining the new mesh, we need to project the solution from the cells $C_j^\nu :=\left[x_{j-\frac{1}{2}}^\nu ,x_{j+\frac{1}{2}}^\nu \right]$ to the new cells $C_j^{\nu +1}:=\left[x_{j-\frac{1}{2}}^{\nu +1},x_{j+\frac{1}{2}}^{\nu +1}\right]$.

Let ${\overline{{\varvec{U}}}}_j^{\,\nu }$ and ${\overline{{\varvec{U}}}}_j^{\,\nu +1}$ be the cell averages over the cells $C_j^\nu$ and $C_j^{\nu +1}$, respectively, and denote the mesh shift by $\mu _{j+\frac{1}{2}}^{\nu +\frac{1}{2}}:=x_{j+\frac{1}{2}}^{\nu +1}-x_{j+\frac{1}{2}}^\nu$. We use the conservative solution projection step from [42] given by

$$\begin{aligned} \Delta x_j^{\nu +1}{\overline{{\varvec{U}}}}_j^{\,\nu +1}=\Delta x_j^\nu \,{\overline{{\varvec{U}}}}_j^{\,\nu }+\mu _{j+\frac{1}{2}}^{\nu +\frac{1}{2}}{\varvec{U}}_{j+\frac{1}{2}}^\nu -\mu _{j-\frac{1}{2}}^{\nu +\frac{1}{2}}{\varvec{U}}_{j-\frac{1}{2}}^\nu , \end{aligned}$$

where

$$\begin{aligned} {\varvec{U}}_{j+\frac{1}{2}}^\nu :=\left\{ \begin{array}{ll} {\varvec{U}}_{j+\frac{1}{2}}^+,&{}\quad \text{ if }\,\,\mu ^{\nu +\frac{1}{2}}_{j+\frac{1}{2}}>0,\\ {\varvec{U}}_{j+\frac{1}{2}}^-,&{}\quad \text{ if }\,\,\mu ^{\nu +\frac{1}{2}}_{j+\frac{1}{2}}<0, \end{array}\right. \end{aligned}$$

and ${\varvec{U}}_{j+\frac{1}{2}}^\pm$ are the point values reconstructed over the grid $C_j^\nu$ as described in Sect. 2.1.

3.2 2-D Algorithm

In this section, we present the AMM method for structured 2-D quadrilateral meshes. Assume that the computational domain $\Omega =[a,b]\times [c,d]$ is covered by the nonuniform mesh $\left\{{x_{j+\frac{1}{2},k+\frac{1}{2}}},{y_{j+\frac{1}{2},k+\frac{1}{2}}}\right\}$. We introduce the uniform rectangular logical mesh

$$\begin{aligned} \left\{ \left({\xi _{j+\frac{1}{2}}},{\eta _{k+\frac{1}{2}}}\right)\,\left| \,{\xi _{j+\frac{1}{2}}}=j\Delta \xi ,\,{\eta _{k+\frac{1}{2}}}=k\Delta \eta \right. \right\} ,\quad j=0,\cdots ,N,\,\,k=0,\cdots ,M, \end{aligned}$$

where $\Delta \xi =1/N$ and $\Delta \eta =1/M$ are the spatial scales in the $\xi$- and $\eta$-directions, respectively. Let us denote the one-to-one coordinate transformation from the logical domain to the computational one by

$$\begin{aligned} (x,y)=(x(\xi ,\eta ),y(\xi ,\eta )),\quad (\xi ,\eta )\in [0,1]\times [0,1], \end{aligned}$$

so that ${x_{j+\frac{1}{2},k+\frac{1}{2}}}=x\left({\xi _{j+\frac{1}{2}}},{\eta _{k+\frac{1}{2}}}\right)$ and ${y_{j+\frac{1}{2},k+\frac{1}{2}}}=y\left({\xi _{j+\frac{1}{2}}},{\eta _{k+\frac{1}{2}}}\right)$. We assume that $x(0,\eta )=a$ and $x(1,\eta )=b$ for all $\eta$ as well as $y(\xi ,0)=c$ and $y(\xi ,1)=d$ for all $\xi$.

3.2.1 Mesh Redistribution

As in the 1-D case, one can use a variational approach (see, e.g., [20]) to obtain the following system of MMPDEs:

$$\begin{aligned} (\omega {\varvec{z}}_\xi )_\xi +(\omega {\varvec{z}}_\eta )_\eta ={\varvec{0}}, \end{aligned}$$

(3.8)

where ${\varvec{z}}:=(x,y).$ Similarly to the 1-D case, the monitor function is chosen to be

$$\begin{aligned} \omega ({\varvec{U}})=1+\alpha \varphi \left( \left\| D{\varvec{U}}\right\| \right) , \end{aligned}$$

(3.9)

where D is a differential operator $\Big({\text{for example, one may use}}$ $D{\varvec{U}}=\nabla U^{(i)}$ or $D{\varvec{U}}=\Delta U^{(i)}$ for some component of ${\varvec{U}}$, where $\nabla :=\left(\frac{\partial }{\partial \xi },\frac{\partial }{\partial \eta }\right)$ and $\Delta :=\frac{\partial ^2}{\partial \xi ^2}+\frac{\partial ^2}{\partial \eta ^2}\Big)$. In this paper, we compute the required numerical derivatives at $(\xi _j,\eta _k)$ by using the second-order centered differences:

$$\begin{aligned} D{\varvec{U}}_{j,k}=\Delta U^{(i)}_{j,k}=\frac{\,{\overline{U}}^{\,(i)}_{j+1,k}-2\,{\overline{U}}^{\,(i)}_{j,k} +\,{\overline{U}}^{\,(i)}_{j-1,k}}{(\Delta \xi )^2}+ \frac{\,{\overline{U}}^{\,(i)}_{j,k+1}-2\,{\overline{U}}^{\,(i)}_{j,k} +\,{\overline{U}}^{\,(i)}_{j,k-1}}{(\Delta \eta )^2}. \end{aligned}$$

The smoothing filter $\varphi$ in (3.9) is employed to prevent the appearance of sharp gradient in the function $\xi =\xi (x,y)$. Similarly to the 1-D case, after $\varphi ^0_{j,k}=|D{\varvec{U}}_{j,k}|,\,j=0,\cdots ,N,\,k=0,\cdots ,M$ are obtained, they are smoothed out by averaging the values over the neighboring cells for each j, k for a prescribed number of iterations, that is, we introduce

$$\begin{aligned} \begin{aligned} \varphi ^{\ell +1}_{j,k}&=\frac{1}{4}\,\varphi ^\ell _{j,k}+ \frac{1}{8}\left( \varphi ^\ell _{j,k-1}+\varphi ^\ell _{j,k+1} +\varphi ^\ell _{j-1,k}+\varphi ^\ell _{j+1,k}\right) \\&\quad +\frac{1}{16}\left( \varphi ^\ell _{j-1,k-1}+\varphi ^\ell _{j+1,k-1} +\varphi ^\ell _{j-1,k+1}+\varphi ^\ell _{j+1,k+1}\right) ,\quad \ell =0,\cdots ,m-1, \end{aligned} \end{aligned}$$

and then set

$$\begin{aligned} \left( \varphi \left( \left\| D{\varvec{U}}\right\| \right) \right) _{j,k}:=\varphi ^m_{j,k}, \end{aligned}$$

(3.10)

which is used in (3.9). In our numerical experiments, we have taken $m=4$.

Finally, $\alpha$ in (3.9) is an intensity parameter needed to control the mesh concentration. In our computation, we choose $\alpha$ to be

$$\begin{aligned} \alpha =\bigg (\frac{1-\beta }{\beta |\Omega |}\iint_\Omega \varphi \left( \left\| D{\varvec{U}}\right\| \right) \,\mathrm{d}x\,\mathrm{d}y\bigg )^{-1}, \end{aligned}$$

where $\beta \in (0,1)$ is the prescribed fraction of mesh points to be concentrated at the “rough” areas of the solution and $|\Omega |$ is the total area of the computational domain.

Equipped with the monitor function $\omega$, we discretize the moving mesh equation (3.8) using the centered difference approximation, which results in the following linear algebraic system for the mesh points locations:

$$\begin{aligned}&\left\{ \begin{array}{l} x_{\frac{1}{2},{k+\frac{1}{2}}}=a,\,\,x_{N+\frac{1}{2},{k+\frac{1}{2}}}=b,\quad k=0,\cdots ,M\\ \displaystyle \frac{\omega _{j+1,k+\frac{1}{2}}(x_{j+\frac{3}{2},{k+\frac{1}{2}}}-{x_{j+\frac{1}{2},k+\frac{1}{2}}})-\omega _{j,k+\frac{1}{2}}({x_{j+\frac{1}{2},k+\frac{1}{2}}}-x_{{j-\frac{1}{2}},{k+\frac{1}{2}}})}{(\Delta \xi )^2}\quad \,\,\,\, j=1,\cdots ,N-1,\\ \displaystyle +\frac{\omega _{{j+\frac{1}{2}},k+1}(x_{{j+\frac{1}{2}},k+\frac{3}{2}}-{x_{j+\frac{1}{2},k+\frac{1}{2}}})-\omega _{j+\frac{1}{2},k}({x_{j+\frac{1}{2},k+\frac{1}{2}}}-x_{{j+\frac{1}{2}},{k-\frac{1}{2}}})}{(\Delta \eta )^2}=0,\quad \,k=0,\cdots ,M,\\ x_{{j+\frac{1}{2}},-\frac{1}{2}}=x_{{j+\frac{1}{2}},\frac{3}{2}},\,\,x_{{j+\frac{1}{2}},M+\frac{3}{2}}=x_{{j+\frac{1}{2}},M-\frac{1}{2}},\quad j=0,\cdots ,N, \end{array}\right. \\&\left\{ \begin{array}{l} y_{{j+\frac{1}{2}},\frac{1}{2}}=c,\,\,y_{{j+\frac{1}{2}},M+\frac{1}{2}}=d,\quad j=0,\cdots ,N\\ \displaystyle \frac{\omega _{j+1,k+\frac{1}{2}}(y_{j+\frac{3}{2},{k+\frac{1}{2}}}-{y_{j+\frac{1}{2},k+\frac{1}{2}}})-\omega _{j,k+\frac{1}{2}}({y_{j+\frac{1}{2},k+\frac{1}{2}}}-y_{{j-\frac{1}{2}},{k+\frac{1}{2}}})}{(\Delta \xi )^2}\quad \,\,\,\, j=0,\cdots ,N,\\ \displaystyle +\frac{\omega _{{j+\frac{1}{2}},k+1}(y_{{j+\frac{1}{2}},k+\frac{3}{2}}-{y_{j+\frac{1}{2},k+\frac{1}{2}}})-\omega _{j+\frac{1}{2},k}({y_{j+\frac{1}{2},k+\frac{1}{2}}}-y_{{j+\frac{1}{2}},{k-\frac{1}{2}}})}{(\Delta \eta )^2}=0,\quad \,k=1,\cdots ,M-1,\\ y_{-\frac{1}{2},{k+\frac{1}{2}}}=y_{\frac{3}{2},{k+\frac{1}{2}}},\,\,y_{N+\frac{3}{2},{k+\frac{1}{2}}}=y_{N-\frac{1}{2},{k+\frac{1}{2}}},\quad k=0,\cdots ,M, \end{array}\right. \end{aligned}$$

where $\omega _{j,k+\frac{1}{2}}:=(\omega _{j,k}+\omega _{j,k+1})/2$ and $\omega _{j+\frac{1}{2},k}:=(\omega _{j,k}+\omega _{j+1,k})/2$, and then proceed similarly to the 1-D case and evolve the mesh according to the following iterative algorithm.

Algorithm 3.2

(Adjusted 2-D Mesh Movement)

• Step 1 Take one Jacobi iteration sweep:

  $$\left\{\begin{aligned} \begin{aligned}&\frac{\omega _{j+1,k+\frac{1}{2}}(x_{j+\frac{3}{2},{k+\frac{1}{2}}}-x_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*)- \omega _{j,k+\frac{1}{2}}(x_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*-x_{{j-\frac{1}{2}},{k+\frac{1}{2}}})}{(\Delta \xi )^2} \quad j=1,\cdots ,N-1,\\&+\frac{\omega _{{j+\frac{1}{2}},k+1}(x_{{j+\frac{1}{2}},k+\frac{3}{2}}-x_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*)- \omega _{j+\frac{1}{2},k}(x_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*-x_{{j+\frac{1}{2}},{k-\frac{1}{2}}})}{(\Delta \eta )^2}=0,\quad k=0,\cdots ,M,\\&\frac{\omega _{j+1,k+\frac{1}{2}}(y_{j+\frac{3}{2},{k+\frac{1}{2}}}-y_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*)- \omega _{j,k+\frac{1}{2}}(y_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*-y_{{j-\frac{1}{2}},{k+\frac{1}{2}}})}{(\Delta \xi )^2} \quad j=0,\cdots ,N,\\&+\frac{\omega _{{j+\frac{1}{2}},k+1}(y_{{j+\frac{1}{2}},k+\frac{3}{2}}-y_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*)- \omega _{j+\frac{1}{2},k}(y_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*-y_{{j+\frac{1}{2}},{k-\frac{1}{2}}})}{(\Delta \eta )^2}=0,\quad k=1,\cdots ,M-1, \end{aligned} \end{aligned}\right.$$

  (3.11)

  which results in $\left\{{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*\right\}=\left \{\left(x_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*,y_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*\right)\right \}$.

• Step 2 Ensure that the mesh remains logically structured by replacing ${\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*$ with

  $$\begin{aligned} {\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{**}=\left(1-\tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}\right){\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^\nu +\tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*, \end{aligned}$$

  (3.12)

  which will be inside the convex hull ${{{\mathcal {C}}}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}:= {{\mathrm{Conv}}}\big ({\varvec{z}}_{j+1,{k+\frac{1}{2}}}^\nu ,\,{\varvec{z}}_{j,{k+\frac{1}{2}}}^\nu , \,{\varvec{z}}_{{j+\frac{1}{2}},k+1}^\nu ,\,{\varvec{z}}_{{j+\frac{1}{2}},k}^\nu \big )$ provided

  $$\begin{aligned} \tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}= \min \left\{ \max _{\tau \in [0,1]}\left\{ \tau \,|\,(1-\tau ) {\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^\nu +\tau {\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*\in {{{\mathcal {C}}}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}\right\} ,1\right\} \end{aligned}$$

  (3.13)

  and denote the new cells based on the grid $\left\{{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{**}\right\}$ by $C_{j,k}^{**}$; see Fig. 3.

• Step 3 Set $\sigma =0$. Prevent rapid change in the cell size as well as the appearance of very small cells as follows. For each $({j+\frac{1}{2}},{k+\frac{1}{2}})$, if either

  $$\begin{aligned}&\frac{\max \{|C^{**}_{j,k}|,|C^{**}_{j+1,k}|,|C^{**}_{j,k+1}|,|C^{**}_{j+1,k+1}|\}}{\min \{|C^{**}_{j,k}|,|C^{**}_{j+1,k}|,|C^{**}_{j,k+1}|,|C^{**}_{j+1,k+1}|\}}>9\,\,\text{ or }\\&\quad \min \{|C^{**}_{j,k}|,|C^{**}_{j+1,k}|,|C^{**}_{j,k+1}|,|C^{**}_{j+1,k+1}|\}<|C|_{\min }, \end{aligned}$$

  where $|C|_{\min }$ is a prescribed minimal allowed cell size, set

  $$\begin{aligned} {\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{***}=(1-\tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}){\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^\nu +\tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}{{\widehat{{\varvec{z}}}}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{\,**}\quad \text{ and }\quad \sigma =1. \end{aligned}$$

  (3.14)

  Here, ${{\widehat{{\varvec{z}}}}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{\,**}:=\big ({\varvec{z}}^{**}_{j,{k+\frac{1}{2}}}+{\varvec{z}}^{**}_{j+1,{k+\frac{1}{2}}}+{\varvec{z}}^{**}_{{j+\frac{1}{2}},k}+{\varvec{z}}^{**}_{{j+\frac{1}{2}},k+1}\big )/4$ and $\tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}$ is computed similarly to (3.13):

  $$\begin{aligned} \tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}= \min \left\{ \max _{\tau \in [0,1]}\left\{ \tau \,|\,(1-\tau ){\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^\nu +\tau {{\widehat{{\varvec{z}}}}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{\,**}\in {{{\mathcal {C}}}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}\right\} ,1\right\} . \end{aligned}$$

• Step 4 If $\sigma =1$, then set

  $$\begin{aligned} {\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{**}={\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{***}, \end{aligned}$$

  and go to Step 3; otherwise, set

  $$\begin{aligned} {\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{\nu +1}={\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{**}. \end{aligned}$$

Fig. 3

Modifying the grid ${\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^*$: $\tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}<1$ (left) vs. $\tau _{{j+\frac{1}{2}},{k+\frac{1}{2}}}=1$ (right) cases

Remark 3.3

We note that according to Algorithm 3.2 the mesh does not evolve purely according to the MMPDE (3.8) as its movement is adjusted in order to ensure better properties of the resulting mesh.

3.2.2 Conservative Solution Projection

After obtaining the new mesh, we need to project the solution from the cells $C^\nu _{j,k}$, whose vertices are ${\varvec{z}}_{j\pm \frac{1}{2},k\pm \frac{1}{2}}^\nu$, to the new cells $C^{\nu +1}_{j,k}$ with the vertices ${\varvec{z}}_{j\pm \frac{1}{2},k\pm \frac{1}{2}}^{\nu +1}$.

Let ${\overline{{\varvec{U}}}}^{\,\nu }_{j,k}$ and ${\overline{{\varvec{U}}}}^{\,\nu +1}_{j,k}$ be the cell averages over the cells $C^\nu _{j,k}$ and $C^{\nu +1}_{j,k}$, respectively, see Fig. 4, and denote the signed areas of the quadrilaterals ${\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^\nu {\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}^\nu {\varvec{z}}_{{j+\frac{1}{2}},{k-\frac{1}{2}}}^{\nu +1}{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{\nu +1}$ and ${\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^\nu {\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}^\nu {\varvec{z}}_{{j-\frac{1}{2}},{k+\frac{1}{2}}}^{\nu +1}{\varvec{z}}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}^{\nu +1}$ by $\mu ^{\nu +\frac{1}{2}}_{j+\frac{1}{2},k}$ and $\mu ^{\nu +\frac{1}{2}}_{j,k+\frac{1}{2}}$, respectively:

$$\begin{aligned} \begin{aligned} \mu ^{\nu +\frac{1}{2}}_{j+\frac{1}{2},k}&=\frac{1}{2}\left[ \big (x_{j+\frac{1}{2},k-\frac{1}{2}} ^{\nu +1}-x_{j+\frac{1}{2},k+\frac{1}{2}}^\nu \big ) \big (y_{j+\frac{1}{2},k+\frac{1}{2}}^{\nu +1}-y_{j+\frac{1}{2},k-\frac{1}{2}}^\nu \big )\right. \\&\quad \left. -\big (x_{j+\frac{1}{2},k+\frac{1}{2}}^{\nu +1}-x_{j+\frac{1}{2},k-\frac{1}{2}}^\nu \big ) \big (y_{j+\frac{1}{2},k-\frac{1}{2}}^{\nu +1}-y_{j+\frac{1}{2},k+\frac{1}{2}}^\nu \big )\right] ,\\ \mu ^{\nu +\frac{1}{2}}_{j,k+\frac{1}{2}}&=\frac{1}{2}\left[ \big (x_{j+\frac{1}{2},k +\frac{1}{2}}^{\nu +1}-x_{j-\frac{1}{2},k+\frac{1}{2}}^\nu \big ) \big (y_{j-\frac{1}{2},k+\frac{1}{2}}^{\nu +1}-y_{j+\frac{1}{2},k+\frac{1}{2}}^\nu \big )\right. \\&\quad \left. -\big (x_{j-\frac{1}{2},k+\frac{1}{2}}^{\nu +1}-x_{j+\frac{1}{2},k+\frac{1}{2}}^\nu \big ) \big (y_{j+\frac{1}{2},k+\frac{1}{2}}^{\nu +1}-y_{j-\frac{1}{2},k+\frac{1}{2}}^\nu \big )\right] . \end{aligned} \end{aligned}$$

Fig. 4

The shift of the cell $C_{j,k}^\nu$ (solid line) to $C_{j,k}^{\nu +1}$ (dashed line)

We use the conservative solution projection step from [42] given by

$$\begin{aligned} |{C}_{j,k}^{\nu +1}|\,{\overline{{\varvec{U}}}}_{j,k}^{\,\nu +1}=|C_{j,k}^\nu |\,{\overline{{\varvec{U}}}}^{\,\nu }_{j,k} +\mu ^{\nu +\frac{1}{2}}_{j+\frac{1}{2},k}{\varvec{U}}^\nu _{j+\frac{1}{2},k}-\mu ^{\nu +\frac{1}{2}}_{j-\frac{1}{2},k}{\varvec{U}}^\nu _{j-\frac{1}{2},k}+\mu ^{\nu +\frac{1}{2}}_{j,k+\frac{1}{2}}{\varvec{U}}^\nu _{j,k+\frac{1}{2}} -\mu ^{\nu +\frac{1}{2}}_{j,k-\frac{1}{2}}{\varvec{U}}^\nu _{j,k-\frac{1}{2}}, \end{aligned}$$

where

$$\begin{aligned} {\varvec{U}}^\nu _{j+\frac{1}{2},k}:=\left\{ \begin{array}{ll} {\varvec{U}}_{j+\frac{1}{2},k}^+,&{}\quad \text{ if }\,\,\mu _{j+\frac{1}{2},k}^{\nu +\frac{1}{2}}>0,\\ {\varvec{U}}_{j+\frac{1}{2},k}^-,&{}\quad \text{ if }\,\,\mu _{j+\frac{1}{2},k}^{\nu +\frac{1}{2}}<0,\end{array}\right. \quad {\varvec{U}}^\nu _{j,k+\frac{1}{2}}:=\left\{ \begin{array}{lc} {\varvec{U}}_{j,k+\frac{1}{2}}^+,&{}\text{ if }\,\,\mu _{j,k+\frac{1}{2}}^{\nu +\frac{1}{2}}>0,\\ {\varvec{U}}_{j,k+\frac{1}{2}}^-,&{}\text{ if }\,\,\mu _{j,k+\frac{1}{2}}^{\nu +\frac{1}{2}}<0,\end{array}\right. \end{aligned}$$

and ${\varvec{U}}_{j+\frac{1}{2},k}^\pm$ and ${\varvec{U}}_{j,k+\frac{1}{2}}^\pm$ are the point values reconstructed over the grid $C_{j,k}^\nu$ as described in Sect. 2.2.

3.3 Solution Algorithm

In this section, we summarize the 1-D and 2-D AMM central-upwind solution algorithm.

Algorithm 3.3

(AMM Central-Upwind Scheme)

• Step 1 Set $t:=0$.

• Step 2 Given the initial condition, we adapt the computational mesh using the iterative method described in Sects. 3.1 and 3.2. These iterations require a starting mesh (for $\nu =0$ at the initial time moment when the mesh from previous time step is unavailable). We take the starting mesh to be uniform in both 1-D and 2-D cases.

• Step 3 Based on the solution at a given time level, compute $\Delta t$ according to the CFL condition (2.17) or (2.18).

• Step 4 Use the central-upwind scheme presented in Sect. 2 to evolve the solution ${\varvec{U}}(t)$ represented in terms of its cell averages over a current mesh to the new time level $t+\Delta t$. We denote the obtained solution by ${\varvec{V}}(t+\Delta t)$.

• Step 5 Based on ${\varvec{V}}(t+\Delta t)$, implement the AMM procedure described in Sects. 3.1 and 3.2 to generate a new finite-volume mesh and the corresponding cell averages. The resulting solution is denoted by ${\varvec{U}}(t+\Delta t)$.

• Step 6 Set $t:=t+\Delta t$.

• Step 7 If the final computational time is not reached yet, go to Step 3.

Remark 3.4

We set up the stopping criteria for the AMM iterations in Sects. 3.1 and 3.2 to be ${\max\limits_{j}}\left\{\left|x^{\nu +1}_{j+\frac{1}{2}}-x^\nu _{j+\frac{1}{2}}\right|\right\}{\text{tol}}$ and ${\max\limits_{j,k}}\left\{\left\Vert {\varvec{z}}^{\nu +1}_{{j+\frac{1}{2}},{k+\frac{1}{2}}}-{\varvec{z}}^\nu _{{j+\frac{1}{2}},{k+\frac{1}{2}}}\right\Vert \right\}<{\text{tol}}$, respectively. However, in practice, since the mesh does not typically change much in one evolution time step (Step 4 of Algorithm 3.3), we improve the efficiency of the resulting AMM method by stopping the iteration process after several iterations even if the required tolerance has not been reached. In our numerical experiments, the upper bound on the number of iterations has been set to 4.

4 Euler Equation of Gas Dynamics—Numerical Examples

In this section, we apply the developed AMM central-upwind schemes to the 1-D and 2-D Euler equations of gas dynamics. We compare the obtained results with the ones computed by the central-upwind scheme from [29] implemented on uniform meshes. These examples clearly demonstrate the ability of the proposed schemes to capture the “rough” parts of the computed solutions with high resolution.

In all of the examples in this section, we use the minmod parameter $\psi =1.3$ and apply the positivity-preserving correction to the reconstructions of the density and total energy.

4.1 Example 1—1-D Riemann Problem

We numerically solve the 1-D Euler Equations of gas dynamics:

$$\begin{aligned} \frac{\partial }{\partial t}\left( \begin{array}{l} \rho \\ {{{\mathcal {M}}}}\\ E\end{array}\right) + \frac{\partial }{\partial x} \left( \begin{array}{c}{{{\mathcal {M}}}}\\ \rho u^2+p\\ u(E+p) \end{array}\right) ={\varvec{0}}, \end{aligned}$$

(4.1)

where $\rho (x,t)$ is the density, u(x, t) is the velocity, ${{{\mathcal {M}}}}(x,t)=\rho (x,t)u(x,t)$ is the momentum, E(x, t) is the total energy, p(x, t) is the pressure satisfying the equation of state

$$\begin{aligned} p=p(\rho ,{{{\mathcal {M}}}},E)=(\gamma -1)\left( E-\frac{{{{\mathcal {M}}}}^2}{2\rho }\right) , \end{aligned}$$

(4.2)

and $\gamma$ is a specific heat ratio taken to be 1.4.

We consider the Riemann problem studied in [26] with the initial conditions

$$\begin{aligned} (\rho (x,0),u(x,0),p(x,0))=\left\{ \begin{array}{ll} (1,-19.597\,\,45,1\,\,000),&{}\quad \text{ if }\,\,x<0.3,\\ (1,-19.597\,\,45,0.01),&{}\quad \text{ if }\,\,x>0.3, \end{array}\right. \end{aligned}$$

and compute the solution until the final time $T=0.012$.

We use the computational domain $[-0.5,0.5]$, which is initially split into $N_{\mathrm{AMM}}=100$ uniform finite-volume cells, and compute the solution by the proposed AMM central-upwind scheme using two different values of the mesh concentration parameter ($\beta =0.3$ and 0.6) and minimal allowed cell size ($\Delta x_{\min }=1/(10N_{\mathrm{AMM}})$ and $1/(100N_{\mathrm{AMM}})$).

We first use $D{\varvec{U}}=\rho _{\xi \xi }$ to compute the monitor function in (3.2) (except for the mesh initialization Step 2 in Algorithm 3.3, in which we have used $D{\varvec{U}}=E_{\xi \xi }$ since $\rho$ is initially constant). The obtained densities together with the time-space distributions of mesh cells are plotted in Figs. 5 and 6. As one can see, when $\Delta x_{\min }=1/(10N_{\mathrm{AMM}})$ is relatively large (Fig. 5) increasing $\beta$ from 0.3 to 0.6 does not lead to a significant improvement in the resolution of either contact or shock waves. However, when a much smaller $\Delta x_{\min }=1/(100N_{\mathrm{AMM}})$ is used, one may observe (Fig. 6) that as $\beta$ increases, more mesh points are concentrated near the shock and contact waves. Also notice that the rarefaction “corners” are slightly better captured as $\beta$ increases. At the same time, the use of larger $\beta$ leads to the appearance of smaller cells, which cause the time steps to become smaller and thus the CPU time increases from 0.85 s to 0.92 s when $\Delta x_{\min }=1/(10N_{\mathrm{AMM}})$ and from 1.12 s to 1.82 s when $\Delta x_{\min }=1/(100N_{\mathrm{AMM}})$. We then compare the AMM results with the solution computed using uniform meshes of the sizes that require about the same CPU times, namely, with $N_{\mathrm{unif}}=r280$, 320, 550 and 900, respectively. The uniform results (densities) are shown in the same Figs. 5 and 6, where they are compared with the corresponding AMM solutions. As one can see, the AMM central-upwind scheme achieves much higher resolution of both the contact and shock waves.

Fig. 5

Example 1: density profiles (top row) computed using the uniform and adaptive meshes using the same CPU times. The AMM central-upwind scheme was used with $\Delta x_{\min }=1/(10N_{\mathrm{AMM}})$, the monitor function $\omega =1+\alpha \varphi (|\rho _{\xi \xi }|)$ and different values of $\beta =0.3$ (left) and 0.6 (right). The corresponding time-space distributions of mesh cells are shown in the bottom row

Fig. 6

Example 1: same as Fig. 5, but with $\Delta x_{\min }=1/(100N_{\mathrm{AMM}})$

Remark 4.1

We note that the physical quantities $\rho$, E and p should be positive at all times. In particular, the reconstructed point values of $\rho$, E and p at the cell interfaces should remain positive. The positivity of $\rho$ and E is guaranteed by the use of the positivity-preserving correction, while the positivity of p is achieved by employing the positivity-preserving limiter proposed in [49].

This limiter is applied as follows. After the reconstruction step described in Sect. 2.1, we obtain the point values $\rho _{j+\frac{1}{2}}^\pm$, ${{{\mathcal {M}}}}_{j+\frac{1}{2}}^\pm$ and $E_{j+\frac{1}{2}}^\pm$ for all j and then use the equation of state (4.2) to compute the corresponding point values of the pressure, $p_{j+\frac{1}{2}}^\pm$. If in a certain cell $C_j$, either $p_{j+\frac{1}{2}}^-<p_\varepsilon$ or $p_{j-\frac{1}{2}}^+<p_\varepsilon$, where $p_\varepsilon$ is a small positive number (taken to be $10^{-12}$ in all of our numerical experiments), we replace the linear piece (2.2) in this cell with a less oscillatory one:

$$\begin{aligned} \tau _j({\varvec{{{\mathcal {P}}}}}_j(x,t)-{\overline{{\varvec{U}}}}_j)+{\overline{{\varvec{U}}}}_j. \end{aligned}$$

(4.3)

Here, $\tau _j=\min \left\{\tau _{j+\frac{1}{2}}^-,\tau _{j-\frac{1}{2}}^+\right\}$, in which

$$\begin{aligned} \tau _{j+\frac{1}{2}}^-=\left\{ \begin{array}{ll} 1,&{}\quad \text{ if }\,\,p_{j+\frac{1}{2}}^->p_\varepsilon ,\\ {{\hat{\tau }}}_{j+\frac{1}{2}}^-,&{}\quad \text{ otherwise }, \end{array}\right. \quad \tau _{j-\frac{1}{2}}^+= \left\{ \begin{array}{ll} 1,&{}\quad \text{ if }\,\,p_{j-\frac{1}{2}}^+>p_\varepsilon ,\\ {{\hat{\tau }}}_{j-\frac{1}{2}}^+,&{}\quad \text{ otherwise }, \end{array}\right. \end{aligned}$$

where ${{\hat{\tau }}}_{j+\frac{1}{2}}^-\in (0,1)$ and ${{\hat{\tau }}}_{j-\frac{1}{2}}^+\in (0,1)$ are the roots of the quadratic equations

$$\begin{aligned} (\gamma -1)\left[ (1-\tau )\,{\overline{E}}_j+\tau E_{j+\frac{1}{2}}^-- \frac{\big ((1-\tau )\,{\overline{{{\mathcal {M}}}}}_j +\tau {{{\mathcal {M}}}}_{j+\frac{1}{2}}^-\big )^2}{2\big ((1-\tau ) \,{\overline{\rho }}_j+\tau \rho _{j+\frac{1}{2}}^-\big )}\right] =p_\varepsilon \end{aligned}$$

and

$$\begin{aligned} (\gamma -1)\left[ (1-\tau )\,{\overline{E}}_j+\tau E_{j-\frac{1}{2}}^+- \frac{\big ((1-\tau )\,{\overline{{{\mathcal {M}}}}}_j +\tau {{{\mathcal {M}}}}_{j-\frac{1}{2}}^+\big )^2}{2\big ((1-\tau )\,{\overline{\rho }}_j+\tau \rho _{j-\frac{1}{2}}^+ \big )}\right] =p_\varepsilon , \end{aligned}$$

respectively. We then recompute $\rho _{j+\frac{1}{2}}^\pm$, ${{{\mathcal {M}}}}_{j+\frac{1}{2}}^\pm$ and $E_{j+\frac{1}{2}}^\pm$ in the cell $C_j$ using the modified reconstruction (4.3).

We note that in the 2-D case, the positivity of the reconstructed values of p can be enforced in a similar manner.

4.2 Example 2—2-D Riemann Problem

In this example, we numerically solve the 2-D Euler equations of gas dynamics:

$$\begin{aligned} \frac{\partial }{\partial t}\left( \begin{array}{l}\rho \\ {{{\mathcal {M}}}}\\ {{{\mathcal {N}}}}\\ E\end{array}\right) + \frac{\partial }{\partial x}\left( \begin{array}{c}{{{\mathcal {M}}}}\\ \rho u^2+p\\ \rho uv\\ u(E+p)\end{array}\right) + \frac{\partial }{\partial y}\left( \begin{array}{c}{{{\mathcal {N}}}}\\ \rho uv\\ \rho v^2+p\\ v(E+p)\end{array}\right) ={\varvec{0}}, \end{aligned}$$

(4.4)

where $\rho (x,y,t)$ is the density, u(x, y, t) and v(x, y, t) are the x- and y-velocities, ${{{\mathcal {M}}}}(x,y,t):=\rho (x,y,t)u(x,y,t)$ and ${{{\mathcal {N}}}}(x,y,t):=\rho (x,y,t)v(x,y,t)$ are the x- and y-momenta, E(x, y, t) is the total energy, p(x, y, t) is the pressure satisfying the equation of state

$$\begin{aligned} p=p(\rho ,{{{\mathcal {M}}}},{{{\mathcal {N}}}},E)=(\gamma -1) \left( E-\frac{{{{\mathcal {M}}}}^2+{{{\mathcal {N}}}}^2}{2\rho }\right) , \end{aligned}$$

(4.5)

and $\gamma$ is a specific heat ratio taken to be 1.4.

We consider the 2-D Riemann problem with the initial condition corresponding to Configuration 7 from [29]:

$$\begin{aligned} (\rho ,p,u,v)=\left\{ \begin{array}{ll} (1,1,0.1,0.1),&{}\quad \text{ if }\,\, x>0.5,\,y>0.5,\\ (0.519\,\,7,0.4,-0.625\,\,9,0.1),&{}\quad \text{ if }\,\, x<0.5,\,y>0.5,\\ (0.8,0.4,0.1,0.1),&{}\quad \text{ if }\,\, x<0.5,\,y<0.5,\\ (0.519\,\,7,0.4,0.1,-0.625\,\,9),&{}\quad \text{ if }\,\, x>0.5,\,y<0.5, \end{array} \right. \end{aligned}$$

and run our simulations until the final time $T=0.25$. We take the computational domain $[0,1]\times [0,1]$, which is initially split into $100\times 100$ uniform finite-volume cells for the AMM calculations.

We first compute the solution by the proposed AMM central-upwind scheme using $D{\varvec{U}}=\Delta \rho$ in the monitor function (3.9) and the minimal allowed cell size $|C|_{\min }=1/(1\,\,000\times 1\,\,000)$. The densities computed using the concentration parameters $\beta =0.6$ and $\beta =0.9$ and the corresponding final time mesh distributions are presented in Figs. 7 (left and middle) and 8 (left and middle), respectively. As one can see, the mesh is concentrated in the contact and shock wave areas with a substantially larger number of mesh cells being moved there in the case of the larger $\beta =0.9$. We then compare the AMM results with the ones computed by the central-upwind scheme using uniform meshes of the sizes that require about the same CPU times, namely, with $210\times 210$ (Fig. 7, right) and $260\times 260$ (Fig.  8, right) uniform cells. It can be observed that both the contact and shock waves are more sharply resolved using the AMM approach.

Fig. 7

Example 2: density profiles computed using the adaptive mesh with $\beta =0.6$ (left) and $210\times 210$ uniform mesh (right), and the final time mesh distribution (middle)

Fig. 8

Example 2: density profiles computed using the adaptive mesh with $\beta =0.9$ (left) and $260\times 260$ uniform mesh (right), and the final time mesh distribution (middle)

5 Granular Hydrodynamics—Numerical Examples

In this section, we apply the AMM central-upwind schemes for the 1-D and 2-D granular hydrodynamics equations, which are used to model granular gases; see, e.g., [8, 14, 34, 38, 39] and references therein. Though this model has recently attracted a great attention from physicists, no rigorous mathematical analysis of the granular hydrodynamics equations is available, especially in the multidimensional case. In contrast to ordinary molecular gases, granular gases cool spontaneously because of the inelastic collisions between the particles. The inelasticity of the collisions generally causes the granular gas to form dense clusters.

The 1-D granular hydrodynamics equations are the 1-D Euler equations of gas dynamics (4.1), (4.2) with an additional inelastic energy loss term:

$$\begin{aligned} \frac{\partial }{\partial t}\left( \begin{array}{l}\rho \\ {{{\mathcal {M}}}}\\ E\end{array}\right) + \frac{\partial }{\partial x}\left( \begin{array}{c}{{{\mathcal {M}}}}\\ \rho u^2+p\\ u(E+p)\end{array}\right) = \left( \begin{array}{c}0\\ 0\\ -\Lambda \rho ^{\frac{1}{2}}p^{\frac{3}{2}}\end{array}\right) , \end{aligned}$$

(5.1)

where $\Lambda$ is a positive constant. Similarly, the 2-D granular hydrodynamics equations are the 2-D Euler equations of gas dynamics (4.4), (4.5) with the same inelastic energy loss term:

$$\begin{aligned} \frac{\partial }{\partial t}\left( \begin{array}{l}\rho \\ {{{\mathcal {M}}}}\\ {{{\mathcal {N}}}}\\ E\end{array}\right) + \frac{\partial }{\partial x}\left( \begin{array}{c}{{{\mathcal {M}}}}\\ \rho u^2+p\\ \rho uv\\ u(E+p)\end{array}\right) + \frac{\partial }{\partial y}\left( \begin{array}{c}{{{\mathcal {N}}}}\\ \rho uv\\ \rho v^2+p\\ v(E+p)\end{array}\right) = \left( \begin{array}{c}0\\ 0\\ 0\\ - \Lambda \rho ^{\frac{1}{2}}p^{\frac{3}{2}}\end{array}\right) . \end{aligned}$$

(5.2)

A characteristic feature of the solutions of (5.1), (4.2) and (5.2), (4.5) is a formation of finite-time singularities, which are different from the shock discontinuities arising in the Euler equations of gas dynamics (4.1), (4.2) and (4.4), (4.5) based on the assumption of elastic interaction between the particles. In particular, the granular gas singularities contain the density blowup, which signals the formation of close-packed clusters. These singularities can be accumulated in points or distributed along a curve (see [38] for the simplest analytical ansatz demonstrating finite-time singularities formation). Moreover, the structure of granular hydrodynamics equations supports the existence of $\delta$-type singularities in the density component. Capturing such solutions numerically is a challenging task and the AMM approach may become a key factor in achieving high resolution of spiky solutions in an efficient and computationally affordable manner.

We apply the developed AMM central-upwind schemes to the systems (5.1), (4.2) and (5.2), (4.5) in a straightforward manner. Namely, we approximate the cell averages of the source terms using the midpoint rule, which results in the following approximations of (2.6) and (2.16):

$$\begin{aligned} {\overline{S}}^{\,(3)}_j=-\Lambda \,{\overline{\rho }}_j^{\,\frac{1}{2}}p_j^{\frac{3}{2}} \quad \text{ and }\quad {\overline{S}}^{\,(4)}_{j,k}=-\Lambda \,{\overline{\rho }}_{j,k}^{\,\frac{1}{2}}\,p_{j,k}^{\frac{3}{2}}, \end{aligned}$$

respectively.

In all of our numerical experiments reported below, we take $\Lambda =10$. In Examples 3 and 4, we use the minmod parameter $\psi =1.3$, while in Example 5, we use both $\psi =1.3$ and a more dissipative minmod reconstruction with $\psi =1$. As in Sect. 4, we apply the positivity-preserving correction to the reconstructions of the density and total energy.

5.1 Example 3—1-D Case

In this example, we numerically solve the 1-D granular hydrodynamics system (5.1), (4.2) on the interval $[-5,5]$ subject to the following initial data:

$$\begin{aligned} \rho (x,0)\equiv 1,\quad u(x,0)\equiv 0,\quad p(x,0)=2-\frac{1}{1+16x^2}, \end{aligned}$$

(5.3)

and the homogeneous Neumann boundary conditions.

Analyzing the initial value problem (5.1), (4.2), (5.3), one can see that the initial minimum of pressure at $x=0$ triggers the development of negative velocity derivative there, which, in turn, causes the increase of the density at the origin. Then, unlike the case of the Euler equations of gas dynamics (4.1), (4.2), the entropy $\ln (p/\rho ^\gamma )$ is not conserved along a sound characteristics $u=0$, but decreases to zero within finite or infinite time. This suggests a formation of spiky structure in the density component along the sound characteristics, that is, at the point $x=0$. To verify this and to study the type of a possible singularity, we first compute the solution at time $t=5$ using the central-upwind scheme on three uniform meshes with $N=201$, 401 and 801 cells. The obtained densities, shown in Fig. 9 (left), indicate that by this time the singularity could have already formed since the maximum of the density increases as the mesh is refined. We then apply the AMM central-upwind scheme with $\beta =0.3$, and minimal allowed cell size $\Delta x_{\min }=1/(1\,000N_{\mathrm{AMM}})$, where $N_{\mathrm{AMM}}=201$ and the monitor function (3.2) with $D{\varvec{U}}=\rho _{\xi \xi }$ (except for the mesh initialization Step 2 in Algorithm 3.3, in which we have used $D{\varvec{U}}=E_{\xi \xi }$ since $\rho$ is initially constant) to the studied IBVP. As one can see in Fig. 9 (middle), the obtained density has a much larger maximum value than its uniform grid counterparts. The time-space distribution of the mesh cells, shown in Fig. 9 (right), suggests that using the AMM approach is crucial in achieving a high resolution of the developed singularity. The velocity and pressure computed by the AMM central-upwind scheme are shown in Fig. 10. We note that the velocity has a sharp gradient at $x=0$ and the pressure values are much smaller than the initial ones due to the energy decay caused by the source term in the third equation in (5.1).

Fig. 9

Example 3: densities computed on the uniform meshes (left) and using the AMM approach (middle) and the corresponding time-space distributions of mesh cells (right)

Fig. 10

Example 3: velocity (left) and pressure (right) computed using the AMM central-upwind scheme

Next, we further study the behavior of both the uniform mesh and AMM solutions by comparing the time evolution of ${\max\limits_{x}}\rho ^{N+1}(x,t)$ (the upper index indicates the number of finite-volume cells used), computed using different values of N. The obtained results are shown in Fig. 11 (left). As one can clearly see, the central-upwind AMM scheme clearly outperforms its uniform counterpart. It is also instructive to compare the ratios ${\max\limits_{x}}\rho ^{2N+1}(x,t)/{\max\limits_{x}}\rho ^{N+1}(x,t)$ for the uniform grid solutions with different values of N. The obtained results, shown in Fig. 11 (right), can be used as an indicator of the nature of the developed singularity. Indeed, after the time $t\approx 3$, the computed ratios are getting close to 2, which indicates that at large times the solution may have a $\delta$-type singularity at $x=0$ since the maximum of such solutions captured by finite-volume methods on uniform grids is typically proportional to $1/\Delta x$.

Fig. 11

Example 3: $\mathop {\max\limits_{x}}\rho (x,t)$ as a function of time for the uniform (with 10 001, 20 001 and 40 001 cells) and AMM (with 201 initially uniform cells) computations (left) and $\mathop {\max\limits_{x}}\rho ^{2N+1}(x,t)/{\max\limits_{x}}\rho ^{N+1}(x,t)$ as a function of time for the sequence of uniform grids with $N=5\,\,000$, 10 000 and 20 000 (right)

5.2 Example 4—Radially Symmetric Data

Next, we consider the 2-D granular hydrodynamics system (5.2), (4.5) on the square domain $[-5,5]\times [-5,5]$ subject to the radially symmetric initial data, which are a modified version of the 1-D initial data (5.3),

$$\begin{aligned} \rho (x,y,0)\equiv 1,\quad u(x,y,0)\equiv v(x,y,0)\equiv 0,\quad p(x,y,0)=2-\frac{1}{1+16(x^2+y^2)}, \end{aligned}$$

and the homogeneous Neumann boundary conditions.

In Fig. 12 (left), we plot the density at time $t=5$ computed by the AMM central-upwind scheme with $\beta =0.3$ and the minimal allowed cell size $|C|_{\min }=1/(201\times 201)$. Initially start with uniform mesh with $201\times 201$ finite-volume cells and the monitor function (3.9) with $D{\varvec{U}}=\Delta \rho$. As one can see, the solution contains a spike at the origin, where the mesh is concentrated; see Fig. 12 (right).

Fig. 12

Example 4: density computed using the AMM central-upwind scheme (left) and the final time mesh distribution (right)

At larger times, $\mathop {\max\limits_{x,y}}\rho (x,y,t)$ keeps increasing (see Fig. 13 (left)) and the mesh is further concentrated at the origin. This may lead to the appearance of very small cells, which may trigger (small) oscillations in the computed energy, which, in turn, may lead to the appearance of negative pressure values near the origin. To prevent this, we use relatively small $\beta =0.3$ both in this example and the next one. As in the 1-D case, we study the singularity formation by computing the ratios $\mathop {\max\limits_{x,y}}\rho ^{2N+1}(x,y,t)/\mathop {\max\limits_{x,y}}\rho ^{N+1}(x,y,t)$. Here, $\rho ^{N+1}(x,y,t)$ stands for the density computed using $(N+1)\times (N+1)$ uniform cells. As one can see, the obtained results are quite similar to the ones reported in Example 3. However, there are two quite important differences: first, the ratios are getting larger than 1 earlier, and second, at large times the ratios approach 4 (and even become a little larger than 4), which clearly indicates that by time $t\approx 5$ the density develops a $\delta$-function at the origin. We note that in the 2-D case, the maximum values of the computed $\delta$-functions are proportional to $1/(\Delta x\Delta y)$, so that we conclude that apparently a $\delta$-function appears in the density component if the aforementioned ratio is 4. We note that the obtained blowup result is in good compliance with the theoretical finite-time blowup results in [38].

Fig. 13

Example 4: $\mathop {\max\limits_{x,y}}\rho (x,y,t)$ as a function of time for the uniform (with $201\times 201$, $401\times 401$ and $801\times 801$ cells) and AMM (with $101\times 101$ initially uniform cells) computations (left) and $\mathop {\max\limits_{x,y}}\rho ^{2N+1}(x,y,t)/{\max\limits_{x,y}}\rho ^{N+1}(x,y,t)$ as a function of time for the sequence of uniform grids with $N=100$, 200 and 400 (right)

5.3 Example 5—Vortex-Like Data

In the final example, we consider the 2-D granular hydrodynamics system (5.2), (4.5) on the square domain $[-10,10]\times [-10,10]$ subject to the following vortex-like initial data:

$$\begin{aligned} \rho (x,y,0)\equiv 1,\quad u(x,y,0)=-y{{{\mathcal {E}}}},\quad v(x,y,0)=x{{{\mathcal {E}}}},\quad p(x,y,0)=\frac{\gamma -1}{\gamma }\left( R_0-\frac{{{{\mathcal {E}}}}^2}{2} \right) \end{aligned}$$

(5.4)

with ${{{\mathcal {E}}}}:={\text{e}}^{-\frac{1}{2}(x^2+y^2)}$, and the homogeneous Neumann boundary conditions. We note that if one replaces $\rho (x,y,0)$ in (5.4) with $\rho (x,y,0)=R_0-{{{\mathcal {E}}}}^2/2$, then the initial data will correspond to the steady vortex for the Euler equations of gas dynamics (4.4), (4.5). Here, $R_0$ is a constant, which determines the size of the vortex: the larger $R_0$ the larger the radius of the vortex. Moreover, as one can easily see, the solution of the initial value problem (5.2), (4.5), (5.4) is expected to preserve its initial radial symmetry. We first take a small $R_0=5$ and compute the solution until the final time $T=10$. The densities, computed by the AMM central-upwind scheme with $\beta =0.3$, $\psi =1.3$, initially uniform mesh with $200\times 200$ finite-volume cells (the minimal allowed cell size $|C|_{\min }=1/(100\times 100)$) and the monitor function (3.9) with $D{\varvec{U}}=\Delta (\log (1+\rho ))$, are shown in the left and middle columns in Fig. 14 at times $t=1$, 5, 10 and 25. As one can see, the solution develops a singularity along the circle-shaped curve, where the mesh is concentrated; see Fig. 14 (right column). The AMM solution at time $t=10$ is similar to the one obtained using the uniform mesh with $800\times 800$ uniform cells, which are plotted in Fig. 15 (top row).

Fig. 14

Example 5, $R_0=5$, densities computed using the AMM central-upwind scheme: three-dimensional (3-D) plot (left column), top view (middle column) and the mesh distribution (right column) at times $t=1$, 5, 10 and 25 (from top to bottom rows)

Fig. 15

Example 5, $R_0=5$, densities computed using the central-upwind scheme on the uniform $800\times 800$ grid: 3-D plot (left column), top view (right column) at times $t=10$ (top row) and 25 (bottom row)

We then numerically study the process of singularity formation by measuring $\mathop {\max\limits_{x,y}}\rho (x,y,t)$ and $\mathop {\max\limits_{x,y}}\rho ^{2N}(x,y,t)/\mathop {\max\limits_{x,y}}\rho ^N(x,y,t)$ as functions of time, presented in Fig. 16. As one can see, the maximum ratios become larger than one at $t\approx 2$, but they do not approach 2 (the maximum of the finite-volume representation of $\delta$-functions spread along curves is expected to be proportional to $1/\sqrt{\Delta x\Delta y}$ rather than to $1/(\Delta x\Delta y)$ as in the case of $\delta$-functions focused at isolated points), which suggests that the observed singular structure along the circle may or may not be the $\delta$-function. Computing the solution at larger times, we observe that the circular singularity structure is unstable. This can be seen in the bottom rows in Figs. 14 and 15, in which the densities, computed at the final time $T=25$ using the AMM and uniform central-upwind schemes, respectively, are plotted.

Fig. 16

Example 5, $R_0=5$: $\mathop {\max\limits_{x,y}}\rho (x,y,t)$ as a function of time for the uniform (with $200\times 200$, $400\times 400$ and $800\times 800$ cells) and AMM (with $200\times 200$ initially uniform cells) computations (left) and $\mathop {\max\limits_{x,y}}\rho ^{2N}(x,y,t)/\mathop {\max\limits_{x,y}}\rho ^N(x,y,t)$ as a function of time for the sequence of uniform grids with $N=100$, 200 and 400 (right)

Finally, we take a large $R_0=100$ and compute the solution until the same final time $T=25$. The densities and corresponding meshes at times $t=1$, 5, 10 and 25, computed by the AMM central-upwind scheme with the same parameters as before, but with $\beta =0.2$ and $\psi =1$ (the latter corresponds to a more dissipative minmod reconstruction) are shown in Fig. 17. As in the case of a smaller $R_0=5$, the solution develops a singularity along the curve, but a breakdown of its circular shape, which signals on the instability development, occurs much earlier now. As one can see, the shape deformation, is much more pronounced than in the case of a smaller $R_0=5$. We also notice that the solutions computed using the AMM and uniform mesh with $800\times 800$ cells (presented in Fig. 18) are not very closed. To further numerically study the developed singular structures, we compute the AMM solution using a sharper minmod reconstruction with $\psi =1.3$. The obtained densities are plotted in Fig. 19. As one can clearly see, the change in $\psi$ leads to a substantial change in the singularity curve, which supports the conclusion that after the singularity is developed the solution becomes unstable. In fact, the numerical study of the solution maximum (see Fig. 20) suggests that the solution develops $\delta$-type singularity along the circle by time $t\approx 1$, that is, long before the final computational time.

Fig. 17

Example 5, $R_0=100$, densities computed using the AMM central-upwind scheme with $\psi =1$: 3-D plot (left column), top view (middle column) and the mesh distribution (right column) at times $t=1$, 5, 10 and 25 (from top to bottom rows)

Fig. 18

Example 5, $R_0=100$, densities computed using the central-upwind scheme on the uniform $800\times 800$ grid: 3-D plot (left column) and top view (right column) at times $t=1$, 5, 10 and 25 (from top to bottom rows)

Fig. 19

Example 5, $R_0=100$: same as Fig. 17 but with $\psi =1.3$

Fig. 20

Example 5, $R_0=100$: $\mathop {\max\limits_{x,y}}\rho (x,y,t)$ as a function of time for the uniform (with $400\times 400$ and $800\times 800$ cells and $\psi =1$) and AMM (with $200\times 200$ initially uniform cells and $\psi =1$ and $\psi =1.3$) computations (left) and $\mathop {\max\limits_{x,y}}\rho ^{2N}(x,y,t)/\mathop {\max\limits_{x,y}}\rho ^N(x,y,t)$ as a function of time for the sequence of uniform grids with $N=200$ and 400 (right)