1 INTRODUCTION

Mathematical modeling of the processes of non-isothermal filtering of a multiphase flow in porous media is of great importance for determining technical parameters and justifying design decisions in many geoengineering applications, including oil field development [1, 2], geological storage of carbon dioxide [3], and artificial freezing of a rock massive [4, 5]. It is prospective to solve the system of equations of non-isothermal filtering of a multi-phase flow numerically using the finite-element method (FEM), where we can introduce the equations that describe the stress–strain state of a rock skeleton to the calculation scheme relatively easily [6, 7]. However, the discretization of the constitutive equations in the FEM based on the standard Galerkin method leads to nonphysical oscillations of the solution in narrow inner and boundary layers. In recent decades stabilized FEMs have been intensively developed to stabilize the computation process [8].

It follows from the analysis of the equations of non-isothermal multiscale filtering with account for phase transition of the first kind that these equations can be classified as the convection–diffusion–reaction equations. The following methods for stabilizing this type of equations have become widely used: the streamline-upwind Petrov–Galerkin (SUPG) method [9–13], the Galerkin least-squares (GLS) method [14–18], the spurious oscillations at layers diminishing (SOLD) method [19–21], and the variation multiscale method (VMM) [22–31]. The common idea of these methods consists in introducing an auxiliary stabilizing term into the notation of the original equation. The value of this term depends on the accuracy of the obtained solution at each calculation step, which allows stabilizing the solution only in those domains where the oscillations appear.

We characterize each method and restrict ourselves with consideration of only the linear convection–diffusion–reaction equation with some initial and boundary conditions

$$Q\left( u \right) \equiv \alpha \Delta u - {\mathbf{b}} \cdot \nabla u - cu + p = 0,\quad \left( {x,y} \right) \in \Omega ,$$

where \(\Omega \subset {{\mathbb{R}}^{2}}\) is a two-dimensional bounded domain with piecewise-smooth boundary, \(\alpha > 0\) is a positive constant, \({\mathbf{b}} = {\mathbf{b}}\left( {x,y} \right)\) is a vector function, and \(c = c\left( {x,y} \right)\) and \(p = p\left( {x,y} \right)\) are functions of the coordinates. In the SUPG method, the stabilizing term depending on the value of residual \(Q\left( u \right)\) and on the gradient of the test function \({v}\) is introduced into the equation in the weak form

$$\int\limits_\Omega {{{\tau }_{{{\text{SUPG}}}}}Q\left( u \right)\left( {{\mathbf{b}} \cdot \nabla {v}} \right)} ,$$

where \({{\tau }_{{{\text{SUPG}}}}}\) is the stabilizing parameter. In the GLS method the product of the gradient of the test function \(u\) and the convective coefficient \({\mathbf{b}}\) is replaced with the result of applying the operator of the considered equation to the test function \({v}\)

$$\int\limits_\Omega {{{\tau }_{{{\text{SUPG}}}}}Q\left( u \right)\left[ {\lambda \Delta {v} - {\mathbf{b}} \cdot \nabla {v} - c{v}} \right]} .$$

These methods allow considerable improvement in the stability and accuracy of the numerical solution under the condition that the exact solution is smooth [32]. However, when there are narrow internal and boundary layers where the solution varies rapidly use of the above methods does not exclude the appearance of nonphysical (spurious) oscillations in the solution.

In the SOLD methods it is proposed to add one more auxiliary stabilizing term to improve the stability of the solution. It is the product of the stabilizing parameter \({{\tau }_{{{\text{SOLD}}}}}\) and the artificial diffusion, which may have one of the following forms:

(1) the isotropic diffusion

$$ - \int\limits_\Omega {{{\tau }_{{{\text{SOLD}}}}}\nabla u \cdot \nabla {v}} ;$$

(2) the crosswind diffusion

$$ - \int\limits_\Omega {{{\tau }_{{{\text{SOLD}}}}}\left[ {\nabla u \cdot \nabla {v} - \frac{1}{{\left\| {\mathbf{b}} \right\|_{2}^{2}}}\left( {{\mathbf{b}} \cdot \nabla u} \right)\left( {{\mathbf{b}} \cdot \nabla {v}} \right)} \right]} ,$$

where \({{\left\| {\, \cdot \,} \right\|}_{2}}\) is the Euclidean norm; and

(3) the diffusion based on the edge stabilization

$$ - \sum\limits_{{{\Omega }_{K}}} {\int\limits_{\partial {{\Omega }_{K}}} {{{\tau }_{{{\text{SOLD}}}}}{\text{sgn}}\left( {{\mathbf{t}} \cdot \nabla u} \right)} } \left( {{\mathbf{t}} \cdot \nabla {v}} \right),$$

where \({\mathbf{t}}\) is the unit tangent vector to the boundary \(\partial {{\Omega }_{K}}\) of an element of the calculation mesh \({{\Omega }_{K}}\).

In [21] different methods based on solving some test boundary-value problems for the convection–diffusion–reaction equation were compared, and the comparison showed that the SOLD stabilization allows a significant decrease in the amplitude of the oscillations. However, in contrast to the SUPG and GLS methods, the introduction of artificial diffusion leads to the fact that the solution to the modified equation does not coincide with the solution to the original equation, that is, the consistency condition is violated. In the computational practice this stabilization leads to an extremely smoothened solution.

We also note that the efficiency of the described methods is to a large extent dependent on the type of stabilizing parameters. In [21, 27, 33] different expressions for these parameters are provided for the convection–diffusion–reaction equation.

In the VMM, the solution to the original equation in the weak form is represented as a sum of solutions to the equations on the grid and subgrid scales to determine the form of the stabilizing term. By using this multiscale splitting, we succeed in including the subgrid peculiarities of the original equation into the mesh problem and thus accounting for the rapid change in the solution in the thin internal and boundary layers on a mesh acceptable for practical calculations. The following modifications of the VMM have become widespread: the VMM with an algebraic sub-scale approximation (VMM-ASA) and the residual-free bubble (RFB) method.

In the first modification the solution to the sub-scale equation is not determined directly but is computed based on the residual of the mesh equation and stabilizing parameters (intrinsic time scales). As a result, it is not needed to solve the subgrid-scale equation, which considerably simplifies the calculation scheme and does not require increasing the computational resources. At the same time, the optimal expressions for the stabilizing parameters are not known and their adjustment requires a series of computations for each equation.

In the RFB method we determine the approximate solution to the equation on the subgrid scale by using the test functions of special type. Functions called bubble functions vanish at the boundary of each element and achieve their maximum value inside it. This approach does not lead to a significant increase in the computational cost and makes it possible to construct the approximate solution to the subgrid-scale equation.

VMMs allow better stabilization of the solution in comparison with the SUPG and GLS methods [23, 31]. Despite the fact that most implementations of the VMM are intended to solve linear convection–diffusion problems, [25] presented an approach to the VMM-ASA application for solving nonlinear equations exemplified by a two-phase filtering problem. Here, the original equation is linearized with respect to the subgrid-scale solution.

In the current work we generalized the VMM-ASA and the RFB method to solve the singularly perturbed nonlinear two-dimensional convection–diffusion–reaction equation. The computer implementation is carried out in the Comsol Multiphysics® finite-element analysis package. We performed a series of computational experiments on a test boundary value problem To study the efficiency of the developed methods.

2 THE WEAK FORMULATION OF THE NONSTATIONARY BOUNDARY VALUE PROBLEM OF THE CONVECTION–DIFFUSION–REACTION

We consider the convection–diffusion–reaction equation for the function \(u = u\left( {x,y} \right)\) in a bounded domain \(\Omega \subset {{\mathbb{R}}^{2}}\) with a piecewise-smooth boundary \(\partial \Omega \)

$$R\left( u \right) \equiv - {{u}_{t}} - \nabla \cdot {\mathbf{f}} + \nabla \cdot \left( {\lambda \nabla u} \right) + q = 0,\quad \left( {x,y} \right) \in \Omega ,\quad t \in (0,T],$$
(1)

with the initial condition

$${{\left. u \right|}_{{t = 0}}} = {{u}_{0}},\quad \left( {x,y} \right) \in \bar {\Omega },$$
(2)

and with the boundary conditions of the first and second kind

$${{\left. u \right|}_{{{{\Gamma }_{D}}}}} = g,\quad \left( {x,y} \right) \in \Omega ,\quad t \in [0,T],$$
(3)
$$ - {{\left. {\left( {{\mathbf{f}} - \lambda \nabla u} \right) \cdot {\mathbf{n}}} \right|}_{{{{\Gamma }_{N}}}}} = h,\quad \left( {x,y} \right) \in \Omega ,\quad t \in [0,T].$$
(4)

Here, the functions \(\lambda = \lambda \left( u \right)\), \(q = q\left( u \right)\), \({{u}_{0}} = {{u}_{0}}\left( {x,y} \right)\), \(g = g\left( {x,y} \right)\), \(h = h\left( {x,y} \right)\), and the vector function \({\mathbf{f}}{ = }{\mathbf{f}}\left( u \right)\) are prescribed, \(\lambda > 0\), \({\mathbf{n}}\) is the external normal to the boundary \(\partial \Omega \), and \({{\Gamma }_{D}}\) and \({{\Gamma }_{N}}\) are the piecewise-smooth boundaries of the domain \(\Omega \) such that \({{\Gamma }_{D}} \cup {{\Gamma }_{N}} = \partial \Omega \). We assume that all values are dimensionless. This type is inherent to the equations of mass conservation when a non-isothermal filtering flow of a multiphase liquid in porous media is described with account for the phase transition of the first kind [2, 4, 6, 7].

Let us proceed to the weak formulation of the problem (1)–(4). To this end, we determine the spaces of the test functions and solutions

$$V = \{ {v} \in {{H}^{1}}(\Omega ){{\left| {v} \right|}_{{\partial \Omega }}} = 0\} ,$$
$$S = \{ u \in {{H}^{1}}(\Omega ){{\left| u \right|}_{{{{\Gamma }_{D}}}}} = g\} ,$$

where \({{H}^{1}}(\Omega )\) is the Sobolev space of square integrable functions that have first derivatives. The weak formulation of the problem (1)–(4) is as follows: for each \(t \in (0,T]\) we need to solve a function \(u \in S\) such that

$$ - \int\limits_\Omega {{{u}_{t}}{v}} + \int\limits_\Omega {{\mathbf{f}} \cdot \nabla {v}} - \int\limits_\Omega {\lambda \nabla u \cdot \nabla {v}} + \int\limits_{{{\Gamma }_{N}}} {h{v}} + \int\limits_\Omega {q{v}} = 0,\quad \forall {v} \in V,$$
(5)
$${{\left. u \right|}_{{t = 0}}} = {{u}_{0}},\quad \left( {x,y} \right) \in \bar {\Omega }{\kern 1pt} .$$
(6)

Here, we assume that the input data of the formulated problem satisfy the conditions of its being well-posed [34].

3 A VARIATIONAL MULTISCALE APPROACH TO CONSTRUCTING A NUMERICAL SOLUTION

Let the studied domain \(\Omega \) be divided into finite elements \({{\Omega }_{K}}\) so that \(\bar {\Omega } = \overline { \cup {{\Omega }_{K}}} \). According to the Galerkin approach, we consider the approximation of the spaces of solutions \(S\) and test functions \(V\) by the spaces of interpolation polynomials \({{S}^{h}}\) and \({{V}^{h}}\) constructed based on the partition \( \cup {{\Omega }_{K}}\) [35].

The convection–diffusion–reaction equation with a small diffusion coefficient is singular perturbed [8]. This equation is characterized by narrow internal and boundary layers where its solution varies rapidly (jump-like). In the numerical calculation we can account only for those peculiarities of the problem that occur at characteristic scales larger than the element mesh size. Due to this, construction of the numerical solution in narrow domains with a large value of derivative with respect to spatial coordinates requires using extremely fine meshes. In the opposite case the solution begins to oscillate, which leads to a significant increase in the error and to the absence of convergence to the exact solution.

In the VMM, to account for peculiarities on the scales smaller than the element size, the solution to the equation is decomposed into the sum of grid-scale and subgrid-scale components. By \(\operatorname{P} \) we denote the linear operator of projecting the space of test functions \(V\) onto the finite-dimensional space \({{V}^{h}}\) of grid-scale (large-scale) test functions: \(\operatorname{P} :V \to {{V}^{h}}\). Then, the space \(V\) may be represented as a direct sum [31]

$$V = {{V}^{h}} \oplus \tilde {V},$$

where \(\tilde {V} = {\text{ker}}(\operatorname{P} )\) is the infinite-dimensional space of subgrid-scale (small-scale) test functions.

A similar decomposition is also valid for the space of solutions

$$S = {{S}^{h}} \oplus \tilde {S},$$

where \({{S}^{h}} = \bar {g} + {{V}^{h}}\) is the finite-dimensional space of grid-scale solutions that satisfy the boundary condition of the first kind on \({{\Gamma }_{D}}\): \({{\left. {\bar {g}} \right|}_{{{{\Gamma }_{D}}}}} = g\) and \(\tilde {S}\) is the infinite-dimensional space of subgrid-scale solutions. Since the subgrid-scale solutions and test functions fulfill the homogeneous boundary conditions on \({{\Gamma }_{D}}\), \(S = V\).

On the basis of this decomposition, we represent the solution and the test function uniquely as

$$u = {{u}^{h}} + \tilde {u},\quad {v} = {{{v}}^{h}} + {\tilde {v}},$$
(7)

where \({{u}^{h}} \in {{S}^{h}}\), \({{{v}}^{h}} \in {{V}^{h}}\), \(\tilde {u},\,\,{\tilde {v}} \in \tilde {V}\). According to the decomposition, we divide the original problem in the weak formulation (5) and (6) into the grid-scale and subgrid-scale problems. Following the approach used in [25], to determine the type of problem, we proceed in Eq. (5) from integration over the domain to the integration over the mesh \( \cup {{\Omega }_{K}}\). Then, we substitute the solution and the test functions (7) into (5) and linearize the derived equation with respect to \(\tilde {u}\). Next, after some manipulations, we formulate the problems: we need to find a grid-scale function \({{u}^{h}} \in S{^{h}}\) and a subgrid-scale function \(\tilde {u} \in \tilde {V}\) that, for each \(t \in (0,T]\), satisfy the grid-scale equation

$$\sum\limits_K {\int\limits_{{{\Omega }_{K}}} { - u_{t}^{h}{{{v}}^{h}}} } { + }\sum\limits_K {\int\limits_{{{\Omega }_{K}}} {{\mathbf{f}}({{u}^{h}}) \cdot \nabla {{{v}}^{h}}} } - \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {\lambda ({{u}^{h}})\nabla {{u}^{h}} \cdot \nabla {{{v}}^{h}}} } + \sum\limits_K {\int\limits_{{{\Gamma }_{N}} \cap {{\Omega }_{K}}} {h({{u}^{h}}){{{v}}^{h}}} } $$
$$ + \;\sum\limits_K {\int\limits_{{{\Omega }_{K}}} {q({{u}^{h}}){{{v}}^{h}}} } - \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {{{{\tilde {u}}}_{t}}{{{v}}^{h}}} } + \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {\tilde {u}[{{{\mathbf{f}}}_{u}}({{u}^{h}}) - {{\lambda }_{u}}({{u}^{h}})\nabla {{u}^{h}}] \cdot \nabla {{{v}}^{h}}} } $$
(8)
$$ - \;\sum\limits_K {\int\limits_{{{\Omega }_{K}}} {\lambda ({{u}^{h}})\nabla \tilde {u} \cdot \nabla {{{v}}^{h}}} } + \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {{{q}_{u}}({{u}^{h}})\tilde {u}{{{v}}^{h}}} } = 0,\quad \forall {{{v}}^{h}} \in {{V}^{h}},$$

and the subgrid-scale equation

$$\begin{gathered} \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {R({{u}^{h}}){\tilde {v}}} } - \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {{{{\tilde {u}}}_{t}}{\tilde {v}}} } + \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {\tilde {u}{\kern 1pt} \text{[}{{{\mathbf{f}}}_{u}}({{u}^{h}}) - {{\lambda }_{u}}({{u}^{h}})\nabla {{u}^{h}}] \cdot \nabla {\tilde {v}}} } - \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {\lambda ({{u}^{h}})\nabla \tilde {u} \cdot \nabla {\tilde {v}}} } \\ + \;\sum\limits_K {\int\limits_{{{\Omega }_{K}}} {{{q}_{u}}({{u}^{h}})\tilde {u}{\tilde {v}}} } = 0,\quad \forall {\tilde {v}} \in \tilde {V}. \\ \end{gathered} $$
(9)

It is well known [8] that the main difficulty in constructing the solution to Eqs. (8) and (9) lies in the fact that the space \(\tilde {V}\) is infinite dimensional. However, it is possible to improve the stability and accuracy of the grid-scale solution either by simulating the effect of the subgrid-scale peculiarities of the studied equation on it or by solving the subgrid-scale problem approximately.

3.1 VMM-ASA

In this method the subgrid-scale solution \(\tilde {u}\) is determined not from the solution to Eq. (9), but from the expression containing the stabilizing parameter \(\tau \) which approximates the inverse operator to the operator of Eq. (9). The form of \(\tau \) is chosen according to the type of the considered equation

$$\tilde {u} = - \tau R({{u}^{h}}).$$
(10)

Expressions of the stabilizing parameters for linear convection–diffusion–reaction equations that were used in the SUPG, GLS, SOLD, and VMM-ASA stabilization were provided in [16, 21, 27, 33]. In the current work, on the basis of the computational experiments, we choose the following expression for the stabilizing parameter

$$\tau = \frac{{h_{K}^{2}}}{{\left| {1 + {{q}_{u}}({{u}^{h}})} \right|h_{K}^{2}\xi ({{w}_{{K,1}}}) + (2\lambda ({{u}^{h}}){\text{/}}{{m}_{K}})\xi ({{w}_{{K,2}}})}},$$

where

$${{w}_{{K,1}}} = \frac{{2\lambda ({{u}_{h}})}}{{{{m}_{K}}\left| {1 + {{q}_{u}}({{u}^{h}})} \right|h_{K}^{2}}},\quad {{w}_{{K,2}}} = \frac{{{{m}_{K}}{{{\left\| {\mathbf{c}} \right\|}}_{2}}{{h}_{k}}}}{{\lambda ({{u}_{h}})}},\quad \xi (z) = \left\{ \begin{gathered} 1,\quad 0 \leqslant z \leqslant 1, \hfill \\ z,\quad z \geqslant 1. \hfill \\ \end{gathered} \right.$$

Here, \({{h}_{K}}\) is the size of the Kth element equal to the length of its longest edge, \({\mathbf{c}} = {{{\mathbf{f}}}_{u}}({{u}^{h}}) - {{\lambda }_{u}}({{u}^{h}})\nabla {{u}^{h}}\), and \({{m}_{K}}\) is the numerical parameter whose value depends on the order of the finite-element approximation. For the linear and quadratic approximations \({{m}_{K}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}\).

3.2 RFB Method

According to this method, the subgrid-scale space of solutions and test functions \(V\) is approximated by the finite-dimensional space of bubble functions \({{B}^{h}}\)

$${{B}^{h}} = \left\{ {{\tilde {v}} \in {\tilde {V}}\,|\,\forall {{\Omega }_{K}}:{\tilde {v}} \in {{H}^{1}}({{\Omega }_{K}}) \wedge {{{\left. {{\tilde {v}}} \right|}}_{{\partial {{\Omega }_{K}}}}} = 0} \right\}.$$

The methods for constructing the bubble functions were given in [23, 24, 28, 29]. In the current work we use the approach implemented in the Comsol Multiphysics® package, Here, each element of the mesh is equipped with a single bubble function with the following properties: it is a polynomial of the lowest possible order that achieves the maximum value in the center of the element and vanishes at its boundary [36].

4 THE RESULTS OF COMPUTATIONAL EXPERIMENTS

To compare the efficiency of the proposed modifications of the VMM-ASA and RFB method, we consider a test boundary value problem for the convection–diffusion–reaction equation under the condition of small diffusion coefficient. We need to find the solution to problem (1)–(4) in the domain \(\Omega \).

The coefficients of Eq. (1) have the form: \({\mathbf{f}}{ = }({{u}^{3}},{{u}^{3}})\), \(\lambda = 6 \times {{10}^{{ - 1}}}\), and \(q = {{u}^{2}}\). The domain \(\Omega \) is a square with two holes whose centers are located on one of its diagonals. The side of the square is 1, the radius of the holes is 0.05, the distance between the holes is \(0.5\sqrt 2 \), and the distance between the square vertices and the holes is \(0.25\sqrt 2 \). At the boundaries of the holes we impose the conditions of the first kind: \(g = 10\) and \(g = 0\) and at the boundaries of the square we impose the zero flow \(h = 0\). The time parameter is changed within the range \(t \in (0;\;0.02]\).

We used the proposed stabilized FEMs in the Comsol Multiphysics® package using the Weak Form PDE Interface module, which allows discretizing the weak formulation of the problem according to the chosen basis functions. Thus, in the module we prescribe only the grid-scale Eq. (8) for the VMM-ASA and we define expression (10) for computing the subgrid-scale solution as a variable; for the RFB method we prescribe both the grid-scale and the subgrid-scale Eqs. (8) and (9). In order to study the efficiency of the proposed methods, we also solve the formulated boundary value problem using the standard Galerkin calculation scheme. Here, we input Eq. (5) into the Weak Form PDE Interface module.

We use the piecewise-linear continuous functions to construct the solution to the grid-scale equation; we used the bubble functions to construct the solution to the subgrid-scale equation, which we prescribe in the form of a third-order polynomial. For approximation in time, we use the first-order implicit Euler scheme. We solve the system of nonlinear algebraic equations using the Newton method. We divide the domain \(\Omega \) into triangular elements with gradual refinement as we approach the boundary of the holes. In Fig. 1 we present the computation mesh with an average element size \({{h}_{{{\text{avr}}}}} = 2.3 \times {{10}^{{ - 2}}}\); the element size at the boundary of the holes is \(1.1 \times {{10}^{{ - 3}}}\).

Fig. 1.
figure 1

The calculation mesh.

Full size image

Artificial diffusion was added to Eq. (12) in [27] to improve the stability of the numerical solution obtained with the VMM-ASA. However, in the computational experiments performed in the current study the efficiency of this trick was not established, because the introduction of some types of the SOLD stabilization did not lead to variation in oscillatory characteristics of the numerical solution. At the same time, when we introduced the artificial isotropic diffusion according to [31]

$$ - \sum\limits_K {\int\limits_{{{\Omega }_{K}}} {\frac{{{{h}_{K}}{{{\left\| {\mathbf{c}} \right\|}}_{2}}}}{{18}}\nabla \tilde {u}} \cdot \nabla {\tilde {v}}} $$

into the subgrid-scale equation in solving with the RFB method, we decreased the amplitude of the oscillations and increased the convergence rate.

We note that the appropriate results in solving with the RFB method were obtained only in the case where the quasi-stationary formulation was used in the subgrid-scale problem; this quasi-stationary formulation implies that the subgrid-scale function \(\tilde {u}\) is time-independent and all the time derivatives in Eq. (9) are equal to zero. In the VMM-ASA elimination of the time derivative from Eq. (10) from the grid-scale solution in computing the subgrid-scale component also led to an improved accuracy.

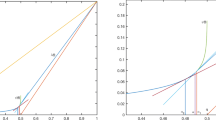
In Fig. 2 we present the levels of error of numerical solutions dependent on the average mesh element size \({{h}_{{{\text{avr}}}}}\). We take the solution \({{u}_{{{\text{ref}}}}}\) obtained on the mesh with \({{h}_{{{\text{avr}}}}} = 1.34 \times {{10}^{{ - 2}}}\) as the reference solution. We computed the relative error by the formula

$$err = \frac{{\int\limits_0^T {\int\limits_\Omega {{{{({{u}^{h}} - u_{{{\text{ref}}}}^{h})}}^{2}}} } }}{{\int\limits_0^T {\int\limits_\Omega {{{{(u_{{{\text{ref}}}}^{h})}}^{2}}} } }} \times 100(\% ).$$
Fig. 2.
figure 2

The errors of numerical solutions obtained by (a) VMM-ASA and (b) RFB method over average mesh element size \({{h}_{{{\text{avr}}}}}\).

Full size image

From the graphs we see that, depending on the element size \({{h}_{{{\text{avr}}}}}\), the considered stabilization methods have practically identical convergence rates and accuracy. In the computations with the VMM-ASA on the coarsest mesh with \({{h}_{{{\text{avr}}}}} = 4.4 \times {{10}^{{ - 2}}}\), the relative error is \(err = 0.33\)%, and in the computations with the RFB method it is \(err = 0.34\)%. Further refinement of the mesh until \({{h}_{{{\text{avr}}}}} = 2.3 \times {{10}^{{ - 2}}}\) leads to a sharp reduction in the error values to \(err = 0.036\)% and \(err = 0.041\)%; after this the convergence of both methods worsens.

Figure 3 contains the distributions of the grid-scale solution \({{u}^{h}}\) at \(t = 3 \times {{10}^{{ - 3}}}\) computed with the VMM-ASA, RFB method, and the standard Galerkin scheme on the mesh with \({{h}_{{{\text{avr}}}}} = 2.3 \times {{10}^{{ - 2}}}\). We see that there are no oscillations in the solutions with the stabilization methods. However, when the RFB method is applied, we observe an unjustified splash of the solution in the neighborhood of the first point of the sharp change in the solution character (see curve 3 in Fig. 3d).

Fig. 3.
figure 3

The distributions of \({{u}^{h}}\) at \(t = 3 \times {{10}^{{ - 3}}}\) and \(\lambda = 6 \times {{10}^{{ - 1}}}\) (a–c) over region \(\Omega \) obtained by (a) VMM-ASA, (b) RFB method, and (c) Galerkin method and (d) over segment between the hole centers: curve 1 for VMM-ASA, curve 2 for RFB method, and curve 3 for Galerkin method.

Full size image

As the parameter \(t\) increases, the grid-scale solution \({{u}^{h}}\) becomes smoother. Near the boundary of the upper hole, no nonphysical oscillations and splashes occur in the solution for both proposed methods.

The solution to the convection–diffusion–reaction equation may be characterized by the Peclet number [33] whose mesh analog for the nonlinear equation may be defined as [25]

$${\text{Pe}} = \frac{{{{{\left\| {\mathbf{c}} \right\|}}_{2}}{{h}_{K}}}}{{2\lambda }}.$$

For the considered equation on the calculation mesh with \({{h}_{{{\text{avr}}}}} = 2.3 \times {{10}^{{ - 2}}}\), the maximum value of this constant is 12. In the case where the diffusion coefficient \(\lambda \) increases to 20 in the equation, the grid-scale solution \({{u}^{h}}\) determined by the Galerkin method contains no oscillations. Here, the Peclet number does not exceed 3.

To investigate the efficiency of the constructed methods, we solve the problem with the diffusion coefficient \(\lambda = 6 \times {{10}^{{ - 6}}}\) on a calculation mesh with \({{h}_{{{\text{avr}}}}} = 2.3 \times {{10}^{{ - 2}}}\). Below, we present the following distributions of \({{u}^{h}}\) in the figures:

(1) the distribution over the domain \(\Omega \) under the following values of the parameter \(t\): 1 × 10–3, 3 × 10–3, 5  × 10–3, and 1 × 10–2 (Fig. 4) and

Fig. 4.
figure 4

The distributions of \({{u}^{h}}\) over region \(\Omega \) at \(\lambda = 6 \times {{10}^{{ - 6}}}\) and different values of parameter \(t\): (a, b) 1 × 10–3, (c, d) 3 × 10–3, (e, f) 5 × 10–3, and (g, h) 1 × 10–2 obtained by (a, c, e, g) VMM-ASA and (b, d, f, h) RFB method.

Full size image

(2) the distribution over the segment between the hole centers for two values of the parameter \(t\): 3 × 10–3 and 5 × 10–3 (Fig. 5).

Fig. 5.
figure 5

Distributions of \({{u}^{h}}\) over segment between the hole centers at (a) \(\lambda = 6 \times {{10}^{{ - 6}}}\) and \(t = 3 \times {{10}^{{ - 3}}}\) and (b) \(\lambda = 6 \times {{10}^{{ - 6}}}\) and \(t = 5 \times {{10}^{{ - 3}}}\) obtained by VMM-ASA (curve 1) and RFB (curve 2) method.

Full size image

The maximum value of the Peclet number is \(1.6 \times {{10}^{6}}\). In this case the standard Galerkin method diverges and we cannot succeed in constructing the solution.

From the presented data we may conclude that both methods give appropriate results; however, the grid-scale solution contains a splash and is not monotonic. Using the distributions of \({{u}^{h}}\) over the domain \(\Omega \), we see that a large splash amplitude is observed along the lateral boundaries of the solution front. The maximum value of the solution calculated with the VMM-ASA does not exceed 11 and the maximum value of the solution calculated with the RFB method is not larger than 11.5. In the segment between the hole centers, the forward edge of the front of the second solution is not smooth (Fig. 5a). The solution with the RFB method has a splash near the boundary of the upper hole (Fig. 5b), which does not vanish as we increase the parameter \(t\). Using the VMM-ASA allows obtaining the smooth solution in the neighborhood of this point. In the rest of the domain adherent to the boundary of the hole, both solutions have a splash (Fig. 4e–4h).

The significant advantage of the VMM-ASA is in the fact that the time needed to solve the problem is shorter than the computation time for the RFB method. It is especially so when the diffusion coefficient \(\lambda = 6 \times {{10}^{{ - 6}}}\) enters the equation. In the case of the VMM-ASA, the computation time is 2 minutes, while in the case of the RFB method it is longer than 1 h.

5 CONCLUSIONS

This paper was devoted to developing and implementing stabilized finite-element methods. We modified the VMM-ASA and the RFB method for numerical solution of the two-dimensional nonstationary nonlinear convection–diffusion–reaction equation. Based on the multiscale decomposition of the solution and subsequent linearization of the weak formulation of the original problem with respect to the subgrid-scale component, we defined the formulations of the grid-scale and subgrid-scale problems. We performed the computer implementation of the stabilized methods in the Comsol Multiphysics® package.

We evaluated the efficiency of the developed modifications of the VMM-ASA and RFB methods by solving a test problem. For the RFB method, we succeeded in obtaining the appropriate results only when we used the quasi-stationary formulation for the subgrid-scale problem. In the VMM-ASA method, the elimination of the time derivative of the grid-scale solution in computing the subgrid-scale component also increased the accuracy. The introduction of artificial diffusion into the subgrid-scale equation in the RFB method led to an improvement of its stabilizing properties. In its turn, in using the SOLD stabilization we could not succeed in correcting the perturbation of the grid-scale solution in the locations of its rapid variation.

On the basis of the results of the computational experiments, we concluded that the VMM-ASA and the RFB methods have a similar rate of decrease in the error of the grid-scale solution dependent on the mesh element size. In comparison with the standard Galerkin method, these methods allow a decrease in the number and amplitude of oscillations in the solution. Here, at the stage of propagation of the grid-scale solution from the boundary of supply (the boundary with the input condition) towards the outflow boundary (the boundary with the output condition), its error in the internal layer in using the RFB method is larger than the error of the VMM-ASA. In the case of large values of the Peclet number when the Galerkin method is not applicable the stabilized methods provide an opportunity to construct a numerical solution with sufficiently small oscillations whose amplitude does not exceed 5% of the solution value at the input boundary. Compared with the VMM-ASA method, the RFB method requires larger computational resources necessary to introduce auxiliary degrees of freedom related with the bubble functions and longer time to solve the problem. Due to this, it is more advantageous to use the VMM-ASA to perform practical calculations.