A new thinning-based INAR(1) process for underdispersed or overdispersed counts

Abstract

Underdispersed and overdispersed phenomena are often observed in practice. To deal with these phenomena, we introduce a new thinning-based integer-valued autoregressive process. Some probabilistic and statistical properties of the process are obtained. The asymptotic normality of the estimators of the model parameters, using conditional least squares, weighted conditional least squares and modified quasi-likelihood methods, are presented. One overdispersed real-data example and one underdispersed real-data example are given to show the flexibility and superiority of the new model.

1 Introduction

During the last three decades, an integer-valued autoregressive (of order 1) model, denoted by INAR(1), has been widely used in real-world applications, such as the insurance actuarial, reliability theory, medicine and social sciences. There is a huge literature on the INAR(1) model [see Weiß (2008b) and Scotto et al. (2015)]. For more details on the INAR(1) model, we refer to Jazi et al. (2012), Schweer and Weiß (2014), Bourguignon and Vasconcellos (2015), Barreto-Souza (2015, 2017), Li et al. (2015), Borges et al. (2016), Bourguignon and Weiß (2017), Kim and Lee (2017) and Bourguignon et al. (2019).

The INAR(1) processes have been constructed by using thinning operators. The binomial thinning operator was originally proposed by Steutel and Van Harn (1979) and defined as

$$\begin{aligned} \alpha \circ X=\sum _{i=1}^{X}B_i, \end{aligned}$$

(1)

where $\{B_i\}$ is a sequence of iid Bernoulli($\alpha$) random variables independent of X. Based on the binomial thinning operator, the Poisson INAR(1) (POINAR(1)) model was introduced by Alzaid and Al-Osh (1987) and defined by

$$\begin{aligned} X_{t}=\alpha \circ X_{t-1}+\epsilon _{t},~t\ge 1, \end{aligned}$$

where $\{\epsilon _t\}$ is a sequence of iid Poisson random variables with mean $\lambda (1-\alpha )$, uncorrelated with the past value of $\{X_{t}\}$. Moreover, $X_0$ is assumed to follow the Poisson distribution with mean $\lambda$.

The POINAR(1) model has been widely used in practice due to its simplicity. For instance, Cossette et al. (2011) generalized the classical discrete time risk models which used the POINAR(1) model to describe the dependence (in time) between the claim frequencies. Freeland and McCabe (2004) applied the POINAR(1) model that exhibited the short-range dependence to analyse a data set.

While the POINAR(1) model is widely used, it has two main limitations in practice. First, the binomial thinning operator in the POINAR(1) model is not appropriate when the observed unit can generate more counting objects or produce more new random events. Second, the Poisson distribution suffers from the equidispersion requirement which can not explain underdispersion and overdispersion. To handle the first limitation, Ristić et al. (2009) introduced the negative binomial thinning operator

$$\begin{aligned} \alpha *X=\sum _{i=1}^{X}W_i, \end{aligned}$$

(2)

where $\{W_i\}$ is a sequence of iid Geometric($\alpha /(1+\alpha )$) random variables independent of X. The negative binomial thinning operator contains geometric counting series which can explain overdispersion. To deal with the second limitation, Ristić et al. (2009) introduced a negative binomial thinning INAR(1) model with the geometric marginal, i.e., NGINAR(1) process. Since the NGINAR(1) model captures overdispersion, during the past ten years, the NGINAR(1) model has become popular in some fields such as the reliability theory, medicine and reservoirs theory.

However, the NGINAR(1) model still has some drawbacks: (i) the counting series in the negative binomial thinning operator can not exhibit equidispersion and underdispersion, (ii) the geometric marginal distributions are not suitable for explaining underdispersion. The aim of this paper is to deal with the above two problems. For the first drawback, we propose a new thinning operator by using a more general discrete distribution. Our thinning operator has three attractive characteristics: (i) the counting series in our thinning operator can exhibit equidispersion, overdispersion, underdispersion, zero inflation and zero deflation; (ii) the probability mass function (pmf) of the counting random variable in our thinning operator is a decreasing function, which is very useful to explain some practical problems; (iii) the counting random variable in our thinning operator can describe both the short and long tailed count data. To the best of our knowledge, there is no thinning operator that can capture all the above three features. For the second drawback, we propose a new thinning-based INAR(1) process to explain both overdispersion and underdispersion.

The contents of this paper are organized as follows. In Sect. 2, we construct a new INAR(1) process based on an alternative thinning operator. In Sect. 3, some probabilistic and statistical properties of the process are derived. In Sect. 4, the estimators of the model parameters are derived by using conditional least squares (CLS), weighted conditional least squares (WCLS) and modified quasi-likelihood (MQL) methods. Also, the asymptotic properties of the estimators are investigated. In Sect. 5, we present some simulation studies to investigate the performances of the proposed estimators. In Sect. 6, we apply the model to two real data sets. Section 7 contains a discussion on the higher-order model. All proofs are given in Appendix.

2 Construction of the new process

Gómez-Déniz et al. (2011) introduced a new discrete distribution taking non-negative integers $\{0, 1, \ldots \}$. For convenience, we call it the Gómez–Déniza–Sarabia–Calderín-Ojeda (GSC) distribution. The pmf of the GSC distribution is given by

$$\begin{aligned} P_n=\mathrm {Pr}(N=n)=\frac{\mathrm {log}(1-\alpha \theta ^n)-\mathrm {log}(1-\alpha \theta ^{n+1})}{\mathrm {log}(1-\alpha )}, \end{aligned}$$

(3)

where $\alpha <1$, $\alpha \ne 0$ and $0<\theta <1$. The moments and the moment generating function (mgf) of the GSC distribution are given as follows:

$$\begin{aligned} \mathrm {E}(N)&=\frac{1}{\mathrm {log}(1-\alpha )}\sum _{s=1}^{\infty }\mathrm {log}(1-\alpha \theta ^s),\\ \mathrm {E}(N^2)&=\frac{1}{\mathrm {log}(1-\alpha )}\sum _{s=1}^{\infty }(2s-1)\mathrm {log}(1-\alpha \theta ^s),\\ \mathrm {E}(t^N)&=\frac{1}{\mathrm {log}(1-\alpha )} \sum _{s=0}^{\infty }t^s\mathrm {log}\bigg (\frac{1-\alpha \theta ^s}{1-\alpha \theta ^{s+1}}\bigg ),~~~t\in [-1,1]. \end{aligned}$$

There are four main advantages of the GSC distribution. Firstly, Gómez-Déniz et al. (2011) found that overdispersion and underdispersion are encountered depending on the values of the distribution parameters. In our study, we found that some parameter combinations can also lead to equidispersion, which means that the GSC distribution can be viewed as an alternative one to the Poisson distribution. To investigate the dispersion characteristic of GSC($\alpha$, $\theta$) with varying values of $\alpha$ and $\theta$, the index of dispersion of the GSC distribution; $\mathrm {Var}(N)/\mathrm {E}(N)$, is shown in Table 1. Secondly, the GSC distribution can be used to explain varying degrees of the zero-inflated and slightly zero-deflated phenomena. To illustrate it, we introduce a zero inflation index; $z_i=p_0\exp (\mu )-1$ (see Weiß et al. 2019), where $p_0$ is the proportion of 0’s and $\mu$ is the mean. $z_i>0$ means that the distribution suffers from zero inflation and $z_i<0$ means the random variable is zero-deflated. The zero inflation indices of GSC($\alpha$, $\theta$) with varying values of $\alpha$ and $\theta$ are shown in Table 2. Thirdly, the GSC distribution represents a general family of distributions. As pointed out by Gómez-Déniz et al. (2011), the GSC distribution can be viewed as a compound Poisson distribution, a specific mixed geometric distribution and a specific mixed Poisson distribution. Furthermore, the GSC distribution can be viewed as a possible alternative one to the negative binomial, generalized Poisson, hyper-Poisson, Poisson-inverse Gaussian distribution, different generalizations of the geometric distribution that have been discussed in the statistical literature. Finally, Gómez-Déniz et al. (2011) pointed out that the pmf (3) is a decreasing function and has the ability to describe the short and long tailed counts.

Table 1 The indices of dispersion of GSC($\alpha$, $\theta$) for different values of $\alpha$ and $\theta$

Table 2 The zero inflation indices of GSC($\alpha$, $\theta$) for different values of $\alpha$ and $\theta$

Although the GSC distribution has some interesting properties, it still has a significant disadvantage: as pointed out by a referee, the GSC distribution does not have explicit formulae for the mean and variance, which leads to some difficulties when it is applied to the statistical model. To analyse this drawback, we discuss it from two aspects. Firstly, we prove that the infinite sum in the mean and variance expressions are convergent (see the top of Appendix). Secondly, the infinite sum in the mean and variance of the GSC distribution can be approximated very precisely by the corresponding finite sum. This conclusion can be supported by Table 3, i.e., the mean and variance of GSC($\alpha$, $\theta$) for different values of $\alpha$ and $\theta$ with varying upper limit in the finite sum. From Table 3, we find that the approximation is precise enough for each parameter combination when the finite sum as the indices running $s=1,\ldots ,200$. Based on these discussions, we conclude that the inexistence of explicit formulae for the mean and variance can be overcomed by approximating the infinite sum by the finite sum.

Table 3 The means (above) and variances (below) of GSC($\alpha$, $\theta$) for different values of $\alpha$ and $\theta$ with varying upper limit in the infinite series

To get a better fit for a serially dependent count data, one should identify the dispersion behavior of the counts before choosing a suitable INAR(1) process. The most popular methods to identify the dispersion behavior of the counts is a test proposed by Schweer and Weiß (2014). Consider the null hypothesis $\mathcal {H}_0$: $X_1$,...,$X_n$ stem from an equidispersed POINAR(1) process ($I_d=1$) against the alternative of an overdispersed (or underdispersed) marginal distribution. Let $z_{1-\beta }$ be the quantile of the $(1-\beta )$-quantile of the N(0, 1)-distribution. We reject the null hypothesis $\mathcal {H}_0$: equidispersion on significance level $\beta$ in favor of alternative hypothesis $\mathcal {H}_1$: overdispersion (or underdispersion) if

$$\begin{aligned} \widehat{I}_d>1+z_{1-\beta }\sqrt{\frac{2(1+\widehat{\rho }_{X}^2(1))}{n(1-\widehat{\rho }_{X}^2(1))}}~ \Bigg (\mathrm {or}~ \widehat{I}_d<1+z_{\beta }\sqrt{\frac{2(1+\widehat{\rho }_{X}^2(1))}{n(1-\widehat{\rho }_{X}^2(1))}}\Bigg ), \end{aligned}$$

where $\widehat{I}_d=\sum _{t=1}^{n}(X_t-\overline{X})^2/\sum _{t=1}^{n}X_t$, $\overline{X}=(1/n)\sum _{t=1}^{n}X_t$ and $\widehat{\rho }_{X}(1)$ is the first-order autocorrelation coefficient of $X_1,\ldots ,X_n$.

After identifying the dispersion behavior of the counts, one may choose a suitable existing INAR(1) model to fit the data. On one hand, the binomial thinning INAR(1) models with different innovation structures are natural choices. For example, Bourguignon and Vasconcellos (2015), Kim and Lee (2017), Bourguignon et al. (2019) introduced the binomial thinning INAR(1) processes with the power series, Katz family, double Poisson and generalized Poisson innovations, respectively. The above models are able to handle equidispersion, underdispersion and overdispersion. On the other hand, the negative binomial thinning INAR(1) models with different marginal distributions are also commonly used. As we mentioned before, the NGINAR(1) model is very popular when the overdispersed counts are suffered. Barreto-Souza (2015) proposed a negative binomial thinning INAR(1) process with the zero-modified geometric marginal to account for underdispersion and overdispersion. However, new thinning-based INAR(1) model is still needed. This statement can be explained from two aspects. Firstly, the binomial and negative binomial thinning operators both have some limitations: (i) the binomial thinning operator is not suitable when the observed unit can generate more counting objects or produce more new random events; (ii) the negative binomial thinning operator can not exhibit equidispersion and underdispersion. Secondly, due to the complexity and diversity of the practical application, the counting series in the thinning operator are expected to have the ability to explain as many data characteristics as possible.

Based on the need for the new thinning operator and the attractive advantages of the GSC distribution, we use this distribution to create a GSC thinning operator which is defined by

$$\begin{aligned} \alpha \diamond X:=\sum _{j=1}^{X}W_j, \end{aligned}$$

(4)

where $\{W_j\}$ is a sequence of iid GSC($\alpha$, $\exp \{-|\alpha |\}$) random variables, $\mathrm {E}(W_j)=\phi$, $\mathrm {Var}(W_j)=\beta$, $\{W_j\}$ and X are independent. The proposed thinning operator (4) not only can overcome the shortcomings of the binomial and negative binomial thinning operators (1) and (2), but also has the ability to describe many data characteristics. To be specific, the GSC thinning operator can capture the feature that the observed unit may generate more counting objects or produce more new random events and the counting series in our thinning operator can show equidispersion, overdispersion and underdispersion. Besides, the counting series in our thinning operator can describe the zero-inflated, zero-deflated, short tailed and long tailed characteristics.

We now introduce GSC thinning-based INAR(1) process, as follows:

Definition 1

An INAR(1) model based on the GSC thinning operator, denoted by GSCINAR(1), is defined by the following difference equation:

$$\begin{aligned} X_{t}=\alpha \diamond X_{t-1}+\epsilon _{t},~t\ge 1, \end{aligned}$$

(5)

where $\{W_j\}$ is a sequence of iid GSC($\alpha$, $\exp \{-|\alpha |\}$) random variables with the finite mean $\phi$ and variance $\beta$, $\alpha <1$, $\alpha \ne 0$. Here, we write $\phi =\frac{1}{\mathrm {log}(1-\alpha )}\sum _{s=1}^{\infty }\mathrm {log}(1-\alpha \exp \{-s|\alpha |\})$ and $\beta =\frac{1}{\mathrm {log}(1-\alpha )}\sum _{s=1}^{\infty }(2s-1)\mathrm {log}(1-\alpha \exp \{-s|\alpha |\})-\phi ^2$. $\{\epsilon _t\}$ is an innovation sequence of iid non-negative integer-valued random variables, uncorrelated with the past values of $\{X_t\}$. Let $\mu _{\epsilon }=\mathrm {E}(\epsilon _t)$, $\sigma _{\epsilon }^{2}=\mathrm {Var}(\epsilon _t)$ (we assume that they exist).

3 Properties of GSCINAR(1) process

In this section, we consider some properties of GSCINAR(1) process.

Proposition 1

Suppose $\{X_t\}$ is a stationary process satisfying (5). Then for $t\ge 1$,

• (i) $\mathrm {E}(X_t|X_{t-1})=\phi X_{t-1}+\mu _{\epsilon }$,

• (ii) $\mathrm {E}(X_t)=\mu _{\epsilon }/(1-\phi )$,

• (iii) $\mathrm {Var}(X_t|X_{t-1})=\beta X_{t-1}+\sigma _{\epsilon }^2$,

• (iv) $\mathrm {Var}(X_t)=[\beta \mu _{\epsilon }+\sigma _{\epsilon }^{2}(1-\phi )]/[(1-\phi )^2(1+\phi )]$,

• (v) $\rho _{k}=\mathrm {Corr}(X_{t+k},X_t)=\phi ^k$, $k=1,2,\ldots ,$

where $\phi$ and $\beta$ are given in Definition 1.

Remark 1

• (i) Proposition 1(i) shows that the GSCINAR(1) model is a member of the non-Gaussian conditional linear AR(1) models discussed by Grunwald et al. (2000).

• (ii) The index of dispersion of $\{X_t\}$ is given by

  $$\begin{aligned} I_X:=\frac{\mathrm {Var}(X_t)}{\mathrm {E}(X_t)} =\frac{\beta \mu _{\epsilon }+\sigma _{\epsilon }^2(1-\phi )}{\mu _{\epsilon }(1+\phi )(1-\phi )}. \end{aligned}$$

Following Li et al. (2015), the existence of the strict stationary and ergodic GSCINAR(1) process can be established in the following theorem.

Theorem 1

If $0<\phi <1$, then there exists an unique strictly stationary integer-valued random series $\{X_t\}$ satisfying

$$\begin{aligned} X_{t}=\alpha \diamond X_{t-1}+\epsilon _{t},~t\ge 1, \end{aligned}$$

$\mathrm {Cov}(X_s,\epsilon _t)=0$ for $s<t$. Furthermore, the process is an ergodic process.

4 Estimation of the unknown parameters

Suppose $\{X_t\}$ is a strictly stationary and ergodic solution of model (5). Our task is to estimate the parameter $\varvec{\eta }=(\alpha ,\mu _{\epsilon })^{'}$ from a sample $(X_1,X_2,\ldots ,X_n)$. Three different methods of parameter estimation, the CLS, WCLS and MQL, are applied. The reason why we take these approaches is that they do not require specifying the exact family of distributions for the innovations.

4.1 Conditional least squares estimator

The CLS estimator $\widehat{\varvec{\eta }}_{CLS}=(\widehat{\alpha }_{CLS},\widehat{\mu _{\epsilon }}_{CLS})^{'}$ of $\varvec{\eta }$ is obtained by minimizing the expression

$$\begin{aligned} Q_1(\varvec{\eta })&:=\sum _{t=1}^{n} (X_t-\phi X_{t-1}-\mu _{\epsilon })^2\nonumber \\&=\sum _{t=1}^{n}\left( X_t-\frac{X_{t-1}}{\log (1-\alpha )}\sum _{s=1}^{\infty }\log (1-\alpha \exp \{-s|\alpha |\})-\mu _{\epsilon }\right) ^2. \end{aligned}$$

(6)

The following result establishes the asymptotic distribution of $\widehat{\varvec{\eta }}_{CLS}$. For convenience, write

$$\begin{aligned} \varvec{V_{\omega }}=\begin{pmatrix} V_{11} &{} V_{12} \\ V_{12} &{} V_{22} \end{pmatrix}, ~\varvec{H_{\omega }}=\begin{pmatrix} H_{11} &{} H_{12} \\ H_{12} &{}H_{22}\end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} V_{11}&=\mathrm {E}[\{\omega (X_0)(\dot{\phi }X_0)(X_1-\phi X_{0}-\mu _{\epsilon })\}^2],\\ V_{22}&=\mathrm {E}[\{\omega (X_0)(X_1-\phi X_{0}-\mu _{\epsilon })\}^2],\\ V_{12}&=\mathrm {E}[\omega ^2(X_0)(\dot{\phi }X_0)(X_1-\phi X_{0}-\mu _{\epsilon })^2]\\ H_{11}&=\mathrm {E}[\omega (X_0)(\dot{\phi }X_0)^2],~H_{12}=\mathrm {E}[\omega (X_0)(\dot{\phi }X_0)],\\ H_{22}&=\mathrm {E}[\omega (X_0)],~ \dot{\phi }=\frac{\partial \phi }{\partial \alpha } =\frac{\sum _{s=1}^{\infty }\log (1-\alpha \exp \{-s|\alpha |\})}{(1-\alpha )\log ^2(1-\alpha )} \nonumber \\&\quad +\sum _{s=1}^{\infty }\frac{(s|\alpha |-1)\exp \{-s|\alpha |\}}{\log (1-\alpha )(1-\alpha \exp \{-s|\alpha |\})}, \end{aligned}$$

$\omega (\cdot )$ is a weight function. It can be verified that $\varvec{H_{\omega }}$ is a invertible matrix.

Theorem 2

Suppose $\mathrm {E}|X_t|^4<\infty$. Then, we have

$$\begin{aligned} \sqrt{n}(\widehat{\varvec{\eta }}_{CLS}-\varvec{\eta })\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{H_{CLS}}^{-1}\varvec{V_{CLS}}\varvec{H_{CLS}}^{-1}), \end{aligned}$$

where $\varvec{V_{CLS}}$ and $\varvec{H_{CLS}}$ are given by $\varvec{V_{\omega }}$ and $\varvec{H_{\omega }}$, with $\omega (X_{0})=1$.

4.2 Weighted conditional least squares estimator

In general, the CLS estimator is not asymptotically efficient. To improve the efficiency, we consider the WCLS estimator as an alternative one to the CLS estimator. In this section, we focus on the WCLS method with a known weight function. The WCLS estimator $\widehat{\varvec{\eta }}_{WCLS}$=$(\widehat{\alpha }_{WCLS}, \widehat{\mu _{\epsilon }}_{WCLS})^{'}$ can be obtained by minimizing

$$\begin{aligned} Q_2(\varvec{\eta })&:=\sum _{t=1}^{n}\omega (X_{t-1}) (X_t-\phi X_{t-1}-\mu _{\epsilon })^2\nonumber \\&=\sum _{t=1}^{n}\omega (X_{t-1})\left( X_t-\frac{X_{t-1}}{\log (1-\alpha )}\sum _{s=1}^{\infty }\log (1-\alpha \exp \{-s|\alpha |\})-\mu _{\epsilon }\right) ^2, \end{aligned}$$

(7)

where $\omega (X_{t-1})$ is a suitably chosen weight function. A natural choice of $\omega (X_{t-1})$ may be

$$\begin{aligned} \omega (X_{t-1})=\frac{1}{X_{t-1}+c_1}, \end{aligned}$$

(8)

where $c_1$ is a positive constant.

The following result establishes the asymptotic distribution of $\widehat{\varvec{\eta }}_{WCLS}$. The proof is similar to the proof of Theorem 2 and we omit it.

Theorem 3

Suppose $\mathrm {E}|X_t|^4<\infty$. Then, we have

$$\begin{aligned} \sqrt{n}(\widehat{\varvec{\eta }}_{WCLS}-\varvec{\eta })\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{H_{WCLS}}^{-1}\varvec{V_{WCLS}}\varvec{H_{WCLS}}^{-1}), \end{aligned}$$

where $\varvec{V_{WCLS}}$ and $\varvec{H_{WCLS}}$ are given by $\varvec{V_{\omega }}$ and $\varvec{H_{\omega }}$, with $\omega (X_{0})=1/(X_0+c_1)$.

4.3 Modified quasi-likelihood estimator

Let $\varvec{\tau }=(\alpha ,\sigma _{\epsilon }^2)^{'}$. Recall that, from Proposition 1(iii), the expression for the one-step conditional variance is

$$\begin{aligned} \mathrm {V_{\varvec{\tau }}}(X_t|X_{t-1})=\mathrm {Var}(X_t|X_{t-1})=\beta X_{t-1}+\sigma _{\epsilon }^2, \end{aligned}$$

where $\beta$ is given in Definition 1. The MQL estimator $\widehat{\varvec{\eta }}_{MQL}=(\widehat{\alpha }_{MQL}, ~\widehat{\mu _{\epsilon }}_{MQL})^{'}$ can be obtained by minimizing

$$\begin{aligned} Q_3(\varvec{\eta })&:=\sum _{t=1}^{n}\mathrm {V_{\widehat{\varvec{\tau }}}^{-1}}(X_{t}|X_{t-1}) (X_t-\phi X_{t-1}-\mu _{\epsilon })^2 \nonumber \\&=\sum _{t=1}^{n}\mathrm {V_{\widehat{\varvec{\tau }}}^{-1}}(X_{t}|X_{t-1})\left( X_t-\frac{X_{t-1}}{\log (1-\alpha )}\sum _{s=1}^{\infty }\log (1-\alpha \exp \{-s|\alpha |\})-\mu _{\epsilon }\right) ^2, \end{aligned}$$

(9)

where $\widehat{\varvec{\tau }}$ is a consistent estimator of $\varvec{\tau }$. Note that $\widehat{\varvec{\eta }}_{CLS}$ is a consistent estimator of $\varvec{\eta }$ (see Theorem 2), while the consistent estimator of $\sigma _{\epsilon }^2$ can be obtained, as follows:

The first method is based on the moment estimator

$$\begin{aligned} \widehat{\sigma }_{\epsilon }^2=(1-\widehat{\phi }^2)s^2-\widehat{\beta }\overline{X}, \end{aligned}$$

(10)

where $s^2=\sum _{t=1}^{n}(X_t-\overline{X})^2/(n-1)$, $\overline{X}=\sum _{t=1}^{n}X_t/n$, $\widehat{\phi }=\frac{1}{\mathrm {log}(1-\widehat{\alpha })}\sum _{s=1}^{\infty }\mathrm {log}(1-\widehat{\alpha }\exp \{-s|\widehat{\alpha }|\})$, $\widehat{\beta }=\frac{1}{\mathrm {log}(1-\widehat{\alpha })}\sum _{s=1}^{\infty }(2s-1)\mathrm {log}(1-\widehat{\alpha }\exp \{-s|\widehat{\alpha }|\})-\widehat{\phi }^2$, $\widehat{\alpha }$ is the CLS estimator of $\alpha$.

The second method is based on the two-step CLS method which has been discussed by Karlsen and Tjøstheim (1988). Let

$$\begin{aligned} S(\alpha ,\mu _{\epsilon },\sigma _{\epsilon }^{2})&=\sum _{t=1}^{n}[\{X_t-\mathrm {E}(X_t|X_{t-1})\}^2-\mathrm {Var}(X_t|X_{t-1})]^2. \end{aligned}$$

Then, the consistent estimator of $\sigma _{\epsilon }^2$ may be obtained by minimizing $S(\widehat{\alpha }_{CLS},\widehat{\mu _{\epsilon }}_{CLS},\sigma _{\epsilon }^{2})$ with respect to $\sigma _{\epsilon }^2$.

Following Zheng et al. (2007), we establish the asymptotic distribution of $\widehat{\varvec{\eta }}_{MQL}$ in the following theorem.

Theorem 4

Suppose $\mathrm {E}|X_t|^4<\infty$. Then, we have

$$\begin{aligned} \sqrt{n}(\widehat{\varvec{\eta }}_{MQL}-\varvec{\eta })\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{H_{MQL}}^{-1}\varvec{V_{MQL}}\varvec{H_{MQL}}^{-1}), \end{aligned}$$

where $\varvec{V_{MQL}}$ and $\varvec{H_{MQL}}$ are given by $\varvec{V_{\omega }}$ and $\varvec{H_{\omega }}$, with $\omega (X_{0})=\mathrm {V_{\varvec{\tau }}^{-1}}(X_1|X_{0})$.

5 Simulation studies

In this section, the estimators described earlier are compared by simulations. Consider

$$\begin{aligned} X_{t}=\alpha \diamond X_{t-1}+\epsilon _{t},~t\ge 1, \end{aligned}$$

where $\{\epsilon _t\}$ is a sequence of iid Poisson random variables (Model A) with mean $\mu _{\epsilon }$ or iid generalized Poisson (GP) random variables (Model B) with $\mu _{\epsilon }=\lambda _{\epsilon }/(1-\kappa _{\epsilon })$ .

Remark 2

A random variable X has a GP distribution with parameters $\lambda$ and $\kappa$, which we denote by GP($\lambda$, $\kappa$), if its pmf is

$$\begin{aligned} \mathrm {P}(X=x)=\left\{ \begin{array}{ll} \lambda (\lambda +\kappa x)^{x-1}\mathrm {e}^{-(\lambda +\kappa x)}/x!,&{} \quad x=0,1,2\ldots ,\\ 0,&{} \quad \mathrm {for}~x>m~\mathrm {if}~\kappa <0,\\ \end{array} \right. \end{aligned}$$

where $\lambda >0$, $\max (-1,-\lambda /m)<\kappa <1$, and m ($\le 4$) is the largest positive integer for which $\lambda +\kappa m>0$ when $\kappa <0$. The mean and variance of GP($\lambda$, $\kappa$) are

$$\begin{aligned} \mathrm {E}(X)=\frac{\lambda }{1-\kappa },~~~\mathrm {Var}(X)=\frac{\lambda }{(1-\kappa )^3}. \end{aligned}$$

In the simulation, we generate the GSCINAR(1) sample with the sample size equals to $n+1000$ and discard the first 1000 observations. We generate the data from the models and set the sample sizes $n=300, 500, 800, 1000$. The true values of the parameters are:

Model A: (A1) $(\alpha , \mu _{\epsilon })=(-2, 2)$; (A2) $(\alpha , \mu _{\epsilon })=(-1.5, 2.5)$;

Model B: (B1) $(\alpha , \lambda _{\epsilon }, \kappa _{\epsilon })=(0.8, 0.5, 0.5)$; (B2) $(\alpha , \lambda _{\epsilon }, \kappa _{\epsilon })=(0.85, 0.75, 0.5)$.

Fig. 1

The sample paths of Models (A1)–(B2) with the sample size $n=500$

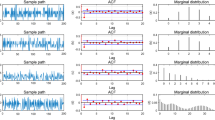
Figure 1 is the sample paths from Models A and B. Table 4 lists some statistics of Models A and B including the mean, variance, first-order autocorrelation coefficient (ACF(1)) and zero probability ($p_0$). Specially, the zero probability is computed from the average percentages of zeros in time series of length 5000 generated from the corresponding models. The average is obtained based on 1000 replications.

Table 4 Some statistics for Models (A1)–(B2)

To compare the three methods, we calculate the mean squared error (MSE) and standard deviation (SD) based on $m=1000$ replications for each combinations; $\mathrm {MSE}=\frac{1}{m}\sum _{k=1}^{m}(\widehat{\alpha }_{k}-\alpha )^2$, $\mathrm {SD}=\sqrt{\frac{1}{m-1}\sum _{k=1}^{m}(\widehat{\alpha }_{k}-\overline{\alpha })^2}$, where $\widehat{\alpha }_{k}$ is the estimator of $\alpha$ at the kth replication and $\overline{\alpha }=\frac{1}{m}\sum _{k=1}^{m}\widehat{\alpha }_{k}$. For simplification of the computation, all the infinite sum in (6), (7) and (9) are approximated by the corresponding finite sum running $s=1, \ldots ,200$.

To choose a more suitable weight for the WCLS method, we firstly compare the WCLS methods with different weights. We suppose that $c_1$ in (8) equals to 1, 3, 5, 7 and 9, respectively. The simulation results are summarized in Table 5, which indicates that there is no significant difference among the five weights and a little better estimator can be obtained when $c_1=3,5,7, 9$. In the following, we set $c_1=3$.

Table 5 The MSEs and SDs of the WCLS estimators with different weights and the sample size $n=1000$

Table 6 The MSEs and SDs of the estimators

From Table 6, the MSEs and SDs of the estimators decrease as the sample size n increases, as expected. This finding can be supported by the box plots shown in Fig. 2 (the box plots are symmetric and centered around the true parameter value). Next, we compare the three methods by observing the MSEs and SDs in Table 6. We find that the WCLS and MQL methods perform better than the CLS method. The smaller SDs indicate that the WCLS method improves the efficiency of the estimation and the weight function is satisfactory. The WCLS and MQL methods give the similar results in most cases and the MQL method can be a little better than the WCLS method. Figure 3 shows the QQ plots of the CLS, WCLS and MQL estimators for Model (B2) with the sample size $n=1000$, which indicates that the CLS, WCLS and MQL estimators are asymptotically normal for all the parameters. Similar results can be obtained for all parameter combinations and the figures are also omitted.

Fig. 2

Box plots from 1000 simulated estimators of $\alpha$ and $\mu _{\epsilon }$ with the sample size $n=1000$. (A1) $\alpha =-2$, (A1) $\mu _{\epsilon }=2$, (A2) $\alpha =-1.5$, (A2) $\mu _{\epsilon }=2.5$, (B1) $\alpha =0.8$, (B1) $\mu _{\epsilon }=1$, (B2) $\alpha =0.85$, (B2) $\mu _{\epsilon }=1.5$

Fig. 3

QQ plots of the CLS, WCLS and MQL estimators for Model (B2) with the sample size $n=1000$

To further compare the three methods, a contaminated model is considered here.

Definition 2

(Contaminated GSCINAR(1) Model). A stochastic process $(Y_k)_{k\in \mathbb {Z_{+}}}$ is called a contaminated GSCINAR(1) model if

$$\begin{aligned} Y_k= X_k+\xi _kc_2,~~~k\in \mathbb {Z_{+}}, \end{aligned}$$

(11)

where $(X_k)_{k\in \mathbb {Z_{+}}}$ is a GSCINAR(1) process given by Definition 1. $c_2$ is a positive integer and it represents the contamination’s size. $(\delta _k)_{k\in \mathbb {Z_{+}}}$ is a sequence of iid Bernoulli($\delta$) random variables. It is obvious to see that the contamination percentage is $\delta$. $(X_k)_{k\in \mathbb {Z_{+}}}$ and $(\xi _k)_{k\in \mathbb {Z_{+}}}$ are independent.

Table 7 The MSEs and SDs of the estimators in the contaminated situation with the sample size $n=1000$

For comparison, we give the simulation results of Models A and B with the sample size $n=1000$ and different contamination percentages $\delta =0.1$, 0.2. Here we suppose $c_2=1$ in (11). From Table 7, we find that the three methods produce the worse estimator as the contamination percentage $\gamma$ increases. The contaminating data have a more significant impact on the WCLS and MQL methods than the CLS method. The explanation for this phenomenon may be that the WCLS and MQL methods use more wrong information in the contaminating data due to the existence of the weight functions. However, the WCLS and MQL methods are still better than the CLS method especially when we consider the SD. As before, the WCLS and MQL methods give the competitive results and the WCLS method is a little worse than the MQL method when the contaminating data exists.

In the two simulation studies, we find that the WCLS and MQL methods can produce more satisfactory results than the CLS method. While the WCLS method is reliable in each situation, it may cause inconvenience because choosing a suitable weight is a problem which can not be avoided. Based on the above discussions, we conclude that the inverse of the conditional variance is a more satisfactory weight function and we recommend the use of the MQL method to estimate the model parameters.

6 Real data analysis

In this section, we conduct two applications to illustrate the usefulness of the GSCINAR(1) process in explaining underdispersed and overdispersed phenomena. The two data sets, exhibiting underdispersion and overdispersion, are used. We compare our process with some INAR(1) models based on the binomial and negative binomial thinning operators:

• POINAR(1) model (Alzaid and Al-Osh 1987);

• NGINAR(1) model (Ristić et al. 2009);

• ZMGINAR(1) model (Barreto-Souza 2015).

The MQL method is used to estimate the unknown parameters of the fitted models. We assume that $\{\epsilon _t\}$ in the GSCINAR(1) model is a sequence of iid GP($\lambda _{\epsilon }$, $\kappa _{\epsilon }$) random variables. The moment estimators of $\lambda _{\epsilon }$, $\kappa _{\epsilon }$ are given by

$$\begin{aligned} \widehat{\kappa }_{\epsilon }=1-\frac{\widehat{\mu }_{\epsilon }}{\widehat{\sigma }_{\epsilon }^2},~~~ \widehat{\lambda }_{\epsilon }=\widehat{\mu }_{\epsilon }(1-\widehat{\kappa }_{\epsilon }), \end{aligned}$$

where $\widehat{\mu }_{\epsilon }$ is the MQL estimator of $\mu _{\epsilon }$ and $\widehat{\sigma }_{\epsilon }^2$ is the moment estimator (see (10)). Also, the following statistics of the fitted models are computed: mean, variance, index of dispersion $I_d$ (the variance to mean ratio), first-order autocorrelation coefficient ACF(1), root mean square of differences between observations and predicted values (RMS) and zero probability $p_0$. As before, the zero probability is computed from the average percentages of zeros in time series of length 5000 generated from the corresponding model and the average is obtained based on 1000 replications.

6.1 Modelling overdispersion

In this section, one real example is applied to show good performance of the GSCINAR(1) model in fitting overdispersed count data. We applied our model to fit the series of a monthly count of criminal mischief reported in the twentyninth police car beat in Pittsburgh. The data consists of 137 observations starting in January 1990 and ending in May 2001.

Table 8 Descriptive statistics for the criminal mischief count data

Fig. 4

The sample path, ACF and PACF of the criminal mischief count data

Table 8 displays some descriptive statistics of the criminal mischief counts. We find that the sample mean is smaller than the sample variance. Thus, the data set seems to be overdispersed. The zero probability equals to zero indicates that the data set is zero-truncated. A time series plot, the autocorrelation function (ACF) and partial autocorrelation function (PACF) are shown in Fig. 4, which indicates that an autoregressive process of order one is suitable to model the series. In Table 9, we provide the estimators, mean, variance, $I_d$, ACF(1), RMS and $p_0$ of the fitted models. From the results presented in Table 9, although the POINAR(1) model can capture the zero-truncated characteristic of the data set, it performs worst when we consider ACF(1) and RMS. Furthermore, it is very clear that the POINAR(1) process is not suitable for modelling this data set since it can not explain overdispersion. While the NGINAR(1) model gives the best fit of ACF(1), it fails to describe the overdispersed phenomenon accurately. The GSCINAR(1) model can capture overdispersion accurately and $I_d$ of the GSCINAR(1) model is very close to the empirical $I_d$. Moreover, the GSCINAR(1) model performs well when we consider ACF(1). During our study, we also applied the ZMGINAR(1) model to fit this data set. However, the constraints on the model parameters lead to the result that the ZMGINAR(1) model is not suitable for the data. Based on these facts, we recommend the use of the GSCINAR(1) model to fit this data set.

Table 9 Estimators of the parameters and statistics for the criminal mischief count data

6.2 Modelling underdispersion

To illustrate the usefulness of the GSCINAR(1) process in modelling underdispersion, we consider an observation of this time series corresponds to the number of different IP addresses ($\approx$ different users) registered within periods of 2-min length at the server of the Department of Statistics of the University of Würzburg in November and December 2005. In particular, we focus on the time series collected on November 29th, 2005, between 10 o’clock in the morning and 6 o’clock in the evening, a time series of length 241. These data have been investigated by Weiß (2007, 2008a) and Zhu (2012a, b).

Table 10 Descriptive statistics for the ip count data

Table 11 Estimators of the parameters and statistics for the ip count data

Fig. 5

The sample path, ACF and PACF of the ip count data

Some descriptive statistics of the data are shown in Table 10, which reveals that the data set shows underdispersion since the empirical $I_d$ is smaller than one. The plots of the data, ACF and PACF are presented in Fig. 5. Within these fitted models, the estimators, mean, variance, $I_d$, ACF(1), RMS and $p_0$ are summarized in Table 11, which shows that the NGINAR(1) model is not a good choice since it gives the wrong information that the data set is overdispersion. The POINAR(1) model has the best results when we consider some statistics. To be specific, it gives the best fit when we consider the mean, ACF(1), RMS and $p_0$. However, the GSCINAR(1) model gives the most satisfactory results among the alternative models based on the variance and $I_d$. It is well-known that the POINAR(1) model encounters the problem that it can only deal with equidispersion. For this data set, the POINAR(1) model fails to account for the underdispersed phenomenon. The ZMGINAR(1) model is practicable in this case, since $\widehat{\pi }=-1.1186$ and $\widehat{\mu }=0.6097$ statisfy the constraint $\pi \in (-1/\mu ,1)$. The ZMGINAR(1) and GSCINAR(1) models capture the underdispersed feature well and the GSCINAR(1) model is a little better than the ZMGINAR(1) model when we consider $I_d$. Based on ACF(1), RMS and $p_0$, the GSCINAR(1) model also gives the better fit than the ZMGINAR(1) model. In summary, the GSCINAR(1) process gives the satisfactory fits based on each statistics and the most comprehensive performances among the alternative models. We conclude that the GSCINAR(1) model is the best choice for fitting this data set.

7 Discussion

In this paper, we have introduced GSCINAR(1) process. The strict stationarity, ergodicity and some statistical properties of the process are obtained. The CLS, WCLS and MQL methods are used to estimate the model parameters. Two real examples show that our model not only can model the underdispersed data but also has the ability to explain the overdispersed phenomenon.

However, more research is still necessary for some aspects of the GSCINAR(1) process. One of the most important issues may be extending the GSCINAR(1) process to the higher-order autoregressive model.

Definition 3

An INAR(p) model based on the GSC thinning operator, denoted by GSCINAR(p), is defined by the following difference equation:

$$\begin{aligned} X_{t}=\alpha _1 \diamond X_{t-1}+\alpha _2 \diamond X_{t-2}+\cdots +\alpha _p \diamond X_{t-p}+\epsilon _{t},~t\ge 1, \end{aligned}$$

(12)

where $\alpha _i\diamond X_{t-i}=\sum _{j=1}^{X_{t-i}}W_j$, $i=1,\ldots ,p$, $\{W_j\}$ is a sequence of iid GSC($\alpha _i$, $\exp \{-|\alpha _i|\}$) random variables with the finite mean $\phi _i$ and variance $\beta _i$, $\alpha _i<1$, $\alpha _i\ne 0$. Here, we write $\phi _i=\frac{1}{\mathrm {log}(1-\alpha _i)}\sum _{s=1}^{\infty }\mathrm {log}(1-\alpha _i\exp \{-s|\alpha _i|\})$ and $\beta _i=\frac{1}{\mathrm {log}(1-\alpha _i)}\sum _{s=1}^{\infty }(2s-1)\mathrm {log}(1-\alpha _i\exp \{-s|\alpha _i|\})-\phi _i^2$. $\{\epsilon _t\}$ is an innovation sequence of iid non-negative integer-valued random variables, uncorrelated with the past values of $\{X_t\}$. Let $\mu _{\epsilon }=\mathrm {E}(\epsilon _t)$, $\sigma _{\epsilon }^{2}=\mathrm {Var}(\epsilon _t)$ (we assume that they exist).

We give some statistical properties of the GSCINAR(p) model in the following proposition. The proof of the proposition is similar to the proof of Proposition 2.1 in Zhang et al. (2010) and we omit it.

Proposition 2

Suppose $\{X_t\}$ is a stationary process satisfying (12). Then for $t\ge 1$,

• (i) $\mathrm {E}(X_t|X_{t-i},i=1,\ldots ,p)=\sum _{i=1}^{p}\phi _i X_{t-i}+\mu _{\epsilon }$,

• (ii) $\mathrm {E}(X_t)=\mu _{\epsilon }/(1-\sum _{i=1}^{p}\phi _i)$,

• (iii) $\mathrm {Var}(X_t|X_{t-i},i=1,\ldots ,p)=\sum _{i=1}^{p}\phi _i X_{t-i}+\sigma _{\epsilon }^2$,

• (iv) $\mathrm {Var}(X_t)=[\mu _{\epsilon }\sum _{i=1}^{p}\phi _i+\sigma _{\epsilon }^2(1-\sum _{i=1}^{p}\phi _i)]\big /[(1-\sum _{i=1}^{p}\phi _i)(1-\sum _{i=1}^{p}\phi _i^2)]$,

• (v) $\rho _k=\mathrm {Corr}(X_{t+k},X_t)=\sum _{i=1}^{p}\phi _i\rho _{k-i}$, $k=1,\ldots$,

where $\phi _i$ and $\beta _i$ are given in Definition 3.

The strict stationarity and ergodicity of the GSCINAR(p) model are given by the following theorem. Again, the proof is omitted because it is similar to the proof of Theorem 2.1 in Zhang et al. (2010).

Theorem 5

If all roots of the polynomial $\lambda ^p-\phi _1\lambda ^{p-1}-\cdots -\phi _{p-1}\lambda -\phi _{p}=0$ are inside the unit circle, then there exists an unique strictly stationary integer-valued random series $\{X_t\}$ satisfying

$$\begin{aligned} X_{t}=\alpha _1 \diamond X_{t-1}+\alpha _2 \diamond X_{t-2}+\cdots +\alpha _p \diamond X_{t-p}+\epsilon _{t},~t\ge 1, \end{aligned}$$

$\mathrm {Cov}(X_s,\epsilon _t)=0$ for $s<t$. Furthermore, the process is an ergodic process.

We must point out that the GSCINAR(p) model deserves a more detailed analysis in a future research. In particular, the topic of parameter estimation should be treated in more detail. For example, it would be interesting in applying the empirical likelihood approach to the GSCINAR(p) model and investigating the asymptotic behavior of the estimators. Furthermore, the forecasting problem for the GSCINAR(p) model would be particularly relevant for practice.

Appendix

As we mentioned in the third paragraph of Sect. 2, the infinite sum in the mean and variance for GSC($\alpha$, $\theta$) are convergent, where $\alpha <1$, $\alpha \ne 0$ and $0<\theta <1$. We illustrate it, as follows:

Let $\alpha <0$. Denote $S_n=\sum _{s=1}^{n}\log (1-\alpha \theta ^{s})$. Then, we have

$$\begin{aligned} 0{\le }\lim _{n\rightarrow \infty }\sup _{p{>}0}|S_{n+p}{-}S_n|{=}\lim _{n\rightarrow \infty }\sup _{p{>}0}\sum _{s{=}n+1}^{n+p}\log (1{-}\alpha \theta ^{s}){\le }\lim _{n\rightarrow \infty }\sup _{p{>}0} [p\log (1{-}\alpha \theta ^{n})]{=}0. \end{aligned}$$

By the Cauchy criterion of series, the infinite sum $\sum _{s=1}^{\infty }\log (1-\alpha \theta ^{s})$ are convergent.

Denote $S_n^{'}=\sum _{s=1}^{n}(2s-1)\log (1-\alpha \theta ^{s})$. Then, we have

$$\begin{aligned} 0&\le \lim _{n\rightarrow \infty }\sup _{p>0}|S_{n+p}^{'}-S_n^{'}|=\lim _{n\rightarrow \infty }\sup _{p>0}\sum _{s=n+1}^{n+p}(2s-1)\log (1-\alpha \theta ^{s})\\&\le \lim _{n\rightarrow \infty }\sup _{p>0}p\cdot 2(n+p)\log (1-\alpha \theta ^{n+1})\le \lim _{n\rightarrow \infty }\sup _{p>0}2p(n+p)(-\alpha )\theta ^{n+1}=0, \end{aligned}$$

using $x\ge \log (1+x)$ for $x\ge 0$. By the Cauchy criterion of series, the infinite sum $\sum _{s=1}^{\infty }(2s-1)\log (1-\alpha \theta ^{s})$ are convergent. Following the same way, we can see that the two infinite sum are convergent when $0<\alpha <1$. $\square$

Proof of Proposition 1

We have (i) and (iii), i.e.,

$$\begin{aligned} \mathrm {E}(X_{t}|X_{t-1})=\mathrm {E}(\alpha \diamond X_{t-1}+\epsilon _{t}|X_{t-1})=\phi X_{t-1}+\mu _{\epsilon } \end{aligned}$$

and

$$\begin{aligned} \mathrm {Var}(X_{t}|X_{t-1})&=\mathrm {Var}(\alpha \diamond X_{t-1}+\epsilon _{t}|X_{t-1})\\&=\mathrm {Var}(\alpha \diamond X_{t-1}|X_{t-1})+\mathrm {Var}(\epsilon _{t}|X_{t-1})\\&=\beta X_{t-1}+\sigma _{\epsilon }^2. \end{aligned}$$

Then, we get

$$\begin{aligned} \mathrm {E}(X_{t})=\mathrm {E}[\mathrm {E}(X_{t}|X_{t-1})]=\phi \mathrm {E}(X_{t-1})+\mu _{\epsilon } \end{aligned}$$

and

$$\begin{aligned} \mathrm {Var}(X_{t})&=\mathrm {Var}[\mathrm {E}(X_{t}|X_{t-1})]+\mathrm {E}[\mathrm {Var}(X_{t}|X_{t-1})]\\&=\mathrm {Var}(\phi X_{t-1}+\mu _{\epsilon })+\mathrm {E}(\beta X_{t-1}+\sigma _{\epsilon }^2)\\&=\phi ^2\mathrm {Var}(X_{t-1})+\beta \mathrm {E}(X_{t-1})+\sigma _{\epsilon }^2, \end{aligned}$$

which yield (ii) and (iv), due to the stationarity; $\mathrm {E}(X_{t})=\mathrm {E}(X_{t-1})$ and $\mathrm {Var}(X_{t})=\mathrm {Var}(X_{t-1})$. Moreover, we have (v), i.e.,

$$\begin{aligned} \mathrm {Cov}(X_{t},X_{t+k})&=\mathrm {Cov}(X_{t}, \underbrace{\alpha \diamond \cdots \diamond \alpha }_{k}\diamond X_{t})+\mathrm {Cov}(X_{t},\sum _{j=0}^{k-1} \underbrace{\alpha \diamond \cdots \diamond \alpha }_{j} \diamond \epsilon _{t+k-j})\\&=\mathrm {E}\{\mathrm {E}[X_{t}(\underbrace{\alpha \diamond \cdots \diamond \alpha }_{k}\diamond X_{t})|X_{t}]\} -\mathrm {E}(\underbrace{\alpha \diamond \cdots \diamond \alpha }_{k}\diamond X_{t})\cdot \mathrm {E}(X_{t})\\&=\phi ^k\{\mathrm {E}(X_t^2)-[\mathrm {E}(X_t)]^2\}\\&=\phi ^k\mathrm {Var}(X_t). \end{aligned}$$

$\square$

Proof of Theorem 1

We first introduce a random sequence $\{X_{t}^{(n)}\}$,

$$\begin{aligned} X_{t}^{(n)}=\left\{ \begin{array}{ll} 0,&{} \quad n<0,\\ \epsilon _t,&{} \quad n=0,\\ \alpha \diamond X_{t-1}^{(n-1)}+\epsilon _{t},&{} \quad n>0,\\ \end{array} \right. \end{aligned}$$

where $\mathrm {Cov}(X_{s}^{(n)},\epsilon _t)=0$ when $s<t$ for any n.

As in Li et al. (2015), we can verify: existence of $\{X_t\}$ satisfying (5), i.e., (A1) $X_{t}^{(n)}\in L^2$, $n>0$, (A2) $X_t^{(n)}$ is a Cauchy sequence, (A3) $\{X_t\}$ satisfies (5), uniqueness, strict stationarity and ergodicity. The details are omitted here to save space. $\square$

Proof of Theorem 2

From (6), solving $\partial Q_1(\varvec{\eta })/\partial \alpha =0$ and $\partial Q_1(\varvec{\eta })/\partial \mu _{\epsilon }=0$ lead to the CLS estimators of $\alpha$ and $\mu _{\epsilon }$. Now, let $\mathcal {F}_n=\sigma \{X_0,X_1,\ldots ,X_n\}$, $M_{n}^{(1)}=-\frac{1}{2}(\partial Q_1(\varvec{\eta })/\partial \alpha )=\sum _{t=1}^{n}\dot{\phi }X_{t-1}\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big )$, $M_0^{(1)}=0$. Also, $M_{n}^{(2)}=-\frac{1}{2}(\partial Q_1(\varvec{\eta })/\partial \mu _{\epsilon })=\sum _{t=1}^{n}\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big )$, $M_0^{(2)}=0$. Then, it is easy to see that $\{M_{n}^{(1)},\mathcal {F}_n\}_{n\ge 0}$ and $\{M_{n}^{(2)},\mathcal {F}_n\}_{n\ge 0}$ are martingales. The martingale central limit theorem and Cramer-Wold’s device imply that

$$\begin{aligned} n^{-1/2}(M_n^{(1)},M_n^{(2)})^{'}\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{V_{CLS}}). \end{aligned}$$

Using Taylor’s expansion, we have

$$\begin{aligned} \mathbf {0}{=-}\frac{1}{2\sqrt{n}}\frac{\partial Q_1(\widehat{\varvec{\eta }}_{CLS})}{\partial \varvec{\eta }}{=-}\frac{1}{2\sqrt{n}}\frac{\partial Q_1(\varvec{\eta })}{\partial \varvec{\eta }} -\frac{1}{2n}\frac{\partial ^2 Q_1(\varvec{\eta })}{\partial \varvec{\eta }\partial \varvec{\eta ^{'}}}\sqrt{n}(\widehat{\varvec{\eta }}_{CLS}{-}\varvec{\eta }){+}o_p(n^{-1/2}). \end{aligned}$$

Since we have proved that $-\frac{1}{2\sqrt{n}}\frac{\partial Q_1(\varvec{\eta })}{\partial \varvec{\eta }} \mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{V_{CLS}})$, after some algebra, we have

$$\begin{aligned} \sqrt{n}(\widehat{\varvec{\eta }}_{CLS}-\varvec{\eta })\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{H_{CLS}}^{-1}\varvec{V_{CLS}}\varvec{H_{CLS}}^{-1}). \end{aligned}$$

This completes the proof. $\square$

Proof of Theorem 4

Following Zheng et al. (2007), we firstly suppose $\varvec{\tau }$ is known. Let

$$\begin{aligned} L_{n}^{(1)}(\varvec{\tau },\varvec{\eta })&=\sum _{t=1}^{n}\mathrm {V_{\varvec{\tau }}^{-1}}(X_t| X_{t-1})\dot{\phi }X_{t-1}\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big ),~L_{0}^{(1)}(\varvec{\tau },\varvec{\eta })=0,\\ L_{n}^{(2)}(\varvec{\tau },\varvec{\eta })&=\sum _{t=1}^{n}\mathrm {V_{\varvec{\tau }}^{-1}}(X_t|X_{t-1})\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big ),~L_{0}^{(2)}(\varvec{\tau },\varvec{\eta })=0. \end{aligned}$$

Similar to Theorem 2, we have

$$\begin{aligned} n^{-1/2}\big (L_{n}^{(1)}(\varvec{\tau },\varvec{\eta }),L_{n}^{(2)}(\varvec{\tau },\varvec{\eta })\big )^{'} \mathop {\longrightarrow }\limits ^{d} N(\mathbf {0},\varvec{V_{MQL}}). \end{aligned}$$

Now, we replace $V_{\varvec{\tau }}^{-2}(X_t|X_{t-1})$ by $V_{\varvec{\widehat{\tau }}}^{-2}(X_t|X_{t-1})$, where $\varvec{\widehat{\tau }}$ is a consistent estimator of $\varvec{\tau }$. Then we want

$$\begin{aligned} n^{-1/2}\big (L_{n}^{(1)}(\varvec{\widehat{\tau }},\varvec{\eta }),L_{n}^{(2)}(\varvec{\widehat{\tau }},\varvec{\eta })\big )^{'} \mathop {\longrightarrow }\limits ^{d} N(\mathbf {0},\varvec{V_{MQL}}). \end{aligned}$$

For this we need to prove that $\frac{1}{\sqrt{n}}L_{n}^{(i)}(\varvec{\widehat{\tau }},\varvec{\eta })- \frac{1}{\sqrt{n}}L_{n}^{(i)}(\varvec{\tau },\varvec{\eta })\mathop {\longrightarrow }\limits ^{P}0,~i=1,2$ [its proof is omitted here, since the argument is the same as in Zheng et al. (2007)]. Following the proof of Theorem 2, by Taylor’s expansion and some algebra, we have

$$\begin{aligned} \sqrt{n}(\widehat{\varvec{\eta }}_{MQL}-\varvec{\eta })\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{H_{MQL}}^{-1}\varvec{V_{MQL}}\varvec{H_{MQL}}^{-1}). \end{aligned}$$

This completes the proof. $\square$