Fixed-Time Disturbance Observer-Based Control for Uncertainty Systems Applied to Permanent-Magnet Speed Control

Abstract

For a class of uncertain systems, a fixed-time disturbance observer is suggested. The proposed observer not only estimated the disturbance but also ensured the fixed-time convergence, leading to the increased accuracy of the disturbance estimation together with the improved estimation speed. Taking the proposed observer in combination with a state-feedback controller and employing it in a fully actuated system, stabilization of the closed-loop system will be assured which allows the control of uncertain systems. With a numerical example to illustrate the efficacy of the scheme, finally, such scheme is successfully applied to the permanent-magnet speed control system, the results show that it has the advantages of rapid convergence speed and favorable control performance.

1 Introduction

Uncertainties are widely occurring in real processes, including but not limited to parameter variations, unmodeled parts, and external unmeasurable disturbances. These uncertainties do adversely affect system performance, leading to stability problems, tracking performance degradation, safety issues, increased cost and complexity, therefore, effective handling of uncertainties is a key challenge in control system design and some elegant schemes are proposed [1,2,3], disturbance observer (DOB)-based strategies linking control strategies with uncertainty and disturbance estimation methods is one efficient and prevalent control technique.

As is known, many uncertainties in control systems are unmeasurable, and DOB methods to estimate uncertainties and disturbances have been made available [4,5,6]. Practical applications of DOB are reported in the literature, including quadrotor helicopter [7], hypersonic vehicle [8] and flexible manipulator [9]. Regarding design methods, notable achievements attained in recent years and that part is reviewed in [10]. Subsequent years also birthed some nice results. Elkayam et al. followed the classical frequency domain DOB design approach with the addition of a multi-resonant term allowing the system an improved periodic signal rejection capability without sacrificing DC gain and crossover frequency [11]. Zheng et al. built a generalized DOB design framework and extended it to a learning scheme with enhanced processing of disturbances featuring repeated components, applicable to non-square or non-minimum phase systems [12]. Guerrero et al. developed an adaptive DOB on the basis of the generalized hyper-twist algorithm, which automatically adjusts the observer gain by introducing an adaptive law to make the model robust to uncertainties [13].

DOB-based control strategies are attractive propositions in which the framework first designs the baseline controller assuming a no-disturbance scenario and then adds an appropriate DOB to compensate for the effect of the estimated uncertainties. First appearing in the late eighties, this has now been in development and application for decades. Yao et al. used Lyapunov and linear matrix inequality (LMI) theory to structure the DOB and controller, respectively, constituting a combined hierarchical control scheme where the availability and uniqueness of the solution guarantee the stochastic admissibility of the system, employed in the multi-disturbance reduction of non-linear Markovian jump singular systems [14]. Vu and Wang combined the unknown input observer and DOB to generate a new form utilized for estimating unknown states and disturbances, weakened constraints, and further solving controllers with LMI-based solutions to asymptotically enable the stability of uncertain polynomial systems [15]. Wang et al. proposed a robust backstepping method integrating DOB and sliding mode control, where the application of DOB simultaneously simplifies the structure of the controller and reduces the switching gain via estimating the centralized uncertainties of the control-oriented model, thereby suppressing the jitter and enabling trajectory tracking of hypersonic vehicles [7].

Following our literature review, it is evident that earlier papers designed asymptotically converging observers and could not guarantee the convergence time, which would result in a bad situation when estimates are too long and the observer-based controller fails as the state escapes before the DOB converges. As a result, in certain practical scenarios, what we require is an accurate estimation in finite time, leading to accurate control. Finite-time DOBs are proposed to let the error converge to zero in finite time, somewhat unfortunately, the estimation time, an important metric as a measure of DOB performance, is hardly available for display expressions [16,17,18]. On this basis, the concept of fixed time was further extended and, as the name denotes, the system can be stabilized over a given time horizon, this wonderful property leading to its application in solving practical issues [19, 20]. Ni et al. described a fixed-time DOB (FTDOB) that is based on the Brunovsky system and consists of two parts: one that achieves uniform convergence for error driving and another that achieves fixed-time convergence for exact estimation and gives a theoretical calculation of an upper boundary on the estimated time [21]. Tian et al. handled matched and mismatched disturbances using a FTDOB and studied the stabilization problem for systems of arbitrary-order integrators via a bi-limit technics to design a switching-free continuous control law and considering the classical finite-time one as a particular exception [22]. Wang and Chen investigated the fixed-time control of mismatched systems and presented a FTDOB as well as a non-singularly sliding mode surface and controller based on it, differing from existing methods in that it guarantees a consistent and bounded convergence time independent of the initial-value condition [23].

The above results are certainly interesting, but one notes that these papers do not cover the problem of fixed-time design of fully actuated (FAC) systems. The unique advantages of FAC systems as being flexible and accurate, safe and efficient have led to a wide range of areas like machine control, aerospace and many others [24,25,26,27,28,29]. Therefore, it is motivating for this study to explore the existence of a similar form of fixed-time observer for FAC systems as in the above mentioned papers. Furthermore, since uncertainty is commonly occurring in practice, the excellence of DOB-based methods in improving the control performance of disturbed systems has attracted our attention to the possibility of following this idea and designing some control algorithms for such systems.

This thesis is used for controlling FAC systems influenced by uncertainties and external unmeasurable disturbances, providing a promising approach for dealing with system uncertainty. The main features are as follows:

• 1. The disturbance estimation is tackled with a novel FTDOB.

• 2. The key advantage of this proposed DOB involves the rapidity of estimating disturbances with high flexibility in adjusting the estimation time to suit different requirements.

• 3. This DOB scheme not only achieves estimation performance comparable to that of conventional DOB, but also exhibits excellent guarantees for convergence performance. In theory, the observer is able to have an exact convergence in a very short time.

• 4. Combining the scheme with feedback control, which allows correct estimation and subsequent elimination of the effects of uncertainties and disturbances, achieves stable control of FAC systems with uncertainties in a simple and straightforward structure.

For the sake of further demonstrating the proposed method, the control of permanent-magnet eddy-current coupler speed control (PECSC) system is considered. Permanent-magnet eddy-current coupler (PEC) is a breakthrough new technology developed in recent years, with high energy efficiency, no rigid contact, low maintenance cost, etc., has been receiving great attention from scholars in various fields [30,31,32,33,34], and since it utilizes the magnetic field to transfer torque and is adjustable and controllable in real-time depending on the load demand, naturally, the related speed control method is worth investigating. The PECSC system is modeled as a fully actuated form, also considering uncertainties and disturbances, employing the new design that is well controlled and achieves a very effective and fast disturbance compensation. The design and simulation results fully demonstrate that this method is a remarkably effective and simple way to tackle such speed control issues.

We proceed as follows. In Sect. 2, a formulation of the problem is given and the solution to be pursued as well as the overall objective are indicated. The design and analysis of the proposed DOB are shown in Sect. 3, and an observer-based synthesis procedure is presented that targets the control law for FAC systems with uncertainties in Sect. 4. Section 5 gives an illustrative numerical example and corresponding simulation results as well as a comprehensive comparison with the conventional method. Section 6 takes the application of the proposed scheme to a PECSC system for simulation studies. As a final point, concluding remarks are derived in Sect. 7.

2 Problem Formulation

In this note, ${\mathbb{R}}$ stands for the set of real numbers, ${\mathbb{R}}^{n}$ for the set of $n \times 1$ column vectors, and ${\mathbb{R}}^{n \times m}$ for the set of $n \times m$ real matrices. $I_{{\left\{ {n,n} \right\}}}$ and $0_{{\left\{ {n,n} \right\}}}$ denote the identity matrix and the zero matrix of dimension $n \times n$, respectively. Besides, for matrix $A$, the inverse matrix is represented by $A^{ - 1}$, the determinant by ${\text{det}}\left( A \right)$, and the eigenvalues by $\lambda (A)$, then if $A$ is a Hurwitz matrix, it satisfies that the real part of all eigenvalues are negative, i.e., ${\text{Re}}(\lambda ) < 0$.

A general system with uncertainties, denoted as

$$\begin{gathered} \dot{x} = Ax + Bu + d(x,t,u,\epsilon(t)), \hfill \\ y = Cx, \hfill \\ \end{gathered}$$

(1)

where $x = \left[ {x_{1} , \cdots ,x_{n} } \right]^{{\text{T}}} \in {\mathbb{R}}^{n}$ represents the states, $y \in {\mathbb{R}}^{p}$ represents the outputs, $\epsilon,u \in {\mathbb{R}}$ represent external disturbances and inputs, $d$ is a function of uncertainties with respect to $x, \, u$ and $\epsilon$, denotes the generalized lumped disturbances, including but not limited to uncertainty, unmodeled components, and external disturbances, written in the form of the expression

$$d = \Delta Ax + \Delta Bu + \sigma (\epsilon,t),$$

where $\sigma$ uniformly signifies the non-linearities contained in the object. $A,B$ and $C$ are known system matrices.

For system (1) discussed, one assumption is considered to be certain and verifiable, that the full state vector can be measured. Another note is that the FAC property of the system is captured by the dimensionality of matrix $B$. An $n \times n$-dimensional $B$ ensures that all degrees of freedom or actuators within the system are controllable independently and finely tuned for achieving the desired effect as required.

This work aims at designing a continuous control strategy $u$ that drives state $x$ of FAC system (1) with uncertainties to zero in fixed time. The general composite control law designing procedure for system (1) consists:

1. Combine uncertainties and external disturbances, then construct DOB for estimating the lumped disturbances.

2. Devise the disturbance compensation gain to achieve the desired specification underlying the disturbance case.

3. Design the feedback controller that guarantees the system stability regardless of the lumped disturbance.

4. Integrate the DOB-based compensation control and feedback controller together with the composite control law such that the system state converges asymptotically.

3 Disturbance Observer Design

3.1 Initial Observer

Using (1) for estimating $d$, the basic DOB is derived as

$$\dot{\hat{d}}(t) = - \Gamma \hat{d}(t) + \Gamma (\dot{x}(t) - Ax(t) - Bu(t))$$

(2)

where $\Gamma$ is the designed gain.

Generally, $d$ is unknown but almost constant over short sample periods, so one can assume that relative to the observer system $d$ varies slowly to reasonably have $\dot{d} = 0$.

Defining the error variable $\vartheta = \hat{d} - d$, and combining (1) and (2) gives

$$\dot{\vartheta } = - \Gamma \vartheta ,$$

(3)

that when choosing a positive diagonal matrix $\Gamma$, then for any $d$ error $\vartheta$ is bounded. This is certainly a good result, yet requires derivatives of states, which makes the above DOB (2) challenging to implement, nevertheless, it provides a basis for further DOB design.

Remark 1:

Convergence of the system (3) has been established under the condition that the disturbance changes slowly with respect to the dynamics of the observer, and in fact one can track some fast time-varying disturbances with bounded errors if the derivative of the disturbance is bounded, as has been corroborated in [35]. Meanwhile, it is a reasonable approximation that the variation rate of the disturbance equals to zero, considering that the changes of certain systems are probably very small and negligible in short time in practical applications.

3.2 Modified Observer

After modifying the above DOB, for the system (1), two auxiliary dynamics linked to the disturbance estimation are regarded in this work

$$\begin{gathered} \dot{z}_{i} (t) = - \Gamma_{i} (z_{i} (t) + \Gamma_{i} x(t)) - \Gamma_{i} (Ax(t) + Bu(t)), \hfill \\ h_{i} (t) = z_{i} (t) + \Gamma_{i} x(t).(i = 1,2) \hfill \\ \end{gathered}$$

(4)

where $z_{i} ,h_{i} \in {\mathbb{R}}^{n} ,$ matrix $\Gamma_{i}$ is constant and of dimension $n \times n$. Redefine the above system by

$$z: = \left[ {\begin{array}{*{20}c} {z_{1} } \\ {z_{2} } \\ \end{array} } \right],h: = \left[ {\begin{array}{*{20}c} {h_{1} } \\ {h_{2} } \\ \end{array} } \right],x^{\prime}: = \left[ {\begin{array}{*{20}c} x \\ x \\ \end{array} } \right],G: = \left[ {\begin{array}{*{20}c} {I_{n,n} } \\ {I_{n,n} } \\ \end{array} } \right],$$

$$\Gamma : = \left[ {\begin{array}{*{20}c} {\Gamma_{1} } & 0 \\ 0 & {\Gamma_{2} } \\ \end{array} } \right],B^{\prime}: = \left[ {\begin{array}{*{20}c} B \\ B \\ \end{array} } \right],A^{\prime}: = \left[ {\begin{array}{*{20}c} A & 0 \\ 0 & A \\ \end{array} } \right],$$

and combine the two observers into one, then a new state $\hat{d}(t)$ is generated using a delay $D$ to estimate the disturbance $d\left( t \right)$, given by the following equations

$$\dot{z}(t) = - \Gamma (z(t) + \Gamma x^{\prime}(t)) - \Gamma (A^{\prime}x^{\prime}(t) + B^{\prime}u(t)),$$

(5)

$$h(t) = z(t) + \Gamma x^{\prime}(t),$$

(6)

$$\hat{d}(t) = \Theta (h(t) - e^{ - \Gamma D} h(t - D)),$$

(7)

where $z,h \in {\mathbb{R}}^{2n} ,$$\hat{d} \in {\mathbb{R}}^{n} ,$ matrices $\Gamma ,\Theta$ are unknowns to be found of dimensions respectively $2n \times 2n$ and $n \times 2n$. Obviously, the observer has to possess the initial state $h(t),t \in \left[ {t_{0} - D,t_{0} } \right]$ due to the delay $D$.

For the above FTDOB (5)-(7), the design and proof are in the following terms:

Theorem 1:

Observer (5)–(7) achieves disturbance estimation in fixed time $D$ with $\Theta = [I_{n,n} ,0_{n,n} ][G,e^{ - \Gamma D} G]^{ - 1} ,$ as well as $\Gamma$ and $D$ satisfying:

1. $\Gamma$ is a positive diagonal matrix;

2. ${\text{det[}}G,e^{ - \Gamma D} G] \ne 0$.

Proof: The error between the observed and actual values is expressed in terms of the variable $\vartheta$, i.e., $\vartheta = \hat{d} - d$, and we prove the validity of Theorem 1 starting from the transient evolution of the state observation error $\vartheta$. Introduce a new error variable $\varpi$ as

$$\varpi = h - Gd,$$

(8)

and with this derivation, for $t\ge{t_{0}}$, one can obtain the error system below

$$ \begin{gathered} \dot{\varpi } = \dot{z} + \Gamma \dot{x^{\prime}} - G\dot{d}, \\ = - \Gamma (z + \Gamma x^{\prime}) - \Gamma (A^{\prime}x^{\prime} + B^{\prime}u) + \Gamma (A^{\prime}x^{\prime} \\ + B^{\prime}u + Gd) - G\dot{d} \\ = - \Gamma (z + \Gamma x^{\prime} - Gd) \\ = - \Gamma \varpi . \\ \end{gathered} $$

(9)

Following the dynamics (5)-(7), when $t \in \left[ {t_{0} - D,t_{0} } \right]$, the observer possesses the initial state, and may be set to $h(t_{0} ) = G\hat{d}_{0}$ with $\hat{d}(t_{0} ) = \hat{d}_{0}$ and

$$h(t) = G\rho (t),\forall t \in \left[ {t_{0} - D,t_{0} } \right)$$

(10)

whereas $\rho (t)$ is arbitrary.

We divide $t\ge{t_{0}}$ into both $t \in \left[ {t_{0} ,t_{0} + D} \right]$ and $t \in \left( {t_{0} + D,\infty } \right).$ For any initial system disturbance $d\left( {t_{0} } \right) = d_{0}$ and consider any observer initial disturbance estimate $\hat{d}_{0}$ and initial value $h(t) = G\hat{d}_{0} ,t \in \left[ {t_{0} - D,t_{0} } \right]$, from (9), it leads to that for $t \in \left[ {t_{0} ,t_{0} + D} \right]$, there is

$$\varpi (t) = e^{ - \Gamma t} (G\hat{d}_{0} - Gd_{0} ),$$

(11)

and then

$$h(t) = Gd(t) + e^{ - \Gamma t} (G\hat{d}_{0} - Gd_{0} ),$$

(12)

thus following (7) to have

$$ \begin{gathered} \hat{d}(t) = \Theta h(t) - \Theta e^{ - \Gamma D} h(t - D) \\ = \Theta Gd(t) + \Theta e^{ - \Gamma t} (G\hat{d}_{0} - Gd_{0} ) - \Theta e^{ - \Gamma D} G\hat{d}_{0} . \\ \end{gathered} $$

(13)

As defined by $\Theta$ in Theorem 1, it holds the fact that

$$\Theta e^{ - \Gamma D} G = 0,\Theta G = I,$$

(14)

and combined with (13) yields the expression for the error variable

$$ \begin{gathered} \vartheta (t) = \hat{d}(t) - d(t) \\ = \Theta Gd(t) + \Theta e^{ - \Gamma t} (G\hat{d}_{0} - Gd_{0} ) - d(t) \\ = \Theta e^{ - \Gamma t} (G\hat{d}_{0} - Gd_{0} ), \\ \end{gathered} $$

(15)

from which we see that the observation error is in exponential form and converges to zero to time $t = t_{0} + D$ as $\Theta e^{ - \Gamma D} G = 0$.

When $t \in \left( {t_{0} + D,\infty } \right)$, (9) leads to

$$\varpi (t) = e^{ - \Gamma D} (h(t - D) - Gd(t - D)),$$

(16)

namely,

$$h(t) = Gd(t) + e^{ - \Gamma D} (h(t - D) - Gd(t - D)),$$

(17)

and

$$\hat{d}(t) = \Theta (Gd(t) - e^{ - \Gamma D} Gd(t - D)),$$

(18)

then with (14) there is $\hat{d}(t) = d(t)$, meaning that $\vartheta (t) = 0$ for all $t \in \left( {t_{0} + D,\infty } \right)$. At this point, dynamics (5)-(7) constitute a disturbance observer for (1) with fixed-time convergence, proof complete.

Remark 2: The creation of the two auxiliary dynamics borrows from the observer in [36] in designing the FTDOB, which in no way means that it is a formal continuation of that, as the convergence of the state observation error to zero is always asymptotic with time for [36], and the convergence rate is exponential, ascribed by the eigenvalues of the observers, lacking a specific metric, whereas this paper takes inspiration of fixed-time convergence in [37], and represents the disturbance with two sub-observer states and one time delay under the observability condition, thus realizing the disturbance observation converged in fixed time, with an even more tremendous improvement compared to [37] to the application point.

Remark 3: For the FTDOB, it is the delay $D$ deciding the convergence speed of the system, as well as the proof explaining that it can take a small value theoretically, and this is a particularly point for practical application, as it can be deployed arbitrarily upon demand to get the “proper” fixed time, for instance, if one expects the system to converge at ${\varrho }$, then $D$ can be randomly taken within a neighborhood smaller than ${\varrho }$, which is all up to the user's mind, and thus generating another point of interest, in that the moment of convergence may be specified, benchmarking with existing methods of exponential or finite time convergence, thereby avoiding the wastage of resources, and facilitating the enhancement of the control efficiency.

4 DOB-Based Composite Control

When dealing with disturbances, the present technique follows the philosophy of active compensation rather than suppression, which has the advantage of responding more quickly to disturbances and bringing the state to zero. For the system (1) with lumped disturbances, the designed composite control law is divided in two parts

$$u = u_{b} + u_{k} ,$$

(19)

$${u_b} = - {B^{ - 1}}\hat d,$$

(20)

$$u_{k} = \Pi x + \xi ,$$

(21)

where $u_{b}$ is the disturbance compensation component, in which $\hat{d}$ is the estimator based on FTDOB (5)-(7), and $u_{k}$ is the feedback control law without considering the disturbance, that we design here as state feedback with $\Pi$ being the feedback gain and $\xi$ being the external signal.

Applying the controller to the system (1), a closed-loop system can be obtaining in the form of

$$ \begin{gathered} \dot{x} = (A + B\Pi )x + B\xi + d - \hat{d} \\ = (A + B\Pi )x + B\xi - \vartheta , \\ \end{gathered} $$

(22)

and if $A + B\Pi$ is Hurwitz, the closed-loop system (22) can be considered BIBO-stable for any bounded $\xi$, since it has been concluded in the preliminaries that the observation error $\vartheta$ converges asymptotically at $\left( {0,D} \right)$ and is constantly equal to zero at $\left[ {D,\infty } \right)$, thus the steady state can be obtained when the DOB dynamics is faster than the closed-loop one. Given this, the main contribution of the subsequent work is to select the feedback gain $\Pi$ in (21) such that $A + B\Pi$ is Hurwitz to obtain the steady state.

Defining the matrix $A_{\Pi } = A + B\Pi$, what we want to see is that $A_{\Pi }$ similar to some given constant matrix, making the closed-loop system with desired structure. Let $\Upsilon$ be some arbitrarily chosen constant matrix, thereby modelling the control rate design as finding the gains $\Pi$ and $\Xi$ that makes

$$A_{\Pi } \Xi = \Xi \Upsilon .$$

(23)

We describe the explicit expression of the composite control law (19) in terms of the following theorem.

Theorem 2.

The gain of controller (19) can be calculated as.

$$\Pi = B^{ - 1} \Omega \Xi^{ - 1} ,$$

(24)

$$\Xi = Z,$$

(25)

$$\Omega = Z\Upsilon - AZ,$$

(26)

with parameter matrices $Z,\Upsilon \in {\mathbb{R}}^{n \times n}$, and the stability of system (22) to be guaranteed by $Z,\Upsilon \in {\mathbb{G}}$, where ${\mathbb{G}}$ being non-empty and satisfying

• 1. $\Upsilon$ is arbitrary and Hurwitz stable;

• 2. $Z$ is free making ${\text{det}}(Z) \ne 0$ holds.

Proof: The proof is in two steps.

Part I, proof of sufficiency. Choose $Z,\Upsilon \in {\mathbb{G}}$, here it is sufficient to show that the gain matrices calculated from Eqs. (24)–(26) satisfy relation (23).

Applying (24)-(26) to the left side of (23) yields

$$ \begin{gathered} A_{\Pi } \Xi = AZ + B\Pi Z \\ = AZ + \Omega \\ = Z\Upsilon , \\ \end{gathered} $$

(27)

this is clearly equal to the right end, and sufficiency is proven.

Part II, proof of necessity. Knowing that there exist matrices $\Xi$ and $\Pi$ satisfying (23), and based on it holds

$$A_{\Pi } \Xi = A\Xi + B\Pi \Xi ,$$

(28)

define $\Omega = B\Pi \Xi$ to further obtain

$$A\Xi + \Omega = \Xi \Upsilon .$$

(29)

The above relation is a standard Sylvester equation, with detailed solutions available in [38], here we give the result directly in the form expressed as (25)-(26), where $Z$ is the free parameter. Also to make the control gain solvable, it is required that $\Xi$ is non-singular, meaning that ${\text{det}}(Z) \ne 0$, to this point the expression (24) is obtained for $\Pi$. Proof ends.

Remark 4: With the composite control law, the closed-loop system (22) is written as

$$\dot{x}(t) = \Xi \Upsilon \Xi^{ - 1} x(t) + B\xi ,$$

having $n$ eigenvalues and corresponding eigenvector determined by $\Upsilon$ and $\Xi$, respectively, which obviously provides more degrees of freedom and is meaningful for system performance improvement.

Remark 5: Confronted with the decline in performance caused by the interaction between the system and the external environment in practical applications, it is desired that the control method possesses both high convergence speed and strong disturbance immunity so as to produce the ideal transient and steady state behaviors. Distinguished from the existing exponential convergence of the poor real-time shortcomings, this paper proposes that the FTDOB-based method is theoretically possible to achieve convergence within an arbitrarily small time, satisfying the demands of some real applications requiring real-time properties for high convergence speed.

Remark 6: The feasibility of the proposed FTDOB-based control method (19) is analyzed below from both implementation and computational perspectives.

For this method, the feasibility of the feedback control part $u_{k}$ is determined by the stability of the system $\dot{x} = (A + B\Pi )x$, equivalent to constructing a matrix $A_{\Pi }$ analogous to the constant matrix $\Upsilon$, where $A_{\Pi } = A + B\Pi$, and this implies that there exists a transformation matrix $\Xi$ such that (23) holds and derives $A\Xi + \Omega = \Xi \Upsilon ,$ with $\Omega = B\Pi \Xi$, the above is a typical Sylvester equation that can be solved according to [38]. As for the compensated control part $u_{b}$, its feasibility is yielded by the asymptotic stability of the FTDOB (5)-(7), and this is simply a matter of choosing the appropriate $\Gamma$ and $D$ to satisfy the two conditions in Theorem 1, thus the method is simple in implementation and computation.

5 A Numerical Example Simulation

In this section, the proposed scheme is evaluated by comparing a FTDOB with a conventional one and also considering a DOB-based controller design for a system with disturbances.

The diversity of practical problems leads to many uncertain systems, and inspired by [39] we choose a common third-dimensional continuous-time system as a specific one to deeply discuss the problem of disturbance estimation as well as control method. A third-dimensional continuous-time object subject to disturbances is regarded as

$$\begin{gathered} \dot{x}(t) = \left[ {\begin{array}{*{20}c} { - 0.8} & 1 & {1.6} \\ 0 & { - 3} & 2 \\ 0 & 0 & { - 6} \\ \end{array} } \right]x(t) + \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]u(t) + d(t), \hfill \\ y(t) = x_{1} (t), \hfill \\ \end{gathered}$$

(30)

there are two objectives that are desired: the former is to estimate system disturbances asymptotically using a DOB, and the latter is to make $y\left( t \right)$ from any initial value to zero by an DOB-based controller with the existence of disturbances, and since $y\left( t \right)$ is a linear combination of states, the second objective above also expands to bring full state convergence to zero for the system.

Part I: Disturbance estimation. Realization and comparison are made between the proposed FTDOB, expressed as shown in (5)-(7), and the conventional DOB in [36], which can be described as (4) when $i$ is equal to 1 or 2, i.e.

$$\begin{gathered} \dot{z}_{c} (t) = - \Gamma_{c} (z_{c} (t) + \Gamma_{c} x(t)) - \Gamma_{c} (Ax(t) + Bu(t)), \hfill \\ h_{c} (t) = z_{c} (t) + \Gamma_{c} x(t). \hfill \\ \end{gathered}$$

(31)

For both cases, the observer gains $\Gamma$ and $\Gamma_{c}$ are set as

$$\Gamma = \left[ {\begin{array}{*{20}c} {0.6} & 0 & 0 & 0 & 0 & 0 \\ 0 & {0.7} & 0 & 0 & 0 & 0 \\ 0 & 0 & {0.8} & 0 & 0 & 0 \\ 0 & 0 & 0 & {1.4} & 0 & 0 \\ 0 & 0 & 0 & 0 & {1.5} & 0 \\ 0 & 0 & 0 & 0 & 0 & {1.6} \\ \end{array} } \right],\Gamma_{c} = \left[ {\begin{array}{*{20}c} {1.4} & 0 & 0 \\ 0 & {1.5} & 0 \\ 0 & 0 & {1.6} \\ \end{array} } \right],$$

respectively, then for the FTDOB, choose $D \, = \, 0.5$, the gain $\Theta$ is generated using Theorem 1 as

$$\begin{gathered} \hfill \Theta = \left[ {\begin{array}{*{20}c} { - 2.0332} & 0 & 0 \\ 0 & { - 2.0332} & 0 \\ 0 & 0 & { - 2.0332} \\ \end{array} } \right. \\ \hfill \left. {\begin{array}{*{20}c} {3.0332} & 0 & 0 \\ 0 & {3.0332} & 0 \\ 0 & 0 & {3.0332} \\ \end{array} } \right]. \\ \end{gathered}$$

Part II: Composite controller design. The input for system (30) is generated by applying (19), whereas $\hat{d}$ in the compensation part $u_{b}$ is replaced with the FTDOB observed in the first step, and the feedback part $u_{k}$ is computed next. With no loss of generality let $\xi = 0$ and choose $\Upsilon$ a diagonal matrix of $3 \times 3$-dimensional, defined as

$$\Upsilon = \left[ {\begin{array}{*{20}c} { - 0.1} & 0 & 0 \\ 0 & { - 0.2} & 0 \\ 0 & 0 & { - 0.3} \\ \end{array} } \right].$$

For this controller, the matrix $Z$ must be properly selected to allow the inverse matrix of $\Xi$ to exist, so set $Z$ to

$$Z = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],$$

in which case the gain matrix $\Pi$ is calculated with (24) in Theorem 2 as

$$\Pi = \left[ {\begin{array}{*{20}c} {0.7} & { - 1} & { - 1.6} \\ 0 & {2.8} & { - 2} \\ 0 & 0 & {5.7} \\ \end{array} } \right].$$

Aiming to verify the effectiveness of this proposed FTDOB-based control method in various scenarios, the system (30) is simulated subject to different types of disturbances, for three cases, including normal, random and time-varying ones, and the results are compared with those of the traditional DOB method.

Case 1. Constant-value disturbance.

Assume that the system (30) is subjected to three typical forms of constant-value disturbances as

$$d_{1} (t) = 0.2,d_{2} (t) = \left\{ {\begin{array}{*{20}c} {0,t < 3,} \\ {0.4,t \ge 3,} \\ \end{array} } \right.d_{3} (t) = \left\{ {\begin{array}{*{20}c} {0,t < 3,} \\ { - 0.5,3 \le t \le 6,} \\ {0,t > 6,} \\ \end{array} } \right.$$

then we assign initial values to the disturbance estimates for more general simulation results and set uniformly for both DOBs, denoted as $z_{0}$ and $z_{c0}$, where,

$$z_{0} = \left[ {0.1,0,0,0.1,0,0} \right]^{{\text{T}}} ,z_{c0} = \left[ {0.1,0,0} \right]^{{\text{T}}} ,$$

meanwhile, the initial system conditions are setting as

$$x_{0} = \left[ {0.1,0, - 0.2} \right]^{{\text{T}}} .$$

The comparison results of the proposed scheme and the conventional DOB are plotted in Figs. 1, 2. The comparative plots of the disturbance observation effects are shown in Fig. 1a–c. It is evident that compared with the conventional disturbance estimation scheme, the proposed one is rapidly adjusting the output to the observed disturbance value, even in the case of a relatively large initial value. Concerning the comparison of the disturbance estimation error are shown in Fig. 2a–c. With respect to the conventional DOB, the proposed scheme exhibits better estimation capabilities as the error decreases sharply toward zero at a quickly convergent rate within the defined fixed-time $D$.

Fig. 1

Disturbance estimation results: original disturbance (yellow line), FTDOB (blue line) as well as conventional DOB (red line). a $d_{1} ,\hat{d}_{1} .$ b $d_{2} ,\hat{d}_{2} .$ c $d_{3} ,\hat{d}_{3}$

Fig. 2

Comparison error of the proposed DOB (blue line) and the conventional DOB (red line). a $\vartheta_{1} .$ b $\vartheta_{2} .$ c $\vartheta_{3}$

The following performance of the system with the proposed scheme are shown in Figs. 3, 4. The state trajectories are plotted in Fig. 3 as well as control inputs for the three channels as Fig. 4, respectively. This shows that the proposed composite control scheme is able to drive the state close to zero very quickly.

Fig. 3

State trajectory of the system

Fig. 4

Control input for three channels

Case 2. Random disturbance.

A bounded unknown disturbance $d = \pm \left[ {0.1,0.1,0.1} \right]^{{\text{T}}}$ is applied to the system (30) during t = 40-100 s, and the initial states of the system and the two DOBs are set to be $x_{0} = \left[ {1,0, - 2} \right]^{{\text{T}}} ,z_{0} = \left[ {0.1,0,0,0.1,0,0} \right]^{{\text{T}}} ,z_{c0} = \left[ {0.1,0,0} \right]^{{\text{T}}} .$

The simulation results of the observer are shown in Fig. 5, and the designed observer is able to respond and estimate the disturbances quickly compared with the conventional DOB. For more clarity, the error is shown in Fig. 6, which converges rapidly for the FTDOB for a fixed time $D = 0.5.$ In addition, the states and inputs of the system with FTDOB-based control are shown in Figs. 7 and 8. Therefore, the FTDOB-based control is effective.

Fig. 5

Disturbance estimation results: original disturbance (yellow line), FTDOB (blue line) as well as conventional DOB (red line). a $d_{1} ,\hat{d}_{1} .$ b $d_{2} ,\hat{d}_{2} .$ c $d_{3} ,\hat{d}_{3}$

Fig. 6

Comparison error of the proposed DOB (blue line) and the conventional DOB (red line). a $\vartheta_{1} .$ b $\vartheta_{2} .$ c $\vartheta_{3}$

Fig. 7

State trajectory of the system

Fig. 8

Control input for three channels

Case 3. Time-varying disturbance.

Consider a time-varying disturbance applied to system (30) as

$$\begin{gathered} d_{1} (t) = 0.01\sin 0.05t + \cos 0.02t, \hfill \\ d_{2} (t) = \left\{ {\begin{array}{*{20}c} {0.1,t\le30,} \\ {0,t > 30,} \\ \end{array} } \right.d_{3} (t) = 0.05\cos 0.05t, \hfill \\ \end{gathered}$$

and the initial conditions of system are given as follows

$$x_{0} = \left[ {1,0, - 2} \right]^{{\text{T}}} ,z_{0} = \left[ {0.1,0,0,0.1,0,0} \right]^{{\text{T}}} ,z_{c0} = \left[ {0.1,0,0} \right]^{{\text{T}}} .$$

Then, within the simulation time of 200 s, we realize the disturbance estimation given by FTDOB and conventional DOB respectively, and the results are shown in Fig. 9, and the errors are shown in Fig. 10. The FTDOB-based control is further implemented with the system state shown in Fig. 11 and inputs shown in Fig. 12. The simulation results fully demonstrate the usability and advantages of the proposed method.

Fig. 9

Disturbance estimation results: original disturbance (yellow line), FTDOB (blue line) as well as conventional DOB (red line). a $d_{1} ,\hat{d}_{1} .$ b $d_{2} ,\hat{d}_{2} .$ c $d_{3} ,\hat{d}_{3}$

Fig. 10

Comparison error of the proposed DOB (blue line) and the conventional DOB (red line). a $\vartheta_{1} .$ b $\vartheta_{2} .$ c $\vartheta_{3}$

Fig. 11

State trajectory of the system

Fig. 12

Control input for three channels

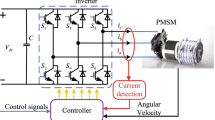
6 Application to Permanent-Magnet Speed Control

This section provides the application of the proposal in a PECSC system through simulation. Here, in the control application, the proposed scheme aims to attain the desired results with disturbances present in the system.

The PEC is a transmission device that utilizes the eddy current effect to transmit torque, containing the drive end and the working end, coupled by the interaction of the magnetic field, and transmitting torque with the eddy currents generated and interacting in the rotor at the working end. Whilst the PECSC system is a control system that uses the PEC to achieve mechanical speed regulation, it controls the motor speed at the drive end and thus the operating state of the eddy current coupling to obtain adjustable speed and torque output.

6.1 Structure of the Speed Control System

In the PECSC system, the prime mover of the PEC, the copper conductor, is connected to the inverter and the motor, and therefore considered to remain immobile in the horizontal direction as a stator, while the permanent magnet disk, together with the supporting steel disk thereof, is pulled into motion under the magnetic field and displaced in the horizontal direction, thus considered to be a rotor. For a straight line movement of the rotor to be enabled, a screw is utilized to adjust the air gap.

During the actual speed regulation process, the screw is connected to the control mechanism at one end and to the permanent magnet at the other end, applying the characteristic of converting the rotary motion into linear motion to convert the circumferential motion of the control mechanism into the linear motion of the rotor in the horizontal direction, so as to realize the adjustment of the air gap thickness between the stator and rotor, and ultimately to carry out the regulation of the speed and torque.

6.2 Modeling of the Speed Control System

Regarding the speed control system of PEC, controlling motor is the key part, especially the selection of motor, after comparing, we choose the permanent magnet synchronous motor (PMSM) as the speed control system, with high rotating speed, high efficiency, low power consumption, good reliability, wide speed control range and fast response speed. When applying the PECSC system, the speed of the mechanical system is regulated by controlling the motor.

For a PMSM, assuming a sinusoidal distribution of the three-phase stator windings spatially, the electromagnetic and kinematic equations can be described in the rotational ${\text{d - q}}$ coordinates using the model below

$$\left\{ \begin{gathered} \frac{{di_{q} }}{dt} = - \frac{R}{{L_{q} }}i_{q} - n\omega \frac{{L_{d} }}{{L_{q} }}i_{d} + \frac{1}{{L_{q} }}u_{q} - n\omega \frac{{\Psi_{f} }}{{L_{q} }}, \hfill \\ \frac{{di_{d} }}{dt} = - \frac{R}{{L_{d} }}i_{d} + n\omega \frac{{L_{q} }}{{L_{d} }}i_{q} + \frac{1}{{L_{d} }}u_{d} , \hfill \\ \frac{d\omega }{{dt}} = \frac{1}{J} \times \frac{3}{2}n(\Psi_{f} i_{q} + (L_{d} - L_{q} )i_{d} i_{q} ) - \frac{1}{J}T_{L} - \frac{{B_{f} }}{J}\omega , \hfill \\ \end{gathered} \right.$$

(32)

where $n$ is the pole number, $\omega$ is the electric angular velocity, $i_{d} , \, i_{q} , \, u_{d} , \, u_{q} , \, L_{d}$ and $L_{q}$ are the stator current, voltage and inductance in the ${\text{d - q}}$ system, respectively, $R$ is the stator resistance, $T_{L}$ is the load torque, $\Psi_{f}$ is the permanent magnetic flux, $B_{f}$ is the coefficient of viscous friction, $J$ is the rotational inertia.

The study is on a face-mounted motor of $L_{d} = L_{q} = L$, utilizing $i_{d} = 0$ control method, with consideration of parameter ingestion, modeling errors and external disturbances, and introducing $\phi = \left[ {\phi_{1} ,\phi_{2} } \right]^{{\text{T}}}$ to simplify the above one:

$$\left\{ \begin{gathered} \frac{d\omega }{{dt}} = \frac{{3n\Psi_{f} }}{2J}i_{q} - \frac{1}{J}T_{L} - \frac{{B_{f} }}{J}\omega + \phi_{1} , \\ \frac{{di_{q} }}{dt} = - \frac{R}{L}i_{q} + \frac{1}{L}u_{q} - n\omega \frac{{\Psi_{f} }}{L} + \phi_{2} . \\ \end{gathered} \right.$$

(33)

Define the desired angular velocity $\omega^{*}$ and the ${\text{q}}$-axis stator current $i_{q}^{*}$, then re-selection of variables for the model (33) to ease the derivation:this yields the model as

$$\begin{gathered} X_{1} = \omega - \omega^{*} ,X_{2} = i_{q} - i_{q}^{*} ,a_{1} = \frac{{3n\Psi_{f} }}{2},a_{2} = - \frac{R}{L}, \\ a_{3} = - \frac{{n\Psi_{f} }}{L},a_{4} = \frac{1}{L},b_{1} = - \frac{1}{J},b_{2} = - \frac{B}{J}, \\ \end{gathered}$$

this yields the model as

$$\left\{ \begin{gathered} \frac{{dX_{1} }}{dt} = b_{2} X_{1} + a_{1} b_{1} X_{2} + b_{2} \omega^{*} + a_{1} b_{1} i_{q}^{*} - \dot{\omega }^{*} + b_{1} T_{L} + \phi_{1} , \hfill \\ \frac{{dX_{2} }}{dt} = a_{3} X_{1} + a_{2} X_{2} + a_{3} \omega^{*} + a_{2} i_{q}^{*} - \dot{i}_{q}^{*} + a_{4} u_{q} + \phi_{2} . \hfill \\ \end{gathered} \right.$$

(34)

Let $x = \left[ {X_{1} ,X_{2} } \right]^{{\text{T}}}$ and $u = \left[ {T_{L} ,u_{q} } \right]^{{\text{T}}}$, then the state space description is obtained from model (1) with the coefficients

$$\begin{gathered} A = \left[ {\begin{array}{*{20}c} {b_{2} } & {a_{1} b_{1} } \\ {a_{3} } & {a_{2} } \\ \end{array} } \right],B = \left[ {\begin{array}{*{20}c} {b_{1} } & 0 \\ 0 & {a_{4} } \\ \end{array} } \right], \\ d = \left[ {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {b_{2} \omega^{*} + a_{1} b_{1} i_{q}^{*} - \dot{\omega }^{*} + \phi_{1} } \\ {a_{3} \omega^{*} + a_{2} i_{q}^{*} - \dot{i}_{q}^{*} + \phi_{2} } \\ \end{array} } \right]. \\ \end{gathered}$$

6.3 Simulation Analysis

For validation of the scheme, one has built the above system using the Simulink tool and executed $i_{d} = 0$ control mode with motor parameters selected from [40] to the Table 1 below.

Table 1 Parameters of motor

For this situation, considered $\phi = \left[ {0.1,0.2} \right]^{{\text{T}}}$, the electrical angular velocity $\omega$ and the ${\text{q}}$-axis stator current $i_{q}$ are expected to track the reference values $\omega^{*} = 500\,{\text{rad/s}}$ and $i_{q}^{*} = 1.5\,{\text{A}}$, respectively. Two DOBs (conventional and fixed-time) are implemented for estimation, and the detailed steps are available along similar lines to the previous section that will be omitted here as appropriate. The poles of observers are located at

$$\Gamma = \left[ {\begin{array}{*{20}c} {0.2} & 0 & 0 & 0 \\ 0 & {0.5} & 0 & 0 \\ 0 & 0 & {0.8} & 0 \\ 0 & 0 & 0 & {0.1} \\ \end{array} } \right],\Gamma_{c} = \left[ {\begin{array}{*{20}c} {0.2} & 0 \\ 0 & {0.5} \\ \end{array} } \right],$$

respectively. Set the delay to $D = 0.5$, then the gain $\Theta$ is designed using Theorem 1 as

$$\Theta = \left[ {\begin{array}{*{20}c} { - 2.8583} & 0 & {3.8583} & 0 \\ 0 & {5.5167} & 0 & { - 4.5167} \\ \end{array} } \right].$$

Here, the conventional DOB is in comparison with the one introduced in this paper, and throughout all the simulations performed, following initial state is kept constant: $x_{0} = \left[ {0.1,0} \right]^{{\text{T}}}$. As can be seen in the Fig. 13a–b, both observers are capable of observing purposes, while the proposed scheme converges faster, with that result being referred to the fixed-time action. The error comparison is plotted in Fig. 14. It is evident that the proposed scheme gives better estimates and improved performance.

Fig. 13

Disturbance estimation results: original disturbance (yellow line), FTDOB (blue line) as well as conventional DOB (red line). a $d_{1} ,\hat{d}_{1} .$ b $d_{2} ,\hat{d}_{2}$

Fig. 14

Comparison error of the proposed DOB (blue line) and the conventional DOB (red line). a $\vartheta_{1} .$ b $\vartheta_{2}$

Using (19) to design the control input, matrix $\Upsilon$ is set to

$$\Upsilon = \left[ {\begin{array}{*{20}c} { - 0.3} & 0 \\ 0 & { - 0.4} \\ \end{array} } \right],$$

the parameter matrix $Z$ can be chosen as

$$Z = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],$$

then $u$ is now defined with

$$\Pi = \left[ {\begin{array}{*{20}c} {0.0031} & { - 3.6} \\ {2.4} & {2.8618} \\ \end{array} } \right].$$

Applied the proposed controller to the system (34), with the state trajectory shown in Fig. 15, it is noticeable that the proposed control has no chattering as well as gives well controlled performance.

Fig. 15

State trajectory of the system. a $x_{1} .$ b $x_{2}$

In summary, the control of permanent magnet speed control system with FTDOB-based controller is actualized, and concluded that in the disturbance estimation part, in contrast to the traditional DOB, FTDOB has a shorter estimation time, enabling the errors converging to the steady state rapidly, furthermore, the controller designed on this observer leads a better system performance and a fast disturbance elimination.

7 Concluding Remarks

In this paper, a FTDOB is introduced for a class of uncertain systems. It is demonstrated that the proposed DOB combines the features of disturbance estimation and fixed-time convergence, as well as increases the estimation speed and enhances the overall system performance with maintaining the estimation accuracy. Further application of the proposed DOB to the FAC system enables the control of uncertain systems, where the performance of the closed-loop system is preserved as the uncertainties have been successfully estimated and compensated via the FTDOB and FTDOB-based control. Numerical simulations validate the proposed scheme, also, the controlling of the PECSC system is successfully achieved using this scheme, where results show that the controller is fast responding and capable of quickly eliminating disturbances to the steady state. As future work, related studies are planned to reduce the restrictiveness by assuming the disturbances as fast time-varying to match more complex working conditions.