Fixed-time stabilization of high-order integrator systems with mismatched disturbances

Abstract

The fixed-time stabilization of high-order integrator systems with both matched and mismatched disturbances is investigated. A continuous non-switching control law is designed based on the bi-limit homogeneous technique for arbitrary-order integrator systems. Combining with fixed-time disturbance observer, the proposed continuous control law for the system with matched and mismatched disturbances guarantees that the convergence time is uniformly bounded with respect to any initial states. Finally, the numerical results are provided to verify the efficiency of the developed method.

1 Introduction

In comparison with the systems with asymptotically stable, the finite-time stable systems show some additional properties, such as faster convergence rate, higher accuracy and better disturbance rejection [1,2,3]. As a result, extensive work has been studied during the last years from the point of view both in theory and in practice [4,5,6].

The homogeneous technique is commonly applied to develop a finite-time stabilizing control law for high-order systems [7]. Subsequently, the method in [7] was extended to deal with the system with mismatched disturbances in [8]. In addition, a sufficient condition was proposed in [9] using Lyapunov method, which has been widely applied in finite-time analysis of nonlinear systems [10, 11]. Nevertheless, the convergence time achieved by these methods aforementioned increases unboundedly together with the initial states. To address the issue, the fixed-time stabilization has received a lot attention [12,13,14,15,16] in the recent years. The systems with fixed-time stabilization show some excellent properties such as uniform finite-time convergence with respect to any initial condition, which is very useful in practice for systems whose initial states are varying or uncertain [17]. In this case, the finite-time control algorithm is not able to provide an estimation of the convergence time which is dependent on the initial condition. However, the fixed-time algorithm avoids the issue due to the fact that the upper bound of the convergence time is independent on the initial condition. In [18], the Lyapunov technique was utilized to achieve a sufficient condition ensuring the fixed-time stability of a class of nonlinear systems. Nevertheless, it is non-trivial to extend the fixed-time stabilizing control algorithms from first-order or second-order systems [13, 19, 20] to high-order cases due to the fact that an analytic Lyapunov function satisfying the sufficient condition is difficult to develop. In spite of the difficulties, some work on this issue has been investigated in the recent years. Specifically, a fixed-time stabilizing control law was proposed based on an implicit Lyapunov function (ILF) for high-order integrator systems in [21]. Instead of providing an analytical control law, an online computation of the ILF value at the current state is required in the algorithm. Hence, it is applicable only in digital controller. Another result on fixed-time stabilization for high-order systems can be found in [22], where a Lyapunov-based homogeneous technique was used for controller design. However, the control law provided in [22] was designed based on switching control strategy. In practice, the non-switching control law with less control effort is more desirable [18].

Motivation It is well known that the classic finite-time stabilizing control law presented in [23] can be easily used to develop a finite-time control algorithm for high-order systems subject to disturbances, such as [11, 24] and [25], to name a few. As aforementioned, it is non-trivial to design a fixed-time control algorithm for high-order systems utilizing the Lyapunov methods. Hence, we are wondering if there exists a fixed-time control law having a similar form with that in [23] for arbitrary-order integrator systems. If it is available, then some fixed-time control algorithms can be designed for high-order systems following the ideas in [11, 24] and [25]. Bearing this in mind, an important motivation of the current work is to design a fixed-time control law covering the one in [23] as a special case. In addition, disturbance-observer-based methods have received much attention in improving the control performance of systems subject to disturbance [26, 27]. Nevertheless, the fixed-time control algorithm based on disturbance observer for systems with both matched and mismatched disturbances is little discussed in the open literature but is common in practice [28], which constitutes the second motivation of the research.

Contributions The main contributions of the work are twofold. First, a novel continuous non-switching fixed-time stabilizing control law is developed for integrator systems with arbitrary-order dynamics, which covers the classic finite-time control law [23] as a special case. Second, both the matched and the mismatched disturbances are dealt with by a fixed-time disturbance observer, and some fine properties of the developed method are expected, such as fixed-time convergence as well as chattering alleviation.

The remainder of the paper is as follows. In Sect. 2, some concepts and lemmas on finite-time stability are recalled, and the problem is formulated. Section 3 is devoted to the construction of a non-switching fixed-time stabilizing control law for arbitrary-order integrator system. In Sect. 4, disturbance-observer-based fixed-time stabilizing control law is proposed for high-order system with matched and mismatched disturbances. In Sect. 5, an illustrative numerical example is given. Finally, concluding remarks are presented in Sect. 6.

2 Preliminaries and problem statement

In this section, some notations and useful lemmas to be used in the subsequent development of the proposed algorithm are provided. Then, the problem discussed in the context is formulated.

2.1 Notations

Let $\alpha >0$ be an arbitrary positive constant, and the notation $x\mapsto {\lceil x\rfloor }^\alpha$ is defined by $\lceil x\rfloor ^{\alpha }=|x|^{\alpha }{{\mathrm {sign}}}(x)$ for all $x\in \mathbb {R}$. For strictly positive numbers $r_i,i=1,\ldots ,n$ and $\lambda >0$, define the vector of weights $r=[r_1,\ldots ,r_n]$ and the dilation function $\varLambda _r(\lambda )={{\mathrm {diag}}}\{\lambda ^{r_1},\ldots ,\lambda ^{r_n}\}$. With the definition, one has $\varLambda _r(\lambda )x={{\mathrm {diag}}}\{\lambda ^{r_1}x_1,\ldots ,\lambda ^{r_n}x_n\}$ for any $x\in \mathbb {R}^n$. Furthermore, for continuous and positive definite function V(x), let set $V^{-1}([\alpha ,\beta ])=\{x\in \mathbb {R}^n: \alpha \le V(x)\le \beta \}$ denote the $[\alpha ,\beta ]$ sublevel set of V(x). Define $\mathcal {B}_\varepsilon [0]=\{x\in \mathbb {R}^n:\Vert x\Vert \le \varepsilon \}$. Denote the n dimensional column vector $x=[x_1,\ldots ,x_n]^T\in \mathbb {R}^n$ by $x=[x_i]^T\in \mathbb {R}^n$.

2.2 Definitions and lemmas

In this context, the following nonlinear system is considered

$$\begin{aligned} \dot{x}=f(x),\quad x(0)=x_0 \end{aligned}$$

(1)

where $x=[x_i]^T \in {\mathbb {R}}^n$ is the state vector, $f(x)=[f_i(x)]^T \in {\mathbb {R}}^n$ ensures forward existence and uniqueness of the system solutions at least locally satisfying $f(0)=0$. Some useful definitions and lemmas on finite-time stability are recalled below, which are required in the subsequent development.

Definition 1

[29] A function $g: \mathbb {R}^n\rightarrow \mathbb {R}$ is r-homogeneous with degree $k\in \mathbb {R}$ if the condition $\lambda ^{-k}g(\varLambda _r(\lambda )x)=g(x)$ holds for any $x\in \mathbb {R}^n$ and any positive real number $\lambda >0$.

Definition 2

[29] A vector field $f: \mathbb {R}^n\rightarrow \mathbb {R}^n$ is r-homogeneous with degree $k\in \mathbb {R}$ if the condition $\lambda ^{-k}\varLambda _r^{-1}f(\varLambda _r(\lambda )x)=f(x)$ holds for any $x\in \mathbb {R}^n$ and any positive real number $\lambda >0$.

Definition 3

[30] A function $g:\mathbb {R}^n\rightarrow \mathbb {R}$ is homogeneous in the p-limit ($p=0$ or $p=\infty$) with triple $(r_p,k_p,g_p)$, where $r_p=[r_{p,1},\ldots ,r_{p,n}]\in \mathbb {R}^n$ denotes the vector of weights, $k_p$ represents the degree, and $g_p$ is the approximating function, if the equality $\lim \nolimits _{\lambda \rightarrow p}\max \nolimits _{x\in C}|\lambda ^{-k_p}g(\varLambda _{\lambda }^{r_p}(x))-g_p(x)| =0$ holds for any $C \in \mathbb {R}^n \backslash \{0\}$.

Definition 4

[30] A vector field $f: \mathbb {R}^n\rightarrow \mathbb {R}^n$ is homogeneous in the p-limit with triple $(r_p,k_p,f_p)$ where $r_p=[r_{p,1},\ldots ,r_{p,n}]\in \mathbb {R}^n$ denotes the vector of weights, $k_p$ represents the degree and $f_p$ is the approximating vector field if the ith component of f is homogeneous in the p-limit under the triple $(r_p,k_p+r_{p,i},f_{p,i})$ with the condition $k_p+r_{p,i}>0$ being hold.

Definition 5

[30] A vector field $f: \mathbb {R}^n\rightarrow \mathbb {R}^n$ is bi-limit homogeneous if it is homogeneous in both 0-limit and $\infty$-limit.

Definition 6

[21] The origin of system (1) is said to be globally finite-time stable if it is globally asymptotically stable and any solution $x(t,x_0)$ of (1) attains it in finite time, i.e., $x(t,x_0)=0$ for $\forall t\ge T(x_0)$ where $T:\mathbb {R}^n\rightarrow R_+\cup {0}$ is the settling-time function.

Definition 7

[21] The origin of system (1) is said to be globally fixed-time stable if it is globally finite-time stable and the settling-time function $T(x_0)$ is bounded, i.e., there exists $T_\mathrm{max}>0$ such that $T(x_0)\le T_\mathrm{max}$ for $\forall x_0 \in \mathbb {R}^n$.

Lemma 1

[12] Consider system (1) with the assumption that f(x) is bi-limit homogeneous with the triples $(r_0,k_0,f_0)$ and $(r_\infty ,k_\infty ,f_\infty )$. Then, the system (1) is called to be fixed-time stable provided that the systems $\dot{x}=f(x),\dot{x}_0=f_0(x)$ and $\dot{x}_\infty =f_\infty (x)$ are globally asymptotically stable with the inequality $k_0<0<k_\infty$ being hold.

Lemma 2

[12] Consider the system $\dot{x}=f(x,\delta ) \in \mathbb {R}^n$ with exogenous disturbance $\delta =[\delta _i]^T\in \mathbb {R}^m$ and suppose that $f(x,\delta )$ is bi-limit homogeneous with triples $((r_0,\tau _0),k_0,f_0)$ and $((r_\infty ,\tau _\infty ),k_\infty ,f_\infty )$, where $\tau _0$ and $\tau _\infty$ are weights with respect to disturbance $\delta$. Then, the system $\dot{x}=f(x,\delta )$ is input-to-state stable (ISS) with $\delta$ as input if its nominal system $\dot{x}=f(x,0)$ satisfies all the hypotheses in Lemma 1.

2.3 Problem statement

Consider the following high-order integrator system subject to both mismatched disturbances $\varDelta _i(t)$ and matched disturbance $\varDelta _n(t)$, which covers many practical systems such as the attitude control of vehicles [25, 28], to name just a few.

$$\begin{aligned} \dot{x}_i=x_{i+1}+\varDelta _i(t),\quad \dot{x}_n=u+\varDelta _n(t),\quad i=1,\ldots ,n-1 \end{aligned}$$

(2)

where $x_i\in \mathbb {R}$ is the state variable, u is the control input, $x=[x_i]^T\in \mathbb {R}^n$ represents the state vector. To proceed, the following assumption is required

Assumption 1

Suppose that the disturbance $\varDelta _i(t)$ in (2) is $n+1-i$ times differentiable such that $\varDelta ^{(n+1-i)}_i(t)$ has a known Lipschitz constant $L_i$ satisfying $|\varDelta ^{(n+1-i)}_i(t)|\le L_i$.

The aim of the work is to design a continuous control law u driving system output $y=x_1$ to zero in finite time which is uniformly bounded with respect to any initial conditions in the presence of matched and mismatched disturbances.

3 Fixed-time stability of integrator systems

In this section, a fixed-time stabilizing control algorithm is developed for integrator systems with arbitrary-order dynamics. To show that, let us consider the system with the following form

$$\begin{aligned} \dot{x}_1=x_2,\quad \dot{x}_2=x_3,\ldots , \dot{x}_n=u,\quad x(0)=x_0 \end{aligned}$$

(3)

where $x=[{x}_i]^T \in {\mathbb {R}}^n$ and $u \in {\mathbb {R}}$ denote the state vector and the control input, respectively, and $x_0\in {\mathbb {R}}^n$ represents the initial condition of the system. In order to guarantee the fixed-time stabilization of system (3) under appropriate control input u, the following control law is developed

$$\begin{aligned} \begin{aligned} u(x)&=-\sum _{i=1}^{n} k_i\left( \lceil x_i \rfloor ^{\varrho _i}+\lceil x_i \rfloor +\lceil x_i \rfloor ^{{\varrho _i'}}\right) \end{aligned} \end{aligned}$$

(4)

where the positive constants $k_i>0, (i=1,\ldots ,n)$ are selected to ensure that the n-order polynomials $s^n+k_ns^{n-1}+\cdots +k_2s+k_1$ and $s^n+3k_ns^{n-1}+\cdots +3k_2s+3k_1$ are Hurwitz, and the detailed implementation of the selection of the parameter $k_i$ is provided in “Appendix.” Furthermore, the parameters $\varrho _i,\varrho _i',(i=1,\ldots ,n)$ are calculated by

$$\begin{aligned} \varrho _{n-j}= & {} \frac{\varrho }{(j+1)-j\varrho },\quad \nonumber \\ {\varrho _{n-j}'}= & {} \frac{2-\varrho }{j\varrho -(j-1)},\quad (j=0,\ldots ,n-1) \end{aligned}$$

(5)

due to the bi-limit homogeneity reasoning to be shown in the subsequent proof. In (5), the parameter $\varrho$ is selected in the interval $(\epsilon ,1)$ with $\epsilon \in (\frac{n-2}{n-1},1)$. In fact, the high-order item $\lceil x_i \rfloor ^{{\varrho _i'}}$ in (4) is responsible for driving the system states into a compact set in finite time independent of any initial condition $x_0$, whereas the low-order item $\lceil x_i \rfloor ^{{\varrho _i}}$ is used to ensure the finite time stabilization of the system (3) with its initial state $x_0$ being in a any compact set. The following theorem is presented to summarize the main result in this section.

Theorem 1

Consider system (3) under the control law (4) with parameters provided in (5); then there exists a positive real number $\epsilon$ in the interval $(\frac{n-2}{n-1},1)$ such that the origin of system (3) is fixed-time stable for any initial condition $x_0\in {\mathbb {R}}^n$ if $\varrho \in (\epsilon ,1)$ and the parameters $k_i>0, (i=1,\ldots ,n)$ are chosen to ensure that the n-order polynomials $s^n+k_ns^{n-1}+\cdots +k_2s+k_1$ and $s^n+3k_ns^{n-1}+\cdots +3k_2s+3k_1$ are Hurwitz.

Proof

The proof proceeds in the following three steps. First, it will be shown that the vector field (denoted by $f_\varrho (x)$) of closed-loop system (3) under control law (4) with parameters (5) is bi-limit homogeneous with the triples $(r_0,k_0,f_{\varrho _0}(x))$ and $(r_\infty ,k_\infty ,f_{\varrho _\infty }(x))$ to be given later, satisfying $k_0<0<k_\infty$. Then, the globally asymptotical stability of its approximating systems $\dot{x}=f_{\varrho _0}(x)$ and $\dot{x}=f_{\varrho _\infty }(x)$ would be proved. Furthermore, it will be illustrated that the origin of system $\dot{x}=f_\varrho (x)$ is also globally asymptotically stable. In terms of Lemma 1, the result in this theorem follows. $\square$

For brevity, the control law in (4) is divided into the following three parts

$$\begin{aligned} u_1(x)= & {} -\sum _{i=1}^{n} k_i\lceil x_i \rfloor ^{\varrho _i}\nonumber \\ u_2(x)= & {} -\sum _{i=1}^{n} k_i\lceil x_i \rfloor ,u_3(x)=-\sum _{i=1}^{n} k_i\lceil x_i \rfloor ^{\varrho _i'} \end{aligned}$$

(6)

Denote the closed-loop vector fields of system (3) under control law $u(x)=u_1(x)$ and $u(x)=u_3(x)$ by $f_{\varrho _0}(x)$ and $f_{\varrho _\infty }(x)$, respectively. For any $\varrho \in (\epsilon ,1)$ with $\epsilon \in (\frac{n-2}{n-1},1)$, it follows from (5) that the conditions $0<\varrho _i<1<\varrho _i', (i=1,\ldots ,n)$ hold. Hence, it can be observed that $f_{\varrho _0}(x)$ and $f_{\varrho _\infty }(x)$ can be considered as the approximating functions for $f_\varrho (x)$ in 0-limit and $\infty$-limit. Furthermore, selecting weight vectors $r_0=[r_{0_i}]^T\in \mathbb {R}^n$ and $r_\infty =[r_{\infty _i}]^T\in \mathbb {R}^n$ with

$$\begin{aligned} r_{0_{n-j}}=\frac{(j+1)-j\varrho }{1-\varrho },\quad r_{\infty _{n-j}}=\frac{j\varrho -(j-1)}{1-\varrho } \end{aligned}$$

(7)

where $j=0,\ldots ,n-1$. It follows from the homogeneity definitions provided in Sect. 2.2 that the vector fields $f_{\varrho _0}(x)$ (resp. $f_{\varrho _\infty }(x)$) are homogeneous with weight $r_0=[r_{0_i}]^T\in \mathbb {R}^n$ (resp. $r_\infty =[r_{\infty _i}]^T \in \mathbb {R}^n$) defined in (7) and degree $k_0=-1$ (resp. $k_\infty =1$).

In the sequel, we will focus to show that the approximating systems $\dot{x}=f_{\varrho _0}(x)$ and $\dot{x}=f_{\varrho _\infty }(x)$ are globally asymptotically stable. To this end, the following lemma is required.

Fig. 1

Visualizations idea of global asymptotic stability for $\dot{x}=f_\varrho (x)$

Lemma 3

[23] Suppose that system (1) is homogeneous and there exists a compact set $\mathcal {A}\subset \mathbb {R}^n$ that is strictly positively invariant with respect to homogeneous system (1), then the origin of system (1) is globally asymptotically stable.

Next, the idea to prove the globally asymptotic stability for systems $\dot{x}=f_{\varrho _0}(x)$ and $\dot{x}=f_{\varrho _\infty }(x)$ follows the method in [23]. It follows from  (5) that $\varrho _i=\varrho _i'=1,(i=1,\ldots ,n)$ if specified with $\varrho =1$. In this case, system $\dot{x}=f_{\varrho _0}(x)$ (resp.$\dot{x}=f_{\varrho _\infty }(x)$) is reduced to

$$\begin{aligned} \dot{x}_1=x_2,\dot{x}_2=x_3,\ldots ,\dot{x}_{n-1}=x_n,\dot{x}_n=-\sum _{i=1}^{n} k_ix_i \end{aligned}$$

(8)

which is globally asymptotically stable when the parameters $k_i,(i=1,\ldots ,n)$ are selected such that the polynomial $s^n+k_ns^{n-1}+\cdots +k_2s+k_1$ is Hurwitz. Therefore, there exists a continuous differentiable, positively definite and proper function V(x) such that $\dot{V}(x)<0$ for system (8) with any $x\in \mathbb {R}^n\backslash \{0\}$. Then, let ${V}(\varrho ,x)=V(x)$ and $\dot{V}(\varrho ,x)$ denote the derivative of V(x) along system $\dot{x}=f_{\varrho _0}(x)$ (resp.$\dot{x}=f_{\varrho _\infty }(x)$), satisfying $\dot{V}(1,x)=\dot{V}(x)$. In addition, it can be easily found that $\dot{V}(\varrho ,x)$ is continuous with respect to $\varrho$ and x. Furthermore, define $\mathcal {A}=V^{-1}([0,\mu ])$ for any $\mu >0$, and $\mathcal {S}=V^{-1}(\{\mu \})$ as the boundary of set $\mathcal {A}$. Since V(x) is proper, it follows that sets $\mathcal {A}$ and $\mathcal {S}$ are compact. Hence, the continuous function $\dot{V}(1,x)=\dot{V}(x)<0$ for any $x\in \mathcal {S}$. Following the tube lemma (Lemma 5.8) in [31] that there exists a constant $\frac{n-2}{n-1}<\epsilon _1<1$ (resp.$\frac{n-2}{n-1}<\epsilon _2<1$), such that $\dot{V}(\varrho ,x)<0$ for $x\in \mathcal {S}$ with $\varrho \in (\epsilon _1,1)$ (resp.$\varrho \in (\epsilon _2,1)$), which is sufficient to ensure that $\mathcal {A}$ is a strictly positively invariant set for system $\dot{x}=f_{\varrho _0}(x)$ (resp.$\dot{x}=f_{\varrho _\infty }(x)$). It follows from Lemma 3 that the global asymptotic stability of system $\dot{x}=f_{\varrho _0}(x)$ (resp.$\dot{x}=f_{\varrho _\infty }(x)$) can be guaranteed. Therefore, there exists a constant $\epsilon _3={{\mathrm {max}}}(\epsilon _1,\epsilon _2)$ ensuring global asymptotic stability for both $\dot{x}=f_{\varrho _0}(x)$ and $\dot{x}=f_{\varrho _\infty }(x)$ when $\varrho \in (\epsilon _3,1)$.

Next, the global asymptotic stability of system $\dot{x}=f_\varrho (x)$ is to be proved. Instead of finding an unified Lyapunov function for this system, we will find different Lyapunov functions, i.e., ${V}_\infty , {V}$, and ${V}_0$, in different regions of $\mathcal {C}_1,\mathcal {C}_2$ and $\mathcal {C}_3$ (see Fig. 1) which covers the whole state spaces. In this case, if $\dot{V}_\infty , \dot{V}$ and $\dot{V}_0$ are strictly negative in $\mathcal {C}_1,\mathcal {C}_2$ and $\mathcal {C}_3\backslash \{0\}$, respectively, then the claim follows. The proof is summarized as below.

Since the bi-limit systems $\dot{x}=f_{\varrho _0}(x)$ and $\dot{x}=f_{\varrho _\infty }(x)$ are globally asymptotically stable for $\varrho \in (\epsilon _3,1)$, it follows from Propositions 2.16 and 2.18 in [12] that the origin of system $\dot{x}=f_\varrho (x)$ is locally asymptotically stable and there exists an invariant compact set which is globally asymptotically stable for this system. Following the results in [12], there exist strictly positive real numbers $\upsilon _0$, $\upsilon _\infty$ and continuous, positive definite as well as proper functions $V_0(x)$ and $V_\infty (x)$ satisfying

$$\begin{aligned} \frac{\partial V_0}{\partial x}f_\varrho (x)<0,\quad x \in \mathcal {C}_3\backslash \{0\} \triangleq \mathcal {B}_{\upsilon _0}[0]\backslash \{0\} \end{aligned}$$

(9)

and

$$\begin{aligned} \frac{\partial V_\infty }{\partial x}f_\varrho (x)<0,\quad x \in \mathcal {C}_1\triangleq V^{-1}_\infty ([\upsilon _\infty ,+\,\infty )) \end{aligned}$$

(10)

Next, our aim is to find a Lyapunov function V(x) in region $\mathcal {C}_2$ (see Fig. 1), satisfying $\dot{V}(x)<0$ for any $x\in \mathcal {C}_2$ and

$$\begin{aligned} \mathcal {C}_1\cup \mathcal {C}_2\cup \mathcal {C}_3=\mathbb {R}^n \end{aligned}$$

(11)

Specifying with $\varrho =1$ in (5), system $\dot{x}=f_\varrho (x)$ is reduced to

$$\begin{aligned} \dot{x}_1=x_2,\quad \dot{x}_2=x_3,\ldots ,\dot{x}_{n-1}=x_n,\quad \dot{x}_n=-\sum _{i=1}^{n} 3k_ix_i \end{aligned}$$

(12)

which is globally asymptotically stable with the selection of $k_i, (i=1,\ldots ,n)$ such that $s^n+3k_ns^{n-1}+\cdots +3k_2s+3k_1$ is Hurwitz. The selection of positive real numbers $k_i$ to ensure that the polynomials $s^n+k_ns^{n-1}+\cdots +k_2s+k_1$ and $s^n+3k_ns^{n-1}+\cdots +3k_2s+3k_1$ are both Hurwitz provided in “Appendix.” Following the same analysis for system (8), it can be concluded that there exists a constant $\epsilon _4$, satisfying $\frac{n-2}{n-1}<\epsilon _4<1$, and continuous, positive definite and proper function V(x) such that

$$\begin{aligned} \frac{\partial V}{\partial x}f_\varrho (x)<0,~~x \in \mathcal {C}_2\triangleq V^{-1}([\upsilon _{{{\mathrm {min}}}},\upsilon _{{{\mathrm {max}}}}]) \end{aligned}$$

(13)

for $\varrho \in (\epsilon _4,1)$ and $\upsilon _{{{\mathrm {min}}}}$ as well as $\upsilon _{{{\mathrm {max}}}}$ being arbitrary positive real numbers satisfying $\upsilon _{{{\mathrm {min}}}}\le \upsilon _{{{\mathrm {max}}}}$. Next, parameters $\upsilon _{{{\mathrm {min}}}}$ and $\upsilon _{{{\mathrm {max}}}}$ are to be selected to ensure that the condition (11) holds. Since function $V_\infty (x)$ is proper, it follows that the sets $\mathcal {C}^{c}_1\triangleq V^{-1}_\infty ([0,\upsilon _\infty ])$ is compact. Taking into account the continuity of V(x), there exists a maximum value for V(x) in $\mathcal {C}^{c}_1$, given by $\upsilon _{{{\mathrm {max}}}}=\max \nolimits _{x\in \mathcal {C}^{c}_1}V(x)$. Consequently, for any $x\in \mathcal {C}^{c}_1$, the condition $V(x)\le \upsilon _{{{\mathrm {max}}}}$ holds, implying that $x\in \mathcal {C}^{1}_2\triangleq V^{-1}([0,\upsilon _{{{\mathrm {max}}}}])$. It follows that

$$\begin{aligned} \mathcal {C}^{c}_1\triangleq V^{-1}_\infty ([0,\upsilon _\infty ])\subseteq \mathcal {C}^{1}_2\triangleq V^{-1}([0,\upsilon _{{{\mathrm {max}}}}]) \end{aligned}$$

(14)

In what follows, we show that there exists a positively real number $\upsilon _\mathrm{min}$ such that the following condition holds.

$$\begin{aligned} \mathcal {C}^{2}_2\triangleq V^{-1}([0,\upsilon _{{{\mathrm {min}}}}])\subseteq \mathcal {C}_3\triangleq \mathcal {B}_{\upsilon _0}[0] \end{aligned}$$

(15)

For linear system (12) with Hurwitz matrix A, the Lyapunov function used in (13) can be chosen as $V(x)=x^TPx$ with positive definite matrix P as the solution to $A^TP+PA\prec 0$. Condition (15) holds if, for any $x\in \mathcal {C}^{2}_2$, we can derive $x\in \mathcal {C}_3$. To this end, note the fact that $\lambda _{{{\mathrm {min}}}}(P){\Vert x\Vert }^2\le V(x)=x^TPx\le \lambda _{{{\mathrm {max}}}}(P){\Vert x\Vert }^2$ holds with $\lambda _{{{\mathrm {min}}}}(P)$ and $\lambda _{{{\mathrm {max}}}}(P)$ being the maximum and minimum eigenvalues of matrix P. As a result, for any $x\in \mathcal {C}^{2}_2$ in (15), it follows that $V(x)\le \upsilon _{{{\mathrm {min}}}}$ implying $\lambda _{{{\mathrm {min}}}}(P){\Vert x\Vert }^2\le \upsilon _{{{\mathrm {min}}}}$. Equivalently, $\Vert x\Vert \le \sqrt{\frac{\upsilon _{{{\mathrm {min}}}}}{\lambda _{{{\mathrm {min}}}}(P)}}=\upsilon _0$ if specified with $\upsilon _{{{\mathrm {min}}}}=\lambda _{{{\mathrm {min}}}}(P)\upsilon ^2_0$. In such case, any $x\in \mathcal {C}^{2}_2$ means $x\in \mathcal {C}_3$ defined in (15), which implies (15) holds.

Next we show that condition (11) holds with parameters $\upsilon _{{{\mathrm {min}}}}$ and $\upsilon _{{{\mathrm {max}}}}$ provided previously. Taking into account that $\mathcal {C}_1\cup \mathcal {C}^{c}_1=\mathbb {R}^n$, it follows from (14) that $\mathcal {C}_1\cup \mathcal {C}^{1}_2=\mathbb {R}^n$. Following the definitions of $\mathcal {C}_{2},\mathcal {C}^{1}_2$ and $\mathcal {C}^{2}_2$ in (13), (14) and (15), we have $\mathcal {C}^{1}_2=\mathcal {C}_{2}\cup \mathcal {C}^{2}_2$, implying $\mathcal {C}_{1}\cup \mathcal {C}_{2}\cup \mathcal {C}^{2}_2=\mathbb {R}^n$. Bearing in mind that $\mathcal {C}^{2}_2\subseteq \mathcal {C}_3$ which can be observed from (15), it follows that condition (11) holds.

From the proof, it can be concluded that there must exist a constant $\epsilon =\mathrm{max}(\epsilon _3,\epsilon _4)$ such that all the conditions in Lemma 1 hold for system $\dot{x}=f_\varrho (x)$ with $\varrho \in (\epsilon ,1)$, which implies the fixed-time stabilization of $\dot{x}=f_\varrho (x)$. This completes the proof.

Remark 1

It should be noted that the developed algorithm in Theorem 1 is different from that in [12]. Specifically, the bi-limit homogeneous control law in [12] is designed recursively by backstepping technique, which relies strongly on the recursive determination of the virtual controllers. However, a non-recursive design procedure is developed in the current work to render a simple construction of a fixed-time stabilizing control law for high-order systems. In addition, the proposed control law covers the classic finite-time stabilizing control law in [23] as a special case if the items $\lceil x_i \rfloor$ and $\lceil x_i \rfloor ^{{\varrho _i'}}$ are removed from (4).

Remark 2

It is worth mentioning that the existence of $\epsilon$ in Theorem 1 is guaranteed by tube lemma [31], and it is difficult to specify $\epsilon$ exactly. Alternatively, the exact selection of $\epsilon$ may be solved via Lyapunov analysis, which has been addressed for double integrator systems in [19]. The rule for the selection of $\epsilon$ for arbitrary-order integrator systems will be investigated in the future work.

4 Disturbance observer based fixed-time stabilization control

Following the idea from the work in [32], the fixed-time convergent arbitrary-order sliding mode differentiator in [33] can be utilized to design the following disturbance observer

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{z}^i_0=v^i_0+x_{i+1}\\ v^i_0=-\lambda ^i_0\theta L^{\frac{1}{m_i+1}}_i\lfloor z^i_0-x_i\rceil ^{\frac{m_i}{m_i+1}}-k^i_0(1-\theta )\lfloor z^i_0-x_i\rceil ^{\alpha _0}+z^i_1\\ \dot{z}^i_1=v^i_1\\ v^i_1=-\lambda ^i_1\theta L^{\frac{1}{m_i}}_i\lfloor z^i_1-v^i_0\rceil ^{\frac{m_i-1}{m_i}}-k^i_1(1-\theta )\lfloor z^i_1-v^i_0\rceil ^{\alpha _1}+z^i_2\\ \vdots \\ \dot{z}^i_{m_i-1}=v^i_{m_i-1}\\ v^i_{m_i-1}=-\lambda ^i_{m_i-1}\theta L^{\frac{1}{2}}_i\lfloor z^i_{m_i-1}-v^i_{m_i-2}\rceil ^{\frac{1}{2}}-k^i_{m_i}(1-\theta )\lfloor z^i_{m_i-1}\\ \qquad \qquad ~~-\,v^i_{m_i-2}\rceil ^{\alpha _{m_i-1}}+z^i_{m_i}\\ \dot{z}^i_{m_i}\in -\lambda ^i_{m_i}\theta L_i\lfloor z^i_{m_i}-v^i_{m_i-1}\rceil ^0-k^i_{m_i}(1-\theta )\lfloor z^i_{m_i}-v^i_{m_i-1}\rceil ^{\alpha _{m_i}}\\ \qquad \quad ~+\,[-\,L_i,L_i] \end{array}\right. } \end{aligned}$$

(16)

to estimate $\varDelta _i$ in (2) and its derivatives $\varDelta ^{(j)}_i,(i=1,\ldots ,n; j=1,\ldots ,m_i)$ , where $m_i=n-i$ and $x_{n+1}=u$ for brevity. Furthermore, the solution of differential inclusion (16) is understood in Filippov’s sense [34].

Lemma 4

Consider the system (2) with assumption 1 being satisfied; then the following equalities are established in a fixed time

$$\begin{aligned} z^i_0=x_1,\quad z^i_1=\varDelta _i,\ldots ,z^i_{m_i}=\varDelta ^{(m_i-1)}_i \end{aligned}$$

(17)

if the following statements hold

• 1. Parameters $\lambda ^i_j,(j=0,\ldots ,m_i)$ are selected in terms of traditional high-order sliding mode differentiator provided in [35];

• 2. Parameters $\alpha _j,(j=0,\ldots ,m_i)$ are calculated by

  $$\begin{aligned} \alpha _j=\frac{(j+1)\alpha -j}{j\alpha -(j-1)} \end{aligned}$$

  (18)

  with $\alpha \in (1,\epsilon _\alpha )$ and $\epsilon _\alpha >1$ close enough to one;

• 3. Parameters $k^i_j$ are chosen such that the following matrix is Hurwitz

  $$\begin{aligned} A^i=\left( \begin{array}{ccccc} -\,k^i_0 &{}\quad 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ -\,k^i_0k^i_1 &{}\quad 0 &{}\quad 1 &{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ -\,\prod \limits _{j=0}^{j=m_i}k^i_j &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \end{aligned}$$

  (19)

• 4. Function $\theta$ is determined by $\theta =0$ if $t\le T_0$; otherwise $\theta =1$, with arbitrarily time constant $T_0$.

Proof

Define variables $\sigma ^i_0={z}^i_0-x_i,\sigma ^i_1={z}^i_1-\varDelta _i,\ldots ,\sigma ^i_{m_i}={z}^i_{m_i}-\varDelta ^{(m_i-1)}_{i}$. Taking into account (2) and (16), the error dynamics are governed by

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\sigma }^i_0=-\lambda ^i_0\theta L^{\frac{1}{m_i+1}}_i\lfloor \sigma ^i_0 \rceil ^{\frac{m_i}{m_i+1}}-k^i_0(1-\theta )\lfloor \sigma ^i_0\rceil ^{\alpha _0}+\sigma _1\\ \dot{\sigma }^i_1=-\lambda ^i_1\theta L^{\frac{1}{m_i}}_i\lfloor \sigma ^i_1-\dot{\sigma }^i_0\rceil ^{\frac{m_i-1}{m_i}}-k^i_1(1-\theta )\lfloor \sigma ^i_1-\dot{\sigma }^i_0\rceil ^{\alpha _1}+\sigma ^i_2\\ \vdots \\ \dot{\sigma }^i_{m_i-1}=-\lambda ^i_{m_i-1}\theta L^{\frac{1}{2}}_i\lfloor \sigma ^i_{m_i-1}-\dot{\sigma }^i_{m_i-2}\rceil ^{\frac{1}{2}}-k^i_{m_i}(1-\theta )\lfloor \sigma ^i_{m_i-1}\\ \qquad \qquad ~~-\,\dot{\sigma }^i_{m_i-2}\rceil ^{\alpha _{m_i-1}}+z^i_{m_i}\\ \dot{\sigma }^i_{m_i}\in -\lambda ^i_{m_i}\theta L_i\lfloor \sigma ^i_{m_i}-\dot{\sigma }^i_{m_i-1}\rceil ^0-k^i_{m_i}(1-\theta )\lfloor \sigma ^i_{m_i}-\dot{\sigma }^i_{m_i-1}\rceil ^{\alpha _{m_i}}\\ \qquad \quad ~+\,[-\,L_i,L_i] \end{array}\right. } \end{aligned}$$

(20)

For $0\le t \le T_0$ implying $\theta =0$, if specified with $\alpha =1$ and $L_i=0$ meaning $\varDelta _i=0$, the error dynamics (20) are reduced to $\dot{\sigma }^i=A^i\sigma ^i$ where $\sigma ^i=[\sigma ^i_0,\ldots ,\sigma ^i_{m_i}]^T$ with $A^i$ being provided in (19). Furthermore, the obtained linear system is globally asymptotically stable when the third condition in Lemma 4 holds. In addition, system (20) with $\theta =0$ and $L_i=0$ is homogeneous with weight $r^i=[\frac{j\alpha -(j-1)}{\alpha -1}]^T \in \mathbb {R}^{m_i+1},(j=0,\ldots ,m_i)$ with respect to degree $d^i=1$ for $\alpha >1$. It follows from the similar analysis in Theorem 1 that there exists a constant $\varepsilon _\alpha >1$ and close enough to 1 such that system (20) with $\theta =0$ and $L_i=0$ is globally asymptotically stable for $\alpha \in (1,\varepsilon _\alpha )$. Following Lemma 1 in [33], it can be known that the trajectories that started at “infinity” for system (20) with $\theta =0$ and arbitrary bounded $L_i>0$ enter into a compact set containing origin for any $T_0>0$.

For $t>T_0$ implying $\theta =1$, the error dynamical system (20) with the selection of parameters $\lambda ^i_j$ in terms of the first condition in Lemma 4 is the same with that provided in [32], which is able to bring the estimation errors to zero in a bounded finite time, i.e., $T_1$, from any compact set. From the analysis, it follows that equalities (17) are established in finite time $T_0+T_1$ which is independent of initial conditions, implying the fixed-time convergence. This completes the proof. $\square$

Now, we are in a position to construct a fixed-time stabilizing control law for system (2). To this end, introduce variables

$$\begin{aligned} y_1=x_1,\quad y_2=x_2+\varDelta _1,\ldots ,y_{n}=x_{n}+\sum _{i=1}^{n-1}\varDelta ^{(n-1-i)}_i \end{aligned}$$

(21)

satisfying

$$\begin{aligned} \dot{y}_1=y_2,\ldots ,\dot{y}_{n-1}=y_n,\quad \dot{y}_{n}=u+\sum _{i=1}^{n}\varDelta ^{(n-i)}_i \end{aligned}$$

(22)

with x being governed by (2). Then, the objective of the work is equivalent to designing control law u for system (22) such that $y_1=x_1$ converges to zero in a fixed time. The main result is summarized by theorem 2 given below.

Theorem 2

Consider system (22) with control law

$$\begin{aligned} {{u(x)\!=\!-\sum _{i=1}^{n}k_i\left( \lceil \widehat{y}_i \rfloor ^{\varrho _i}+\lceil \widehat{y}_i \rfloor +\lceil \widehat{y}_i \rfloor ^{{\varrho _i'}}\right) \!-\!\sum _{i=1}^{n}\widehat{\varDelta }^{(n-i)}_i}}\nonumber \\ \end{aligned}$$

(23)

where $\widehat{y}_1=x_1,\widehat{y}_2=x_2+\widehat{\varDelta }_1,\ldots ,\widehat{y}_n=x_n+\sum _{i=1}^{n-1}\widehat{\varDelta }^{(n-1-i)}_i$ are measurable with $\widehat{\varDelta }^{k}_i=z^i_k,(i=1,\ldots ,n; k=0,\ldots ,n-i)$ obtained from (16). If the parameters $k_i>0$ and $\varrho _i,\varrho _i',(i=1,\ldots ,n)$ are selected in terms of Theorem 1 and the parameters $\lambda ^i_j,k^i_j,(i=1,\ldots ,n;j=0,\ldots ,m_j)$ and $\theta$ in observer (16) are chosen based on Lemma 4, then $y_1=x_1\rightarrow 0$ in a fixed time.

Proof

For brevity, define variables $\widehat{\varDelta }_0^{i-1}\triangleq {\varDelta }_0^{i-1},(i=1,\ldots ,n)$ such that, following from (21) and (22), the equalities $\widehat{y}_i=y_i+e_i$ hold with $e_i=\sum _{j=0}^{i-1}[\widehat{\varDelta }^{(i-1-j)}_j-{\varDelta }^{(i-1-j)}_j]$. Then, substituting (23) into (22) results in

$$\begin{aligned} \begin{aligned} \dot{y}_i&=y_{i+1}\\ \dot{y}_{n}&=-\sum _{i=1}^{n}k_i\left( \lceil {y}_i+e_i \rfloor ^{\varrho _i}\right. \\&\left. +\,\lceil {y}_i+e_i \rfloor +\lceil {y}_i+e_i \rfloor ^{{\varrho _i'}}\right) +e'_n \end{aligned} \end{aligned}$$

(24)

with $e'_n=\sum _{i=1}^{n}[{\varDelta }^{(n-i)}_i-\widehat{\varDelta }^{(n-i)}_i]$. Based on the results in Lemma 4, it can be known that $e_i$ and $e'_n$ are bounded and there exists a finite time, i.e., $T_0+T_1$, such that $e_i=e'_n=0$ for all $t\ge T_0+T_1$. Taking into account $\widehat{y}_i=y_i+e_i$, it follows that $y_i=\widehat{y}_i$ holds for $t\ge T_0+T_1$. After that, the system (24) is equivalent to $\dot{\widehat{y}}_i=\widehat{y}_{i+1}, \dot{\widehat{y}}_{n}=-\sum _{i=1}^{n}k_i(\lceil {\widehat{y}}_i \rfloor ^{\varrho _i}+\lceil {\widehat{y}}_i \rfloor +\lceil {\widehat{y}}_i \rfloor ^{{\varrho _i'}})$ which is fixed-time stability based on Theorem 1. Hence, the last step to prove Theorem 2 is to show that the trajectory of system (24) does not escape in any finite time interval, i.e., $[0,T_0+T_1]$.

To this end, let $f(y,\delta )\in \mathbb {R}^n$ with $y=[y_i]^T\in \mathbb {R}^n$ and $\delta =[e_i~e'_n]^T\in \mathbb {R}^{n+1}$ be the closed-loop vector field of system (24) with $\varrho _i$ and $\varrho _i'$ in (5). It can be verified that $f(y,\delta )$ is bi-limit homogeneous with triples $((r_0,\tau _0),k_0,f_{\delta _0})$ and $((r_\infty ,\tau _\infty ),k_\infty ,f_{\delta _\infty })$, where $r_0$ and $r_\infty$ are provided in (7) and $\tau _{0_i}=r_{0_i},~\tau _{\infty _i}=r_{\infty _i},(i=1,\ldots ,n),~\tau _{0_{n+1}}=\frac{\varrho }{1-\varrho },~ \tau _{\infty _{n+1}}=\frac{2-\varrho }{1-\varrho },~k_0=-1,~k_\infty =1,~f_{\delta _0}=[y_2,\ldots ,y_n,-\sum _{i=1}^{n}k_i\lceil {y}_i+e_i \rfloor ^{\varrho _i}+e'_n]^T$ and $f_{\delta _\infty }=[y_2,\ldots ,y_n,-\sum _{i=1}^{n}k_i\lceil {y}_i+e_i \rfloor ^{\varrho '_i}+e'_n]^T$. Moreover, system $\dot{y}=f(y,0)$ (see Theorem 1) satisfies all the conditions in Lemma 1. It follows from Lemma 2 that system $\dot{y}=f(y,\delta )$ is ISS with respect to bounded disturbance $\delta$, which means that the system trajectory in (24) is always bounded in any finite time interval. This completes the proof. $\square$

5 Numerical example

Considering the following integrator system with mismatched disturbances $\varDelta _1$ as well as $\varDelta _2$ and matched disturbances $\varDelta _3$

$$\begin{aligned} \dot{x}_1=x_2+\varDelta _1,\quad \dot{x}_2=x_3+\varDelta _2,\quad \dot{x}_3=u+\varDelta _3 \end{aligned}$$

(25)

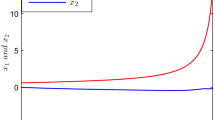
In the simulation, the disturbances are set to $\varDelta _1={{\mathrm {sin}}}(t),\varDelta _2={{\mathrm {cos}}}(t)$ and $\varDelta _3=\frac{1}{2}({{\mathrm {sin}}}(t)+{{\mathrm {cos}}}(t))$. The controller parameters are chosen as $k_1=2,k_2=3,k_3=5$ and $\varrho =0.85$. The disturbance observer parameters are given by $\alpha =1.05,k^i_0=21,k^i_1=15/21,k^i_2=1/2,k^i_3=1/5,L^i=100,\lambda ^i_0=3,\lambda ^i_1=2,\lambda ^i_2=1.5,\lambda ^i_3=1.1, (i=1,2,3)$ and $T_0=1.5$. The simulation is carried out in Matlab/Simulink by Euler method with a fixed sampling step 0.1 ms. As a comparison, the classic finite-time control algorithm in [23] is selected which can be recovered from the proposed control law (4) by omitting high-order items $\lceil x_i \rfloor$ and $\lceil x_i \rfloor ^{{\varrho _i'}}$. The other parameters are the same with those provided previously. The simulation results are presented in Fig. 2 for initial values $x(0)=[10^2,0,0]$, $x(0)=[10^3,0,0]$ and $x(0)=[10^4,0,0]$. From Fig. 2, it can be observed that the convergence time under our proposed control law with different initial values is similar, implying a weak dependence of the convergence time on the initial conditions. However, it can be observed that the convergence time under finite-time control law grows significantly with initial conditions. Correspondingly, the control signals obtained by finite-time and fixed-time algorithms are provided in Fig. 3. From that, it can be seen that the fixed-time property is achieved at the cost of large control magnitude.

Remark 3

It should be noted that the fixed-time control algorithm has many applications in practice. For example, the fixed-time approach helps to design a control law, which is able to preserve the convergence time even with the variation of operation region. In addition, the fixed-time property is especially useful for either hybrid or switching systems with some kind of dwell time [33].

Fig. 2

System responses with different initial values $x(0)=(10^2,0,0)$ for (a), $x=(10^3,0,0)$ for (b), and $x=(10^4,0,0)$ for (c)

Fig. 3

Control signals with different initial values $x(0)=(10^2,0,0)$ for (a), $x=(10^3,0,0)$ for (b), and $x=(10^4,0,0)$ for (c)

6 Conclusions

A fixed-time stabilizing control law is presented for high-order integrator systems with matched and mismatched disturbances. The stability of closed-loop system under controller and disturbance is analyzed through Lyapunov function and bi-limit homogeneous techniques, ensuring that the convergence time is uniformly bounded with respect to any initial states.

Appendix

For brevity, define $A^n_1(s)$ and $A^n_2(s)$ as follows

$$\begin{aligned} A^n_1(s)=s^n+k_ns^{n-1}+\cdots +k_2s+k_1 \end{aligned}$$

(26)

and

$$\begin{aligned} A^n_2(s)=s^n+k'_ns^{n-1}+\cdots +k'_2s+k'_1 \end{aligned}$$

(27)

with

$$\begin{aligned} k'_i=3k_i,\quad i=1,2,\ldots ,n \end{aligned}$$

(28)

For $n\le 4$, a direct application of Routh criterion [36] shows that $A^n_2(s)$ is Hurwitz if the parameters $k_i$ are selected such that the polynomial $A^n_1(s)$ is Hurwitz. For example, $A^4_1(s)$ with $n=4$ in (26) is Hurwitz if and only if the condition

$$\begin{aligned} k_2k_3k_4>k^2_2+k^2_4k_1,\quad k_i>0, \quad i=1,\ldots ,4 \end{aligned}$$

(29)

holds. Obviously, the condition $k'_2k'_3k'_4>k'^2_2+k'^2_4k'_1$ with $k'_i>0,i=1,\ldots ,4$ holds when $k'_i$ are defined by (28) with the selection of $k_i$ in (29). It follows that $A^4_2(s)$ is Hurwitz if $A^4_1(s)$ is Hurwitz. Similarly, it can be easily found that the conclusion holds for $n=1,2,3$.

For $n>4$, the polynomial $A^n_2(s)$ may not be Hurwitz even if $A^n_1(s)$ is Hurwitz. In this case, the following lemma can be applied to select $k_i,i=1,\ldots ,n$ such that $A^n_1(s)$ and $A^n_2(s)$ are both Hurwitz.

Lemma 5

[37] The polynomial $a_ns^n+\cdots +a_1x+a_0$ is Hurwitz if the condition $a_ia_{i+1}\ge 3a_{i-1}a_{i+2},i=1,\ldots ,n-2$ with $a_j>0,j=0,\ldots ,n$ holds.

Lemma 5 was first proposed in [38] using Chinese, and its English description was provided in [37]. It follows from Lemma 5 that the positive real numbers $k_j,j=1,\ldots ,n$ can be chosen as

$$\begin{aligned} k_ik_{i+1}\ge 3k_{i-1}k_{i+2},\quad i=2,\ldots ,n-1 \end{aligned}$$

(30)

with the definition $k_{n+1}=1$ such that $A^n_1(s)$ is Hurwitz. An equivalent expression of (30) is

$$\begin{aligned} (3k_i)(3k_{i+1})\ge 3(3k_{i-1})(3k_{i+2}),\quad i=2,\ldots ,n-1 \end{aligned}$$

(31)

Taking into account (28), (31) means the following inequality

$$\begin{aligned} k'_ik'_{i+1}\ge 3k'_{i-1}k'_{i+2},\quad i=2,\ldots ,n-1 \end{aligned}$$

(32)

holds with the definition $k'_{n+1}=1$. Although $k'_{n+1}=k_{n+1}=1$ does not satisfy the relationship (28), it can be easily verified that (32) can be derived from (31) when $i=n-1$. It follows from Lemma 5 that the polynomial $A^n_2(s)$ is Hurwitz with the positive real numbers $k'_i$ satisfying (28) and (30). Therefore, the positive real numbers $k_i$ can be selected in terms of (30) to ensure that $A^n_1(s)$ and $A^n_2(s)$ are both Hurwitz.